Stripping Model for Short Gamma-Ray Bursts in Neutron Star Mergers
Abstract
1. Introduction
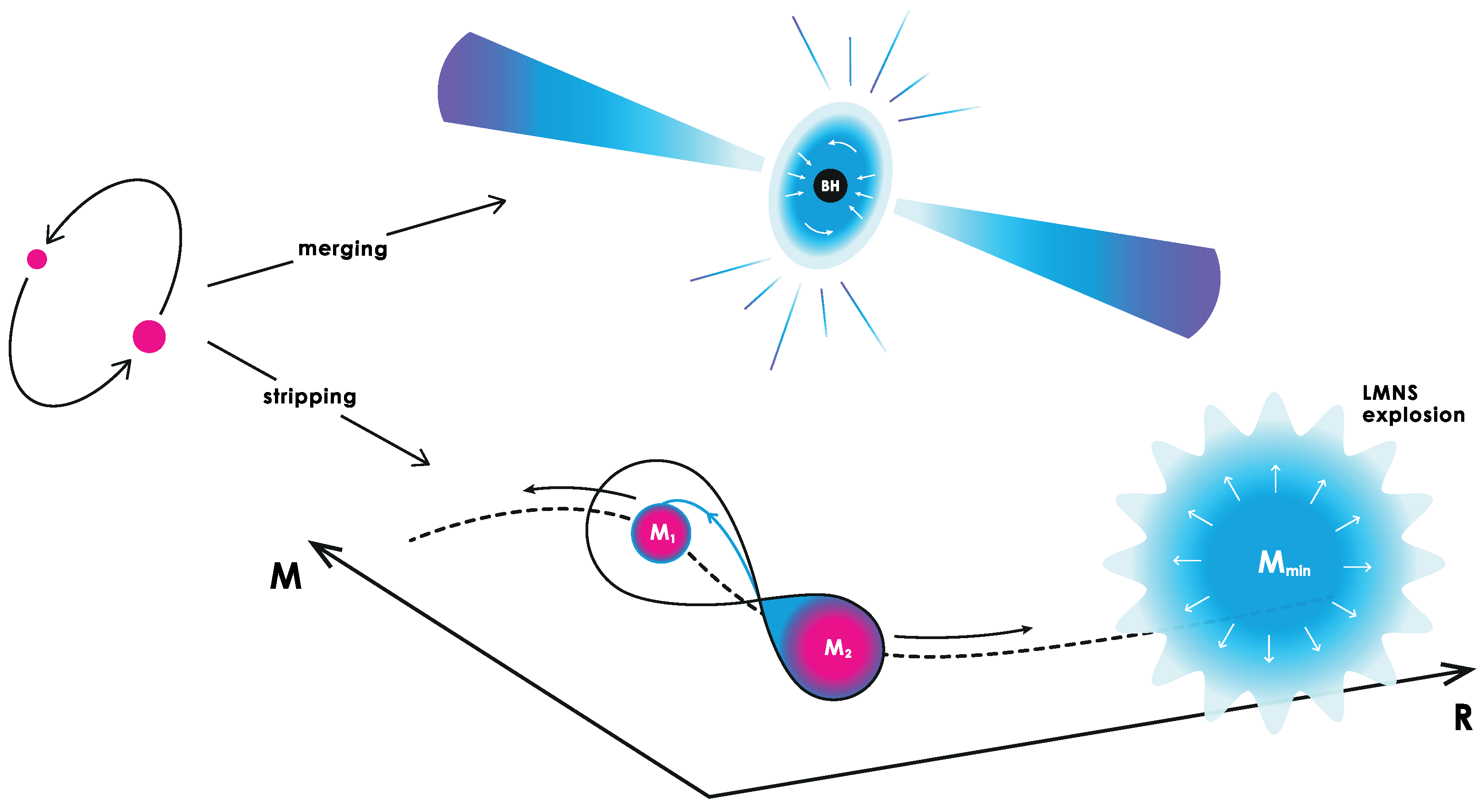
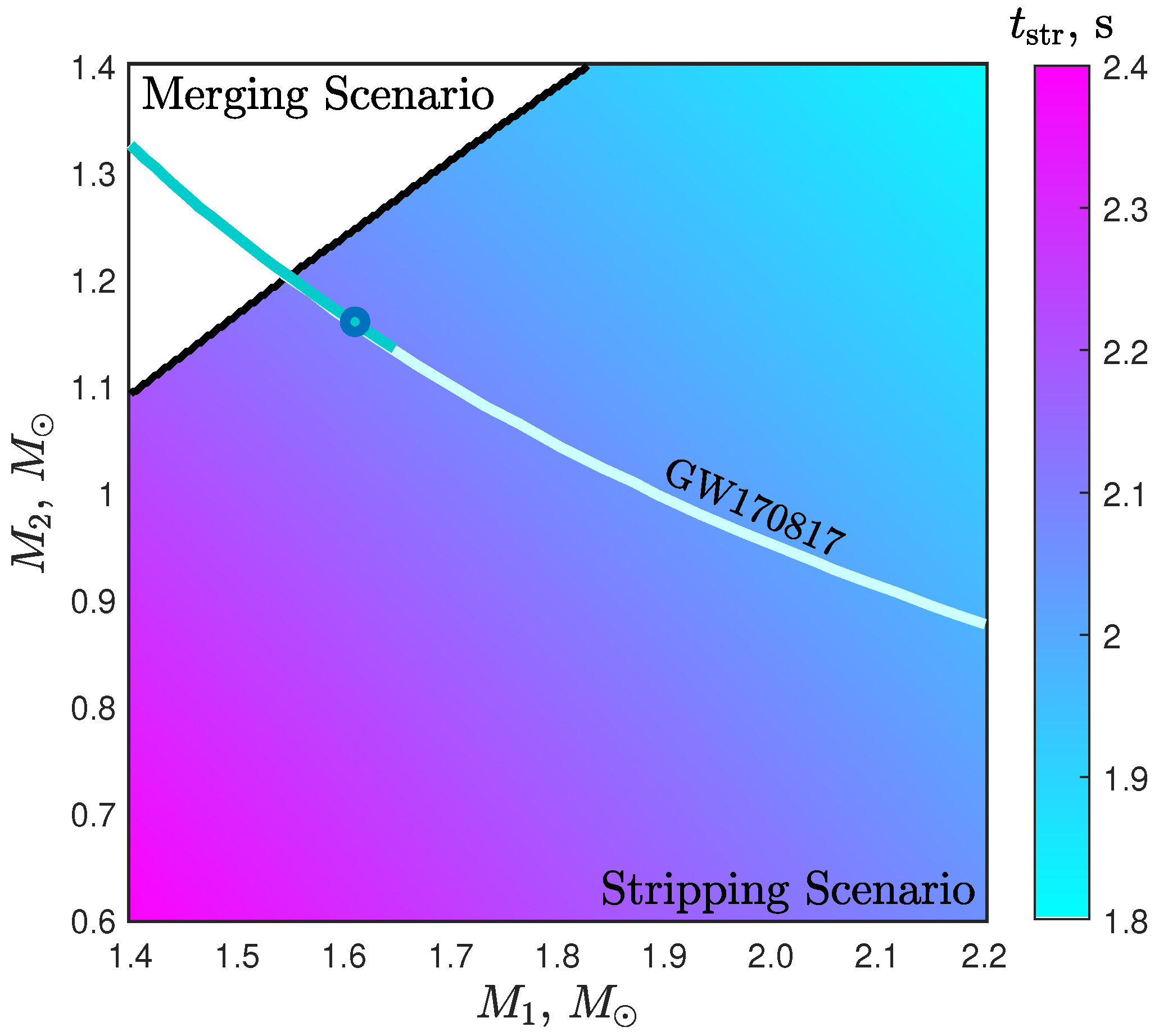
2. GRB170817A and the Stripping Model
Boundary between the Two Scenarios
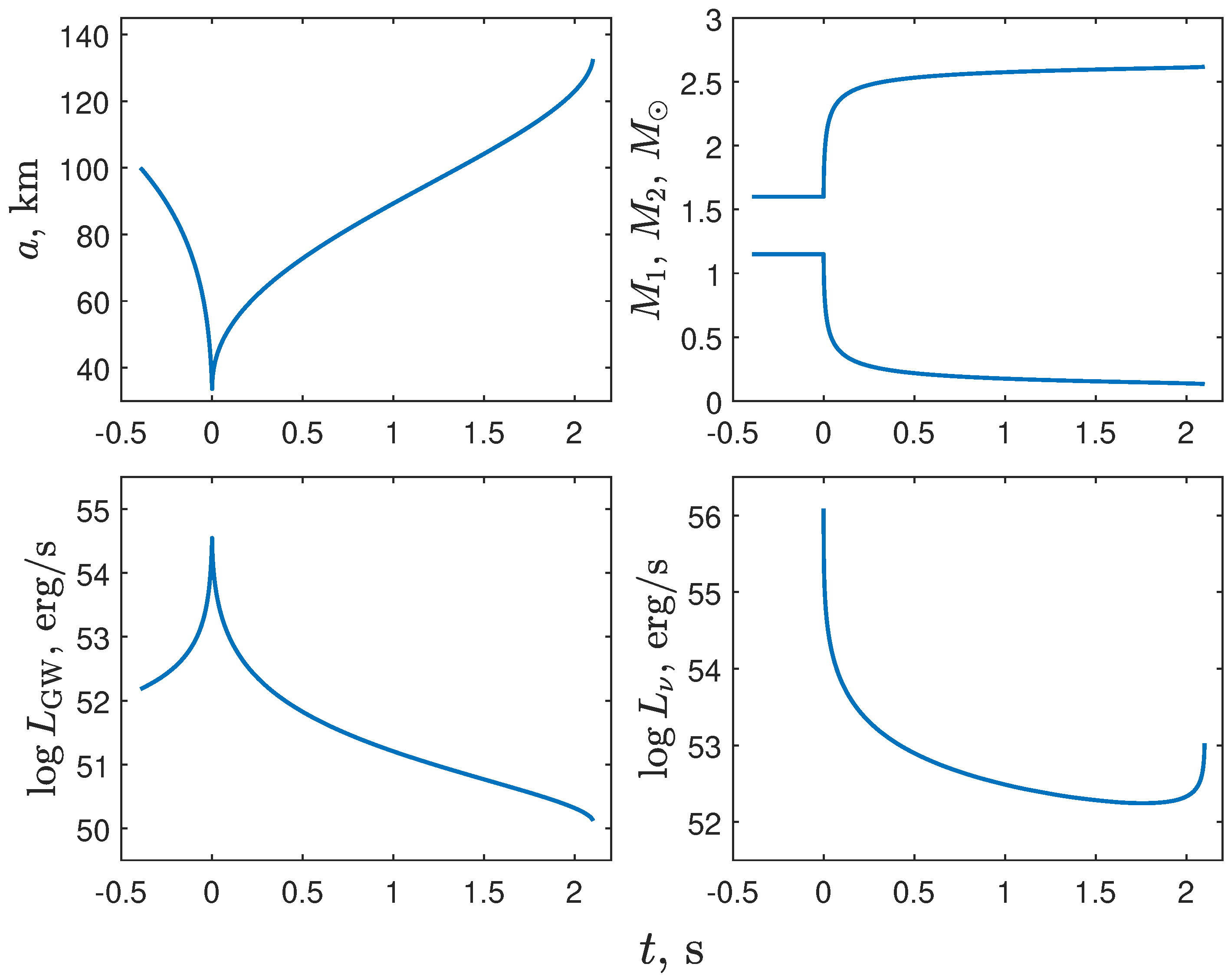
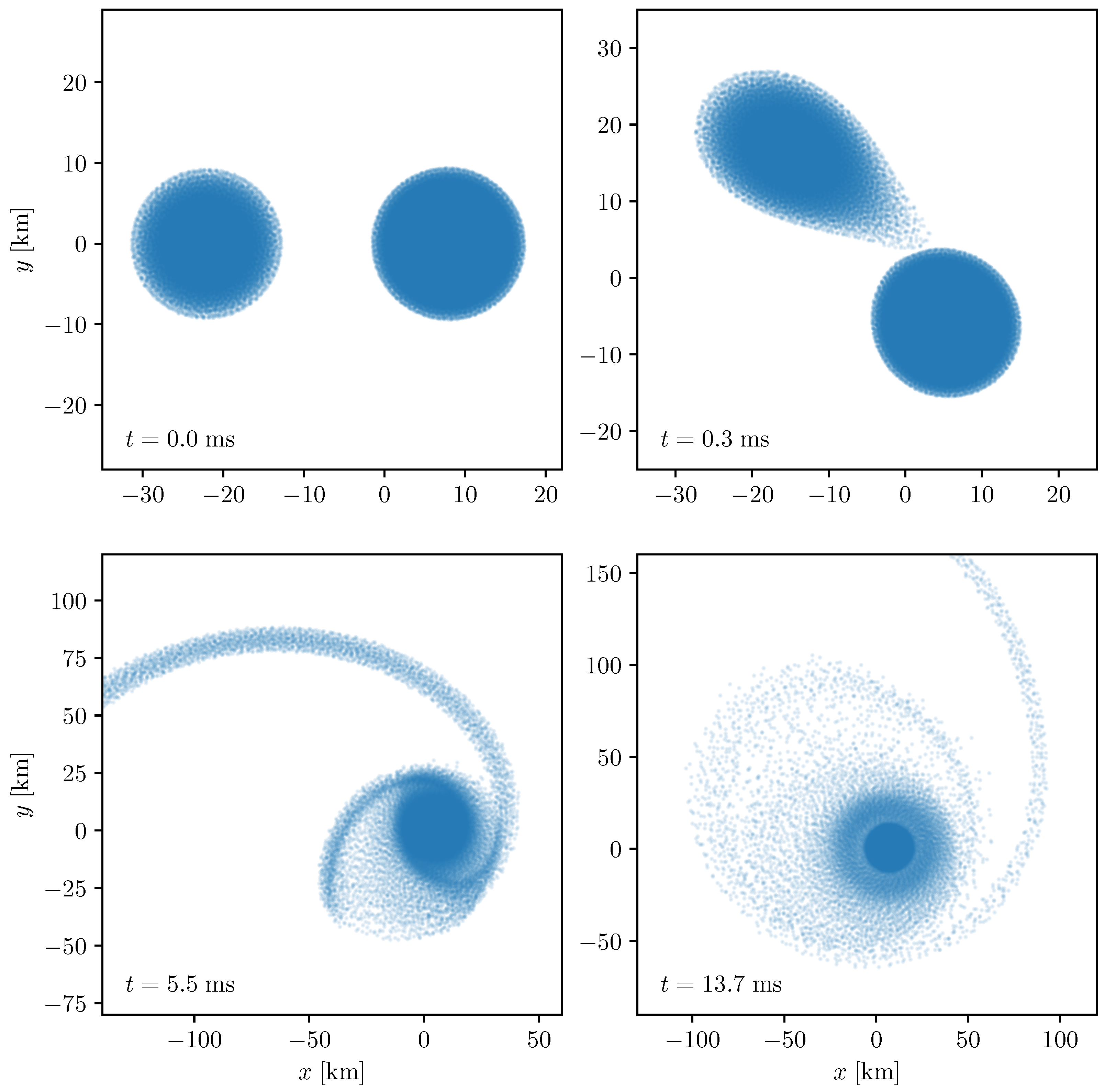
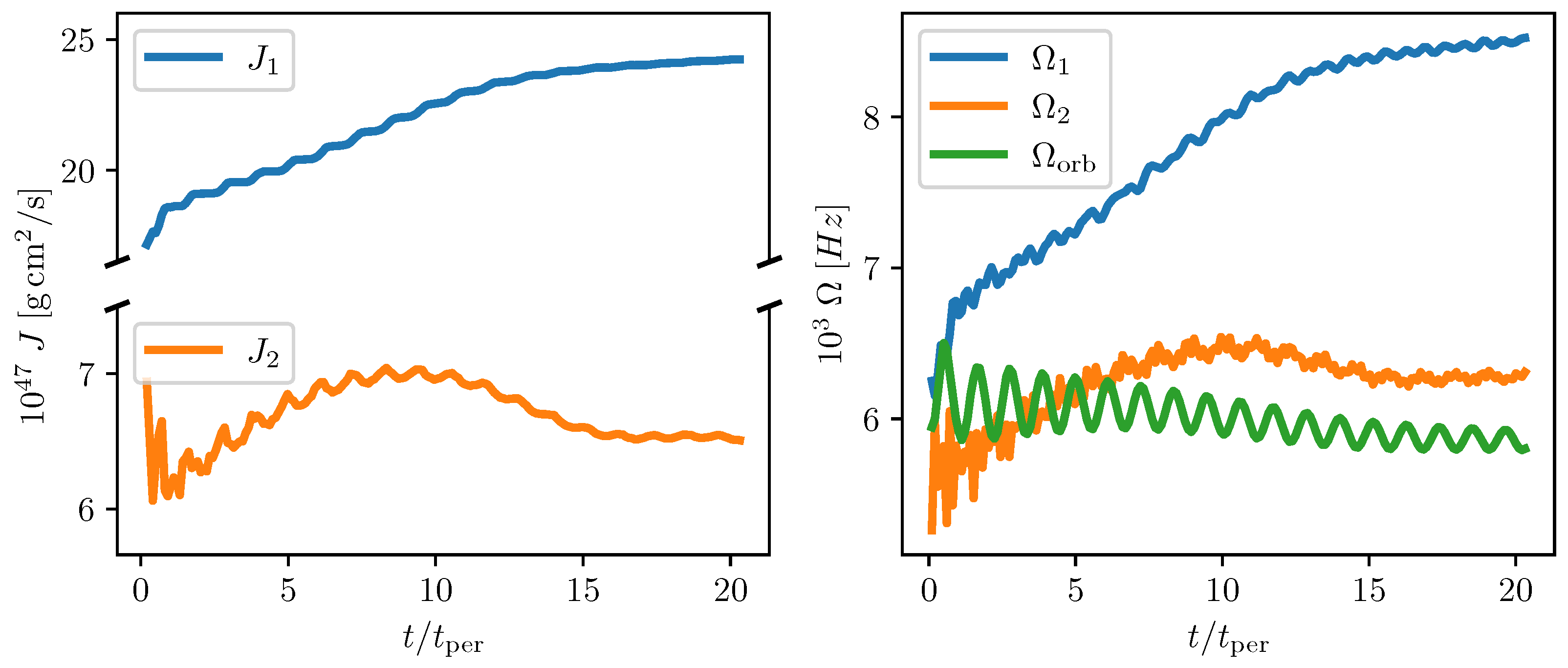
3. Stripping vs Merging: PHANTOM Modelling
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| EoS | Equation of State |
| GRB | Gamma-Ray Burst |
| GW | Gravitational Wave |
| LMNS | Low-Mass NS |
| NS | Neutron Star |
| SN | Supernova |
| SPH | Smoothed Particle Hydrodynamics |
| VLBI | Very Long Baseline Interferometry |
References
- Hjorth, J.; Sollerman, J.; Møller, P.; Fynbo, J.P.U.; Woosley, S.E.; Kouveliotou, C.; Tanvir, N.R.; Greiner, J.; Andersen, M.I.; Castro-Tirado, A.J.; et al. A very energetic supernova associated with the γ-ray burst of 29 March 2003. Nature 2003, 423, 847–850. [Google Scholar] [CrossRef] [PubMed]
- Nomoto, K.; Tanaka, M.; Tominaga, N.; Maeda, K.; Mazzali, P.A. Hypernovae and their Gamma-Ray Bursts Connection. arXiv 2007, arXiv:0707.2219. [Google Scholar] [CrossRef][Green Version]
- Woosley, S.E. Models for Gamma-Ray Burst Progenitors and Central Engines. arXiv 2011, arXiv:1105.4193. [Google Scholar]
- Mazzali, P.A.; Deng, J.; Pian, E.; Malesani, D.; Tominaga, N.; Maeda, K.; Nomoto, K.I.; Chincarini, G.; Covino, S.; Della Valle, M.; et al. Models for the Type Ic Hypernova SN 2003lw associated with GRB 031203. Astrophys. J. 2006, 645, 1323–1330. [Google Scholar] [CrossRef]
- Yu, Y.W.; Zhu, J.P.; Li, S.Z.; Lü, H.J.; Zou, Y.C. A Statistical Study of Superluminous Supernovae Using the Magnetar Engine Model and Implications for Their Connection with Gamma-Ray Bursts and Hypernovae. Astrophys. J. 2017, 840, 12. [Google Scholar] [CrossRef]
- Suzuki, A.; Maeda, K.; Shigeyama, T. Relativistic Supernova Ejecta Colliding with a Circumstellar Medium: An Application to the Low-luminosity GRB 171205A. Astrophys. J. 2019, 870, 38. [Google Scholar] [CrossRef]
- Lattimer, J.M.; Schramm, D.N. Black-Hole-Neutron-Star Collisions. Astrophys. J. Lett. 1974, 192, L145. [Google Scholar] [CrossRef]
- Lattimer, J.M.; Schramm, D.N. The tidal disruption of neutron stars by black holes in close binaries. Astrophys. J. 1976, 210, 549–567. [Google Scholar] [CrossRef]
- Clark, J.P.A.; Eardley, D.M. Evolution of close neutron star binaries. Astrophys. J. 1977, 215, 311–322. [Google Scholar] [CrossRef]
- Bernuzzi, S.; Breschi, M.; Daszuta, B.; Endrizzi, A.; Logoteta, D.; Nedora, V.; Perego, A.; Radice, D.; Schianchi, F.; Zappa, F.; et al. Accretion-induced prompt black hole formation in asymmetric neutron star mergers, dynamical ejecta, and kilonova signals. Mon. Not. R. Astron. Soc. 2020, 497, 1488–1507. [Google Scholar] [CrossRef]
- Baiotti, L.; Rezzolla, L. Binary neutron star mergers: A review of Einstein’s richest laboratory. Rep. Prog. Phys. 2017, 80, 096901. [Google Scholar] [CrossRef] [PubMed]
- Blandford, R.D.; Znajek, R.L. Electromagnetic extraction of energy from Kerr black holes. Mon. Not. R. Astron. Soc. 1977, 179, 433–456. [Google Scholar] [CrossRef]
- Christie, I.M.; Lalakos, A.; Tchekhovskoy, A.; Fernández, R.; Foucart, F.; Quataert, E.; Kasen, D. The role of magnetic field geometry in the evolution of neutron star merger accretion discs. Mon. Not. R. Astron. Soc. 2019, 490, 4811–4825. [Google Scholar] [CrossRef]
- Berezinskii, V.S.; Prilutskii, O.F. Neutrino-antineutrino annihilation around a collapsar. Astron. Astrophys. 1987, 175, 309–311. [Google Scholar]
- Woosley, S.E. Gamma-Ray Bursts from Stellar Mass Accretion Disks around Black Holes. Astron. J. 1993, 405, 273. [Google Scholar] [CrossRef]
- Just, O.; Obergaulinger, M.; Janka, H.T.; Bauswein, A.; Schwarz, N. Neutron-star Merger Ejecta as Obstacles to Neutrino-powered Jets of Gamma-Ray Bursts. Astrophys. J. Lett. 2016, 816, L30. [Google Scholar] [CrossRef]
- MacFadyen, A.I.; Woosley, S.E.; Heger, A. Supernovae, Jets, and Collapsars. Astrophys. J. 2001, 550, 410–425. [Google Scholar] [CrossRef]
- Usov, V.V. Millisecond pulsars with extremely strong magnetic fields as a cosmological source of γ-ray bursts. Nature 1992, 357, 472–474. [Google Scholar] [CrossRef]
- Thompson, C. A model of gamma-ray bursts. Mon. Not. R. Astron. Soc. 1994, 270, 480–498. [Google Scholar] [CrossRef]
- Thompson, T.A.; Chang, P.; Quataert, E. Magnetar Spin-Down, Hyperenergetic Supernovae, and Gamma-Ray Bursts. Astrophys. J. 2004, 611, 380–393. [Google Scholar] [CrossRef]
- Metzger, B.D.; Giannios, D.; Thompson, T.A.; Bucciantini, N.; Quataert, E. The protomagnetar model for gamma-ray bursts. Mon. Not. R. Astron. Soc. 2011, 413, 2031–2056. [Google Scholar] [CrossRef]
- Ciolfi, R.; Kalinani, J.V. Magnetically Driven Baryon Winds from Binary Neutron Star Merger Remnants and the Blue Kilonova of 2017 August. Astrophys. J. Lett. 2020, 900, L35. [Google Scholar] [CrossRef]
- Ciolfi, R. Collimated outflows from long-lived binary neutron star merger remnants. Mon. Not. R. Astron. Soc. 2020, 495, L66–L70. [Google Scholar] [CrossRef]
- Mösta, P.; Radice, D.; Haas, R.; Schnetter, E.; Bernuzzi, S. A Magnetar Engine for Short GRBs and Kilonovae. Astrophys. J. Lett. 2020, 901, L37. [Google Scholar] [CrossRef]
- Blinnikov, S.I.; Novikov, I.D.; Perevodchikova, T.V.; Polnarev, A.G. Exploding Neutron Stars in Close Binaries. Sov. Astron. Lett. 1984, 10, 177–179. [Google Scholar]
- Blinnikov, S.I.; Imshennik, V.S.; Nadezhin, D.K.; Novikov, I.D.; Perevodchikova, T.V.; Polnarev, A.G. Explosion of a Low-Mass Neutron Star. Sov. Astron. 1990, 34, 595. [Google Scholar]
- Manukovskii, K.V. Model for the explosion of a critical-mass neutron star in a binary system. Astron. Lett. 2010, 36, 191–203. [Google Scholar] [CrossRef]
- Lai, D.; Rasio, F.A.; Shapiro, S.L. Hydrodynamic Instability and Coalescence of Binary Neutron Stars. Astroph. J. 1994, 420, 811. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. Multi-messenger Observations of a Binary Neutron Star Merger. Astrophys. J. Lett. 2017, 848, L12. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X. Gravitational Waves and Gamma-Rays from a Binary Neutron Star Merger: GW170817 and GRB 170817A. Astrophys. J. Lett. 2017, 848, L13. [Google Scholar] [CrossRef]
- Metzger, B.D. Kilonovae. Living Rev. Relativ. 2019, 23, 1. [Google Scholar] [CrossRef] [PubMed]
- Dobie, D.; Kaplan, D.L.; Murphy, T.; Lenc, E.; Mooley, K.P.; Lynch, C.; Corsi, A.; Frail, D.; Kasliwal, M.; Hallinan, G. A Turnover in the Radio Light Curve of GW170817. Astrophys. J. Lett. 2018, 858, L15. [Google Scholar] [CrossRef]
- Mooley, K.P.; Deller, A.T.; Gottlieb, O.; Nakar, E.; Hallinan, G.; Bourke, S.; Frail, D.A.; Horesh, A.; Corsi, A.; Hotokezaka, K. Superluminal motion of a relativistic jet in the neutron-star merger GW170817. Nature 2018, 561, 355–359. [Google Scholar] [CrossRef] [PubMed]
- Nakar, E.; Gottlieb, O.; Piran, T.; Kasliwal, M.M.; Hallinan, G. From γ to Radio: The Electromagnetic Counterpart of GW170817. Astrophys. J. 2018, 867, 18. [Google Scholar] [CrossRef]
- Nynka, M.; Ruan, J.J.; Haggard, D.; Evans, P.A. Fading of the X-Ray Afterglow of Neutron Star Merger GW170817/GRB 170817A at 260 Days. Astrophys. J. Lett. 2018, 862, L19. [Google Scholar] [CrossRef]
- Hajela, A.; Margutti, R.; Bright, J.S.; Alexander, K.D.; Metzger, B.D.; Nedora, V.; Kathirgamaraju, A.; Margalit, B.; Radice, D.; Guidorzi, C.; et al. Evidence for X-Ray Emission in Excess to the Jet-afterglow Decay 3.5 yr after the Binary Neutron Star Merger GW 170817: A New Emission Component. Astrophys. J. Lett. 2022, 927, L17. [Google Scholar] [CrossRef]
- Troja, E.; O’Connor, B.; Ryan, G.; Piro, L.; Ricci, R.; Zhang, B.; Piran, T.; Bruni, G.; Cenko, S.B.; van Eerten, H. Accurate flux calibration of GW170817: Is the X-ray counterpart on the rise? Mon. Not. R. Astron. Soc. 2022, 510, 1902–1909. [Google Scholar] [CrossRef]
- Blinnikov, S.I.; Nadyozhin, D.K.; Kramarev, N.I.; Yudin, A.V. Neutron Star Mergers and Gamma-Ray Bursts: Stripping Model. Astron. Rep. 2021, 65, 385–391. [Google Scholar] [CrossRef]
- Jaranowski, P.; Krolak, A. Detectability of the Gravitational Wave Signal from a Close Neutron Star Binary with Mass Transfer. Astrophys. J. 1992, 394, 586. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshitz, E.M. The Classical Theory of Fields; Elsevier: Amsterdam, The Netherlands, 1975. [Google Scholar]
- Koshut, T.M.; Kouveliotou, C.; Paciesas, W.S.; van Paradijs, J.; Pendleton, G.N.; Briggs, M.S.; Fishman, G.J.; Meegan, C.A. Gamma-Ray Burst Precursor Activity as Observed with BATSE. Astrophys. J. 1995, 452, 145. [Google Scholar] [CrossRef]
- Pearson, J.M.; Chamel, N.; Potekhin, A.Y.; Fantina, A.F.; Ducoin, C.; Dutta, A.K.; Goriely, S. Unified equations of state for cold non-accreting neutron stars with Brussels-Montreal functionals—I. Role of symmetry energy. Mon. Not. R. Astron. Soc. 2018, 481, 2994–3026. [Google Scholar] [CrossRef]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. Properties of the Binary Neutron Star Merger GW170817. Phys. Rev. X 2019, 9, 011001. [Google Scholar] [CrossRef]
- Kopal, Z. Close Binary Systems; Springer Science & Business Media: Berlin/Heidelberg, Germany, 1959. [Google Scholar]
- Eggleton, P.P. Aproximations to the radii of Roche lobes. Astrophys. J. 1983, 268, 368–369. [Google Scholar] [CrossRef]
- Paczyński, B. Gravitational Waves and the Evolution of Close Binaries. Acta Astron. 1967, 17, 287. [Google Scholar]
- Radice, D.; Perego, A.; Hotokezaka, K.; Fromm, S.A.; Bernuzzi, S.; Roberts, L.F. Binary Neutron Star Mergers: Mass Ejection, Electromagnetic Counterparts, and Nucleosynthesis. Astrophys. J. 2018, 869, 130. [Google Scholar] [CrossRef]
- Baiotti, L. Gravitational waves from binary neutron stars. Arab. J. Math. 2022. [Google Scholar] [CrossRef]
- Price, D.J.; Wurster, J.; Tricco, T.S.; Nixon, C.; Toupin, S.; Pettitt, A.; Chan, C.; Mentiplay, D.; Laibe, G.; Glover, S.; et al. Phantom: A Smoothed Particle Hydrodynamics and Magnetohydrodynamics Code for Astrophysics. Publ. Astron. Soc. Aust. 2018, 35, e031. [Google Scholar] [CrossRef]
- Dan, M.; Rosswog, S.; Guillochon, J.; Ramirez-Ruiz, E. Prelude to A Double Degenerate Merger: The Onset of Mass Transfer and Its Impact on Gravitational Waves and Surface Detonations. Astrophys. J. 2011, 737, 89. [Google Scholar] [CrossRef]
- Silva, H.O.; Sotani, H.; Berti, E. Low-mass neutron stars: Universal relations, the nuclear symmetry energy and gravitational radiation. Mon. Not. R. Astron. Soc. 2016, 459, 4378–4388. [Google Scholar] [CrossRef]
- Toscani, M.; Lodato, G.; Price, D.J.; Liptai, D. Gravitational waves from tidal disruption events: An open and comprehensive catalog. Mon. Not. R. Astron. Soc. 2022, 510, 992–1001. [Google Scholar] [CrossRef]
- Haas, R.; Ott, C.D.; Szilagyi, B.; Kaplan, J.D.; Lippuner, J.; Scheel, M.A.; Barkett, K.; Muhlberger, C.D.; Dietrich, T.; Duez, M.D.; et al. Simulations of inspiraling and merging double neutron stars using the Spectral Einstein Code. Phys. Rev. D 2016, 93, 124062. [Google Scholar] [CrossRef]
- Dietrich, T.; Ujevic, M.; Tichy, W.; Bernuzzi, S.; Brügmann, B. Gravitational waves and mass ejecta from binary neutron star mergers: Effect of the mass ratio. Phys. Rev. D 2017, 95, 024029. [Google Scholar] [CrossRef]
- Dietrich, T.; Moldenhauer, N.; Johnson-McDaniel, N.K.; Bernuzzi, S.; Markakis, C.M.; Brügmann, B.; Tichy, W. Binary neutron stars with generic spin, eccentricity, mass ratio, and compactness: Quasi-equilibrium sequences and first evolutions. Phys. Rev. D 2015, 92, 124007. [Google Scholar] [CrossRef]
- Kaplan, J.D.; Nichols, D.A.; Thorne, K.S. Post-Newtonian approximation in Maxwell-like form. Phys. Rev. D 2009, 80, 124014. [Google Scholar] [CrossRef]
- Siegel, D.M. GW170817 -the first observed neutron star merger and its kilonova: Implications for the astrophysical site of the r-process. Eur. Phys. J. A 2019, 55, 203. [Google Scholar] [CrossRef]
- Blinnikov, S.I.; Röpke, F.K.; Sorokina, E.I.; Gieseler, M.; Reinecke, M.; Travaglio, C.; Hillebr, T.W.; Stritzinger, M. Theoretical light curves for deflagration models of type Ia supernova. Astron. Astrophys. 2006, 453, 229–240. [Google Scholar] [CrossRef]
- Finstad, D.; De, S.; Brown, D.A.; Berger, E.; Biwer, C.M. Measuring the Viewing Angle of GW170817 with Electromagnetic and Gravitational Waves. Astrophys. J. Lett. 2018, 860, L2. [Google Scholar] [CrossRef]
- Lazzati, D.; López-Cámara, D.; Cantiello, M.; Morsony, B.J.; Perna, R.; Workman, J.C. Off-axis Prompt X-Ray Transients from the Cocoon of Short Gamma-Ray Bursts. Astrophys. J. Lett. 2017, 848, L6. [Google Scholar] [CrossRef]
- Gottlieb, O.; Nakar, E.; Piran, T.; Hotokezaka, K. A cocoon shock breakout as the origin of the γ-ray emission in GW170817. Mon. Not. R. Astron. Soc. 2018, 479, 588–600. [Google Scholar] [CrossRef]
- Panov, I.V.; Yudin, A.V. Production of Heavy Elements during the Explosion of a Low-Mass Neutron Star in a Close Binary. Astron. Lett. 2020, 46, 518–527. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Blinnikov, S.; Yudin, A.; Kramarev, N.; Potashov, M. Stripping Model for Short Gamma-Ray Bursts in Neutron Star Mergers. Particles 2022, 5, 198-209. https://doi.org/10.3390/particles5020018
Blinnikov S, Yudin A, Kramarev N, Potashov M. Stripping Model for Short Gamma-Ray Bursts in Neutron Star Mergers. Particles. 2022; 5(2):198-209. https://doi.org/10.3390/particles5020018
Chicago/Turabian StyleBlinnikov, Sergei, Andrey Yudin, Nikita Kramarev, and Marat Potashov. 2022. "Stripping Model for Short Gamma-Ray Bursts in Neutron Star Mergers" Particles 5, no. 2: 198-209. https://doi.org/10.3390/particles5020018
APA StyleBlinnikov, S., Yudin, A., Kramarev, N., & Potashov, M. (2022). Stripping Model for Short Gamma-Ray Bursts in Neutron Star Mergers. Particles, 5(2), 198-209. https://doi.org/10.3390/particles5020018





