Experimental Determination of the QCD Effective Charge αg1(Q)
Abstract
1. Introduction
2. Experimental Extraction of
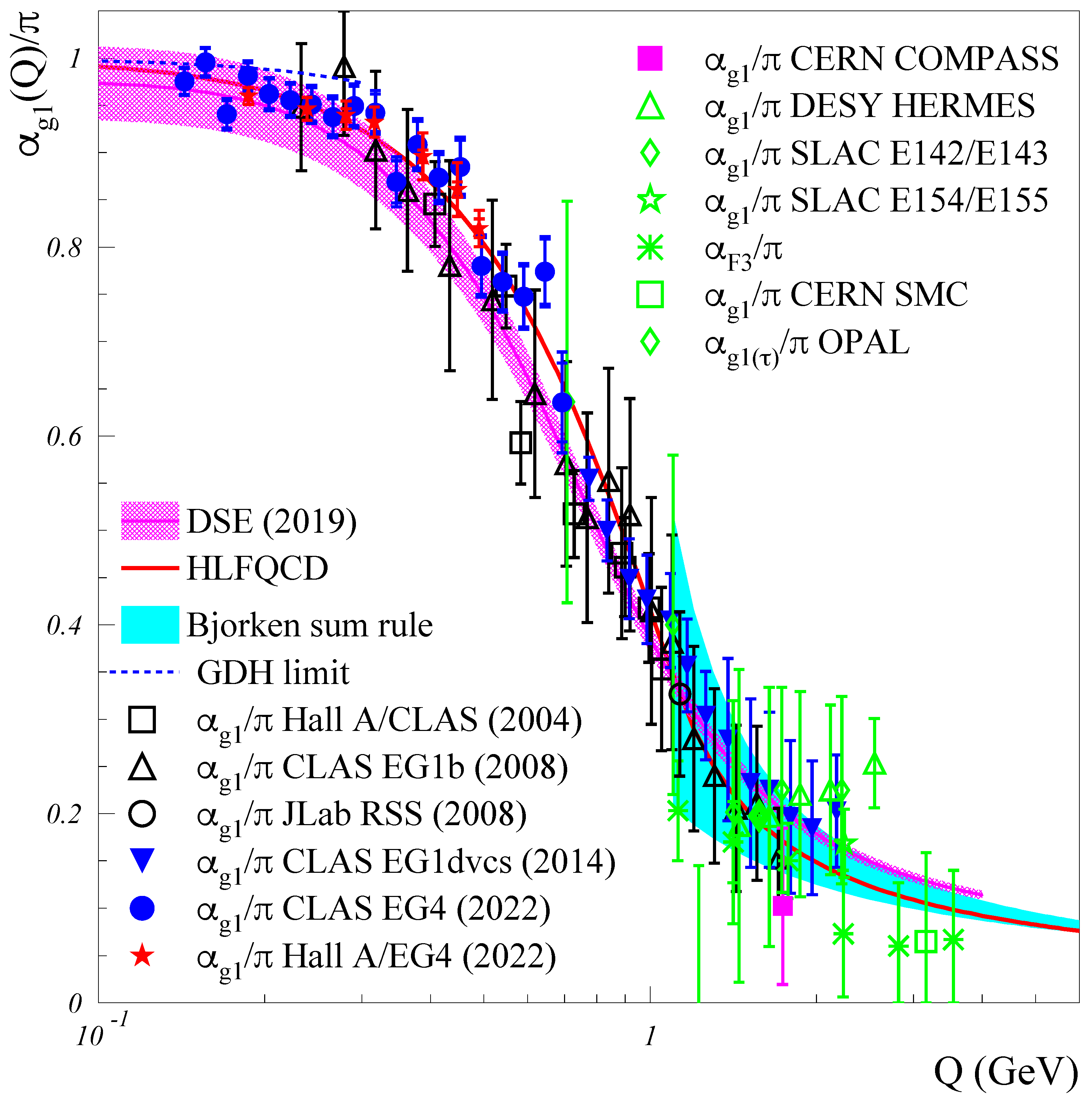
3. Summary and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- D’Enterria, D.; Kluth, S.; Zanderighi, G.; Ayala, C.; Benitez-Rathgeb, M.A.; Bluemlein, J.; Xie, K. The strong coupling constant: State of the art and the decade ahead. arXiv 2022, arXiv:2203.08271. [Google Scholar]
- Yao, W.M.; Amsler, C.; Asner, D.; Barnett, R.M.; Beringer, J.; Burchat, P.R.; Staney, T. Review of Particle Physics. J. Phys. G Nucl. Part. Phys. 2006, 33, 1–1232. [Google Scholar] [CrossRef]
- Brodsky, S.J.; de Téramond, G.F.; Dosch, H.G.; Erlich, J. Light-front holographic QCD and emerging confinement. Phys. Rep. 2015, 584, 1–105. [Google Scholar] [CrossRef]
- Dobado, A.; Espriu, D. Strongly coupled theories beyond the Standard Model. Prog. Part. Nucl. Phys. 2020, 115, 103813. [Google Scholar] [CrossRef]
- Dirac, P.A.M. Forms of relativistic dynamics. Rev. Mod. Phys. 1949, 21, 392. [Google Scholar] [CrossRef]
- Brodsky, S.J.; de Téramond, G.F. Light-front hadron dynamics and AdS/CFT correspondence. Phys. Lett. B 2004, 582, 211–221. [Google Scholar] [CrossRef]
- Maris, P.; Roberts, C.D. Dyson-Schwinger equations: A Tool for hadron physics. Int. J. Mod. Phys. E 2003, 12, 297–365. [Google Scholar] [CrossRef]
- Deur, A.; Brodsky, S.J.; de Téramond, G.F. The QCD Running Coupling. Prog. Part. Nucl. Phys. 2016, 90, 1. [Google Scholar] [CrossRef]
- Grunberg, G. Renormalization Group Improved Perturbative QCD. Phys. Lett. 1980, 95B, 70, Erratum in Phys. Lett. 1982, 110B, 501. [Google Scholar] [CrossRef]
- Gell-Mann, M.; Low, F.E. Quantum electrodynamics at small distances. Phys. Rev. 1954, 95, 1300. [Google Scholar] [CrossRef]
- Brodsky, S.J.; Lu, H.J. Commensurate scale relations in quantum chromodynamics. Phys. Rev. D 1995, 51, 3652. [Google Scholar] [CrossRef] [PubMed]
- Bjorken, J.D. Applications of the Chiral U(6)×U(6) Algebra of Current Densities. Phys. Rev. 1966, 148, 1467. [Google Scholar] [CrossRef]
- Gross, D.J.; Smith, C.H.L. High-energy neutrino-nucleon scattering, current algebra and partons. Nucl. Phys. B 1969, 14, 337. [Google Scholar] [CrossRef]
- Brodsky, S.J.; Menke, S.; Merino, C.; Rathsman, J. On the behavior of the effective QCD coupling alpha(tau)(s) at low scales. Phys. Rev. D 2003, 67, 055008. [Google Scholar] [CrossRef]
- Gorishnii, S.G.; Kataev, A.L.; Larin, S.A. The O(αs3)-corrections to σtot(e+e-→hadrons) and Γ(τ-→ντ+hadrons) in QCD. Phys. Lett. B 1991, 259, 144–150. [Google Scholar] [CrossRef]
- Deur, A.; Brodsky, S.J.; de Téramond, G.F. Connecting the hadron mass scale to the fundamental mass scale of quantum chromodynamics. Phys. Lett. B 2015, 750, 528. [Google Scholar] [CrossRef]
- Bjorken, J.D. Asymptotic Sum Rules at Infinite Momentum. Phys. Rev. 1969, 179, 1547–1553. [Google Scholar] [CrossRef]
- Deur, A.; Brodsky, S.J.; de Téramond, G.F. The Spin Structure of the Nucleon. Rep. Prog. Phys. 2019, 82, 7. [Google Scholar] [CrossRef]
- Kataev, A.L. The Ellis-Jaffe sum rule: The estimates of the next-to-next-to-leading order QCD corrections. Phys. Rev. D 1994, 50, 5469. [Google Scholar] [CrossRef]
- Burkardt, M. Transverse force on quarks in deep-inelastic scattering. Phys. Rev. D 2013, 88, 114502. [Google Scholar] [CrossRef]
- Deur, A. Spin Sum Rules and the Strong Coupling Constant at large distance. AIP Conf. Proc. 2009, 1155, 112–121. [Google Scholar]
- Gerasimov, S.B. A Sum rule for magnetic moments and the damping of the nucleon magnetic moment in nuclei. Sov. J. Nucl. Phys. 1966, 2, 430. [Google Scholar]
- Burkert, V.D. Comment on the generalized Gerasimov-Drell-Hearn sum rule in chiral perturbation theory. Phys. Rev. D 2001, 63, 097904. [Google Scholar] [CrossRef]
- Brodsky, S.J.; de Téramond, G.F.; Deur, A. Nonperturbative QCD Coupling and its β-function from Light-Front Holography. Phys. Rev. D 2010, 81, 096010. [Google Scholar] [CrossRef]
- Binosi, D.; Mezrag, C.; Papavassiliou, J.; Roberts, C.D.; Rodriguez-Quintero, J. Process-independent strong running coupling. Phys. Rev. D 2017, 96, 054026. [Google Scholar] [CrossRef]
- Deur, A.; Burkert, V.; Chen, J.P.; Korsch, W. Experimental determination of the effective strong coupling constant. Phys. Lett. B 2007, 650, 244. [Google Scholar] [CrossRef]
- Adeva, B.; Ahmad, S.; Arvidson, A.; Badelek, B.; Ballintijn, M.K.; Bardin, G.; Voss, R. Measurement of the spin dependent structure function g1(x) of the deuteron. Phys. Lett. B 1993, 302, 533. [Google Scholar] [CrossRef][Green Version]
- Airapetian, A.; Akopov, N.; Akushevich, I.; Amarian, M.; Arrington, J.; Aschenauer, E.C.; Schüler, K.P. The Q2 dependence of the generalized Gerasimov-Drell-Hearn integral for the proton. Phys. Lett. B 2000, 494, 1–8. [Google Scholar] [CrossRef]
- Deur, A.; Bosted, P.; Burkert, V.; Cates, G.; Chen, J.P.; Choi, S.; Yun, J. Experimental determination of the evolution of the Bjorken integral at low Q2. Phys. Rev. Lett. 2004, 93, 212001. [Google Scholar] [CrossRef]
- Anthony, P.L.; Arnold, R.G.; Band, H.R.; Borel, H.; Bosted, P.E.; Breton, V.; Zapalac, G. Deep inelastic scattering of polarized electrons by polarized He-3 and the study of the neutron spin structure. Phys. Rev. D 1996, 54, 6620. [Google Scholar] [CrossRef]
- Alekseev, M.G.; Alexakhin, V.Y.; Alexandrov, Y.; Alexeev, G.D.; Amoroso, A.; Austregesilo, A.; Padee, A. The Spin-dependent Structure Function of the Proton and a Test of the Bjorken Sum Rule. Phys. Lett. B 2010, 690, 466–472. [Google Scholar] [CrossRef]
- Deur, A.; Prok, Y.; Burkert, V.; Crabb, D.; Girod, F.X.; Griffioen, K.A.; Kvaltine, N. High precision determination of the Q2 evolution of the Bjorken Sum. Phys. Rev. D 2014, 90, 012009. [Google Scholar] [CrossRef]
- Deur, A.; Chen, J.P.; Kuhn, S.E.; Peng, C.; Ripani, M.; Sulkosky, V.; Zheng, X. Experimental study of the behavior of the Bjorken sum at very low Q2. Phys. Lett. B 2022, 825, 136878. [Google Scholar] [CrossRef]
- Rodríguez-Quintero, J.; Binosi, D.; Mezrag, C.; Papavassiliou, J.; Roberts, C.D. Process-independent effective coupling. From QCD Green’s functions to phenomenology. Few Body Syst. 2018, 59, 121. [Google Scholar] [CrossRef]
- Deur, A.; Shen, J.M.; Wu, X.G.; Brodsky, S.J.; de Téramond, G.F. Implications of the Principle of Maximum Conformality for the QCD Strong Coupling. Phys. Lett. B 2017, 773, 98. [Google Scholar] [CrossRef]
- Deur, A.; Brodsky, S.J.; de Téramond, G.F. Determination of at five loops from holographic QCD. J. Phys. G 2017, 44, 105005. [Google Scholar] [CrossRef]
- Cui, Z.F.; Ding, M.; Gao, F.; Raya, K.; Binosi, D.; Chang, L.; Roberts, C.D.; Rodríguez-Quintero, J.; Schmidt, S.M. Kaon and pion parton distributions. Eur. Phys. J. C 2020, 80, 1064. [Google Scholar] [CrossRef]
- Janik, R.A. The Dynamics of Quark-Gluon Plasma and AdS/CFT. Lect. Notes Phys. 2011, 828, 147–181. [Google Scholar]
- Busza, W.; Rajagopal, K.; van der Schee, W. Heavy Ion Collisions: The Big Picture, and the Big Questions. Ann. Rev. Nucl. Part. Sci. 2018, 68, 339–376. [Google Scholar] [CrossRef]
- Florkowski, W.; Heller, M.P.; Spalinski, M. New theories of relativistic hydrodynamics in the LHC era. Rept. Prog. Phys. 2018, 81, 046001. [Google Scholar] [CrossRef]
- Jokela, N.; Järvinen, M.; Remes, J. Holographic QCD in the Veneziano limit and neutron stars. JHEP 2019, 3, 41. [Google Scholar] [CrossRef]
- Sulkosky, V.; Singh, J.T.; Peng, C.; Chen, J.P.; Deur, A.; Abrahamyan, S.; Zhu, L. Measurement of the 3He spin-structure functions and of neutron (3He) spin-dependent sum rules at 0.035 ≤ Q2 ≤ 0.24 GeV2. Phys. Lett. B 2020, 805, 135428. [Google Scholar] [CrossRef]
- Alcorn, J.; Anderson, B.D.; Aniol, K.A.; Annand, J.R.M.; Auerbach, L.; Arrington, J.; McKeown, R.D. Basic Instrumentation for Hall A at Jefferson Lab. Nucl. Instrum. Meth. A 2004, 522, 294–346. [Google Scholar] [CrossRef]
- Mecking, B.A.; Adams, G.; Ahmad, S.; Anciant, E.; Anghinolfi, M.; Asavapibhop, B.; Vlassov, A.V. The CEBAF Large Acceptance Spectrometer (CLAS). Nucl. Instrum. Meth. A 2003, 503, 513–553. [Google Scholar] [CrossRef]
- Prok, Y.; Bosted, P.; Kvaltine, N.; Adhikari, K. Precision measurements of g1 of the proton and the deuteron with 6 GeV electrons. Phys. Rev. C 2014, 90, 025212. [Google Scholar] [CrossRef]
- Zheng, X.; Deur, A.; Kang, H.; Kuhn, S.E.; Ripani, M.; Zhang, J.; Zachariou, N. Measurement of the proton spin structure at long distances. Nat. Phys. 2021, 17, 736. [Google Scholar] [CrossRef]
- Adhikari, K.P.; Deur, A.; El Fassi, L.; Kang, H.; Kuhn, S.E.; Ripani, M.; CLAS Collaboration. Measurement of the Q2-dependence of the deuteron spin structure function g1 and its moments at low Q2 with CLAS. Phys. Rev. Lett. 2018, 120, 062501. [Google Scholar] [CrossRef]
- Sulkosky, V. The Spin Structure of 3He and the Neutron at Low Q2: A Measurement of the Generalized Gdh Integrand. Ph.D. Thesis, College of William & Mary, Williamsburg, VA, USA, 2007. [Google Scholar]
- Keith, C.D.; Anghinolfi, M.; Battaglieri, M.; Bosted, P.; Branford, D.; Bültmann, S.; Witherspoon, S. A polarized target for the CLAS detector. Nucl. Instrum. Meth. A 2003, 501, 327–339. [Google Scholar] [CrossRef][Green Version]
- Garibaldi, F.; Acha, A.; Ambrozewicz, P.; Aniol, K.A.; Baturin, P.; Benaoum, H.; Jefferson Lab Hall A Collaboration. High-resolution hypernuclear spectroscopy at Jefferson Lab, Hall A. Phys. Rev. C 2019, 99, 054309. [Google Scholar] [CrossRef]
- Kim, J.H.; Harris, D.A.; Arroyo, C.G.; de Barbaro, L.; de Barbaro, P.; Bazarko, A.O.; Bernstein, R.H.; Bodek, A.; Bolton, T.; Budd, H.; et al. A measurement of αs(Q2) from the Gross–Llewellyn Smith sum rule. Phys. Rev. Lett. 1998, 81, 3595. [Google Scholar] [CrossRef]
- De Alfaro, V.; Fubini, S.; Furlan, G. Conformal invariance in quantum mechanics. Nuovo Cim. A 1976, 34, 569. [Google Scholar] [CrossRef]
- Trawinski, A.P.; Glazek, S.D.; Brodsky, S.J.; de Téramond, G.F.; Dosch, H.G. Effective confining potentials for QCD. Phys. Rev. D 2014, 90, 074017. [Google Scholar] [CrossRef]
- Cornwall, J.M. Dynamical Mass Generation in Continuum QCD. Phys. Rev. D 1982, 26, 1453. [Google Scholar] [CrossRef]
- Abbott, L.F. The Background Field Method Beyond One Loop. Nucl. Phys. B 1981, 185, 189–203. [Google Scholar] [CrossRef]
- Binosi, D.; Chang, L.; Papavassiliou, J.; Roberts, C.D. Bridging a gap between continuum-QCD and ab initio predictions of hadron observables. Phys. Lett. B 2015, 742, 183–188. [Google Scholar] [CrossRef]
- Aguilar, A.C.; Binosi, D.; Papavassiliou, J. Gluon and ghost propagators in the Landau gauge: Deriving lattice results from Schwinger-Dyson equations. Phys. Rev. D 2008, 78, 025010. [Google Scholar] [CrossRef]
- Brodsky, S.J.; Shrock, R. Maximum wavelength of confined quarks and gluons and properties of quantum chromodynamics. Phys. Lett. B 2008, 666, 95. [Google Scholar] [CrossRef][Green Version]
- Sufian, R.S.; Liu, T.; de Téramond, G.F.; Dosch, H.G.; Brodsky, S.J.; Deur, A.; Hlfhs Collaboration. Nonperturbative strange-quark sea from lattice QCD, light-front holography, and meson-baryon fluctuation models. Phys. Rev. D 2018, 98, 114004. [Google Scholar] [CrossRef]
| Q (GeV) | |
|---|---|
| 0.143 | 3.064 |
| 0.156 | 3.129 |
| 0.171 | 2.955 |
| 0.187 | 3.083 |
| 0.204 | 3.022 |
| 0.223 | 3.002 |
| 0.243 | 2.988 |
| 0.266 | 2.947 |
| 0.291 | 2.983 |
| (GeV) | |
| 0.317 | 2.961 |
| 0.347 | 2.730 |
| 0.379 | 2.853 |
| 0.414 | 2.745 |
| 0.452 | 2.779 |
| 0.494 | 2.451 |
| 0.540 | 2.397 |
| 0.590 | 2.349 |
| 0.645 | 2.431 |
| 0.704 | 1.996 |
| (GeV) | |
| 0.187 | 3.016 |
| 0.239 | 2.973 |
| 0.281 | 2.952 |
| 0.316 | 2.929 |
| 0.387 | 2.815 |
| 0.447 | 2.704 |
| 0.490 | 2.575 |
| 0.775 | 1.743 |
| 0.835 | 1.571 |
| 0.917 | 1.419 |
| 0.986 | 1.341 |
| 1.088 | 1.272 |
| 1.167 | 1.121 |
| 1.261 | 0.955 |
| 1.384 | 0.874 |
| 1.522 | 0.730 |
| 1.645 | 0.708 |
| 1.795 | 0.617 |
| 1.967 | 0.581 |
| 2.177 | 0.636 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Deur, A.; Burkert, V.; Chen, J.-P.; Korsch, W. Experimental Determination of the QCD Effective Charge αg1(Q). Particles 2022, 5, 171-179. https://doi.org/10.3390/particles5020015
Deur A, Burkert V, Chen J-P, Korsch W. Experimental Determination of the QCD Effective Charge αg1(Q). Particles. 2022; 5(2):171-179. https://doi.org/10.3390/particles5020015
Chicago/Turabian StyleDeur, Alexandre, Volker Burkert, Jian-Ping Chen, and Wolfgang Korsch. 2022. "Experimental Determination of the QCD Effective Charge αg1(Q)" Particles 5, no. 2: 171-179. https://doi.org/10.3390/particles5020015
APA StyleDeur, A., Burkert, V., Chen, J.-P., & Korsch, W. (2022). Experimental Determination of the QCD Effective Charge αg1(Q). Particles, 5(2), 171-179. https://doi.org/10.3390/particles5020015





