Rabi Frequency Management of Collapsing Quasi-Two-Dimensional Bose-Einstein Condensates with Pseudospin-1/2

Abstract

The collapse of quasi-two-dimensional pseudospin-1/2 Bose-Einstein condensate of attracting atoms with intra- and cross-spin interaction is studied in the presence of the Rabi coupling. The condensate dynamics is presented as a function of the self-interaction and Rabi frequency. The evolution of two components of the condensate by using the Gross-Pitaevskii equations is investigated. The initial Gaussian ansatz for two-component wave functions is selected for the better interpretation of the numerical results. The intra-spin-coupling modifies the critical number of atoms causing the collapse while the collapse is observed only in a single pseudospin component. It is demonstrated that for cross-spin-coupling only double spin-components collapse can occur.

1. Introduction

Understanding of behavior of nonlinear quantum systems, including solitons and instantons, is critically important for understanding of quantum field and particles physics [1]. Thus, studies of experimentally available nonlinear quantum condensed matter systems can shed light on variety of processes occuring on much smaller spatial scales and involving much higher energies. One of those nonlinear quantum condensed matter systems is Bose-Einstein condensate (BEC) of interacting atoms [2]. The BECs open new research avenues in low-energy quantum physics as well as in astrophysics and cosmology, where they are actively studied for the understanding of the nature of mysterious Dark Matter [3] and possible alternatives of the relativistic neutron stars as boson stars. The nonlinear self-interaction that can be “repulsive” or “attractive” due to the Feshbach resonance [4] or dipolar interactions [5,6] is critically important for the BECs properties. The attractive interaction in the BEC can produce solitons [7], quantum droplets [8,9], collapse processes [10], and many other phenomena.

The BEC collapse is a dynamical process, corresponding to the squeezing of the characteristic size of the condensate into a point and sequentially an explosion as occurs in the experiments [11,12,13,14]. The collapse process depends on the dimension of the system and interatomic interaction. For instance, in a one-dimensional system, a cubic interatomic attraction in the condensate characterizes soliton dynamics [15] rather than the collapse. However, in the presence of the stronger quintic nonlinearity, the condensate can collapse [16]. In three dimensional systems with cubic nonlinearity attractive interaction always leads to the BEC collapse while in two dimensions a critical number of atoms is needed for the collapse to occur. The stabilization of the collapse opens a wide range of possible features of self-attracting BEC with the studies carried out by introducing a variety of obstacles into the self-attraction of the condensate [17,18,19,20,21,22,23].

In this paper we study the quasi-two-dimensional BEC of atoms with pseudospin-1/2. Studying the cubic nonlinearity, the main focus will be on two types of interactions: intra- and cross-spin coupling of components [24,25,26]. To produce the spin dynamics, we use an external synthetic Rabi magnetic field which leads to redistribution of the condensate density between the spin components. As a result, we will demonstrate the collapse of the condensate depending on the type of interactions: (i) with the intra-spin interaction the collapse can be observed only in one spin component depending on the Rabi field strength; (ii) with the cross-spin interaction the collapse can be observed only in both spin components for a sufficient strength of the Rabi field.

Controlled collapse of two and three-dimensional condensate is demonstrated in [17] through changing scattering length of atoms, that is in the framework of time-dependent inter-atomic interaction g. As a result, the stability of the condensate is limited in time, eventually switching into collapse. Here, we apply a Rabi field to rotate the BEC pseudospin and the spin rotation leads to the oscillation of condensate density between spin components consequently modifying inter-atomic interaction. Thus we obtain the effect being similar to the oscillated interatomic scattering length used in Ref. [17]. Despite this similarity, the physics of the problem studied here is considerably richer since, as it will be shown, various forms of collapse and collapse inhibition can occur here.

2. The Model and Main Parameters

The collapse dynamics of quasi-two-dimensional BEC with pseudospin-1/2 coupled by the synthetic Rabi magnetic field is characterized by evolution of the wave functions ${\psi }_i\equiv {\psi }_i(\mathit{r},t)(i=1,2)$ with the total norm N, $\mathit{r}\equiv (x,y)$. The evolution of the wave functions is described by the Gross-Pitaevskii equations (GPEs) in the form:

$$\begin{array}{cc}\hfill i\hslash {\partial }_t{\psi }_1& =-\frac{{\hslash }^2}{2m}\Delta {\psi }_1-\frac{g}{1+\left|\kappa \right|}\left[(1-\kappa )|{\psi }_1{|}^2+(1+\kappa ){\left|{\psi }_2\right|}^2\right]{\psi }_1+\frac{\Omega }{2}{\psi }_2,\hfill \\ \hfill i\hslash {\partial }_t{\psi }_2& =-\frac{{\hslash }^2}{2m}\Delta {\psi }_2-\frac{g}{1+\left|\kappa \right|}\left[(1-\kappa )|{\psi }_2{|}^2+(1+\kappa ){\left|{\psi }_1\right|}^2\right]{\psi }_2+\frac{\Omega }{2}{\psi }_1.\hfill \end{array}$$

(1)

Here m is the atomic mass, the interaction constant $g=4\pi {\hslash }^2\left|a_s\right|/m{a}_z$, $a_z$ is the condensate extension along the z axis, and $a_s<0$ is the s-wave scattering length. The Rabi frequency $\Omega$ corresponds to the effective Zeeman magnetic field directed along the x-axis. In the system of GPEs (1) $\kappa =-1,0,1$ describes the intra-, total and cross-spin interaction, correspondingly. The spin components are normalized by

$$N_i=2\pi {\int }_0^{\infty }{\left|{\psi }_i(r,t)\right|}^{2}r\mathrm{d}r,$$

(2)

where $(i=1,2)$, $N_i\equiv N_i\left(t\right)$ and the total norm $N=N_1+N_2$ is conserved.

Since the dynamics of the collapse is characterized by the density profile of the condensate components, we study the evolution of widths of the spin components and spin dynamics driven by Rabi field for given inter-atomic interactions. The evolution of the width of the spin components is characterized by time-dependent inverse participation ratio in the form:

$$a_i\left(t\right)=\frac{N_i}{\sqrt{2\pi }}{\left[{\int }_0^{\infty }{\left|{\psi }_i(r,t)\right|}^{4}r\mathrm{d}r\right]}^{-1/2}.$$

(3)

The nonlinear condensate dynamics has a strong impact on the evolution of spin components defined by

$$⟨{\sigma }_j\left(t\right)⟩=\frac{2\pi }{N}{\int }_0^{\infty }{\{{\psi }_1^{*},{\psi }_2^{*}\}}^{\mathrm{T}}{\sigma }_j\{{\psi }_1,{\psi }_2\}r\mathrm{d}r,$$

(4)

where ${\sigma }_j(j=x,y,z)$ are corresponding Pauli matrices, “*” stands for the complex conjugate and “$\mathrm{T}$” is the transposition. Consequently, the length of the spin vector $P\left(t\right)$ [27]

$$P\left(t\right)=\sqrt{\sum _j{⟨{\sigma }_j\left(t\right)⟩}^2}\le 1,$$

(5)

corresponding to the decreased purity of the condensate in the spin subspace.

From Equation (1) the total energy of the system is given by

$$E_T^{\kappa }=E_K+E_I^{\kappa }+E_R.$$

(6)

Here $E_K$, $E_I^{\kappa }$, and $E_R$ are the kinetic, interaction, and Rabi magnetic field energies, respectively, determined by

$$\begin{array}{ll}{E}_K& =-2\pi {\int }_0^{\infty }\frac{{\hslash }^2}{2m}\left[{\psi }_1^{*}\Delta {\psi }_1+{\psi }_2^{*}\Delta {\psi }_2\right]r\mathrm{d}r,\end{array}$$

(7)

$$\begin{array}{ll}{E}_I^{\kappa }& =-\frac{\pi g}{1+\left|\kappa \right|}{\int }_0^{\infty }\left[(1-\kappa )\left[|{\psi }_1{|}^4+{\left|{\psi }_2\right|}^4\right]+2(1+\kappa )|{\psi }_1{|}^2{\left|{\psi }_2\right|}^2\right]r\mathrm{d}r,\end{array}$$

(8)

$$\begin{array}{ll}{E}_R& =\pi \Omega {\int }_0^{\infty }\left[{\psi }_1^{*}{\psi }_2+{\psi }_2^{*}{\psi }_1\right]r\mathrm{d}r.\end{array}$$

(9)

From Equations (4) and (9) follows, the Rabi magnetic field energy can be characterized with spin parameter $⟨{\sigma }_x⟩$ by $E_R=N⟨{\sigma }_x⟩/2$.

For the numerical solution of Equation (1) we assume that at $t=0$ one has $g=0$ and $\Omega =0$, and the condensate is prepared in the ground state of harmonic potential. At $t>0$ the harmonic potential is suddenly switched off and simultaneously the interaction and the Rabi magnetic field are switched on causing the BEC dynamics. Thus, we start with the Gaussian ground state wave function with the initial spin along the z-axis

$${\psi }_1(r,t=0)=\begin{array}{c}\hfill \sqrt{\frac{N}{\pi a_0^2}}\end{array}exp\left[-\frac{r^2}{2a_0^2}\right],$$

(10)

where $a_0$ is initial width of the condensate and ${\psi }_2(r,t=0)=0$. Hereafter we use the units with $m=\hslash \equiv 1$ and consequently dimensionless $g=4\pi |a_s|/a_z$, unit of length ℓ is arbitrary and unit of time is ${\ell }^2$.

To have a reference point we assume that the condensate is prepared in the ground state form (10) and in Equation (1) $\Omega =0,\kappa =0.$ Thus, Equation (6) yields

$$E_0=-\frac{N}{2\pi }\frac{\Lambda }{a_0^2},$$

(11)

where $\Lambda =(gN-{\lambda }_{\mathrm{cr}})/2$ and ${\lambda }_{\mathrm{cr}}=2\pi$ is the critical interaction parameter $gN$ to obtain the collapse as characterized by condition $E_0\to -\infty$ for $a_0\to \infty$ satisfied only if $\Lambda >0$ [28]. In this case the corresponding time dependent width is given by [29]

$$a_{\mathrm{v}}\left(t\right)=a_0\sqrt{1-\frac{\Lambda t^2}{a_0^4}},$$

(12)

with the collapse time being $T_c=a_0^2/\sqrt{\Lambda }.$

For a qualitative explanation of the Rabi magnetic field effect, we use Gaussian ansatz for two-component wave functions in the form,

$$\begin{array}{cc}\hfill & {\psi }_1(r,t)={\left(\frac{N}{\pi {\tilde{a}}_1^{\prime }{}^2\left(t\right)}\right)}^{1/2}exp\left[-\frac{r^2}{2{\tilde{a}}_1^2\left(t\right)}\right]cos\left(\frac{\Omega }{2}t\right),\hfill \\ \hfill & {\psi }_2(r,t)={\left(\frac{N}{\pi {\tilde{a}}_2^{\prime }{}^2\left(t\right)}\right)}^{1/2}exp\left[-\frac{r^2}{2{\tilde{a}}_2^2\left(t\right)}\right]sin\left(\frac{\Omega }{2}t\right).\hfill \end{array}$$

(13)

Here, we assume the ${\tilde{a}}_i^2\left(t\right)$ is a complex number. The real part $\mathrm{Re}\left[{\tilde{a}}_i^2\left(t\right)\right]>0$ in order to have a wave function of Gaussian form with ${\tilde{a}}_i^{\prime }{}^2\left(t\right)=\mathrm{Re}\left[{\tilde{a}}_i^2\left(t\right)\right]$.

In the wave functions (13), $\Omega$ is the spin precession rate corresponding to oscillations of the condensate density between spin components. From the ansatz functions (13) we can characterize widths of spin components by

$$\begin{array}{c}\hfill {\left(\frac{2\pi }{N}{\int }_0^{\infty }{r}^3{\left|{\psi }_1(r,t)\right|}^2\mathrm{d}r\right)}^{1/2}=\frac{|{\tilde{a}}_1{\left(t\right)|}^2}{{\tilde{a}}_1^{\prime }\left(t\right)}\left|cos\left(\frac{\Omega }{2}t\right)\right|,\\ \hfill {\left(\frac{2\pi }{N}{\int }_0^{\infty }{r}^3{\left|{\psi }_2(r,t)\right|}^2\mathrm{d}r\right)}^{1/2}=\frac{|{\tilde{a}}_2{\left(t\right)|}^2}{{\tilde{a}}_2^{\prime }\left(t\right)}\left|sin\left(\frac{\Omega }{2}t\right)\right|.\end{array}$$

(14)

Here the widths of the spin-projected wave packets are characterized by $|{\tilde{a}}_1{\left(t\right)|}^2/{\tilde{a}}_1^{\prime }\left(t\right)$ where factors with cosine and sine functions are explicitly related to the spin rotation. If in Equation (14) $\mathrm{Im}\left[{\tilde{a}}_i^2\left(t\right)\right]=0$, then the spin components widths are characterized by ${\tilde{a}}_i\left(t\right)$.

Since the kinetic and Rabi-field related energies do not explicitly depend on the self-interaction type, then for ansatz functions (13) the Equations (7) and (9) become:

$$\begin{array}{cc}\hfill & E_K=\frac{N}{2}\left[\frac{1}{{\tilde{a}}_1^{\prime }{}^2\left(t\right)}{cos}^2\left(\frac{\Omega }{2}t\right)+\frac{1}{{\tilde{a}}_2^{\prime }{}^2\left(t\right)}{sin}^2\left(\frac{\Omega }{2}t\right)\right],\hfill \end{array}$$

(15)

$$\begin{array}{cc}\hfill & E_R=\Omega N\frac{{\tilde{a}}_1^{\prime }\left(t\right){\tilde{a}}_2^{\prime }\left(t\right)}{|{\tilde{a}}_1\left(t\right){\tilde{a}}_2{\left(t\right)|}^2}\frac{{\tilde{a}}_1^{\prime }{}^2\left(t\right)|{\tilde{a}}_2{\left(t\right)|}^4+{\tilde{a}}_2^{\prime }{}^2\left(t\right){\left|{\tilde{a}}_1\left(t\right)\right|}^4}{|{\tilde{a}}_1^2\left(t\right)+{\tilde{a}}_2^{*2}{\left(t\right)|}^2}sin\left(\Omega t\right).\hfill \end{array}$$

(16)

Consequently, as can be seen from (16), the Rabi energy can be positive or negative, in order to compensate kinetic and self-interaction energies depending on the spin state.

3. Numerical Results and Discussion

3.1. Intra-Spin Interaction

In this section we discuss the dynamics of the intra-spin interacting condensate with $\kappa =-1$ in Equation (1). Since at time $t=0,$ the initial spin (10) is directed along the z-axis, at time $t>0$ the applied Rabi magnetic field starts to rotate the spin and the wave function of the second spin component became nonzero. Correspondingly, the density of the condensate included in (1) splits between two spin components, thus reducing the interaction between atoms because of the absence of spin cross-coupling term. As a result, although for a weak Rabi field, the attractive self-interaction will be reduced by reorientation of spin and density redistribution, the condensate eventually collapses. However, for a sufficiently strong Rabi field, spin rotation provides oscillations of interaction on the $2\pi /\Omega$ timescale and can prevent the collapse, similar to the effect studied in Ref. [17].

Now, for intra-spin interaction $\kappa =-1$ we apply the ansatz functions (13) to (8) and we obtain the interaction energy in the form

$$E_I^{\kappa =-1}=-\frac{g{N}^2}{4\pi }{cos}^4\left(\frac{\Omega }{2}t\right)\frac{{\tilde{a}}_1^{\prime }{}^2\left(t\right)}{|{\tilde{a}}_1{\left(t\right)|}^4}-\frac{g{N}^2}{4\pi }{sin}^4\left(\frac{\Omega }{2}t\right)\frac{{\tilde{a}}_2^{\prime }{}^2\left(t\right)}{|{\tilde{a}}_2{\left(t\right)|}^4}.$$

(17)

On the right hand side of the Equation (17), the first and second terms characterize the interaction energies of the intra-spin components and the Rabi field. They are introduced to demonstrate oscillations of these energies between the spin components. As follows from Equation (14), in Equation (17) factors ${\tilde{a}}_i^{\prime }{}^2\left(t\right)/{\left|{\tilde{a}}_i\left(t\right)\right|}^4$ characterize the inverse square of the widths of spin components. Then the condensate collapses at least in one spin component, if ${\tilde{a}}_i^{\prime }{}^2\left(t\right)/{\left|{\tilde{a}}_i\left(t\right)\right|}^4\to 0$ and $E_I^{\kappa =-1}\to -\infty ,$ respectively. On the other hand, it is difficult to collapse both spin components due to the cosine and sine functions in Equation (17), since due to the fourth power, these functions can remain close to zero for a significantly long time compared to the collapse time.

Since the spin rotation frequency is $\Omega$, the characteristic spin flip time is $T_{sf}=\pi /\Omega +2\pi k/\Omega ,k=0,1,2,\dots$. At the time $\pi /2\Omega$, the occupations of the spin components become close, then the interaction energy (17) has decreased by a factor of $2.$ As a result, $T_c=\pi /2\Omega$ could, in general, be a probable moment of collapse of the double spin components under the condition of sufficiently large self-interaction, $gN>4\pi$. On the other hand, at $t=\pi /2\Omega$ it follows from Equation (16) that the Rabi field-related energy can be either positive or negative with corresponding kinetic and self-interaction energies being dependent on the spin state. Therefore, simultaneous collapse in both spin components is difficult to achieve. Eventually, $\pi /2\Omega$ is a border time of collapse due to the transfer of density between two spin components. As a result, the condition for the collapse of the first spin component before the first spin flip is $T_{sf}>2T_c$ ($k=0$), i.e., $\Omega <\pi \sqrt{gN-2\pi }/\left(2\sqrt{2}{a}_0^2\right)$. This means that for a weak Rabi field, the first spin component collapses, and for a sufficiently large $\Omega$, one of the spin components can collapse, as depends on the Rabi field.

The Figure 1 presents the stability and collapse of diagram of the two spin components in the $(gN,\Omega )$-plane. In the figure, the panels (a) and (b) are plotted for two different initial widths presented in the caption, and the initial wave function is described by (10). The results show that when the Rabi coupling is switched on, the critical value of $gN$ is shifted up from $2\pi$ to $\approx 2\pi \times 1.33.$ The transitions between different types of collapse show a complex domain structure. For $gN<4\pi ,$ the Rabi frequency can provide a stable BEC at $\Omega \approx \pi \sqrt{gN-2\pi }/\left(2\sqrt{2}{a}_0^2\right)$. Also, comparing panels (a) and (b) of the Figure 1, it can be seen that decreasing the initial width of the condensate increases the Rabi collapse field of each spin component, requiring a stronger Rabi field.

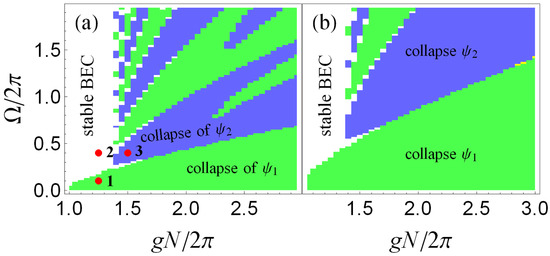
Figure 1. The diagram of stable and collapsing condensate is plotted in $(gN,\Omega )-$plane for intra-spin interaction $\kappa =-1$ given in Equation (1). The left panel (a) and the right panel (b) are plotted for initial width of condensate $a_0=1$ and $a_0=1/\sqrt{2}$, correspondingly. Below in the next figures we will present characteristic dynamics of the condensate for the values of $(gN,\Omega )$ from the fixed points (1,2,3) in the panel (a).

The Figure 2 demonstrate dynamics of the condensate width and spin evolution, defined by Equations (3) and (4). The panels (a), (b), (c) a related to the values $(gN,\Omega )$ given by points (1,2,3) in Figure 1, correspondingly. The panel (a1) presents collapse of the first spin component because for given values of $(gN,\Omega )=(1.32{\lambda }_{\mathrm{cr}},0.1{\lambda }_{\mathrm{cr}})$ the condition $\Omega <\pi \sqrt{gN-2\pi }/\left(2\sqrt{2}{a}_0^2\right)$ is satisfied. Nonetheless, by comparing $a_1\left(t\right)$ and $a\left(t\right)$ one can see that this weak Rabi frequency changes the collapse time with respect to $\Omega =0$. Also, for the same interaction and Rabi frequency, from the Figure 2(a2) it follows that the total spin is reoriented in another direction rather that follows for a rotation expected due to the Rabi field, because $⟨{\sigma }_x⟩\ne 0.$ Consequently, the length of the spin vector $P\left(t\right)<1$ near the $T_c.$

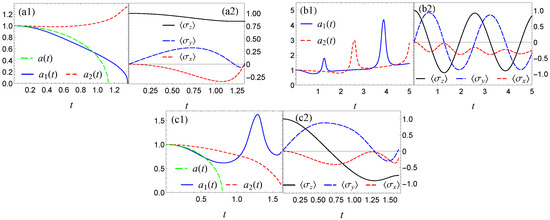
Figure 2. The plot of spin-components width (a1–c1) and spin rotation dynamics (a2–c2) versus time for intra-spin interaction $\kappa =-1$ in Equation (1). The panels (a–c) correspond to the values of $(gN,\Omega )$ given as $(1.32{\lambda }_{\mathrm{cr}},0.1{\lambda }_{\mathrm{cr}})$, $(1.32{\lambda }_{\mathrm{cr}},0.42{\lambda }_{\mathrm{cr}})$, $(1.57{\lambda }_{\mathrm{cr}},0.42{\lambda }_{\mathrm{cr}})$ from fixed points (1,2,3) in the Figure 1, correspondingly. In the panels (a1,c1) the width $a\left(t\right)$ are plotted for $\Omega =0$ to compare the collapse times with non-spin effect.

The panel (b1) of Figure 2 shows that a relatively strong Rabi frequency at $(gN,\Omega )=(1.32{\lambda }_{\mathrm{cr}},0.42{\lambda }_{\mathrm{cr}})$ can stabilize the BEC and, correspondingly, the spin (b2) is rotating perfectly in the spin subspace $({\sigma }_y,{\sigma }_z)$, with the conserved length $P\left(t\right)\approx 1$. The panel (c1) of Figure 2 demonstrates collapse of the second spin component for the interaction $gN>1.33{\lambda }_{\mathrm{cr}}$ (point (3), $(gN,\Omega )=(1.57{\lambda }_{\mathrm{cr}},0.42{\lambda }_{\mathrm{cr}}))$. One can see from the panel (c1) that at time $t<T_{sf}/2$ the widths $a\left(t\right)$ and $a_1\left(t\right)$ are the same because the interaction is relatively strong therefore first spin component is squeezed. From panel (c2) it follows that at time $T_{sf}<T_c$ the spin is flipped to spin-down and then the condensate collapses. Here also close to time $T_c$ the spin length is $P\left(t\right)<1$. Comparison of $a\left(t\right)$ and collapsing $a_i\left(t\right)$ in panels (a1) and (c1) implies that switching the collapse between spin components increases the collapse time $T_c$ compared the realization without the spin-related effects. It may be noticed that in the panels (a2), (b2) and (c2) always $⟨{\sigma }_x⟩<0$ that is reorientation of the initial spin state. The sharp jump of the widths $a_i\left(t\right)$ in panels (b1) and (c1) corresponds to spin flip time $T_{sf}.$

The Figure 3 presents density cross-section profiles of the condensate for the same values of the Rabi frequency and interaction parameters from panels (a) and (b) of the Figure 2 for collapse and stable, BEC correspondingly. The panels (a1), (a2) and (c1), (c2) of Figure 3 demonstrate the density evolution of the spin components. The panels (b1) and (d1) demonstrate spin rotation of ${\sigma }_z$ and panels (b2) and (d2) show spin reorientation in the ${\sigma }_x$ direction. From panels (a1) and (b1) it follows that the condensate collapses in the first spin component at a time $T_c<T_{sf}$ because of a weak the Rabi frequency. It follows from panel (a2) that the density of the second spin component is almost zero since spin cannot rotate but it is reoriented because ${\sigma }_x\ne 0$. The panels (c1) and (c2) clearly show the evolution of the density transition between spin-up and spin-down states and panel (d1) shows pure spin rotation due to a large Rabi frequency. It follows from the panels (b2) and (d2) that the initial spin is reoriented and ${\sigma }_x<0$ that can compensate the interaction energy for collapse or stable BEC. All presented density plots are in the same scales shown on the right side with arbitrary units.

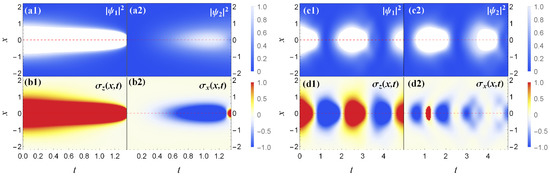
Figure 3. The density plot of the condensate parameters taken from panels (a,b) of Figure 2 is presented for the corresponding values of $(gN,\Omega )$. The panels (a1,c1) are demonstrating $|{\psi }_1{|}^2$ and (a2,c2) are demonstrating $|{\psi }_2{|}^2$. The panels (b1,d1) are demonstrating ${\sigma }_z$ and (b2,d2) are demonstrating ${\sigma }_x$. The plots are presented in the plane $(x,t)$ for intra-spin interaction $\kappa =-1$ in Equation (1). The values of $(gN,\Omega )$ are given from the points (1, 2) of the Figure 1, correspondingly, for collapsing and stable BEC. The density scales on the right side are the same for all panels with arbitrary units. Here the panels (a,b) are presenting collapse of the first spin component with corresponding spin dynamics and the panels (c,d) are presenting stable condensate with total density transition between spin components and corresponding spin rotation.

As a result, we numerically demonstrated that in the case of intra-spin interaction, the Rabi frequency oscillations lead to different time dependence of the density profiles in the spin up to spin down components. Density redistribution between the components decrease self-interaction in each component. Thus, the Rabi rotation at frequency $\Omega$ can produce BEC stable against the collapse or collapse of one of the components. The intra-spin interaction can lead to the reorientation of the spin from that expected for the Rabi rotation by producing $⟨{\sigma }_x⟩<0$ state. In addition, the initial extension of the condensate strongly modifies the effect of the Rabi field on the BEC collapse.

3.2. Cross-Spin Interaction

In this section we discuss the cross-spin interaction with $\kappa =1$ in Equation (1), that can provide collapse of the condensate by applying the Rabi field. Since we take the initial spin (10) along z-axis (${\psi }_2(x,t=0)=0$), then it follows from Equation (1) that to switch on the cross-spin interaction the Rabi frequency should be nonzero.

With the cross-spin coupling the self-interaction energy (8) is given by

$$E_I^{\kappa =1}=-\frac{g{N}^2}{4\pi }{sin}^2[\Omega t]{\tilde{a}}_{12}^{-1}\left(t\right),$$

(18)

where ${\tilde{a}}_{12}\left(t\right)$ is

$${\tilde{a}}_{12}\left(t\right)=\frac{|{\tilde{a}}_1{\left(t\right)|}^2}{{\tilde{a}}_1^{\prime }\left(t\right)}+\frac{|{\tilde{a}}_2{\left(t\right)|}^2}{{\tilde{a}}_2^{\prime }\left(t\right)}.$$

(19)

On the other hand, at the moment of time $T_k=\pi k/\Omega$ the energy (18) also becomes zero due to ${sin}^2[\Omega t]$ function. Thus, a sufficient self-interaction occurs only if the BEC spin $|⟨{\sigma }_z\left(t\right)⟩|<1.$ Eventually, the condensate can collapse only at ${\tilde{a}}_{12}\left(t\right)\to 0$, and it follows from Equation (19) that the collapse can be ensured only in two spin components simultaneously.

The Figure 4 demonstrates the stability and collapse diagram of two spin components in the $(gN,\Omega )$-plane. It follows from the figure that collapse can occur as $\Omega$ exceeding a certain critical value of $\approx 0.4\pi$ and sufficiently large $gN>6\pi$.

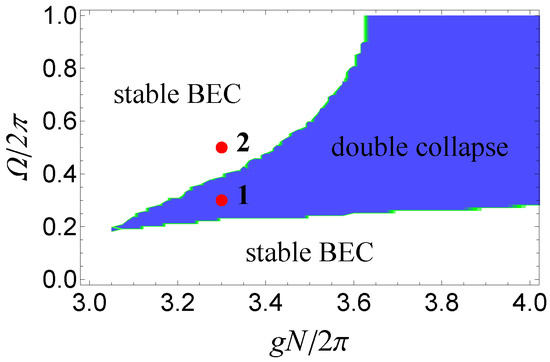
Figure 4. The diagram of the stable and collapsing BEC is presented in $(gN,\Omega )$-plane for cross-spin interaction with $\kappa =1$ in Equation (1). The plot corresponds to initial width $a_0=1$. For the values of $(gN,\Omega )$ from fixed points (1,2) characteristic condensate dynamics will be presented below in the next figures.

The Figure 5 demonstrates the collapse and stable dynamics of the BEC for given values of $(gN,\Omega )$ from fixed points (1) and (2) of Figure 4, correspondingly. The panels (a1) and (b1) correspond to the time evolution of the width, and the panels (a2) and (b2) correspond to the total spin rotation dynamics. The plot (a1) demonstrates the widths of both spin components tend to zero, as consistent with the interaction energy (18). Near the collapse time $T_c,$ the widths show some increase since, as it follows from plot (a2), at this time the spin is flipped to spin-down and $⟨{\sigma }_x⟩\le 0$ leading to a decrease in the self-interaction. Thus, this behavior of the widths of the spin components can be explained as follows. Since $E_R\sim ⟨{\sigma }_x⟩$, it follows from the plot (a2) that the attraction interaction energy (18) is compensated by the Rabi magnetic field energy at $⟨{\sigma }_x⟩>0$ and a sharp change in this energy at $⟨{\sigma }_x⟩\le 0$ leads to expanding of the condensate. Finally, due to a relatively fast spin rotation, one obtains $⟨{\sigma }_x⟩>0$ and consequently, the condensate collapses. Also, due to this interplay of the energies in the panel (a1) one can see the collapse time with cross-spin interaction is considerably larger than $a\left(t\right)$ that corresponds to the spinless condensate. The panel (b1) of Figure 5 demonstrates the widths of spin components with their interrelated behavior for stable condensate with the values of $(gN,\Omega )$ from the fixed point (2) of Figure 4. The sharp changes in the widths correspond to transitions between the spin up and down states with the Rabi frequency. It follows from panel (b2) that the spin is rotating in the $({\sigma }_y,{\sigma }_z)-$plane with the length $P\left(t\right)\approx 1$. In this case, due to fast oscillations of $⟨{\sigma }_x\left(t\right)⟩$, Rabi magnetic field cannot inhibit collapse, but it still keeps the condensate from expanding for a relatively long time. The panels (c1) and (c2) demonstrate cross-section density plot of spin components and panels (d1) and (d2) show corresponding spin rotation dynamics in $(x,t)$ plane. In fact, the panels (c) and (d) present the density plot simulation of the panels (a1) and (a2), correspondingly. Here the condensate is squeezed and spin dynamics are clearly demonstrated.

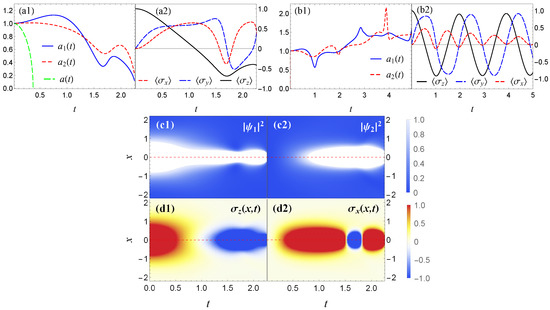
Figure 5. The panels (a1,b1) present the widths of the spin components defined by Equation (3) and the panels (a2,b2) present the spin rotation dynamics defined by Equation (4) versus time. The panels (a,b) are plotted for the values of $(gN,\Omega )$ given as $(3.3{\lambda }_{\mathrm{cr}},0.3{\lambda }_{\mathrm{cr}})$, $(3.3{\lambda }_{\mathrm{cr}},0.5{\lambda }_{\mathrm{cr}})$ from the fixed points (1, 2) of Figure 4 for collapse and stable BEC, correspondingly. In the panel (a1) the width $a\left(t\right)$ is plotted for $\Omega =0$ to compare the collapse time with that in the spinless condensate. The panels (c1,c2) are the cross section density plots of the collapse dynamics of $|{\psi }_1{|}^2$ and $|{\psi }_2{|}^2$, and the panels (d1,d2) present the cross section density plot of spin rotation of ${\sigma }_z$ and ${\sigma }_x$ in the plane $(x,t)$, with correspondingly values of $(gN,\Omega )$ from the panel (a), correspondingly.

To summarize, in this section we presented numerical evidence that the condensate with cross-spin interaction and initially non-coupled spin components can collapse in the presence of Rabi magnetic field. For the self-interaction exceeding some critical value, the collapse of the condensate can be produced by spin reorientation from the initial state even for a relatively small $\Omega$. This implies that the self-interaction energy could be compensated by interaction with the Rabi field when the spin state with $⟨{\sigma }_x(t>0)⟩>0$ is formed.

Moreover, Figure 6 demonstrates for intra- and cross-spin interaction that the initially Gaussian wave functions become non-Gaussian with time. The plots of Figure 6 show the evolution of the expectation values of ${⟨r^4⟩}_i$ and ${⟨r^2⟩}_i^2$ defined as:

$$⟨r^d⟩i=\frac{2\pi }{\begin{array}{c}\hfill N_i\end{array}}{\int }_0^{\infty }{r}^d{\left|{\psi }_i(r,t)\right|}^{2}r\mathrm{d}r,$$

(20)

where ${\psi }_i(r,t)$ is numerical solution of Equation (1) and $N_i$ is defined by Equation (2). For two-dimensional Gaussians one has ${⟨r^4⟩}_i-2{⟨r^2⟩}_i^2=0,$ and the nonzero values demonstrate that the BEC shape strongly deviates from the Gaussian profile.

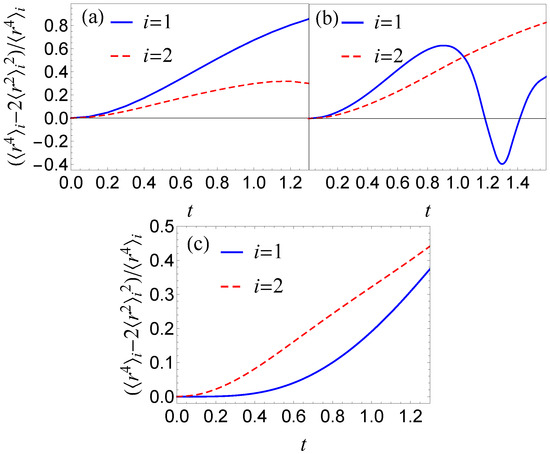
Figure 6. The plot of non-Gaussian behavior of the spin components versus time. Blue lines correspond to the spin up and red dashed lines corresponds to the spin down. The panels (a,b) correspond to intra-spin interaction with the value of $(gN,\Omega )$ from fixed points (1) and (2) of Figure 1, correspondingly. The panel (c) corresponds to cross-spin interaction with the value of $(gN,\Omega )$ from fixed points (1) of the Figure 4.

4. Conclusions

In this paper, we investigated the collapse of quasi-two-dimensional BEC of atoms with pseudospin-1/2 and in a synthetic Rabi magnetic field. The collapse of condensate is explored assuming intra- or cross-spin attractive interactions. With the intra-spin interaction, the Rabi magnetic field affects the collapse of the condensate by modifying number of atoms in each spin component. In this case the spin rotation leads to oscillations in the self-interaction energy with the double Rabi frequency that can stabilize the condensate. With the cross-spin interaction, the condensate collapses by rotation of the spin, which enhances the self-interaction.

We obtained that for the intra- and cross-spin coupling both, the initially Gaussian wave function becomes non-Gaussian at time $t>0$. As a result, we determine collapse and stability diagram in the $(gN,\Omega )-$plane for both interactions. The intra-spin-coupling modifies the critical number of atoms causing the collapse while the collapse is observed only in a single pseudospin component. It is demonstrated that for cross-spin-coupling only double spin-components collapse can occur.

To connect the results with the realization of the BEC experiments, for s-wave scattering length $|a_s|\sim 100a_B\sim 5\times {10}^{-3}$$\mathsf{\mu }\mathrm{m}$ ($a_B$ being the Bohr radius) and the condensate extension along the z axis $a_z\sim 1$ $\mathsf{\mu }\mathrm{m}$, the dimensionless interaction constant $g=4\pi |a_s|/a_z\sim 0.05.$ The velocity of the collapse is $v_c\sim \hslash \sqrt{gN}/Ma\left(0\right)$. For the BEC of ${}^{87}\mathrm{Rb}$ atoms at $a\left(0\right)\sim 10$ $\mathsf{\mu }\mathrm{m}$ and $N\sim {10}^4$ this estimate yields $v_c\sim 0.1$ cm/s and the corresponding time scale $T_c=a\left(0\right)/v_c\sim 0.01$ s. Therefore, the Rabi frequency providing the cross-over condition $\Omega T_c\sim 1$ is of the order of $\Omega \sim 100$ Hz. The conditions of weak and strong Rabi frequency against the BEC collapse, $\Omega T_c\ll 1$ and $\Omega T_c\gg 1,$ correspondingly, can be achieved by modifying initial $a\left(0\right),$ the number of particles $N,$ and Rabi frequency $\Omega$ in the available experimental range [30].