Abstract
An algorithm of pre-equilibrium clustering of spectator matter based on the construction of the minimum spanning tree (MST) is presented. The algorithm was implemented in the Abrasion-Ablation Monte Carlo for Colliders (AAMCC) model designed to study the characteristics of spectator matter in collisions of relativistic nuclei. Due to accounting for the pre-equilibrium clusters in modelling Pb–Pb collisions at the LHC, the agreement of simulation results with experimental data on the average multiplicities of spectator nucleons was improved. The results of the AAMCC-MST were compared with experimental data on the interactions of Au nuclei in nuclear photoemulsion. Comparison of the yields of spectator nuclei calculated for O–O collisions with the yields measured in interactions of O with light nuclei of photoemulsion made it possible to estimate the effect of MST-clustering in small nuclear systems.
1. Introduction
The characteristics of the secondary particles formed as a result of collisions of relativistic nuclei, as well as the conditions of formation of quark–gluon plasma, significantly depend on the initial geometry of the collision. One of the methods to determine the geometry of a nucleus–nucleus collision event, including its centrality and reaction plane, is the detection of forward nucleons using Zero Degree Calorimeters (ZDC) [1]. Such nucleons represent spectator matter outside the overlap region of the colliding nuclei, and they are emitted at small angles with respect to the beam axis. The calculations with the Abrasion-Ablation Monte Carlo for Colliders (AAMCC) model [2] demonstrated [3,4] that spectator matter is represented not only by free nucleons but also by nuclear fragments. In addition to the numbers of free spectator neutrons, other characteristics of spectator nucleons and nuclear fragments can be considered to improve the determination of collision centrality [5]. Multiple production of intermediate mass fragments (IMF) with charges known as multifragmentation was studied in several experiments. In particular, the multifragmentation of 600 MeV/nucleon Au projectiles on Cu target was studied in ALADIN experiments [6]. According to the predictions of the well-known Statistical Model of Multifragmentation SMM [7], a hot thermalized nuclear system (prefragment) with an excitation energy above 3 MeV/nucleon undergoes an explosive decay into three or more fragments of comparable masses. Such less hot fragments may remain excited and their de-excitation occurs later by sequential evaporation of nucleons and light nuclei.
The SMM is based on the assumption that the prefragment is an undivided system in which thermodynamic equilibrium has been established by the time of its decay due to intensive interaction of constituent nucleons [7]. It is assumed that the average density of the decaying system is less than of the normal nuclear density. It is obvious that the shape of a prefragment significantly affects the establishment of thermodynamic equilibrium. In particular, in central collisions of identical spherical heavy nuclei, prefragments have narrow crescent-shaped structures mostly arranged along semicircles. As a result, the establishment of the thermodynamic equilibrium in the entire system is hindered by a poor connectivity between nucleons. The connectivity of spectator matter is reduced also in ultracentral collisions (with impact parameter fm) of elongated deformed nuclei, such as U, if the long axes of the nuclear ellipsoids are perpendicular to each other. With such orientations called tip-body and side-side [8,9], spectator prefragments from nuclei with long axes perpendicular to the direction of their movement are divided into two independent clusters by the overlapping zone of the nuclei. The possibility of modeling the statistical decay of a prefragment is also questionable in the case of central collisions of light nuclei, in which the spectator matter is represented by a small number of weakly bound nucleons.
In the AAMCC model described in our previous publications [2,3,4,5], each nucleus–nucleus collision is considered as a two-stage abrasion-ablation process. At the abrasion stage, the removal of all participating nucleons from the primary nuclei is simulated. At the subsequent ablation stage, the decay of both prefragments representing spectator matter from the initial nuclei is simulated. The above-described effects of the loss of connectivity between nucleons in prefragments of specific shape were not taken into account in the previous version of AAMCC. In the present study, the AAMCC model is supplemented by a mechanism of pre-equilibrium clusterization of spectator matter to account for such effects. In this extension of AAMCC called AAMCC-MST, pre-equilibrium clusterization is simulated immediately after the abrasion stage on the basis of the Minimum Spanning Tree (MST) clustering algorithm.
In Section 2 of the present paper, an updated AAMCC-MST model, including the algorithm for the pre-equilibrium clustering modeling based on MST-clusterisation (MST-clustering), is presented. In Section 3, the influence of MST-clustering on various distributions of spectator fragments formed as a result of the collisions of 10.7 GeV/nucleon Au nuclei with Ag nuclei is discussed, and a comparison with experimental data is provided [10]. In Section 4, the impact of such clustering on the average multiplicity of spectator neutrons and protons as functions of the impact parameter in Pb–Pb collisions at the LHC at TeV is examined, and calculations are compared with preliminary data [11]. In Section 5, the influence of MST-clustering on the probabilities of the formation of various elements as spectator fragments in interactions of 200 GeV/nucleon O nuclei with light nuclei is discussed, and a comparison with data [12] is made. In Section 6, the findings of the present work are summarized.
2. Description of AAMCC-MST Model
In this paper, the AAMCC model [2,3,5,13] is used to describe the formation of spectator matter in nucleus–nucleus collisions as a two-stage process:
- Removal of participating nucleons from the initial nuclei (abrasion) resulting in the formation of an excited prefragments;
- De-excitation of prefragments (ablation) by their decay into spectator nucleons and nuclear fragments.
At the abrasion stage, the collision impact parameter and the positions of neutrons and protons in the initial nuclei are sampled using the Glauber Monte Carlo (GMC) model v3.2 [14] according to the corresponding distributions of neutron and proton densities. Nucleons that have experienced collisions with the nucleons of the other nucleus are considered as participants, while others are treated as spectators.
The secondary ablation stage begins with the calculation of the excitation energy of the spectator prefragments from each side. Depending on the relative mass of the prefragment , where and A are the mass numbers of the prefragment and the initial nucleus, respectively, several methods of calculating the total or specific excitation energy are available in AAMCC.
The Ericson formula is applied [15] to events with a small number of nucleons removed from each of the initial nuclei. In this case, the probability distribution of calculated for each prefragment is determined by a or, in other words, by the numbers of the respective hole states in the potential of the initial nucleus. The Ericson formula [15] is obtained by convoluting energy distributions of single-hole states. Each removed nucleon numbered as a adds excitation energy to the prefragment. On average, this value is equal to the following:
where MeV sets the maximum energy of a single hole state in the initial nucleus [16]. In Ref. [16], it is also shown that after the removal of more than 20% of nucleons from initial Pb in peripheral or semi-central collisions with various targets, the average excitation energy per nucleon obtained on the basis of the Ericson formula:
significantly exceeds the typical binding energy (∼8 MeV) per prefragment nucleon. This implies a complete disintegration of the prefragment into individual nucleons. This contradicts the data of the ALADIN [6] experiment, which show that spectator matter in peripheral collisions of heavy nuclei is represented not only by free nucleons but also by nuclear fragments. This suggests that with a large number a of removed nucleons the properties of the initial nuclear potential change significantly, and the Ericson formula becomes inapplicable. Therefore, for events with significant numbers of removed nucleons , a phenomenological dependence of on is used:
as proposed by the ALADIN [6] collaboration. The methods (2) and (3) were discussed in detail in Ref. [16].
In the present study, a hybrid method to calculate the correlation between and is used. The dependence (2) is switched to (3) at the value of determined from the condition of continuity of the expressions (2) and (3) used at low and high , respectively. The term can be neglected for heavy nuclei, and equating the expressions (2) and (3) provides the following.
The term cannot be neglected for light nuclei; thus, the resulting equation is solved numerically by the iteration method with the values used in this study ( MeV and MeV) for heavy projectile nuclei, including Pb and , while is used for O projectiles.
In previous implementations of abrasion–ablation models, particularly in Refs. [2,16,17], spectator matter formed after the ablation stage is considered as a single system with thermodynamic equilibrium established by the time of its decay. It is assumed that equilibrium is achieved due to the intense interaction between all constituent nucleons. However, as shown in Figure 1 for PbPb collisions, such a condition of connectivity is fulfilled in peripheral collisions but violated in central ones. Indeed, in central collisions of identical spherical nuclei, spectator matter has a shape of a narrow crescent and, therefore, looses connectivity due to the low density of nucleons and larger distances between them. This is in contrast to peripheral collisions with spectator nucleons located densely in relatively large prefragments (see Figure 1). It can be expected that in central collisions a separation of spectator matter into clusters occurs before the establishment of thermodynamic equilibrium as a result of pre-equilibrium processes. Similarly, in central collisions of light projectiles with heavy nuclei, a specific ring shape of spectator matter may hinder the establishment of a thermodynamic equilibrium in the entire spectator system.
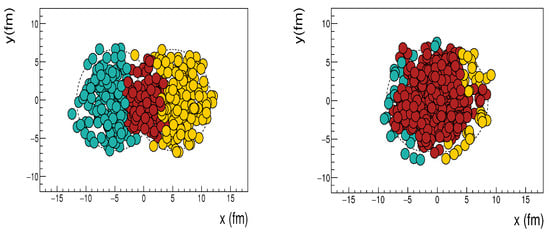
Figure 1.
Peripheral (left) and central (right) events of PbPb interactions at TeV simulated by the Glauber Monte Carlo model v3.2 [14]. The directions of motion of the initial nuclei are perpendicular to the figure plane. The spectator nucleons of the nucleus A are indicated by turquoise circles, nucleus B is indicated by yellow ones, while all participant nucleons are indicated by dark red ones.
An advanced algorithm based on the construction of a minimum spanning tree (MST) [18] was developed in the present study to take into account the above-described features of the shape of spectator matter resulting in pre-equilibrium clustering. The coordinates of the centers of spectator nucleons in three-dimensional space are used to determine individual nucleons and groups of nucleons that can be attributed to clusters. The MST-clustering algorithm is implemented in the following steps. All prefragment nucleons are represented as vertices of a complete weighted undirected graph for which its edge weights are equal to the moduli of the distances in 3D space between the corresponding vertex nucleons. Then, using the Kruskal algorithm [19], a minimum spanning tree with the minimum possible sum of all the edge weights is found. In the next step, the heavy edges for which their lengths are greater than some critical distance d between the nucleons are removed. This critical distance d is considered as a free parameter of the model. After that, a depth-first search algorithm is used to determine the nucleons connected by light edges that form clusters. A typical result of the MST algorithm is presented in Figure 2.
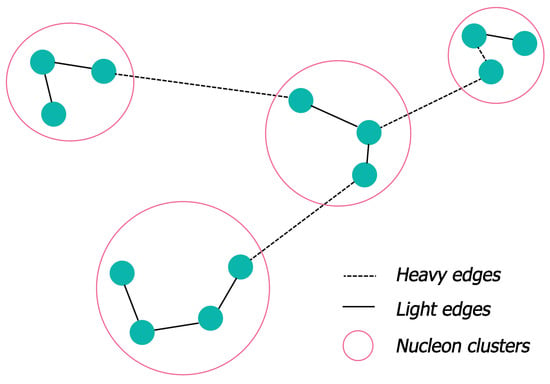
Figure 2.
Schematic representation of a result of the MST-clustering algorithm. Solid turquoise circles denote nucleons (vertices) and red circles denote the resulting clusters of nucleons.
The number of free nucleons and nucleon clusters found by the MST algorithm significantly depends on the parameter d. It is clear, that the application of the MST algorithm to large prefragments formed in peripheral collisions should not result in their separation into many clusters. Therefore, the value of d should not be less than the average distance of 1.6–1.8 fm between the centers of nucleons in nuclei in their ground states. This defines the values fm tested in the present study. In modeling peripheral collisions with fm, the model underestimates the numbers of light spectator fragments and overestimates the numbers of heavy fragments. In contrast, in modeling peripheral collisions with fm spectator matter becomes unstable and emits many nucleons even at very low excitation energy. As a result, fm was found to be optimal. However, calculations with fm underestimate the number of free spectator neutrons in central Pb–Pb collisions with respect to measurements [11].
It can be expected that the average multiplicity of nucleons and nucleon clusters defined by the MST algorithm for prefragments should increase with the decrease in the their average (bulk) density. The average distance between the groups of nucleons forming different clusters increases in diluted nuclear systems. However, in the AAMCC model based on the Glauber theory, nucleons of colliding nuclei are considered frozen. During a short collision time, any changes of the spatial coordinates of nucleons are neglected, and the radial expansion of the spectator system in the plane transverse to the beam axis is not taken into account. The AAMCC model also neglects the mutual Coulomb repulsion of the prefragment protons. For these reasons, direct estimation of the prefragment density at the pre-equilibrium stage is not possible in AAMCC.
However, the lower limit for the prefragment density at the pre-equilibrium stage can be estimated from the average prefragment density at a later stage, after reaching the thermodynamic equilibrium. This is motivated by the expansion of the prefragment on its way to the thermal equilibrium. Following [20], one can conclude that pre-equilibrium and eqilibrium densities correlate, , when they are evaluated from remnant masses for events with given fragment multiplicity. In Ref. [21] break-up densities were calculated from the fractional Coulomb barrier energy, determined by fitting spectra of intermediate mass fragments produced in He–Au, He–Au, and N–Au collisions. It was assumed that for the considered reactions, the heavy thermal source is spherical, and its expansion is radial. It was found [21] that the average density of a hot nuclear system with excitation energy MeV is similar to the ground state nuclear density fm. At higher , drops significantly [21], and at MeV it reaches a plateau value of . A similar estimation is adopted by the Statistical Multifragmentation Model (SMM) [7]. There it is assumed that at the moment of an explosive decay of a hot termalized nuclear system with 3–4 MeV into fragments, its average density is also lower than : 1/4–1/3.
In Ref. [22], was extracted by considering the level density parameters required to fit the caloric curves measured in several experiments for various fragmenting systems with . A useful compilation of results for obtained in [21,22] is presented in Ref. [23], where it is discussed that while they agree at MeV, the break-up densities derived from Coulomb barrier systematics [21] are lower at MeV compared to those from caloric curve data [22]. A moderate decrease in to at MeV was reported in Ref. [22]. We attribute the difference between [21,22] to very different techniques used in these papers and consider it as an estimate of systematic uncertainties of the methods.
The dependence of on the excitation energy at the time of pre-equilibrium clusterization is postulated in the AAMCC-MST model taking into account the above-mentioned experimental results [21,22]. It is assumed that at . At higher excitation energies , a phenomenological approximation of by a power function is introduced to account for the expansion:
where and MeV are the fit parameters that ensure the continuity of .
The dependence (5) is presented in Figure 3 together with the data obtained in Refs. [21,22]. As can be seen from this figure, the results of [21,22] differ from each other at MeV. Our approximation (5) is closer to the data of Ref. [21] at 3–4 MeV, and they are consistent with the values 1/4–1/3 adopted in the SMM model [6,7], which is used in the present work to simulate subsequent decays of clusters resulting from the MST algorithm.
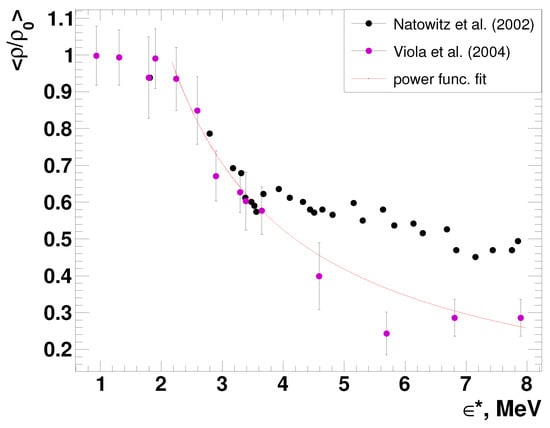
Figure 3.
Average relative density of prefragment as a function of the excitation energy per nucleon (solid line) assumed in AAMCC-MST. Points represent data from Refs. [21,22].
In the AAMCC-MST model, the phenomenological approximation (5) is used to determine the dependence of the clustering parameter d on the excitation energy at the pre-equilibrium stage. It is assumed that the excitation energy of the spectator prefragment is divided between the resulting clusters proportionally to the number of nucleons they contain. In this manner, the of each cluster on average corresponds to the specific excitation energy of the entire prefragment. At the same time, it can be expected that for a given cluster partition, the spatial dimensions of clusters increase with an increase in their excitation energy per nucleon due to an increase in the motion of intracluster nucleons and outward pressure. As a result, the internal density of clusters decreases, approaching the density at which thermodynamic equilibrium is established. Due to a short duration of the pre-equilibrium stage, there is no significant global expansion of the cluster system. Therefore, with an increase in the excitation energy of the system, the distances between the cluster boundaries correlating with the parameter d of the MST algorithm decrease on average. The exact dependence of d on the internal density of clusters is unknown; thus, in the AAMCC-MST model, a phenomenological dependence of is assumed. Using this dependence and Equation (5), the clustering parameter d is estimated as follows:
where fm is the clustering parameter at the normal nuclear density and MeV. The decrease in d with the increase in reflects a decrease in the connectivity of the prefragment system with the growth of . All these effects increase the number of free nucleons in central nucleus–nucleus collisions.
Statistical models of the Geant4 [24] toolkit are used in AAMCC-MST to simulate decays of clusters formed at the pre-equilibrium stage. At MeV, the Weisskopf–Ewing model [25] is used to simulate sequential evaporation of nucleons. For large , the Statistical Multifragmentation Model (SMM) [7] of Geant4 [24] is enabled. A version of the Fermi Break-Up model [26] is used to simulate the decays of excited light nuclei up to O.
3. Fragmentation of Au in Nuclear Emulsion
Various distributions and correlations between charged secondary fragments were measured in experiments on fragmentation of heavy relativistic nuclei in nuclear emulsion, particularly in Ref. [10]. This technique does not allow registering neutrons and accurately determining the mass numbers of spectator fragments, but it allows determining the charges of all fragments in each fragmentation event. Several charge distributions of fragments measured by the EMU-01/12 collaboration for collisions of 10.7 GeV/nucleon Au nuclei with nuclear photoemulsion (AgBrC) [10] are shown in Figure 4. The results of calculations using the AAMCC model with and without the MST algorithm are presented in the same figure. The dependences of the average maximum fragment charge in each event and the average numbers of hydrogen and helium fragments, and , respectively, are presented as functions of the sum of charges of fragments with in each event. The average number of intermediate mass fragments () in the event, denoted by as a function of , is of particular interest as an indicator of multifragment decays of spectator matter. The values and are directly connected with the size of the prefragment and, accordingly, with event centrality.
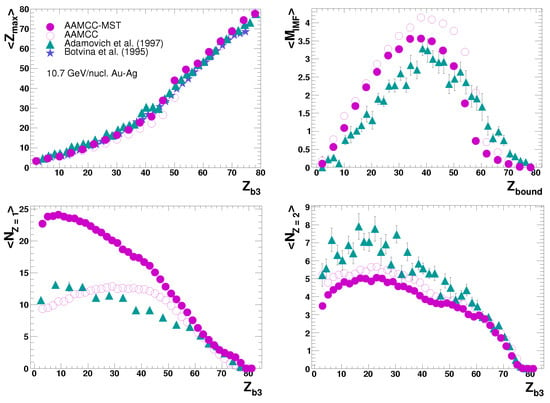
Figure 4.
Average maximum charge of the fragment , the average multiplicity of intermediate mass fragments , and the average multiplicities of hydrogen and helium fragments, and , in collisions of 10.7 GeV/nucleon Au with Ag nuclei calculated using the AAMCC model with (solid points) or without (open points) the MST algorithm as functions of or , see the definitions in the text. Experimental data [10] on projectile fragmentation in NIKFI BR-2 nuclear emulsion are represented by triangles. The data obtained for fragmentation of 600A MeV/nucleon Au on a copper target using the ALADIN [6] detector are represented by stars.
The dependence of on , measured for fragmentation of 600 MeV/nucleon Au on a copper target using the ALADIN detector [6], is also presented in Figure 4. This dependence almost coincides with the one measured in Ref. [10] at significantly higher energy of Au projectiles. This indicates the universality of this dependence. As can be seen from Figure 4, both variants of the AAMCC model describe well the dependence of on measured in two different experiments. Since, by definition, in each event, cannot exceed , all the points of such dependence are located below the diagonal line. The points near the diagonal at large characterize peripheral events in which all spectator matter, except the lightest fragments, such as neutrons, protons, deuterons, tritium nuclei, He, and He, is represented mainly by a single fragment with . In semi-central events represented by points below the diagonal in the range , the prefragment charge is distributed among several spectator fragments of comparable charge. Both variants of calculation of the dependence of on agree with the data in general, but the agreement improves when MST-clustering is enabled.
The results obtained with MST also turn out to be closer to the measured correlation between and , which has a characteristic shape with a maximum in semi-central events, see Figure 4. In Ref. [27] such an evolution of the average multiplicity of intermediate mass fragments with an increase in the impact parameter was identified as rise and fall of multifragmentation [27] (see also [6,28]). Both AAMCC variants qualitatively reflect the dependence of on but overestimate the multiplicity in central and semi-central events at . Still, the calculation with MST turns out to be closer to the data at .
As observed from Figure 4, the average multiplicities of the spectator hydrogen and helium fragments essentially depend on , and, accordingly, on centrality. The general shape of these dependencies is correctly reproduced by the model, with a satisfactory quantitative description of the multiplicity in peripheral events. At the same time, the multiplicity of helium nuclei is underestimated by AAMCC both with and without taking into account pre-equilibrium MST-clustering. The most noticeable difference between calculated with AAMCC-MST and the data is found for central and semi-central collisions. As expected, the inclusion of MST significantly increases the yields of protons and deuterons in central collisions. Such a discrepancy between the AAMCC-MST model and the data may stem from the restriction imposed in measurements [10] on the proton emission angle. The efficiency of a similar cut in calculations depends on the transverse momentum distribution of spectator protons obtained with the AAMCC model and requires further investigation.
4. Multiplicity of Spectator Nucleons in Pb–Pb Collisions
The average multiplicities of spectator neutrons and protons were measured in Pb–Pb collisions at TeV depending on the impact parameter b [11]. These preliminary results were obtained by means of the forward neutron (ZN) and proton (ZP) Zero Degree Calorimeters (ZDC) [1] installed in the ALICE experiment at the LHC. The value of b was estimated from the multiplicity of hadrons produced in the overlap region of colliding nuclei. It was measured using other detectors of the ALICE setup by means of various methods for centrality determination [29]. According to Ref. [11], ZN calorimeters provided full acceptance (>99%) for detecting spectator neutrons. However, the reported acceptance of ZP calorimeters for protons was significantly lower. It was defined by the settings of the LHC magnetic field and in general did not exceed 70–75%.
In Figure 5, and calculated by means of the AAMCC model with and without the pre-equilibrium MST-clustering are presented in comparison with the ALICE data [11]. The measured values of were divided by 0.7 to account for the acceptance of ZP. As can be seen from Figure 5, the average multiplicities of neutrons calculated by the AAMCC model are lower than those measured at all impact parameters. The inclusion of MST-clustering in the calculations reduces the discrepancy between the theory and experiment in central and semi-central events with fm. In such events, the spectator matter at the pre-equilibrium stage, due to its shape, is more susceptible to separation into fragments and free nucleons, as explained in Section 2. As expected, the inclusion of MST-clustering has practically no effect on the multiplicity of nucleons calculated for peripheral events. In general, the application of MST-clustering moves the calculated and closer to the measured ones, but further tuning of the AAMCC parameters is necessary for an accurate description of the data.
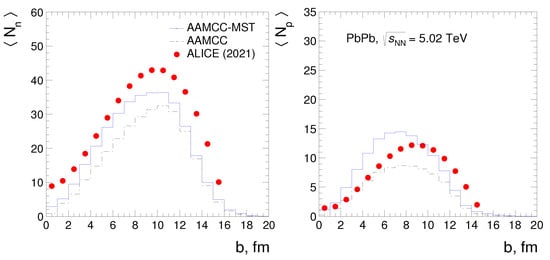
Figure 5.
Average multiplicities of neutrons (left) and protons (right) in Pb–Pb collisions at TeV as functions of the collision impact parameter calculated using the AAMCC model with and without MST-clustering (solid and dotted histograms, respectively). ALICE data [11] are represented by circles.
As known [30], in addition to deuterons, tritons, and He produced directly in nucleus–nucleus collisions, some additional H, H, and He are formed at a later stage by the coalescence of free neutrons and protons. Among other publications, in Refs. [30,31,32], the formation of deuterons was modeled by the phase space coalescence of protons and neutrons. Within this approach, the probability of creating deuterons in a certain momentum space volume is proportional to the numbers of produced neutrons and protons in this volume and to the coalescence parameter . As shown [31], the d/p ratio in nucleus–nucleus collisions calculated by the coalescence model remains well below 0.01 at GeV, in full agreement with the corresponding data. Therefore, in the case of spectator neutrons and protons, their conversion to deuterons is also expected to be unlikely, and the primary yields of free nucleons calculated with AAMCC-MST, Figure 5, will not be significantly affected.
5. Yields of Various Elements from Fragmentation of O
Since in collisions of light nuclei spectator matter consists of a small number of nucleons, its properties should be studied separately. The results of modeling of collisions of O with light nuclei (CNO) in nuclear photoemulsion are presented in Figure 6. In this figure, the multiplicity distribution of spectator -particles and the probability of production of spectator nuclei of elements He, Li, Be, B, C, and N are presented. Calculations were performed with and without MST-clustering, and the results are compared in this figure with the data on the fragmentation of O in photoemulsion [12].
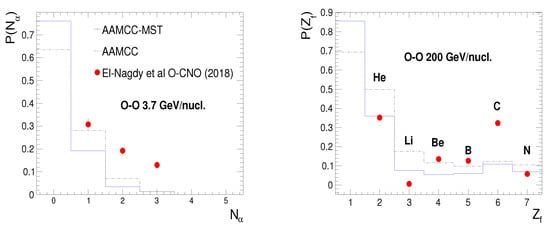
Figure 6.
Probabilities of production of a certain number of -particles (left) and certain elements (right) as spectators in collisions of O with energies of 3.7 GeV/nucleon and 200 GeV/nucleon, respectively, with O nuclei calculated by the AAMCC model with and without the MST-clustering (solid and dotted histograms). Points represent experimental data on the fragmentation of O on light nuclei (CNO) of photoemulsion [12].
According to [12], the reduced measured yields of lithium and nitrogen nuclei can be explained by the odd numbers of nucleons in these nuclei. This behavior is considered as an experimental evidence for the formation of -clusters in primary colliding nuclei and in produced fragments. The consideration of the multiplicity distribution of -particles presented in Figure 6 does not allow us to make a definite conclusion in favor of selecting MST-clustering in the AAMCC model, because both variants of the model significantly underestimate the probabilities of the formation of two and three spectator -particles. At the same time, the probabilities of production of certain elements calculated by AAMCC with MST-clustering, which are presented in Figure 6, turn out to be quite close to the data [12] for He and N nuclei. A satisfactory description of the yield of B nuclei is achieved with both calculation options, but the probability of the production of Li nuclei is overestimated by the present model. At the same time, the calculated probabilities of the production of Be+He+He and C+He in fragmentation of O are markedly underestimated by the AAMCC-MST model, as can be understood from both panels of Figure 6. A possible reason for such underestimation may be due to neglecting -particle clustering [33,34] in initial O nuclei in calculations. Such clustering may increase the probability of breakup channels containing -particles. It is planned to take into account the cluster structure O in future versions of AAMCC. This will allow predicting the composition of spectator fragments in O–O collisions in future runs [35] at a large hadron collider.
6. Conclusions
A new version of the Abrasion–Ablation Monte Carlo for Colliders model supplemented with the pre-equilibrium MST-clustering algorithm (AAMCC-MST) is presented. The inclusion of the MST-clustering makes it possible to take into account the peculiarities of the geometry of spectator matter in central collisions of medium and heavy relativistic nuclei. Due to MST-clustering, the probability of separation of spectator matter into excited clusters increases at the pre-equilibrium stage of fragmentation. As a result, the yields of free spectator nucleons in central and semi-central collisions of nuclei also increase. It was shown that the average multiplicities of neutrons and protons measured [11] by the ALICE collaboration as functions of the impact parameter in Pb–Pb in collisions at TeV are better described by the new version of AAMCC-MST taking into account MST-clustering compared to the version of the AAMCC without MST. The dependence of the clustering parameter on the excitation energy of the system made it possible to improve the description of the charge distributions of spectator fragments measured in experiments on fragmentation of Au in nuclear photoemulsion.
At the same time, the inclusion of MST-clustering in AAMCC does not improve significantly the description of experimental data on fragmentation of relativistic O nuclei on light nuclei in photoemulsion. It is expected that by taking into account the -clustering structure of O in next versions of AAMCC, the agreement with the experiment will be improved. While the production of H, H, and He via the coalescence of free spectator nucleons does not play the main role, the inclusion of this process in AAMCC-MST is also considered as a possible future development of this model.
Author Contributions
Conceptualization, R.N., A.S. and I.P.; data curation, R.N and A.S.; formal analysis, R.N., A.S. and I.P.; funding acquisition, I.P.; investigation, R.N., A.S., N.K. and I.P.; methodology, R.N., A.S., N.K. and I.P.; project administration, I.P.; resources, I.P.; software, R.N., A.S. and N.K.; supervision, I.P.; validation, R.N.; visualization, R.N.; writing—original draft, R.N.; writing—review and editing, A.S., N.K. and I.P. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by RFBR grant number 18-02-40035-mega.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data sharing is not applicable to this article as no new data were created or analysed in this study.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| MST | Minimum Spaning Tree; |
| SMM | Statistical model of multifragmentation; |
| AAMCC | Abrasion-Ablation Monte Carlo for Colliders; |
| AAMCC-MST | AAMCC model with MST-clustering algorithm. |
References
- Puddu, G.; Arnaldi, R.; Chiavassa, E.; Cicaló, C.; Cortese, P.; De Falco, A.; Dellacasa, G.; Ferretti, A.; Floris, M.; Gagliardi, M.; et al. The zero degree calorimeters for the ALICE experiment. Nucl. Instrum. Methods A 2007, 581, 397–401. [Google Scholar] [CrossRef]
- Svetlichnyi, A.; Nepeyvoda, R.; Pshenichnov, I. Using Spectator Matter for Centrality Determination in Nucleus-Nucleus Collisions. Particles 2021, 4, 227–235. [Google Scholar] [CrossRef]
- Svetlichnyi, A.O.; Pshenichnov, I.A. Formation of Free and Bound Spectator Nucleons in Hadronic Interactions between Relativistic Nuclei. Bull. Russ. Acad. Sci. Phys. 2020, 84, 911–916. [Google Scholar] [CrossRef]
- Pshenichnov, I.A.; Dmitrieva, U.A.; Svetlichnyi, A.O. Secondary Nuclei from Peripheral and Ultraperipheral Collisions of Relativistic Heavy Ions. Bull. Russ. Acad. Sci. Phys. 2020, 84, 1007–1011. [Google Scholar] [CrossRef]
- Pshenichnov, I.A.; Kozyrev, N.A.; Nepeivoda, R.S.; Svetlichnyi, A.O.; Dmitrieva, U.A. Properties of Spectator Matter in Nuclear Collisions at NICA. Phys. Part. Nucl. 2021, 52, 591–597. [Google Scholar] [CrossRef]
- Botvina, A.S.; Mishustin, I.N.; Begemann-Blaich, M.; Hubele, J.; Imme, G.; Iori, I.; Kreutz, P.; Kunde, G.J.; Kunze, W.D.; Lindenstruth, V.; et al. Multifragmentation of spectators in relativistic heavy-ion reactions. Nucl. Phys. A 1995, 584, 737–756. [Google Scholar] [CrossRef]
- Bondorf, J.; Botvina, A.; Iljinov, A.; Mishustin, I.; Sneppen, K. Statistical multifragmentation of nuclei. Phys. Rep. 1995, 257, 133–221. [Google Scholar] [CrossRef]
- Bairathi, V.; Haque, M.R.; Mohanty, B. Selecting specific initial configurations using spectator neutrons in U+ U collisions. Phys. Rev. C 2015, 91, 054903. [Google Scholar] [CrossRef]
- Bairathi, V.; Chatterjee, S.; Haque, M.R.; Mohanty, B. Probing Pb+Pb collisions at GeV with spectators. Phys. Lett. B 2016, 754, 144–150. [Google Scholar] [CrossRef]
- Adamovich, M.I.; Aggarwal, M.M.; Alexandrov, Y.A.; Amirikas, R.; Andreeva, N.P.; Anzon, Z.V.; Avetyan, F.A.; Badyal, S.K.; Bakich, A.M.; Baklitskaya, E.; et al. Multifragmentation of Gold nuclei in the interactions with photoemulsion nuclei at 10.7 GeV/nucleon. Z. Phys. A 1997, 359, 277–290. [Google Scholar] [CrossRef]
- Acharya, S.; Adamová, D.; Adler, A.; Adolfsson, J.; Aggarwal, M.M.; Aglieri Rinella, G.; Agnello, M.; Agrawal, N.; Ahammed, Z.; Ahmad, S.; et al. Data-Driven Model for the Emission of Spectator Nucleons as a Function of Centrality in Pb-Pb Collisions at Lhc Energies. Available online: https://cds.cern.ch/record/2712412?ln=bg (accessed on 28 December 2021).
- El-Nagdy, M.; Abdelsalam, A.; Badawy, B.; Zarubin, P.; Abdalla, A.; Yasin, M.N.; Saber, A.; Mohamed, M.; Ahmed, M. Channels of projectile fragmentation of 16O nucleus in nuclear emulsion. J. Phys. Commun. 2018, 2, 035010. [Google Scholar] [CrossRef]
- Nepeivoda, R.S.; Svetlichnyi, A.O. Dependence of n/p-ratio in spectator matter on the energy and mass of colliding nuclei. Mem. Fac. Phys. 2021, 1, 2110302. [Google Scholar]
- Loizides, C.; Kamin, J.; d’Enterria, D. Improved Monte Carlo Glauber predictions at present and future nuclear colliders. Phys. Rev. C 2018, 97, 054910. [Google Scholar] [CrossRef]
- Ericson, T. The statistical model and nuclear level densities. Adv. Phys. 1960, 9, 425–511. [Google Scholar] [CrossRef]
- Scheidenberger, C.; Pshenichnov, I.A.; Sümmerer, K.; Ventura, A.; Bondorf, J.P.; Botvina, A.S.; Mishustin, I.N.; Boutin, D.; Datz, S.; Geissel, H.; et al. Charge-changing interactions of ultrarelativistic Pb nuclei. Phys. Rev. C 2004, 70, 014902. [Google Scholar] [CrossRef]
- Gaimard, J.J.; Schmidt, K.H. A reexamination of the abrasion-ablation model for the description of the nuclear fragmentation reaction. Nucl. Phys. A 1991, 531, 709–745. [Google Scholar] [CrossRef]
- Prim, R.C. Shortest connection networks and some generalizations. Bell Syst. Tech. J. 1957, 36, 1389–1401. [Google Scholar] [CrossRef]
- Cormen, T.H.; Leiserson, C.E.; Rivest, R.L.; Stein, C. Introduction to Algorithms; MIT Press: Cambridge, MA, USA, 2009; pp. 624–642. [Google Scholar]
- Hauger, J.A.; Warren, P.; Albergo, S.; Bieser, F.; Brady, F.P.; Caccia, Z.; Cebra, D.A.; Chacon, A.D.; Chance, J.L.; Choi, Y.; et al. Multifragmentation of the remnant produced in the reaction of 1A GeV gold with carbon. Phys. Rev. C 1998, 57, 764–783. [Google Scholar] [CrossRef]
- Viola, V.E.; Kwiatkowski, K.; Natowitz, J.B.; Yennello, S.J. Breakup densities of hot nuclei. Phys. Rev. Lett. 2004, 93, 132701. [Google Scholar] [CrossRef]
- Natowitz, J.B.; Hagel, K.; Ma, Y.; Murray, M.; Qin, L.; Shlomo, S.; Wada, R.; Wang, J. Caloric curves and nuclear expansion. Phys. Rev. C 2002, 66, 031601. [Google Scholar] [CrossRef]
- De, J.N.; Samaddar, S.K.; Viñas, X.; Centelles, M. Nuclear expansion with excitation. Phys. Lett. B 2006, 638, 160–165. [Google Scholar] [CrossRef][Green Version]
- Allison, J.; Amako, K.; Apostolakis, J.; Arce, P.; Asai, M.; Aso, T.; Bagli, E.; Bagulya, A.; Banerjee, S.; Barrand, G.; et al. Recent developments in Geant4. Nucl. Instrum. Methods A 2016, 835, 186–225. [Google Scholar] [CrossRef]
- Weisskopf, V. Statistics and Nuclear Reactions. Phys. Rev. 1937, 52, 295–303. [Google Scholar] [CrossRef]
- Fermi, E. High Energy Nuclear Events. Prog. Theor. Phys. 1950, 5, 570–583. [Google Scholar] [CrossRef]
- Trautmann, W.; Adloff, J.C.; Begemann-Blaich, M.; Bouissou, P.; Hubele, J.; Imme, G.; Iori, I.; Kreutz, P.; Kunde, G.J.; Leray, S.; et al. The rise and fall of multifragment production in 197Au + C, Al, and Cu reactions at E/A = 600 MeV. Nucl. Phys. A 1992, 538, 473–481. [Google Scholar] [CrossRef]
- Cherry, M.; Dabrowska, A.; Deines-Jones, P.; Holynski, R.; Jones, W.; Kolganova, E.; Olszewski, A.; Sengupta, K.; Skorodko, T.Y.; Szarska, M.; et al. Fragmentation and multifragmentation of 10.6 A GeV gold nuclei. Phys. Rev. C 1995, 52, 2652. [Google Scholar] [CrossRef]
- Abelev, B.; Adam, J.; Adamova, D.; Adare, A.M.; Aggarwal, M.M.; Aglieri Rinella, G.; Agnello, M.; Agocs, A.G.; Agostinelli, A.; Ahammed, Z.; et al. Centrality determination of Pb-Pb collisions at TeV with ALICE. Phys. Rev. C 2013, 88, 044909. [Google Scholar] [CrossRef]
- Barrette, J.; Bellwied, R.; Bennett, S.; Bersch, R.; Chang, W.C.; Cleland, W.E.; Clemen, M.; Cole, J.D.; Cormier, T.M.; Dai, Y.; et al. Light fragment yields from central Au+Au collisions at 11.5A GeV/c. Phys. Rev. C 2000, 61, 044906. [Google Scholar] [CrossRef]
- Bleicher, M.; Hillmann, P.; Reichert, T.; Steinheimer, J.; Sombun, S.; Herold, C.; Limphirat, A.; Yan, Y. Transport model calculations of deuteron production in relativistic hadron and heavy-ion collisions. Astron. Nachr. 2019, 340, 977–982. [Google Scholar] [CrossRef]
- Gaebel, V.; Bonne, M.; Reichert, T.; Burnic, A.; Hillmann, P.; Bleicher, M. Understanding the energy dependence of B2 in heavy ion collisions: Interplay of volume and space-momentum correlations. Eur. Phys. J. A 2021, 57, 1–7. [Google Scholar] [CrossRef]
- Sosin, Z.; Błocki, J.; Kallunkathariyil, J.; Łukasik, J.; Pawłowski, P. Alpha-cluster model of atomic nuclei. Eur. Phys. J. A 2016, 52, 1–12. [Google Scholar] [CrossRef][Green Version]
- Wang, X.; Dong, G.; Gao, Z.; Chen, Y.; Shen, C. Tetrahedral symmetry in the ground state of 16O. Phys. Lett. B 2019, 790, 498–501. [Google Scholar] [CrossRef]
- Brewer, J.; Mazeliauskas, A.; van der Schee, W. Opportunities of OO and pO collisions at the LHC. arXiv 2021, arXiv:2103.01939. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).