Direct-Channel Option of the Forward Slope Increase

Abstract

The LHC data on the elastic scattering indicate that the forward slope increase is not consistent with the contributions of the simple Regge poles only with the linear Regge trajectories. The dynamics might be associated with unitarization in the direct channel of reaction. We discuss the problems of the Regge model and provide a respective illustration of the direct-channel option.

1. Introduction and Problems with Forward Slope Increase Revealed at the LHC

The recent LHC measurements of the differential cross-section of $pp$-scattering have revealed new trends in the forward slope increase. This is a speed up of this steady increase [1,2,3]. A linear logarithmic shrinkage of the diffraction cone at $t=0$ and its relation to the Regge trajectory parameter ${\alpha }^{\prime }\left(0\right)$ (The Regge model predicts the scattering amplitude to have the form $F(s,t)\sim s^{\alpha \left(t\right)}$. The standard assumption of the model corresponds to the choice of the linear trajectories with t-dependence in the form $\alpha \left(t\right)=\alpha \left(0\right)+{\alpha }^{\prime }\left(0\right)t$.) was an evident success of the Regge model application to the relativistic hadron scattering (cf. e.g., [4]). All the secondary Regge trajectories have different values of intercepts ${\alpha }_{R{}_i}\left(0\right)$ (${\alpha }_{R_i}\left(0\right)-1<0$) but positive and approximately the same values of ${\alpha }_{R_i}^{\prime }\left(0\right)\simeq 0.9$${(GeV/c)}^{-2}$, i.e., the trajectories are linear and almost parallel (see, for a recent review, [5]). The Pomeron trajectory has been introduced to reconcile the Regge model with the experimental data on the total cross-sections. Currently, this trajectory has an intercept ${\alpha }_P\left(0\right)-1>0$ and positive slope ${\alpha }_P^{\prime }\left(0\right)\simeq 0.25$${(GeV/c)}^{-2}$ or even less [6], i.e., it is significantly lower than ${\alpha }_R^{\prime }\left(0\right)$. Since ${\alpha }_P\left(0\right)-1>0$, the respective model amplitude needs to be unitarized. Absence of unitarization would lead to the conflict of the partial amplitude magnitude at high energies with the unitarity limit.

The main assumption of the Regge model is an unjustified replacement of the whole amplitude by its asymptotic form in the cross channel. This is reformulated as the statement that asymptotic amplitude analytically continued from the cross-channel will give asymptotics of the amplitude in the direct channel of the reaction.

It appeared that the actual rate of the diffraction cone parameter

$$B\left(s\right)\equiv \frac{d}{dt}ln\frac{d\sigma }{dt}{|}_{t=0}$$

(1)

growth exceeds the linear logarithmic extrapolation to the LHC energy range. In Equation (1), $d\sigma /dt$ is a differential cross-section of the proton–proton elastic scattering. To bring the Regge model closer to the experiment on the diffraction cone slope growth rate, it has been suggested that the slope of the Pomeron trajectory ${\alpha }_P^{\prime }\left(0\right)$ is an energy-dependent function (cf. [7]). Such a dependence can reflect the negative contribution of absorption correction due to increasing contribution of multi-Pomeron exchanges. It might also be due to Odderon presence [8], while complication of the Regge model in the form of Dipole Pomeron itself does not help [9].

Regarding the possible form of transition from a linear logarithmic dependence

$$B\left(s\right)=B_0+2{\alpha }_P^{\prime }\left(0\right)lns$$

of the Regge model with poles only in the region of the Pomeron dominance to the asymptotic ${ln}^{2}s$ dependence [10], the following observation should be mentioned here. The use of function

$$B\left(s\right)=B_0+Alns+C{ln}^{2}s$$

(2)

to fit the data provides a negative or zero value for the factor A [7],

$$A\le 0,$$

and therefore leads to the problems with its consideration as the Pomeron trajectory slope ${\alpha }_P^{\prime }\left(0\right)$ inherited from the Regge-pole model. The use of nonanalytic functions for description of $B\left(s\right)$ (hints for a possible threshold energy dependence of $B\left(s\right)$ are given in [3]) can preserve a positive factor in front of $lns$ term but requires extra justifications for a nonanalytical form of the scattering amplitude.

Even putting aside these fits, one should note that there is another problem regarding the Regge model predictions in the whole energy range. Namely, many papers suggest that the secondary Regge trajectories give a negligible contribution to the elastic amplitude and the Pomeron contribution is the only significant one at the LHC energies. Moreover, it has been claimed that a contribution of the secondary trajectories can already be neglected at lower energies of $\sqrt{s}\sim 100$ GeV [7].

The latter statement on the Pomeron dominance proceeds from the analysis of the total cross-sections data. However, since the Pomeron trajectory has a significantly lower slope ${\alpha }_P^{\prime }\left(0\right)$ compared to ${\alpha }_R^{\prime }\left(0\right)$ and conclusions on vanishing contributions of the secondary trajectories inevitably leads to associated prediction of the slowdown of $B\left(s\right)$ increase in the energy range where the Pomeron starts to dominate. Thus, the Regge-pole model predicts a break of $B\left(s\right)$ due to vanishing secondary poles’ contributions and transition to the regime

$$B\left(s\right)=B_0+2{\alpha }_R^{\prime }\left(0\right)lns$$

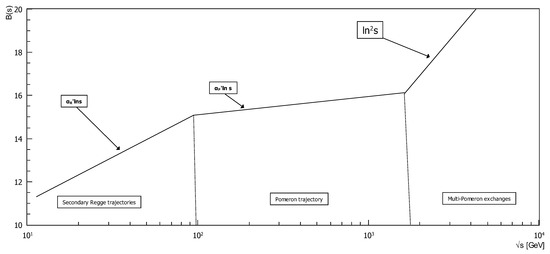
at low energies (Note that ${\alpha }_R^{\prime }\left(0\right)/{\alpha }_P^{\prime }\left(0\right)\simeq 4$). Schematically, the predicted regimes in the energy dependence of $B\left(s\right)$ can be depicted at Figure 1.

The break in $B\left(s\right)$ in the region of$\sqrt{s}\simeq 100$ GeV should be treated as a signal of the Pomeron dominance, but such a break has not been observed yet (see [3]). (This conclusion assumes an approximate equality of the diffraction cone slopes of $pp$ and $\overline{p}p$ elastic scattering in the energy range between CERN ISR and the LHC.).

To this end, there is a problem regarding agreement of the whole set of data for the forward slope of the $pp$ elastic scattering differential cross-section with the Regge model predictions. The main point of this note is to make a statement on its existence.

The resolution of the Regge case might be a twofold one. First, the energy range between CERN ISR and the LHC should be thoroughly scanned experimentally with higher statistics without an assumption on the approximate equality of $pp$ and $\overline{p}p$ diffraction cone parameters. This is correlated with the searches for possible signals of the Odderon contributions to the scattering amplitude (cf. [11,12] and references therein). Evidently, it would be interesting to perform experimental studies of the cross-sections difference $\Delta {\sigma }_{tot}\left(s\right)\equiv {\sigma }_{tot}^{\overline{p}p}\left(s\right)-{\sigma }_{tot}^{pp}\left(s\right)$ in the unexplored energy region to extract a possible nonvanishing contribution of the Odderon at $t=0$.

Recent experimental results on Odderon effects are based on the combined analysis of the D0 and TOTEM Collaborations results [13]. This analysis considers the LHC data set at $t=0$ together with Tevatron data set in the dip region ($-t>0$) and assumes that the same object (Odderon) gives contributions into the scattering amplitude in both of the different regions of t. It also neglects a possible role of spin dependence.

Another solution of the above qualitative discrepancy is the use of an approach supposing an alternative origin of the diffraction cone slope $B\left(s\right)$ growth due to unitarization of an input amplitude in the direct channel. We further illustrate such possibility using a specific form of unitarization.

2. Unitarization and Forward Slope Increase

The form of the input amplitude can be obtained using its asymptotics in the region of large l–values. This procedure is quite similar to taking the Regge-form of the scattering amplitude.

To demonstrate this possibility, we have considered a wide class of the geometrical models [14,15]. These models presuppose a factorized form of the input amplitude. The input amplitudes of these models have an energy independent slopes of the diffraction cone and its unitarization generates the respective energy dependence. The Regge-type models for the input amplitude do not allow clear separation of the unitarity effects since the logarithmic forward slope parameter increase is implied ab initio in the input amplitude.

The slope associated with the interaction radius increases at low and moderate energy values, where the total cross-section does not demonstrate any increase yet [16]. Growth of the forward slope of a diffraction cone is another reason for unitarization in geometrical approaches, and this serves as an argument for unitarization at low and medium energies. The results are found to be common for different unitarization schemes. For definiteness, we consider here the one based on the U-matrix form of the scattering amplitude (see for more details [17] and references therein).

The relation of the scattering amplitude $f(s,b)$ (Here, the variable b denotes a collision impact parameter) with the input quantity $u(s,b)$ in the U–matrix approach (pure imaginary case, $f\to if$, $u\to iu$) (Note that saturation of the unitarity relation, i.e., when $\mathrm{Im}f(s,b)\to 1$ at $s\to \infty$ and b–fixed, implies $\mathrm{Re}f(s,b)\to 0$) in the impact parameter representation has a rational form:

$$f(s,b)=u(s,b)/[1+u(s,b\left)\right].$$

(3)

It can easily be inverted

$$u(s,b)=f(s,b)/[1-f(s,b\left)\right].$$

(4)

Let us first consider the domain of fixed values of s and large increasing impact parameters b. A factorized form should be valid in this limit for the function $u(s,b)$ since

$$f(s,b)\simeq g\left(s\right)exp(-\mu b)$$

and

$$u(s,b)/f(s,b)\to 1$$

(5)

in this region. Assuming that such form for $u(s,b)$ takes place at finite impact parameter values, one arrives to Equations (7) and (8) that follow.

Then, to get an idea on the energy dependence of $u(s,b)$, we evaluate energy dependence at $s\to \infty$ and fixed b. Assuming saturation of the unitarity limit $f\to 1$ at $s\to \infty$, we obtain $u(s,b)\to \infty$. This assumption corresponds to the principle of maximal strength of strong interactions proposed long ago by Chew and Frautchi [18]. Thus, the limiting behavior $u(s,b)\to \infty$ at $s\to \infty$ and b-fixed corresponds to application of the principle of maximal strength in this approach.

A general expression for the function $u(s,b)$ can be written as the ratio of elastic and inelastic distribution functions [19]:

$$u(s,b)={\sigma }_{el}(s,b)/{\sigma }_{inel}(s,b).$$

(6)

Equation (6) characterizes relative spacial distribution of the elastic and inelastic interactions. Central impact parameter dependence of the function $u(s,b)$ implies central character of the elastic scattering and its domination over the inelastic interactions at a small and vanishing ratio ${\sigma }_{el}(s,b)/{\sigma }_{inel}(s,b)$ at large impact parameters. Conclusions on the central character of the elastic scattering is quite general and is not connected with a particular unitarization scheme used [17]. The geometrical models use a factorized form of the input amplitude, i.e., the function $u(s,b)$ is taken as a product:

$$u(s,b)=g\left(s\right)\omega \left(b\right),$$

(7)

where dependence $g\left(s\right)\sim s^{\lambda }$ can be associated with the effective rate of the kinetic energy to mass conversion [20,21,22]. This mass conversion rate reflects increasing contribution with energy of the newly opened inelastic channels into the input amplitude $u(s,b)$. Its power-like dependence corresponds to the polynomial boundedness of the function $u(s,b)$ which does not include elastic channel contributions [23].

As it was noted above, the function $\omega \left(b\right)$ is taken in the form to be consistent with the analyticity of the scattering amplitude in the Lehmann–Martin ellipse (see [24])

$$\omega \left(b\right)\sim exp(-\mu b).$$

(8)

Of course, this conjecture is the simplest option for the function $\omega \left(b\right)$. There are no reasons besides simplicity to expect that a function is to be identical with its asymptotics. The $u(s,b)$ can also be treated as a convolution of the two matter distributions $D_1\otimes D_2$ of the colliding hadrons having respective impact parameter dependencies [25].

Unitarization adjusts energy behavior of $B\left(s\right)$ to the experimental odservations. It has been shown that the resulting energy dependence of the diffraction cone slope is consistent with the data and can be described up to the LHC energies by a power–like preasymptotic function [14]. It can be estimated that $\sqrt{s}\simeq {10}^4$ GeV is the beginning of the transition energy region to asymptotics. The parameter $B\left(s\right)$ has the following asymptotic behavior

$$B\left(s\right)\sim {ln}^{2}s$$

(9)

which replaces a power-like dependence in the limit of $s\to \infty$. The transformation of these two dependencies is provided by the unitarization procedure [15].

Thus, unitarity plays an essential role at the LHC energies and the observed speeding up of the slope B shrinkage can be qualitatively explained as follows. The slope B is related to the average

$$2B={\langle b^2\rangle }_{tot}\equiv {\int }_0^{\infty }{b}^{3}db{\sigma }_{tot}(s,b)/{\int }_0^{\infty }bdb{\sigma }_{tot}(s,b)$$

and a major contribution to the interaction radius ${\langle b^2\rangle }_{tot}$ at the LHC energies is given by the inelastic interactions since the ratio ${\sigma }_{inel}/{\sigma }_{tot}\ge 2/3$. Speed up of the B increase at the LHC is a combined effect of a steady increase of ${\sigma }_{inel}$ and reaching the maximal value of the inelastic overlap function $h_{inel}$ allowed by unitarity. Indeed, the inelastic overlap function $h_{inel}(s,b)$ is very close to its limiting value $h_{inel}^{max}=1/4$ in the region of small and moderate impact parameters: $0\le b\le 0.4$ fm at the LHC energy $\sqrt{s}=13$ TeV [26,27]. Deviation of $h_{inel}$ from its maximal value is small and negative in this region of impact parameters and the following inequalities take place:

$$h_{el}>1/4>h_{inel},$$

where $h_{el}$ is the elastic overlap function and its deviation from $1/4$ is also small but positive. The unitarity relation in the impact parameter representation written in terms of the overlap functions $h_i(s,b)$ has the following form:

$$h_{tot}(s,b)=h_{el}(s,b)+h_{inel}(s,b).$$

The unitarity stops growth of the inelastic interaction intensity in vicinity of $b=0$ and further increase of ${\sigma }_{inel}$,

$${\sigma }_{inel}=8\pi {\int }_0^{\infty }bdb{h}_{inel},$$

becomes only possible due to proliferation of the inelastic interactions into the region of higher impact parameter values with the respective acceleration of the slope parameter B increase.

There is also an enhancing effect connected with peripheral form of the inelastic overlap function developed with the energy growth. Therefore, one obtains an extra augmentation of the speed of B growth due to contribution of emerging reflective scattering mode [28] (aka hollowness) associated with the hadron structure having a central core [17].

3. Conclusions

The available experimental results indicate their inconsistency with the Regge model predictions. We have discussed the Regge model problems with an unobserved break in the energy dependence of the slope parameter in this regard. This is one but not the only reason to address the models of a different, e.g., geometrical origin.

The increasing behavior of the diffraction cone forward slope with energy is illustrated here considering it as a result of unitarization of the input explicit form which is prescribed by the geometrical models when the forward slope of the input amplitude does not depend on energy.

The measurements of B at the LHC and their proposed interpretations make similar measurements in $pp$-scattering even at higher energies as well as at lower energies very promising for the studies of soft hadron interaction dynamics.