Abstract
This paper reviews the main experimental techniques and the most significant results in the searches for the , and decay modes. Efforts related to the study of these decay modes are important, since they can potentially offer complementary information with respect to the cases of decays, which allow a better constraint of models for the nuclear structure calculations. Some positive results that have been claimed will be mentioned, and some new perspectives will be addressed shortly.
1. Introduction
The double beta decay (DBD) is a powerful tool for studying the nuclear instability, the electroweak interaction, the nature of the neutrinos, and physics beyond the Standard Model (SM) of Particle Physics. The theoretical interpretations of the double beta decay with the emission of two neutrinos is well described in the SM; the process is characterized by a nuclear transition changing the atomic number Z of two units while leaving the atomic mass number A unchanged. According to the Weizsäcker mass formula [1], the double beta decay can proceed between two even-even nuclei. Reference [2] initially discussed the theoretical description of the double beta decay; four kinds of DBD decay modes are possible. In particular, the DBDs predicted from the SM are:
In the case of a DBD decay with the emission of two neutrinos, the half-life () is given by the formula (see e.g., Reference [3]):
where: (i) the function is the result of the integration in the phase space of the leptons; (ii) is the energy difference between the initial and final states; (iii) the matrix elements and contain the nuclear structure information for Gamow–Teller and Fermi transitions; and, (iv) and are the vector and axial-vector weak interaction effective coupling constants.
On the other hand, DBD modes without the presence of neutrinos are possible beyond the SM and, if observed, they will open windows on new physics [4,5,6,7,8,9,10]. The half-life of a neutrinoless DBD can parameterised by the following formula (using the formalism presented in Reference [11]):
where: (i) the function is the result of two-electron phase space integration; (ii) the nuclear matrix elements and contain the nuclear structure information for Gamow–Teller and Fermi transitions for the case of neutrinoless emission; and, (iii) is the Majorana effective mass definition for the electronic neutrino:
where are the masses of the neutrino eigenstates; , are the Majorana phases; and, are the electronic neutrino elements of the PMNS mixing matrix [12].
Among the many theoretical frameworks, an interesting one is the case of weak interactions with the right-handed lepton current. In this case, while assuming , , and as three new coupling constants, the effective general Hamiltonian is [11]:
where and are the lepton and quark left- (right-) handed currents, respectively, and is the Fermi constant. Thus, combining the contributions from the mass and the right-handed current terms, we have a general formula that has the form [11]:
The functions contain the nuclear matrix elements and phase space integrals (all of the definitions are in Reference [11]); for example, the term is derivable from Equation (2) [11,13]:
Instead, and are the effective values of and over the mixing matrix for left- and right-handed neutrinos (see Reference [11] for their explicit definitions). We emphasize that , , and are quantities that can be evaluated by the analysis of neutrinoless double beta decay experiments.
The nuclear matrix elements contain the wave function of the initial and final even-even nuclear states, but—especially for the calculation of the mode (in the mode the virtual neutrinos have relatively high energy with respect to the average energy transition among the initial and final states and the intermediate states, known as the “closure approximation”. Thus, in the “closure approximation”, only the wave functions of the initial and final states are required. Moreover, the nuclear matrix elements for both and modes are the same)—a sum of all the matrix elements of the intermediate odd-odd nuclear states is also required. Ideally, in order to determine the matrix elements, it is necessary to solve a many-body problem assuming a relativistic nucleon–nucleon interaction and, thus, infer the total wave function. Unfortunately, such a procedure is not practically feasible, and several assumptions and approximations on the nuclear structure and interactions are needed, which affect the evaluation of the matrix elements and the vector and axial-vector form factors. Moreover, some approximations are more efficient for light nuclei than heavy ones, or vice-versa.
Focusing on the Feynman diagrams (see Figure 1), the 2 are topologically equal to the decays; therefore, the differences in the decay rates are dominated by the phase space terms and the mass difference between the parent and daughter nuclei (). However, the positrons emission allows for implementing a mighty signature, especially when coincidence logic is adopted. In perturbation theory, the nuclear matrix elements of the and the decays are of the same order as the decay, but, generally, the phase space is higher (the kinetic energy that is available for each DBD+, where M(A,Z) is the atomic mass of the isotope with mass number A and atomic number Z, is: , , and , where is the excitation energy of the atomic shell of the daughter); thus, the corresponding is lower. Reference [14] lists the 35 isotopes, which can decay through the mode (DBD-) with forbidden or suppressed decay. Typically, they have a larger Q-value with respect to the DBD in positive channels (DBD+) and, thus, a lower half-life.
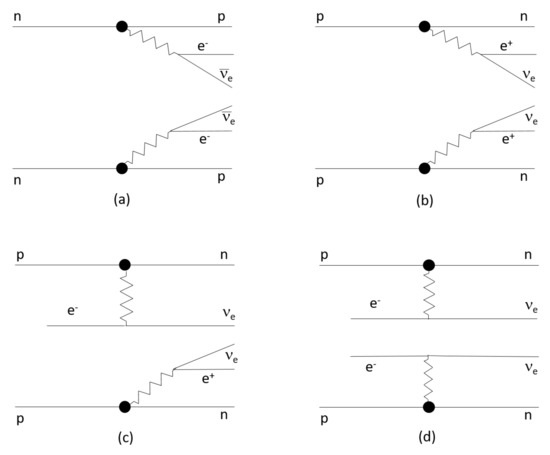
Figure 1.
Leading-order schematic Feynman diagrams for the (a), (b), (c), and (d) decay modes.
However, the 34 DBD+ emitters (as listed in the following Sections and Tables therein) allow us to study the DBD for other nuclei and, thus, test the calculations of a different nucleus shape and decay modes that involve the vector and axial-vector weak effective coupling constants, etc. (see the next Sections). This expands the possibilities of the experimental tests for the achievement of important complementary information. Instead, the case of the mode involves the neutrino mass and new specific theoretical scenarios; but, in some model cases, one can consider the nuclear matrix element as a test case for the modes.
Moreover, several new features arise while assuming either a non-vanishing neutrino mass or lepton number violating () processes. The possible “resonant effect” on the mode when the initial and final states are energetically degenerate is a remarkable example. In this case, the process can profit from an increased counting rate of several orders of magnitude and, in some cases, the sensitivity can approach that of the DBD- (e.g., the case of the resonant transition of Gd →Sm yr) [15]. Actually, the counting rate can increase by a factor if the energetic degeneration between the initial and final states is about 10 keV [16,17,18,19,20,21,22]. Another relevant aspect, with regards to the modes, is that the mutual information from the simultaneous study of positive and negative DBD can constrain the theoretical parameters with very high confidence (see, e.g., Reference [23]).
Furthermore, the DBD without neutrinos emission also breaks the SM accidental symmetry [24]. In theory, where such a global symmetry is spontaneously broken, Goldstone bosons, known as Majorons, can appear. In DBD, three kinds of Majoron models have been proposed: singlet, doublet, and triplet Majoron field. The emission of Majorons can be experimentally inferred by studying the energy spectrum of the SM particles that are emitted during the DBD.
In the case of DBD, adopting a model-dependent framework and assuming the experimental results from the neutrino oscillation experiments, a range of values of effective-DBD-neutrino mass ( [25]) can be obtained as a function of the lightest neutrino mass (see Figure 2). Thus, the experimental limits on the half-lives and, consequently, the limits on , can be compared with the present theoretical expectations.
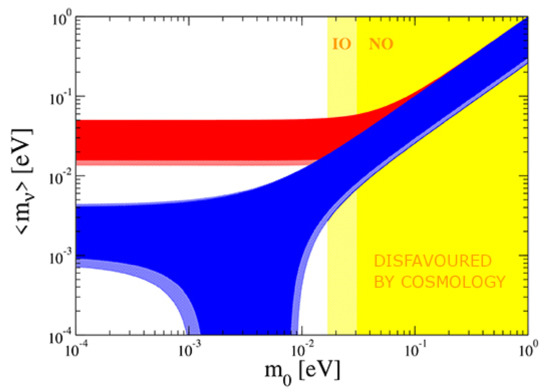
Figure 2.
Predictions on the from neutrino oscillations versus the lightest neutrino mass, , in the two cases of the normal (NO, the on-line blue region) and inverted (IO, the on-line red region) hierarchy of the neutrinos’ masses. The 2 and 3 values of neutrino oscillation parameters are considered. The region that is disfavored by cosmological data ( eV) is presented in (on-line) yellow (>30 meV for the NO and >16 meV for the IO). Reprinted from Reference [25]. The upper limits on inferred by some DBD experiments are: (61–165) meV (KamLAND-Zen, Xe) [26], (75–350) meV (CUORE, Te) [27], (79–180) meV (GERDA, Ge) [28], (0.33–0.62) eV (NEMO-3, Mo) [29], and (1.0–1.7) eV (AURORA, Cd) [30,31].
For all of these arguments, it is very important to evaluate the calculations (matrix elements, coupling constant, CP-phases [32,33], etc.) and the assumptions that are considered in a model via experimental verifications. In addition, having assumed a nuclear model, the nuclear matrix element for the two-neutrino mode differs from the neutrinoless mode, but they are related to each other through relevant parameters. For instance, the g and the strength of the particle–particle interaction in the quasi-particle random-phase approximation model (that is often known by the acronym QRPA) are obtained from the -decay and -DBD measurements [34,35]. Moreover, in the free nucleon interaction, the g value is [36], but, when considering a nuclear decay, there are indications that the phenomenological axial-vector coupling value is reduced at g [37,38,39], more precisely: g or g, depending on the nuclear model adopted to infer the g value [39,40,41]. Thus, DBD investigation with various nuclei would shed new light on constraining these and other important parameters. On the other hand, from an experimental point of view, important developments, in terms of radio-purification, isotopes enrichment, and new detectors, are needed for broadening the study of the DBD, including more potential nuclei.
To this purpose, there are different experimental approaches, such as those that are capable of distinguishing—while properly accounting for the energy resolution—the beta spectrum of the and modes or those that are able to detect the gamma emitted from the excited final states (see also, e.g., Reference [42] for DBDs in excited states and Reference [19] for decay modes).
2. Experimental Techniques to Study the Double Beta Decay in Positive Modes
Three main experimental methods exist for investigating the DBD: geochemical, radiochemical, and direct. The geochemical experiments use double-beta emitters in geological ores and have an advantage in the long geological times during which the daughter nuclei have been accumulated. The DBD parent is usually part of an ore sample from which the atom of a daughter isotope is chemically extracted and analyzed by mass spectroscopy. Such an approach has different possible sources of errors to be carefully considered: the estimation of the ore sample age, possible release of gas in the ore sample, fission or neutron-capture processes, an initial high concentration of daughter nucleus, etc. Moreover, this type of measurement does not allow the separation of the and modes; therefore, the measured decay rate is a global rate that considers all of the possible decay modes and transitions. Historically, the method was initially applied when the daughter was a rare gas, as Se Kr, Te Xe; recently, the technique has also been extended to the case of Ba Xe, Ba Xe.
The radiochemical method uses double-beta emitters, having the daughter nuclei with a shorter decay time than the geochemical experiments. The basic idea utilized in the radiochemical experiments is picking out the produced atoms in the final state (that are radioactive) from a vast amount of target material, concentrating and purifying them, and then finally counting their number through their decay. However, differently from geochemical experiments, some uncertainties—such as estimating the ore sample age, the defection on the retention of the gas in the ore sample, etc.—are less problematic. Nevertheless, as in the previous method, the measured decay rate is a global rate over all the possible decay modes and transitions.
The direct experimental approach allows for the study of the energy spectrum due to the emitted particles in the DBD processes. In this approach, the specific DBD transition can be pointed out. We have two main methods in this contest: one in which the source of the DBD is external to the detector (“source ≠ detector") and the second one in which the “source = detector”. The first one is commonly used to study the gammas that are emitted from a pure sample containing the isotope of interest and/or, in a few cases, the emitted positrons/electrons. Instead, the second one guarantees a very high detection efficiency and the possible exploitation of coincidence techniques among the emitted positrons/electrons and gammas.
We briefly summarize the advantages and problems to be overcome in order to profit from the direct detection approach—besides the theoretical features, which are basically addressed in the previous section—that marks the experimental efforts.
The DBD is an extremely rare phenomenon; thus, a very low background counting rate in the energy of interest is mandatory. The increase of the signal-to-background ratio is of crucial importance. In fact, the experimental half-life in the case of a positive signal is given by:
where T is the measuring time, is the detection efficiency, N is the number of double-beta decaying nuclei, and S is the number of counts attributed to the signal searched for.
If no signal is detected, then the sensitivity of an experiment is usually defined as the minimum half-life compatible with the background fluctuations at a certain C.L. corresponding to a number of sigma, . While assuming that the background counts scale linearly with the mass of the detector, the sensitivity can be written:
where is the isotopic abundance of the double-beta candidate, is the stoichiometric multiplicity of the element containing the DBD candidate, is the Avogadro number, B is the background rate per unit mass and energy, is the FWHM energy resolution (the region where conventionally B is integrated assuming that the signal shape is a peak), and is the compound molecular mass. Thus, there are some crucial key experimental parameters for improving the experimental sensitivity. In addition, when considering the arguments drafted in Section 1, isotopes with high Q-values and large nuclear matrix elements are favored.
In the energy of interest, the main sources of background (that have to be mitigated in all of the experiments concerning rare event investigations; even though, an irreducible background can be present due to the solar neutrino interaction with the detector materials [41,43]) come from:
- cosmic rays: this implies installing the experiment deep underground;
- neutrons that are induced by muons and neutrinos in the rock or by (,n) reactions: a suitable dedicated shield has to be implemented when necessary;
- natural radioactivity due to the U/Th chains, K isotope, Pb, etc.;
- anthropogenic activities, in particular for Cs;
- cosmogenic activation: radio-isotopes that are induced by spallation in the material during their storage at sea level or during transportation; and,
- radio-isotopic activation that is induced by neutron calibration procedures when applied.
Choosing a suitable Deep Underground Laboratory (DUL) is the first condition in achieving the highest sensitivity in ultra-low level detection. The main advantage of a DUL is to reduce the cosmic ray muons flux. Currently, fourteen DULs are operating and three new ones are in construction. The first ones are: Boulby Underground Laboratory (BUL) in UK; Baksan Neutrino Observatory (Baksan) in Russia; Callio Laboratory (CLAB) in Finland; China Jinping Underground Laboratory (CJPL) in China; India-based Neutrino Observatory (INO) in India; Kamioka in Japan; Gran Sasso Underground Laboratories (LNGS) in Italy; Canfranc Underground Laboratory (LSC) in Spain; Modane Underground Laboratory (LSM) in France; Sudbury Neutrino Observatory (SNOlab) in CANADA; Sanford Underground Research Facility (SURF) in USA; Soudan Underground Laboratory (Soudan) in USA; Waste Isolation Pilot Plant (WIPP) in USA; and, Laboratories at the Yangyang pumped storage power plant (Y2L) in South Korea. The DULs under construction are: Agua Negra Deep Experiment Site(ANDES) between Chile and Argentina; Astroparticle Research Laboratory (ARF) in South Korea; and, Stawell Underground Physics Laboratory (SUPL) in Australia. The cosmic ray muons flux in the DULs is shown in Figure 3. The depth, the nature, and the quality of the rock, in terms, for example, of radioactivity, play an important role.
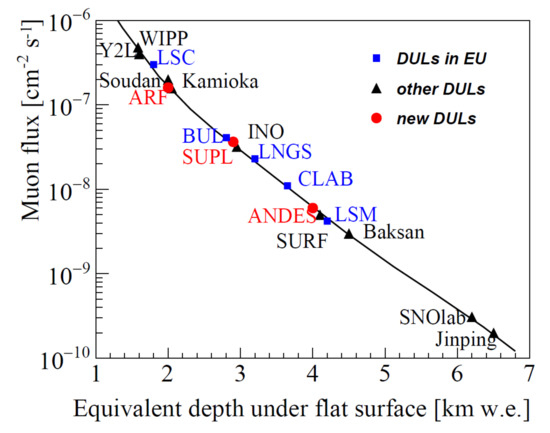
Figure 3.
Cosmic ray muon flux as a function of the overburden of rock in kilometers water equivalent (km w.e.). The DULs are indicated. In particular the DULs operating in Europe are indicated with blue square marker; the DULs operating in the others continents are indicated with black triangles and the DULs under construction are indicated with red circles. Reprinted from Reference [44].
Indeed, exposure of powders, materials, and compounds to the cosmic rays can produce possible non-standard cosmogenic contaminants. In fact, during the powders storage, the crystal growing, or the handling at sea level, radioactive isotopes can be generated by cosmic rays’ interactions. The same is for the shielding compounds or for the materials that are used to build the experimental infrastructure. In general, it is good practice to wait for the decay of the short-life cosmogenic isotopes before starting the measurements. Figure 4 shows an example of the activation processes at sea level and the subsequent decay in underground site.
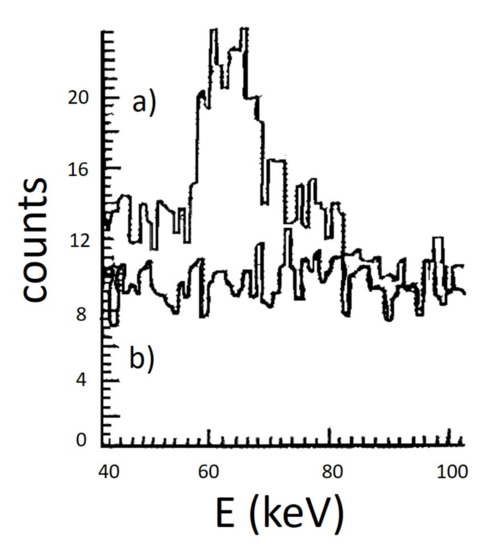
Figure 4.
An example of activation at sea level: the energy spectrum collected at LNGS with a NaI(Tl) detector just stored underground (a) and eight months later (b). The role of keV peak due to I ( days) activation at sea level is evident. Reprinted from Reference [45].
From the muons surviving the coverage of an underground laboratory—typically the flux is of a few ’s m h at m water equivalent depth—either can have direct interactions in the experimental set-up or can produce in the surroundings and/or inside the set-up secondary particles, such as fast neutrons, ’s, electrons, spallation nuclei, etc. Such direct or indirect events are a potential background for low counting rate experiments, such as those in DBD investigation. Thus, in order to moderate the surviving muons in the DBD experiments, a good strategy is to use a multi-detector set-up to identify their passage by topological methods. In some cases, a muon veto could be used, especially if the detector area is very wide or the underground laboratory’s depth is not enough. Instead, the background event due to the neutrons emerging from the surrounding rock can be mitigated by a moderation material (rich in nuclei with light atomic mass) plus a shielding material with a high cross-section for thermal neutron capture, such as, e.g., cadmium, gadolinium, boron, etc. Typically, the overall neutron flux in underground laboratories is of the order of cm s [46].
A significant background contribution would come from radio-isotopes into the detector itself. Figure 5 shows an example of such a background; in particular, the energy spectrum of events due to the radio-nuclides of the U/Th chains inside a CdWO detector is shown [47]. The authors report how the radioactive contamination of a sample of CdWO crystal scintillator by thorium was reduced by a factor , down at the level of 0.01 mBq/kg (Th), and the total activity of uranium and thorium daughters was reduced by a factor , down to 1.6 mBq/kg, by exploiting a re-crystallization procedure. The application of chemical/physical purification procedures is another important aspect for reducing the internal contamination in both a sample and detector. These techniques are in continuous development. In particular, the initial material—often obtained from a commercial site—is purified or further purified by exploiting different techniques (depending on the compound in use) as electron-beam melting, chemical separation, micro-distillation, and many others. Some examples, among these techniques, are discussed in [30,31,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62] and the references therein. Moreover, the neutron calibrations—if any—can activate new radioactive isotopes, e.g., by neutron-capture or spallation processes with the material of the detectors and its frame/structure. Such a type of calibration is strongly disfavored in the DBD set-up.
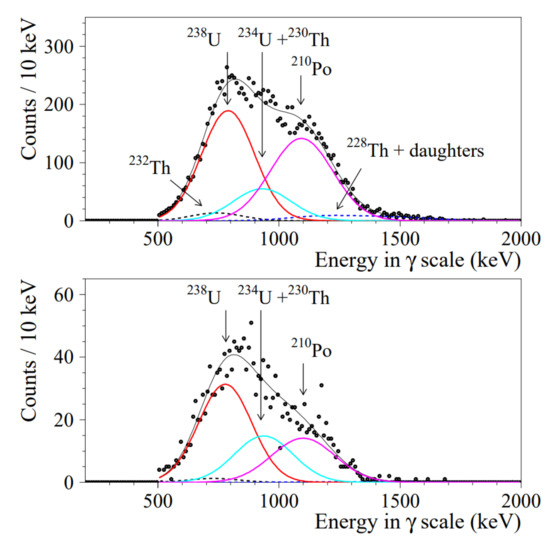
Figure 5.
An example of the effect of the re-crystallization procedure in order to reduce the radioactive contamination of a detector to improve a double beta decay experiment’s sensitivity. In particular, (color on-line) the energy spectra of events that were selected by the pulse-shape discrimination from the data that accumulated in the low-background set-up with a CdWO crystal scintillator before (top) and after the re-crystallization (bottom) are shown. Reprinted from Reference [47].
The most commonly considered detectors in DBD experiments are: (i) semiconductor detectors, (ii) scintillation detectors, (iii) ionization chambers, (iv) bolometric detectors, and their possible combinations (in addition, passive experiments, also utilizing the kinds of detectors listed above, are built as tracking detectors. It is the case, e.g., of SuperNEMO [63] or ELEGANT [64] that, nevertheless, are focusing on the DBD-). In many applications, solid detector medium is of great advantage, thanks to the high-density with respect to gaseous and liquid media. These are the cases of semiconductor, crystal scintillation, and bolometric detectors. In particular, semiconductor detectors offer high energy resolution, and germanium diodes are widely used in the DBD experiments. This detector type provides the possibility to study the DBD of process in Ge, where the source and detector are the same. Nevertheless, germanium-diodes are widely used as a gamma spectrometer in DBD experiments to excite levels of daughter nuclei and in a more general manner in the case of DBD+. In the former case and when considering a ground-state transition, only the two electrons’ sum energy is measured. In the second case, instead, the X-rays and/or -rays coming out of the DBD+ and the quanta that are emitted from the positron annihilation can be measured. In the latter case, the thickness of dead layer can play a crucial role in the energy threshold: the crossed dead layer strongly suppresses the - or X-rays flux at low energy and, thus, the detection efficiency is poor. At the moment, the most used type of germanium detectors is the high pure germanium diode (HP-Ge) operating at cryogenic temperature. Other attempts to perform semiconductor experiments concern the use of CdTe or CdZnTe detectors that allow for the operation at room temperature [65,66]. In this case, there are seven possible DBD emitters, but, at present, the technology seems to not yet be mature.
Many other DBD emitters can be used in solid (or liquid) scintillator detectors (also taking advantage of the possible “source = detector” approach). Typically, the energy resolution (especially for liquids) is worse than in the ionization detectors; however, the technique offers several other advantages: the availability of many nuclei to be used as target, the possibility to operate at room temperature, a high duty cycle, high operation stability, often no environmental impact, etc. In addition, there is also great interest in many other different applications. For example, the NaI(Tl) scintillator is being used to the search for solar axions, possible charge non-conservation processes, matter stability, rare nuclear decay modes, exotics in cosmic rays, DM, and others [67,68,69,70,71,72,73,74,75,76,77]. Moreover, low background crystal scintillators are being used for a long time in rare and decays (see e.g., [78]). Hoverer, a very wide choice of scintillators is available for DBD experiments, such as CdWO (due to Cd, Cd, Cd, Cd, W, W), CaMoO (due to Mo), and their enrichments (such as Cd, Cd and Mo) [31,79,80,81,82,83,84]. Meanwhile, new developments on scintillation materials, like CeCl, CeF, and SrI(Eu), gave encouraging results [85,86,87,88,89,90]. Efforts are also in progress regarding further improvements of BaF, BaWO, ZnWO, CaWO, CaMoO, CdWO, CaF, BGO, LiF, PbWO, PbMoO, and CsHfCl, see e.g., [51,52,53,58,91,92,93,94,95,96,97,98,99,100,101,102,103,104]. Moreover, as other example, rare-earth-doped scintillators (CaF(Eu), LaCl(Ce), etc.) or scintillators, such as CdWO and CaWO, are used to study very specific nuclear rare processes [105,106,107,108]. Extensive literature on historical benchmarks and the industrial production of crystals is available, see, e.g., [51,52,58,85,86,87,88,89,90,91,92,93,94,95,96,97,98,99,100,101,102,103,105,106,107,108,109,110,111,112,113,114,115,116,117,118,119].
A case apart concerns the liquid scintillators as liquid noble gases. Liquid noble gas detectors have been proposed and used in different research fields for more than forty years [120,121,122,123,124,125,126,127,128,129,130,131,132,133,134,135,136,137,138,139,140,141]. In particular, the application of liquid xenon as a pure scintillator in direct Dark Matter particle investigations dates back to 1990 with the pioneering work conducted by DAMA/LXe [124,127,128,129,130,131,132,133,134,135,136,137] and later one by the UK coll. [142]. The liquid noble gases have also been used to study double beta decay in Xe, Xe, and Xe (see, e.g., [135,136,137,143,144,145,146] and the References therein). Nevertheless, the use of liquid noble gases, especially at low energy, can encounter a number of technical and performance difficulties, in terms of energy resolution, light yield, efficiency, light collection and stability, linearity response, rejection procedure, etc., as reported, for example, in [122,123,138,147,148,149,150,151] and the References therein. The noble gases have also been considered in either gaseous detectors or two-phase liquid/gaseous detectors, combining the scintillation and ionization responses. These latter experiments are mostly built in the form of time projection chambers (TPC), where the DBD emitter is either the noble gas itself (e.g., Xe) or included in liquid scintillators. As already mentioned, the main disadvantages regard the worse energy resolution and stability of the large number of apparatus features (especially in a very large detector).
The cryogenic solid calorimeter is another technique exploited in the DBD, whose detectors are also known as bolometric ones [152]; these detectors work at approximately 10 mK, and the energy resolution is typically very good. Nevertheless, they pay some difficulty in the apparatus stability at that temperature, microphonic problems, etc. [153,154,155,156]. Reference [42] reports examples of such detectors in the DBD sector.
In all of the experimental techniques, the natural abundance of the isotope of interest is a common problem. In the Tables of the next Sections, the natural abundance () of all DBD+ emitters is listed. In particular, Ca, Ni, and Zn have a very high natural abundance > 40%; Cr, Fe, Mo, and Ru have ; Pd, Cd, Sm, and Er have % and all other isotopes have a very low natural abundance, . Thus, the isotopic enrichment is often a critical experimental requirement.
The modern techniques for isotopic enrichment have their origin in the developments to separate the U. In fact, apart from the oldest method known as calutrons (usable for a small sample: a few grams), the gas centrifugation is one of the most adopted techniques, which requires—to be implemented—a stable hexafluoride gaseous compound for the element of interest. An alternative method uses a high-power laser to preferentially ionize the element of interest to remove it using an electric field. The molecular laser isotope separation is a hybrid technique between the two previous ones that operates on a gaseous hexafluoride compound as an alternative to centrifugal gas separation. Finally, the so-called isotopic distillation is another common technique [157,158].
Besides all of these points, the use of simulations and the control of key parameters to extract accurate and reliable measures and uncertainties from the data analysis are crucial aspects to consider [159]. These methods are usually dependent upon experimental techniques, but we can underline some general aspects. The Monte Carlo method is widely used to estimate the presence of some contaminants. It can profit from the preliminary screening of the materials to estimate the abundance of some radio-nuclides, but, in any case, strong assumptions regarding their distribution into the detectors and the housing are required. Thus, it is practically impossible to precisely know the background events distribution. However, while assuming to know the shape of the pulses that are searched for (as in the case of events with respect to the ones), procedures adopting the Pulse Shape Discrimination (PSD) method can be helpful in the statistical reduction of the background, especially at relatively high energy where the PSD is more effective. Another technique for tagging quite fast sequences of correlated events is the so-called Time-Amplitude Analysis (see e.g., Reference [80] and the references therein). Other key aspects are the control of the stability of important parameters that can affect the energy scale and detection efficiency; they are, e.g., the temperature, the light-yield, the self-absorption of the light scintillation, the gain of PMT or sensors in general, the contaminant dispersion in the experimental environmental or in the liquid/gaseous detectors, etc.
2.1. Examples of Energy Distributions in Case of an Experiment of DBD+ with “Source = Detector”
When considering a DBD- in mode, the energy spectrum of the two electrons’ energy sum has a continuum shape with an endpoint at due to neutrinos carrying part of the energy away. In the mode, the spectrum is a delta at energy. Typically, a calorimetric experiment for DBD- with an active source has size and density dimensions significant enough to stop the emitted electrons; thus, the energy spectrum is broadened due to the detector’s energy response. Instead, in the case of DBD+, the energy spectrum that is convoluted with the detector response is more complicated, due to the gamma quanta that are emitted by the positron(s) annihilation and/or the emission of X-rays following electron capture. This section briefly describes the energy distributions while considering some DBD+ transitions (adopting the active source approach) to emphasize the differences in the case of a DBD- transition. In particular, we simulate some DBD+ processes in Cd that occur in a cadmium tungstate crystal scintillator enriched in Cd at 66% (CdWO), with a cylindrical shape, size of Ø27 mm × 50 mm, and mass of 215.4 g [160]. The energy resolution—as measured in dedicated calibrations (see Reference [160])—can be written as: . The Monte-Carlo simulation uses the GEANT4 toolkit [161,162], with the initial kinematics of the decay products being provided by the DECAY0 event generator [163,164]. Thus, the results of the simulation of the DBD+ transitions to the ground state (g.s.) of Pd (, , and , with and without neutrinos) and of the resonant transitions for the case of decay to the excited energy levels of Pd (2718 keV and 2741 keV, respectively), , and electron captures, are reported in Figure 6.
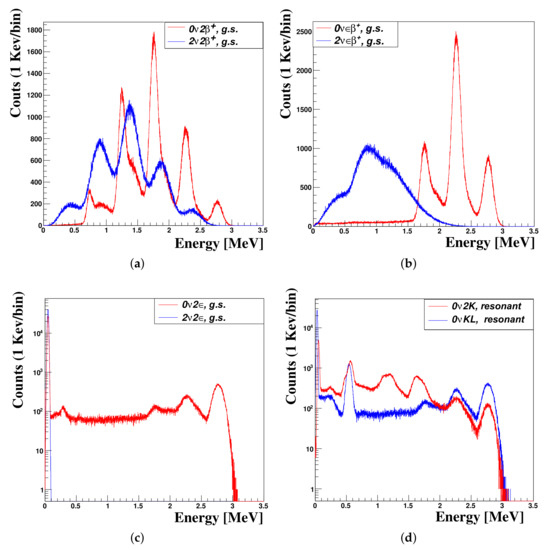
Figure 6.
(Color on-line) Some examples of the simulated response functions of the CdWO detector to , and processes in Cd ( [165]) with and without neutrinos. The structures are due to the gamma quanta detection efficiency, the number of escaping annihilation photons, the presence/absence of the neutrinos, and the possible decay in an excited state of daughter Pd (see text). In the panels (a–d) are respectively reported the energy distributions of the following transitions: and → g.s.; and → g.s.; and → g.s.; and resonants. Reprinted from Reference [160].
In case of the “source = detector” approach the energy distribution of is characterized, while taking the gamma-quanta detection efficiency into account, by five peaks (see Figure 6a) at the energy ( is the electron’s mass) due to the energy deposition of the positrons plus the full deposition of energy of the detected annihilation ’s; and, k is the number of how many annihilation ’s escape the detector. In the mode, the energy distribution is similar to the previous one, but with the following differences: (i) the peak due to positron detection is broadened due to the energy fraction that is carried out by the neutrinos; (ii) the peaks due to the annihilation photons show the same trend as in the mode, but shifted by a quantity of due to the lower mean energy of the positrons.
In the case of decay, the energy distribution is mainly composed of three main peaks (see Figure 6b). In the mode, the average position of the peaks is at , , and . The mode has a similar energy distribution, but with the following important differences: (i) the peaks are enlarged due to the energy that is carried away by the neutrinos; and, (ii) the peaks are shifted of due to the lower energy of the emitted positron; is the bounding atomic energy of the captured electron.
In the mode, the emitted energy () is carried out by the two neutrinos. On the contrary, in the mode, the full energy is carried out by a single bremsstrahlung gamma quanta. Besides this, the energy distributions show two peaks at and , due to the atomic shell re-organization (see Figure 6c, the binding energies of the electrons on the K and L shell are keV and keV, respectively).
Finally, the transition from either or shells in which the released energy is approximatively equal (taking the errors into account) to the two excited energy levels of daughter Pd (in the present case, the energy levels are 2718 keV and 2741 keV, respectively) can show the so-called resonant effect. As before, the lowest energy peak is due to the X-rays/Auger electrons cascades. The peak shown at is given by the absorption of all the energy of the decay. Instead, the intermediate structures are mainly due to the photons coming out the excited state of Pd.
3. Status of Experimental Sensitivities
The most sensitive DBD experiments are decay experiments with the sensitivity at the level of yr and, thus, a sensitivity for the effective Majorana neutrino mass in the range eV is achieved (see, e.g., References [27,28]). The uncertainties are mainly due to the nuclear matrix elements calculations and the assumptions on the nuclear model and the axial-vector coupling constant, as mentioned in Section 1. Instead, the best present sensitivities of experiments for DBD in positive modes are more modest, at the level of yr.
The different experimental sensitivities reached are due, for example, to the progress about the germanium detectors’ developments often used in gamma spectroscopy and in the screening of the materials. Historically, progress and efforts in improving the low-level radioactivity measurements technique have favored studies on the double beta decay of the Ge isotope. This is the case, e.g., of the half-life limits achieved for the of Ge to excited states of Se deduced from the background screening of a passive shield using an HP-Ge detector, as shown in Reference [166]. The present results have profited from a long story of experimental technical improvements, new deep underground laboratories, and an increase in researcher expertise in the sector. Most recently, important efforts are in progress to increase the sensitivity on DBD+ to profit from the advantages that are listed in Section 1.
In the following, the experimental limits and positive claims on half-life of some DBD+ modes are given for both and modes. All of the measured transitions and the experimental techniques are also reported.
3.1. Positive Claims for Some DBD+ Modes
In this Section, we briefly address the few positive claims for the detection of decay in Kr, Xe, Ba, and Ba present in literature. These isotopes can decay to the daughters Se, Te, Xe, and Xe, respectively, by , , , and transitions. In Table 1, we report the results, both positive claims and experimental limits, for those isotopes.

Table 1.
The present best half-lives limits or claims on and DBD+ in Kr, Ba, Ba, and Xe (if not specified, the C.L. of experimental limits is 90%). In the square bracket, the experimental technique is reported: Low background Proportional Counter (LPC), High Pressure Ionization Chamber (HPIC), Geochemical method (GEO), Scintillator detector (S), Liquid Xenon (LXe), and Time Projection Chamber (TPC).
The natural abundance of Kr is 0.355(3)% [167] and its value is 2847.67(26) keV [165] (Figure 7 presents a simplified decay scheme of Kr). The theoretical half-life of DBD+ of Kr decay to the g.s. of Se spreads over a wide range [178,179,180,181,182,183]: – yr for the case and – yr for the and cases. The first positive claim of DBD+ of Kr occurred in 2013 [168] using a low background proportional counter (LPC). The adopted LPC was a cylinder with inner and outer diameters of 140 mm and 150 mm, respectively. A gold-plated tungsten wire of 10 m in diameter was stretched along the LPC axis and it was used as anode. A potential of +2400 V was applied to the wire, and the casing (the cathode) was grounded. The LPC volume was 9.159 L; it was placed inside a shielding of 18 cm of copper, 15 cm of lead, and 8 cm of borated polyethylene layers. The installation was located at the Baksan Neutrino Observatory, INR RAS, (4700 m water equivalent depth), where the cosmic ray flux is lowered by ∼10 times as compared to the flux at sea level. The counter was filled with pure krypton gas (enriched in Kr to 99.81%) up to 4.42 bar having no quenching or accelerating gaseous additions. After a total exposure of 0.343 kg × yr, the authors of Reference [168] quotes a possible hint at 2.5 of statistical significance with a half-life of Kr relative to capture: yr [168]. Later, a comparative study on double electron capture re-estimated the previous value at yr [169] (see Table 1). We also remind the previous limits at the level of – yr set since 1994 [170,184,185].
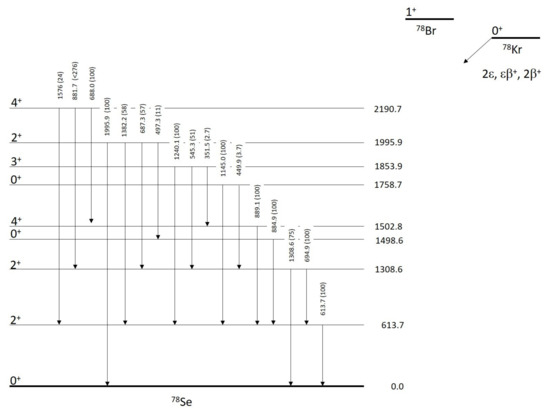
Figure 7.
The simplified decay scheme of Kr to the ground state and to the first excited levels of Se. The energies of the levels (in keV) and relative main branching ratios (in %) are taken from Reference [186].
The natural abundance of Xe is 0.095(5)% [167] and its value is 2863.9(22) keV [165] enough to account for all of the DBD+ modes (Figure 8 presents a simplified decay scheme of Xe). The theoretical half-life of the transition in Xe to the g.s. of Te spreads over a wide range between yr [178,179,187,188,189,190]. Assuming that the two vacancies of the daughter atom are in the K-shell, the Te relaxing emits X-rays and/or Auger electrons with a total energy of E keV [191]. XENON1T is a detector exploiting the primary scintillation in the liquid phase and the secondary proportional scintillation in the gas phase with the limitations addressed in [147,148] and References therein. It uses 3.2 t of ultra-pure liquid xenon (LXe), and 2 t of them are within the sensitive volume of the time projection chamber (TPC): a cylinder of ∼96 cm diameter and height with walls of highly-reflective PTFE that is instrumented with 248 photomultipliers (Hamamatsu R11410-21, with 76.2 mm diameter) in two arrays (top and bottom). Both of the arrays consist of a massive OFHC copper support plate with circular cut-outs for the PMTs. The TPC is surrounded by 74 field-shaping electrodes with a cross-section of ∼10 mm; they are made from low-radioactivity oxygen-free high thermal conductivity (OFHC) copper. The LXe-TPC is encapsulated in a stainless-steel cryostat that is installed inside a 740 m water shield equipped with 84 PMTs deployed on the lateral walls. A neutron gun is placed close the side external layer of the stainless-steel cryostat. The neutrons, with energies that are around 2.2 MeV and 2.7 MeV from a neutron generator exploiting the deuterium–deuterium fusion, are used for routine calibrations despite their effects in the activation of all the set-up’s materials. The collaboration quoted a signal due to the decay in Xe with the half-life of yr [171]. However, the significance of the effect is only 4.4 , as addressed in the literature (see e.g., Reference [192]). To be thorough, it should also be noted that a limit yr was previously obtained in Reference [172] (see Table 1). We are also reminded of the previous limits at the level of (0.65–4.7) × yr [193,194,195].
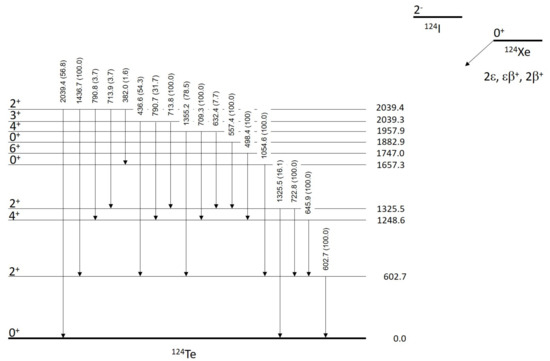
Figure 8.
A simplified decay scheme of Xe to the ground state and the first excited levels of Te. The energies of the levels (in keV) and relative main branching ratios (in %) are taken from Reference [196].
Finally, the natural abundance of Ba is 0.11(1)% [167] and its value is 2618.9(26) keV [165] (a simplified decay scheme of Ba is presented in Figure 9). The theoretical half-life of DBD+ in Ba to the g.s. of Xe spreads over a wide range [3,178,179,180,190,197]: – yr for the case, – yr for the case, and – yr for the case. In 1976, an anomalous amount of Xe in a sedimentary barite sample (BaSO) from South Africa and Western Australia ( years old) was found [177]. The adopted experimental technique was the geochemical method that relies on the extraction of decay products (Xe noble gas) from ancient minerals using mass spectrometer analysis. In Reference [176], reanalyzing the data presented in Reference [177], the limit of yr was set for all of the decay modes of DBD in Ba. In the same work of Reference [176], but using a different sample of barite in Reference [177], the authors set a DBD indication with yr. Later, in Reference [174], using the geochemical measurement of Xe amount in natural barite (from the Belorechenskoe deposit in North Caucasus, Russia), the half-life for Ba for all of the DBD decay modes was set to yr. However, in a following geochemical experiment, a yr [175] was obtained in disagreement with the previous results. More recently, in Reference [198], a summary of the previous measurements was attempted while considering a more reliable value of yr, as recommended in Reference [192] (see Table 1).
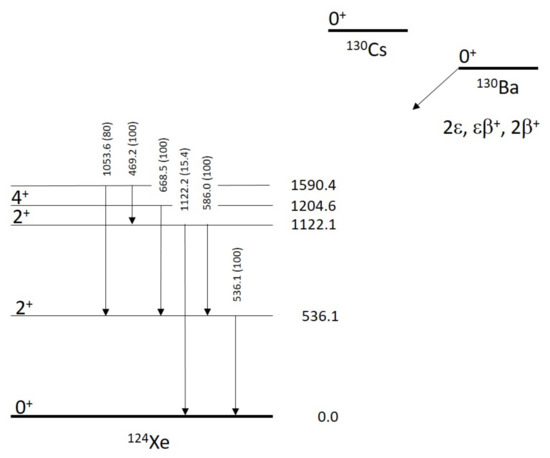
Figure 9.
The simplified decay scheme of Ba to the ground state and to the first excited levels of Xe. The energies of the levels (in keV) and the relative main branching ratios (in %) are taken from Reference [199].
To be thorough, a possible claim also exists for the transitions in Ba to the g.s. of Xe (see Table 1). In fact, in Reference [174], the apparent excess in one barite sample of Xe (not evident in the other samples) can be used to estimate the half-life of DBD+ in Ba yr. However, in the same work, the authors also give a cautious lower limit: yr. Moreover, a more stringent half-life limit is also addressed ( yr) in Reference [176]. The related theoretical half-life prediction spans over a range of – yr [190].
Recently, several developments are aimed at increasing the performance of some low radioactive Ba-based scintillation detectors, as in References [93,95], with the goal to improve the experimental sensitivity to DBD+ in Ba and Ba by direct measurements.
3.2. Experiments Using Solid Detectors as “Source = Detector”
The use of a solid detection medium, thanks, for example, to their high densities and the possibility to implement a modularity approach, is of great advantage. Moreover, when considering the “source = detector” approach, three kinds of solid detectors can be addressed: semiconductor, scintillator, and bolometric detectors. Among them, the most diffused detection method for DBD+ investigations uses the crystal scintillator detectors, since almost all of the best limits of DBD+ transitions are achieved by their use (see the Tables in this Section). In the following, we will first summarize some of the results of bolometers and semiconductors and, later, those of scintillators.
The bolometer/scintillating-bolometers (B/SB) and the semiconductors (SC) (“source = detector”) only obtained the best limits for a few DBD+ transitions in Ca, Zn, Te, and W achieved by the CRESST (SB), COBRA (SC), CUORE (B), and CUPID (SB) collaborations. CUPID, the upgrade of CUORE, in turn the upgrade of CUORE-0 (B), which was the upgrade of CUORICINO (B) experiment.
CRESST (SB, Cryogenic Rare Event Search with Superconducting Thermometers) consists of scintillating bolometers that are based on CaWO crystals. The detector volume (installed deep underground at LNGS in Italy) is surrounded by a passive shield that consists of 14 cm thick low background copper and 20 cm of lead. This inner shield is entirely enclosed within a gas-tight radon box that is continuously flushed with N gas. The data that were collected with the phase-II of the experiment (exposure of 2 kg × yr) have been used to study some DBD+ transition in Ca and W [200] (also see Table 2).
COBRA (SC, Cadmium zinc telluride 0-neutrino double-Beta Research Apparatus) collaboration aims at using semiconductor detectors at room temperature, adopting CdTe or CdZnTe crystals (mainly to explore the DBD- in Cd and Te decays). The experiment, in the upgrading phase at LNGS, is composed by an array of 64 cubic CdZnTe detectors that are arranged in four layers of 16 detectors each one (with 1 cm edge and mass of ∼6 g), and, in 2018, nine new crystals (with a size of 1.5 cm × 2 cm × 2 cm, mass of ∼28 g) have been added [201]. The technology is not yet mature and, thus, the sensitivity for the DBD+ in Te is at the level of – yr. However, CdZnTe crystals have nine double-beta emitters: Zn, Zn, Cd, Cd, Cd, Cd, Te, Te, and Te, but, as before, the sensitivity that is reached for their DBD+ is often not competitive [202].
CUORE-0 (B, Cryogenic Underground Observatory for Rare Events, step 0) consisted of 52 TeO crystals with natural Te composition. The crystals were 5 cm cubes mounted in a tower of 13 floors, with four crystals per floor (the total crystals array is named tower). They were operated at a temperature of ∼10 mK and read-out with neutron transmutation-doped germanium thermistors. The total TeO mass is 39 kg and the Te mass was 28 g, which correponded to atoms of Te. At present, its upgrade, the CUORE experiment, is running using 19 towers of CUORE-0 with an isotopic mass of Te of 532 g. Different layers of shielding, such as, e.g., an internal low-background Roman lead layer and an external anti-radon box, surround the cryostat and the crystals [203,204,205].
CUPID (SB, CUORE Upgrade with Particle Identification [206]) aims at upgrading the CUORE experiment, but using its infrastructure. The idea is to exploit the scintillator-bolometers technique. For this purpose, the project has been testing a few crystal bolometers. The first phase adopting ZnSe crystals was named CUPID-0 (B), and it uses the CUORICINO cryostat.
The bolometric experiments have only achieved the best limits for only a few DBD+ transitions in Ca, Zn, and Te, as previously mentioned. In particular, Ca has a natural abundance of 96.941(156)% [167], and its value is 193.51(2) keV [165]; it can decay via the mode. The theoretical half-life for the DBD+ of Ca to the g.s. of Ar is yr [207]. The best limits currently established are at the level of yr by the CRESST experiment (or by a based scintillator experiment using a CaF(Eu) crystal [208]), as reported in Table 2.

Table 2.
The present best half-life limits on and DBD+ in Ca, Zn, Te, and W (if not specified, the C.L. is at 90%). Only for such isotopes the bolometers (B) or scintillating-bolometers (SB) have achieved the best limits. In the square bracket, the experimental technique and adopted crystal detector are reported: crystal Scintillator detector (S), High Pure Germanium detector (HPGe), B, SB, and crystal semiconductors in CdTe and CdZnTe working at room temperature (SC).
Table 2.
The present best half-life limits on and DBD+ in Ca, Zn, Te, and W (if not specified, the C.L. is at 90%). Only for such isotopes the bolometers (B) or scintillating-bolometers (SB) have achieved the best limits. In the square bracket, the experimental technique and adopted crystal detector are reported: crystal Scintillator detector (S), High Pure Germanium detector (HPGe), B, SB, and crystal semiconductors in CdTe and CdZnTe working at room temperature (SC).
| Transition | Q (keV) [165] | Natural Abundance (%) [167] | Process | (yr) | |
|---|---|---|---|---|---|
| Ca →Ar | 193.51(2) | 96.941(156) | ≥ [CaWO (SB)] [200] | – | |
| ≥ [CaF(Eu) (S)] [208] | ≥ [CaWO (SB)] [200] | ||||
| Zn →Ni | 1094.9(7) | 49.17(75) | 2K | ≥ [ZnWO (S)] [100] | – |
| – | ≥ [HPGe] [209] | ||||
| ≥ (a) [ZnWO (S)] [100] | ≥ [ZnSe (SB)] [210] | ||||
| ≥ (b) [HPGe] [209] | |||||
| Te →Sn | 1730(3) | 0.09(1) | ≥ [CdTe, CdZnTe (SC)] [211] | – | |
| KK/KL/LL | – | ≥ [HPGe] [212] | |||
| ( 1171.3) | ≥ (b) [HPGe] [212] | ≥ [CdZnTe (SC)] [213] | |||
| ≥ [TeO (B)] [214] | ≥ [TeO (B)] [203] | ||||
| W →Hf | 143.23(28) | 0.12(1) | KK | ≥ [CaWO (SB)] [200] | – |
| – | ≥ [CaWO (SB)] [200] | ||||
(†) The nucleus is unstable with respect to the decay [51,78]. (a) We also remind a quoted claim with T yr in Reference [215]. (b) double beta decay.
The Zn nuclide has a natural abundance of 49.17(75)% [167], and its value is 1094.9(7) keV [165], and it can decay via and modes. The half-life that is predicted in the literature for the DBD+ in Zn to the g.s. of Ni spreads over a range of [182,183]: – yr for the case and – yr for the case. The best limit for the transition (g.s.) is achieved by the CUPID-0 with yr, while all of the other transitions are measured by the DAMA-INR Kyiv collaboration with the help of ZnWO crystal scintillators [100]; the sensitivity reached is at the level of – yr. To be thorough, a quoted claim with T yr [215] is present in the literature while using a passive source approach.
The Te nuclide has a natural abundance of 0.09(1)% [167], and its value is 1730(3) keV [165] and it can decay via and modes. The half-life that is predicted in the literature for the DBD+ in Te to the g.s. of Sn spreads over a wide range [216]: – yr for the case and – yr for the case. Instead, the theoretical prediction for decay of Te to the first exited level of Sn spans [216] in – yr. The COBRA experiment [211] and a passive source approach, using an HP-Ge detector [212], determined the best limits for the transition to g.s. of daughter nucleus and to the exited level of the daughter nucleus (see Table 2). Instead, the best limits of were achieved by the CUORICINO and CUORE-0 collaborations [203,214] (see Table 2).
Finally, W has a natural abundance of 0.12(1)% [167] and its value is 143.23(28) keV [165], and it can decay via he modes. The best limits currently established are at the level of – yr by the CRESST experiment, as reported in Table 2 (or by a based scintillator experiment using a CdWO crystal scintillator, as in Reference [217]).
The most competitive crystal scintillators used to study the DBD+ are: CaMoO, ZnWO, CaF, SrI, CsHfCl, CdWO, BaF, and CeCl. Most of the listed crystal scintillators have been developed in the framework of DAMA and DAMA-INR Kyiv collaborations. These scintillators contain DBD+ emitters that are of great interest in the sector: Ca, Zn, Sr, Cd, Cd, Ba, Ba, Ce, Ce, and Hf. This motivated the DAMA and DAMA-INR Kyiv efforts. Besides this, the intriguing possibility to either develop or improve new low background crystal scintillators for both rare event investigations and industrial/medical applications has further motivated different DAMA and DAMA-INR Kyiv R&Ds [30,42,50,55,59]. Table 3 shows the best limits that are mainly achieved using crystal scintillator detectors, besides those already listed in Table 1, Table 2 and Table 4. In the following, as an interesting example, the experimental results on DBD+ in Cd will be summarized.

Table 3.
The present best half-lives limits on and DBD+ of Sr, Mo, Cd, Cd, Xe, and Ce mainly obtained by crystal scintillator detectors (if not specified, the C.L. is at 90%). In the square bracket, the experimental technique and adopted crystal detector is reported: crystal Scintillator detector (S) and High Pure Germanium detector (HPGe). To be thorough, some other best limits for transitions using S are also shown in Table 1, Table 2 and Table 4.
In 2012, the result of a search for the double processes in Cd was carried out at the LNGS (Italy) with the help of a CdWO crystal scintillator (215 g) enriched in Cd up to 66% [80]. After 6590 h of data taking, several half-life limits on the double beta processes, including the possible resonant transitions (see Section 2.1), in Cd were established at the level of – yr (Figure 10 presents a simplified decay scheme of Cd).
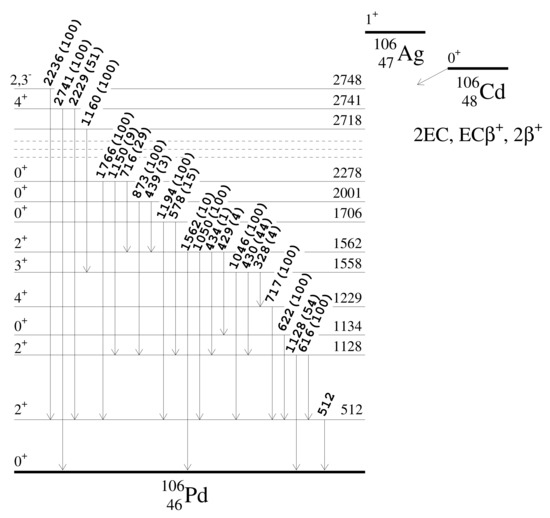
Figure 10.
The simplified decay scheme of Cd to the ground state and to the first excited levels of Pd. The energies of the levels (in keV) and the relative main branching ratios (in %) are taken from Reference [225]. Reprinted from Reference [48].
The CdWO scintillator was placed inside a low background HPGe detector with four Ge crystals to increase the experimental sensitivity to the processes with emission of quanta. The final result of this stage, after 13085 h of data taking, with the CdWO scintillation detector operated in coincidence (anticoincidence) with the four crystals HPGe detector, further improved the lower limits of several DBD+ [82]. The preliminary results of the experiment have been presented in conference proceedings [81,226,227,228].
The third stage of the experiment, which was hosted in the DAMA/CRYS set-up at LNGS, added two other low background CdWO detectors to profit from the coincidences with gammas emitted in the DBD+. After 26033 h of data taking, new improved half-life limits were set on the different channels and modes of the Cd double beta decay at a level of – yr. The limit for the two neutrino electron capture with positron emission in Cd to the ground state of Pd, yr, was set by the analysis of the CdWO data in coincidence with the energy release 511 keV in both of the CdWO counters [48]. The sensitivity approaches the theoretical predictions for the half-life that is in the range of – yr [48]. The resonant neutrinoless double-electron capture to the 2718 keV excited state of Pd is restricted at the level of yr (see Table 3). In particular, Figure 11 shows the energy spectrum of the and events that were measured for 26033 h by the CdWO detector in coincidence with 511 keV events in at least one of the CdWO counters [48]. The fit of the data by the background model and the excluded distributions for and decays of Cd to the ground state of Pd with the half-lives yr and yr, respectively, are also shown [48].
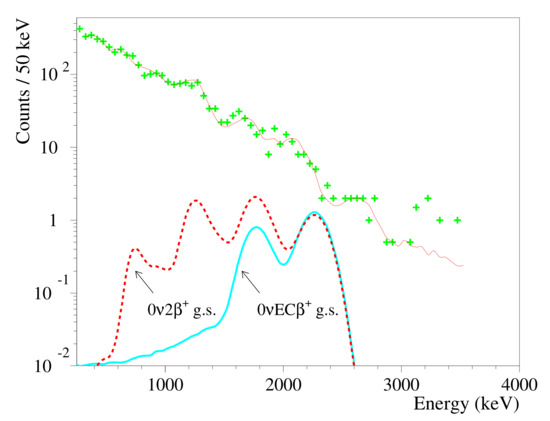
Figure 11.
The energy spectrum of the and events measured for 26,033 h by the CdWO detector in coincidence with events in at least one of the CdWO counters with energy ) keV (crosses). The solid red line shows the fit of the data by the background model (see Reference [48]). The excluded distributions of and decays of Cd to the ground state of Pd with the half-lives yr and yr, respectively, are shown. Reprinted from Reference [48].
Being aimed at the possibility to cover the theoretical predictions for the decay half-life of in Cd, a new stage with an improved apparatus is in data taking in the DAMA/R&D set-up. Figure 12 shows the scheme of the improved experimental set-up. The two CdWO crystal scintillators include a cylindrical cut-out to house the CdWO crystal. The detector system is surrounded by four high purity copper bricks, low radioactive copper and lead, cadmium, and polyethylene in order to reduce the external background.
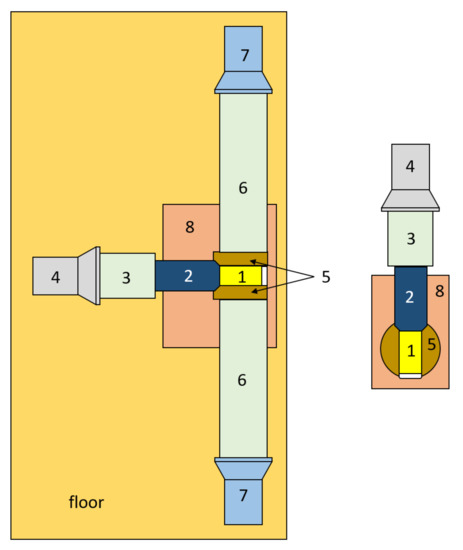
Figure 12.
The scheme of the experimental set-up with the CdWO crystal scintillation detector (1), viewed through plastic scintillator (2) and a quartz light-guide (3) by a metallic PMT (4). The two CdWO crystal scintillators (5) are viewed through two quartz light-guides (6) by PMTs (7). The detector system was shielded by copper, lead, cadmium, and polyethylene (not shown). Only part of the copper details (8) is shown.

Table 4.
The present best half-lives limits on and DBD+ in Ce, Sm, Gd, and Dy being mainly achieved using the passive source approach (if not specified, the C.L. is at 90%). In the square brackets, the adopted detector is reported: High Pure Germanium detector (HPGe) and Geochemical method (GEO). A few other best limits for transitions using such approach are also listed in Table 1, Table 2, Table 3, Table 4, Table 5 and Table 6.
Table 4.
The present best half-lives limits on and DBD+ in Ce, Sm, Gd, and Dy being mainly achieved using the passive source approach (if not specified, the C.L. is at 90%). In the square brackets, the adopted detector is reported: High Pure Germanium detector (HPGe) and Geochemical method (GEO). A few other best limits for transitions using such approach are also listed in Table 1, Table 2, Table 3, Table 4, Table 5 and Table 6.
| Transition | Q (keV) [165] | Natural Abundance (%) [167] | Process | (yr) | |
|---|---|---|---|---|---|
| Ce →Ba | 2378.55(27) | 0.186(2) | KK/KL/LL | ≥ [CeCl (S)] [86] | ≥ [HPGe] [224] |
| ( 818.5) | ≥ [HPGe] [224] | ≥ [HPGe] [224] | |||
| ( 1551.0) | ≥ [HPGe] [224] | ≥ [HPGe] [224] | |||
| ( 1579.0) | ≥ [HPGe] [224] | ≥ [HPGe] [224] | |||
| ( 2080.1) | ≥ [HPGe] [224] | ≥ [HPGe] [224] | |||
| ( 2128.9) | ≥ [HPGe] [224] | ≥ [HPGe] [224] | |||
| ( 2141.4) | ≥ [HPGe] [224] | ≥ [HPGe] [224] | |||
| ( 2222.7) | ≥ [HPGe] [224] | ≥ [HPGe] [224] | |||
| ( 2315.3) | ≥ [HPGe] [224] | ≥ [HPGe] [224] | |||
| ≥ (a) [HPGe] [224] | ≥ [HPGe] [224] | ||||
| ( 818.5) | ≥ [HPGe] [224] | ≥ [HPGe] [224] | |||
| ≥ [HPGe] [224] | ≥ [HPGe] [224] | ||||
| Sm →Nd | 1782.4(8) | 3.08(4) | KK/KL/LL | – | ≥ [HPGe] [56] |
| KK ( 696.6) | ≥ [HPGe] [56] | ≥ [HPGe] [56] | |||
| KK ( 1560.9) | ≥ [HPGe] [56] | ≥ [HPGe] [56] | |||
| ≥ [HPGe] [56] | ≥ [HPGe] [56] | ||||
| ( 696.6) | ≥ [HPGe] [56] | ≥ [HPGe] [56] | |||
| Gd →Sm | 55.69(18) | 0.20(3) | ≥ (b,c) [GEO] [229] | ||
| Dy →Gd | 2005.95(10) | 0.056(3) | KK/KL/LL | ≥ [HPGe] [230] | ≥ [HPGe] [230] |
| ( 89.0) | ≥ [HPGe] [230] | ≥ [HPGe] [230] | |||
| ( 1049.5) | ≥ [HPGe] [230] | ≥ [HPGe] [230] | |||
| ( 1129.4) | ≥ [HPGe] [230] | ≥ [HPGe] [230] | |||
| ( 1154.2) | ≥ [HPGe] [230] | ≥ [HPGe] [230] | |||
| ( 1168.2) | ≥ [HPGe] [230] | ≥ [HPGe] [230] | |||
| (0 1715.2) | ≥ [HPGe] [230] | ≥ [HPGe] [230] | |||
| (2 1771.1) | ≥ [HPGe] [230] | ≥ [HPGe] [230] | |||
| (2 1827.8) | ≥ [HPGe] [230] | ≥ [HPGe] [230] | |||
| (0 1851.3) | ≥ [HPGe] [230] | ≥ [HPGe] [230] | |||
| KK ( 1914.8) (d) | ≥ (c) [HPGe] [230] | ||||
| KL ( 1946.4) (d) | ≥ (c) [HPGe] [230] | ≥ [HPGe] [231] | |||
| KL ( 1952.4) (d) | ≥ (c) [HPGe] [230] | ≥ [HPGe] [231] | |||
| 2L ( 1988.5) (d) | ≥ (c) [HPGe] [230] | ≥ [HPGe] [231] | |||
| 2L ( 2003.7) (d) | ≥ [HPGe] [230] | ≥ [HPGe] [231] | |||
| ≥ (c) [HPGe] [230] | |||||
| ( 89.0) | ≥ (c) [HPGe] [230] | ||||
(†) The nucleus is unstable with respect to the decay [78]. (a) The limit obtained in Reference [224] is erroneously swapped with the limit of Reference [223]. (b) The limit takes all possible processes into account. (c) double beta decay. (d) Resonant effect.
3.3. Experiments Based on the “Source ≠ Detector” Approach
Despite the numerous efforts to implement the “source=detector” approach, since it also offers a good detection efficiency, several DBD+ emitters can be investigated by the passive source method. The isotopes that were studied by this technique, with the best performance in terms of half-life for different DBD+ transitions, are: Cr, Fe, Ni, Se, Mo, Ru, Pd, Sn, Te, Ce, Ce, Sm, Dy, Dy, Er, Yb, Hf, Os, Pt, and Hg.
The most adopted passive-source experiments use the HPGe spectrometers, as shown in Table 4, Table 5 and Table 6. The DAMA-INR Kyiv collaboration holds the most stringent limits for mostly all of the isotopes investigated by this technique. Thus, in this Section, we briefly summarize the measurements that were carried out by the HPGe spectrometers at the STELLA facility of LNGS [232] by the DAMA-INR Kyiv collaboration (also see [42,59] and the References therein).

Table 5.
The present best half-lives limits on and DBD+ in Ar, Cr, Fe, Ni, Se, Ru, Pd, and Sn mainly achieved using the passive source approach (if not specified, the C.L. is at 90%). In the square brackets, the detector adopted is reported: High Pure Germanium detector (HPGe). A few other best limits for transitions using such approach are also listed in Table 1, Table 2, Table 3 and Table 4 and Table 6.
Table 5.
The present best half-lives limits on and DBD+ in Ar, Cr, Fe, Ni, Se, Ru, Pd, and Sn mainly achieved using the passive source approach (if not specified, the C.L. is at 90%). In the square brackets, the detector adopted is reported: High Pure Germanium detector (HPGe). A few other best limits for transitions using such approach are also listed in Table 1, Table 2, Table 3 and Table 4 and Table 6.
| Transition | Q (keV) [165] | Natural Abundance (%) [167] | Process | (yr) | |
|---|---|---|---|---|---|
| Ar →Se | 432.58(19) | 0.3336(210) | – | ≥ [HPGe] [233] | |
| Cr →Ti | 1169.6(5) | 4.345(13) | ≥ (68%)(a) [HPGe] [234] | ||
| ≥ (95%)(a) [HPGe] [235] | |||||
| Fe →Cr | 680.3(4) | 5.845(105) | KK/KL/LL | – | ≥ (68%) [HPGe] [236] |
| Ni →Fe | 1926.4(3) | 68.0769(100) | – | ≥(b) [HPGe] [237] | |
| (, 810.8) | ≥ [HPGe] [237] | – | |||
| (, 1674.7) | ≥ [HPGe] [237] | – | |||
| ≥ [HPGe] [237] | – | ||||
| (, 810.8) | ≥ [HPGe] [237] | – | |||
| Se →Ge | 1209.24(1) | 0.86(3) | 2 | ≥ (a) [HPGe] [238] | |
| KK/KL/LL | – | ≥ [HPGe] [239] | |||
| KK/KL/LL (, 595.9) | ≥ [HPGe] [239] | ≥ [HPGe] [239] | |||
| (, 1204.2) | ≥ (a,c) [HPGe] [240] | ≥ [HPGe] [239] | |||
| ≥ (a) [HPGe] [239] | |||||
| Ru →Mo | 2714.50(12) | 5.54(14) | KK/KL/LL | – | ≥ [HPGe] [241] |
| KL (b)/LL (b) | – | ≥ [HPGe] [241] | |||
| ( 778.2) | ≥ [HPGe] [241] | ≥ [HPGe] [241] | |||
| ( 1148.1) | ≥ [HPGe] [241] | ≥ [HPGe] [241] | |||
| ( 1497.8) | ≥ [HPGe] [241] | ≥ [HPGe] [241] | |||
| ( 1625.9) | ≥ [HPGe] [241] | ≥ [HPGe] [241] | |||
| ( 2095.7) | ≥ [HPGe] [241] | ≥ [HPGe] [241] | |||
| ( 2426.1) | ≥ [HPGe] [241] | ≥ [HPGe] [241] | |||
| ( 2622.5) | ≥ [HPGe] [241] | ≥ [HPGe] [241] | |||
| ≥ [HPGe] [241] | ≥ [HPGe] [241] | ||||
| ( 778.2) | ≥ [HPGe] [241] | ≥ [HPGe] [241] | |||
| ( 1148.1) | ≥ [HPGe] [241] | ≥ [HPGe] [241] | |||
| ( 1497.8) | ≥ [HPGe] [241] | ≥ [HPGe] [241] | |||
| ( 1625.9) | ≥ [HPGe] [241] | ≥ [HPGe] [241] | |||
| ≥ [HPGe] [241] | ≥ [HPGe] [241] | ||||
| Pd →Ru | 1203.3(4) | 1.02(1) | – | – | |
| (, 475.1) | ≥(a) [HPGe] [242] | ||||
| (, 943.7) | ≥(a) [HPGe] [242] | ||||
| (, 1103.0) | ≥(a) [HPGe] [242] | ||||
| – | – | ||||
| (, 475.1) | ≥(a) [HPGe] [242] | ||||
| Sn →Cd | 1919.80(16) | 0.97(1) | KK/KL/LL | – | ≥ [HPGe] [243] |
| ( 617.5) | ≥ [HPGe] [243] | ≥ [HPGe] [243] | |||
| ( 1224.3) | ≥ [HPGe] [243] | ≥ [HPGe] [243] | |||
| ( 1312.4) | ≥ [HPGe] [243] | ≥ [HPGe] [243] | |||
| ( 1415.5) | ≥ [HPGe] [243] | ≥ [HPGe] [243] | |||
| ( 1433.3) | ≥ [HPGe] [243] | ≥ [HPGe] [243] | |||
| ( 1468.8) | ≥ [HPGe] [243] | ≥ [HPGe] [243] | |||
| ( 1870.7) | ≥ [HPGe] [243] | ≥ [HPGe] [243] | |||
| ( 1871.0) | ≥ [HPGe] [243] | ≥ [HPGe] [243] | |||
| ≥ (a) [HPGe] [243] | |||||
| ( 617.5) | ≥ (a) [HPGe] [243] | ||||
(a) double beta decay. (b) Resonant effect. (c) The value quoted in Reference [240] for the (, 1204.2) transition was re-evaluated in Reference [244] with yr, and it further decreased to yr in Reference [245], as reported in [19]. Recently, a new upper limit at was reported in [239].
HPGe detectors can offer high performances in the measurements on samples at very low radioactivity levels, being typically down to the Bq kg. The usual experimental approach consists of two phases: in the first one, the sample (source) can be purified at different stages to decease the background for the effect searched for; then, the DBD+ measurements can be done. Examples of purification technique include the evaporation of the impurities from the melted sample, the sedimentation, the liquid-liquid extraction, or, if possible, their combination. However, the protocol is strictly isotope/sample dependent. Some details regarding the different adopted/developed purifications and protocols can be found in [62,224,241,246] and the references therein. Besides this, the material contamination can also be investigated by Inductively Coupled Plasma-Mass Spectrometry [247], especially to evaluate the radio-isotopes concentration in the case their decay is not accompanied with a emission. For example, present studies on the purification protocol for GdO are in progress at the STELLA facility of LNGS [232], due to the great interest in the DBD+ of Gd (and DBD- of Gd). There is also great interest in the development of purification techniques for lanthanide’s and rare-earth nuclides [57,62,230,247,248,249].

Table 6.
The best half-lives limits on and DBD+ in Dy, Er, Er, Yb, Hf, Os, Pt, and Hg mainly achieved using the passive source approach (if not specified, the C.L. is at 90%). In the square brackets, the adopted detector is reported, where HPGe means High Pure Germanium detector and GEO means the Geochemical method. A few other best limits for transitions using such approach are also listed in Table 1, Table 2, Table 3 and Table 4.
Table 6.
The best half-lives limits on and DBD+ in Dy, Er, Er, Yb, Hf, Os, Pt, and Hg mainly achieved using the passive source approach (if not specified, the C.L. is at 90%). In the square brackets, the adopted detector is reported, where HPGe means High Pure Germanium detector and GEO means the Geochemical method. A few other best limits for transitions using such approach are also listed in Table 1, Table 2, Table 3 and Table 4.
| Transition | Q (keV) [165] | Natural Abundance (%) [167] | Process | (yr) | |
|---|---|---|---|---|---|
| Dy →Gd | 282.2(24) | 0.095(3) | KK | ≥ [HPGe] [230] | ≥ [HPGe] [230] |
| ( 79.5) | ≥ [HPGe] [230] | ≥ [HPGe] [230] | |||
| 2L ( 261.5) (a) | ≥ (b) [HPGe] [230] | ||||
| Er →Dy | 1846.96(30) | 0.139(5) | KK/KL/LL | ≥ [HPGe] [62] | ≥ [HPGe] [62] |
| ( 80.7) | ≥ [HPGe] [62] | – | |||
| ( 888.2) | ≥ [HPGe] [62] | – | |||
| ( 1400.3) | ≥ [HPGe] [62] | – | |||
| ( 1453.5) | ≥ [HPGe] [62] | – | |||
| ( 1666.3) | ≥ [HPGe] [62] | – | |||
| ( 1728.3) | ≥ [HPGe] [62] | – | |||
| KL ( 1782.7) | ≥ [HPGe] [62] | – | |||
| KK ( 80.7) | – | ≥ [HPGe] [62] | |||
| KK ( 888.2) | – | ≥ [HPGe] [62] | |||
| KK ( 1400.3) | – | ≥ [HPGe] [62] | |||
| KK ( 1453.5) | – | ≥ [HPGe] [62] | |||
| KK ( 1666.3) | – | ≥ [HPGe] [62] | |||
| KK ( 1728.3) | – | ≥ [HPGe] [62] | |||
| KL (a) ( 1782.7) | – | ≥ [HPGe] [62] | |||
| ≥ [HPGe] [62] | ≥ [HPGe] [62] | ||||
| ( 80.7) | ≥ [HPGe] [62] | ≥ [HPGe] [62] | |||
| Er →Dy | 25.08(11) | 1.601(3) | ≥(b,c) [GEO] [229] | ||
| Yb →Er | 1409.27(25) | 0.123(3) | KK/KL/LL | ≥ [HPGe] [57] | ≥ [HPGe] [57] |
| ( 78.8) | ≥ [HPGe] [57] | ≥ [HPGe] [57] | |||
| ( 821.2) | ≥ [HPGe] [57] | ≥ [HPGe] [57] | |||
| ( 1217.2) | ≥ [HPGe] [57] | ≥ [HPGe] [57] | |||
| ( 1276.3) | ≥ [HPGe] [57] | ≥ [HPGe] [57] | |||
| MM ( 1403.7) (a) | – | ≥ [HPGe] [57] | |||
| ≥ [HPGe] [57] | ≥ [HPGe] [57] | ||||
| ( 78.8) | ≥ [HPGe] [57] | ≥ [HPGe] [57] | |||
| Hf →Yb | 1100.0(23) | 0.16(12) | KK/KL/LL | ≥ [HPGe] [250] | ≥ [HPGe] [250] |
| KK/KL/LL ( 76.5) | ≥ [HPGe] [250] | ≥ [HPGe] [250] | |||
| K | ≥(b) [HPGe] [250] | ||||
| L | ≥(b) [HPGe] [250] | ||||
| Os →W | 1452.8(7) | 0.02(2) | KK/KL/LL | ≥ [HPGe] [251] | ≥ [HPGe] [252] |
| KK/KL/2 ( 112.2) | ≥ [HPGe] [251] | ≥ [HPGe] [251,252] | |||
| ( 903.3) | ≥ [HPGe] [251] | ≥ [HPGe] [251] | |||
| ( 1002.5) | ≥ [HPGe] [252] | ≥ [HPGe] [252] | |||
| ( 1121.5) | ≥ [HPGe] [251] | ≥ [HPGe] [251] | |||
| KK ( 1322.2) | ≥ [HPGe] [251] | ≥ (a) [HPGe] [251] | |||
| KL ( 1386.3) | ≥ [HPGe] [251] | ≥ (a) [HPGe] [252] | |||
| LL ( 1425.0) | ≥ [HPGe] [251] | ≥ [HPGe] [251] | |||
| LL ( 1431.0) | ≥ [HPGe] [251] | ≥ (a) [HPGe] [252] | |||
| ( 112.2) | ≥ [HPGe] [251] | ≥ [HPGe] [251] | |||
| ( 112.2) | ≥ [HPGe] [251] | ≥ [HPGe] [251] | |||
| Pt →Os | 1401.3(4) | 0.012(2) | KK/KL/LL | ≥ [HPGe] [253] | ≥ [HPGe] [253] |
| KK ( 186.7) | ≥ [HPGe] [253] | – | |||
| KK ( 558.0) | ≥ [HPGe] [253] | – | |||
| KK ( 911.8) | ≥ [HPGe] [253] | – | |||
| KK ( 1114.7) | ≥ [HPGe] [253] | – | |||
| ( 186.7) | – | ≥ [HPGe] [253] | |||
| ( 558.0) | – | ≥ [HPGe] [253] | |||
| ( 911.8) | – | ≥ [HPGe] [253] | |||
| ( 1114.7) | – | ≥ [HPGe] [253] | |||
| MM/MN/NN (0, 1, 2 1382.4) (a) | ≥(b) [HPGe] [253] | ||||
| ≥ [HPGe] [253] | ≥ [HPGe] [253] | ||||
| ( 186.7) | ≥(b) [HPGe] [253] | ||||
| Hg →Pt | 818.6(30) | 0.15(1) | KK | – | ≥ [HPGe] [254] |
| KK ( 355.7) | ≥(b) [HPGe)] [254] | ||||
(†) The nucleus is unstable with respect to the decay [49,51,78]. (a) Resonant effect. (b) double beta decay. (c) The limit takes in account all the possible processes.
The experimental set-ups, in the STELLA facility of LNGS [232], are placed in an air-tight poly-methyl-methacrylate box and then flushed with high purity nitrogen gas to remove the environmental radon (some set-ups are also covered by borated polyethylene of ≈10 cm). Inside this box, the detectors are surrounded by a passive shield made of low radioactivity copper (5–10 cm) and low radioactivity lead (20–25 cm). The samples are typically enclosed in a polystyrene box on the HPGe detector end-cap. The most commonly used HPGe detectors are: (i) GeCris, it is a 465 cm with 120 % relative efficiency with respect to a 3” × 3” sodium iodine detector [232]. (ii) GeMulti, it is made of four HPGe detectors inside the same cryostat with ∼225 cm volume each one. (iii) GeBer with a 244 cm volume. The typical energy resolution of the detectors is 2.0 keV at the 1332.5 keV peak of Co. Other HPGe detectors are also used for radio-purity measurements [232]. The detection efficiencies of the DBD+ that are searched for are estimated while using dedicated Monte-Carlo simulations: EGSnrc [255] and GEANT4 toolkits [161,162], with initial kinematics being provided by the DECAY0 event generator [163,164].
Thanks to these efforts, the DAMA and DAMA-INR Kyiv collaborations have obtained samples with very high-purity levels and high sensitivities to many DBD+ transitions with levels up to yr (see Table 4, Table 5 and Table 6), even with small-scale experiments. In particular, as an example, Figure 13 shows the results of the first direct search for and of Sm to the ground state and the excited levels of Nd [56]. The experiment was realized by measuring—over 1899 h—a 342 g sample of highly purified samarium oxide (SmO) with the ultra-low background HPGe spectrometer GeCris. No effect was observed, and the half-life limits were estimated at the level of (0.1–3.6) × yr (90% C.L.) (see Table 4).
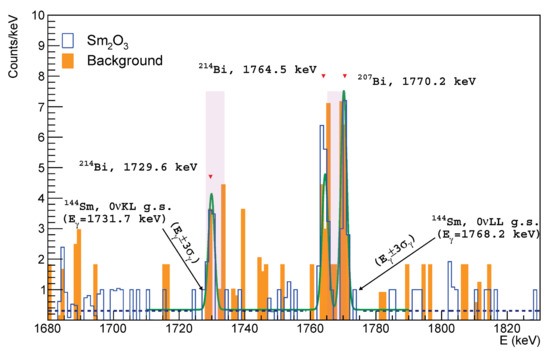
Figure 13.
An example: part of the energy spectrum accumulated with a SmO sample of 342 g over 1899 h [56], where the peaks from the and processes in Sm to the Nd g.s. are expected. The fit (green on-line line) of the background data (a straight line plus the 1729.6 keV and 1764.5 keV Gaussian peaks from Bi and 1770.2 keV peak from Bi) is shown [56]. The constant fit (dashed blue on-line) of the data with the SmO far from the mentioned lines of Bi and Bi is also reported. The boxes (transparent pink on-line) indicate the energy range () expected for the and decay processes to the g.s. of Nd in the energy spectra that were measured with SmO sample [56]. Reprinted from Reference [56].
4. Perspectives and Conclusions
The current interest and status of the experimental searches for DBD+ to the ground state and excited states of daughter nuclei have been outlined. An introduction regarding the theoretical aspect and interests to the DBD+ studies has been addressed. The great interest in the field is clearly evident: it is aimed at studying the important nuclear processes predicted from the SM or its extensions; crucial theoretical tests can be inferred. Moreover, very important complementary information in nuclear and interaction theoretical models can be achieved with respect to the DBD- modes (as widely discussed in Section 1). The case of mode involves the neutrino mass and new specific theoretical scenarios; but, in some models, one can consider the nuclear matrix element as a test case for the modes, which is crucial in studying, as much as possible, all of the DBD+ emitters. Another relevant aspect, concerning the modes, is that the mutual information from the contemporary study of positive and negative DBD can strongly constrain the theoretical parameters with very high confidence (as discussed in Section 1). In addition, a remarkable new effect is the possible so-called “resonant effect" on the decay, if the initial and final states are energetically degenerate. Besides this, continuous efforts in this field push an evident progression in new or more performing detectors, which can also be profitable in many other fields. Thus, the experimental methods that are used in the field and the status of art have been summarized. Some claims, which are present in literature, have been reviewed. Many other experimental results using different detector types, sizes, and materials have been discussed.
In the future, improvements in the purification protocol, growing materials, and new detector concept can strongly increase the experimental sensitivity on DBD+ transitions. In particular, dedicated efforts are enlarging the number of DBD+ emitters that can be studied using the “source=detector” approach. In fact, among the other existing efforts (such as, e.g., attempts to use crystal bolometers), the DAMA-INR Kyiv collaboration works to purify several compounds aiming at improving the sensitivity in the passive source approach and enhancing the growing procedure of crystal scintillators with the DBD+ emitters.
Moreover, some positive claims on DBD+ need further experimental investigation. Some other DBD+ emitters are poorly investigated, such as Gd and Er. Thus, these latter deficits push the experimentalists to improve new related detectors and methods. In addition, the sensitivity that is reached for a few DBD+ emitters is in the range of theoretical expectations (as some DBD+ transition in Cd), which could allow their observations.
Author Contributions
All the authors of this paper have been significantly contributing to the presented review of experimental results. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Acknowledgments
It is a pleasure to thank all our collaborators in the searches on related fields.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Weizsäcker, C.F. Zur Theorie der Kernmassen. Z. Phys. 1935, 96, 431. [Google Scholar] [CrossRef]
- Goeppert-Mayer, M. Double Beta-Disintegration. Phys. Rev. 1935, 48, 512. [Google Scholar] [CrossRef]
- Suhonen, J.; Civitarese, O. Weak-interaction and nuclear-structure aspects of nuclear double beta decay. Phys. Rep. 1998, 300, 123–214. [Google Scholar] [CrossRef]
- Mohapatra, R.N. New contributions to neutrinoless double-beta decay in supersymmetric theories. Phys. Rev. D 1986, 34, 3457–3461. [Google Scholar] [CrossRef]
- Babu, K.S.; Mohapatra, R.N. New Vector-Scalar contributions to neutrinoless double beta decay and constraints on R-parity violation. Phys. Rev. Lett. 1995, 75, 2276–2279. [Google Scholar] [CrossRef]
- Faessler, A.; Gutsche, T.; Kovalenko, S.; Šimkovic, F. Pion dominance in R-parity violating supersymmetry induced neutrinoless double beta decay. Phys. Rev. D 2008, 77, 113012. [Google Scholar] [CrossRef]
- Vergados, J.D. Pion-double-charge-exchange contribution to neutrinoless double-decay. Phys. Rev. D 1982, 25, 914–917. [Google Scholar] [CrossRef]
- Hirsch, M.; Klapdor-Kleingrothaus, H.V.; Kovalenko, S.G. New contributions to supersymmetric mechanism of neutrinoless double beta decay. Phys. Lett. B 1995, 352, 1–7. [Google Scholar] [CrossRef]
- Frank, M.; Majumdar, C.; Poulose, P.; Senapati, S.; Yajnik, U.A. Exploring 0νββ and leptogenesis in the alternative left-right model. Phys. Rev. D 2020, 102, 075020. [Google Scholar] [CrossRef]
- Mitra, M.; Senjanović, G.; Vissani, F. Neutrinoless double beta decay and heavy sterile neutrinos. Nucl. Phys. B 2012, 856, 26–73. [Google Scholar] [CrossRef]
- Masaru Doi, M.; Kotani, T.; Takasugi, E. Double beta decay and Majorana neutrino. Prog. Theo. Phys. Supp. 1985, 83, 1–175. [Google Scholar]
- Zyla, P.A.; Barnett, R.M.; Beringer, J.; Dahl, O.; Dwyer, D.A.; Groom, D.E.; Lin, C.J.; Lugovsky, K.S.; Pianori, E.; Robinson, D.J.; et al. Review of Particle Physics. Prog. Theor. Exp. Phys. 2020, 8, 083C01. [Google Scholar]
- Hirsch, H. Calculation of double beta plus decay matrix elements. Nulc. Phys. A 1994, 557, 411c–414c. [Google Scholar] [CrossRef]
- Tretyak, V.I.; Zdesenko, Y.G. Tables of double beta decay data: An update. Atom. Data Nucl. Data Tabl. 2020, 80, 83–116. [Google Scholar] [CrossRef]
- Maalampi, J.; Suhonen, J. Neutrinoless Double β+/EC Decays. Adv. High Energy Phys. 2013, 2013, 505874. [Google Scholar] [CrossRef]
- Winter, R.G. Double K capture and single K capture with positron emission. Phys. Rev. 1955, 100, 142–144. [Google Scholar] [CrossRef]
- Voloshin, M.B.; Mitselmakher, G.V.; Eramzhyan, R.A. Conversion of an atomic electron into a positron and double β+ decay. JETP Lett. 1982, 35, 656–659. [Google Scholar]
- Bernabeu, J.; De Rujula, A.; Jarlskog, C. Neutrinoless double electron capture as a tool to measure the electron neutrino mass. Nucl. Phys. B 1983, 223, 15–28. [Google Scholar] [CrossRef]
- Blaum, K.; Eliseev, S.; Danevich, F.A.; Tretyak, V.I.; Kovalenko, S.; Krivoruchenko, M.I.; Novikov, Y.N.; Suhonen, J. Neutrinoless double-electron capture. Rev. Mod. Phys. 2020, 92, 045007. [Google Scholar] [CrossRef]
- Krivoruchenko, M.I.; Šimkovic, F.; Frekers, D.; Faessler, D. Resonance enhancement of neutrinoless double electron capture. Nucl. Phys. A 2011, 859, 140. [Google Scholar] [CrossRef]
- Georgi, H.M.; Glashow, S.L.; Nussinov, S. Unconventional model of neutrino masses. Nucl. Phys. B 1981, 193, 297–316. [Google Scholar] [CrossRef]
- Eliseev, S.A.; Novikov, Y.N.; Blaum, K. Search for resonant enhancement of neutrinoless double-electron capture by high-precision Penning-trap mass spectrometry. J. Phys. G 2012, 39, 124003. [Google Scholar] [CrossRef]
- Klapdor-Kleingrothaus, H.V.; Krivosheina, I.V. Nuclear Double Beta Decay, Fundamental Particle Physics, Hot Dark Matter, And Dark Energy. In Proceedings of the 7th International Heidelberg Conference: Dark Matter in Astrophysics and Particle Physics, Christchurch, New Zealand, 18–24 January 2009; pp. 137–169. [Google Scholar]
- Kuzmin, V.A.; Rubakov, V.A.; Shaposhnikov, M.E. On anomalous electroweak baryon-number non-conservation in the early universe. Phys. Lett. B 1985, 155, 36–42. [Google Scholar] [CrossRef]
- Barabash, A.S. Possibilities of future double beta decay experiments to investigate inverted and normal ordering region of neutrino mass. Front. Phys. 2019, 6, 160. [Google Scholar] [CrossRef]
- Gando, A.; Gando, Y.; Hachiya, T.; Hayashi, A.; Hayashida, S.; Ikeda, H.; Inoue, K.; Ishidoshiro, K.; Karino, Y.; Koga, M.; et al. Search for Majorana Neutrinos Near the Inverted Mass Hierarchy Region with KamLAND-Zen. Phys. Rev. Lett. 2016, 117, 082503. [Google Scholar] [CrossRef] [PubMed]
- Adams, D.Q.; Alduino, C.; Alfonso, K.; Avignone, F.T.; Azzolini, O.; Bari, G.; Bellini, F.; Benato, G.; Biassoni, M.; Branca, A.; et al. Improved Limit on Neutrinoless Double-Beta Decay in 130Te with CUORE. Phys. Rev. Lett. 2020, 124, 122501. [Google Scholar] [CrossRef] [PubMed]
- Agostini, M.; Araujo, G.R.; Bakalyarov, A.M.; Balata, M.; Barabanov, I.; Baudis, L.; Bauer, C.; Bellotti, E.; Belogurov, S.; Bettini, A.; et al. Final Results of GERDA on the Search for Neutrinoless Double–β Decay. Phys. Rev. Lett. 2020, 125, 252502. [Google Scholar] [CrossRef]
- Arnold, R.; Augier, C.; Baker, J.D.; Barabash, A.S.; Basharina-Freshville, A.; Blondel, S.; Blot, S.; Bongrand, M.; Brudanin, V.; Busto, J.; et al. Results of the search for neutrinoless double-β decay in 100Mo with the NEMO-3 experiment. Phys. Rev. D 2015, 92, 072011. [Google Scholar] [CrossRef]
- Tretyak, V.I.; Barabash, A.S.; Belli, P.; Bernabei, R.; Cappella, F.; Caracciolo, V.; Cerulli, R.; Chernyak, D.M.; Danevich, F.A.; d’Angelo, S.; et al. Aurora experiment: Final results of studies of 116Cd 2β decay with enriched 116CdWO4 crystal scintillators. AIP Conf. Proc. 2019, 2165, 020029. [Google Scholar]
- Barabash, A.S.; Belli, P.; Bernabei, R.; Cappella, F.; Caracciolo, V.; Cerulli, R.; Chernyak, D.M.; Danevich, F.A.; d’Angelo, S.; Incicchitti, A.; et al. Final results of the Aurora experiment to study 2β decay of 116Cd with enriched 116CdWO4 crystal scintillators. Phys. Rev. D 2018, 98, 092007. [Google Scholar] [CrossRef]
- Abada, A.; Bhattacharyya, G. Impact of CP phases on neutrinoless double beta decay. Phys. Rev. D 2003, 68, 033004. [Google Scholar] [CrossRef]
- Cremonesi, O.; Pavan, M. Challenges in Double Beta Decay. Adv. High Energy Phys. 2014, 2014, 951432. [Google Scholar] [CrossRef]
- Bilenky, S.M.; Giunti, C. Neutrinoless double-beta decay: A probe of physics beyond the Standard Model. Int. J. Mod. Phys. A 2015, 30, 1530001. [Google Scholar] [CrossRef]
- Suhonen, J.T. Value of the axial-vector coupling strength in β and ββ decays: A review. Front. Phys. 2017, 5, 55. [Google Scholar] [CrossRef]
- Beringer, J.; Arguin, J.F.; Barnett, R.M.; Copic, K.; Dahl, O.; Groom, D.E.; Lin, C.J.; Lys, J.; Murayama, H.; Wohl, C.G.; et al. Review of particle physics. Phys. Rev. D 2012, 86, 010001. [Google Scholar] [CrossRef]
- Engel, J.; Menendez, J. Status and future of nuclear matrix elements for neutrinoless double-beta decay: A review. Rep. Prog. Phys. 2017, 80, 046301. [Google Scholar] [CrossRef] [PubMed]
- Suhonen, J. Impact of the quenching of gA on the sensitivity of 0νββ experiments. Phys. Rev. C 2017, 96, 055501. [Google Scholar] [CrossRef]
- Suhonen, J.; Kostensalo, J. Double β decay and the axial strength. Front. Phys. 2019, 7, 00029. [Google Scholar] [CrossRef]
- Ejiri, H. Axial-vector weak coupling at medium momentum for astro neutrinos and double beta decays. J. Phys. G Nucl. Part. Phys. 2019, 46, 125202. [Google Scholar] [CrossRef]
- Ejiri, H.; Suhonen, J.; Zuber, K. Neutrino–nuclear responses for astro-neutrinos, single beta decays and double beta decays. Phys. Rep. 2019, 797, 1–102. [Google Scholar] [CrossRef]
- Belli, P.; Bernabei, R.; Cappella, F.; Caracciolo, V.; Cerulli, R.; Incicchitti, A.; Merlo, V. Double beta decay to excited states of daughter nuclei. Universe 2020, 6, 239. [Google Scholar] [CrossRef]
- Ejiri, H.; Elliott, S.R. Charged current neutrino cross section for solar neutrinos, and background to ββ(0ν) experiments. Phys. Rev. C 2014, 89, 055501. [Google Scholar] [CrossRef]
- Ianni, A. Considerations on Underground Laboratories. J. Phys. Conf. Ser. 2020, 1342, 012003. [Google Scholar] [CrossRef]
- Bernabei, R.; Belli, P.; Montecchia, F.; Di Nicolantonio, W.; Ignesti, G.; Incicchitti, A.; Prosperi, D.; Dai, C.J.; Ding, L.K.; Kuang, H.H.; et al. Performances of the ≃100 kg NaI(Tl) set-up of the DAMA experiment at Gran Sasso. Nuovo Cimento A 1999, 112, 6. [Google Scholar] [CrossRef]
- Belli, P.; Bernabei, R.; d’Angelo, S.; De Pascale, M.P.; Paoluzi, L.; Santonico, R.; Taborgna, R.; Iucci, N.; Villoresi, G. Deep Underground Neutron Flux Measurement With Large BF3 Counters. Nuovo Cimento A 1998, 101, 959–966. [Google Scholar] [CrossRef]
- Barabash, A.S.; Belli, P.; Bernabei, R.; Borovlev, Y.A.; Cappella, F.; Caracciolo, V.; Cerulli, R.; Danevich, F.A.; Incicchitti, A.; Kobychev, V.V.; et al. Improvement of radiopurity level of enriched 116CdWO4 and ZnWO4 crystal scintillators by recrystallization. Nucl. Instrum. Methods 2016, 883, 77–81. [Google Scholar] [CrossRef]
- Belli, P.; Bernabei, R.; Brudanin, V.B.; Cappella, F.; Caracciolo, V.; Cerulli, R.; Danevich, F.A.; Incicchitti, A.; Kasperovych, D.V.; Klavdiinienko, V.R.; et al. Search for Double Beta Decay of 106Cd with an Enriched 106CdWO4 Crystal Scintillator in Coincidence with CdWO4 Scintillation Counters. Universe 2020, 6, 182. [Google Scholar] [CrossRef]
- Belli, P.; Bernabei, R.; Cappella, F.; Caracciolo, V.; Cerulli, R.; Danevich, F.A.; Incicchitti, A.; Kasperovych, D.V.; Kobychev, V.V.; Kovtun, G.P.; et al. Search for α decay of naturally occurring osmium nuclides accompanied by γ quanta. Phys. Rev. C 2020, 102, 024605. [Google Scholar] [CrossRef]
- Barabash, A.S.; Belli, P.; Bernabei, R.; Cappella, F.; Caracciolo, V.; Cerulli, R.; Danevich, F.A.; Di Marco, A.; Incicchitti, A.; Kasperovych, D.V.; et al. Low background scintillators to investigate rare processes. JINST 2020, 15, C07037. [Google Scholar] [CrossRef]
- Caracciolo, V.; Nagorny, S.S.; Belli, P.; Bernabei, R.; Cappella, F.; Cerulli, R.; Incicchitti, A.; Laubenstein, M.; Merlo, V.; Nisi, S.; et al. Search for α decay of naturally occurring Hf-nuclides using a Cs2HfCl6 scintillator. Nucl. Phys. A 2002, 1002, 121941. [Google Scholar] [CrossRef]
- Belli, P.; Bernabei, R.; Cappella, F.; Caracciolo, V.; Cerulli, R.; Cherubini, N.; Danevich, F.A.; Incicchitti, A.; Kasperovych, D.V.; Merlo, V.; et al. Developments and improvements of radiopure ZnWO4 anisotropic scintillators. JINST 2020, 15, C05055. [Google Scholar] [CrossRef]
- Belli, P.; Bernabei, R.; Cappella, F.; Caracciolo, V.; Cerulli, R.; Danevich, F.; Incicchitti, A.; Kasperovych, D.; Merlo, V.; Polischuk, O.; et al. The Future Role of Inorganic Crystal Scintillators in Dark Matter Investigations. Instruments 2021, 5, 16. [Google Scholar] [CrossRef]
- Polischuk, O.G.; Belli, P.; Bernabei, R.; Brudanin, V.B.; Cappella, F.; Caracciolo, V.; Cerulli, R.; Danevich, F.A.; Incicchitti, A.; Kasperovych, D.V.; et al. New limit on two neutrino electron capture with positron emission in 106Cd. AIP Conf. Proc. 2019, 2165, 020020. [Google Scholar]
- Kasperovych, D.V.; Barabash, A.S.; Belli, P.; Bernabei, R.; Boiko, R.S.; Cappella, F.; Caracciolo, V.; Cerulli, R.; Danevich, F.A.; Di Marco, A.; et al. Study of double-β decay of 150Nd to the first 0+ excited level of 150Sm. AIP Conf. Proc. 2019, 2165, 020014. [Google Scholar]
- Belli, P.; Bernabei, R.; Boiko, R.S.; Cappella, F.; Caracciolo, V.; Cerulli, R.; Danevich, F.A.; Di Marco, A.; Incicchitti, A.; Kropivyansky, B.N.; et al. First direct search for 2ϵ and ϵβ+ decay of 144Sm and 2β− decay of 154Sm. Eur. Phys. J. A 2019, 55, 201. [Google Scholar] [CrossRef]
- Belli, P.; Bernabei, R.; Boiko, R.S.; Cappella, F.; Caracciolo, V.; Cerulli, R.; Danevich, F.A.; di Vacri, M.L.; Incicchitti, A.; Kropivyansky, B.N.; et al. First search for 2ϵ and ϵβ+ processes in 168Yb. Nucl. Phys. A 2019, 990, 64–78. [Google Scholar] [CrossRef]
- Belli, P.; Bernabei, R.; Borovlev, Y.A.; Cappella, F.; Caracciolo, V.; Cerulli, R.; Danevich, F.A.; Incicchitti, A.; Kasperovych, D.V.; Polischuk, O.G.; et al. New development of radiopure ZnWO4 crystal scintillators. Nucl. Instrum. Methods A 2019, 935, 89–94. [Google Scholar] [CrossRef]
- Di Marco, A.; Barabash, A.S.; Belli, P.; Bernabei, R.; Boiko, R.S.; Brudanin, V.B.; Cappella, F.; Caracciolo, V.; Cerulli, R.; Chernyak, D.M.; et al. Recent Developments and Results on Double Beta Decays with Crystal Scintillators and HPGe Spectrometry. Universe 2018, 4, 147. [Google Scholar] [CrossRef]
- Barabash, A.S.; Belli, P.; Bernabei, R.; Boiko, R.S.; Brudanin, V.B.; Cappella, F.; Caracciolo, V.; Cerulli, R.; Chernyak, D.M.; Dai, C.J.; et al. Search for rare processes with DAMA experimental set-ups. EPJ Web Conf. 2018, 182, 02027. [Google Scholar] [CrossRef]
- Barabash, A.S.; Belli, P.; Bernabei, R.; Boiko, R.S.; Cappella, F.; Caracciolo, V.; Cerulli, R.; Danevich, F.A.; Di Marco, A.; Incicchitti, A.; et al. Double beta decay of 150Nd to the first excited 0+ level of 150Sm: Preliminary results. Nucl. Phys. Atom. Energy 2018, 19, 95–102. [Google Scholar] [CrossRef]
- Belli, P.; Bernabei, R.; Boiko, R.S.; Cappella, F.; Caracciolo, V.; Cerulli, R.; Danevich, F.A.; Incicchitti, A.; Kropivyansky, B.N.; Laubenstein, M.; et al. First search for 2ϵ and ϵβ+ decay of 162Er and new limit on 2β− decay of 170Er to the first excited level of 170Yb. J. Phys. G 2018, 45, 095101. [Google Scholar] [CrossRef]
- Barabash, A.S.; Basharina-Freshville, A.; Blot, S.; Bongrand, M.; Bourgeois, C.; Breton, D.; Brudanin, V.; Burešovà, H.; Busto, J.; Caffrey, A.J.; et al. Calorimeter development for the SuperNEMO double beta decay experiment. Nucl. Instrum. Methods A 2017, 868, 98–108. [Google Scholar] [CrossRef]
- Ejiri, H.; Higa, K.; Kamada, T.; Kobiki, H.; Matsuoka, K.; Okada, K.; Sano, H.; Shibata, T.; Shima, T.; Tanabe, N.; et al. The high sensitivity beta-gamma spectrometer ELEGANTS V for rare β(e) and ββ(ee) decays. Nucl. Instrum. Methods A 1991, 302, 304–314. [Google Scholar] [CrossRef]
- Zuber, K. COBRA-double beta decay searches using CdTe detectors. Phys. Lett. B 2001, 519, 1–7. [Google Scholar] [CrossRef]
- Ebert, J.; Fritts, M.; Gehre, D.; Gößling, C.; Göpfert, T.; Hagner, C.; Heidrich, N.; Klingenberg, R.; Köttig, T.; Kröninger, C.; et al. The COBRA demonstrator at the LNGS underground laboratory. Nucl. Instrum. Methods A 2016, 807, 114–120. [Google Scholar] [CrossRef]
- Belli, P.; Bernabei, R.; Cerulli, R.; Danevich, F.A.; d’Angelo, A.; Goriletsky, V.I.; Grinyov, B.V.; Incicchitti, A.; Kobychev, V.V.; Laubenstein, M.; et al. 7Li solar axions: Preliminary results and feasibility studies. Nucl. Phys. A 2008, 806, 388. [Google Scholar] [CrossRef]
- Bernabei, R.; Belli, P.; Montecchia, F.; Nozzoli, F.; d’Angelo, A.; Cappella, F.; Incicchitti, A.; Prosperi, D.; Castellano, S.; Cerulli, R.; et al. Search for possible charge non-conserving decay of 139La into 139Ce with LaCl3(Ce) scintillator. Ukr. J. Phys. 2006, 51, 1037. [Google Scholar]
- Belli, P.; Bernabei, R.; Dai, C.J.; He, H.L.; Ignesti, G.; Incicchitti, A.; Kuang, H.H.; Ma, J.M.; Montecchia, F.; Ponkratenko, O.A.; et al. New experimental limit on the electron stability and non-paulian transitions in iodine atoms. Phys. Lett. B 1999, 460, 236. [Google Scholar] [CrossRef]
- Belli, P.; Bernabei, R.; Dai, C.J.; He, H.L.; Ignesti, G.; Incicchitti, A.; Kuang, H.H.; Ma, J.M.; Montecchia, F.; Ponkratenko, O.A.; et al. New limits on the nuclear levels excitation of 127I and 23Na during charge nonconservation. Phys. Rev. C 1999, 60, 065501. [Google Scholar] [CrossRef]
- Bernabei, R.; Belli, P.; Cerulli, R.; Montecchia, F.; Nozzoli, F.; Incicchitti, A.; Prosperi, D.; Dai, C.J.; He, H.L.; Kuang, H.H.; et al. Search for solar axions by Primakoff effect in NaI crystals. Phys. Lett. B 2001, 515, 6. [Google Scholar] [CrossRef]
- Cappella, F.; Cerulli, R.; Incicchitti, A. A preliminary search for Q-balls by delayed coincidences in NaI(Tl). Eur. Phys. J. C 2002, 14, 1. [Google Scholar] [CrossRef]
- Bernabei, R.; Belli, P.; Cappella, F.; Montecchia, F.; Nozzoli, F.; d’Angelo, A.; Incicchitti, A.; Prosperi, D.; Cerulli, R.; Dai, C.J.; et al. Search for spontaneous transition of nuclei to a superdense stat. Eur. Phys. J. A 2005, 23, 7. [Google Scholar] [CrossRef]
- Bernabei, R.; Belli, P.; Cappella, F.; Montecchia, F.; Nozzoli, F.; d’Angelo, A.; Incicchitti, A.; Prosperi, D.; Cerulli, R.; Dai, C.J.; et al. A search for spontaneous emission of heavy clusters in the 127I nuclide. Eur. Phys. J. A 2005, 24, 51. [Google Scholar] [CrossRef]
- Bernabei, R.; Belli, P.; Cappella, F.; Cerulli, R.; Dai, C.J.; d’Angelo, A.; He, H.L.; Incicchitti, A.; Kuang, H.H.; Ma, X.H.; et al. New search for processes violating the Pauli-Exclusion-Principle in Sodium and in Iodine. Eur. Phys. J. C 2009, 62, 327. [Google Scholar] [CrossRef]
- Bernabei, R.; Belli, P.; Montecchia, F.; De Sanctis, M.; Di Nicolantonio, W.; Incicchitti, A.; Prosperi, D.; Bacci, C.; Dai, C.J.; Ding, L.K.; et al. Search for non-paulian transitions in 23Na and 127I. Phys. Lett. B 1997, 408, 439. [Google Scholar] [CrossRef]
- Bernabei, R.; Belli, P.; Cerulli, R.; Montecchia, F.; Amato, M.; Ignesti, G.; Incicchitti, A.; Prosperi, D.; Dai, C.J.; He, H.L.; et al. Extended limits on neutral strongly interacting massive particles and nuclearites from NaI(Tl) scintillators. Phys. Rev. Lett. 1999, 83, 4918. [Google Scholar] [CrossRef]
- Belli, P.; Bernabei, R.; Danevich, F.A.; Incicchitti, A.; Tretyak, V.I. Experimental searches for rare alpha and beta decays. Eur. Phys. J. A 2019, 55, 140. [Google Scholar] [CrossRef]
- Barabash, A.S. Average and recommended half-life values for two-neutrino double beta decay: Upgrade-2019. AIP Conf. Proc. 2019, 2165, 020002. [Google Scholar]
- Belli, P.; Bernabei, R.; Boiko, R.A.; Brudanin, V.B.; Cappella, F.; Caracciolo, V.; Cerulli, R.; Chernyak, D.M.; Danevich, F.A.; d’Angelo, S.; et al. Search for double-β decay processes in 106Cd with the help of a 106CdWO4 crystal scintillator. Phys. Rev. C 2012, 85, 044610. [Google Scholar] [CrossRef]
- Polischuk, O.G.; Belli, P.; Bernabei, R.; Brudanin, V.D.; Cappella, F.; Caracciolo, V.; Cerulli, R.; Chernyak, D.M.; Danevich, F.A.; d’Angelo, S.; et al. Search for 2β processes in 106Cd with 106CdWO4 crystal scintillator. Funct. Mater. 2005, 22, 135. [Google Scholar] [CrossRef]
- Belli, P.; Bernabei, R.A.; Brudanin, V.B.; Cappella, F.; Caracciolo, V.; Cerulli, R.; Danevich, F.A.; Incicchitti, A.; Kasperovych, V.D.; Klavdiienko, V.R.; et al. Search for double-β decay in 106Cd with an enriched 106CdWO4 crystal scintillator in coincidence with four HPGe detectors. Phys. Rev. C 2016, 93, 045502. [Google Scholar] [CrossRef]
- Polischuk, O.G. Enriched Crystal Scintillators for 2β Experiments. Physics 2021, 3, 103–119. [Google Scholar] [CrossRef]
- Cappella, F.; Incicchitti, A. Techniques for background identification in the search for rare processes with crystal scintillators. Physics 2021, 3, 187–206. [Google Scholar] [CrossRef]
- Belli, P.; Bernabei, R.; Cerulli, R.; Dai, C.J.; Danevich, F.A.; Incicchitti, A.; Kobychev, V.V.; Ponkratenko, O.A.; Prosperi, D.; Tretyak, V.I.; et al. Performances of a CeF3 crystal scintillator and its application to the search for rare processes. Nucl. Instrum. Methods A 2003, 498, 352. [Google Scholar] [CrossRef]
- Belli, P.; Bernabei, R.; Cappella, F.; Cerulli, R.; Danevich, F.A.; d’Angelo, A.; Di Marco, A.; Incicchitti, A.; Nozzoli, F.; Tretyak, V.I. Search for 2β decay of cerium isotopes with CeCl3 scintillator. J. Phys. G Nucl. Part. Phys. 2011, 38, 015103. [Google Scholar] [CrossRef]
- Belli, P.; Bernabei, R.; d’Angelo, S.; Cappella, F.; Cerulli, R.; Incicchitti, A.; Laubenstein, M.; Prosperi, D.; Tretyak, V.I. First limits on neutrinoless resonant 2ϵ captures in 136Ce and new limits for other 2β processes in 136Ce and 138Ce isotopes. Nucl. Phys. A 2009, 824, 101. [Google Scholar] [CrossRef]
- Bernabei, R.; Belli, P.; Incicchitti, A.; Prosperi, D.; Bacci, C.; De Notaristefani, F.; Davies, G.J.; Dai, C.J. Feasibility of 2β decay searches with Ce isotopes using CeF3 scintillators. Nuovo Cimento A 1997, 110, 189. [Google Scholar]
- Belli, P.; Bernabei, R.; Cerulli, R.; Danevich, F.A.; Galenin, E.; Gektin, A.; Incicchitti, A.; Isaienko, V.; Kobychev, V.V.; Laubenstein, D.; et al. Radioactive contamination of SrI2(Eu) crystal scintillator. Nucl. Instrum. Methods A 2012, 670, 10. [Google Scholar] [CrossRef]
- Danevich, F.A.; Chernyak, D.M.; Dubovik, A.M.; Grinyov, B.V.; Henry, S.; Kraus, H.; Kudovbenko, V.M.; Mikhailik, V.B.; Nagornay, L.L.; Podviyanuk, R.B.; et al. MgWO4 a new crystal scintillator. Nucl. Instrum. Methods A 2009, 608, 107. [Google Scholar] [CrossRef]
- Belli, P.; Bernabei, R.; Boiko, R.S.; Brudanin, V.B.; Bukilic, N.; Cerulli, R.; Chernyak, D.M.; Danevich, F.A.; d’Angelo, S.; Degoda, V.Y.; et al. Development of enriched 106CdWO4 crystal scintillators to search for double beta decay processes in 106Cd. Nucl. Instrum. Methods A 2010, 615, 301. [Google Scholar] [CrossRef]
- Belli, P.; Bernabei, R.; Cappella, F.; Cerulli, R.; Danevich, F.A.; d’Angelo, S.; Incicchitti, A.; Kobychev, V.V.; Nagorny, S.S.; Nozzoli, F.; et al. Search for double beta decay processes in 108Cd and 114Cd with the help of low background CdWO4 crystal scintillator. Eur. Phys. J. A 2008, 36, 167. [Google Scholar] [CrossRef]
- Cerulli, R.; Belli, P.; Bernabei, R.; Cappella, F.; Nozzoli, F.; Montecchia, F.; d’Angelo, A.; Incicchitti, A.; Prosperi, D.; Dai, C.J. Performances of a BaF2 detector and its application to the search for 2β decay modes in 130Ba. Nucl. Instrum. Methods A 2004, 525, 535. [Google Scholar] [CrossRef]
- Belli, P.; Bernabei, R.; Cappella, F.; Caracciolo, V.; Cerulli, R.; Danevich, F.A.; Di Marco, A.; Incicchitti, A.; Poda, D.V.; Polischuk, O.G.; et al. Investigation of rare nuclear decays with BaF2 crystal scintillator contaminated by radium. Eur. Phys. J. A 2014, 50, 134. [Google Scholar] [CrossRef]
- Caracciolo, V.; Cappella, F.; Cerulli, R.; Di Marco, A.; Laubenstein, M.; Nagorny, S.S.; Safonova, O.E.; Shlegel, V.N. Limits and Performances of a BaWO4 Single Crystal. Nucl. Instrum. Methods A 2018, 901, 150. [Google Scholar] [CrossRef]
- Belli, P.; Bernabei, R.; Cappella, F.; Cerulli, R.; Danevich, F.A.; Dubovik, A.M.; d’Angelo, S.; Galashov, E.N.; Grinyov, B.V.; Incicchitti, A.; et al. Radioactive contamination of ZnWO4 crystal scintillators. Nucl. Instrum. Methods A 2011, 626, 31. [Google Scholar] [CrossRef]
- Belli, P.; Bernabei, R.; Cappella, F.; Cerulli, R.; Danevich, F.A.; Dubovik, A.M.; d’Angelo, S.; Galashov, E.N.; Grinyov, B.V.; Incicchitti, A.; et al. Radiopurity of ZnWO4 crystal scintillators. Acta Phys. Polonica A 2010, 117, 139. [Google Scholar] [CrossRef]
- Belli, P.; Bernabei, R.; Cappella, F.; Cerulli, R.; Danevich, F.A.; Grinyov, B.V.; Incicchitti, A.; Kobychev, V.V.; Mokina, V.M.; Nagorny, S.S.; et al. Search for double beta decay of zinc and tungsten with low background ZnWO4 crystal scintillators. Nucl. Phys. A 2009, 826, 256. [Google Scholar] [CrossRef]
- Belli, P.; Bernabei, R.; Cappella, F.; Cerulli, R.; Danevich, F.A.; Grinyov, B.V.; Incicchitti, A.; Kobychev, V.V.; Nagornaya, L.L.; Nagorny, S.S.; et al. Search for 2β processes in 64Zn with the help of ZnWO4 crystal scintillator. Phys. Lett. B 2008, 658, 193. [Google Scholar] [CrossRef]
- Belli, P.; Bernabei, R.; Cappella, F.; Cerulli, R.; Dai, C.J.; Danevich, F.A.; d’Angelo, S.; Incicchitti, A.; Kobychev, V.V.; Poda, D.V.; et al. Final results of experiment to search for 2β processes in zinc and tungsten with the help of radiopure ZnWO4 crystal scintillators. J. Phys. G Nucl. Part. Phys. 2011, 38, 115107. [Google Scholar] [CrossRef]
- Belli, P.; Bernabei, R.; Cappella, F.; Danevich, F.A.; Denisov, V.Y.; d’Angelo, S.; Incicchitti, A.; Kobychev, V.V.; Poda, D.V.; Polischuk, O.G.; et al. Search for long-lived superheavy eka-tungsten with radiopure ZnWO4 crystal scintillator. Phys. Scr. 2015, 90, 085301. [Google Scholar] [CrossRef]
- Belli, P.; Bernabei, R.; Cappella, F.; Caracciolo, V.; Cerulli, R.; Cherubini, N.; Danevich, F.A.; Incicchitti, A.; Kasperovych, D.V.; Piccinelli, E.; et al. Measurements of ZnWO4 anisotropic response to nuclear recoils for the ADAMO project. Eur. Phys. J. A 2020, 56, 83. [Google Scholar] [CrossRef]
- Danevich, F.A.; Barabash, A.S.; Belli, P.; Bernabei, R.; Boiko, R.S.; Brudanin, V.B.; Cappella, F.; Caracciolo, V.; Cerulli, R.; Chernyak, D.M.; et al. Development of radiopure cadmium tungstate crystal scintillators from enriched 106Cd and 116Cd to search for double beta decay. AIP Conf. Proc. 2013, 1549, 201. [Google Scholar]
- Ejiri, H. Double Beta Decays and Neutrino Masses. J. Phys. Soc. Jpn. 2005, 74, 2101–2127. [Google Scholar] [CrossRef]
- Belli, P.; Bernabei, R.; Bukilic, N.; Cappella, F.; Cerulli, R.; Dai, C.J.; Danevich, F.A.; de Laeter, J.R.; Incicchitti, A.; Kobychev, V.V.; et al. Investigation of beta decay of 113Cd. Phys. Rev. C 2007, 76, 064603. [Google Scholar]
- Danevich, F.A.; Georgadze, A.S.; Kobychev, V.V.; Nagorny, S.S.; Nikolaiko, A.S.; Ponkratenko, O.A.; Tretyak, V.I.; Zdesenko, S.Y.; Zdesenko, Y.G.; Bizzeti, P.G.; et al. Alpha activity of natural tungsten isotopes. Phys. Rev. C 2003, 67, 014310. [Google Scholar] [CrossRef]
- Belli, P.; Bernabei, R.; Cappella, F.; Cerulli, R.; Dai, C.J.; Danevich, F.A.; d’Angelo, A.; Incicchitti, A.; Kobychev, V.V.; Nagorny, S.S.; et al. Search for alpha decay of natural Europium. Nucl. Phys. A 2007, 789, 15. [Google Scholar] [CrossRef]
- Zdesenko, Y.G.; Avignone, F.T.; Brudanin, V.B.; Danevich, F.A.; Nagorny, S.S.; Solsky, I.M.; Tretyak, V.I. Scintillation properties and radioactive contamination of CaWO4 crystal scintillators. Nucl. Instrum. Methods A 2005, 538, 657. [Google Scholar] [CrossRef]
- Belli, P.; Bernabei, R.; Boiko, R.S.; Cappella, F.; Cerulli, R.; Danevich, F.A.; d’Angelo, S.; Incicchitti, A.; Kobychev, V.V.; Kropivyansky, B.N.; et al. New observation of 2β2ν decay of 100Mo to the 01+ level of 100Ru in the ARMONIA experiment. Nucl. Phys. A 2010, 846, 143–156. [Google Scholar] [CrossRef]
- Polischuk, O.G.; Barabash, A.S.; Belli, P.; Bernabei, R.; Cappella, F.; Caracciolo, V.; Cerulli, R.; Chernyak, D.M.; Danevich, F.A.; d’Angelo, S.; et al. Investigation of 2β decay of 116Cd with the help of enriched 116CdWO4 crystal scintillators. AIP Conf. Proc. 2017, 1894, 020018. [Google Scholar]
- Bernabei, R.; Belli, P.; Cappella, F.; Cerulli, R.; Montecchia, F.; Nozzoli, F.; Incicchitti, A.; Prosperi, D.; Tretyak, V.I.; Zdesenko, Y.G.; et al. Search for β and ββ decays in 48Ca. Nucl. Phys. A 2002, 705, 29–39. [Google Scholar] [CrossRef]
- Belli, P.; Bernabei, R.; Cappella, F.; Cerulli, R.; Danevich, F.A.; d’Angelo, A.; Incicchitti, A.; Kobychev, V.V.; Laubenstein, M.; Polischuk, O.G.; et al. Search for 7Li solar axions using resonant absorption in LiF crystal: Final results. Phys. Lett. B 2012, 711, 41–45. [Google Scholar] [CrossRef]
- Bernabei, R.; Belli, P.; Montecchia, F.; Nozzoli, F.; d’Angelo, A.; Cappella, F.; Incicchitti, A.; Prosperi, D.; Castellano, S.; Cerulli, R.; et al. Performances and potentialities of a LaCl3:Ce scintillator. Nucl. Instrum. Methods A 2005, 555, 270–281. [Google Scholar] [CrossRef]
- Elwell, D.; Scheel, H.J. Crystal Growth from High-Temperature Solutions; Academic Press: London, UK, 2003. [Google Scholar]
- Scheel, H.J. Historical Introduction, Chapter 1 in Handbook of Crystal Growth; Hurle, D.T.J., Ed.; Elsevier: Amsterdam, The Netherlands, 1993; Volume 1. [Google Scholar]
- Scheel, H.J.; Fukuda, T. Crystal Growth Technology; Wiley: Hoboken, NJ, USA, 2003. [Google Scholar]
- Feigelson, R.S. 50 Years Progress in Crystal Growth; Elsevier: Amsterdam, The Netherlands, 2004. [Google Scholar]
- Lecoq, P.; Gektin, A.; Korzhik, M. Inorganic Scintillators for Detector Systems; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Dhanaraj, G.; Byrappa, K.; Prasad, V.; Dudley, M. Handbook of Crystal Growth; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Kubota, S.; Hishida, M.; Suzuki, M.; Ruan, J.Z. Dynamical behavior of free electrons in the recombination process in liquid argon, krypton, and xenon. Phys. Rev. B 1979, 20, 3486. [Google Scholar] [CrossRef]
- Barabanov, I.R.; Gavrin, V.N.; Pshukov, A.M. Liquid xenon scintillation spectrometer. Nucl. Instrum. Methods A 1987, 254, 355–360. [Google Scholar] [CrossRef]
- Incicchitti, A.; Belli, P.; Scafi, M. Liquid Xenon as a detector medium. Nucl. Instrum. Methods A 1990, 289, 236–242. [Google Scholar] [CrossRef]
- Belli, P.; Bernabei, R.; d’Angelo, S.; Andreanelli, L.; Bronzini, F.; Buccheri, A.; Incicchitti, A.; Prosperi, D. Liquid Xenon detectors and their applications. Nucl. Instrum. Methods A 1990, 299, 191–194. [Google Scholar] [CrossRef]
- Belli, P.; Bernabei, R.; d’Angelo, S.; Incicchitti, A.; Prosperi, D. Detecting ’dark matter’ using a liquid xenon scintillation detector. Nuovo Cimento A 1990, 103, 767–771. [Google Scholar] [CrossRef]
- Belli, P.; Bernabei, R.; d’Angelo, S.; Incicchitti, A.; Prosperi, D. Liquid xenon scintillators. Nucl. Instrum. Methods A 1991, 310, 150–153. [Google Scholar] [CrossRef]
- Belli, P.; Bernabei, R.; Bacci, C.; Incicchitti, A.; Marcovaldi, R.; Prosperi, D. Liquid xenon detectors for dark matter experiments. Nucl. Instrum. Methods A 1992, 316, 55–57. [Google Scholar] [CrossRef]
- Belli, P.; Bernabei, R.; Di Nicolantonio, W.; Landoni, V.; Montecchia, F.; Incicchitti, A.; Prosperi, D.; Bacci, C.; Besida, O.; Dai, C.J. Search for WIMPs with enriched xenon at Gran Sasso. Nuovo Cimento C 1996, 19, 537–544. [Google Scholar] [CrossRef]
- Belli, P.; Bernabei, R.; Di Nicolantonio, W.; Landoni, V.; Incicchitti, A.; Prosperi, D.; Dai, C.J.; Bacci, C. Charge conservation and electron lifetime: Limits from a liquid xenon scintillator. Astropart. Phys. 1996, 5, 217–219. [Google Scholar] [CrossRef]
- Belli, P.; Bernabei, R.; Di Nicolantonio, W.; Landoni, V.; Montecchia, F.; Incicchitti, A.; Prosperi, D.; Bacci, C.; Dai, C.J. Limits on WIMP–129Xe inelastic scattering. Phys. Lett. B 1996, 387, 222–226. [Google Scholar] [CrossRef]
- Bernabei, R.; Belli, P.; Montecchia, F.; Incicchitti, A.; Prosperi, D.; Dai, C.J.; Angelone, M.; Batistoni, P.; Pillon, M. New limits on particle dark matter search with a liquid Xenon target-scintillator. Phys. Lett. B 1998, 436, 379–388. [Google Scholar] [CrossRef]
- Belli, P.; Bernabei, R.; Dai, C.J.; Ignesti, G.; Incicchitti, A.; Montecchia, F.; Ponkratenko, O.A.; Prosperi, D.; Tretyak, V.I.; Zdesenko, Y.G. Charge non–conservation restrictions from the nuclear levels excitation of Xe–129 induced by the electron’s decay on the atomic shell. Phys. Lett. B 1999, 465, 315–322. [Google Scholar] [CrossRef]
- Belli, P.; Bernabei, R.; Dai, C.J.; Ignesti, G.; Incicchitti, A.; Montecchia, F.; Ponkratenko, O.A.; Prosperi, D.; Tretyak, V.I.; Zdesenko, Y.G. Quest for electron decay e−→νeγ with a liquid xenon scintillator. Phys. Rev. D 2000, 61, 117301. [Google Scholar] [CrossRef]
- Bernabei, R.; Amato, M.; Belli, P.; Cerulli, R.; Dai, C.J.; Denisov, V.Y.; He, H.L.; Incicchitti, A.; Kuang, H.H.; Ma, J.M.; et al. Search for the nucleon and di-nucleon decay into invisible channels. Phys. Lett. B 2000, 493, 12–18. [Google Scholar] [CrossRef]
- Bernabei, R.; Belli, P.; Cerulli, R.; Montecchia, F.; Incicchitti, A.; Prosperi, D.; Dai, C.J.; Angelone, M.; Batistoni, P.; Pillon, M. Light response of a pure liquid xenon scintillator irradiated with 2.5 MeV neutrons. Eur. Phys. J. 2001, 3, 1–11. [Google Scholar] [CrossRef]
- Bernabei, R.; Belli, P.; Cappella, F.; Cerulli, R.; Montecchia, F.; Incicchitti, A.; Prosperi, D.; Dai, C.J. Search for neutrinoless beta beta decay in 134Xe. Phys. Lett. B 2002, 527, 182–186. [Google Scholar] [CrossRef]
- Bernabei, R.; Belli, P.; Cappella, F.; Cerulli, R.; Montecchia, F.; Incicchitti, A.; Prosperi, D.; Dai, C.J. Investigation of beta beta decay modes in 134Xe and 136Xe. Phys. Lett. B 2002, 546, 23–28. [Google Scholar] [CrossRef]
- Bernabei, R.; Belli, P.; Bussolotti, A.; Cappella, F.; Cerulli, R.; Montecchia, F.; Dai, C.J.; Incicchitti, A.; Mattei, A.; Prosperi, D. The liquid xenon set-up of the DAMA experiment. Nucl. Instrum. Methods A 2002, 482, 728–743. [Google Scholar] [CrossRef]
- Collar, J.I. A Realistic Assessment of the Sensitivity of XENON10 and XENON100 to Light-Mass WIMPs. arXiv 2011, arXiv:1106.0653. [Google Scholar]
- Doke, T. Fundamental properties of liquid argon, krypton and xenon as radiation detector media. Port. Phys. 1981, 12, 9. [Google Scholar]
- Brassard, C. Liquid ionization detectors. Nucl. Instrum. Methods 1979, 162, 29. [Google Scholar] [CrossRef]
- Feltesse, J. Liquid noble gas and warm liquid detectors. Nucl. Instrum. Methods A 1989, 283, 375. [Google Scholar] [CrossRef]
- Davies, G.J.; Davies, J.D.; Lewin, J.D.; Smith, P.F.; Jones, W.G. Liquid xenon as a dark matter detector. Prospects for nuclear recoil discrimination by photon timing. Phys. Lett. B 1994, 320, 395. [Google Scholar] [CrossRef]
- Asakura, K.; Gando, A.; Gando, Y.; Hachiya, T.; Hayashida, S.; Ikeda, H.; Inouea, K.; Ishidoshiro, K.; Ishikawa, T.; Ishio, S.; et al. Search for double-beta decay of 136Xe to excited states of 136Ba with the KamLAND-Zen experiment. Nucl. Phys. A 2016, 946, 171–181. [Google Scholar] [CrossRef]
- Galan, J. Microbulk MicrOMEGAs for the search of 0νββ of 136Xe in the PandaX-III experiment. JINST 2016, 11, P04024. [Google Scholar] [CrossRef]
- Albert, J.B.; Auger, M.; Auty, D.J.; Barbeau, P.S.; Beauchamp, E.; Beck, D.; Belov, V.; Benitez-Medina, C.; Bonatt, J.; Breidenbach, M.; et al. Improved measurement of the 2νββ half-life of 136Xe with the EXO-200 detector. Phys. Rev. C 2014, 89, 015502. [Google Scholar] [CrossRef]
- Agostini, F.; Ahmed Maouloud, S.E.M.; Althueser, L.; Amaro, F.; Antunovic, B.; Aprile, E.; Baudis, L.; Baur, D.; Biondi, Y.; Bismark, A.; et al. Sensitivity of the DARWIN observatory to the neutrinoless double beta decay of 136Xe. Eur. Phys. J. C 2020, 80, 808. [Google Scholar] [CrossRef]
- Bernabei, R.; Belli, P.; Incicchitti, A.; Prosperi, D. Liquid Noble Gases for Dark Matter Searches: A Synoptic Survey; Exorma: Rome, Italy, 2009; ISBN 978-88-95688-12-1. [Google Scholar]
- Bernabei, R.; Belli, P.; Incicchitti, A.; Cappella, F.; Cerulli, R. Liquid Noble gases for Dark Matter searches: An updated survey. Int. J. Mod. Phys. A 2015, 30, 1530053. [Google Scholar] [CrossRef]
- Doke, T.; Hitachi, A.; Kikuchi, J.; Masuda, K.; Okada, H.; Shibamura, E. Absolute Scintillation Yields in Liquid Argon and Xenon for Various Particles. Jpn. J. Appl. Phys. 2002, 41, 1538. [Google Scholar] [CrossRef]
- Shutt, T.; Dahl, C.E.; Kwong, J.; Bolozdynya, A.; Brusov, P. Performance and fundamental processes at low energy in a two-phase liquid xenon dark matter detector. Nucl. Phys. B 2007, 173, 160. [Google Scholar] [CrossRef]
- Chepel, V.; Araújo, H. Liquid noble gas detectors for low energy particle physics. JINST 2013, 8, R04001. [Google Scholar] [CrossRef]
- Fiorini, E.; Niinikoski, T.O. Low-temperature calorimetry for rare decays. Nucl. Instrum. Methods A 1984, 224, 83. [Google Scholar] [CrossRef]
- Goulding, F.S.; Landis, D.A. Semiconductor Detector Spectrometer Electronics. Pure Appl. Phys. 1974, 40, 413–481. [Google Scholar]
- Swartz, E.T.; Pohl, R.O. Thermal boundary resistance. Rev. Mod. Phys. 1989, 61, 605–668. [Google Scholar] [CrossRef]
- Pirro, S. Further developments in mechanical decoupling of large thermal detectors. Nucl. Instrum. Methods A 2009, 559, 672–674. [Google Scholar] [CrossRef]
- Barucci, M.; Beeman, J.W.; Caracciolo, V.; Pagnanini, L.; Pattavina, L.; Pessina, G.; Pirro, S.; Rusconi, C.; Schäffner, K. Cryogenic light detectors with enhanced performance for rare event physics. Nucl. Instrum. Methods A 2019, 935, 150–155. [Google Scholar] [CrossRef]
- Razeti, M. Distillation and separation of some rare isotopes and their applications. Nuovo Cimento C 2017, 41, 84. [Google Scholar]
- Agnes, P.; Albergo, S.; Albuquerque, I.F.M.; Alexander, T.; Alici, A.; Alton, A.K.; Amaudruz, P.; Arba, M.; Arpaia, P.; Arcelli, S. Separating 39Ar from 40Ar by cryogenic distillation with Aria for dark matter searches. arXiv 2021, arXiv:2101.08686. [Google Scholar]
- Dell’Oro, S.; Marcocci, S.; Vissani, F. New expectations and uncertainties on neutrinoless double beta decay. Phys. Rev. D 2014, 90, 033005. [Google Scholar] [CrossRef]
- Caracciolo, V. Feasibility Study of an Experiment to Investigate the Double Beta Decay Modes in 106Cd. Ph.D. Thesis, University of L’Aquila, L’Aquila, Italy, 2012. [Google Scholar]
- Agostinelli, S.; Allison, J.; Amako, K.; Apostolakis, L.; Araujoa, H.; Arce, P.; Asaiga, M.; Axeni, D.; Banerjee, S.; Barrand, G.; et al. GEANT4—A simulation toolkit. Nucl. Instrum. Methods A 2003, 506, 250. [Google Scholar] [CrossRef]
- Allison, J.; Amako, K.; Apostolakis, J.; Araujo, H.; Arce Dubois, P.; Asai, M.; Barrand, G.; Capra, R.; Chauvie, S.; Chytracek, R.; et al. Geant4 developments and applications. IEEE Trans. Nucl. Sci. 2006, 53, 270. [Google Scholar] [CrossRef]
- Ponkratenko, O.A.; Tretyak, V.I.; Zdesenko, Y.G. Event generator DECAY4 for simulating double-beta processes and decays of radioactive nuclei. Phys. At. Nucl. 2000, 63, 1282. [Google Scholar] [CrossRef]
- Tretyak, V.I.; (Institute for Nuclear Research of NASU, Kyiv, Ukraine). Private communication, 2007.
- Wang, M.; Audi, G.; Kondev, F.G.; Huang, W.J.; Naimi, S.; Xu, X. The Ame2016 atomic mass evaluation. Chin. Phys. C 2017, 41, 030003. [Google Scholar] [CrossRef]
- Beck, M.; Bockholt, J.; Echternach, J.; Heusse, G.; Hirsch, M.; Klapdor-Kleingrothaus, H.V.; Piepke, A.; Strecker, H.; Zuber, K.; Bakalyarov, A.; et al. New half life limits for the ββ2ν+0ν decay of 76Ge to the excited states of 76Se from the Heidelberg-Moscow ββ experiment. Z. Phys. A 1992, 343, 397. [Google Scholar] [CrossRef]
- Meija, J.; Coplen, T.B.; Berglund, M.; Brand, A.; De Biévre, P.; Gröning, M.; Holden, N.E.; Irrgeher, J.; Loss, R.D.; Walczyk, T.; et al. Isotopic compositions of the elements 2013 (IUPAC Technical Report). Pure Appl. Chem. 2016, 88, 293. [Google Scholar] [CrossRef]
- Gavrilyuk, Y.M.; Gangapshev, A.M.; Kazalov, V.V.; Kuzminov, V.V.; Panasenko, S.I.; Ratkevich, S.S. Indications of 2ν2K capture in 78Kr. Phys. Rev. C 2013, 87, 035501. [Google Scholar] [CrossRef]
- Ratkevich, S.S.; Gangapshev, A.M.; Gavrilyuk, Y.M.; Karpeshin, F.F.; Kazalov, V.V.; Kuzminov, V.V.; Panasenko, S.I.; Trzhaskovskaya, M.B.; Yakimenko, S.P. Comparative study of the double-K-shell-vacancy production in single- and double-electron-capture decay. Phys. Rev. C 2017, 96, 065502. [Google Scholar] [CrossRef]
- Sáenz, C.; Cerezo, E.; García, E.; Morales, A.; Morales, J.; Núñez-Lagos, R.; Ortiz de Solórzano, A.; Puimedón, J.; Salinas, A.; Sarsa, M.L.; et al. Results of a search for double positron decay and electron-positron conversion of 78Kr. Phys. Rev. C 1994, 50, 1170. [Google Scholar] [CrossRef]
- Aprile, E.; Aalbers, J.; Agostini, F.; Alfonsi, M.; Althueser, L.; Amaro, F.D.; Anthony, M.; Antochi, V.C.; Arneodo, F.; Baudis, L.; et al. Observation of two-neutrino double electron capture in 124Xe with XENON1T. Nature 2019, 568, 532–535. [Google Scholar]
- Abe, K.; Hiraide, K.; Ichimura, K.; Kishimoto, Y.; Kobayashi, K.; Kobayashi, M.; Moriyama, S.; Nakahata, M.; Norita, T.; Ogawa, H.; et al. Improved search for two-neutrino double electron capture on 124Xe and 126Xe using particle identification in XMASS-I. Prog. Theor. Exp. Phys. 2018, 5, 053D03. [Google Scholar]
- Barabash, A.S.; Kuzminov, V.V.; Lobashev, V.M.; Movikov, V.M.; Ovchinnikov, B.M.; Pomansky, A.A. Results of the experiment on the search for double beta decay of 136Xe, 134Xe and 124Xe. Phys. Lett. B 1989, 223, 273–276. [Google Scholar] [CrossRef]
- Meshik, A.P.; Hohenberg, C.M.; Pravdivtseva, O.V.; Kapusta, Y.S. Weak decay of 130Ba and 132Ba: Geochemical measurements. Phys. Rev. C 2001, 64, 035205. [Google Scholar] [CrossRef]
- Pujol, M.; Marty, B.; Burnard, P.; Philippot, P. Xenon in Archean barite: Weak decay of 130Ba, mass-dependent isotopic fractionation and implication for barite formation. Geochim. Cosmochim. Acta 2009, 73, 6834–6846. [Google Scholar] [CrossRef]
- Barabash, A.S.; Saakyan, R.R. Experimental limits on 2β+, Kβ+, and 2K processes for 130Ba and on 2K capture for 132Ba. Phys. At. Nucl. 1996, 59, 179–184. [Google Scholar]
- Srinivasan, B. Barite: Anomalous xenon from spallation and neutron-induced reactions. Earth Planet. Sci. Lett. 1976, 31, 129–141. [Google Scholar] [CrossRef]
- Aunola, M.; Suhonen, J. Systematic study of beta and double beta decay to excited final states. Nucl. Phys. A 1996, 602, 133. [Google Scholar] [CrossRef]
- Rumyantsev, O.A.; Urin, M.H. The strength of the analog and Gamow-Teller giant resonances and hindrance of the 2νβ+β+ decay rate. Phys. Lett. B 1998, 51, 443. [Google Scholar]
- Staudt, A.; Muto, K.; Klapdor-Kleingrothaus, H.V. Nuclear matrix elements for double positron emission. Phys. Let. B 1991, 268, 312–316. [Google Scholar] [CrossRef]
- Mishra, S.; Shukla, A.; Sahu, R.; Kota, V.K.B. Deformed shell model calculations of half lives for β+/EC decay and 2ν β+β+/β+EC/ECEC decay in medium-heavy NZ nuclei. Phys. Rev. C 2008, 78, 024307. [Google Scholar] [CrossRef]
- Domir, P.; Kovalenko, S.; Šimkovic, F.; Semeno, S.V. Neutrino accompanied βpmβpm, β+/EC and EC/EC processes within single state dominance hypothesis. Nucl. Phys. A 2005, 753, 337–363. [Google Scholar]
- Sahu, R.; Kota, V.K.B. Deformed shell model studies of spectroscopic properties of 64Zn and 64Ni and the positron double beta decay of 64Zn. Pramana 2014, 82, 757. [Google Scholar] [CrossRef]
- Gavriljuk, J.M.; Kuzminov, V.V.; Osetrova, N.Y.; Ratkevich, S.S. New limit on the half-life of 78Kr with respect to the 2K(2ν)-capture decay mode. Phys. At. Nucl. 2000, 63, 2201–2204. [Google Scholar] [CrossRef][Green Version]
- Gavrilyuk, Y.M.; Gangapshev, A.M.; Kazalov, V.V.; Kuzminov, V.V.; Panasenko, S.I.; Ratkevich, S.S.; Yakimenko, S.P. Investigating 2K capture in 78Kr with a large-volume copper proportional counter. Bull. Russ. Ac. Sci. Phys. 2011, 75, 526. [Google Scholar] [CrossRef]
- Ameenah, R.F.; Balraj, S. Nuclear Data Sheets for A = 78. Nucl. Data Sheets 2009, 110, 1917–2080. [Google Scholar]
- Hirsch, M.; Muto, K.; Oda, T.; Klapdor-Kleingrothaus, H.V. Nuclear structure calculation of β+β+, β+/EC and EC/EC decay matrix elements. Z. Phys. A 1994, 347, 151. [Google Scholar] [CrossRef]
- Suhonen, J. Double beta decays of 124Xe investigated in the QRPA framework. J. Phys. G 2013, 40, 075102. [Google Scholar] [CrossRef]
- Singh, S.; Chandra, R.; Rath, P.K.; Raina, P.K.; Hirsch, J.G. Nuclear deformation and the two-neutrino double-β decay in 124,126Xe, 128,130Te, 130,132Ba and 150Nd isotopes. Eur. Phys. J. A 2007, 33, 375. [Google Scholar] [CrossRef]
- Shukla, A.; Raina, P.K.; Rath, P.K. Study of two neutrino β+β+/β+EC/ECEC decay of 124,126Xe and 130,132Ba for 0+→0+ transition in PHFB model. J. Phys. G Nucl. Part. Phys. 2007, 34, 549. [Google Scholar] [CrossRef]
- Nesterenko, D.A.; Blaum, K.; Block, M.; Droese, C.; Eliseev, S.; Herfurth, F.; Minaya Ramirez, E.; Novikov, Y.N.; Schweikhard, L.; Shabaev, V.M.; et al. Double-β transformations in isobaric triplets with mass numbers A = 124, 130 and 136. Phys. Rev. C 2012, 86, 044313. [Google Scholar] [CrossRef]
- Barabash, A. Precise Half-Life Values for Two-Neutrino Double-β Decay: 2020 review. Universe 2020, 6, 159. [Google Scholar] [CrossRef]
- Gavrilyuk, Y.M.; Gangapshev, A.M.; Kazalov, V.V.; Kuzminov, V.V.; Panasenko, S.I.; Ratkevich, S.S.; Tekueva, D.A.; Yakimenko, S.P. Search for 2K(2ν)-capture of 124Xe. Phys. Part. Nucl. 2017, 48, 38. [Google Scholar] [CrossRef]
- Abe, K.; Hiraide, K.; Ichimura, K.; Kishimoto, Y.; Kobayashi, K.; Kobayashi, M.; Moriyama, S.; Nakagawa, K.; Nakahata, M.; Norita, T. Search for two-neutrino double electron capture on 124Xe with the XMASS-I detector. Phys. Lett. B 2016, 759, 64. [Google Scholar] [CrossRef]
- Aprile, E.; Aalbers, J.; Agostini, F.; Alfonsi, M.; Amaro, F.D.; Anthony, M.; Arneodo, F.; Barrow, P.; Baudis, L.; Bauermeister, B. Search for two-neutrino double electron capture of 124Xe with XENON100. Phys. Rev. C 2017, 95, 024605. [Google Scholar] [CrossRef]
- Katakura, J.; Wu, Z.D. Nuclear Data Sheets for A = 124. Nucl. Data Sheets 2008, 109, 1655–1877. [Google Scholar] [CrossRef]
- Barabash, A.S. How to detect two-neutrino double K capture in a direct (counter) experiment. JETP Lett. 1994, 59, 644. [Google Scholar]
- Meshik, A.; Pravdivtseva, O. Weak Decay of Tellurium and Barium Isotopes in Geological Samples: Current Status. JPS Conf. Proc. 2017, 14, 020702. [Google Scholar]
- Balraj, S. Nuclear Data Sheets for A = 130. Nucl. Data Sheets 2001, 93, 33–242. [Google Scholar]
- Angloher, G.; Bauer, M.; Bauer, P.; Bavykina, I.; Bento, A.; Bucci, C.; Canonica, L.; Ciemniak, C.; Defay, X.; Deuter, G.; et al. New limits on double electron capture of 40Ca and 180W. Nucl. Phys. G 2016, 43, 095202. [Google Scholar] [CrossRef]
- Latest COBRA Annual Report. Available online: https://www.cobra-experiment.org/ (accessed on 1 January 2021).
- Joachim, E.; Fritts, M.; Gehre, D.; Gößling, C.; Hagner, C.; Heidrich, N.; Klingenberg, R.; Kröninger, K.; Nitsch, K.; Oldorf, C.; et al. Results of a search for neutrinoless double-β decay using the COBRA demonstrator. Phys. Rev. C 2016, 94, 024603. [Google Scholar]
- Alduino, C.; Alfonso, K.; Artusa, D.R.; Avignone, F.T., III; Azzolini, O.; Bari, G.; Bellini, F.; Benato, G.; Bersani, A.; Biassoni, M.; et al. Search for neutrinoless β+EC decay of 120Te with CUORE-0. Phys. Rev. C 2018, 97, 055502. [Google Scholar] [CrossRef]
- Alduino, C.; Alfonso, K.; Artusa, D.R.; Avignone, F.T., III; Azzolini, O.; Bari, G.; Bellini, F.; Benato, G.; Bersani, A.; Biassoni, M.; et al. CUORE-0 detector: Design, construction and operation. J. Instrum. 2016, 11, P07009. [Google Scholar] [CrossRef]
- Alfonso, K.; Artusa, D.R.; Avignone, F.T., III; Azzolini, O.; Balata, M.; Banks, T.I.; Bari, G.; Beeman, J.W.; Bellini, F.; Bersani, A.; et al. Search for Neutrinoless Double-Beta Decay of 130Te with CUORE-0. Phys. Rev. Lett. 2015, 115, 102502. [Google Scholar] [CrossRef]
- Armstrong, W.R.; Chang, C.; Hafidi, K.; Lisovenko, M.; Novosad, V.; Pearson, J.; Polakovic, T.; Wang, G.; Yefremenko, V.; Zhang, J.; et al. CUPID pre-CDR. arXiv 2019, arXiv:1907.09376. [Google Scholar]
- Ching, C.; Ho, T.; Zhao, W. Is 40Ca A Stable Isotope? Commun. Theor. Phys. 1984, 3, 517–520. [Google Scholar] [CrossRef]
- Belli, P.; Bernabei, R.; Dai, C.J.; Grianti, F.; He, H.L.; Ignesti, G.; Incicchitti, A.; .Kuang, H.H.; Ma, J.M.; Montecchia, F.; et al. New limits on spin-dependent coupled WIMPs and on 2β processes in 40Ca and 46Ca by using low radioactive CaF2(Eu) crystal scintillators. Nucl. Phys. B 1999, 563, 97–106. [Google Scholar] [CrossRef]
- Bellini, F.; Beretta, M.; Cardani, L.; Carniti, P.; Casali, N.; Celi, E.; Chiesa, D.; Clemenza, M.; Dafinei, I.; Di Domizio, S.; et al. Search for double β-decay modes of 64Zn using purified zinc. Eur. Phys. J. C 2021, 81, 106. [Google Scholar] [CrossRef]
- Azzolini, O.; Beeman, J.W.; Bellini, F.; Beretta, M.; Biassoni, M.; Brofferio, C.; Bucci, C.; Capelli, S.; Cardani, L.; Celi, C. Search for neutrinoless double beta decay of 64Zn and 70Zn with CUPID-0. Eur. Phys. J. C 2020, 80, 702. [Google Scholar] [CrossRef]
- Kiel, H.; Münstermann, D.; Zuber, K. A search for various double beta decay modes of Cd, Te, and Zn isotopes. Nucl. Phys. A 2003, 723, 499–514. [Google Scholar] [CrossRef][Green Version]
- Barabash, A.S.; Hubert, F.; Hubert, P.; Umatov, V. New limits on the β+EC and ECEC processes in 120Te. J. Phys. G 2007, 34, 1721–1728. [Google Scholar] [CrossRef][Green Version]
- Dawson, J.V.; Goessling, C.; Janutta, B.; Junker, M.; Koettig, M.; Muenstermann, D.; Rajek, S.; Reeve, C.; Schulz, O.; Wilson, J.R.; et al. Experimental study of double-β decay modes using a CdZnTe detector array. Phys. Rev. C 2009, 80, 025502. [Google Scholar] [CrossRef]
- Andreotti, E.; Arnaboldi, C.; Avignone, F.T., III; Balata, M.; Bandac, I.; Barucci, M.; Beeman, J.W.; Bellini, F.; Broferio, C.; Bryant, A.; et al. Search for β+/EC double beta decay of 120Te. Astropart. Phys. 2011, 34, 643–648. [Google Scholar] [CrossRef][Green Version]
- Bikit, I.; Slivka, J.; Anicin, I.; Veskovic, M.; Conkic, L. Electron-positron conversion decay of 64Zn. Appl. Radiat. Isot. 1995, 46, 455. [Google Scholar] [CrossRef]
- Pirinen, P.; Suhonen, J. Systematic approach to β and 2νββ decays of mass A=100-136 nuclei. Phys. Rev. C 2015, 91, 054309. [Google Scholar] [CrossRef]
- Danevich, F.A.; Georgadze, A.S.; Kobychev, V.V.; Nikolaiko, A.S.; Ponkratenko, O.A.; Tretyak, V.I.; Zdesenko, S.Y.; Zdesenko, Y.G.; Bizzeti, P.G.; Fazzini, T.F.; et al. Two-neutrino 2βdecay of 116Cd and new half-lifelimits on 2β decay of 180W and 186W. Nucl. Phys. A 2003, 717, 129–145. [Google Scholar] [CrossRef]
- Kang, W.G.; Choi, J.H.; Jeon, E.J.; Lee, J.I.; Kim, H.J.; Kim, S.K.; Kim, Y.D.; Lee, J.H.; Maa, K.J.; Myung, S.S.; et al. Ultra-low gamma-ray measurement system for neutrinoless double beta decay. Appl. Rad. Isot. 2013, 81, 290–293. [Google Scholar] [CrossRef] [PubMed]
- Barabash, A.S.; Gurrianin, R.; Hubert, F.; Hubert, P.; Umatov, V.I. Improved limits on double beta processes in 92Mo. Z. Phys. A 1997, 357, 351–352. [Google Scholar] [CrossRef]
- Bellotti, E.; Fiorini, E.; Liguori, C.; Pullia, A.; Sarbacino, A.; Zanotti, L. An experimental investigation on lepton number conservation in double-beta processes. Lett. Nuovo Cimento 1982, 33, 273. [Google Scholar] [CrossRef]
- Lee, J.I.; Bhang, H.C.; Choi, J.H.; Jeon, E.J.; Kang, W.G.; Kim, H.J.; Kim, S.C.; Kim, S.K.; Kim, Y.D.; Leeet, J.H.; et al. Experimental study on neutrinoless double beta decay of 92Mo. Nucl. Instrum. Met. A 2011, 654, 157–161. [Google Scholar] [CrossRef]
- Rukhadze, N.I.; Briancon, C.; Brudanin, B.B.; Egorov, V.G.; Klimenko, A.A.; Kovalik, A.; Timkin, V.V.; Čhermák, P.; Shitov, Y.A.; Šimkovic, F.; et al. Search for double-β decay of 106Cd. Bull. Russ. Acad. Sci. Phys. 2011, 75, 879. [Google Scholar] [CrossRef]
- Belli, P.; Bernabei, R.; Boiko, R.S.; Cappella, R.; Cerulli, R.; Danevich, F.A.; Incicchitti, A.; Kropivyansky, B.N.; Laubenstein, M.; Poda, D.V.; et al. Search for double beta decay of 136Ce and 138Ce with HPGe gamma detector. Nulc. Phys. A 2014, 930, 195–208. [Google Scholar] [CrossRef]
- Belli, P.; Bernabei, R.; Boiko, R.S.; Cappella, F.; Cerulli, R.; Danevich, F.A.; Incicchitti, A.; Kropivyansky, B.N.; Laubenstein, M.; Mokina, V.M.; et al. New limits on 2ϵ, ϵβ+ and 2ϵ decay of 136Ce and 138Ce with deeply purified cerium sample. Eur. Phys. J. A 2017, 53, 172. [Google Scholar] [CrossRef]
- De Frenne, D.; Negret, A. Nuclear data sheets for A = 106. Nucl. Data Sheets 2008, 109, 943–1102. [Google Scholar] [CrossRef]
- Tretyak, V.I.; Belli, P.; Bernabei, R.; Brudanin, V.B.; Cappella, F.; Caracciolo, V.; Cerulli, R.; Chernyak, D.M.; Danevich, D.F.; d’Angelo, S.; et al. First results of the experiment to search for 2β decay of 106Cd with 106CdWO4 crystal scintillator in coincidence with four crystals HPGe detector. EPJ Web Conf. 2014, 65, 01003. [Google Scholar] [CrossRef]
- Danevich, F.A.; Belli, P.; Bernabei, R.; Brudanin, V.B.; Cappella, F.; Caracciolo, V.; Cerulli, R.; Chernyak, D.M.; d’Angelo, S.; Incicchitti, A.; et al. Search for double beta processes in 106Cd with enriched 106CdWO4 crystal scintillator in coincidence with four crystals HPGe detector. AIP Conf. Proc. 2015, 1686, 020006. [Google Scholar]
- Tretyak, V.I.; Belli, P.; Bernabei, R.; Brudanin, V.B.; Cappella, F.; Caracciolo, V.; Cerulli, R.; Chernyak, D.M.; Danevich, D.F.; d’Angelo, S.; et al. New limits on 2β processes in 106Cd. J. Phys. Conf. Ser. 2016, 718, 062062. [Google Scholar] [CrossRef]
- Nozzoli, F. 146Nd, 144Sm, and other unexplored 2β-decay isotopes. Phys. Rev. C 2018, 97, 015501. [Google Scholar] [CrossRef]
- Belli, P.; Bernabei, R.; Cappella, F.; Cerulli, R.; Danevich, F.A.; d’Angelo, S.; Di Vacri, M.L.; Incicchitti, A.; Laubenstein, M.; Nagaorny, S.S. First search for double β decay of dysprosium. Nucl. Phys. A 2011, 859, 126–139. [Google Scholar] [CrossRef]
- Finch, S.W.; Tornow, W. Search for neutrinoless double-electron capture of 156Dy. Phys. Rev. C 2015, 92, 065503. [Google Scholar] [CrossRef]
- Laubenstein, M. Screening of materials with high purity germanium detectors at the Laboratori Nazionali del Gran Sasso. Int. J. Mod. Phys. A 2017, 32, 1743002. [Google Scholar] [CrossRef]
- Agostini, M.; Allardt, M.; Bakalyarov, A.M.; Balata, M.; Barabanov, I.; Barros, N.; Baudis, L.; Bauer, C.; Bellotti, E.; Belogurov, S.; et al. Limit on the radiative neutrinoless double electron capture of 36Ar from GERDA Phase I. Eur. Phys. J. C 2016, 76, 652. [Google Scholar] [CrossRef][Green Version]
- Bikit, I.; Zikić-Todorović, N.; Slivka, J.; Vesković, M.; Krmar, M.; Čonkić, L.J.; Puzović, J.; Aničin, I.V. Double β decay of 50 Cr. Phys. Rev. C 2003, 67, 065801. [Google Scholar] [CrossRef]
- Norman, E.B. Improved limits on the double beta decay half-lives of 50Cr, 64Zn, 92Mo and 96Ru. Phys. Rev. C 1973, 31, 1937. [Google Scholar] [CrossRef]
- Bikit, I.; Krmat, M.; Slivka, J.; Vesković, M.; Čonkić, L.J.; Aničin, I.V. New results on the double β decay of Iron. Phys. Rev. C 1998, 58, 2566. [Google Scholar] [CrossRef]
- Rukhadze, N.I.; Brudanin, V.B.; Klimenko, A.A.; Piquemal, F.; Rukhadze, E.N.; Shitov, Y.A.; Štekl, I.; Warot, G. Investigating the Double Beta Decay of 58Ni. Bull. Rus. Ac. Sci. Phys. 2018, 82, 708–711. [Google Scholar] [CrossRef]
- Jeskovsky, M.; Frekers, D.; Kovacik, A.; Povinec, P.P.; Puppe, P.; Stanicek, J.; Sykora, I.; Simkovic, F.; Thies, J.H. A search for double-electron capture in 74Se using coincidence/anticoincidence gamma-ray spectrometry. arXiv 2015, arXiv:1507.02200. [Google Scholar]
- Barabash, A.S.; Brudanin, V.B.; Klimenko, A.A.; Konovalov, S.I.; Rakhimov, A.V.; Rukhadze, E.N.; Rukhadze, N.I.; Shitov, Y.A.; Stekl, I.; Warot, G.; et al. Improved limits on β+EC and ECEC processes in 74Se. Nucl. Phys. A 2020, 996, 121697. [Google Scholar] [CrossRef]
- Frekers, D.; Puppe, P.; Thies, J.H.; Povinec, P.P.; Šimkovic, F.; Staniček, J.; Sýkora, I. Double-electron capture of 74Se and the search for neutrinoless decay. Nucl. Phys. A 2011, 860, 1–7. [Google Scholar] [CrossRef]
- Belli, P.; Bernabei, R.; Cappella, F.; Cerulli, R.; Danevich, F.A.; d’Angelo, S.; Incicchitti, A.; Kovtun, G.P.; Kovtun, N.G.; Laubenstein, M.; et al. Search for 2β decays of 96Ru and 104Ru by ultralow-background HPGe γ spectrometry at LNGS: Final results. Phys. Rev. C 2013, 87, 034607. [Google Scholar] [CrossRef]
- Lehnert, B.; Andreotti, E.; Degering, D.; Hult, M.; Laubenstein, M.; Wester, T.; Zuber, K. Double beta decays into excited states in 110Pd and 102Pd. J. Phys. G 2016, 43, 115201. [Google Scholar] [CrossRef][Green Version]
- Barabash, A.S.; Hubert, P.; Nachab, A.; Konovalov, S.I.; Umatov, V. Improved limits on β+EC and ECEC processes in 112Sn. Phys. Rev. C 2011, 83, 045503. [Google Scholar] [CrossRef]
- Ješkovský, M.D.; Fekers, D.; Kováčik, A.; Povinec, P.P.; Puppe, P.; Staníček, J.; Sýcora, I.; Šimkovic, F.; Thies, J.H. A search for double-electron capture of 74Se to excited levels using coincidence/anticoincidence gamma-ray spectrometry. Nucl. Instrum. Methods A 2015, 795, 268–275. [Google Scholar] [CrossRef]
- Lehnert, B.; Wester, T.; Degering, D.; Somme, D.; Wagner, L.; Zuber, K. Double electron capture searches in 74Se. J. Phys. G 2016, 43, 085201. [Google Scholar] [CrossRef][Green Version]
- Boiko, R.S. Chemical purification of lanthanides for low-background experiments. Int. J. Mod. Phys. A 2017, 32, 1743005. [Google Scholar] [CrossRef]
- Marchegiani, F.; Ferella, F.; Nisi, S. Material screening with mass spectrometry. Physics 2021, 3, 71–84. [Google Scholar] [CrossRef]
- Polischuk, O.G.; Barabash, A.S.; Belli, P.; Bernabei, R.; Boiko, R.S.; Cappella, F.; Cerulli, R.; Danevich, F.A.; Incicchitti, A.; Laubenstein, M.; et al. Purification of Lanthanides for Double Beta Decay Experiments. AIP Conf. Proc. 2013, 1549, 124. [Google Scholar]
- Boiko, R.S.; Barabash, A.S.; Belli, P.; Bernabei, R.; Cappella, F.; Cerulli, R.; Danevich, F.A.; Incicchitti, A.; Laubenstein, M.; Mokina, V.M.; et al. Purification of cerium, neodymium and gadolinium for low background experiments. EPJ Web Conf. 2014, 65, 04001. [Google Scholar] [CrossRef]
- Danevich, F.A.; Hult, M.; Kasperovych, D.V.; Kovtunc, G.P.; Kovtun, K.V.; Lutter, G.; Marissens, G.; Polischuk, O.G.; Stetsenko, S.P.; Tretyak, V.I. First search for 2ϵ and ϵβ+ decay of 174Hf. Nucl. Phys. A 2020, 996, 121703. [Google Scholar] [CrossRef]
- Belli, P.; Bernabei, R.; Cappella, F.; Caracciolo, V.; Cerulli, R.; Danevich, F.A.; Incicchitti, A.; Kasperovych, D.V.; Kobychev, V.V.; Kovtun, G.G.; et al. New experimental limits on double-beta decay of osmium. J. Phys. G Nucl. Part. Phys. 2021. accepted for publication. [Google Scholar] [CrossRef]
- Belli, P.; Bernabei, R.; Cappella, F.; Cerulli, R.; Danevich, F.A.; d’Angelo, S.; Di Marco, A.; Incicchitti, A.; Kovtun, G.P.; Kovtun, N.G.; et al. First search for double-β decay of 184Os and 192Os. Eur. Phys. J. A 2013, 49, 24. [Google Scholar] [CrossRef]
- Belli, P.; Bernabei, R.; Cappella, F.; Cerulli, R.; Danevich, F.A.; Di Marco, A.; Incicchitti, A.; Laubenstein, M.; Nagorny, S.S.; Nisi, S. First search for double-β decay of platinum by ultra-low background HPGe γ spectrometry. Eur. Phys. J. A 2011, 47, 91. [Google Scholar] [CrossRef]
- Bukhner, E.; Vishnevskij, I.N.; Danevich, F.A. Rare decays of mercury nuclei. Sov. J. Nucl. Phys. 1990, 52, 193–197. [Google Scholar]
- Kawrakow, I.; Rogers, D.W.O. The EGSnrc Code System: Monte Carlo Simulation of Electron and Photon Transport; NRCC Rep. (National Research Council Canada) Report PIRS-701; NRCC: Ottawa, ON, Canada, 2003. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).