Abstract
We derive a set of coupled equations for the gravitational and electromagnetic perturbation in the Reissner–Nordström geometry using the Newman–Penrose formalism. We show that the information of the physical gravitational signal is contained in the Weyl scalar function , as is well known, but for the electromagnetic signal, the information is encoded in the function , which relates the perturbations of the radiative Maxwell scalars and the Weyl scalar . In deriving the perturbation equations, we do not impose any gauge condition and as a limiting case, our analysis contains previously obtained results, for instance, those from Chandrashekhar’s book. In our analysis, we also include the sources for the perturbations and focus on a dust-like charged fluid distribution falling radially into the black hole. Finally, by writing the functions on the basis of spin-weighted spherical harmonics and the Reissner–Nordström spacetime in Kerr–Schild type coordinates, a hyperbolic system of coupled partial differential equations is presented and numerically solved. In this way, we completely solve a system that generates a gravitational signal as well as an electromagnetic/gravitational one, which sets the basis to find correlations between them and thus facilitates gravitational wave detection via electromagnetic signals.
1. Introduction
Gravitational wave astronomy was born in 2015 with the discovery of the first astronomical source named GW150914 [1,2,3]. This was the first observation of a binary black hole system and was done with the gravitational wave interferometer LIGO [4], which detected the gravitational wave signal produced by the merger of two black holes in a binary system. The two black holes were not surrounded by a significant amount of matter that could generate electromagnetic emissions; therefore, in this respect, the emission of the merger was purely in the gravitational channel. Unlike black hole binaries, a system involving neutron stars does possess an electromagnetic counterpart, as demonstrated by the detection of the neutron star merger event in gravitational and electromagnetic messenger channels in 2017, named GW170817 [5,6].
During the formation of an accretion disk around a black hole, electrons may escape from the influence of the central object leaving a net charge in the system, these charged particles may be captured by the black hole, producing a charged black hole [7]. Thus, the study of the electromagnetic and gravitational perturbations can be used to describe the scattering of both types of waves. However, for a charged black hole, a gravitational perturbation of the metric inevitably accompanies a perturbation on the electromagnetic field and vice versa. The description of coupled electromagnetic and gravitational perturbations on charged black holes have been discussed in several studies [8,9,10,11,12,13,14] using different techniques including dispersion of waves due to curvature potentials [15,16,17] and the Newman–Penrose formalism [18,19,20].
Chandrasekhar described the scattering of electromagnetic waves on a Reissner–Nordström black hole and the resulting generation of outgoing gravitational waves, and using the gauge freedom of the Maxwell equations in a curved background, he derived the electromagnetic equations by finding a gauge that restores the symmetry to the perturbation equations [21]. He showed that the curved spacetime produced by a black hole is sensitive to the electromagnetic field part of the spacetime and this awareness is manifested in the symmetry of the equations for the scalars and in a curved background. With the introduction of this particular gauge, the electromagnetic and gravitational perturbation equations simplify greatly. Furthermore, using this gauge, the equations for the gravitational and electromagnetic Weyl scalars decouple from the rest of the functions appearing in the system of equations. As a result of the apparent cognizance of the curved geometry to the existence of the Maxwell field, in which the symmetry in the equations is recovered, Chandrasekhar dubbed this gauge the phantom gauge. Since then, the scattering of both gravitational and electromagnetic waves have been described using this gauge in a variety of studies [22,23,24]. In [22], Lee found a pair of equations for only two gauge invariant quantities involving electromagnetic and gravitational perturbations in a Kerr–Newman spacetime without using the phantom gauge. In this work, we revisit the findings of Lee, explicitly including the matter sources that may cause the perturbation in a Reissner–Nordström background.
As a direct application of our setting, we consider a pressureless charged perfect fluid (dust) falling radially into the black hole as the cause of the perturbation. We explicitly write the equations in a coordinate system and expand the functions using a spherical harmonic basis with the appropriate spin weight. With this choice, we show that the dynamics of the perturbed functions and are completely determined by a set of partial differential equations that depend on the radial and temporal coordinates only. We numerically solve this set of equations and obtain the waveforms for several representative values of the parameters of the system. This sets the basis for a thorough comparative analysis that might find correlations between the waveforms and thus, by the detection of one of these electromagnetic/gravitational signals, one will be able to infer the presence of a purely gravitational one. This will be carried out in future research.
The paper is structured as follows: In Section 2, we introduce the basics of the Newman–Penrose formalism including the Bianchi and Maxwell identities. In Section 3, we provide a detailed derivation of the perturbation equations in a Reisnner–Nordström background. In Section 4, we describe the sources of the perturbation and show that by choosing an adequate decomposition in spin-weighted spherical harmonics, it is possible to separate the time-spatial structure of the equations. In Section 5, we introduce the tetrad and geometric quantities in the Reissner–Nördstrom background described in horizon penetrating coordinates, present a numerical scheme to solve the equations for a particular scenario of matter falling into the black hole, and present some waveforms: gravitational as well as those related with . Finally some concluding remarks are given in Section 6. In the rest of the paper, we use to indicate the signature of the metric: for signature , and for the signature , and we use geometric units where .
2. Foundations: Newman–Penrose Formalism
The starting point in the Newman–Penrose formalism is to define a tetrad of null vectors [25]. The choice of the tetrad is made to reflect symmetries of spacetime, since certain components may vanish, leading to simplification of field equations. In this work, we use and to denote ingoing and outgoing null vectors, respectively, which satisfy the normalization conditions
and The metric tensor can be represented by , where means the complex-conjugate, and the Greek index runs from 0 to 3. The directional derivative operators are defined as , and . The spin coefficients are obtained from the projections
where “;” stands for covariant derivative. The Weyl scalars related with the curvature , , , , and , and the source terms , are defined as
and
where is the Weyl tensor and is the stress energy tensor of the matter content. The information of the electromagnetic fields is encoded in the scalars,
where is the Faraday tensor [24]. The stress energy tensor for the electromagnetic field has the form
where is the magnetic permeability in vacuum. In the rest of this work, we set .
From the definition of the scalars and Equations (4) and (5), we consider that The Latin index runs from 1 to 3. In order to obtain the electromagnetic and gravitational perturbation equations, we depart from the projected Maxwell equations, and the Bianchi identities [21,26] as explained below.
2.1. Maxwell Equations
The dynamics of the electromagnetic fields with sources are described by the Maxwell equations , where is the external electric current. The Maxwell equations projected along the tetrad (“” means intrinsic derivative) written in terms of the spin coefficients and the electromagnetic scalars are [27]
where and .
2.2. Bianchi Identities
By projecting the equations on the tetrad, one gets a set of equations which include the spin coefficients and operators acting on the Weyl scalars known as the Bianchi identities. In the following, we use two of them: Equations (10) and (11) from [21]:
For a detailed description on the projections, we refer the reader to [26]. Similarly, projecting the Weyl tensor on the tetrad, we obtain the following expression,
The equations above are the three equations needed in the forthcoming derivation.
3. Equations for the Perturbations
Corresponding to the six parameters of the Lorentz group of transformation, there are six degrees of freedom to rotate a chosen tetrad frame. It is usual to encode a general Lorentz transformation in terms of the basis vectors l, k, and m, and classify them in three classes of rotations, each one leaving an invariant vector under such transformation. The effect of the basis transformation on the various Newman–Penrose quantities can be found in [21]. For instance, an infinitesimal rotation of class I will change the Weyl and the Maxwell scalars to first order in a, according to the following scheme:
and
where the superscript denotes a perturbed quantity. For the Reissner–Nordström spacetime, the background scalars and are the only ones that are nonzero. Consequently, , , , , , and are unaffected to first order under an infinitesimal rotation. However, and are indeed affected since and are different from zero in the background. Nevertheless, the radiative combination
is invariant to first order and, as it is shown below, one can get a coupled system of equations for this function, , and the perturbed Weyl component . In the following, we describe the general procedure to find such a coupled set of equations in detail.
3.1. Perturbed Maxwell Equations
The ingoing and outgoing electromagnetic radiation is given by the perturbations of the scalars and , respectively. However, in a charged spacetime, the outgoing electromagnetic perturbations couple with the perturbations of the Weyl scalar , which carries the so-called electromagnetic part of the spacetime. A similar coupling occurs with the ingoing perturbation , and . In this section, we derive an equation for the perturbation of .
First, consider the following identities relating the derivative operators [21]:
Second, on the projected Maxwell’s Equations (6)–(9), operate on Equation (8) and on Equation (9); then, subtract these equations and, after some algebra, one arrives to the following expression:
where
In order to describe the perturbation of , let us perform a first-order perturbation of the form in all the functions on Equation (19). In a Reissner–Nordström-like background, considering that the spacetimes are type D, in Petrov classification, the spinor quantities are zero. Furthermore, we consider spherical symmetry and that are also zero. These considerations imply
with the perturbed current term defined as
In previous equation, we only kept first-order and nonvanishing background quantities. Equation (21) can be further simplified using background Maxwell equations Equation (6): ; and Equation (7): , in order to obtain
This equation can be written in a more convenient form using the commutation expressions for the operators acting on ,
and the Ricci identities [28]:
in Equation (23). After some algebra, one arrives to the following expression relating the perturbations with the current
In order to simplify the notation, let us define the derivative operators as follows:
where N takes integer values. In terms of these expressions, we can rewrite the electromagnetic perturbation Equation (28) as
With the notation of Equations (29) and (30), we denoted for for , and analogously for other values and operators.
3.2. Perturbed Bianchi Identities
In order to derive the equations for the perturbations and , we start by perturbing the the Bianchi identities Equations (10) and (11). As mentioned above, in a Petrov-type D space-time background, the background Weyl scalars vanish except , and the spinor coefficients are equal to zero. Furthermore, we consider spacetimes, such as the Schwarzschild or the Reissner–Nördstrom, in which it is always possible to choose a tetrad so that the nonzero spinor coefficients are real. Finally, we consider stress energy tensors of the same form as the Reissner–Nordström one, so that the only nonzero Ricci scalar is .
By performing a first-order perturbation in Equations (10) and (11), one gets the following two equations:
In the forthcoming analysis, we consider that the external matter that causes the perturbation satisfies . As we show below, this condition is consistent with matter falling in the radial direction only.
In an analogous manner, the perturbation of Equation (12) gives
Finally, the following Ricci identities describing the action of the operators D and on the unperturbed fields are also useful:
3.3. System of Equations for the Perturbations
In the previous subsection, we obtained four equations relating the perturbations , , and due to the perturbed sources and . It is an underdetermined system, with four equations for five unknowns. However, as we show, one can partially solve such a system using the particular combination of and given by Equation (15) and obtain a subsystem of coupled equations for and . This remarkable combination has been related to a freedom in the rotation of the tetrad [21], although its physical meaning is not clearly understood and, to our knowledge, the physical meaning of such a combination has not been discussed in the literature. In this section, we present a detailed derivation of such a subsystem of equations.
Acting with on Equation (32), and with on Equation (33), adding and using the identity with , one gets
A further simplification can be done using the fact that the action of the operator on is
for an arbitrary function f. Thus, using Equations (38) and (39), it takes the form
Substituting in the previous equation given by Equation (34) and after collecting terms, one gets
Simplifying and using the definition of the operator in Equation (29), one obtains
Next, one can use Equations (32) and (33) to express the perturbed spinors as
and substitute them in Equation (42). The resulting equation is
where we have defined the operators
Remarkably, the operator acting on takes the same form as the operator acting on . Indeed, one can write the action of and on and as
and using this remarkable property in Equation (45), one gets
where
and
In order to derive a second equation for and , we first apply the operator on Equation (32), and the operator on Equation (33), and adding up and using the rule of commutation , we eliminate in the equation. The resulting equation is
Considering that , we can use the Maxwell Equation (31) to expand this last equation as follows:
After some algebra, the previous equation becomes
From Equations (32) and (33), one can obtain the following expressions for the terms involving the perturbed spinor coefficients:
Using these expressions in Equation (57), and after some simplifications, we obtain an equation involving only , and the sources
where the operators have the form
We have collected the operators acting on and on in those involving and , and the rest, as long as they involve more algebraic manipulation in the next steps in the derivation. Indeed, using and in , one gets
and for the radial operators
where , , and have the form
and
We have written the operator as a sum of different operators, since, as shown below, each element of the sum is equal to the corresponding element of :
thus, each of the coefficients of take the same form as the corresponding coefficients of acting on the variable defined in Equation (53). As a result, we can again express the operators acting on with the operators acting on as a single operator acting on , and obtain in this way the second equation for and ,
where . We have shown that it is possible to obtain a couple of equations for and that are independent of and . However, the complete system is not solved as long as, in order to determine the perturbed spinor coefficients, one must obtain , , and independently, which is not possible within this formalism because, as mentioned above, the system is underdetermined.
4. Sources of the Perturbation and Harmonic Decomposition
Because the previous section is quite lengthy due to all the calculations, we briefly present the two important equations that describe the gravitational and electromagnetic/gravitational perturbations for and and further comment on the sources that may cause these perturbations. From Equations (60) and (78), we have
where
As the source of perturbation, let us consider a charged dust-like matter falling radially into the black hole with stress energy tensor , where is the four velocity and is the rest mass density of the fluid. In our analysis, we consider that the fluid is falling radially into the black hole with four velocities:
When the fluid is charged, it induces an electric current given by , where the electric density is , and q is the charge per unit of the mass of each particle.
An important property of the system of Equations (79) and (80) with the given form of the sources is that the system can be decoupled into an angular and radial set of equations.
First, one must notice that the different functions of the system, Equations (79) and (80), have different spin weights. For instance, the Weyl scalar has a spin weight of minus two, whereas has spin weight of minus one. Furthermore, the rest mass density and the density of charge are scalar functions with zero spin. Thus, the different operators acting on these functions have to be such that they finally produce quantities with the same spin weight. Indeed, as we show below, Equation (79) has spin weight of and Equation (80) has a spin weight of . With this in mind and using the fact that the spin-weighted spherical harmonics form a basis for each weight s, we write
In spherical symmetry, we can choose the vector such that the operators and in Equation (30) can be written in terms of the eth and eth-bar operators, and as follows:
The action of the eth, eth-bar operators on is to raise or lower the spin weight as follows:
Given the action of the operators on the spin weight, one gets the following identities for the terms in the perturbation equations:
Thus, the angular dependence of the dynamical equations is encoded in the spin weighted spherical harmonics. Furthermore, all the terms that appear in Equation (79) have spin weights of , and those appearing in Equation (80) have spin weights of , which confirms that the equations are balanced with respect to the spin weight.
The angular part of the perturbation equations can be factorized using the orthogonality properties of the spherical harmonics and each equation, and can be reduced to a set of equations for each mode as follows: multiply Equation (79) by , and Equation (79) by ; then, integrate the element of solid angle. As a result of the orthogonality of the spherical harmonics, each sum reduces and one obtains an equation for each mode ().
Finally, recalling the Peeling theorem [29] that states that the Weyl scalars have the asymptotic decay , it proves convenient to rewrite the equation for the gravitational perturbation in terms of the quantity , which does not decay in the asymptotic region. For the electromagnetic/gravitational perturbation, the product between the Weyl and Maxwell scalars forming decays as ; thus, the product has a constant amplitude. For simplicity, let us define the amplitudes for each radial mode:
Then, the perturbation equations take the form
where
Equations (98) and (99) are the final coupled dynamical equations for the gravitational and electromagnetic perturbations in the time domain, which can be written in any coordinate basis.
5. Perturbations in Reissner–Nordström Spacetime in Kerr–Schild Coordinates
Following our previous work [28], we focus on the Reissner–Nordström metric in Kerr–Schild-type coordinates:
where the null tetrad is
and the nonvanishing components of the Weyl, Ricci, and Maxwell scalars associated to this geometry are
For this spacetime and with our choice of null tetrad, the nonzero spin coefficients are
In order to solve the perturbation equations, the first step is to write the equations in a dimensionless form. For this purpose, we recover the physical constants G, c, and . We start by defining the characteristic length of the system , the we write the radial coordinate r, as , with as a dimensionless quantity. We also define a characteristic time, , such that . In terms of the dimensionless quantities, we find it useful to define the quantity
The maximum value of the charge to get an extreme black hole is ; therefore, we can normalize the value of the charge defining a dimensionless quantity .
The dimensionless electromagnetic and gravitational scalars are
where
and:
Furthermore, the dimensionless radial functions and are
By replacing the Weyl scalars Equation (103) and the spin coefficients Equation (104) in the perturbation Equations (98) and (99), we obtain the following system in terms of dimensionless quantities:
and
where, for simplicity in the notation, we dropped the indices on each mode.
5.1. Matter Models
We shall consider that there are two sources of matter that cause a perturbation in the black hole: one associated with neutral matter characterized by the rest mass density and the other associated to charged particles with density . We consider that neutral particles only move in the radial direction and are free falling into the black hole. The conservation of the number of particles , where , for the metric Equation (101) gives
where we defined the three velocity as and we assumed that the dimensionless four velocity has components . For charged particles, we make the same assumptions, so we obtain that the conservation of the number of particles implies
Considering the normalization of the four velocity for both types of particles, we can express in terms of as [28]
where . As previously stated, this expression is valid for neutral and charged particles.
For spherically symmetric static spacetimes, one can determine the motion of test particles up to quadrature by means of the Euler–Lagrange equations in the following way: Let us consider the dimensionless Lagrangian for neutral particles
using the Euler–Lagrange equation for and the metric Equation (101), one obtains a conserved quantity associated to the energy of the particles at infinity and, consequently,
where . Proceeding in a similar way for charged particles, the dimensionless Lagrangian is
where the vector potential was taken as and we have written . From the staticity of the spacetime via the Euler–Lagrange equation for t, we get
where and . Using Equation (113) in both Equations (115) and (117), we obtain
Finally, the projection of the four velocity along the null vector for both types of particles provides a couple of expressions that are useful: , and .
Given the components of the velocity for both neutral and charged particles and the evolution of the densities, one can numerically solve the perturbation equations given an initial distribution of matter and compute the resultant gravitational signal due to the gravitational and electromagnetic perturbation induced in the black hole.
5.2. First-Order Reduction and Numerical Implementation
In terms of the 3+1 decomposition of the spacetime , one can determine the lapse function , the shift vector , and the metric component from metric Equation (101), yielding
In order to write the system of second-order differential Equations (98) and (99) as a first-order system suitable for numerical integration, we introduce the auxiliary functions
From the definition of , one obtains the time evolution of ; however, by taking the time derivative of and replacing the lapse and shift, one gets
The equations for and are obtained by substituting first-order functions into Equations (109) and (110):
5.3. Waveforms
For our simulations, we solved the system of equations for the gravitational perturbation and the electromagnetic/gravitational perturbation with sources using Equations (124) and (125). For the source, we are considering nonspherical shell of particles falling into the hole. The numerical code evolves the first-order variables with a third-order Runge–Kutta integrator with a fourth-order spatial stencil. For a more detailed description of the code see [28]. As initial data, we used a Gaussian packet in the density describing a nonspherical shell of particles falling into the hole ; where , and . For the simulation, we used Kerr–Schild-type coordinates, lies inside the event horizon, and we chose and . The gravitational and electromagnetic/gravitational waveforms produced by the infalling matter were extracted at a fixed radius. The gravitational and electromagnetic/gravitational functions, , , were initially set to zero, as were their time derivatives. The outer boundary was set far enough from the horizon to ensure that any possible incoming radiation had no effect on our results.
In Figure 1a,b, we show the radial profile for the gravitational and the electromagnetic/gravitational component for the mode , respectively. The simulation was preformed for different values of charge , and . We can observe that the waveforms are quite similar in structure and that the amplitude changes for different values of . The gravitational waveform amplitude is greater and presents more oscillations than that of the electromagnetic/gravitational case. It is interesting to observe that the amplitude decreases for greater values of in the gravitational case. On the other hand, in the electromagnetic/gravitational case, the amplitude increases for greater values of . The time response for both gravitational and electromagnetic/gravitational waveforms starts and finishes at almost the same times.
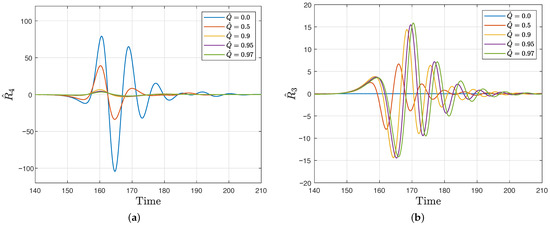
Figure 1.
Radial profiles of the gravitational signal (a), and electromagnetic/gravitational (b) signals for the quadrupolar mode with different values of , and .
In Figure 2, we plotted the absolute value on a logarithmic scale to show the different stages of the signal: the initial burst due to the initial data, the quasinormal ringing, and the tail. Figure 2a shows the gravitational signal and Figure 2b shows the electromagnetic/gravitational signal. We found no sign of mixing between gravitational and electromagnetic/gravitational frequencies. Each signal displays its characteristic ring-down frequency and the power-law decay. The ring-down frequencies were extracted from ∼50 to ∼350 for the gravitational case and from ∼50 to 400 for the electromagnetic/gravitational case. The frequency of the gravitational waves is the one associated with the quadrupolar quasinormal mode. In order to find the frequencies, we fitted the data with a sinusoidal waveform. The numerical values of the corresponding frequencies are shown in Table 1. The values we found are consistent with the values given in [21]. Although it is known that quasinormal mode frequencies are complex, we were interested in the oscillatory behavior of the signal. For black holes with masses of , the electromagnetic frequencies are in the interval 8–800 Hz, whereas the gravitational waves produced for such a range of masses are in the interval of 12– kHz [28]. As has been pointed out, quasinormal ringing can be used to determine the intrinsic properties of the black hole [30]. Electromagnetic waves with such low frequencies, however, could be easily absorbed by the interstellar medium during propagation, making it almost impossible to detect them directly.
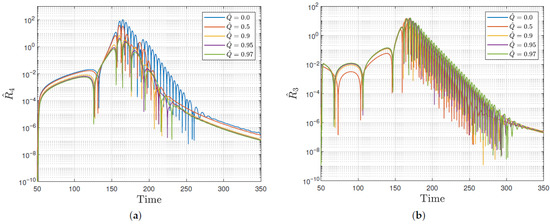
Figure 2.
The gravitational and electromagnetic/gravitational signals in logarithmic scale for different values of charge , and . The signals show the characteristic phases: the initial burst, the quasinormal ringing, the power-law decay, and the tail.

Table 1.
Frequency of the quasinormal modes of the black hole produced by the perturbation of the accreting matter. The frequencies are consistent with the values given in [21].
Next, we present the behavior of the energy carried by the gravitational wave for several values of the charge of the infalling matter for the mode (any ), obtained from the energy loss formula, i.e., the power of the gravitational wave, , (see [27]):
From Figure 3, we notice how the flux of energy carried by the gravitational wave reaches a constant value. This value decreases for large values of the charge of the black hole. Although the same integral can be made for the gauge invariant quantity , as long as it is coupled to the gravitational radiation through , its classification as electromagnetic energy cannot be immediately made; thus, it deserves a deeper discussion. Here, we only mention that it is zero for and opposite in behavior to ; and its asymptotic value increases with .
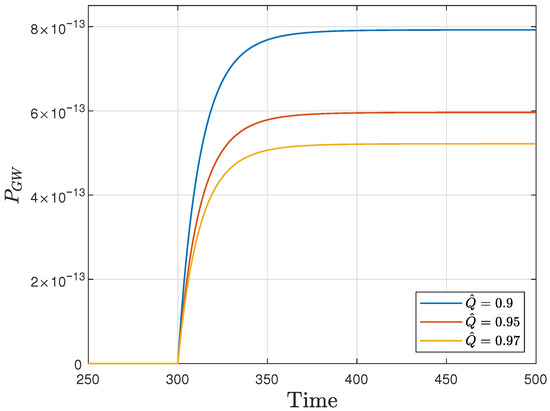
Figure 3.
Energy carried by the gravitational wave, , according to Equation (126), for the values proportional to the charge of the black hole.
Our system of equations allows for a purely electromagnetic/gravitational response (encoded in the function ). Indeed, for the case, which corresponds to a dipole angular distribution, there is no gravitational response, as the gravitational waves occur starting from the quadrupolar angular distribution [31], but there might be an electromagnetic one. We see that this is the case in the following: in solving the system of equations with , we only obtain a response in , which we present in Figure 4.
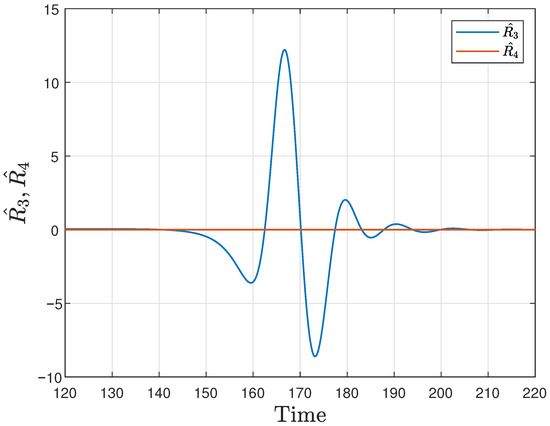
Figure 4.
Waveforms for dipole perturbation, , with , , and . Data were collected at . Notice how in this case, there is no gravitational response, , as there should be, but there is the response associated with .
6. Final Remarks
In this work, we revisited the gravitational and electromagnetic perturbations in a Reissner–Nordström black hole by means of the Newman–Penrose formalism. In our analysis, we include the sources that cause the perturbations and discuss the particular case of a charged perfect fluid falling radially into the black hole. Using both Maxwell equations for the Maxwell scalars and the Bianchi identities for the Weyl scalars, we found a system of coupled equations for the gravitational and electromagnetic perturbations without choosing a specific gauge. A common practice to study electromagnetic and gravitational perturbations within the Newman–Penrose formalism is to choose the so-called phantom gauge (imposing ), since using this gauge, one can obtain a subsystem of equations for the perturbation of the Weyl scalars and . However, although convenient, this choice is not unique. In this work, we show that a similar system of equations can be obtained for and , which involves perturbations of the electromagnetic field and perturbations of the electromagnetic part of the Weyl tensor . Our results thus open up the possibility to explore electromagnetic and gravitational perturbations without any a priori assumption regarding the value of any of the scalars.
It is remarkable that it is not possible to obtain a perturbation equation for independently of without choosing a particular gauge, and only the combination given by can be determined via this formalism. However, this fact is not related to any physical property of the fields since one can always obtain the fields by numerically solving the Einstein–Maxwell field equations and computing all the gravitational scalars at each time step. The actual physical meaning of such a constraint in the Newman–Penrose formalism is an ongoing focus of research.
We also considered a dust-like charged fluid as a source of the perturbations. We used the spin-weighted spherical harmonics as a basis to expand the functions and obtain a system of partial differential equations for the temporal and radial components, leaving all the angular dependence of the functions on the respective basis of spherical harmonics. The resulting system of partial differential equations constitutes a hyperbolic system that can be solved numerically by standard means. In this way, we see that we have a robust procedure which sets the basis to accurately determine the simultaneous generation of gravitational and electromagnetic waveforms. A thorough study comparing amplitudes, frequencies, harmonic dependence, and power between the gravitational and the electromagnetic/gravitational signals for several fiducial values of the parameters will allow for the determination of correlations between these waveforms. This will not only give a better understanding of the process, but might also shed light on the multimessenger program in a general sense, as long as it is possible to extrapolate the correlations found in the system presented in this work to other scenarios in which signals of different interactions are generated.
Furthermore, our analysis can be used as a simple model to describe the correlation that exists between electromagnetic and gravitational wave signals that occur during the accretion of charged matter around a compact object. This is because the frequency of the gravitational waves resulting from the quasinormal ringing of black holes of – with moderate charge lies within the range of sensitivity of current ground-based gravitational wave interferometers.
Finally, we would like to remark that studies performed in a Reissner–Nordström spacetime frequently give valuable insights into Kerr geometry. The relationships arising from the interaction of the electromagnetic field of matter with the charge of a black hole might have a similarity with the interaction of the angular momentum of the accreting matter with the angular momentum of the black hole. The results and derivations presented in this work might prove to be useful in the perturbation analysis generated by accreting rotating matter in a Kerr background. Further studies are currently underway.
Author Contributions
Conceptualization: C.M., J.C.D., D.N.; methodology: C.M., J.C.D., D.N., C.R.-L.; formal analysis: C.M., J.C.D., D.N., C.R.-L.; investigation: C.M., J.C.D., D.N., C.R.-L.; writing—original draft preparation: C.M., J.C.D., D.N., C.R.-L. All authors have read and agreed to the published version of the manuscript.
Funding
This work was partially supported by DGAPA-UNAM through grants IN110218 and IN105920; by CONACyT Ciencia de Frontera Projects No. 376127 “Sombras, lentes y ondas gravitatorias generadas por objetos compactos astrofísicos”, and No. 304001 “Estudio de campos escalares con aplicaciones en cosmología y astrofísica”. Moreover, the European Union’s Horizon 2020 research and innovation (RISE) program H2020-MSCA-RISE-2017 Grant No. FunFiCO-777740. C.M. acknowledges support from PROSNI-UDG. C.R.-L. acknowledges CONACYT scholarship.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data sharing is not applicable to this article as no new data were created or analyzed in this study.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abernathy, M.R.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; et al. Observation of Gravitational Waves from a Binary Black Hole Merger. Phys. Rev. Lett. 2016, 116, 061102. [Google Scholar] [CrossRef] [PubMed]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abernathy, M.R.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; et al. GW150914: First results from the search for binary black hole coalescence with Advanced LIGO. Phys. Rev. D 2016, 93, 122003. [Google Scholar] [CrossRef] [PubMed]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Abernathy, M.R.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; et al. GW151226: Observation of Gravitational Waves from a 22-Solar-Mass Binary Black Hole Coalescence. Phys. Rev. Lett. 2016, 116, 241103. [Google Scholar] [CrossRef]
- Aston, S.; Guenther, M.; Hammond, G.D.; Brady, P.R.; Mukherjee, S.; Byer, R.L.; Rainer, N.; Yoshida, S.; Schilling, R.; McIntyre, G.; et al. LIGO: The Laser Interferometer Gravitational-Wave Observatory. Rep. Prog. Phys. 2009, 72, 076901. [Google Scholar]
- Abbott, B.P.; Abbott, R.; Abbott, T.D.; Acernese, F.; Ackley, K.; Adams, C.; Adams, T.; Addesso, P.; Adhikari, R.X.; Adya, V.B.; et al. GW170817: Observation of Gravitational Waves from a Binary Neutron Star Inspiral. Phys. Rev. Lett. 2017, 119, 161101. [Google Scholar] [CrossRef]
- Aasi, J.; Abadie, J.; Abbott, B.P.; Abbott, R.; Abbott, T.; Abernathy, M.R.; Accadia, T.; Acernese, T.; Adams, C.; Adams, T.; et al. First Searches for Optical Counterparts to Gravitational-wave Candidate Events. Astrophys. J. Suppl. Ser. 2014, 211, 7. [Google Scholar] [CrossRef]
- Zakharov, A.F. Constraints on a charge in the Reissner-Nordström metric for the black hole at the Galactic Center. Phys. Rev. D 2014, 90, 062007. [Google Scholar] [CrossRef]
- Moncrief, V. Odd-parity stability of a Reissner-Nordström black hole. Phys. Rev. D 1974, 9, 2707–2709. [Google Scholar] [CrossRef]
- Moncrief, V. Stability of Reissner-Nordström black holes. Phys. Rev. D 1974, 10, 1057–1059. [Google Scholar] [CrossRef]
- Bicak, J.; Dvorak, L. Stationary electromagnetic fields around black holes. Phys. Rev. D 1980, 22, 2933–2940. [Google Scholar]
- Chitre, D.M. Perturbations of Charged Black Holes. Phys. Rev. D 1976, 13, 2713–2719. [Google Scholar] [CrossRef]
- Leaute, B.; Linet, B. Electrostatics in a Reissner-Nordström space-time. Phys. Lett. A 1976, 58, 5–6. [Google Scholar] [CrossRef]
- Chrzanowski, P.L. Vector Potential and Metric Perturbations of a Rotating Black Hole. Phys. Rev. D 1975, 11, 2042–2062. [Google Scholar] [CrossRef]
- Fabbri, R. Electromagnetic and Gravitational Waves in the Background of a Reissner-Nordström Black Hole. Nuovo Cim. B 1977, 40, 311–329. [Google Scholar] [CrossRef]
- Zerilli, F.J. Perturbation analysis for gravitational and electromagnetic radiation in a Reissner-Nordström geometry. Phys. Rev. D 1974, 9, 860–868. [Google Scholar] [CrossRef]
- Ferrari, V.; Mashhoon, B. New approach to the quasinormal modes of a black hole. Phys. Rev. D 1984, 30, 295–304. [Google Scholar] [CrossRef]
- Khanna, G.; Price, R.H. Black Hole Ringing, Quasinormal Modes, and Light Rings. Phys. Rev. D 2017, 95, 081501. [Google Scholar] [CrossRef]
- Chandrasekhar, S. On the Equations Governing the Perturbations of the Reissner-Nordström Black Hole. Proc. R. Soc. Lond. Ser. Math. Phys. Sci. 1979, 365, 453–465. [Google Scholar]
- Teukolsky, S.A. Perturbations of a rotating black hole. 1. Fundamental equations for gravitational electromagnetic and neutrino field perturbations. Astrophys. J. 1973, 185, 635–647. [Google Scholar] [CrossRef]
- Mino, Y.; Sasaki, M.; Shibata, M.; Tagoshi, H.; Tanaka, T. Black hole perturbation: Chapter 1. Prog. Theor. Phys. Suppl. 1997, 128, 1–121. [Google Scholar] [CrossRef]
- Chandrasekhar, S. The Mathematical Theory of Black Holes; Oxford University Press: Oxford, UK, 1983. [Google Scholar]
- Lee, C.H. Coupled gravitational and electromagnetic perturbations around a charged black hole. J. Math. Phys. 1976, 17, 1226. [Google Scholar] [CrossRef]
- Lee, C.H. Coupled gravitational and electromagnetic perturbations equations with the source terms. Il Nuovo Cimento 1977, 41, 305. [Google Scholar] [CrossRef]
- Chandrasekhar, S.; Detweiler, S. The quasi-normal modes of the Schwarzschild black hole. R. Soc. Lond. Proc. Ser. A 1975, 344, 441–452. [Google Scholar] [CrossRef]
- Newman, E.T.; Penrose, R. An Approach to Gravitational Radiation by a Method of Spin Coefficients. J. Math. Phys. 1962, 3, 566–578, Erratum in J. Math. Phys. 1963, 4, 998. [Google Scholar] [CrossRef]
- Degollado, J.C.; Nunez, D. Perturbation theory of black holes: Generation and properties of gravitational waves. AIP Conf. Proc. 2011, 1473, 3–25. [Google Scholar] [CrossRef]
- Degollado, J.C.; Nunez, D.; Palenzuela, C. Signatures of the sources in the gravitational waves of a perturbed Schwarzschild black hole. Gen. Rel. Grav. 2010, 42, 1287–1310. [Google Scholar] [CrossRef]
- Moreno, C.; Degollado, J.C.; Núñez, D. Gravitational and electromagnetic signatures of accretion into a charged black hole. Gen. Rel. Grav. 2017, 49, 83. [Google Scholar] [CrossRef]
- Wald, R.M. General Relativity; The University of Chicago Press: Chicago, IL, USA, 1984. [Google Scholar]
- Kokkotas, K.; Konoplya, R.; Zhidenko, A. Quasinormal modes, scattering and Hawking radiation of Kerr-Newman black holes in a magnetic field. Phys. Rev. D 2011, 83, 024031. [Google Scholar] [CrossRef]
- Schutz, B.F. Geometrical Methods of Mathematical Physics; Cambridge University Press: Cambridge, UK, 1980. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).