New Canonical and Grand Canonical Density of States Techniques for Finite Density Lattice QCD
Abstract
1. Introduction
2. The Canonical Density of States Approach
2.1. Canonical Ensemble and Density of States
2.2. Parametrization of the Density
2.3. Evaluation of the Parameters of the Density
3. An Exploratory Test of the Canonical DoS Approach in the Free Case
3.1. Setting and Reference Results from Fourier Transformation
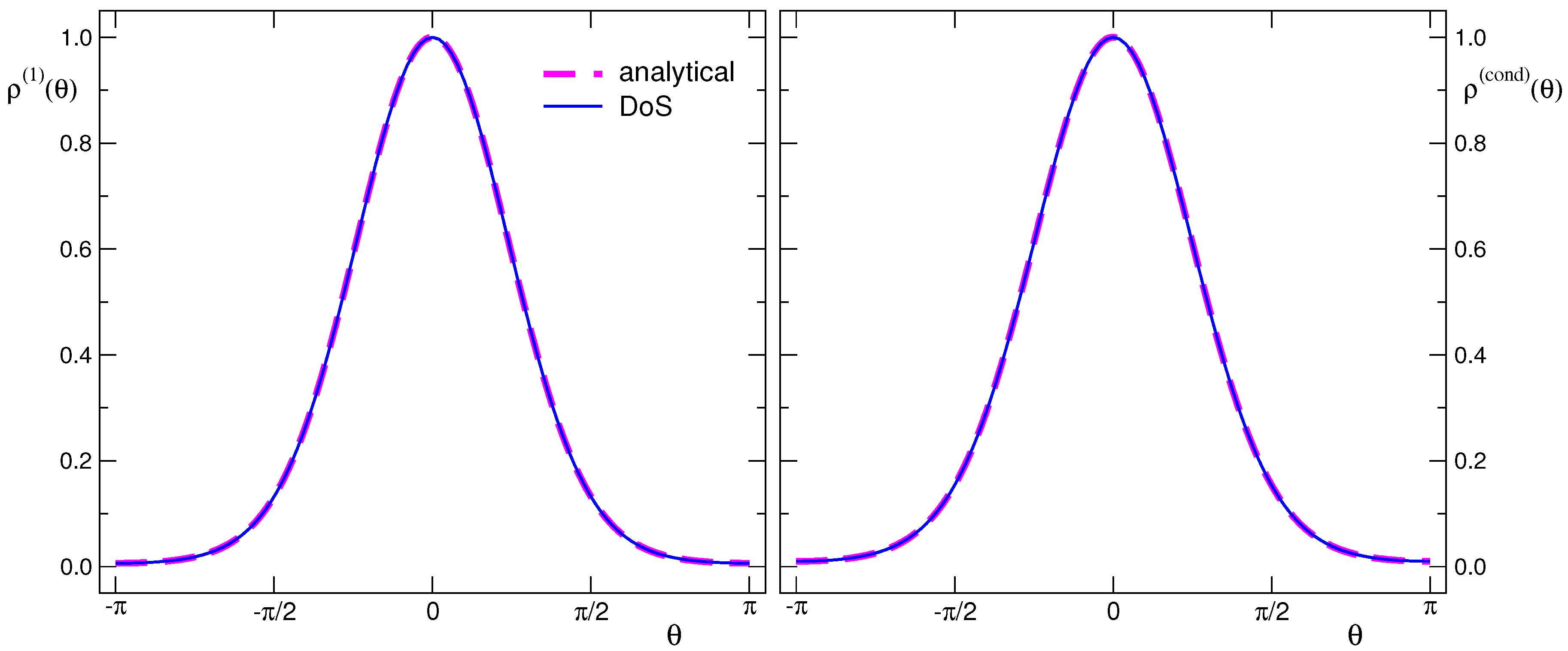
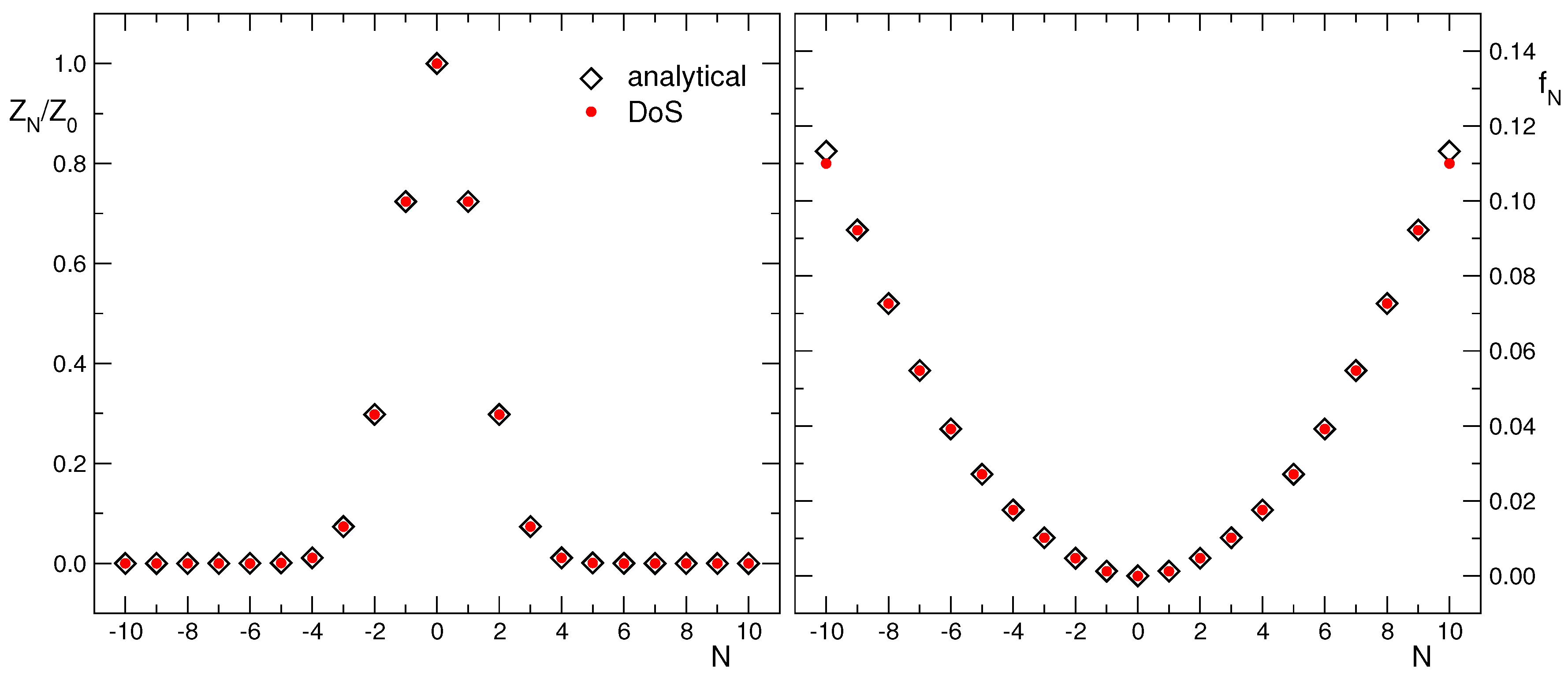
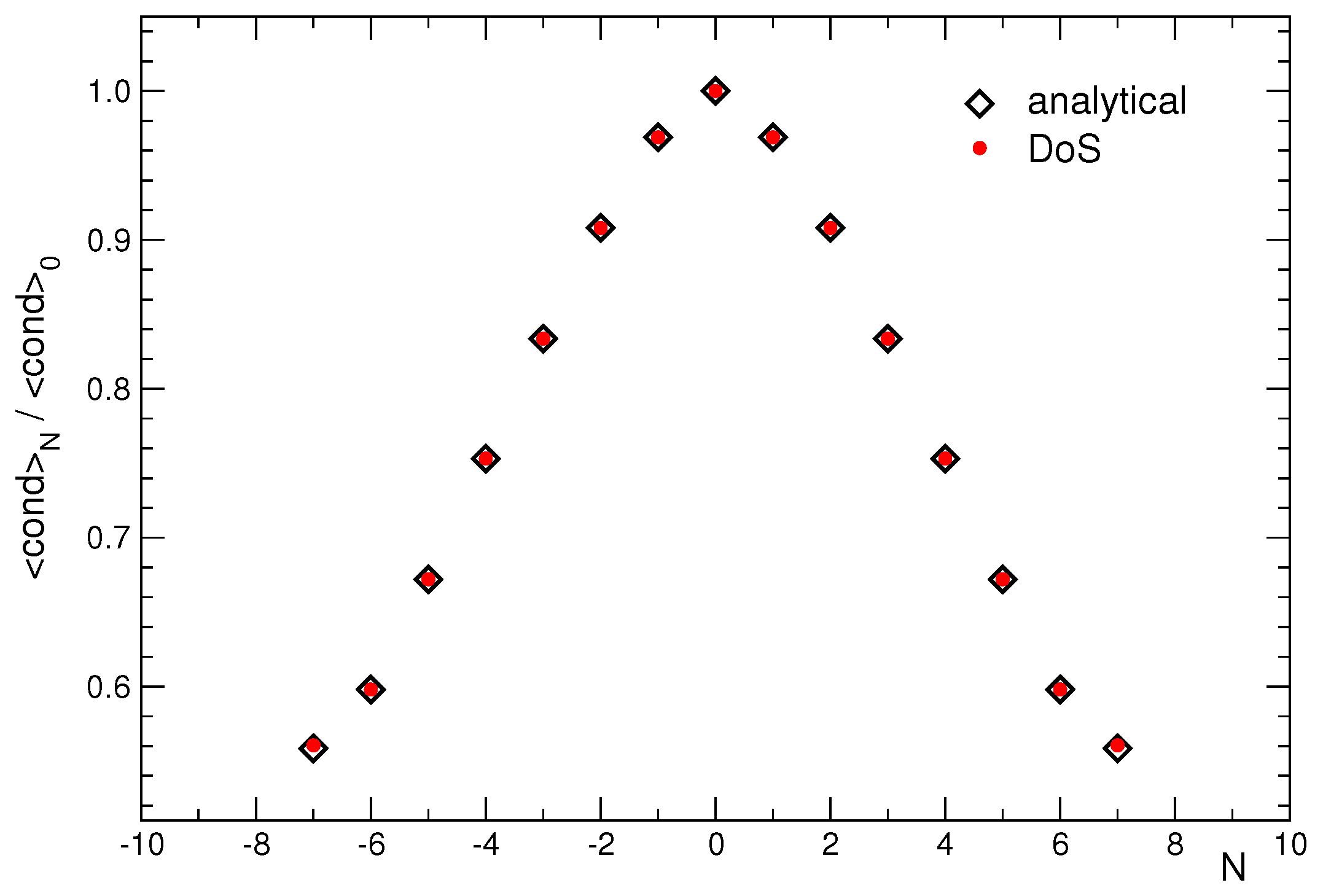
3.2. Numerical Results for CanDos in the Free Case
4. Direct Grand Canonical DoS Approach
4.1. Pseudo-Fermion Representation and Introduction of Densities
4.2. Evaluation of the Densities with FFA
5. Summary and Outlook
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Gocksch, A.; Rossi, P.; Heller, U.M. Quenched hadronic screening lengths at high temperature. Phys. Lett. B 1988, 205, 334–338. [Google Scholar] [CrossRef]
- Gocksch, A. Simulating lattice QCD at finite density. Phys. Rev. Lett. 1988, 61, 2054. [Google Scholar] [CrossRef]
- Schmidt, C.; Fodor, Z.; Katz, S.D. The QCD phase diagram at finite density. arXiv 2005, arXiv:hep-lat/0510087. [Google Scholar]
- Fodor, Z.; Katz, S.D.; Schmidt, C. The Density of states method at non-zero chemical potential. J. High Energy Phys. 2007, 2007, 121. [Google Scholar] [CrossRef]
- Ejiri, S. On the existence of the critical point in finite density lattice QCD. Phys. Rev. D 2008, 77, 014508. [Google Scholar] [CrossRef]
- Ejiri, S.; Aoki, S.; Hatsuda, T.; Kanaya, K.; Nakagawa, Y.; Ohno, H.; Saito, H.; Umeda, T. Numerical study of QCD phase diagram at high temperature and density by a histogram method. Open Phys. 2012, 10, 1322–1325. [Google Scholar] [CrossRef]
- Langfeld, K.; Lucini, B.; Rago, A. The density of states in gauge theories. Phys. Rev. Lett. 2012, 109, 111601. [Google Scholar] [CrossRef] [PubMed]
- Wang, F.; Landau, D.P. Efficient, Multiple-Range Random Walk Algorithm to Calculate the Density of States. Phys. Rev. Lett. 2001, 86, 2050. [Google Scholar] [CrossRef] [PubMed]
- Langfeld, K.; Pawlowski, J.M. Two-color QCD with heavy quarks at finite densities. Phys. Rev. D 2013, 88, 071502. [Google Scholar] [CrossRef]
- Langfeld, K.; Lucini, B. Density of states approach to dense quantum systems. Phys. Rev. D 2014, 90, 094502. [Google Scholar] [CrossRef]
- Langfeld, K.; Lucini, B.; Pellegrini, R.; Rago, A. An efficient algorithm for numerical computations of continuous densities of states. Eur. Phys. J. C 2016, 76, 306. [Google Scholar] [CrossRef][Green Version]
- Garron, N.; Langfeld, K. Anatomy of the sign-problem in heavy-dense QCD. Eur. Phys. J. C 2016, 76, 569. [Google Scholar] [CrossRef]
- Gattringer, C.; Langfeld, K. Approaches to the sign problem in lattice field theory. Int. J. Mod. Phys. A 2016, 31, 1643007. [Google Scholar] [CrossRef]
- Garron, N.; Langfeld, K. Controlling the Sign Problem in Finite Density Quantum Field Theory. Eur. Phys. J. C 2017, 77, 470. [Google Scholar] [CrossRef]
- Francesconi, O.; Holzmann, M.; Lucini, B.; Rago, A. Free energy of the self-interacting relativistic lattice Bose gas at finite density. Phys. Rev. D 2020, 101, 014504. [Google Scholar] [CrossRef]
- Francesconi, O.; Holzmann, M.; Lucini, B.; Rago, A.; Rantaharju, J. Computing general observables in lattice models with complex actions. arXiv 2019, arXiv:1912.04190. [Google Scholar]
- Gattringer, C.; Giuliani, M.; Lehmann, A.; Törek, P. Density of states techniques for lattice field theories using the functional fit approach (FFA). arXiv 2015, arXiv:1511.07176. [Google Scholar]
- Giuliani, M.; Gattringer, C.; Törek, P. Developing and testing the density of states FFA method in the SU(3) spin model. Nucl. Phys. B 2016, 913, 627–642. [Google Scholar] [CrossRef][Green Version]
- Giuliani, M.; Gattringer, C. Density of States FFA analysis of SU(3) lattice gauge theory at a finite density of color sources. Phys. Lett. B 2017, 773, 166–171. [Google Scholar] [CrossRef]
- Mercado, Y.D.; Törek, P.; Gattringer, C. The ℤ3 model with the density of states method. arXiv 2014, arXiv:1410.1645. [Google Scholar]
- Gattringer, C.; Törek, P. Density of states method for the ℤ3 spin model. Phys. Lett. B 2015, 747, 545–550. [Google Scholar] [CrossRef][Green Version]
- Gattringer, C.; Mandl, M.; Törek, P. New DoS approaches to finite density lattice QCD. Phys. Rev. D 2019, 100, 114517. [Google Scholar] [CrossRef]
- Manteuffel, T.A. The Tchebychev iteration for nonsymmetric linear systems. Numer. Math. 1977, 28, 307–327. [Google Scholar] [CrossRef]
- Saad, Y. Iterative Methods for Sparse Linear Systems, 2nd ed.; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2003. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gattringer, C.; Mandl, M.; Törek, P. New Canonical and Grand Canonical Density of States Techniques for Finite Density Lattice QCD. Particles 2020, 3, 87-98. https://doi.org/10.3390/particles3010008
Gattringer C, Mandl M, Törek P. New Canonical and Grand Canonical Density of States Techniques for Finite Density Lattice QCD. Particles. 2020; 3(1):87-98. https://doi.org/10.3390/particles3010008
Chicago/Turabian StyleGattringer, Christof, Michael Mandl, and Pascal Törek. 2020. "New Canonical and Grand Canonical Density of States Techniques for Finite Density Lattice QCD" Particles 3, no. 1: 87-98. https://doi.org/10.3390/particles3010008
APA StyleGattringer, C., Mandl, M., & Törek, P. (2020). New Canonical and Grand Canonical Density of States Techniques for Finite Density Lattice QCD. Particles, 3(1), 87-98. https://doi.org/10.3390/particles3010008




