Abstract
The Compressed Baryonic Matter (CBM) experiment is one of four scientific pillars of the future Facility for Antiproton and Ion Research (FAIR) in Darmstadt. In collisions between heavy nuclei at FAIR energies, it is expected that the matter in the reaction zone is compressed to more than five times saturation density, corresponding to the density in the core of a massive neutron star. This offers the unique opportunity to study in the laboratory the high-density equation-of-state (EOS) of nuclear matter, and to search for new phases of Quantum Chromo Dynamics (QCD) matter at large baryon-chemical potentials. Promising experimental observables sensitive to the EOS and to possible phase transitions will be discussed, together with a brief description of the CBM experiment.
1. Introduction
Heavy-ion collision experiments at moderate beam energies, as provided by the future accelerator centers “Facility for Antiproton and Ion Research” (FAIR) in Darmstadt, Germany, and the “Nuclotron-based Ion Collider fAcility” (NICA) at the Joint Institute for Nuclear Research (JINR) in Russia, will offer the unique possibility to produce and explore baryonic matter at high densities. At collision energies in the range of = 3–10 GeV, the baryons in the reaction zone of two heavy nuclei are expected to be piled-up to 3–8 times the density of an atomic nucleus. In nature, such densities are expected to exist in the core of massive neutron stars.
In contrast, in collisions at the Relativistic Heavy Ion Collider (RHIC) at the Brookhaven National Laboratory (BNL) in USA or at the Large Hadron Collider (LHC) at the “Centre Européen de Recherche Nucléaire (CERN) in Switzerland, a mixture of matter and antimatter is produced at vanishing baryon-chemical potential. In this case, the fundamental theory of strong interaction, Quantum Chromo Dynamics (QCD), predicts a smooth crossover transition from hadronic matter to a plasma of quarks and gluons at a pseudo-critical temperature of about 155 MeV [1,2]. This plasma is more than a hundred-thousand times hotter than the core of the sun, and resembles the primordial soup in the early universe about a microsecond after the big bang.
The conception of the three-dimensional phase diagram of QCD matter as a function of temperature, baryon-chemical and isospin-chemical potentials is sketched in Figure 1 [3]. QCD still is not able to make firm statements on the properties of matter at large baryon-chemical potentials. Therefore, the only theoretical guideline is provided by effective-model calculations which predict structures in the QCD phase diagram like a critical endpoint followed by a first-order phase transition, or new forms of exotic matter [4,5]. Figure 1 includes the conjectured landmarks such as the chiral and deconfinement phase transition, their critical endpoint, exotic phases like quarkyonic matter, together with the expected locations of cosmic matter such as neutron stars, neutron star mergers, and supernovae, in the region of large baryon-chemical potentials, low temperatures, and finite isospin-chemical potential.
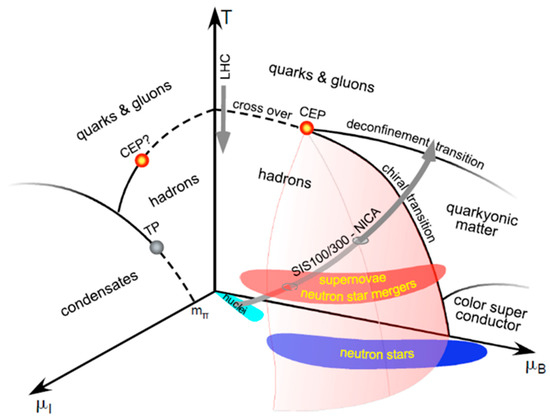
Figure 1.
Sketch of the three-dimensional phase diagram of strongly interacting matter as a function of temperature, baryon-chemical and isospin-chemical potential. The plot illustrates characteristic landmarks such as the critical endpoint (CEP) and the tri-critical point (TP). Taken from [3].
This article focusses on observables from laboratory experiments which are relevant for our understanding of the structure of neuron stars and the dynamics of neutron star mergers. Emphasis is put on the prospects for heavy-ion collisions, to measure the high-density nuclear matter equation-of-state, to find experimental indications for new phases of QCD matter at high net-baryon densities, and to shed light on the hyperon puzzle in neutron stars by the possible discovery and investigation of new (double-) strange hypernuclei. Future experimental progress requires multi-differential measurements of promising diagnostic probes, and, hence, extremely high reaction rates. The “Compressed Baryonic Matter” experiment at FAIR, which is designed to meet these requirements, will be briefly described.
2. The High-Density Nuclear-Matter Equation-of-State
The evolution of supernova explosions, the mass and radius of neutron stars, and the dynamics of neutron star mergers is governed by the equation-of-state (EOS) of nuclear matter. Figure 2 depicts results of calculations based on the Tolman–Oppenheimer–Volkoff (TOF) equation for the mass of neutron stars as a function of central density for different EOS. Depending on the chosen EOS, the density in the core of neutron stars reaches values of 3–5 ρ0 for star masses between 1.3 and 1.8 solar masses, and values of 5–8 ρ0 for star masses between 1.8 and 2.0 solar masses [6]. The most recent relativistic Shapiro delay measurements of an extremely massive millisecond pulsar found a mass of 2.14 + 0.10 − 0.09 solar masses [7]. In order to accommodate such large neutron star masses, the EOS has to be stiff at high densities [8].
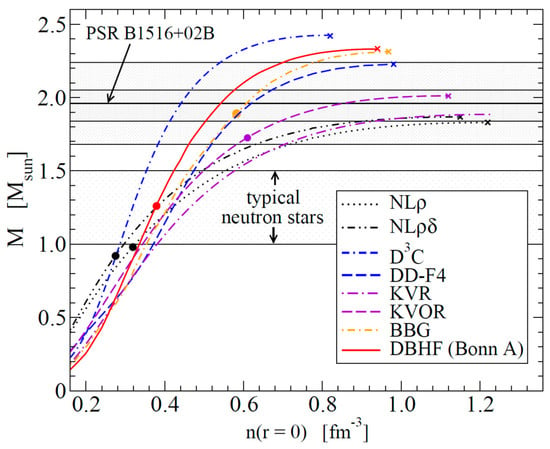
Figure 2.
Mass versus central density of neutron stars calculated from the Tolman–Oppenheimer–Volkoff (TOF) equation using different equation-of-state (EOS). For explanation of the abbreviations please look at table 1 in [6].
The EOS describes the relation between density, pressure, volume, temperature, energy, and isospin asymmetry. The pressure can be written as
with energy E, volume V, and temperature T. With V = A/ρ and δV/δρ = −A/ρ2, where A is the atomic number of the nucleus and ρ the density, one obtains
P = δE/δV |T = const
P = ρ2 δ(E/A)/δρ |T = const
The energy per nucleon depends on the isospin, and can be expressed as
with the asymmetry parameter δ = (ρn − ρp)/ρ. Symmetric matter is stable around saturation density ρ0 with a binding energy of E/A(ρo) = −16 MeV, the slope δ(E/A)(ρo)/δρ = 0, and the curvature Knm = 9ρ2 δ2(E/A)/δρ2 with Knm the nuclear incompressibility. The incompressibility of symmetric matter at saturation density has been determined from giant monopole resonances of heavy nuclei, and found to be Knm (ρ0) = 230 ± 10 MeV [9].
EA(ρ,δ) = EA(ρ,0) + Esym(ρ)·δ2 + O(δ4)
The symmetry energy Esym(ρ) can be parameterized as
Esym(ρ) = Esym(ρ0) + L/3·(ρ − ρ0)/ρ0 + Ksym/18·((ρ − ρ0)/ρ0)2
At saturation density, empirical average values have been found to be Esym(ρ0) = 32 MeV, and L(ρ0) = 59 MeV for the slope [10]. For the curvature at saturation density, a value of Ksym(ρ0) = 500 ± 100 MeV was extracted from giant monopole resonances of nuclei with different isospin [9].
Various EOS are shown in the left panel of Figure 3 as a function of density, calculated for symmetric nuclear matter (lower set of curves) and for neutron matter (higher set of curves) [11]. The difference between the two sets of curves is the symmetry energy Esym(ρ) which is plotted in the right panel of Figure 3. Most of the experiments performed so far have measured Esym and the slope L at densities around ρ0, and model calculations then try to extrapolate Esym to higher densities [12].
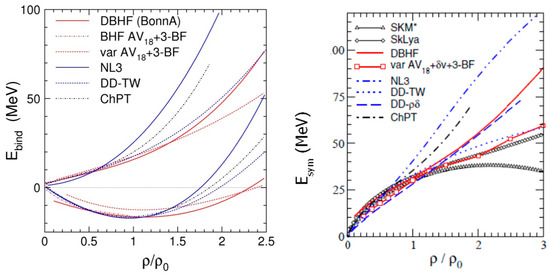
Figure 3.
Left panel: EOS of in isospin-symmetric nuclear matter (lower curves) and neutron matter (upper curves). Right panel: symmetry energy as a function of density. BHF/DBHF and variational calculations are compared to phenomenological density functionals NL3 and DD-TW and ChPT. For explanation of the abbreviations see [11].
Extensive experimental investigations have been undertaken at GSI in order to study the EOS of symmetric matter at densities up to about 2 ρ0. The KaoS collaboration measured the excitation of K+ meson production in Au + Au and C + C collisions at subthreshold beam energies from 0.8 A and 1.5 A GeV [13]. At subthreshold beam energies, kaons are produced in multi-step collisions involving pions and Delta resonances, and, hence, are sensitive to the density of the reaction volume, which depends on the EOS. According to Relativistic Quantum Molecular Dynamics (RQMD) and Isospin Quantum Molecular Dynamics (IQMD) transport model calculations, the K+ meson data can only be reproduced when using momentum-dependent interactions and a soft EOS with a nuclear incompressibility of about 200 MeV [14,15]. The FOPI collaboration measured the elliptic flow protons, deuterons, tritons and 3He in Au + Au collisions at beam kinetic energies between 0.4 A and 1.5 A GeV. The experimental data could be reproduced by IQMD transport calculations, when taking into account momentum-dependent interactions and assuming a soft EOS for symmetric matter, i.e., a nuclear incompressibility of Knm = 190 ± 30 MeV [16]. Some of the harder EOS shown in the left panel of Figure 3 are in contradiction with these results.
The symmetry energy at densities above saturation density has been investigated by the FOPI and the ASY–EOS (Asymmetric Equation-Of-State) collaborations, which both measured the elliptic flow of neutrons and protons in Au+Au collisions at a beam kinetic energy of 400 A MeV at the GSI SIS18 accelerator [17,18]. When comparing the experimental data with results of Ultra Relativistic Quantum Molecular Dynamics (UrQMD) transport code calculations, which took into account a symmetry potential between protons and neutrons, a value for the symmetry energy of about Esym= 60 ± 10 MeV at 2 ρ0 was extracted from the FOPI data. The result of the ASY–EOS experiment, which took place more than 20 years later, corresponds to a value of about Esym= 55 ± 5 MeV at twice saturation density. This value rules out some of the Esym curves depicted in the right panel of Figure 3.
According to Figure 2, the central densities of massive neutron stars reach values well above 3 ρ0 for most of the EOS. On the other hand, Figure 3 demonstrates that the various EOS vastly differ already above 2 ρ0, and extrapolations to 4 or 5 ρ0 are not conclusive. Moreover, Figure 3 illustrates that it is not sufficient to determine the symmetry energy Esym at high densities, but one has to measure the EOS for symmetric nuclear matter as well, in order to shed light on the EOS for neutron star matter. Such densities can be reached in heavy-ion collisions for beam kinetic energies which are well above the energies available at the GSI SIS18 synchrotron. According to model calculations, the nuclear fireball will be compressed to densities of about 5 ρ0 in central Au+Au collisions already at kinetic beam energies of 5 A GeV, and densities above 8 ρ0 are reached at 10 A GeV [19]. Above densities of about 5 ρ0, the nucleons are expected to percolate, start to melt and to dissolve into their constituents [8].
Pioneering experiments in this density regime have been performed at the AGS, where the collective flow of protons has been measured in Au + Au collisions at kinetic energies from 2 A to 11 A GeV [20]. Both the directed flow as well as the elliptic flow are driven by the pressure gradient inside the reaction volume, and, hence, are sensitive to the EOS. The experimental data have been compared to the results of BUU transport model calculations, which take into account the nuclear incompressibility [21]. It turned out that the directed flow data are compatible with a soft EOS (Knm = 210 MeV), whereas the data on the elliptic flow can be better reproduced assuming a stiff EOS (Knm = 300 MeV). In conclusion, the analysis of the flow data is incompatible with extremely soft or stiff EOS’s, but still is consistent with values for the nuclear incompressibility ranging from about Knm = 200 MeV to more than 300 MeV.
The future Compressed Baryonic Matter experiment at FAIR will improve the data quality on the proton flow in the kinetic beam energy range up to 11A GeV, and will add data on the collective flow of light fragments and strange particles. Another promising observable to study the high-density EOS of symmetric matter is the excitation function of multi-strange (anti-)hyperons. According to transport models, Ξ and Ω hyperons are produced in sequential collisions involving kaons and Lambdas, and, therefore, are sensitive to the density in the fireball [22,23]. This sensitivity is expected to increase at beam energies close to or even below the production threshold, as was the case for kaon production at beam energies around 1 A GeV at SIS18. Preliminary results of calculations with the novel Parton-Hadron-Quantum-Molecular Dynamics (PHQMD) transport model indicate that the yields of Ξ− and Ω− hyperons and even more of Ξ+ and Ω+ anti-hyperons produced in A+A collisions at FAIR energies depend significantly on the EOS [24]. For a soft EOS, higher densities are reached than for a stiff EOS, and, hence, the number of multiple-collisions increases, resulting in a higher yield of multi-strange hyperons. Therefore, the measurement of the excitation functions of multi-strange (anti-) hyperons at SIS100 beam energies is an essential part of the Compressed Baryonic Matter (CBM) research program with a substantial discovery potential regarding the high-density nuclear matter equation-of-state at neutron star core densities.
In order to shed light on the properties of dense neutron star matter, one has to explore the symmetry energy at high densities, in addition to the EOS for symmetric matter. This could be done by measuring the elliptic flow of neutrons and charged particles at FAIR energies. Another possibility is to study the production of particles of opposite isospin, i.e., with I3 = ±1, which reflect the neutron and proton densities in the fireball. According to transport model calculations, the π−/π+ ratio is sensitive to Esym at beam energy close to the pion production threshold. However, this sensitivity decreases with increasing beam energy. Moreover, the yet unknown Δ(1232) in-medium potentials also effects the measured π−/π+ ratio [25]. At higher beam energies and matter densities, the Σ−/Σ+ ratio may take over the role of the π−/π+ ratio, providing information on the Esym at high baryon densities. The experimental challenge is to identify instable particles with one neutral daughter, which will be realized in the CBM experiment by its high-resolution tracking systems based on the missing mass method.
3. Searching for New Phases of QCD Matter at Large Baryon-Chemical Potentials
The conjectured QCD phase diagram shown in Figure 1 exhibits structures at large baryon-chemical potentials such as a chiral and a deconfinement first-order phase transition merging at a critical endpoint with a region of quarkyonic matter in between. None of these structures or phases has been found so far. As mentioned in the beginning, first-principle theories, such as perturbative QCD, still fail to make reliable predictions for properties of matter at large baryon-chemical potentials. In order to get an idea on the degrees-of-freedoms of matter in the core of neutron stars, we have to rely on effective models. Calculations of the evolution of a neutron star merger with a total mass of 2.8 solar masses based on Chiral Mean Field model predict a phase transition to pure quark matter at a density of 4 ρ0 and at a temperature of about 50 MeV [26]. This phase transition occurs shortly before the high-mass neutron star collapses into a black hole.
3.1. Probing the Fireball Temperature with Di-Leptons
Similar temperatures and densities can be reached in heavy-ion collisions at moderate beam energies. The HADES (High-Acceptance Di-Electron Spectrometer) collaboration has performed di-electron measurements in Au + Au collisions at GSI-SIS18 with a beam kinetic energy of 1.25 A GeV, where densities of up to about 2.5 ρ0 can be reached. After subtraction of the known contributions from vector meson decays from the di-electron invariant mass spectrum, it was found that this so-called excess spectrum exhibits an exponential shape corresponding to thermal distribution with a temperature of about 72 MeV [27]. This spectrum can be regarded as an experimental measure of the temperature of the fireball produced in the collision of the two nuclei.
The HADES result demonstrates that the precise measurement of the di-lepton invariant mass spectrum as a function of beam energy opens the unique possibility to determine the caloric curve, which would be the first direct experimental signature for a phase transition in high-density nuclear matter. This method is illustrated in Figure 4, which sketches the fireball temperature as a function of collision energy for two scenarios: a smooth curve in the case of no phase transition or a crossover transition, and a caloric curve for a first order phase transition [28]. Such a measurement would also provide indications for the onset of deconfinement, the duration of phase coexistence, and the location of the critical endpoint. In the FAIR beam energy range, the di-lepton invariant mass spectrum between 1 and about 2.5 GeV/c2 is even a cleaner probe of the average fireball temperature, as it is not contaminated by di-leptons from vector meson decays [29].
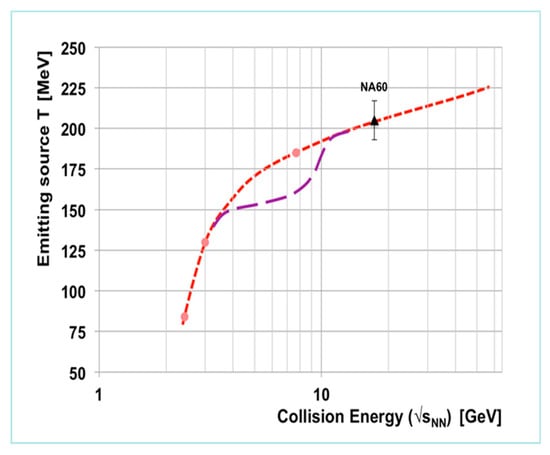
Figure 4.
Sketch of the emitting source temperature as a function of collision energy for two scenarios: no phase transition or crossover (red dashed line), and first order phase transition (purple dashed line) [28].
3.2. Scouting the QCD Phase Transition with Multi-Strange Hyperons
Multi-strange hyperons including Ω− and Ω+ produced in ultra-relativistic heavy-ion collisions are found to be in agreement with the predictions of the statistical hadronization model, which is based on the assumption of thermal equilibrium. This observation was interpreted as a signature for a phase transition from the quark-gluon plasma to the hadronic final state [30]. The argument is that equilibration cannot be achieved in the hadronic phase because of the small hyperon-nucleon scattering cross section, and multi-body collisions in the high particle density regime near the phase boundary are needed to establish equilibrium. The hyperon yields measured in Pb + Pb collisions at 40 A GeV at the SPS are found to be also in agreement with thermal model calculations [31]. The HADES collaboration has measured the particle yields in Ar + KCl collisions at a beam kinetic energy of 1.76 A GeV, and found also agreement with the thermal model for the most abundantly produced hadrons [32]. The measured yield of Ξ− hyperons, however, is underestimated by the thermal model by a factor 24 ± 9. Future experiments at SIS100 will perform beam energy scans, and search for the energy where the multi-strange hyperons are driven into equilibrium, indicating the onset of deconfinement in the high-density fireball created in heavy-ion collisions
3.3. Searching the QCD Critical Endpoint with Event-By-Event Fluctuations
According to Lattice QCD calculations, the higher moments of thermo-dynamical susceptibilities are sensitive to the vicinity of the critical point. These susceptibilities can be related to the multiplicity distributions of conserved quantities such as baryon number, strangeness and electrical charge, measured in heavy-ion collisions event-by-event. A classical analogy of this effect is critical opalescence in binary liquids caused by density fluctuations, which grow near the critical point. The STAR collaboration found an increase of the 4th order cumulant (kurtosis) of the net-baryon distribution measured event-by-event at the lowest beam energy measured in the beam energy scan [33]. At densities below the critical endpoint, in the region of phase coexistence, spinodal decomposition is expected occur. Calculations based on state-of-the-art machine learning methods find imprints of the spatial net-density distributions on higher-order cumulants of the net-baryon number multiplicity distribution integrated over many events. According to these calculations, the third order cumulant, the skewness, exhibits a peak in a central rapidity window at a beam energy Elab = 3–4 A GeV, where the transient hot and dense system created in the heavy ion collision is expected to reach the first-order phase transition [34]. Both for the confirmation of the critical fluctuations related to critical opalescence, and for the measurement of possible signatures for spinodal decomposition, precise data on the net-baryon number multiplicity distributions in the FAIR energy range are required.
3.4. Exploring the Role of Hyperons in Dense Nuclear Matter
The role of hyperons in neutron stars is a long-standing puzzle. With increasing density in the core on neutron stars, the chemical potential of neutrons and protons will also increase, and, at some point of density, exceed the chemical potential of hyperons. The appearance of a new degree-of-freedom should lead to a softening of the EOS, and prevent the formation of massive neutron stars, which, however, have been observed. In order to avoid this contradiction, different model calculations propose different solutions. Calculations describing the hadronic phase by non-linear relativistic field theory, and the quark phase by a non-local extension of the 3-flavor Nambu Jona-Lasinio model with repulsive vector interactions among the quarks [35]. Depending on the strength of the quark vector repulsion, the model predicts phase existence of hadrons and quarks in the core of massive neutron stars. Calculations based on the Quark–Meson-Coupling model predict hyperon contributions in neutron stars above densities of 3 ρ0, and at the presence of Ξ−,0 and anti-Λ hyperons at higher densities [36]. The model takes into account 3-body forces to prevent a strong softening of the EOS, and is able to explain neutron stars with more than two solar masses, with a central density of up to 6 ρ0. Calculations based on chiral effective field theory predict no hyperon contributions up to densities of 3–4 ρ0 when taking into account a repulsive ΛN potential at high density, and shift the appearance of hyperons to densities beyond 5 ρ0 when including repulsive 3-body ΛNN interactions [37].
The ΛN and ΛNN interactions can be studied in the laboratory by the measurement of hypernuclei. According to thermal model calculations, the production probability of light hypernuclei exhibits a maximum in heavy-ion collisions in the FAIR energy range [38]. The excitation functions of hypernuclei production can be understood as a coalescence of hyperons with light nuclei, where the hyperon yield increases with increasing beam energy, while the yield of light nuclei decreases with increasing beam energy. A saturation of the hypernuclei yield in heavy-ion collisions at FAIR energies is also predicted by calculations based on transport models [39]. The discovery of yet unknown (double-) lambda hypernuclei, and the determination of their lifetimes will provide valuable information on the ΛN, ΛNN, and ΛΛ interactions, which will shed light on the role of hyperons in neutron stars. The CBM experiment is well suited to identify hydrogen and helium hypernuclei, including light double-lambda hypernuclei, in heavy-ion collisions.
4. The Compressed Baryonic Matter Experiment at FAIR
The Facility for Antiproton and Ion Research (FAIR) in Darmstadt will be the leading research center in accelerator based fundamental science and applications for the coming decades. The FAIR research program covers hadron and nuclear physics, atomic physics and plasma physics, and applications in the fields of materials research and radiation biophysics including novel medical treatments and space science. High-intensity primary beams of protons with kinetic energies of up to 29 GeV, Uranium beams with energies of up to 11A GeV, and beams of N=Z nuclei with energies of up to 15 A GeV will be delivered by the SIS100 synchrotron. Primary heavy-ion beams will be converted into secondary beams of rare isotopes by a large-acceptance Superconducting Fragment Separator. The properties of short-lived neutron-rich or neutron-deficient isotopes will be studied by the subsequent experimental facilities of the NUSTAR (Nuclear Structure, Astrophysics and Reactions) collaboration, in order to explore the nucleosynthesis in the universe. The High-Energy Storage Ring (HESR) will accelerate and cool intense secondary beams of antiprotons, which will be used for hadron physics experiments with the PANDA detector. A variety of setups will be available for experiments in atomic, plasma, and biophysics, and in material science. The Compressed Baryonic Matter (CBM) detector system will investigate high-energy nucleus-nucleus collisions. The construction of the accelerator components and civil construction is ongoing. According to the actual planning, installation and commissioning of the experiments is planned during the period 2022–2024, and in 2025 FAIR will be fully operational.
The mission of the Compressed Baryonic Matter (CBM) experiment at FAIR is to explore the properties of QCD matter under extreme conditions as produced in high-energy heavy-ion collisions. As discussed in the previous chapters, the beam energies available at SIS100 appear to be especially well suited for studying the properties of QCD matter at high baryon-chemical potentials, and, therefore, offer the opportunity to address fundamental scientific questions related to nuclear and astrophysics. A review of the theoretical concepts and the experimental programs devoted to the exploration of the QCD phase diagram with focus on high net-baryon densities is given in the CBM Physics Book [40].
Many of the diagnostic probes discussed above such as anti-hyperons or dileptons are very rarely produced at beam energies where the highest baryon densities will be created. Moreover, extremely high statistics is needed to generate multi-differential data with sufficient precision. Therefore, the experimental challenge is to combine a large-acceptance and fast detector setup with a high-speed data read-out system and a high luminosity beam. The rate capabilities of existing and heavy-ion experiments under construction are plotted in Figure 5 as a function of collision energy. The comparison clearly demonstrates the uniqueness of the CBM setup in terms of interaction rates.
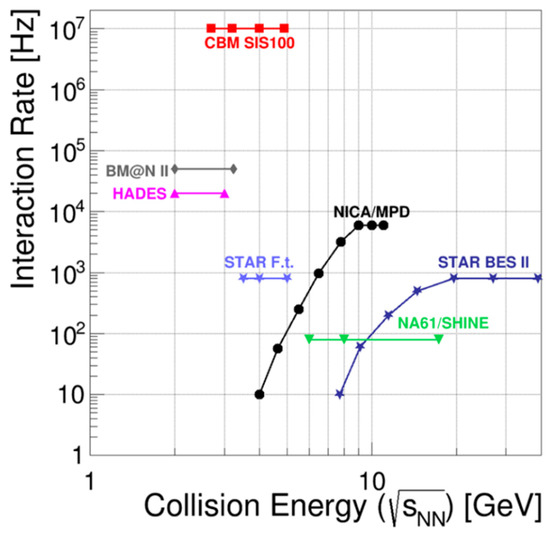
Figure 5.
Interaction rates achieved by existing and heavy-ion experiments under construction as a function of collision energy (taken from [28]).
The research program on dense QCD matter at FAIR will be performed by the experiments CBM and HADES, which will be operated alternatively. A sketch of the setups is shown in Figure 6. The HADES detector covers polar angles from 18 to 85 degrees, and will be used for reference measurements of electron–positron pairs and hadrons including multi-strange hyperons in collision systems with moderate particle multiplicities, such as proton–nucleus collisions or medium-size nucleus–nucleus collisions at lower SIS100 energies.

Figure 6.
The HADES detector (left) and the Compressed Baryonic Matter (CBM) experimental setup (right). The HADES setup comprises the following components: A diamond START detector, a Ring Imaging Cherenkov (RICH), four sets of Multi-wire Drift Chambers (MDC), a superconducting toroidal magnet and a multiplicity/electron trigger array consisting of granular pre-shower detectors at forward angles and two time of flight walls: a scintillator based time-of-flight wall (TOF) and the RPC wall built from resistive plate chambers. The CBM components are described in the text.
The CBM setup is a fixed target experiment which will be capable of measuring hadrons, electrons and muons in heavy-ion collisions over the full FAIR beam energy range. In a central collision of two gold nuclei at FAIR energies, about 700 charged particles are emitted. The tracks of these particles will be measured by a Silicon Tracking System consisting of eight layers of double-sided micro-strip sensors located in a magnetic field of a superconducting dipole magnet. The identification of hadrons requires an additional time-of-flight measurement, which is performed by a wall of Multi-Gap Resistive Plate Chambers (MRPC) with an active area of 100 m2 located about 7 m downstream the target. The identification of electrons and positrons is performed by a Ring Imaging Cherenkov (RICH) detector and a Transition Radiation Detector (TRD). The RICH can be replaced by a Muon Chamber (MuCh) system, which consists of hadron absorbers (graphite and iron plates) sandwiching triplets of Gas Electron Multiplier (GEM) detectors. For high-precision measurements of the primary vertex and of secondary decay vertices close to the target (e.g., from open charm decays), a Micro-Vertex-Detector (MVD) will be installed between the target and the first STS station. The MVD comprises four layers of silicon monolithic active pixel sensors (MAPS). The Project Spectator Detector, which is a hadronic calorimeter about 10 m downstream the target, will be used to determine the centrality and the reaction plane angle of the collision. For most of the observables, no trigger can be generated. Therefore, the data are read-out in a free streaming mode without any event correlation. The read-out electronics generates a time-stamp for each signal, which is used, together with the 3-d position information, to reconstruct first the particle tracks, and then the events. Finally, the particles will be identified based on the track topology, the time-of-flight information, and, in case of the leptons, using the signals from RICH, TRD, and MuCh. The entire reconstruction chain is performed online by high-speed algorithms, which run on a high-performance computing farm.
5. Conclusions
The Compressed Baryonic Matter (CBM) experiment is one of the four scientific pillars of the Facility for Antiproton and Ion Research (FAIR). The CBM research program is devoted to the exploration of the QCD phase diagram in the region of high baryon-chemical potentials using high-energy nucleus–nucleus collisions. This includes the study of the equation-of-state of nuclear matter at neutron star core densities and the search for new phases of nuclear matter at high densities. The CBM detector is designed to measure promising diagnostic probes such as the collective flow of identified particles, event-by-event fluctuations, multi-strange hyperons, lepton pairs, and hypernuclei with unprecedented precision and statistics. In order to achieve the required statistics, the measurements will be performed at reaction rates up to 10 MHz. The unique combination of an accelerator which delivers a high-intensity heavy-ion beam, and a modern high-rate experiment based on innovative detector and computer technology offers the optimal prerequisite for a research program with substantial discovery potential regarding the fundamental properties of QCD matter.
Funding
The CBM project is supported by the German Ministry of Education and Research, the Helmholtz Association, and national funds of the CBM member institutions. The author acknowledges support from the Ministry of Science and Higher Education of the Russian Federation, grant N 3.3380.2017/4.6 and by the National Research Nuclear University MEPhI in the framework of the Russian Academic Excellence Project (contract No. 02.a03.21.0005, 27.08.2013). This research received no external funding.
Acknowledgments
The development of the CBM experiment is performed by the CBM Collaboration, which consists of more than 470 persons from 55 institutions and 12 countries.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Bazavov, A.; Bhattacharya, T.; Cheng, M.; De Tar, C.; Ding, H.-T.; Gottlieb, S.; Gupta, R.; Hegde, P.; Heller, U.M.; Karsch, F.; et al. The chiral and deconfinement aspects of the QCD transition. Phys. Rev. D 2012, 85, 054503. [Google Scholar] [CrossRef]
- Aoki, Y.; Endrődi, G.; Fodor, Z.; Katz, S.D.; Szabó, K.K. The order of the quantum chromodynamics transition predicted by the standard model of particle physics. Nature 2006, 443, 675–678. [Google Scholar] [CrossRef] [PubMed]
- NUPECC Long Range Plan 2017. Available online: http://www.nupecc.org/?display=lrp2016/main (accessed on 31 October 2019).
- McLerran, L.; Pisarski, R.D. Phases of dense quarks at large Nc. Nucl. Phys. A 2007, 796, 83. [Google Scholar] [CrossRef]
- Fukushima, K.; Hatsuda, T. The phase diagram of dense QCD. Rep. Prog. Phys. 2011, 74, 014001. [Google Scholar] [CrossRef]
- Blaschke, D.; Klaehn, T.; Weber, F. Constraints on the high-density nuclear equation of state from neutron star observables. arXiv 2008, arXiv:0808.1279. [Google Scholar]
- Cromartie, H.T.; Fonseca, E.; Ransom, S.M.; Demorest, P.B.; Arzoumanian, Z.; Blumer, H.; Brook, P.R.; De Cesar, M.E.; Dolch, T.; Ellis, J.A.; et al. Relativistic Shapiro delay measurements of an extremely massive millisecond pulsar. Nat. Astron. 2019. [Google Scholar] [CrossRef]
- Baym, G.; Hatsuda, T.; Kojo, T.; Powell, P.D.; Song, Y.; Takatsuka, T. From hadrons to quarks in neutron stars: A review. Rep. Prog. Phys. 2018, 81, 056902. [Google Scholar] [CrossRef]
- Blaizot, J.P.; Berger, J.F.; Dechargé, J.; Girod, M. Microscopic and macroscopic determination of nuclear compressibility. Nucl. Phys. A 1995, 591, 435–457. [Google Scholar] [CrossRef]
- Li, B.-A.; Han, X. Constraining the neutron–proton effective mass splitting using empirical constraints on the density dependence of nuclear symmetry energy around normal density. Phys. Lett. B 2013, 727, 276. [Google Scholar] [CrossRef]
- Fuchs, C. The Nuclear Equation of State at high densities. arXiv 2006, arXiv:nucl-th/0610038. [Google Scholar]
- Li, B.-A. Nuclear Symmetry Energy Extracted from Laboratory Experiments. Nucl. Phys. News 2017, 27, 7. [Google Scholar] [CrossRef]
- Sturm, C.; Böttcher, I.; Dȩbowski, M.; Förster, A.; Grosse, E.; Koczoń, P.; Kohlmeyer, B.; Laue, F.; Mang, M.; Naumann, L.; et al. Evidence for a soft nuclear equation of state from kaon production in heavy ion collisions. Phys. Rev. Lett. 2001, 86, 39. [Google Scholar] [CrossRef] [PubMed]
- Fuchs, C.; Faessler, A.; Zabrodin, E.; Zheng, Y.-M. Probing the Nuclear Equation of State by K+ Production in Heavy-Ion Collisions. Phys. Rev. Lett. 2001, 86, 1974. [Google Scholar] [CrossRef] [PubMed]
- Hartnack, C.; Aichelin, J. Analysis of kaon production around the threshold. J. Phys. G 2002, 28, 1649. [Google Scholar] [CrossRef]
- Le Fèvre, A.; Leifels, Y.; Reisdorf, W.; Aichelin, J.; Hartnack, C. Constraining the nuclear matter equation of state around twice saturation density. Nucl. Phys. A 2016, 945, 112–133. [Google Scholar] [CrossRef]
- Leifels, Y.; Blaich, T.; Elze, T.W.; Emling, H.; Freiesleben, H.; Grimm, K.; Henning, W.; Holzmann, R.; Keller, J.G.; Klingler, H. Exclusive studies of neutron and charged particle emission in collisions of Au 197+ 197Au at 400 MeV/nucleon. Phys. Rev. Lett. 1993, 71, 963. [Google Scholar] [CrossRef] [PubMed]
- Russotto, P.; Gannon, S.; Kupny, S.; Lasko, P.; Acosta, L.; Adamczyk, M.; Al-Ajlan, A.; Al-Garawi, M.; Al-Homaidhi, S.; Amorini, F. Results of the ASY-EOS experiment at GSI: The symmetry energy at supra-saturation density. Phys. Rev. C 2016, 94, 034608. [Google Scholar] [CrossRef]
- Arsene, I.C.; Bravina, L.V.; Cassing, W.; Ivanov Yu, B.; Larionov, A.; Randrup, J.; Russkikh, V.N.; Toneev, V.D.; Zeeb, G.; Zschiesche, D. Dynamical phase trajectories for relativistic nuclear collisions. Phys. Rev. C 2007, 75, 034902. [Google Scholar] [CrossRef]
- Pinkenburg, C.; Ajitanand, N.N.; Alexander, J.M.; Anderson, M.; Best, D.; Brady, F.P.; Case, T.; Caskey, W.; Cebra, D.; Chance, J.L. Elliptic Flow: Transition from Out-of-Plane to In-Plane Emission in Au + Au Collisions. Phys. Rev. Lett. 1999, 83, 1295. [Google Scholar] [CrossRef]
- Danielewicz, P.; Lacey, R.; Lynch, W.G. Determination of the Equation of State of Dense Matter. Science 2002, 298, 1592. [Google Scholar] [CrossRef]
- Li, F.; Chen, L.-W.; Ko, C.M.; Lee, S.H. Contributions of hyperon-hyperon scattering to subthreshold cascade production in heavy ion collisions. Phys. Rev. C 2012, 85, 064902. [Google Scholar] [CrossRef]
- Graef, G.; Steinheimer, J.; Li, F.; Bleicher, M. Deep sub-threshold Ξ and Λ production in nuclear collisions with the UrQMD transport model. Phys. Rev. C 2014, 90, 064909. [Google Scholar] [CrossRef]
- Aichelin, J.; Bratkovskaya, E.; Fevre, A.L.; Kireyeu, V.; Kolesnikov, V.; Leifels, Y.; Voronyuk, V. Parton-Hadron-Quantum-Molecular Dynamics (PHQMD)—A Novel Microscopic N-Body Transport Approach for Heavy-Ion Collisions, Dynamical Cluster Formation and Hypernuclei Production. arXiv 2019, arXiv:1907.03860. [Google Scholar]
- Cozma, M.D. The impact of energy conservation in transport models on the π−/π+ multiplicity ratio in heavy-ion collisions and the symmetry energy. Phys. Lett. B 2016, 753, 166–172. [Google Scholar] [CrossRef]
- Most, E.R.; Papenfort, L.J.; Dexheimer, V.; Hanauske, M.; Schramm, S.; Stocker, H.; Rezzolla, L. Signatures of Quark-Hadron Phase Transitions in General-Relativistic Neutron-Star Mergers. Phys. Rev. Lett. 2019, 122, 061101. [Google Scholar] [CrossRef] [PubMed]
- Adamczewski-Musch, J.; Arnold, O.; Behnke, C.; Belounnas, A.; Belyaev, A.; Berger-Chen, J.C.; Biernat, J.; Blanco, A.; Blume, C.; Böhmer, M. Probing baryon-rich matter with virtual photons, The HADES Collaboration. Nat. Phys. 2019, 15, 1040–1045. [Google Scholar] [CrossRef]
- Ablyazimov, T.; Abuhoza, A.; Adak, R.P.; Adamczyk, M.; Agarwal, K.; Aggarwal, M.M.; Ahammed, Z.; Ahmad, F.; Ahmad, N.; Ahmad, S.; et al. Challenges in QCD matter physics—The Compressed Baryonic Matter experiment at FAIR. arXiv 2016, arXiv:1607.01487. [Google Scholar]
- Rapp, R.; van Hees, H. Thermal Dileptons as Fireball Thermometer and Chronometer. Phys. Lett. B 2016, 753, 586. [Google Scholar] [CrossRef]
- Braun-Munzinger, P.; Stachel, J.; Wetterich, C. Chemical Freeze-out and the QCD Phase Transition Temperature. Phys. Lett. B 2004, 596, 61–69. [Google Scholar] [CrossRef]
- Andronic, A.; Braun-Munzinger, P.; Stachel, J. Thermal hadron production in relativistic nuclear collisions. Acta Phys. Polon. B 2009, 40, 1005–1012. [Google Scholar]
- Agakishiev, G.; Balanda, A.; Bannier, B.; Bassini, R.; Belver, D.; Belyaev, A.; Blanco, A.; Böhmer, M.; Boyard, J.L.; Cabanelas, P.; et al. Hyperon production in Ar + KCl collisions at 1.76A GeV. Eur. Phys. J. A 2011, 47, 21. [Google Scholar] [CrossRef]
- Adamczyk, L.; Balanda, A.; Bannier, B.; Bassini, R.; Belver, D.; Belyaev, A.; Blanco, A.; Böhmer, M.; Boyard, J.L.; Cabanelas, P.; et al. Beam Energy Dependence of Moments of the Net-Charge Multiplicity Distributions in Au + Au Collisions at RHIC. Phys. Rev. Lett. 2014, 113, 092301. [Google Scholar] [CrossRef] [PubMed]
- Steinheimer, J.; Pang, L.G.; Zhou, K.; Koch, V.; Randrup, J.; Stoecker, H. A machine learning study to identify spinodal clumping in high nergy nuclear collisions. arXiv 2019, arXiv:1906.06562. [Google Scholar]
- Orsaria, M.; Rodrigues, H.; Weber, F.; Contrera, G.A. Quark deconfinement in high-mass neutron stars. Phys. Rev. C 2014, 89, 015806. [Google Scholar] [CrossRef]
- Rikovska-Stone, J.; Guichon, P.A.M.; Matevosyan, H.H.; Thomas, A.W. Cold uniform matter and neutron stars in the quark-mesons-coupling mode. Nucl. Phys. A 2007, 792, 341. [Google Scholar] [CrossRef]
- Weise, W. Dense Baryonic Matter and Strangeness in Neutron Stars. arXiv 2019, arXiv:1905.03955. [Google Scholar]
- Andronic, A.; Braun-Munzinger, P.; Stachel, J.; Stocker, H. Production of light nuclei, hypernuclei and their antiparticles in relativistic nuclear collisions. Phys. Lett. B 2011, 697, 203–207. [Google Scholar] [CrossRef]
- Botvina, A.S.; Steinheimer, J.; Bratkovskaya, E.; Bleicher, M.; Pochodzalla, J. Formation of hypermatter and hypernuclei within transport models in relativistic ion collisions. Phys. Lett. B 2015, 742, 7–14. [Google Scholar] [CrossRef]
- Friman, B.; Höhne, C.; Knoll, J.; Leupold, S.; Randrup, J.; Rapp, R.; Senger, P. (Eds.) The CBM Physics Book; Series: Lecture Notes in Physics; Springer: Berlin/Heidelberg, Germany, 2011; Volume 814. [Google Scholar]
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).