Anomaly-Induced Transport Phenomena from Imaginary-Time Formalism
Abstract
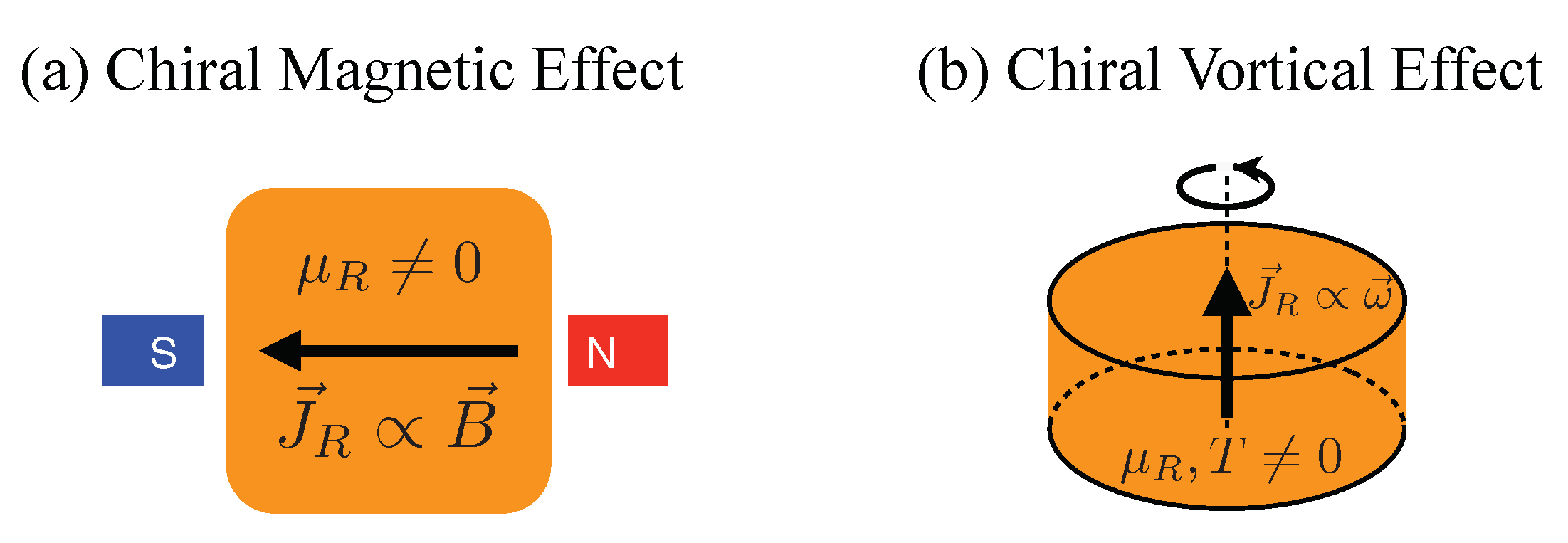
:1. Introduction
2. Preliminaries for the Anomaly-Induced Transport Phenomena
2.1. Anomalous (Non-)Conservation Laws for a Single Weyl Fermion
2.2. Zubarev’s Formula: Decomposing Dissipative and Nondissipative Transport
3. Perturbative Evaluation of Anomalous Transport Coefficients
3.1. Derivative Expansion of the Local Gibbs Distribution
3.2. One-loop Evaluation of Anomalous Transport Coefficients
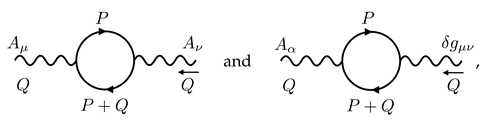
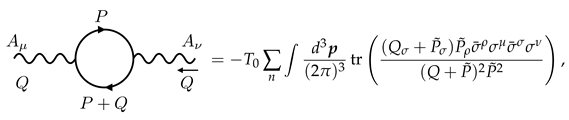
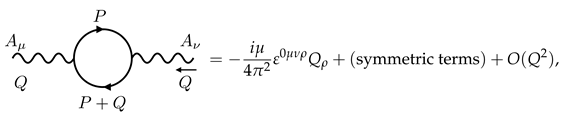
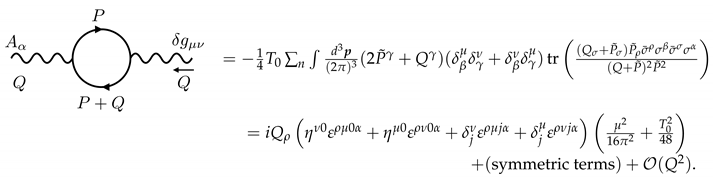
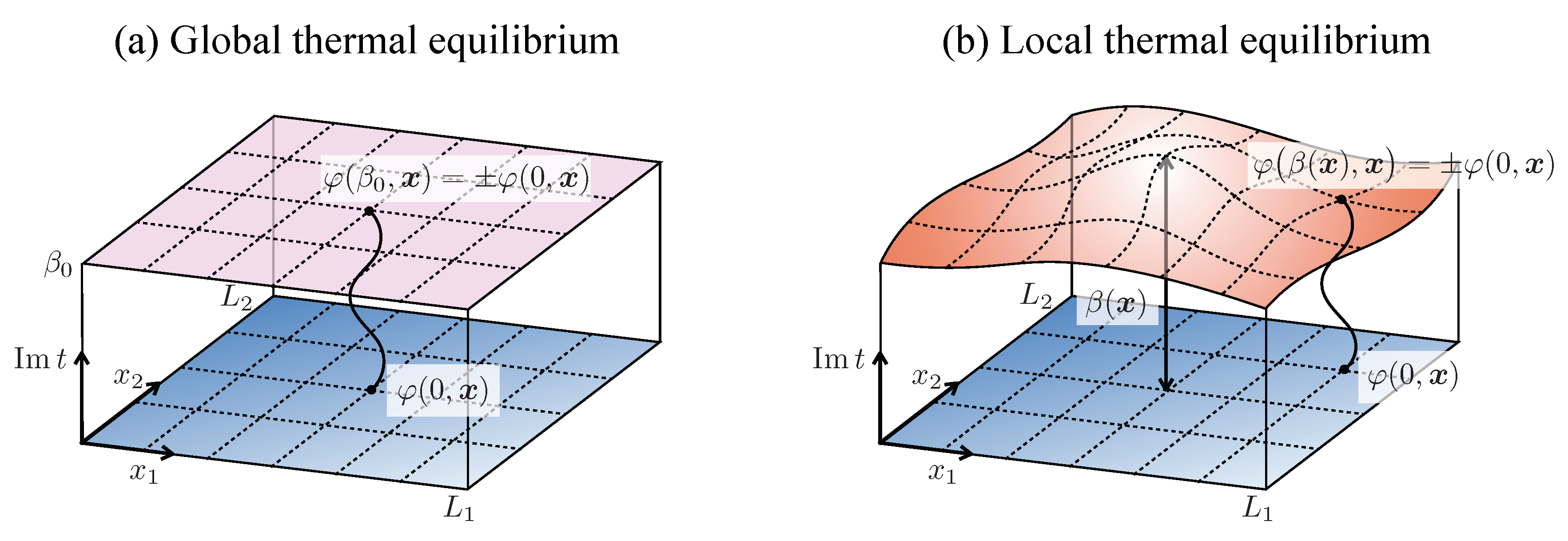
4. Anomaly Matching for Local Thermodynamic Functional
4.1. Basic Properties of Local Thermodynamic Functional
4.1.1. Path-Integral Formula and Resulting Symmetry
4.1.2. Variational Formula in the Presence of Quantum Anomaly
4.2. Anomaly Matching for Local Thermodynamic Functional
4.2.1. Chiral Anomaly in Thermal Spacetime
4.2.2. Global Anomaly for Kaluza-Klein Gauge Transformation
5. Summary and Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Bertlmann, R.A. Anomalies in Quantum Field Theory; Oxford University Press: Oxford, UK, 2000; Volume 91. [Google Scholar]
- Fujikawa, K.; Suzuki, H. Path Integrals and Quantum Anomalies; Oxford University Press on Demand: Oxford, UK, 2004; Volume 122. [Google Scholar]
- Fukuda, H.; Miyamoto, Y. On the γ-Decay of Neutral Meson. Prog. Theor. Phys. 1949, 4, 347–357. [Google Scholar] [CrossRef] [Green Version]
- Adler, S.L. Axial vector vertex in spinor electrodynamics. Phys. Rev. 1969, 177, 2426–2438. [Google Scholar] [CrossRef]
- Bell, J.S.; Jackiw, R. A PCAC puzzle: π0 → γγ in the σ model. Nuovo Cim. 1969, A60, 47–61. [Google Scholar] [CrossRef]
- ’t Hooft, G. Naturalness, chiral symmetry, and spontaneous chiral symmetry breaking. In Recent Developments in Gauge Theories. NATO Advanced Study Institutes Series (Series B. Physics); Springer: Boston, MA, USA, 1979; Volume 59. [Google Scholar]
- Frishman, Y.; Schwimmer, A.; Banks, T.; Yankielowicz, S. The Axial Anomaly and the Bound State Spectrum in Confining Theories. Nucl. Phys. 1981, B177, 157–171. [Google Scholar] [CrossRef]
- Wen, X.G. Classifying gauge anomalies through symmetry-protected trivial orders and classifying gravitational anomalies through topological orders. Phys. Rev. 2013, D88, 045013. [Google Scholar] [CrossRef]
- Tachikawa, Y.; Yonekura, K. On time-reversal anomaly of 2+1d topological phases. PTEP 2017, 2017, 033B04. [Google Scholar] [CrossRef]
- Gaiotto, D.; Kapustin, A.; Komargodski, Z.; Seiberg, N. Theta, Time Reversal, and Temperature. J. High Energy Phys. 2017, 5, 091. [Google Scholar] [CrossRef]
- Tanizaki, Y.; Kikuchi, Y. Vacuum structure of bifundamental gauge theories at finite topological angles. J. High Energy Phys. 2017, 6, 102. [Google Scholar] [CrossRef]
- Shimizu, H.; Yonekura, K. Anomaly constraints on deconfinement and chiral phase transition. Phys. Rev. 2018, D97, 105011. [Google Scholar] [CrossRef]
- Tanizaki, Y.; Misumi, T.; Sakai, N. Circle compactification and ’t Hooft anomaly. J. High Energy Phys. 2017, 12, 56. [Google Scholar] [CrossRef]
- Tanizaki, Y.; Kikuchi, Y.; Misumi, T.; Sakai, N. Anomaly matching for phase diagram of massless -QCD. Phys. Rev. 2018, D97, 054012. [Google Scholar] [CrossRef]
- Sulejmanpasic, T.; Tanizaki, Y. C-P-T anomaly matching in bosonic quantum field theory and spin chains. Phys. Rev. 2018, B97, 144201. [Google Scholar] [CrossRef]
- Yao, Y.; Hsieh, C.T.; Oshikawa, M. Anomaly matching and symmetry-protected critical phases in SU(N) spin systems in 1 + 1 dimensions. arXiv 2018, arXiv:1805.06885. [Google Scholar]
- Tanizaki, Y.; Sulejmanpasic, T. Anomaly and global inconsistency matching: θ-angles, SU(3)/U(1)2 nonlinear sigma model, SU(3) chains and its generalizations. Phys. Rev. 2018, B98, 115126. [Google Scholar] [CrossRef]
- Tanizaki, Y. Anomaly constraint on massless QCD and the role of Skyrmions in chiral symmetry breaking. J. High Energy Phys. 2018, 8, 171. [Google Scholar] [CrossRef]
- Yonekura, K. Anomaly matching in QCD thermal phase transition. arXiv 2019, arXiv:1901.08188. [Google Scholar] [CrossRef]
- Fukushima, K.; Kharzeev, D.E.; Warringa, H.J. The Chiral Magnetic Effect. Phys. Rev. 2008, D78, 074033. [Google Scholar] [CrossRef]
- Erdmenger, J.; Haack, M.; Kaminski, M.; Yarom, A. Fluid dynamics of R-charged black holes. J. High Energy Phys. 2009, 1, 55. [Google Scholar] [CrossRef]
- Banerjee, N.; Bhattacharya, J.; Bhattacharyya, S.; Dutta, S.; Loganayagam, R.; Surowka, P. Hydrodynamics from charged black branes. J. High Energy Phys. 2011, 1, 094. [Google Scholar] [CrossRef]
- Torabian, M.; Yee, H.U. Holographic nonlinear hydrodynamics from AdS/CFT with multiple/non-Abelian symmetries. J. High Energy Phys. 2009, 8, 20. [Google Scholar] [CrossRef]
- Son, D.T.; Surowka, P. Hydrodynamics with Triangle Anomalies. Phys. Rev. Lett. 2009, 103, 191601. [Google Scholar] [CrossRef] [PubMed]
- Amado, I.; Landsteiner, K.; Pena-Benitez, F. Anomalous transport coefficients from Kubo formulas in Holography. J. High Energy Phys. 2011, 5, 081. [Google Scholar] [CrossRef]
- Landsteiner, K.; Megias, E.; Pena-Benitez, F. Gravitational Anomaly and Transport. Phys. Rev. Lett. 2011, 107, 021601. [Google Scholar] [CrossRef]
- Gao, J.H.; Liang, Z.T.; Pu, S.; Wang, Q.; Wang, X.N. Chiral Anomaly and Local Polarization Effect from Quantum Kinetic Approach. Phys. Rev. Lett. 2012, 109, 232301. [Google Scholar] [CrossRef]
- Son, D.T.; Yamamoto, N. Berry Curvature, Triangle Anomalies, and the Chiral Magnetic Effect in Fermi Liquids. Phys. Rev. Lett. 2012, 109, 181602. [Google Scholar] [CrossRef]
- Banerjee, N.; Bhattacharya, J.; Bhattacharyya, S.; Jain, S.; Minwalla, S.; Sharma, T. Constraints on Fluid Dynamics from Equilibrium Partition Functions. J. High Energy Phys. 2012, 9, 46. [Google Scholar] [CrossRef]
- Jensen, K.; Kaminski, M.; Kovtun, P.; Meyer, R.; Ritz, A.; Yarom, A. Towards hydrodynamics without an entropy current. Phys. Rev. Lett. 2012, 109, 101601. [Google Scholar] [CrossRef]
- Jensen, K. Triangle Anomalies, Thermodynamics, and Hydrodynamics. Phys. Rev. 2012, D85, 125017. [Google Scholar] [CrossRef]
- Banerjee, N.; Dutta, S.; Jain, S.; Loganayagam, R.; Sharma, T. Constraints on Anomalous Fluid in Arbitrary Dimensions. J. High Energy Phys. 2013, 3, 48. [Google Scholar] [CrossRef]
- Stephanov, M.A.; Yin, Y. Chiral Kinetic Theory. Phys. Rev. Lett. 2012, 109, 162001. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Landsteiner, K.; Megias, E.; Pena-Benitez, F. Anomalous Transport from Kubo Formulae. Lect. Notes Phys. 2013, 871, 433–468. [Google Scholar] [CrossRef] [Green Version]
- Jensen, K.; Loganayagam, R.; Yarom, A. Thermodynamics, gravitational anomalies and cones. J. High Energy Phys. 2013, 2, 88. [Google Scholar] [CrossRef]
- Son, D.T.; Yamamoto, N. Kinetic theory with Berry curvature from quantum field theories. Phys. Rev. 2013, D87, 085016. [Google Scholar] [CrossRef]
- Chen, J.W.; Pu, S.; Wang, Q.; Wang, X.N. Berry Curvature and Four-Dimensional Monopoles in the Relativistic Chiral Kinetic Equation. Phys. Rev. Lett. 2013, 110, 262301. [Google Scholar] [CrossRef]
- Jensen, K.; Kovtun, P.; Ritz, A. Chiral conductivities and effective field theory. J. High Energy Phys. 2013, 10, 186. [Google Scholar] [CrossRef]
- Jensen, K.; Loganayagam, R.; Yarom, A. Anomaly inflow and thermal equilibrium. J. High Energy Phys. 2014, 5, 134. [Google Scholar] [CrossRef]
- Jensen, K.; Loganayagam, R.; Yarom, A. Chern-Simons terms from thermal circles and anomalies. J. High Energy Phys. 2014, 5, 110. [Google Scholar] [CrossRef]
- Manuel, C.; Torres-Rincon, J.M. Kinetic theory of chiral relativistic plasmas and energy density of their gauge collective excitations. Phys. Rev. 2014, D89, 096002. [Google Scholar] [CrossRef]
- Chen, J.Y.; Son, D.T.; Stephanov, M.A.; Yee, H.U.; Yin, Y. Lorentz Invariance in Chiral Kinetic Theory. Phys. Rev. Lett. 2014, 113, 182302. [Google Scholar] [CrossRef] [PubMed]
- Haehl, F.M.; Loganayagam, R.; Rangamani, M. Adiabatic hydrodynamics: The eightfold way to dissipation. J. High Energy Phys. 2015, 5, 060. [Google Scholar] [CrossRef]
- Chen, J.Y.; Son, D.T.; Stephanov, M.A. Collisions in Chiral Kinetic Theory. Phys. Rev. Lett. 2015, 115, 021601. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Golkar, S.; Sethi, S. Global Anomalies and Effective Field Theory. J. High Energy Phys. 2016, 5, 105. [Google Scholar] [CrossRef]
- Chowdhury, S.D.; David, J.R. Global gravitational anomalies and transport. J. High Energy Phys. 2016, 12, 116. [Google Scholar] [CrossRef]
- Landsteiner, K. Notes on Anomaly Induced Transport. Acta Phys. Pol. B 2016, B47, 2617. [Google Scholar] [CrossRef]
- Gorbar, E.V.; Miransky, V.A.; Shovkovy, I.A.; Sukhachov, P.O. Consistent Chiral Kinetic Theory in Weyl Materials: Chiral Magnetic Plasmons. Phys. Rev. Lett. 2017, 118, 127601. [Google Scholar] [CrossRef] [PubMed]
- Hidaka, Y.; Pu, S.; Yang, D.L. Relativistic Chiral Kinetic Theory from Quantum Field Theories. Phys. Rev. 2017, D95, 091901. [Google Scholar] [CrossRef]
- Buzzegoli, M.; Grossi, E.; Becattini, F. General equilibrium second-order hydrodynamic coefficients for free quantum fields. J. High Energy Phys. 2017, 10, 091. [Google Scholar] [CrossRef]
- Hidaka, Y.; Pu, S.; Yang, D.L. Nonlinear Responses of Chiral Fluids from Kinetic Theory. Phys. Rev. 2018, D97, 016004. [Google Scholar] [CrossRef]
- Mueller, N.; Venugopalan, R. The chiral anomaly, Berry’s phase and chiral kinetic theory, from world-lines in quantum field theory. Phys. Rev. 2018, D97, 051901. [Google Scholar] [CrossRef]
- Mueller, N.; Venugopalan, R. Worldline construction of a covariant chiral kinetic theory. Phys. Rev. 2017, D96, 016023. [Google Scholar] [CrossRef]
- Glorioso, P.; Liu, H.; Rajagopal, S. Global Anomalies, Discrete Symmetries, and Hydrodynamic Effective Actions. J. High Energy Phys. 2019, 1, 043. [Google Scholar] [CrossRef]
- Hidaka, Y.; Yang, D.L. Nonequilibrium chiral magnetic/vortical effects in viscous fluids. Phys. Rev. 2018, D98, 016012. [Google Scholar] [CrossRef]
- Stone, M.; Kim, J. Mixed Anomalies: Chiral Vortical Effect and the Sommerfeld Expansion. Phys. Rev. 2018, D98, 025012. [Google Scholar] [CrossRef]
- Carignano, S.; Manuel, C.; Torres-Rincon, J.M. Consistent relativistic chiral kinetic theory: A derivation from on-shell effective field theory. Phys. Rev. 2018, D98, 076005. [Google Scholar] [CrossRef]
- Buzzegoli, M.; Becattini, F. General thermodynamic equilibrium with axial chemical potential for the free Dirac field. J. High Energy Phys. 2018, 12, 002. [Google Scholar] [CrossRef]
- Dayi, O.F.; Kilinçarslan, E. Quantum Kinetic Equation in the Rotating Frame and Chiral Kinetic Theory. Phys. Rev. 2018, D98, 081701. [Google Scholar] [CrossRef]
- Liu, Y.C.; Gao, L.L.; Mameda, K.; Huang, X.G. Chiral kinetic theory in curved spacetime. arXiv 2018, arXiv:1812.10127. [Google Scholar] [CrossRef]
- Mueller, N.; Venugopalan, R. Constructing phase space distributions with internal symmetries. arXiv 2019, arXiv:1901.10492. [Google Scholar] [CrossRef]
- Vilenkin, A. Macroscopic parity violating effects: Neutrino fluxes from rotating black holes and in rotating thermal radiation. Phys. Rev. 1979, D20, 1807–1812. [Google Scholar] [CrossRef]
- Vilenkin, A. Equilibrium parity violating current in a magnetic field. Phys. Rev. 1980, D22, 3080–3084. [Google Scholar] [CrossRef]
- Kharzeev, D.E.; McLerran, L.D.; Warringa, H.J. The Effects of topological charge change in heavy ion collisions: ‘Event by event P and CP violation’. Nuclear Phys. 2008, A803, 227–253. [Google Scholar] [CrossRef]
- Kharzeev, D.E.; Yee, H.U. Chiral Magnetic Wave. Phys. Rev. 2011, D83, 085007. [Google Scholar] [CrossRef]
- Burnier, Y.; Kharzeev, D.E.; Liao, J.; Yee, H.U. Chiral magnetic wave at finite baryon density and the electric quadrupole moment of quark-gluon plasma in heavy ion collisions. Phys. Rev. Lett. 2011, 107, 052303. [Google Scholar] [CrossRef]
- Hongo, M.; Hirono, Y.; Hirano, T. Anomalous-hydrodynamic analysis of charge-dependent elliptic flow in heavy-ion collisions. Phys. Lett. 2017, B775, 266–270. [Google Scholar] [CrossRef]
- Yee, H.U.; Yin, Y. Realistic Implementation of Chiral Magnetic Wave in Heavy Ion Collisions. Phys. Rev. 2014, C89, 044909. [Google Scholar] [CrossRef]
- Hirono, Y.; Hirano, T.; Kharzeev, D.E. The chiral magnetic effect in heavy-ion collisions from event-by-event anomalous hydrodynamics. arXiv 2014, arXiv:1412.0311. [Google Scholar]
- Adamczyk, L.; Adkins, J.K.; Agakishiev, G.; Aggarwal, M.M. Observation of charge asymmetry dependence of pion elliptic flow and the possible chiral magnetic wave in heavy-ion collisions. Phys. Rev. Lett. 2015, 114, 252302. [Google Scholar] [CrossRef] [PubMed]
- Yin, Y.; Liao, J. Hydrodynamics with chiral anomaly and charge separation in relativistic heavy ion collisions. Phys. Lett. 2016, B756, 42–46. [Google Scholar] [CrossRef]
- Huang, X.G. Electromagnetic fields and anomalous transports in heavy-ion collisions—A pedagogical review. Rept. Prog. Phys. 2016, 79, 076302. [Google Scholar] [CrossRef]
- Kharzeev, D.E.; Liao, J.; Voloshin, S.A.; Wang, G. Chiral magnetic and vortical effects in high-energy nuclear collisions—A status report. Prog. Part. Nucl. Phys. 2016, 88, 1–28. [Google Scholar] [CrossRef] [Green Version]
- Shi, S.; Jiang, Y.; Lilleskov, E.; Liao, J. Anomalous Chiral Transport in Heavy Ion Collisions from Anomalous-Viscous Fluid Dynamics. Ann. Phys. 2018, 394, 50–72. [Google Scholar] [CrossRef]
- Charbonneau, J.; Zhitnitsky, A. Topological Currents in Neutron Stars: Kicks, Precession, Toroidal Fields, and Magnetic Helicity. J. Cosmol. Astropart. Phys. 2010, 1008, 010. [Google Scholar] [CrossRef]
- Grabowska, D.; Kaplan, D.B.; Reddy, S. Role of the electron mass in damping chiral plasma instability in Supernovae and neutron stars. Phys. Rev. 2015, D91, 085035. [Google Scholar] [CrossRef]
- Kaminski, M.; Uhlemann, C.F.; Bleicher, M.; Schaffner-Bielich, J. Anomalous hydrodynamics kicks neutron stars. Phys. Lett. 2016, B760, 170–174. [Google Scholar] [CrossRef]
- Sigl, G.; Leite, N. Chiral Magnetic Effect in Protoneutron Stars and Magnetic Field Spectral Evolution. J. Cosmol. Astropart. Phys. 2016, 1601, 025. [Google Scholar] [CrossRef]
- Yamamoto, N. Chiral transport of neutrinos in supernovae: Neutrino-induced fluid helicity and helical plasma instability. Phys. Rev. 2016, D93, 065017. [Google Scholar] [CrossRef]
- Masada, Y.; Kotake, K.; Takiwaki, T.; Yamamoto, N. Chiral magnetohydrodynamic turbulence in core-collapse supernovae. Phys. Rev. 2018, D98, 083018. [Google Scholar] [CrossRef]
- Zyuzin, A.A.; Burkov, A.A. Topological response in Weyl semimetals and the chiral anomaly. Phys. Rev. 2012, B86, 115133. [Google Scholar] [CrossRef]
- Goswami, P.; Tewari, S. Axionic field theory of (3 + 1)-dimensional Weyl semimetals. Phys. Rev. 2013, B88, 245107. [Google Scholar] [CrossRef]
- Chen, Y.; Wu, S.; Burkov, A.A. Axion response in Weyl semimetals. Phys. Rev. 2013, B88, 125105. [Google Scholar] [CrossRef]
- Basar, G.; Kharzeev, D.E.; Yee, H.U. Triangle anomaly in Weyl semimetals. Phys. Rev. 2014, B89, 035142. [Google Scholar] [CrossRef]
- Hosur, P.; Qi, X. Recent developments in transport phenomena in Weyl semimetals. Comptes Rendus Phys. 2013, 14, 857–870. [Google Scholar] [CrossRef] [Green Version]
- Landsteiner, K. Anomalous transport of Weyl fermions in Weyl semimetals. Phys. Rev. 2014, B89, 075124. [Google Scholar] [CrossRef]
- Chernodub, M.N.; Cortijo, A.; Grushin, A.G.; Landsteiner, K.; Vozmediano, M.A.H. Condensed matter realization of the axial magnetic effect. Phys. Rev. 2014, B89, 081407. [Google Scholar] [CrossRef]
- Gorbar, E.V.; Miransky, V.A.; Shovkovy, I.A. Chiral anomaly, dimensional reduction, and magnetoresistivity of Weyl and Dirac semimetals. Phys. Rev. 2014, B89, 085126. [Google Scholar] [CrossRef]
- Armitage, N.P.; Mele, E.J.; Vishwanath, A. Weyl and Dirac Semimetals in Three Dimensional Solids. Rev. Mod. Phys. 2018, 90, 015001. [Google Scholar] [CrossRef]
- Gorbar, E.V.; Miransky, V.A.; Shovkovy, I.A.; Sukhachov, P.O. Anomalous transport properties of Dirac and Weyl semimetals (Review Article). Low Temp. Phys. 2018, 44, 487–505. [Google Scholar] [CrossRef]
- Li, Q.; Kharzeev, D.E.; Zhang, C.; Huang, Y.; Pletikosic, I.; Fedorov, A.V.; Zhong, R.D.; Schneeloch, J.A.; Gu, G.D.; Valla, T. Observation of the chiral magnetic effect in ZrTe5. Nat. Phys. 2016, 12, 550–554. [Google Scholar] [CrossRef]
- Lv, B.Q.; Weng, H.M.; Fu, B.B.; Wang, X.P.; Miao, H.; Ma, J. Experimental discovery of Weyl semimetal TaAs. Phys. Rev. 2015, X5, 031013. [Google Scholar] [CrossRef]
- Xu, S.Y.; Belopolski, I.; Alidoust, N.; Neupane, M.; Bian, G.; Zhang, C.; Sank, R. Discovery of a Weyl Fermion semimetal and topological Fermi arcs. Science 2015, 349, 613–617. [Google Scholar] [CrossRef]
- Matsubara, T. A New Approach to Quantum-Statistical Mechanics. Prog. Theor. Phys. 1955, 14, 351–378. [Google Scholar] [CrossRef] [Green Version]
- Abrikosov, A.A.; Gorkov, L.P.; Dzyaloshinskii, I.E. On the Application of Quantum-Field-Theory Methods to Problems of Quantum Statistics at Finite Temperatures. Sov. Phys. JETP 1959, 9, 636–641. [Google Scholar]
- Le Bellac, M. Thermal Field Theory; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Kapusta, J.I.; Gale, C. Finite-Temperature Field Theory: Principles and Applications; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
- Zubarev, D.N.; Prozorkevich, A.V.; Smolyanskii, S.A. Derivation of nonlinear generalized equations of quantum relativistic hydrodynamics. Theor. Math. Phys. 1979, 40, 821–831. [Google Scholar] [CrossRef]
- Zubarev, D.N.; Morozov, V.; Ropke, G. Statistical Mechanics of Nonequilibrium Processes, Volume 1: Basic Concepts, Kinetic Theory, 1st ed.; Wiley-VCH: Hoboken, NJ, USA, 1996. [Google Scholar]
- Zubarev, D.N.; Morozov, V.; Ropke, G. Statistical Mechanics of Nonequilibrium Processes, Volume 2: Relaxation and Hydrodynamic Processes; Wiley-VCH: Hoboken, NJ, USA, 1997. [Google Scholar]
- Becattini, F.; Bucciantini, L.; Grossi, E.; Tinti, L. Local thermodynamical equilibrium and the beta frame for a quantum relativistic fluid. Eur. Phys. J. 2015, C75, 191. [Google Scholar] [CrossRef]
- Hayata, T.; Hidaka, Y.; Noumi, T.; Hongo, M. Relativistic hydrodynamics from quantum field theory on the basis of the generalized Gibbs ensemble method. Phys. Rev. 2015, D92, 065008. [Google Scholar] [CrossRef]
- Hongo, M. Path-integral formula for local thermal equilibrium. Ann. Phys. 2017, 383, 1–32. [Google Scholar] [CrossRef] [Green Version]
- Hongo, M. Nonrelativistic Hydrodynamics from Quantum Field Theory: (I) Normal Fluid Composed of Spinless Schrödinger Fields. J. Stat. Phys. 2019. [Google Scholar] [CrossRef]
- Bardeen, W.A.; Zumino, B. Consistent and Covariant Anomalies in Gauge and Gravitational Theories. Nucl. Phys. 1984, B244, 421–453. [Google Scholar] [CrossRef]
- Nakai, R.; Ryu, S.; Nomura, K. Laughlin’s argument for the quantized thermal Hall effect. Phys. Rev. 2017, B95, 165405. [Google Scholar] [CrossRef]
- Witten, E. Global Aspects of Current Algebra. Nucl. Phys. 1983, B223, 422–432. [Google Scholar] [CrossRef]
- Witten, E. Global gravitational anomalies. Commun. Math. Phys. 1985, 100, 197. [Google Scholar] [CrossRef]
- Golkar, S.; Son, D.T. (Non)-renormalization of the chiral vortical effect coefficient. J. High Energy Phys. 2015, 2, 169. [Google Scholar] [CrossRef]
- Boyarsky, A.; Frohlich, J.; Ruchayskiy, O. Self-consistent evolution of magnetic fields and chiral asymmetry in the early Universe. Phys. Rev. Lett. 2012, 108, 031301. [Google Scholar] [CrossRef]
- Tashiro, H.; Vachaspati, T.; Vilenkin, A. Chiral Effects and Cosmic Magnetic Fields. Phys. Rev. 2012, D86, 105033. [Google Scholar] [CrossRef]
- Akamatsu, Y.; Yamamoto, N. Chiral Plasma Instabilities. Phys. Rev. Lett. 2013, 111, 052002. [Google Scholar] [CrossRef]
- Akamatsu, Y.; Yamamoto, N. Chiral Langevin theory for non-Abelian plasmas. Phys. Rev. 2014, D90, 125031. [Google Scholar] [CrossRef]
- Manuel, C.; Torres-Rincon, J.M. Dynamical evolution of the chiral magnetic effect: Applications to the quark-gluon plasma. Phys. Rev. 2015, D92, 074018. [Google Scholar] [CrossRef]
- Gorbar, E.V.; Miransky, V.A.; Shovkovy, I.A.; Sukhachov, P.O. Chiral magnetic plasmons in anomalous relativistic matter. Phys. Rev. 2017, B95, 115202. [Google Scholar] [CrossRef]
- Rybalka, D.; Gorbar, E.; Shovkovy, I. Hydrodynamic modes in a magnetized chiral plasma with vorticity. Phys. Rev. 2019, D99, 016017. [Google Scholar] [CrossRef]
- Hattori, K.; Hirono, Y.; Yee, H.U.; Yin, Y. MagnetoHydrodynamics with chiral anomaly: Phases of collective excitations and instabilities. arXiv 2017, arXiv:1711.08450. [Google Scholar]
- Giovannini, M.; Shaposhnikov, M.E. Primordial hypermagnetic fields and triangle anomaly. Phys. Rev. 1998, D57, 2186. [Google Scholar] [CrossRef]
- Giovannini, M. Anomalous Magnetohydrodynamics. Phys. Rev. 2013, D88, 063536. [Google Scholar] [CrossRef]
- Boyarsky, A.; Frohlich, J.; Ruchayskiy, O. Magnetohydrodynamics of Chiral Relativistic Fluids. Phys. Rev. 2015, D92, 043004. [Google Scholar] [CrossRef]
- Gorbar, E.V.; Shovkovy, I.A.; Vilchinskii, S.; Rudenok, I.; Boyarsky, A.; Ruchayskiy, O. Anomalous Maxwell equations for inhomogeneous chiral plasma. Phys. Rev. 2016, D93, 105028. [Google Scholar] [CrossRef]
- Yamamoto, N. Scaling laws in chiral hydrodynamic turbulence. Phys. Rev. 2016, D93, 125016. [Google Scholar] [CrossRef]
- Giovannini, M. Anomalous magnetohydrodynamics in the extreme relativistic domain. Phys. Rev. 2016, D94, 081301. [Google Scholar] [CrossRef]
- Rogachevskii, I.; Ruchayskiy, O.; Boyarsky, A.; Fröhlich, J.; Kleeorin, N.; Brandenburg, A.; Schober, J. Laminar and turbulent dynamos in chiral magnetohydrodynamics-I: Theory. Astrophys. J. 2017, 846, 153. [Google Scholar] [CrossRef]
- Huang, X.G.; Sedrakian, A.; Rischke, D.H. Kubo formulae for relativistic fluids in strong magnetic fields. Ann. Phys. 2011, 326, 3075–3094. [Google Scholar] [CrossRef]
- Grozdanov, S.; Hofman, D.M.; Iqbal, N. Generalized global symmetries and dissipative magnetohydrodynamics. Phys. Rev. 2017, D95, 096003. [Google Scholar] [CrossRef]
- Hernandez, J.; Kovtun, P. Relativistic magnetohydrodynamics. J. High Energy Phys. 2017, 5, 001. [Google Scholar] [CrossRef]
- Armas, J.; Jain, A. Magnetohydrodynamics as superfluidity. arXiv 2018, arXiv:1808.01939. [Google Scholar] [CrossRef] [PubMed]
- Glorioso, P.; Son, D.T. Effective field theory of magnetohydrodynamics from generalized global symmetries. arXiv 2018, arXiv:1811.04879. [Google Scholar]
- Armas, J.; Jain, A. One-form superfluids & magnetohydrodynamics. arXiv 2018, arXiv:1811.04913. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hongo, M.; Hidaka, Y. Anomaly-Induced Transport Phenomena from Imaginary-Time Formalism. Particles 2019, 2, 261-280. https://doi.org/10.3390/particles2020018
Hongo M, Hidaka Y. Anomaly-Induced Transport Phenomena from Imaginary-Time Formalism. Particles. 2019; 2(2):261-280. https://doi.org/10.3390/particles2020018
Chicago/Turabian StyleHongo, Masaru, and Yoshimasa Hidaka. 2019. "Anomaly-Induced Transport Phenomena from Imaginary-Time Formalism" Particles 2, no. 2: 261-280. https://doi.org/10.3390/particles2020018





