Causality and Renormalization in Finite-Time-Path Out-of-Equilibrium ϕ3 QFT
Abstract
1. Introduction and Survey
2. Results
2.1. Conservation and Non-Conservation of Energy at Vertices
- If the vertex time is lower than the other times of all incoming propagators, there are additional contributions, and energy is not conserved at this vertex. The oscillations are just what we would expect from the Heisenberg uncertainty relations. It is how the time dependence emerges in the finite-time-path out-of-equilibrium QFT. The ill-defined pinching singularities—products of retarded and advanced propagators with the same , only partially eliminated for the Keldysh time-path [30]—do not appear here as the propagator energies and are different variables, so that the singularities do not coincide except at the point . Thus, the pertinent mathematical expressions are well defined.
- For some vertices, at least one incoming propagator is advanced (or more generally, time is lower at the other vertex of this propagator); then, integration over the (supposed to be UV finite) re-establishes energy conservation.
- The case of UV divergent integrals is interesting; looking at integrations done separately, one would expect energy conservation, but performing other integrals before, one notices that the result is ill-defined. The solution is in regularization: regulated quantities are finite, and (say, in the dimensional regularization) the energy conservation is re-established (as far as ).
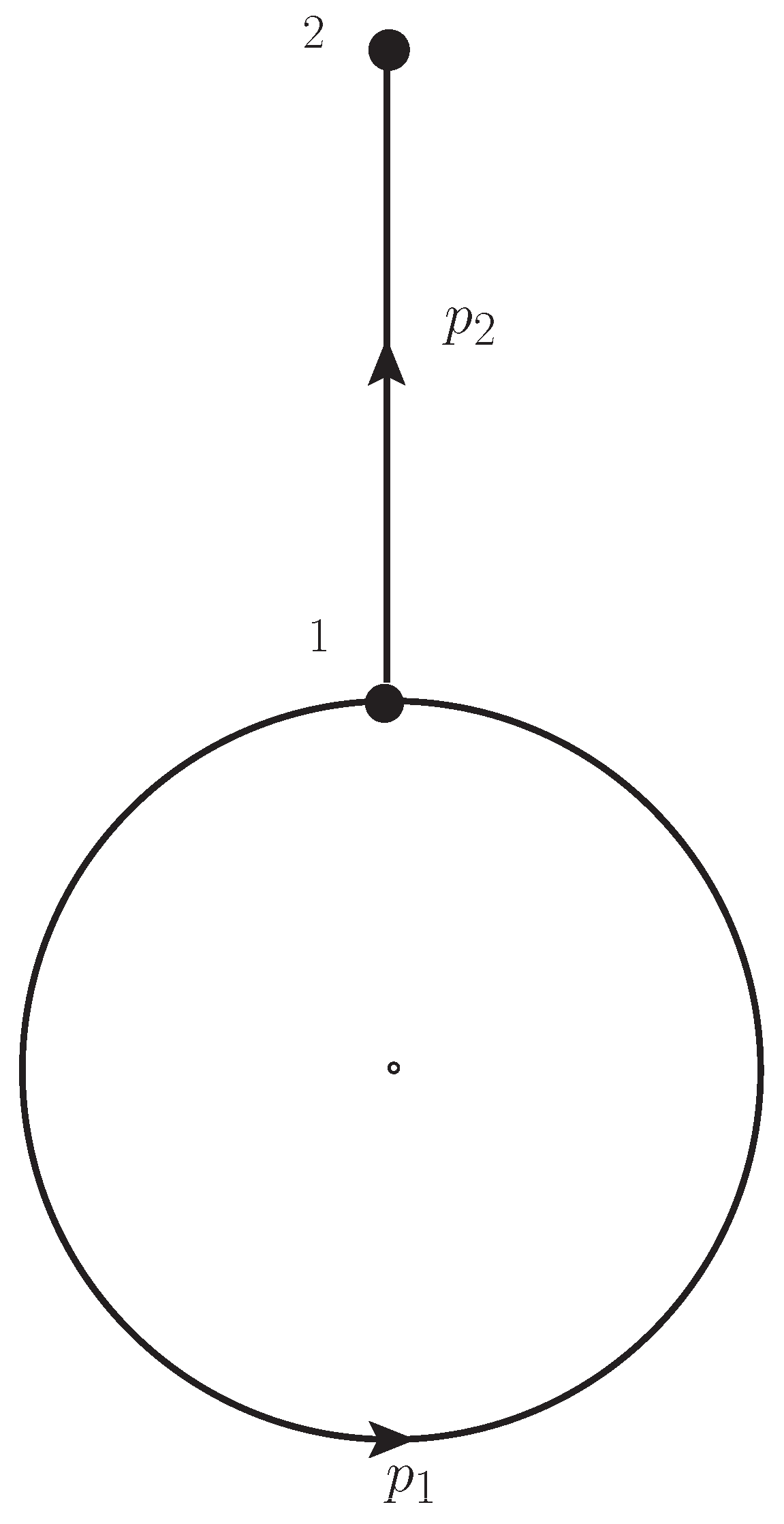
2.2. UV Divergence at the Tadpole Subdiagram
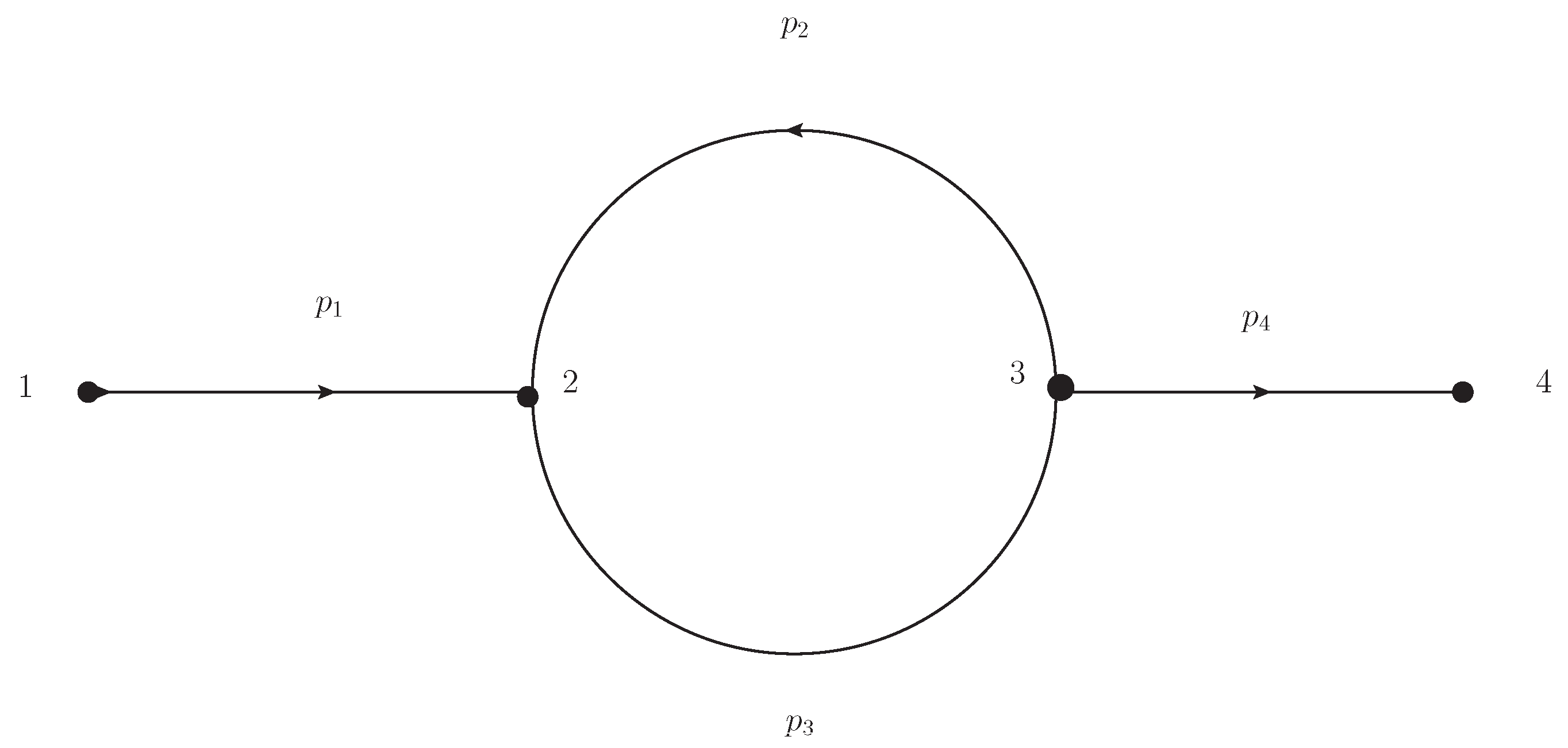
2.3. UV Divergence at the Self-Energy Subdiagram
2.4. Self-Energy Diagram with Legs
3. Discussion and Conclusions
- The integrals ensuring the energy conservation at the vertices above and should have been done before taking the limit .
- The renormalized self-energies (, , and ) are not a linear combination of true retarded and advanced components. This is directly readable from the final result, which does not vanish as in all directions in a complex plane . This problem is present already in S-matrix theory, and we only recognize it properly as a causality problem, in the sense that the expected properties of the theta-function fail: or . While it is not clear what harm it does to the theory, one may introduce “composite objects” , , and to improve convergence, and the causality is “repaired”. Indeed in the Glaser–Epstein approach, they consider the perturbation expansion, in which only self-energy with a leg appears.
- The tadpole contribution splits into the energy-conserving, constant component, which is eliminated by renormalization condition, and the other energy nonconserving, time-dependent component, is finite after subtraction. These tadpole contributions are strongly oscillating with time and vanish as , in good agreement with the renormalization condition of the S-matrix theory.
- The regularization () is extended till the late phase of calculation.
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| QFT | quantum field theory |
| FTP | finite-time-path |
| RT | renormalization theory |
| DR | dimensional regularization |
| UV | ultra-violet |
| QED | quantum electrodynamics |
| QCD | quantum chromodynamics |
Appendix A
References
- Bollini, C.G.; Giambiagi, J.J. Dimensional Renormalization: The Number of Dimensions as a Regularizing Parameter. Nuovo Cim. B 1972, 12, 20–26. [Google Scholar]
- ’t Hooft, G.; Veltman, M.J.G. Regularization and Renormalization of Gauge Fields. Nucl. Phys. B 1972, 44, 189. [Google Scholar] [CrossRef]
- Ashmore, J.F. A Method of Gauge Invariant Regularization. Nuovo Cim. Lett. 1972, 4, 289. [Google Scholar] [CrossRef]
- Cicuta, G.M.; Montaldi, E. Analytic renormalization via continuous space dimension. Nouvo Cim. Lett. 1972, 4, 329. [Google Scholar] [CrossRef]
- Wilson, K.G. Quantum field theory models in less than four-dimensions. Phys. Rev. D 1973, 7, 2911. [Google Scholar] [CrossRef]
- Donoghue, J.F.; Holstein, B.R. Renormalization and Radiative Corrections at Finite Temperature. Phys. Rev. D 1983, 28, 340. [Google Scholar] [CrossRef]
- Donoghue, J.F.; Holstein, B.R. Renormalization and Radiative Corrections at Finite Temperature, Erratum. Phys. Rev. D 1984, 29, 3004. [Google Scholar] [CrossRef]
- Chapman, I.A. Finite temperature wave function renormalization: A Comparative analysis. Phys. Rev. D 1997, 55, 6287–6291. [Google Scholar] [CrossRef]
- Nakkagawa, H.; Yokota, H. Effective potential at finite temperature: RG improvement versus high temperature expansion. Prog. Theor. Phys. Suppl. 1997, 129, 209–214. [Google Scholar] [CrossRef]
- Baacke, J.; Heitmann, K.; Patzold, C. Renormalization of nonequilibrium dynamics at large N and finite temperature. Phys. Rev. D 1998, 57, 6406–6419. [Google Scholar] [CrossRef]
- Esposito, S.; Mangano, G.; Miele, G.; Pisanti, O. Wave function renormalization at finite temperature. Phys. Rev. D 1998, 58, 105023. [Google Scholar] [CrossRef]
- van Hees, H.; Knoll, J. Renormalization in selfconsistent approximation schemes at finite temperature. 3. Global symmetries. Phys. Rev. D 2002, 66, 025028. [Google Scholar] [CrossRef]
- Jakovac, A.; Szep, Z. Renormalization and resummation in finite temperature field theories. Phys. Rev. D 2005, 71, 105001. [Google Scholar] [CrossRef]
- Arrizabalaga, A.; Reinosa, U. Renormalized finite temperature phi**4 theory from the 2PI effective action. Nucl. Phys. A 2007, 785, 234–237. [Google Scholar] [CrossRef]
- Blaizot, J.-P.; Ipp, A.; Mendez-Galain, R.; Wschebor, N. Perturbation theory and non-perturbative renormalization flow in scalar field theory at finite temperature. Nucl. Phys. A 2007, 784, 376–406. [Google Scholar] [CrossRef]
- Blaizot, J.-P.; Wschebor, N. Massive renormalization scheme and perturbation theory at finite temperature. Phys. Lett. B 2015, 741, 310–315. [Google Scholar] [CrossRef]
- Schwinger, J. Brownian motion of a quantum oscillator. J. Math. Phys. 1961, 2, 407. [Google Scholar] [CrossRef]
- Keldysh, L.V. Diagram technique for nonequilibrium processes. ZH. Eksp. Teor. Fiz. 1964, 47, 1515. [Google Scholar]
- Kadanoff, L.P.; Baym, G. Quantum Statistical Mechanics; Benjamin: New York, NY, USA, 1962. [Google Scholar]
- Danielewicz, P. Quantum Theory Of Nonequilibrium Processes. Ii. Application To Nuclear Collisions. Ann. Phys. 1984, 152, 239. [Google Scholar] [CrossRef]
- Rammer, J.; Smith, H. Quantum field-theoretical methods in transport theory of metals. Rev. Math. Phys. 1986, 58, 323. [Google Scholar] [CrossRef]
- Landsman, N.P.; van Weert, C.G. Real and Imaginary Time Field Theory at Finite Temperature and Density. Phys. Rep. 1987, 145, 141. [Google Scholar] [CrossRef]
- Calzetta, E.; Hu, B.L. Nonequilibrium Quantum Fields: Closed Time Path Effective Action, Wigner Function and Boltzmann Equation. Phys. Rev. D 1988, 37, 2878. [Google Scholar] [CrossRef]
- le Bellac, M. Thermal Field Theory; Cambridge University Press: Cambridge, UK, 1996. [Google Scholar]
- Brown, D.A.; Danielewicz, P. Partons in phase space. Phys. Rev. D 1998, 58, 094003. [Google Scholar] [CrossRef]
- Blaizot, J.-P.; Iancu, E. The Quark gluon plasma: Collective dynamics and hard thermal loops. Phys. Rept. 2002, 359, 355–528. [Google Scholar] [CrossRef]
- Dadić, I. Out-of-equilibrium thermal field theories: Finite time after switching on the interaction: Fourier transforms of the projected functions. Phys. Rev. D 2001, 63, 025011. [Google Scholar] [CrossRef]
- Dadić, I. Erratum: Out of equilibrium thermal field theories: Finite time after switching on the interaction and Wigner transforms of projected functions. Phys. Rev. D 2002, 66, 069903. [Google Scholar] [CrossRef]
- Dadić, I. Out-of-equilibrium thermal field theories: Finite time after switching on the interaction: Fourier transforms of the projected functions, Erratum. Nucl. Phys. A 2002, 702, 356. [Google Scholar] [CrossRef]
- Bedaque, P.F. Thermalization and pinch singularities in nonequilibrium quantum field theory. Phys. Lett. B 1995, 344, 23. [Google Scholar] [CrossRef]
- Dadić, I. Retarded propagator representation of out-of-equilibrium thermal field theories. Nucl. Phys. A 2009, 820, 267C–270D. [Google Scholar] [CrossRef]
- Kirillov, A.A.; Savelova, E.P. On the possible dynamical realization of the Pauli–Villars regularization. Phys. Atom. Nucl. 2015, 78, 1069. [Google Scholar] [CrossRef]
- Ryder, L.H. Quantum Field Theory; Cambridge University Press: Cambridge, UK, 1985. [Google Scholar]
- Epstein, H.; Glaser, V. The Role of locality in perturbation theory. Ann. Inst. Henri Poincare Phys. Theor. A 1973, 19, 211. [Google Scholar]
- Scharf, G. Finite Quantum Electrodynamics—The Causal Approach; Springer: Berlin/Heidelberg, Germany, 1995. [Google Scholar]
- Lazzarini, S.; Gracia-Bondıa, J.M. Improved Epstein-Glaser renormalization in coordinate space. 1. Euclidean framework. J. Math. Phys. 2003, 44, 3863. [Google Scholar] [CrossRef]
- Millington, P.; Pilaftsis, A. Perturbative Non-Equilibrium Thermal Field Theory to all Orders in Gradient Expansion. Phys. Lett. B 2013, 724, 56–62. [Google Scholar] [CrossRef]
- Millington, P.; Pilaftsis, A. Perturbative nonequilibrium thermal field theory. Phys. Rev. D 2013, 88, 085009. [Google Scholar] [CrossRef]
- Dickinson, R.; Forshaw, J.; Millington, P.; Cox, B. Manifest Causality in quantum field theory with sources and detectors. JHEP 2014, 1406, 049. [Google Scholar] [CrossRef]
- Urmossy, K.; Xu, Z. PoS DIS 2016, 265, 054.
- Wang, S.-Y.; Boyanovsky, D. Enhanced photon production from quark—gluon plasma: Finite lifetime effect. Phys. Rev. D 2001, 63, 051702. [Google Scholar] [CrossRef]
- Wang, S.-Y.; Boyanovsky, D.; Ng, K.-W. Direct photons: A nonequilibrium signal of the expanding quark gluon plasma at RHIC energies. Nucl. Phys. A 2002, 699, 819–846. [Google Scholar] [CrossRef]
- Arleo, F.; Aurenche, P.; Bopp, F.; Dadic, I.; David, G.; Delagrange, H.; d’Enterria, D.; Eskola, K.J.; Gelis, F.; Guillet, J.-Ph.; et al. Photon Physics in Heavy Ion Collisions at the LHC. 2004. Available online: http://cds.cern.ch/record/815045 (accessed on 30 November 2018).
- Dadić, I.; Klabučar, D.; Kuić, D. Direct Photons from Hot Quark Matter in Renormalized Finite-Time-Path QED, (unpublished).
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dadić, I.; Klabučar, D. Causality and Renormalization in Finite-Time-Path Out-of-Equilibrium ϕ3 QFT. Particles 2019, 2, 92-102. https://doi.org/10.3390/particles2010008
Dadić I, Klabučar D. Causality and Renormalization in Finite-Time-Path Out-of-Equilibrium ϕ3 QFT. Particles. 2019; 2(1):92-102. https://doi.org/10.3390/particles2010008
Chicago/Turabian StyleDadić, Ivan, and Dubravko Klabučar. 2019. "Causality and Renormalization in Finite-Time-Path Out-of-Equilibrium ϕ3 QFT" Particles 2, no. 1: 92-102. https://doi.org/10.3390/particles2010008
APA StyleDadić, I., & Klabučar, D. (2019). Causality and Renormalization in Finite-Time-Path Out-of-Equilibrium ϕ3 QFT. Particles, 2(1), 92-102. https://doi.org/10.3390/particles2010008




