Turbulence Generation by Shock-Acoustic-Wave Interaction in Core-Collapse Supernovae
Abstract
:1. Introduction
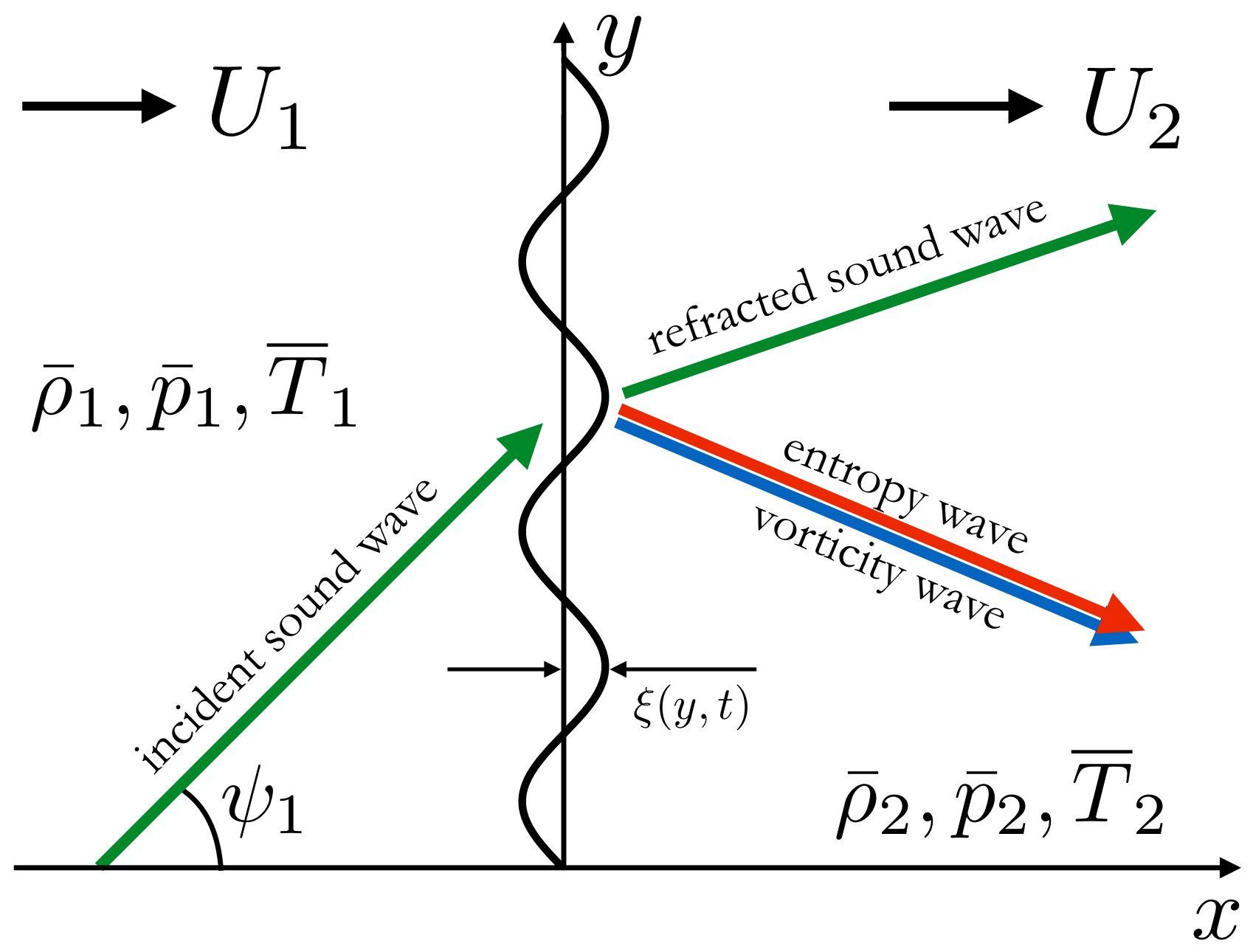
2. Method and Setup
3. Results
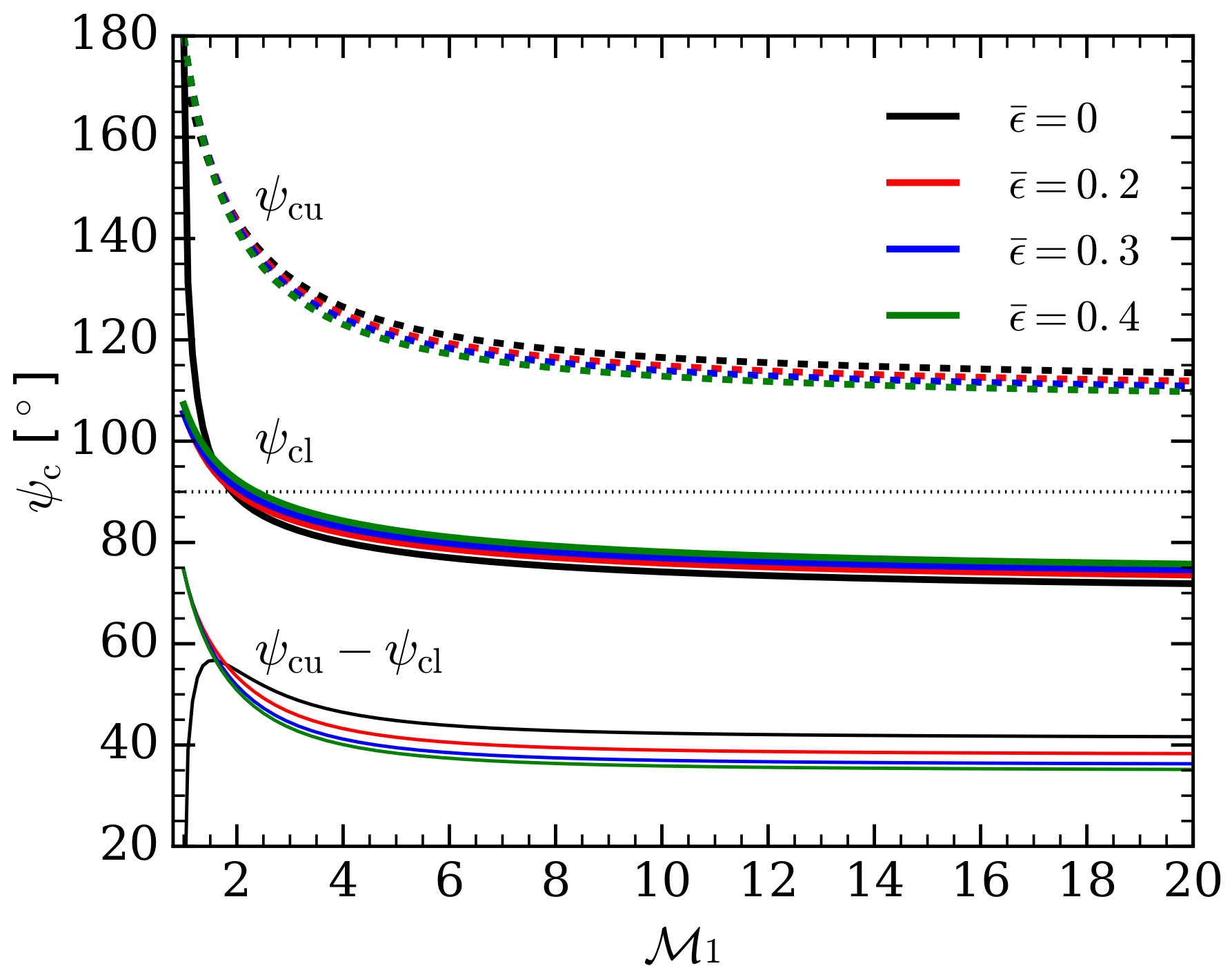
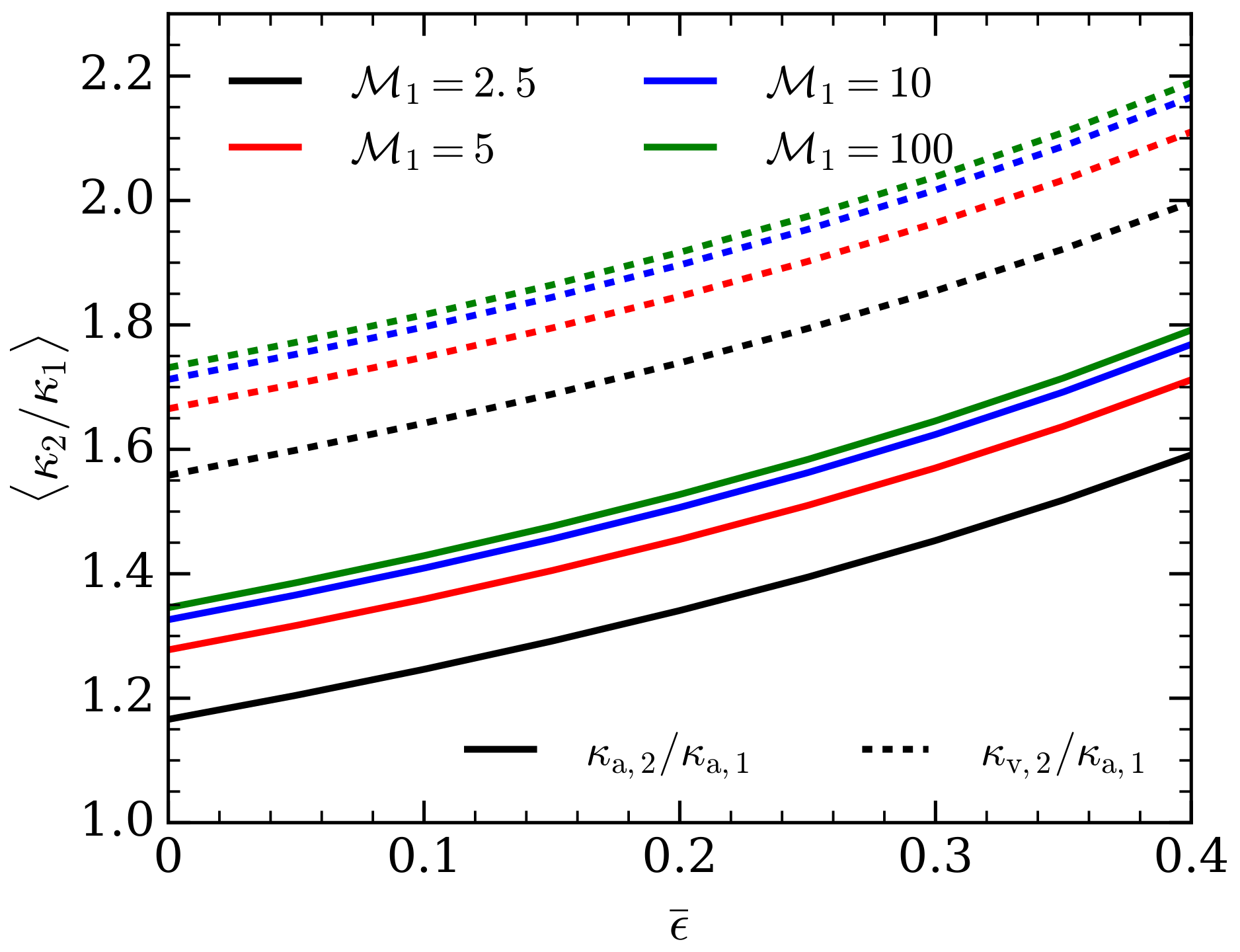
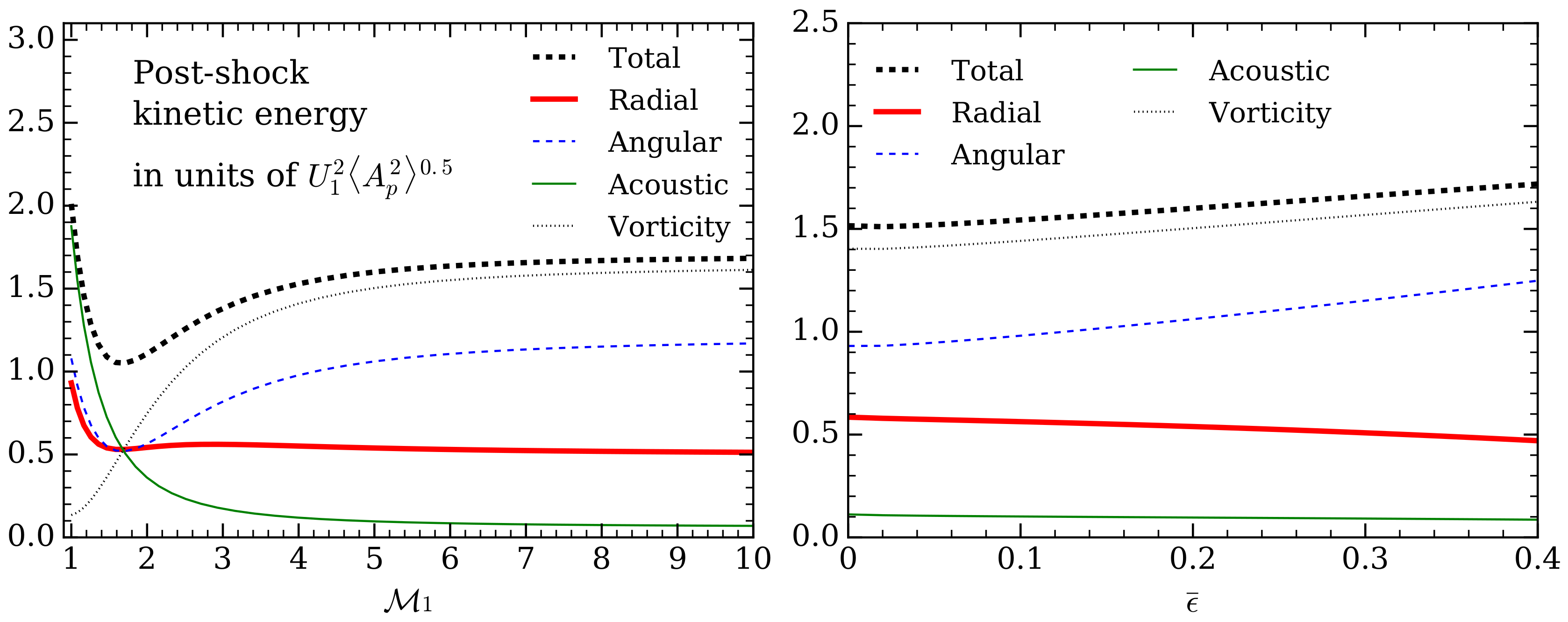
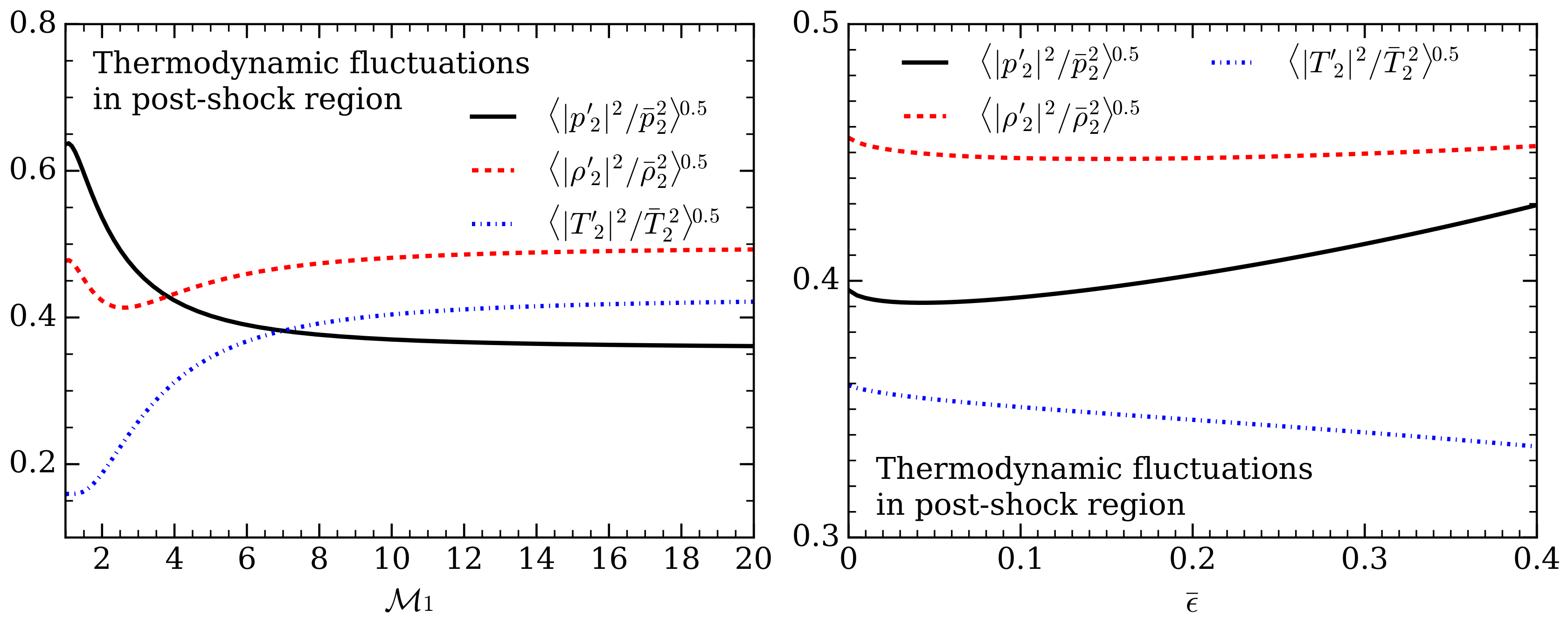
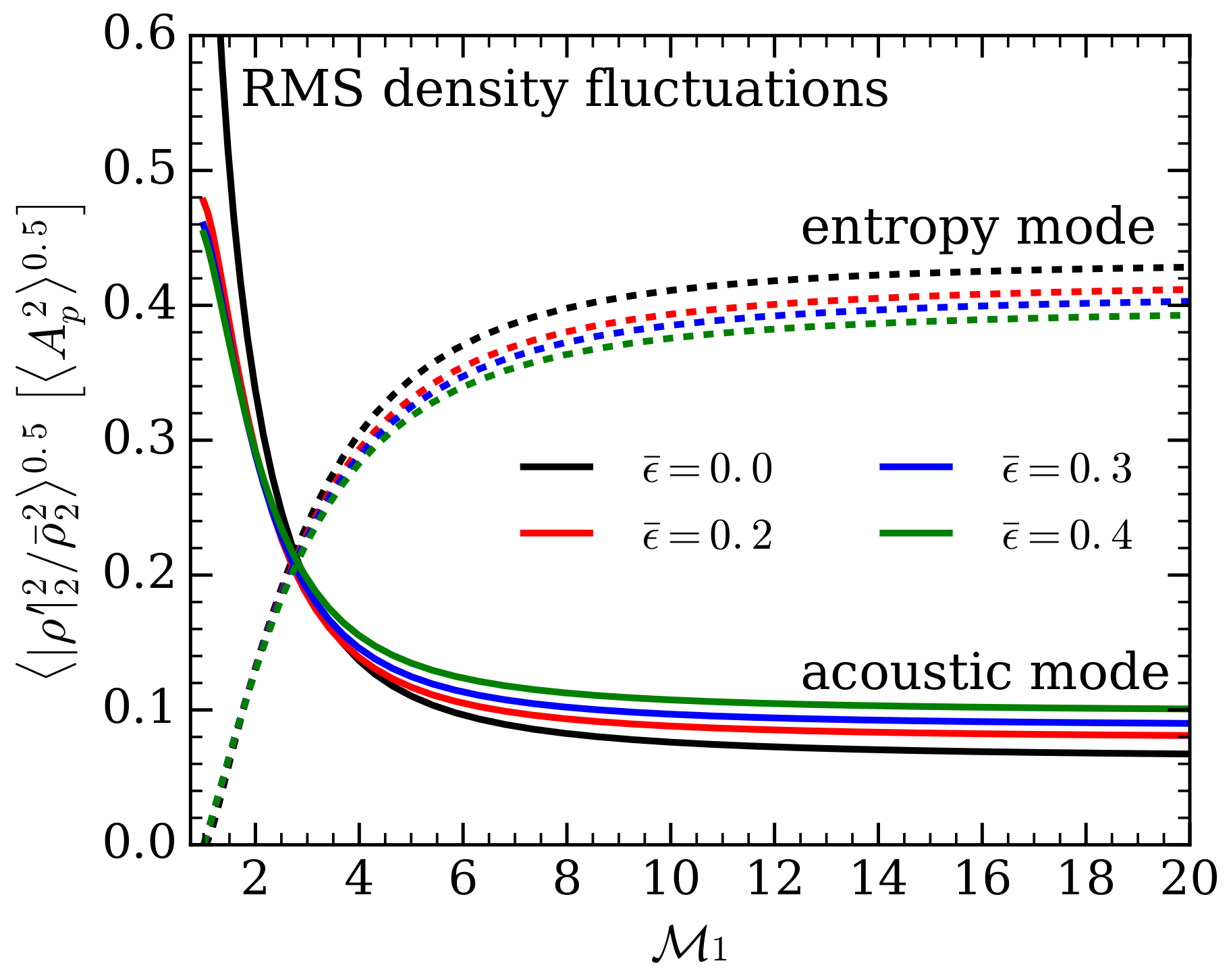
3.1. Dependence on Incidence Angle
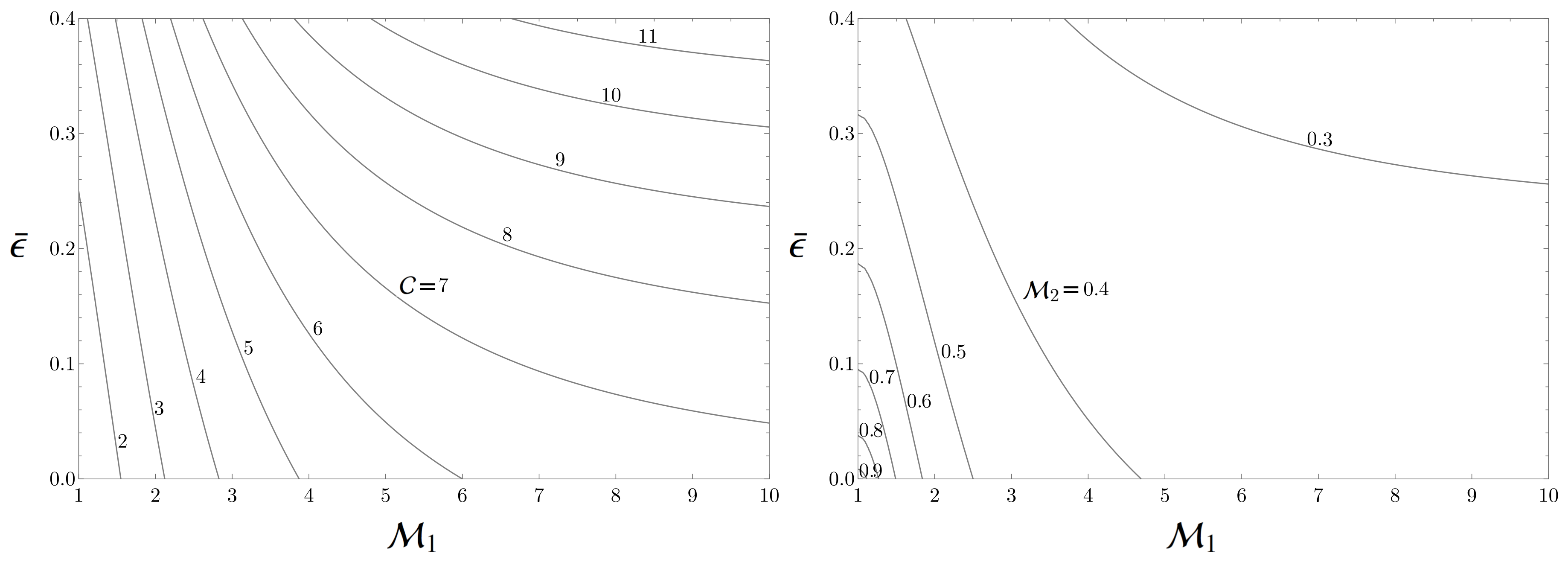
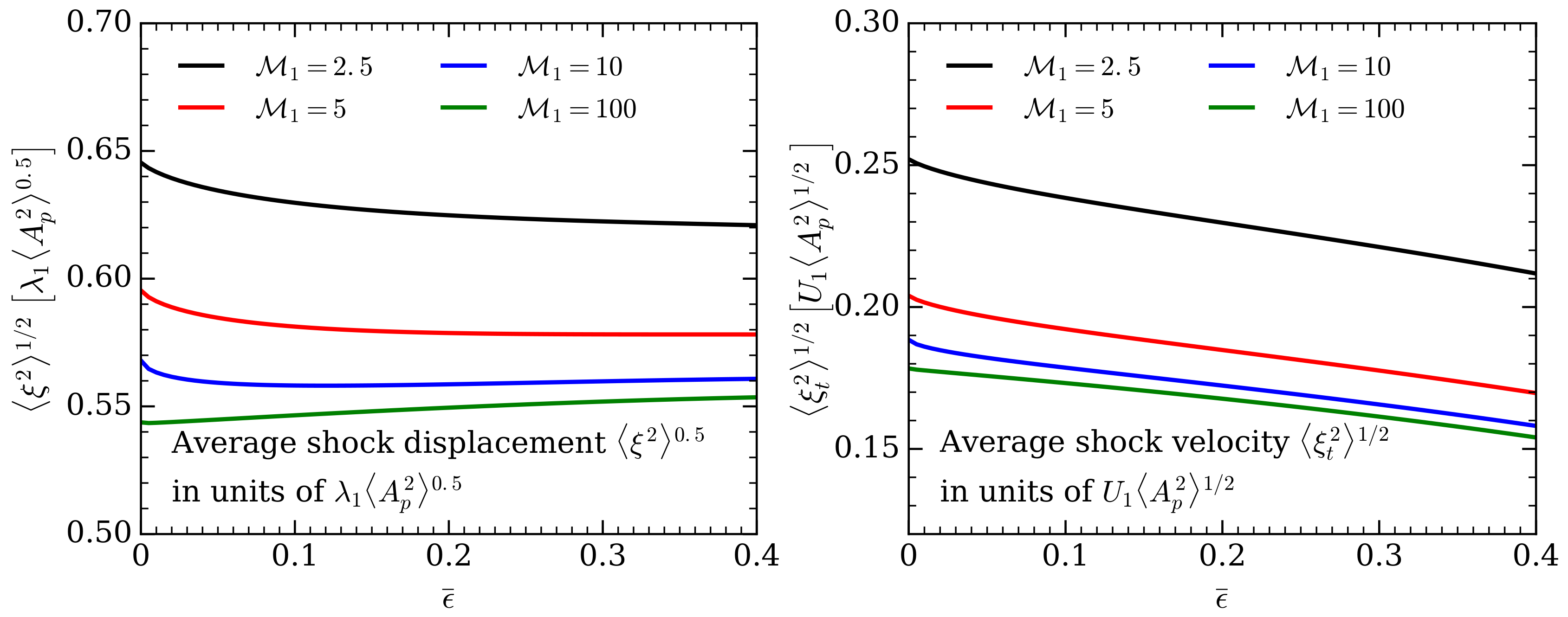
3.2. Interaction with an Isotropic Field of Acoustic Waves
3.3. Implications for CCSN Explosion Condition
4. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Fryxell, B.; Arnett, D.; Mueller, E. Instabilities and clumping in SN 1987A. I-Early evolution in two dimensions. Astrophys. J. 1991, 367, 619–634. [Google Scholar] [CrossRef]
- Herant, M. The convective engine paradigm for the supernova explosion mechanism and its consequences. Phys. Rep. 1995, 256, 117–133. [Google Scholar] [CrossRef]
- Burrows, A.; Hayes, J.; Fryxell, B.A. On the Nature of Core-Collapse Supernova Explosions. Astrophys. J. 1995, 450, 830. [Google Scholar] [CrossRef]
- Janka, H.T.; Müller, E. Neutrino heating, convection, and the mechanism of Type-II supernova explosions. Astron. Astrophys. 1996, 306, 167. [Google Scholar]
- Mösta, P.; Richers, S.; Ott, C.D.; Haas, R.; Piro, A.L.; Boydstun, K.; Abdikamalov, E.; Reisswig, C.; Schnetter, E. Magnetorotational Core-collapse Supernovae in Three Dimensions. Astrophys. J. Lett. 2014, 785, L29. [Google Scholar] [CrossRef]
- Boggs, S.E.; Harrison, F.A.; Miyasaka, H.; Grefenstette, B.W.; Zoglauer, A.; Fryer, C.L.; Reynolds, S.P.; Alexander, D.M.; An, H.; Barret, D.; et al. 44Ti gamma-ray emission lines from SN1987A reveal an asymmetric explosion. Science 2015, 348, 670–671. [Google Scholar] [CrossRef] [PubMed]
- Mao, J.; Ono, M.; Nagataki, S.; Hashimoto, M.a.; Ito, H.; Matsumoto, J.; Dainotti, M.G.; Lee, S.H. Matter Mixing in Core-collapse Supernova Ejecta: Large Density Perturbations in the Progenitor Star? Astrophys. J. 2015, 808, 164. [Google Scholar] [CrossRef]
- Wongwathanarat, A.; Müller, E.; Janka, H.T. Three-dimensional simulations of core-collapse supernovae: From shock revival to shock breakout. Astron. Astrophys. 2015, 577, A48. [Google Scholar] [CrossRef]
- Müller, B. The Status of Multi-Dimensional Core-Collapse Supernova Models. Publ. Astron. Soc. Aust. 2016, 33, e048. [Google Scholar] [CrossRef]
- Katsuda, S.; Morii, M.; Janka, H.T.; Wongwathanarat, A.; Nakamura, K.; Kotake, K.; Mori, K.; Müller, E.; Takiwaki, T.; Tanaka, M.; et al. Intermediate-mass Elements in Young Supernova Remnants Reveal Neutron Star Kicks by Asymmetric Explosions. Astrophys. J. 2018, 856, 18. [Google Scholar] [CrossRef]
- Blondin, J.M.; Mezzacappa, A.; DeMarino, C. Stability of Standing Accretion Shocks, with an Eye toward Core-Collapse Supernovae. Astrophys. J. 2003, 584, 971. [Google Scholar] [CrossRef]
- Foglizzo, T.; Scheck, L.; Janka, H.T. Neutrino-driven Convection versus Advection in Core-Collapse Supernovae. Astrophys. J. 2006, 652, 1436. [Google Scholar] [CrossRef]
- Foglizzo, T.; Galletti, P.; Scheck, L.; Janka, H.T. Instability of a Stalled Accretion Shock: Evidence for the Advective-Acoustic Cycle. Astrophys. J. 2007, 654, 1006. [Google Scholar] [CrossRef]
- Hanke, F.; Marek, A.; Müller, B.; Janka, H.T. Is Strong SASI Activity the Key to Successful Neutrino-driven Supernova Explosions? Astrophys. J. 2012, 755, 138. [Google Scholar] [CrossRef]
- Hanke, F.; Müller, B.; Wongwathanarat, A.; Marek, A.; Janka, H.T. SASI Activity in Three-dimensional Neutrino-hydrodynamics Simulations of Supernova Cores. Astrophys. J. 2013, 770, 66. [Google Scholar] [CrossRef]
- Janka, H.T.; Hanke, F.; Hüdepohl, L.; Marek, A.; Müller, B.; Obergaulinger, M. Core-collapse supernovae: Reflections and directions. Prog. Theor. Exp. Phys. 2012, 2012, 01A309. [Google Scholar] [CrossRef]
- Dolence, J.C.; Burrows, A.; Murphy, J.W.; Nordhaus, J. Dimensional Dependence of the Hydrodynamics of Core-collapse Supernovae. Astrophys. J. 2013, 765, 110. [Google Scholar] [CrossRef]
- Murphy, J.W.; Dolence, J.C.; Burrows, A. The Dominance of Neutrino-driven Convection in Core-collapse Supernovae. Astrophys. J. 2013, 771, 52. [Google Scholar] [CrossRef]
- Burrows, A. Colloquium: Perspectives on core-collapse supernova theory. Rev. Mod. Phys. 2013, 85, 245. [Google Scholar] [CrossRef]
- Takiwaki, T.; Kotake, K.; Suwa, Y. A Comparison of Two- and Three-dimensional Neutrino-hydrodynamics Simulations of Core-collapse Supernovae. Astrophys. J. 2014, 786, 83. [Google Scholar] [CrossRef]
- Ott, C.D.; O’Connor, E.P.; Gossan, S.; Abdikamalov, E.; Gamma, U.C.T.; Drasco, S. Core-Collapse Supernovae, Neutrinos, and Gravitational Waves. Nucl. Phys. B Proc. Suppl. 2013, 235, 381. [Google Scholar] [CrossRef]
- Ott, C.D.; Abdikamalov, E.; Mösta, P.; Haas, R.; Drasco, S.; O’Connor, E.P.; Reisswig, C.; Meakin, C.A.; Schnetter, E. General-relativistic Simulations of Three-dimensional Core-collapse Supernovae. Astrophys. J. 2013, 768, 115. [Google Scholar] [CrossRef]
- Abdikamalov, E.; Ott, C.D.; Radice, D.; Roberts, L.F.; Haas, R.; Reisswig, C.; Mösta, P.; Klion, H.; Schnetter, E. Neutrino-driven Turbulent Convection and Standing Accretion Shock Instability in Three-dimensional Core-collapse Supernovae. Astrophys. J. 2015, 808, 70. [Google Scholar] [CrossRef]
- Radice, D.; Couch, S.M.; Ott, C.D. Implicit large eddy simulations of anisotropic weakly compressible turbulence with application to core-collapse supernovae. Comput. Astrophys. Cosmol. 2015, 2, 7. [Google Scholar] [CrossRef]
- Melson, T.; Janka, H.T.; Marek, A. Neutrino-driven Supernova of a Low-mass Iron-core Progenitor Boosted by Three-dimensional Turbulent Convection. Astrophys. J. Lett. 2015, 801, L24. [Google Scholar] [CrossRef]
- Melson, T.; Janka, H.T.; Bollig, R.; Hanke, F.; Marek, A.; Müller, B. Neutrino-driven Explosion of a 20 Solar-mass Star in Three Dimensions Enabled by Strange-quark Contributions to Neutrino–Nucleon Scattering. Astrophys. J. Lett. 2015, 808, L42. [Google Scholar] [CrossRef]
- Lentz, E.J.; Bruenn, S.W.; Hix, W.R.; Mezzacappa, A.; Messer, O.E.B.; Endeve, E.; Blondin, J.M.; Harris, J.A.; Marronetti, P.; Yakunin, K.N. Three-dimensional Core-collapse Supernova Simulated Using a 15 M⊙ Progenitor. Astrophys. J. Lett. 2015, 807, L31. [Google Scholar] [CrossRef]
- Fernández, R.; Müller, B.; Foglizzo, T.; Janka, H.T. Characterizing SASI- and convection-dominated core-collapse supernova explosions in two dimensions. Mon. Not. R. Astron. Soc. 2014, 440, 2763–2780. [Google Scholar] [CrossRef]
- Fernández, R. Three-dimensional simulations of SASI- and convection-dominated core-collapse supernovae. Mon. Not. R. Astron. Soc. 2015, 452, 2071–2086. [Google Scholar] [CrossRef]
- Foglizzo, T.; Kazeroni, R.; Guilet, J.; Masset, F.; González, M.; Krueger, B.K.; Novak, J.; Oertel, M.; Margueron, J.; Faure, J.; et al. The Explosion Mechanism of Core-Collapse Supernovae: Progress in Supernova Theory and Experiments. Publ. Astron. Soc. Aust. 2015, 32, e009. [Google Scholar] [CrossRef]
- Cardall, C.Y.; Budiardja, R.D. Stochasticity and Efficiency in Simplified Models of Core-collapse Supernova Explosions. Astrophys. J. Lett. 2015, 813, L6. [Google Scholar] [CrossRef]
- Radice, D.; Ott, C.D.; Abdikamalov, E.; Couch, S.M.; Haas, R.; Schnetter, E. Neutrino-driven Convection in Core-collapse Supernovae: High-resolution Simulations. Astrophys. J. 2016, 820, 76. [Google Scholar] [CrossRef]
- Bruenn, S.W.; Lentz, E.J.; Hix, W.R.; Mezzacappa, A.; Harris, J.A.; Messer, O.E.B.; Endeve, E.; Blondin, J.M.; Chertkow, M.A.; Lingerfelt, E.J.; et al. The Development of Explosions in Axisymmetric Ab Initio Core-collapse Supernova Simulations of 12-25 M⊙ Stars. Astrophys. J. 2016, 818, 123. [Google Scholar] [CrossRef]
- Roberts, L.F.; Ott, C.D.; Haas, R.; O’Connor, E.P.; Diener, P.; Schnetter, E. General-Relativistic Three-Dimensional Multi-group Neutrino Radiation-Hydrodynamics Simulations of Core-Collapse Supernovae. Astrophys. J. 2016, 831, 98. [Google Scholar] [CrossRef]
- Kuroda, T.; Kotake, K.; Hayama, K.; Takiwaki, T. Correlated Signatures of Gravitational-wave and Neutrino Emission in Three-dimensional General-relativistic Core-collapse Supernova Simulations. Astrophys. J. 2017, 851, 62. [Google Scholar] [CrossRef]
- Ott, C.D.; Roberts, L.F.; da Silva Schneider, A.; Fedrow, J.M.; Haas, R.; Schnetter, E. The Progenitor Dependence of Core-collapse Supernovae from Three-dimensional Simulations with Progenitor Models of 12-40 M⊙. Astrophys. J. Lett. 2018, 855, L3. [Google Scholar] [CrossRef]
- Takiwaki, T.; Kotake, K. Anisotropic emission of neutrino and gravitational-wave signals from rapidly rotating core-collapse supernovae. Mon. Not. R. Astron. Soc. 2018, 475, L91–L95. [Google Scholar] [CrossRef]
- Kazeroni, R.; Krueger, B.K.; Guilet, J.; Foglizzo, T.; Pomarède, D. The non-linear onset of neutrino-driven convection in two and three-dimensional core-collapse supernovae. arXiv, 2018; arXiv:1802.08125. [Google Scholar]
- Radice, D.; Abdikamalov, E.; Ott, C.D.; Moesta, P.; Couch, S.M.; Roberts, L.F. Turbulence in Core-Collapse Supernovae. J. Phys. G Nucl. Part. Phys. 2018, 45, 053003. [Google Scholar] [CrossRef]
- Couch, S.M.; Ott, C.D. Revival of The Stalled Core-Collapse Supernova Shock Triggered by Precollapse Asphericity in the Progenitor Star. Astrophys. J. Lett. 2013, 778, L7. [Google Scholar] [CrossRef]
- Couch, S.M.; Ott, C.D. The Role of Turbulence in Neutrino-driven Core-collapse Supernova Explosions. Astrophys. J. 2015, 799, 5. [Google Scholar] [CrossRef]
- Müller, B.; Janka, H.T. Non-radial instabilities and progenitor asphericities in core-collapse supernovae. Mon. Not. R. Astron. Soc. 2015, 448, 2141–2174. [Google Scholar] [CrossRef]
- Müller, B.; Viallet, M.; Heger, A.; Janka, H.T. The Last Minutes of Oxygen Shell Burning in a Massive Star. Astrophys. J. 2016, 833, 124. [Google Scholar] [CrossRef]
- Kovalenko, I.G.; Eremin, M.A. Instability of spherical accretion—I. Shock-free Bondi accretion. Mon. Not. R. Astron. Soc. 1998, 298, 861–870. [Google Scholar] [CrossRef]
- Lai, D.; Goldreich, P. Growth of Perturbations in Gravitational Collapse and Accretion. Astrophys. J. 2000, 535, 402. [Google Scholar] [CrossRef]
- Takahashi, K.; Yamada, S. Linear Analysis on the Growth of Non-spherical Perturbations in Supersonic Accretion Flows. Astrophys. J. 2014, 794, 162. [Google Scholar] [CrossRef]
- Müller, B.; Melson, T.; Heger, A.; Janka, H.T. Supernova simulations from a 3D progenitor model—Impact of perturbations and evolution of explosion properties. Mon. Not. R. Astron. Soc. 2017, 472, 491–513. [Google Scholar] [CrossRef]
- Abdikamalov, E.; Zhaksylykov, A.; Radice, D.; Berdibek, S. Shock-turbulence interaction in core-collapse supernovae. Mon. Not. R. Astron. Soc. 2016, 461, 3864–3876. [Google Scholar] [CrossRef]
- Huete, C.; Abdikamalov, E.; Radice, D. The impact of vorticity waves on the shock dynamics in core-collapse supernovae. Mon. Not. R. Astron. Soc. 2018, 475, 3305–3323. [Google Scholar] [CrossRef]
- Collins, C.; Müller, B.; Heger, A. Properties of convective oxygen and silicon burning shells in supernova progenitors. Mon. Not. R. Astron. Soc. 2018, 473, 1695–1704. [Google Scholar] [CrossRef]
- Ribner, H.S. Convection of a Pattern of Vorticity through a Shock Wave; Technical Report TN 2864; NACA (National Advisory Committee for Aeronautics): Cleveland, OH, USA, 1954. [Google Scholar]
- Chang, C.T. Interaction of a Plane Shock and Oblique Plane Disturbances With Special Reference to Entropy Waves. J. Aeronaut. Sci. 1957, 24, 675–682. [Google Scholar] [CrossRef]
- Mahesh, K.; Moin, P.; Lele, S.K. The Interaction of a Shock Wave with a Turbulent Shear Flow; Technical Report TF-69; Thermosciences division, Department of Mechanical Engineering, Stanford University: Stanford, CA, USA, 1997. [Google Scholar]
- Wouchuk, J.G.; Huete Ruiz de Lira, C.; Velikovich, A.L. Analytical linear theory for the interaction of a planar shock wave with an isotropic turbulent vorticity field. Phys. Rev. E 2009, 79, 066315. [Google Scholar] [CrossRef] [PubMed]
- Huete Ruiz de Lira, C.; Velikovich, A.L.; Wouchuk, J.G. Analytical linear theory for the interaction of a planar shock wave with a two- or three-dimensional random isotropic density field. Phys. Rev. E 2011, 83, 056320. [Google Scholar] [CrossRef] [PubMed]
- Huete, C.; Wouchuk, J.G.; Velikovich, A.L. Analytical linear theory for the interaction of a planar shock wave with a two- or three-dimensional random isotropic acoustic wave field. Phys. Rev. E 2012, 85, 026312. [Google Scholar] [CrossRef] [PubMed]
- Kovasznay, L.S.G. Turbulence in Supersonic Flow. J. Aeronaut. Sci. 1953, 20, 657–674. [Google Scholar] [CrossRef]
- Lighthill, M.J. On Sound Generated Aerodynamically. I. General Theory. Proc. R. Soc. Lond. Ser. A 1952, 211, 564–587. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshitz, E.M. Fluid Mechanics, 2nd ed.; Butterworth-Heinemann: Oxford, UK, 1959. [Google Scholar]
- Foglizzo, T.; Tagger, M. Entropic-acoustic instability in shocked accretion flows. Astron. Astrophys. 2000, 363, 174–183. [Google Scholar]
- Foglizzo, T. Entropic-acoustic instability of shocked Bondi accretion I. What does perturbed Bondi accretion sound like? Astron. Astrophys. 2001, 368, 311–324. [Google Scholar] [CrossRef]
- Moore, F.K. Unsteady Oblique Interaction of a Shock Wave with a Plane Disturbance; Technical Report TR 1165; NACA (National Advisory Committee for Aeronautics): Cleveland, OH, USA, 1953. [Google Scholar]
- Sagaut, P.; Cambon, C. Homogeneous Turbulence Dynamics; Cambridge University Press: Cambridge, UK, 2008. [Google Scholar]
- Mahesh, K.; Lee, S.; Lele, S.K.; Moin, P. The interaction of an isotropic field of acoustic waves with a shock wave. J. Fluid Mech. 1995, 300, 383–407. [Google Scholar] [CrossRef]
- Bethe, H.A. Supernova mechanisms. Rev. Mod. Phys. 1990, 62, 801. [Google Scholar] [CrossRef]
- Fernández, R.; Thompson, C. Stability of a Spherical Accretion Shock with Nuclear Dissociation. Astronphys. J. 2009, 697, 1827. [Google Scholar] [CrossRef]
- Fernández, R.; Thompson, C. Dynamics of a Spherical Accretion Shock with Neutrino Heating and Alpha-Particle Recombination. Astrophys. J. 2009, 703, 1464. [Google Scholar] [CrossRef]
- Takahashi, K.; Iwakami, W.; Yamamoto, Y.; Yamada, S. Links between the Shock Instability in Core-collapse Supernovae and Asymmetric Accretions of Envelopes. Astrophys. J. 2016, 831, 75. [Google Scholar] [CrossRef]
- Mabanta, Q.A.; Murphy, J.W. How Turbulence Enables Core-collapse Supernova Explosions. Astrophys. J. 2018, 856, 22. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abdikamalov, E.; Huete, C.; Nussupbekov, A.; Berdibek, S. Turbulence Generation by Shock-Acoustic-Wave Interaction in Core-Collapse Supernovae. Particles 2018, 1, 97-110. https://doi.org/10.3390/particles1010007
Abdikamalov E, Huete C, Nussupbekov A, Berdibek S. Turbulence Generation by Shock-Acoustic-Wave Interaction in Core-Collapse Supernovae. Particles. 2018; 1(1):97-110. https://doi.org/10.3390/particles1010007
Chicago/Turabian StyleAbdikamalov, Ernazar, César Huete, Ayan Nussupbekov, and Shapagat Berdibek. 2018. "Turbulence Generation by Shock-Acoustic-Wave Interaction in Core-Collapse Supernovae" Particles 1, no. 1: 97-110. https://doi.org/10.3390/particles1010007




