Realistic Compactification Models in Einstein–Gauss–Bonnet Gravity
Abstract
:1. Introduction
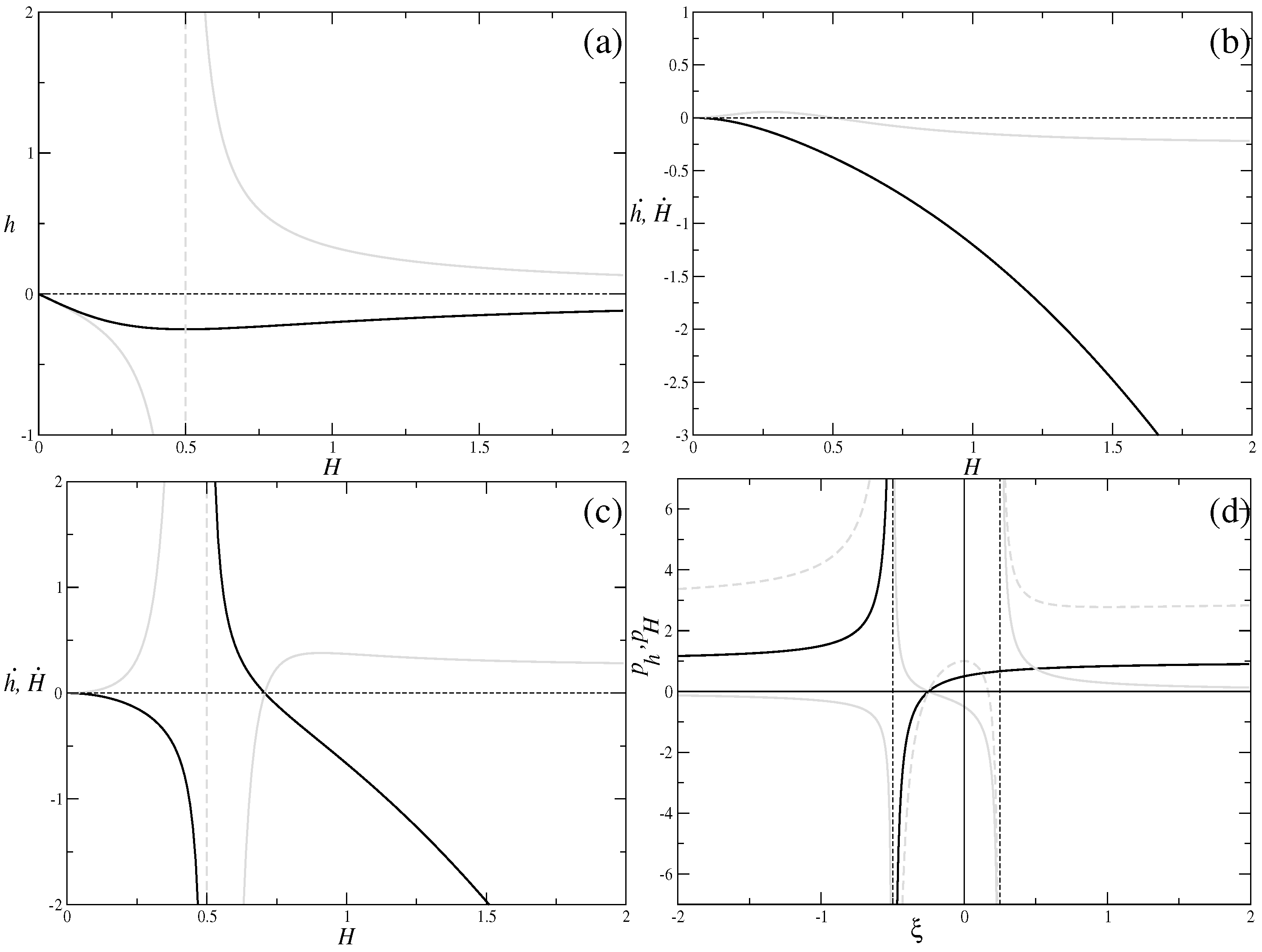
2. Equations of Motion
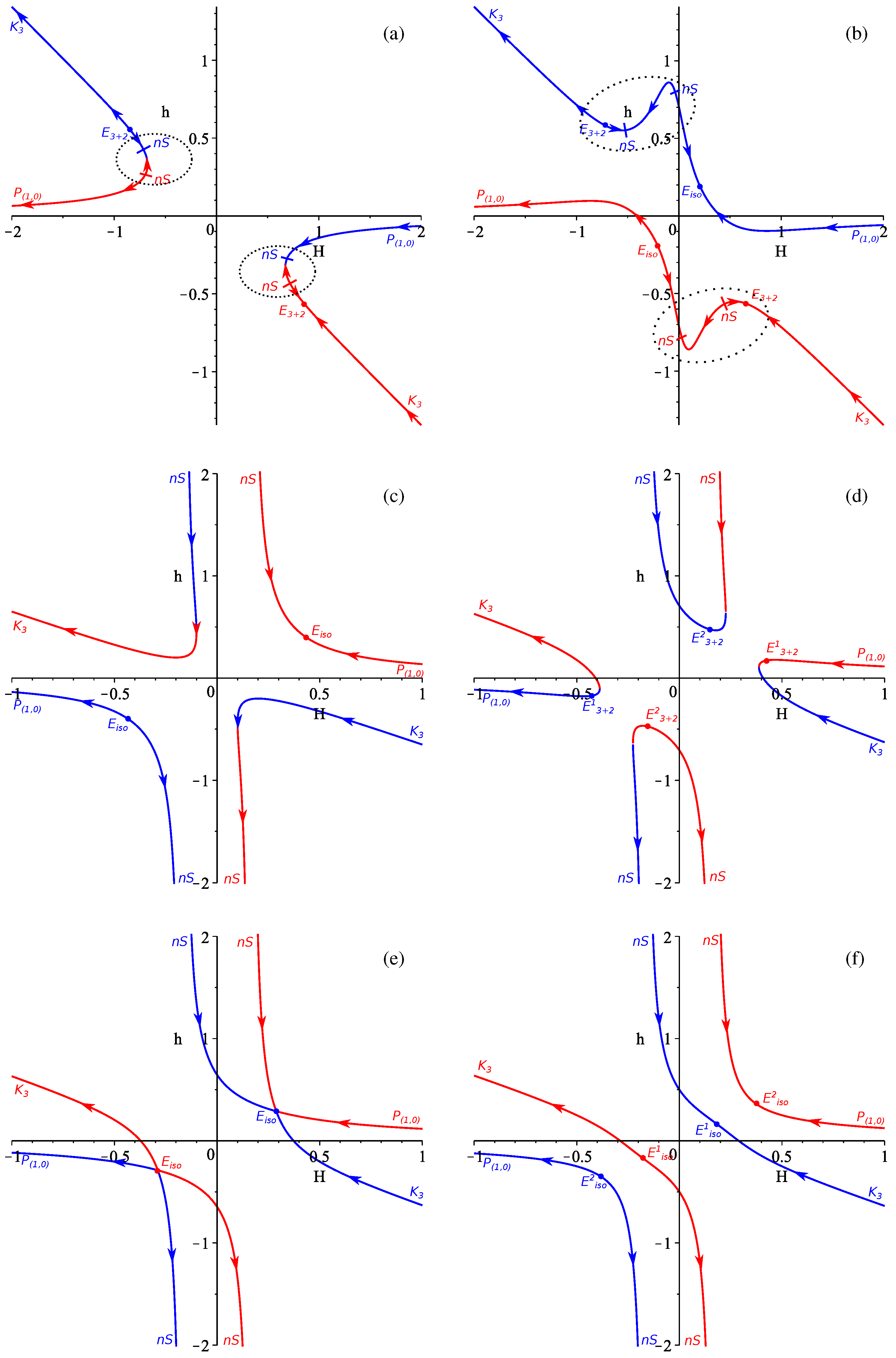
3. The Vacuum Case
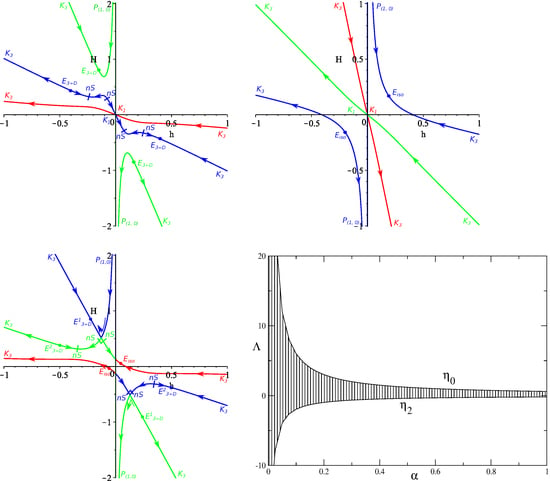
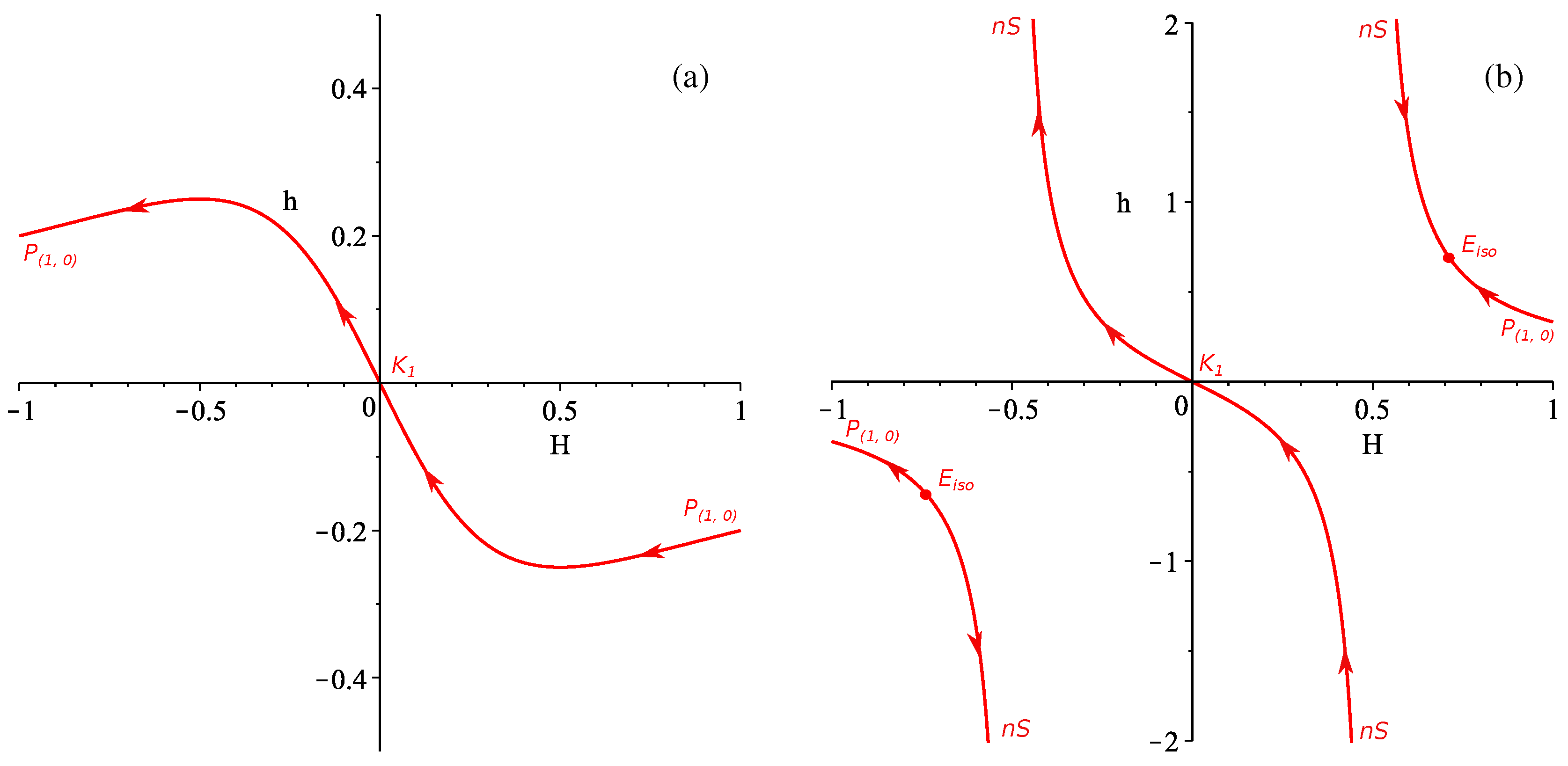
3.1. Case
3.2. Case
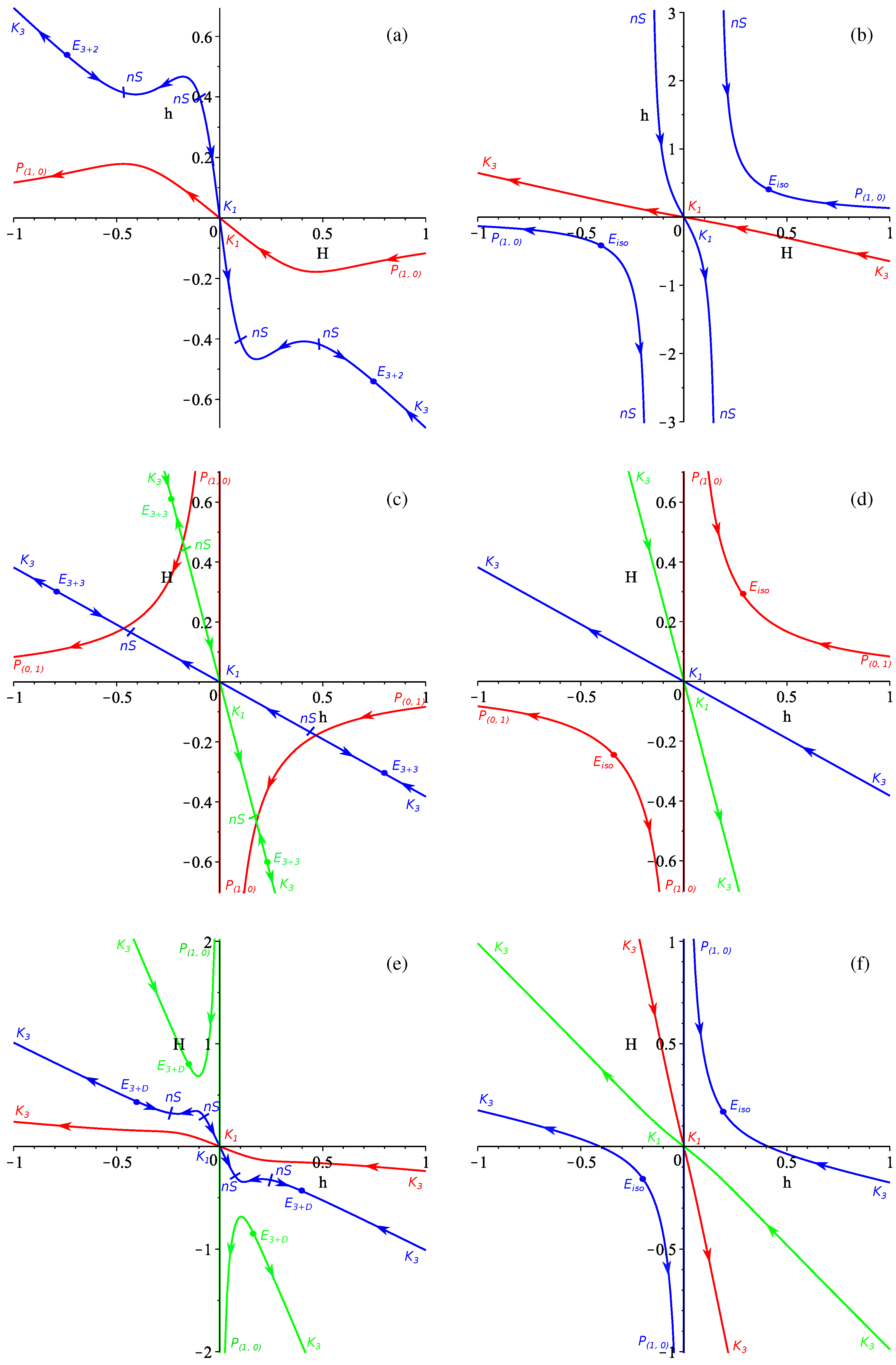
3.3. Case
3.4. General Case
3.5. Conclusions on the Vacuum Case
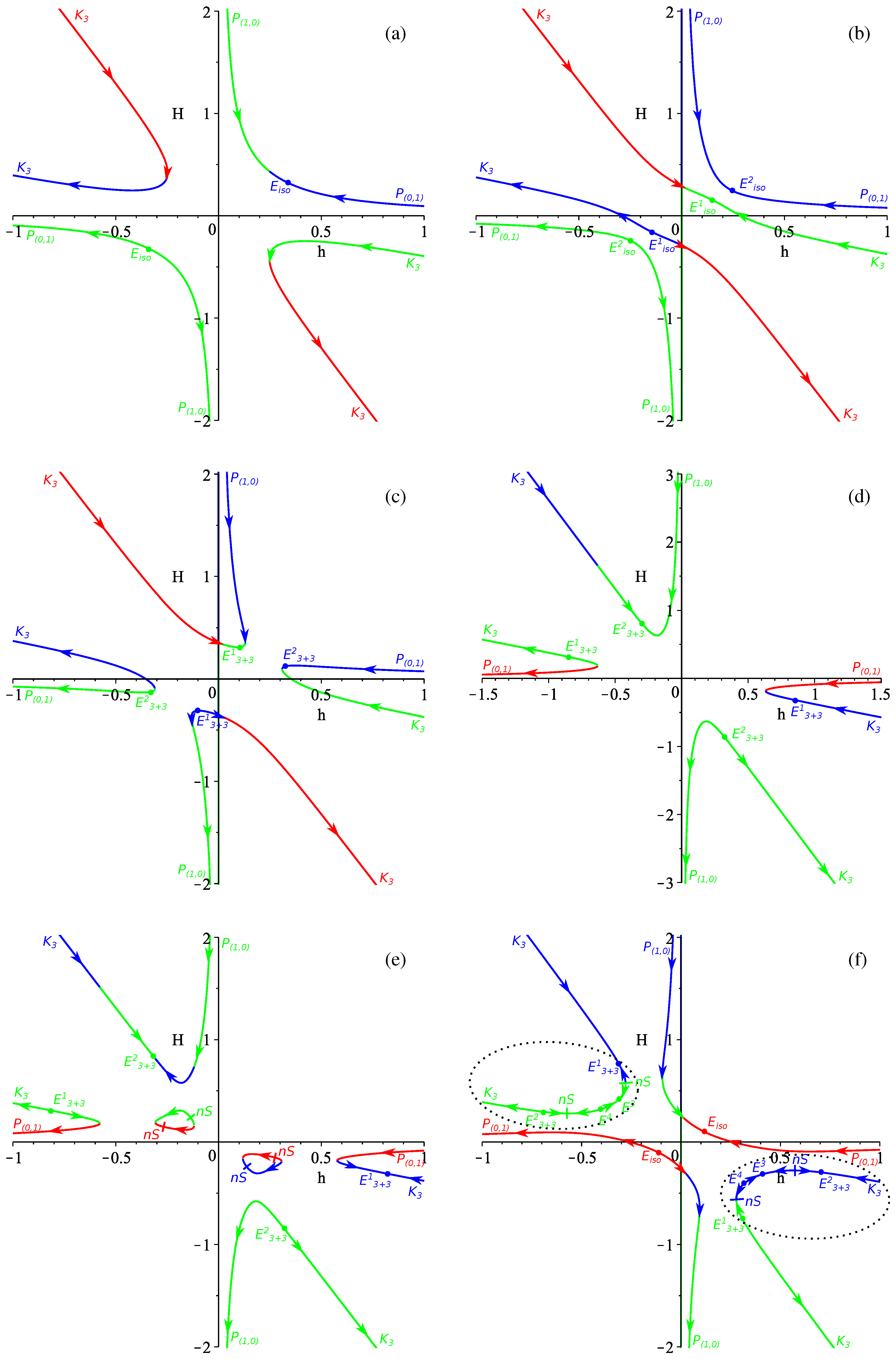
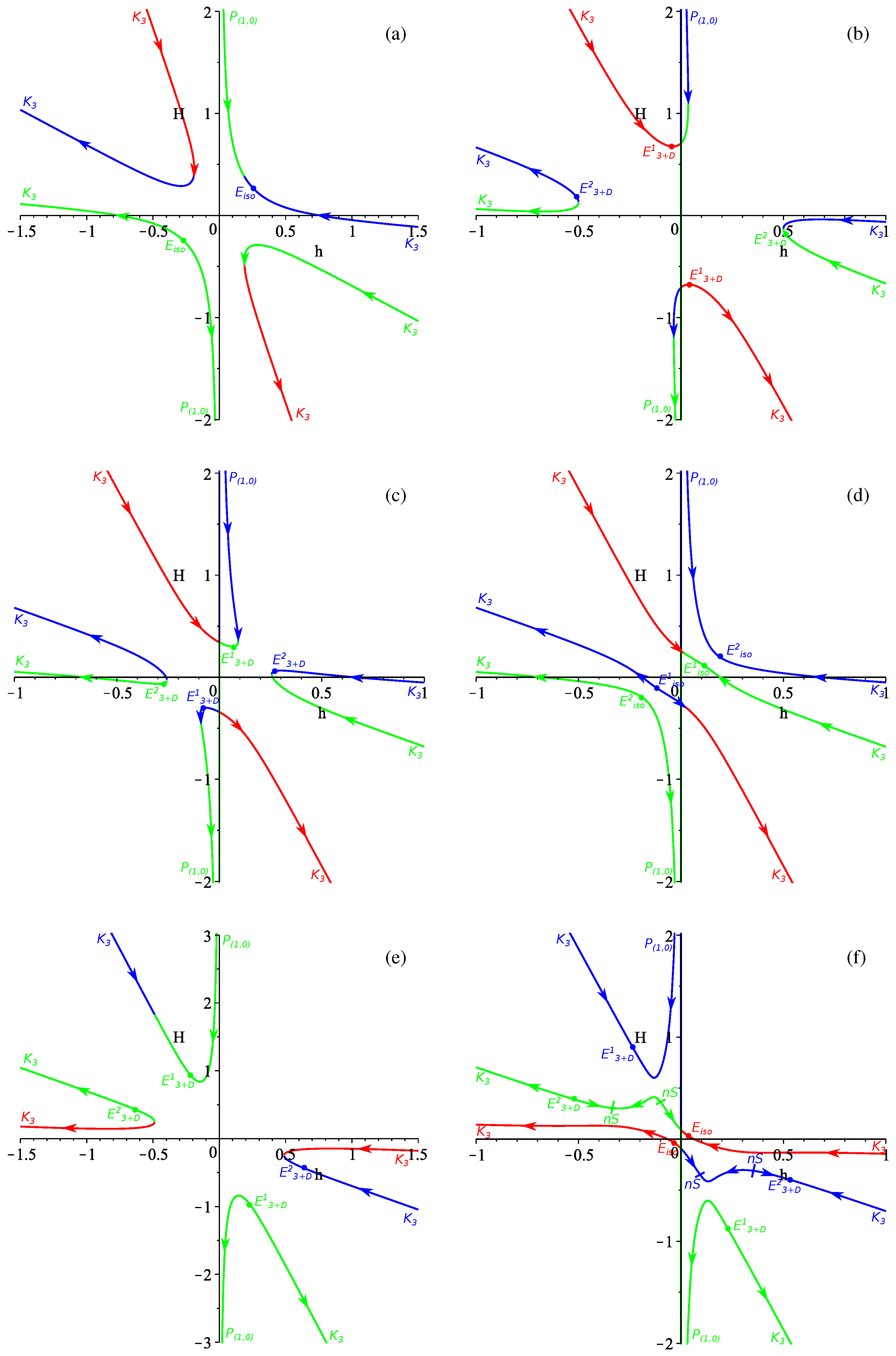
4. The -Term Case
4.1. The Case
4.2. The Case
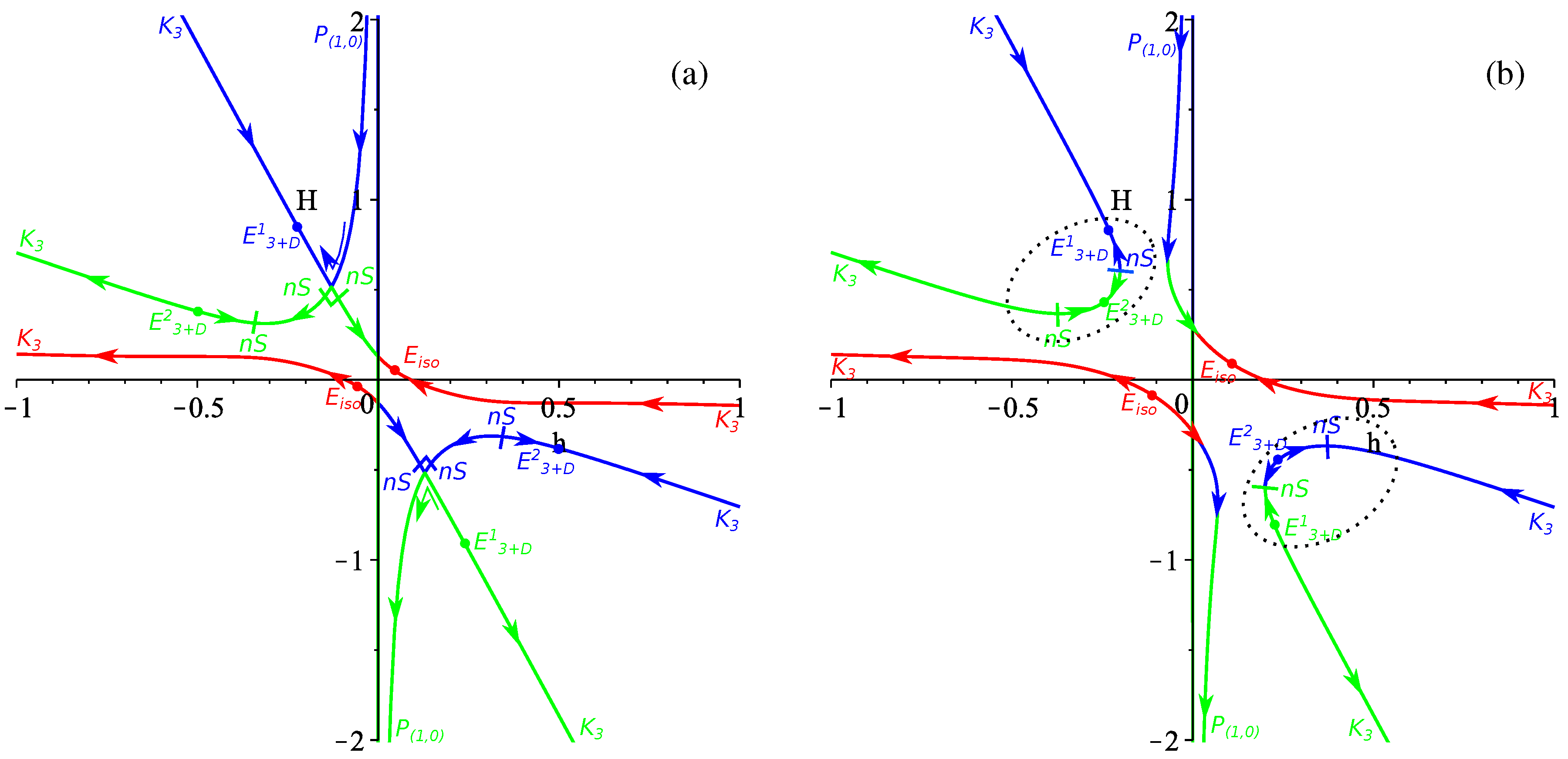
4.3. The Case
4.4. General Case
4.5. Conclusions on the -Term Case
5. Discussion
6. Conclusions
Conflicts of Interest
References
- Nordström, G. Über die Möglichkeit, das Elektromagnetische Feld und das Gravitationsfeld zu vereiningen. Phys. Z. 1914, 15, 504–506. [Google Scholar]
- Nordström, G. Zur Theorie der Gravitation vom Standpunkt des Relativitätsprinzips. Ann. Phys. 1913, 347, 533–554. [Google Scholar] [CrossRef]
- Kaluza, T. Zum Unitätsproblem der Physik. Sit. Preuss. Akad. Wiss. 1921, K1, 966. [Google Scholar]
- Klein, O. Quantentheorie und fünfdimensionale Relativitätstheorie. Z. Phys. 1926, 37, 895–906. [Google Scholar] [CrossRef]
- Klein, O. The Atomicity of Electricity as a Quantum Theory Law. Nature 1926, 118, 516. [Google Scholar] [CrossRef]
- Zwiebach, B. Curvature squared terms and string theories. Phys. Lett. B 1985, 156, 315–317. [Google Scholar] [CrossRef]
- Zumino, B. Gravity theories in more than four dimensions. Phys. Rep. 1986, 137, 109–114. [Google Scholar] [CrossRef]
- Lovelock, D. The Einstein Tensor and Its Generalizations. J. Math. Phys. 1971, 12, 498–501. [Google Scholar] [CrossRef]
- Deruelle, N.; Fariña-Busto, L. Lovelock gravitational field equations in cosmology. Phys. Rev. D 1990, 41, 3696–3708. [Google Scholar] [CrossRef]
- Mu¨ller-Hoissen, F. Dimensionally continued Euler forms: Kaluza-Klein cosmology and dimensional reduction. Class. Quant. Grav. 1986, 3, 665–677. [Google Scholar] [CrossRef]
- Deruelle, N. On the approach to the cosmological singularity in quadratic theories of gravity: The Kasner regimes. Nucl. Phys. B 1989, 327, 253–266. [Google Scholar] [CrossRef]
- Pavluchenko, S.A. General features of Bianchi-I cosmological models in Lovelock gravity. Phys. Rev. D 2009, 80, 107501. [Google Scholar] [CrossRef]
- Pavluchenko, S.A.; Toporensky, A.V. A note on differences between (4 + 1)- and (5 + 1)-dimensional anisotropic cosmology in the presence of the Gauss-Bonnet term. Mod. Phys. Lett. A 2009, 24, 513–521. [Google Scholar] [CrossRef]
- Pavluchenko, S.A. The dynamics of the flat anisotropic models in the Lovelock gravity. I: The even-dimensional case. Phys. Rev. D 2010, 82, 104021. [Google Scholar] [CrossRef]
- Ivashchuk, V. On cosmological-type solutions in multi-dimensional model with Gauss-Bonnet term. Int. J. Geom. Meth. Mod. Phys. 2010, 07, 797–819. [Google Scholar] [CrossRef]
- Kirnos, I.V.; Makarenko, A.N.; Pavluchenko, S.A.; Toporensky, A.V. The nature of singularity in multidimensional anisotropic Gauss-Bonnet cosmology with a perfect fluid. Gen. Rel. Grav. 2010, 42, 2633–2641. [Google Scholar] [CrossRef]
- Pavluchenko, S.A.; Toporensky, A.V. Note on properties of exact cosmological solutions in Lovelock gravity. Gravit. Cosmol. 2014, 20, 127–131. [Google Scholar] [CrossRef]
- Kirnos, I.V.; Pavluchenko, S.A.; Toporensky, A.V. New features of flat (4+1)-dimensional cosmological model with a perfect fluid in Gauss-Bonnet gravity. Gravit. Cosmol. 2010, 16, 274–282. [Google Scholar] [CrossRef]
- Chirkov, D.; Pavluchenko, S.; Toporensky, A. Exact exponential solutions in Einstein-Gauss-Bonnet flat anisotropic cosmology. Mod. Phys. Lett. A 2014, 29, 1450093. [Google Scholar] [CrossRef]
- Chirkov, D.; Pavluchenko, S.; Toporensky, A. Constant volume exponential solutions in Einstein-Gauss-Bonnet flat anisotropic cosmology with a perfect fluid. Gen. Rel. Grav. 2014, 46, 1799. [Google Scholar] [CrossRef]
- Chirkov, D.; Pavluchenko, S.; Toporensky, A. Non-constant volume exponential solutions in higher-dimensional Lovelock cosmologies. Gen. Rel. Grav. 2015, 47, 137. [Google Scholar]
- Pavluchenko, S.A. Stability analysis of the exponential solutions in Lovelock cosmologies. Phys. Rev. D 2015, 92, 104017. [Google Scholar] [CrossRef]
- Ivashchuk, V.D. On stability of exponential cosmological solutions with nonstatic volume factor in the Einstein-Gauss-Bonnet model. Eur. Phys. J. C 2016, 76, 431. [Google Scholar] [CrossRef]
- Ivashchuk, V.D.; Kobtsev, A.A. Stable exponential cosmological solutions with 3- and l-dimensional factor spaces in the Einstein-Gauss-Bonnet model with a Λ-term. Eur. Phys. J. C 2018, 78, 100. [Google Scholar] [CrossRef]
- Canfora, F.; Giacomini, A.; Pavluchenko, S.A. Dynamical compactification in Einstein-Gauss-Bonnet gravity from geometric frustration. Phys. Rev. D 2013, 88, 064044. [Google Scholar] [CrossRef]
- Canfora, F.; Giacomini, A.; Pavluchenko, S.A. Cosmological dynamics in higher-dimensional Einstein-Gauss- Bonnet gravity. Gen. Rel. Grav. 2014, 46, 1805. [Google Scholar] [CrossRef]
- Canfora, F.; Giacomini, A.; Pavluchenko, S.A.; Toporensky, A. Friedmann dynamics recovered from compactified Einstein-Gauss-Bonnet cosmology. Gravit. Cosmol. 2018; arXiv:1605.00041. [Google Scholar]
- Pavluchenko, S.A. The generality of inflation in closed cosmological models with some quintessence potentials. Phys. Rev. D 2003, 67, 103518. [Google Scholar] [CrossRef]
- Pavluchenko, S.A. Constraints on inflation in closed universe. Phys. Rev. D 2004, 69, 021301. [Google Scholar] [CrossRef]
- Pavluchenko, S.; Toporensky, A. Effects of spatial curvature and anisotropy on the asymptotic regimes in Einstein-Gauss-Bonnet gravity. arXiv, 2017; arXiv:1709.04258. [Google Scholar]
- Pavluchenko, S.A. Cosmological dynamics of spatially flat Einstein-Gauss-Bonnet models in various dimensions. Vacuum case. Phys. Rev. D 2016, 94, 024046. [Google Scholar] [CrossRef]
- Pavluchenko, S.A. Cosmological dynamics of spatially flat Einstein-Gauss-Bonnet models in various dimensions: Low-dimensional Λ-term case. Phys. Rev. D 2016, 94, 084019. [Google Scholar] [CrossRef]
- Pavluchenko, S.A. Cosmological dynamics of spatially flat Einstein-Gauss-Bonnet models in various dimensions: High-dimensional Λ-term case. Eur. Phys. J. C 2017, 77, 503. [Google Scholar] [CrossRef]
- Ivashchuk, V.D. On anisotropic Gauss-Bonnet cosmologies in (n+1) dimensions, governed by an n-dimensional Finslerian 4-metric. Grav. Cosmol. 2010, 16, 118–125. [Google Scholar] [CrossRef]
- Taub, A.H. Empty Space-Times Admitting a Three Parameter Group of Motions. Ann. Math. 1951, 53, 472–490. [Google Scholar] [CrossRef]
- Tipler, F.J. Singularities in conformally flat spacetimes. Phys. Lett. A 1977, 64, 8–10. [Google Scholar] [CrossRef]
- Kitaura, T.; Wheeler, J.T. Anisotropic, time-dependent solutions in maximally Gauss-Bonnet extended gravity. Nucl. Phys. B 1991, 355, 250–277. [Google Scholar] [CrossRef]
- Kitaura, T.; Wheeler, J.T. New singularity in anisotropic, time-dependent, maximally Gauss-Bonnet extended gravity. Phys. Rev. D 1993, 48, 667–672. [Google Scholar] [CrossRef]
- Brigante, M.; Liu, H.; Myers, R.C.; Shenker, S.; Yaida, S. Viscosity Bound Violation in Higher Derivative Gravity. Phys. Rev. D 2008, 77, 126006. [Google Scholar]
- Brigante, M.; Liu, H.; Myers, R.C.; Shenker, S.; Yaida, S. Viscosity Bound and Causality Violation. Phys. Rev. Lett. 2008, 100, 191601. [Google Scholar]
- Buchel, A.; Myers, R.C. Causality of Holographic Hydrodynamics. JHEP 2008, 0908, 016. [Google Scholar] [CrossRef]
- Hofman, D.M. Higher Derivative Gravity, Causality and Positivity of Energy in a UV complete QFT. Nucl. Phys. B 2009, 823, 174–194. [Google Scholar] [CrossRef]
- De Boer, J.; Kulaxizi, M.; Parnachev, A. AdS_7/CFT_6, Gauss-Bonnet Gravity, and Viscosity Bound. JHEP 2010, 1003, 087. [Google Scholar] [CrossRef]
- Camanho, X.O.; Edelstein, J.D. Causality constraints in AdS/CFT from conformal collider physics and Gauss-Bonnet gravity. JHEP 2010, 1004, 007. [Google Scholar] [CrossRef]
- Buchel, A.; Escobedo, J.; Myers, R.C.; Paulos, M.F.; Sinha, A.; Smolkin, M. Holographic GB gravity in arbitrary dimensions. JHEP 2010, 1003, 111. [Google Scholar]
- Ge, X.-H.; Sin, S.-J. Shear viscosity, instability and the upper bound of the Gauss-Bonnet coupling constant. JHEP 2009, 0905, 051. [Google Scholar] [CrossRef]
- Cai, R.G.; Guo, Q. Gauss-Bonnet black holes in dS spaces. Phys. Rev. D 2004, 69, 104025. [Google Scholar] [CrossRef]
- Cai, R.G. Gauss-Bonnet black holes in AdS spaces. Phys. Rev. D 2002, 65, 084014. [Google Scholar] [CrossRef]
- Cai, R.G. A note on thermodynamics of black holes in Lovelock gravity. Phys. Lett. B 2004, 582, 237–242. [Google Scholar] [CrossRef]
- Boulware, D.G.; Deser, S. String-generated gravity models. Phys. Rev. Lett. 1985, 55, 2656–2660. [Google Scholar] [CrossRef] [PubMed]
- Ogawa, N.; Takayanagi, T. Higher Derivative Corrections to Holographic Entanglement Entropy for AdS Solitons. JHEP 2011, 1110, 147. [Google Scholar] [CrossRef]

© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pavluchenko, S. Realistic Compactification Models in Einstein–Gauss–Bonnet Gravity. Particles 2018, 1, 36-55. https://doi.org/10.3390/particles1010004
Pavluchenko S. Realistic Compactification Models in Einstein–Gauss–Bonnet Gravity. Particles. 2018; 1(1):36-55. https://doi.org/10.3390/particles1010004
Chicago/Turabian StylePavluchenko, Sergey. 2018. "Realistic Compactification Models in Einstein–Gauss–Bonnet Gravity" Particles 1, no. 1: 36-55. https://doi.org/10.3390/particles1010004