Current-Carrying Performance Degradation Mechanisms of Outdoors Power Connectors Under External Vibrations

Abstract

The environmental adaptability of outdoor power connectors exerts a crucial influence on the reliability of electrical systems. In this work, the current-carrying performance degradation of commercial power connectors under forced mechanical vibration conditions is investigated comprehensively. The variations in the instantaneous electrical contact resistance (ECR) of power connectors are accurately recorded in real time, and then effects of vibration amplitude, frequency, and load current on the ECR are interpreted explicitly. Furthermore, multi-cycle swept-sine vibration tests are carried out, and the open circuit failure of power connectors is reproduced. The continuous carrying of a heavy current combined with the mechanical fretting between socket and plug results in surface coating wear, debris melting, and the formation of copper oxide. The observed surface morphology and element contents support the presented failure mechanisms of power connectors under external vibrations.

1. Introduction

Power connectors, as an irreplaceable electrical component, are primarily used to establish detachable electrical connections between power sources and electrical devices [1]. The power connector should be more mechanically and electrically robust, particularly for outdoor application [2]. With the continuous increase in outdoor electrical equipment’s power, the current-carrying capacity of the power connectors is expanded from several amperes to several hundred amperes [3]. Meanwhile, this kind of connector is required to be designed with excellent properties such as corrosion resistance, UV resistance, and vibration resistance [4,5] and meet high-protection level standards, such as IP 68, IP 69K, etc. [6].

As the demand for system reliability continues to rise, much attention has been given to the assessment of the contact’s physical condition and fault diagnosis of electrical connectors. The electrical contact resistance (ECR) of connectors or the loop resistance of the electrical circuit is selected as the health indicator, and the upper spread of contact resistance, time to surge, and quotient have been used to characterize the performance degradation of electrical connectors [7]. Cheng et al. investigated the transient responses of ECR of electrical connectors under sweep-frequency vibrations and concluded that the occurrence of intermittent fault concentrates at the resonance points of the vibration system [8]. Ren et al. comprehensively researched the influences of vibration stress on the ECR of an electrical connector with a counterbored socket, and the possible failure mechanisms of the connector exposed to the vibration environment are interpreted with the introduced structural dynamic model [9]. In another work, Fu et al. stated that the variation in ECR of power connectors with the crown spring socket under vibration is approximated with an equation that is proportional to the product of relative displacement and frequency squared [10]. In addition to resistance-based degradation studies, research in high-frequency connectors has also shown the diagnostic value of electrical response parameters. Zhang et al. demonstrates that both contact resistance and contact impedance exhibit strong sensitivity to interface degradation under fast signal transmission [11].

For long-term service outdoor application scenarios, it has been confirmed that fretting between detachable contact pairs can lead to electrical contact failures, such as increased ECR or significant fluctuations in ECR, and even temporary interruptions of circuit current [12]. Key features of these behaviors are intermittency and non-reproducibility. The failure mechanism of electrical contact is considered as coating wear, as well as associated material corrosion, fatigues, and cracks on the micro scale [13]. Fretting faults have become an insurmountable bottleneck limiting the development of high-reliability connectors.

To clearly interpret the electrical contact failure mechanisms occurring in industrial applications, a series of fretting experiments on electrical contact materials were carried out using an electric motor or an electrodynamic vibration table and a thermostatic chamber [14]. The effects of fretting amplitude, fretting frequency, normal contact force, and environment temperature on the wear track morphologies, wear debris, and friction force of copper alloy materials were systematically investigated. Additionally, the differences in fretting failure mechanisms between tin plating, silver plating, and gold plating were compared [15].

Considering the effect of Joule heating, fretting-induced damage to power connectors is manifested in the melting of wear debris and the re-solidification of the contact region [16]. It indicates that the above-mentioned research results obtained under a test current of less than 100 milliamperes are only applicable to electronic connectors. The impact of the load current on the environmental adaptability of power connectors has emerged as a research focus [17]. It is found that the wear particles become smaller and the oxide layer becomes more stable with the increase in the load current [18,19]. Park et al. believed the ECR could remain at 1.0 ± 0.02 Ω due to the synergistic effect of oxide debris formation and electrical breakdown under a rated current ranging from 1 to 3 A [20].

In a previous paper by the present authors, the wear and melt erosion behavior of tin-plated copper alloy contacts was observed under fretting conditions with current loads ranging from 0.1 to 12.5 A [21]. The results indicate that when the load current reaches a certain level, phenomena such as melting, erosion, and splashing will inevitably occur due to the substantial heat generated at the contact interface. However, the current-carrying performance degradation of real power connectors exposed to mechanical vibration environments still remains unknown.

In this work, a series of mechanical vibration experiments were conducted to investigate the effects of vibration parameters (i.e., amplitude and frequency) on the ECR response of a commercial power connector under a rated load current. Subsequent sections detail the degradation process of power connectors through multi-cycle swept-sine vibration testing. The current-carrying degradation mechanisms of power connectors with the silver-coated pin-and-socket contact pairs under external vibrations are proposed.

2. Experimental Details

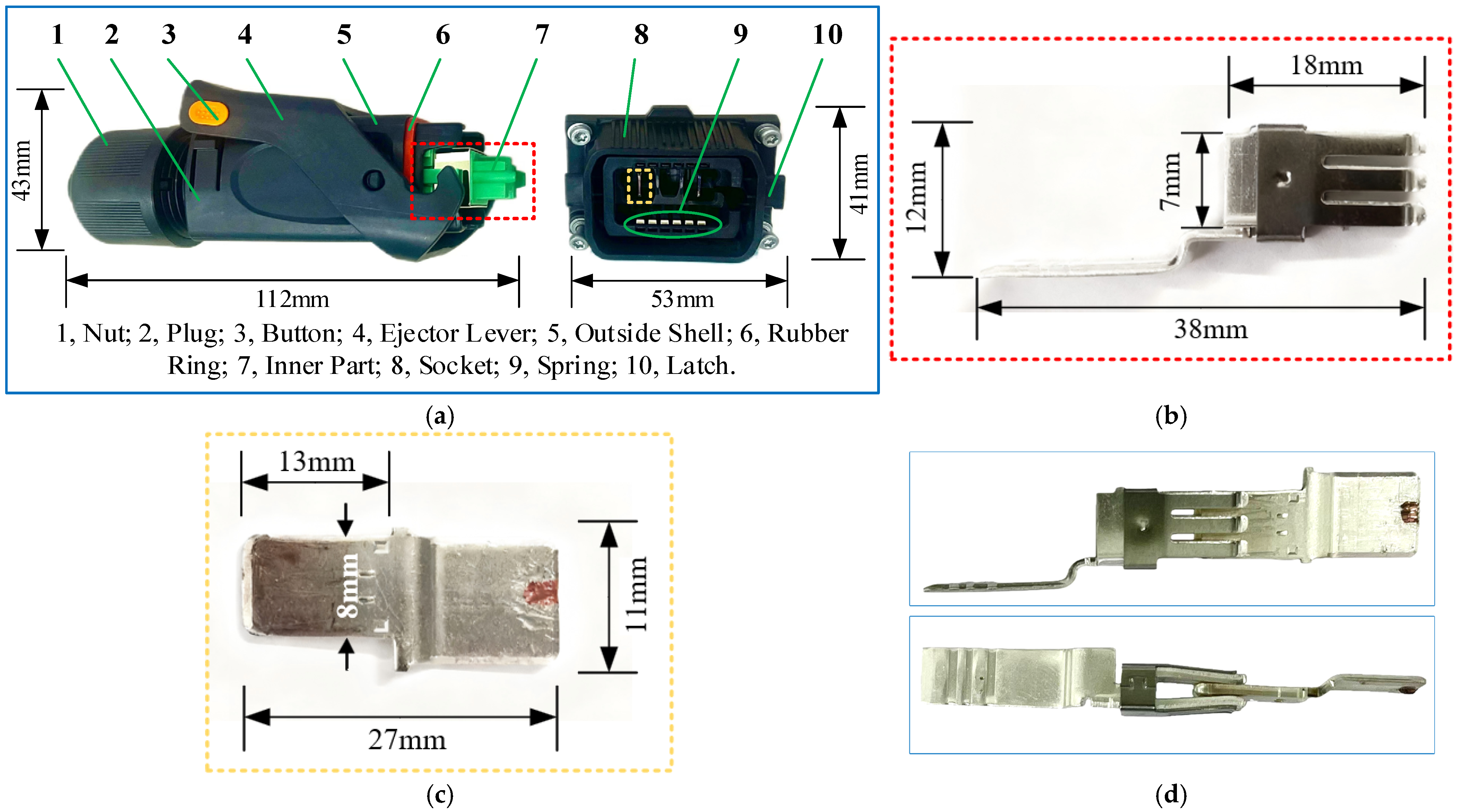
2.1. Description of Power Connectors

This work analyzes a commercial power connector (shown in Figure 1), which is vertically installed at the bottom of mobile communication towers supplying electricity from the ground directing current (DC) power supply to 5G base station equipment. The power connector consists of two sets of plugs and sockets, namely the male terminals and female terminals. One set is for input, and the other is for output. As shown in Figure 1b, the plug component adopts a blade-type structure, and the socket uses a multi-contact-fingers structure to improve the current-carrying capability. The male terminal is made of electrolytic tough pitch copper (C11000), and the female terminal is made of chromium-zirconium copper alloy (C18150). The combination of these two materials can achieve high normal force after matching. Both terminals are silver-plated and nickel-plated with the thickness of 2.5 μm and 1.3 μm, respectively. The connector integrates several anti-vibration features that limit the relative motion between mating terminals. As shown in Figure 1a, the socket’s spring beams provide normal-force stability and lateral constraint, while the housing’s latching structures secure the plug–socket engagement and suppress excessive displacement. An elastic retaining ring further absorbs vibration and restricts the fretting amplitude. These structural constraints keep the interface motion within a controlled range.

2.2. Test Rig

The test rig (shown in Figure 2) consists of two parts; that is, the mechanical vibration excitation module and the measurement module. The periodic sine vibration is provided by the electrodynamic vibration table (DC-300-3, SUSHI, Suzhou, China). The tensile state refers to the condition in which the current-carrying lead attached to the rear of the connector is fixed to the ground and kept under slight tension. To simulate the impact of wind and cable galloping on connector performance in 5G base station towers, an adapter flange and fixture, as shown in Figure 3, is used to connect with the socket part of connector. The mechanical vibration in X-direction could realize the fretting behaviors between the blade and the contact fingers. An acceleration sensor is attached to the adapter flange to provide real-time feedback from the sample vibration status, enabling closed-loop control of vibration signals. The connector was fixed to the vibrating table using a rigid adapter flange, following standard vibration–qualification practice for outdoor power connectors. This method ensures stable and repeatable lateral excitation. Although alternative fixing approaches (e.g., soft clamps or flexible brackets) may slightly change the transmitted displacement, the key degradation mechanisms are intrinsic to the contact interface and are not affected by the specific fixing method.

The measurement module is designed to record the contact current and the contact drop signals in real time. A Hall-effect current sensor (LHB-Y2, XINGHUI, Yueqing, China) is employed to characterize the contact current with a resolution of 0.05 A. The contact voltage drop signal is processed by low-noise amplification and low-pass filter. The measurement module is configured for the four-wire method, which could eliminate the lead resistance including the resistance of soldered joints. All the above signals including contact current and contact voltage drop are collected by the data acquisition system (PCI-1716, ADVANTECH, Taiwan) with a sampling rate of 250 kHz and measurement resolution of 16 bits. The ECR could be calculated by the ratio of the voltage signal and contact current, and the accuracy of the ECR is within 1% after calibration. The data acquisition, storage, and processing are controlled by a PC with the help of LabVIEW software 16.0.

2.3. Experimental Conditions

To investigate the effects of vibration frequency and vibration amplitude on the ECR of the power connector under current load, a series of fixed-frequency and fixed-amplitude vibration tests are carried out. Further, the multi-cycle swept-sine vibration experiment is also conducted. The experiment will be terminated once an open circuit failure occurs. The details of experimental conditions are listed in

Table 1. Experimental conditions.

Parameter	Value
Vibration frequency	5 Hz~1000 Hz
Vibration amplitude	0.5 mm~5 mm
Environment temperature	25 °C
Current load	3~70 A
Humidity	62 ± 2% RH

.

3. Results and Discussion

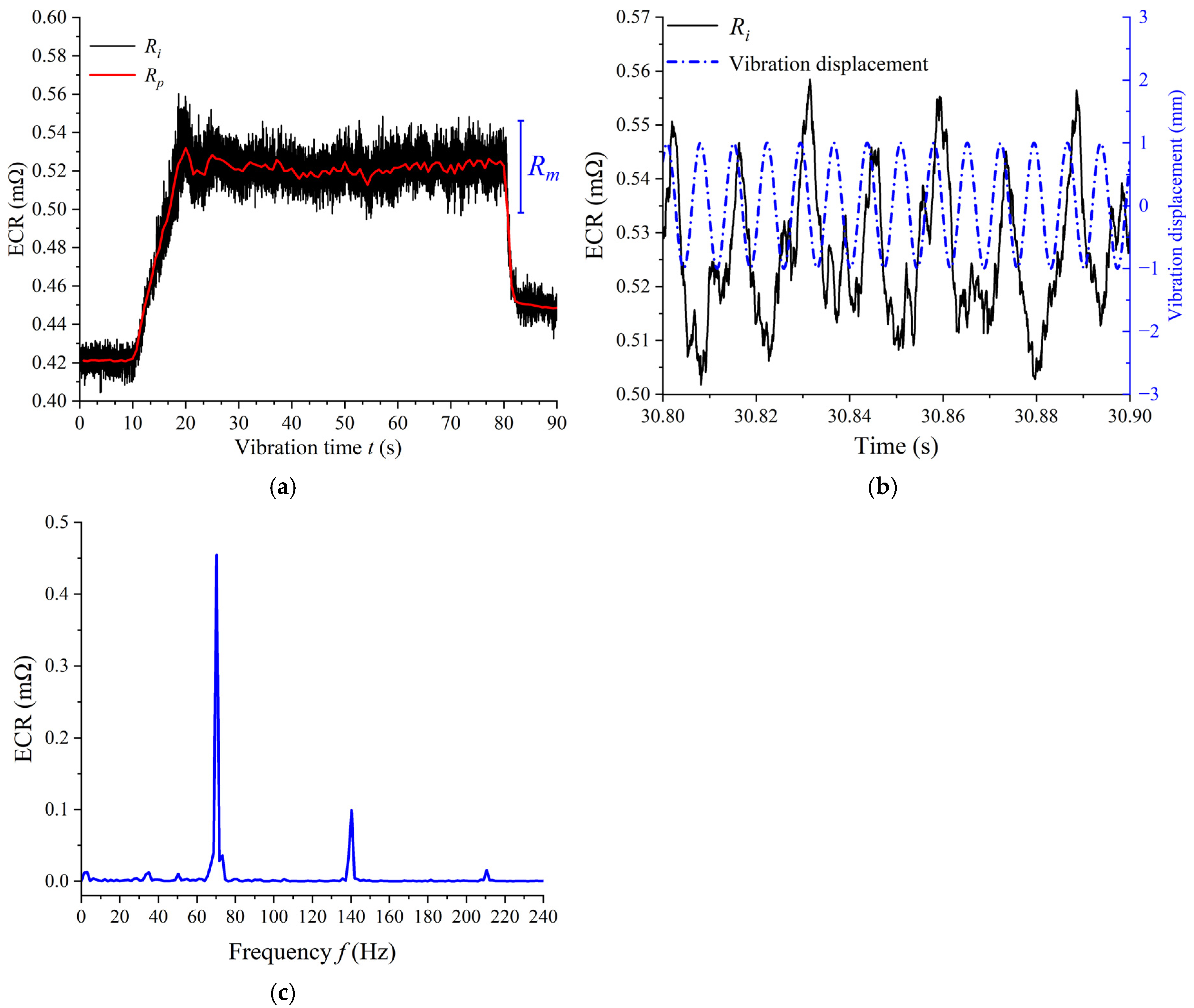
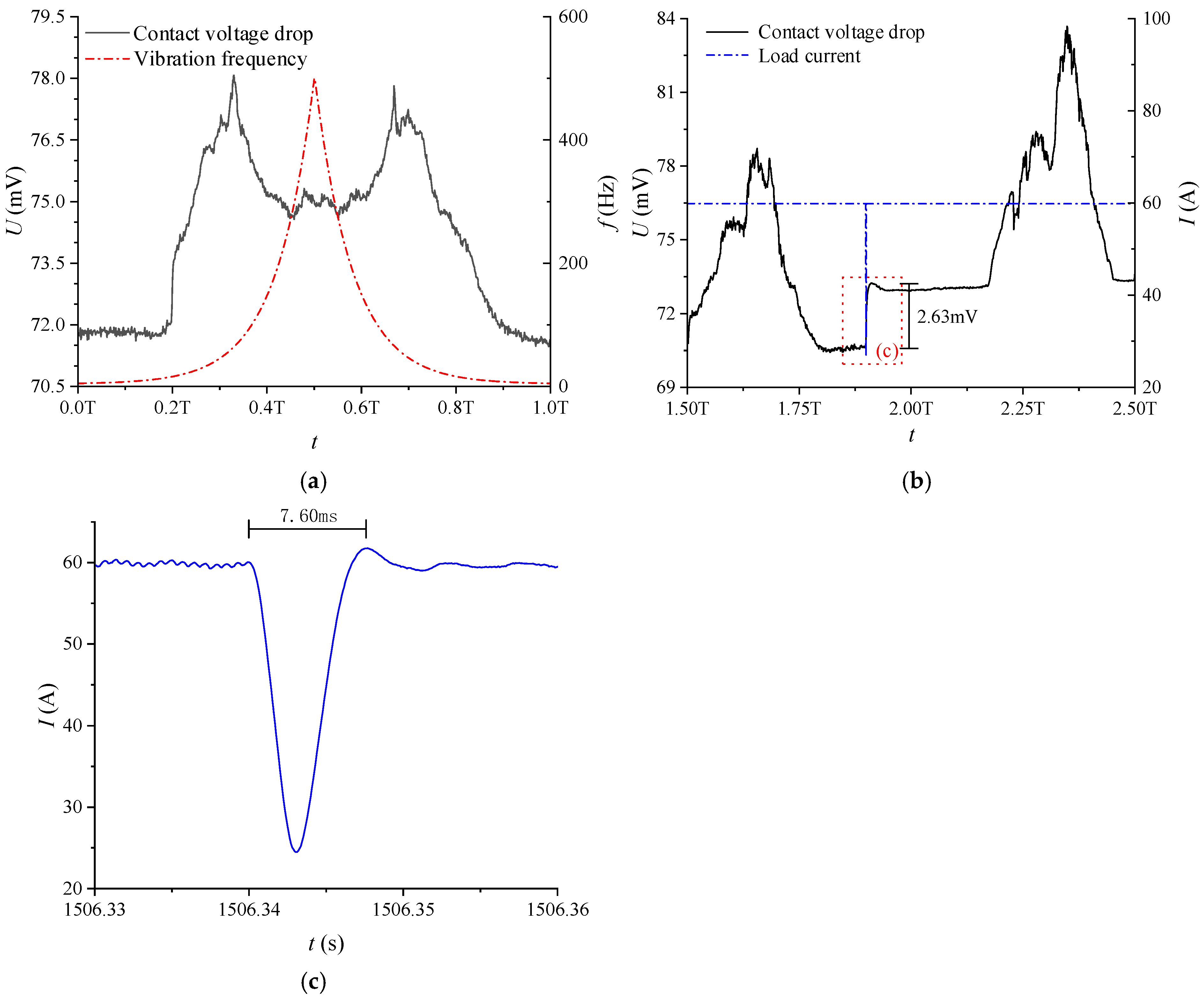
3.1. ECR Data Processing Methodology

The recorded each instantaneous ECR value, denoted as R_i, is defined as

$$R_i={\displaystyle \frac{U_i}{I_i}}$$

(1)

where U_i is the transient contact voltage drop, and I_i is the transient contact current.

Considering the irregular nature of the fluctuation amplitude of R_i, the peak-to-peak value of these fluctuations is defined as the difference between adjacent local maximum and minimum in R_i; then, these peak-to-peak values are averaged, and the result is defined as R_m, which is

$$R_m={\displaystyle \frac{1}{p}}{\displaystyle \sum _{k=1}^p\Delta R_k}$$

(2)

where p denotes the number of peak-to-peak values under identical vibration conditions, and ΔR_k represents the difference between adjacent local maximum and minimum.

In order to gain the obvious variation trend of ECR, 12,500 instantaneous values collected within each 0.5 s sampling cycle are averaged and named as the periodic average value R_p:

$$R_p={\displaystyle \frac{1}{\mathrm{12,500}}}{\displaystyle \sum _{i=1}^{\mathrm{12,500}}{R}_i}$$

(3)

The ECR values obtained during time periods with the same vibration conditions are averaged and define R_g as the average value of ECR under the specified vibration conditions:

$$R_g={\displaystyle \frac{1}{m}}{\displaystyle \sum _{i=1}^m{R}_p}={\displaystyle \frac{1}{n}}{\displaystyle \sum _{j=1}^n{R}_i}$$

(4)

where m is the number of sampling cycles under identical vibration conditions, and n is the number of samples under the same conditions.

Figure 4 shows the variations in R_i and R_p of one set contact pair within power connectors as a function of vibration time with the fixed vibration frequency of 70 Hz and the fixed vibration amplitude of 2 mm at a load current of 60 A. As seen, the initial average value of the ECR is 0.421 mΩ. The vibration stability is turned on at the 10th second, and then R_g linearly increases to 0.522 mΩ and remains constant for 50 s. At the 80th second, the vibration stops and R_g drops to 0.454 mΩ. Figure 4b provides the enlargement of the ECR variation during 30.80~30.90 s. The power spectral density (PSD) of these instantaneous ECR shown in Figure 4c indicates that the main frequency is 70.19 Hz, which is very close to the fundamental vibration frequency, and a secondary peak occurs at 140.38 Hz (twice of the dominant frequency). The occurrence of the first and second harmonics of ECR is consistent with the results in [10,22,23]. This phenomenon mainly arises from the relative sliding motion between the mated terminals under tangential vibration excitation. Since both the tangential friction force and the vibration acceleration vary sinusoidally, the normal force and the real contact area also fluctuate in a sinusoidal manner, which lead to periodic variations in the ECR. Therefore, the harmonic component at the excitation frequency originates directly from the vibration excitation itself. Meanwhile, within each vibration cycle, the acceleration reaches its maximum magnitude twice in the positive and negative directions, which causes the ECR to reach its minimum value twice as well. As a result, the fundamental frequency components of the ECR signal include both the excitation frequency and its second harmonic.

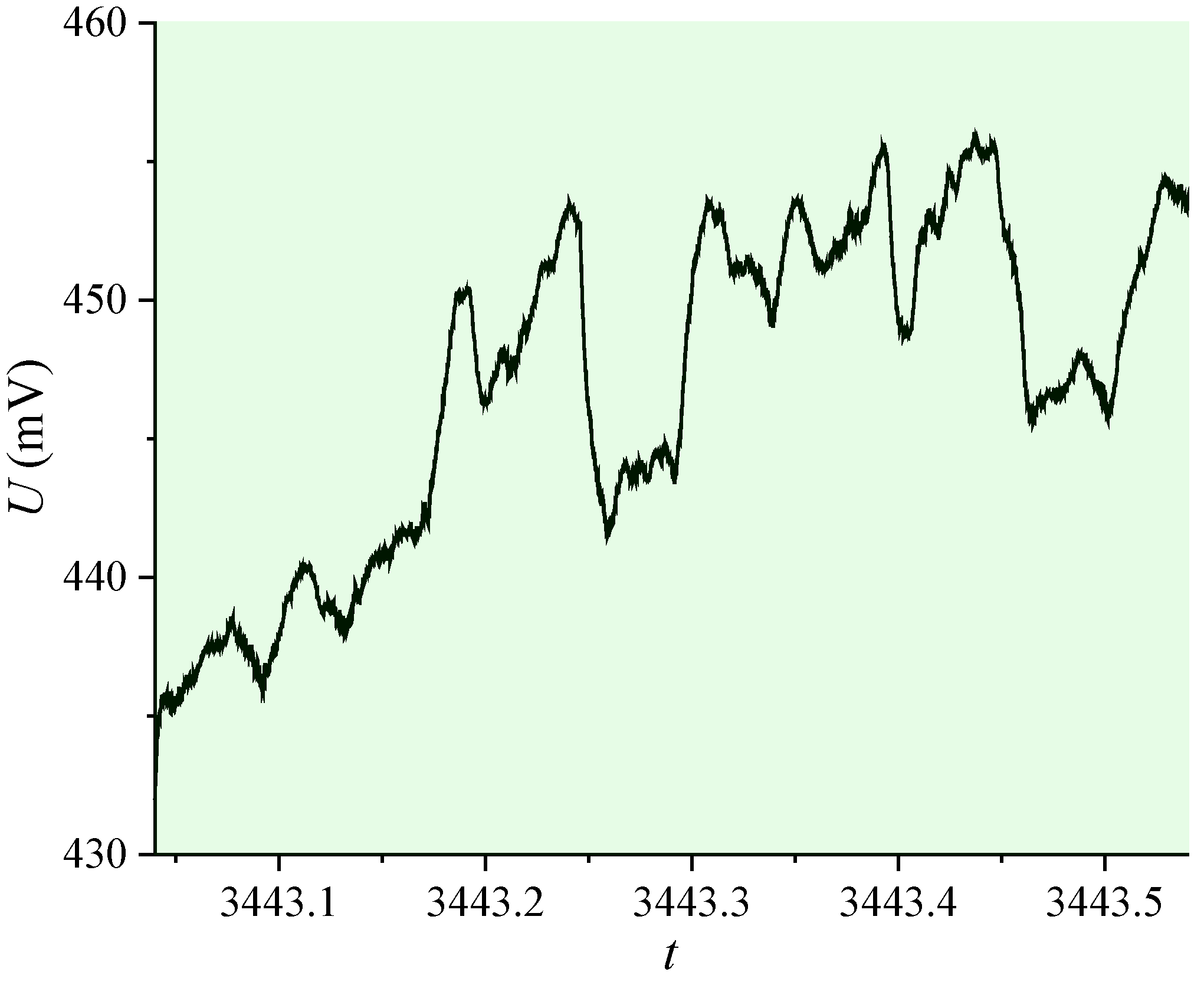
3.2. Effect of Vibration Amplitude

Figure 5 shows the recorded instantaneous ECR of the power connector with a constant vibration frequency of 70 Hz and a varied vibration amplitude ranging from 0.5 mm to 5 mm at a 60 A load current. It should be noted for each set vibration amplitude condition that the vibration table requires 20 s to establish stable vibration output, followed by 30 s vibration hold time and a 40 s recovery time before proceeding to the next amplitude level. As expected, the instantaneous ECR of R_i and calculated R_p both show an increasing trend as the vibration amplitude increases continuously. Figure 6a illustrates the variations in the average ECR R_g of the power connector as a function of vibration amplitude for vibration frequencies of 40 Hz, 70 Hz, and 100 Hz, respectively. The direct consequence of the increase in vibration intensity is the continuous rise in the ECR, which is consistent with the results of most previous studies [9,10,24]. The evolution of ECR with increasing vibration amplitude exhibits an initial rise followed by saturation behavior. A similar phenomenon has also been reported in fretting studies of Cu–Be alloy contacts at sufficiently large vibration amplitudes and high current loads [25]. When the amplitude is small, the imposed micro-slip disrupts the original asperity junctions and forms new, smaller, and less stable contact spots, resulting in a rapid increase in contact resistance. As the amplitude grows, a large portion of the active fretting region has already undergone repeated slip cycles, so the increment of newly generated contact areas becomes smaller and the rate of resistance increase gradually diminishes. Once the amplitude reaches the mechanical limit of relative motion allowed by the connector structure, no further enlargement of the fretting zone occurs, and the ECR approaches saturation. Then, a logarithmic function relationship is exhibited between the ECR and vibration amplitude, and the minimum value of the goodness of fit is 0.95. To compare the fluctuations in the transient ECR values during vibration, the ECR R_m of the power connector at different frequencies and amplitudes with the load current are also extracted and plotted in Figure 6b. As seen, the fluctuation of ECR becomes intense as the vibration amplitude increases. However, the influence of vibration frequency is limited.

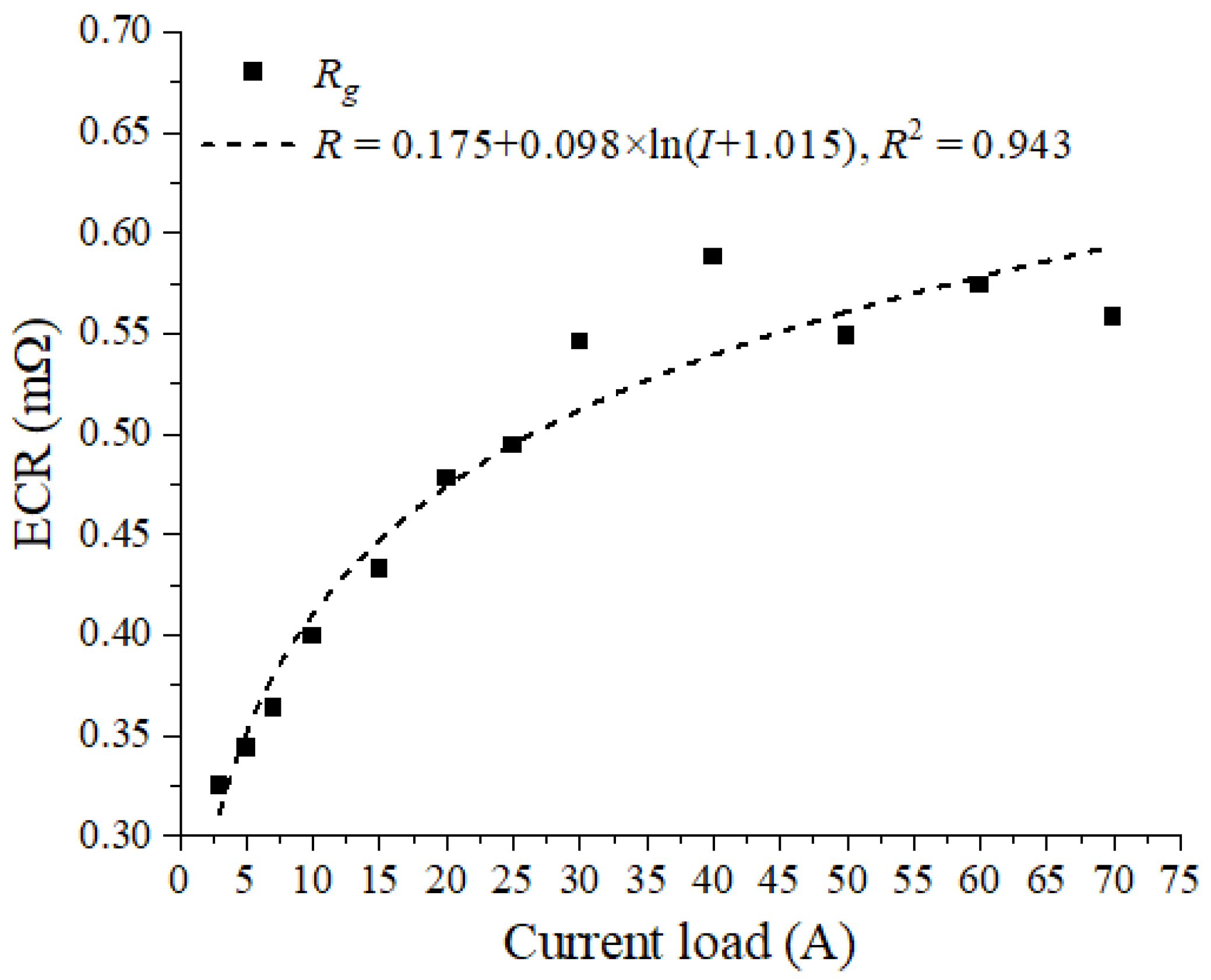
3.3. Effect of Load Current

Set the mechanical vibration frequency to 70 Hz and the vibration amplitude to 2 mm, then gradually increase the load current from 3 A to 70 A. It should be noted that vibration is applied only after the power connector reaches a stable temperature at a given load current. The duration of each vibration application is 30 s, and the entire experiment lasts for 2100 vibration cycles. The average ECR values are extracted and plotted in Figure 7. When the load current is lower than 30 A, the ECR increases significantly. After that, as the load current increases, changes in ECR response diminish. At low currents, limited heating allows fretting-induced degradation—such as debris formation, oxide growth, and coating removal—to dominate, leading to a clear increase in ECR. As the current rises, the interface temperature increases sharply, causing local softening and micro-melting of asperities. The resulting thermally assisted material flow can partially enlarge or reconnect conductive paths, offsetting part of the resistance growth from ongoing fretting wear. As a result, the change in ECR decreases and the response appears to approach a saturated state, reflecting a temporary balance between thermal enlargement of contact spots and mechanically induced degradation. This nonlinear relationship could be well described by the logarithmic function, and the goodness of fit is 0.943.

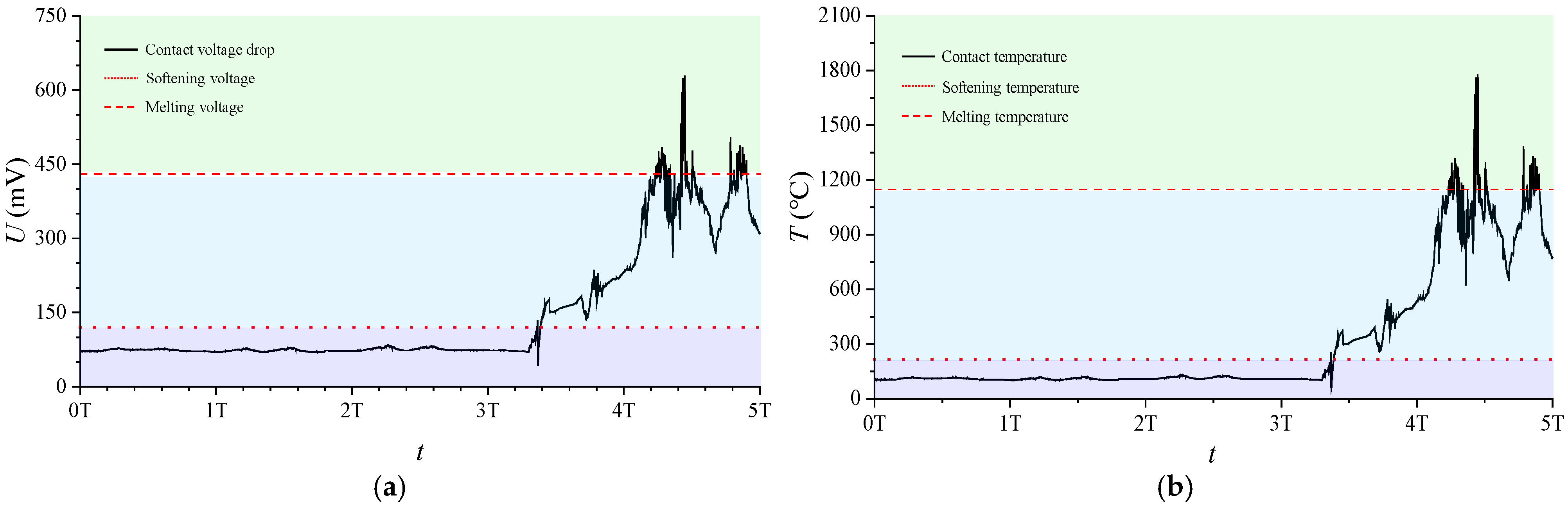
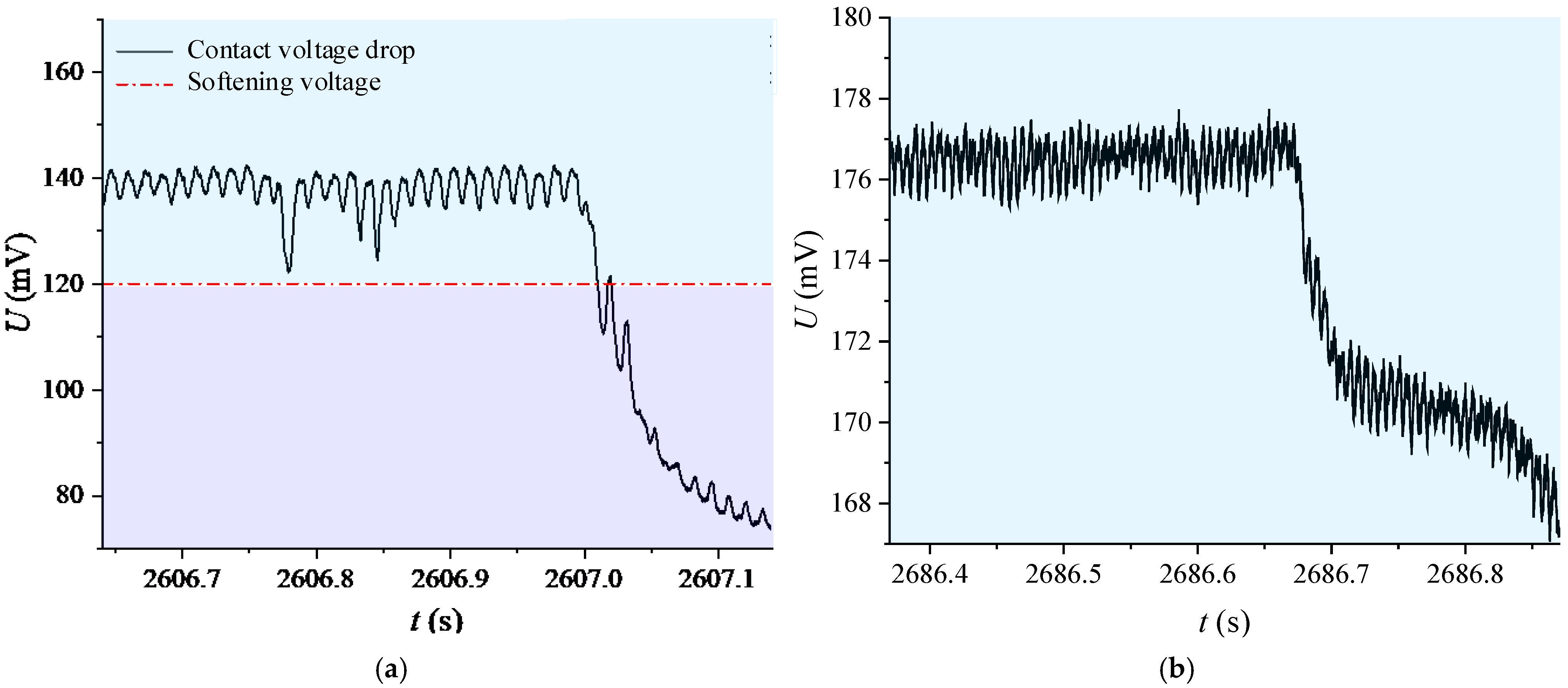
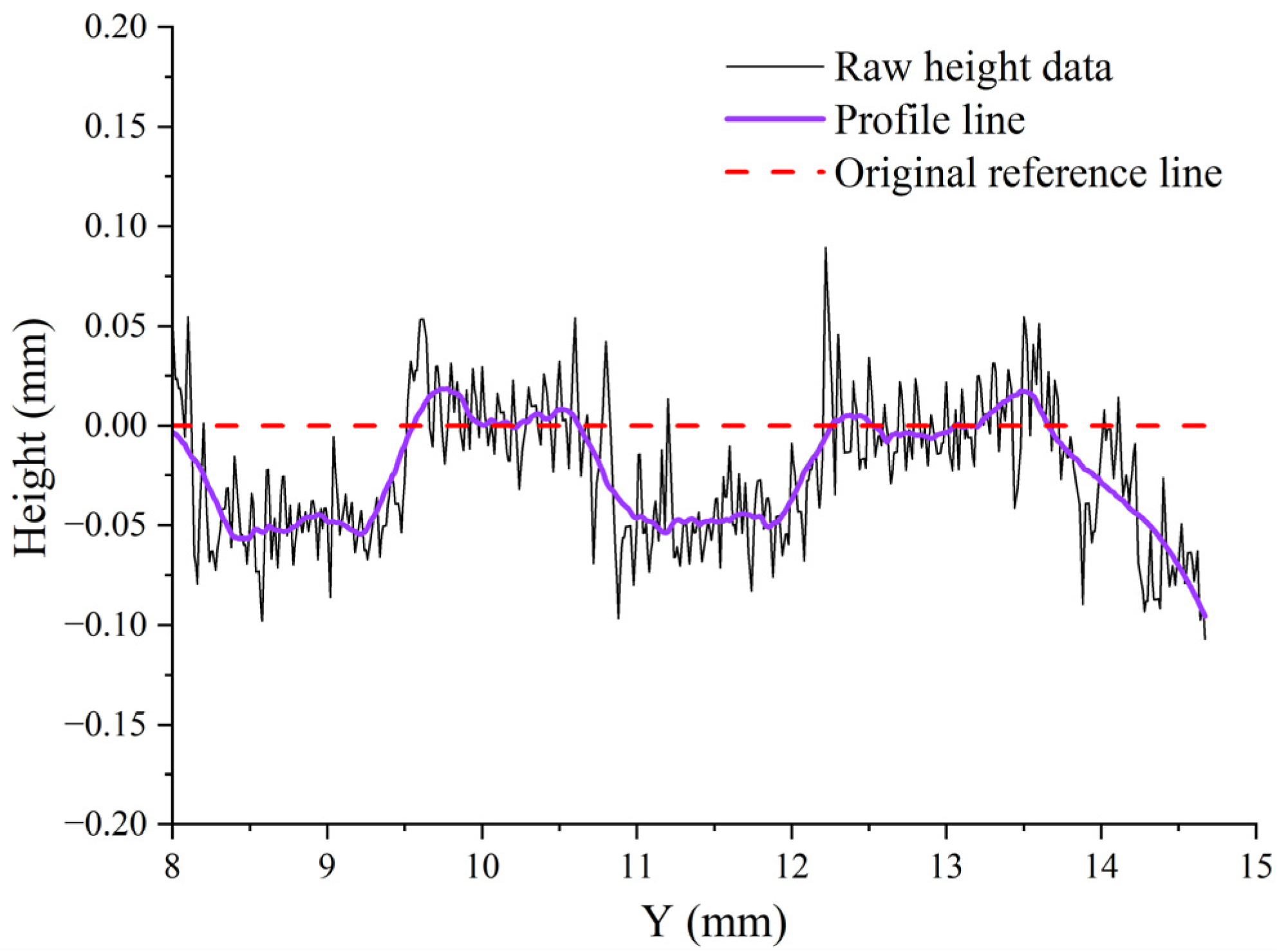
3.4. Failure Phenomena Induced by Swept-Sine Vibration Testing

The frequency-sweep vibration conditions applied during the experiments are shown in Figure 8. The frequency-sweep range is set from 5 Hz to 500 Hz at a rate of 1 oct/min with the current maintained at 60 A. The vibration acceleration is 196 m/s².

Figure 9a illustrates the variations in the contact voltage drop of power connectors carrying a current of 60 A during five cycles of swept-sine vibration testing. The contact voltage drop behavior appears to be characterized by a few distinct stages. The contact voltage drop remains stable with about 80 mV below 3.27 T swept-sine vibration cycles. There is a slight increment in the contact voltage drop from 3.4 T to 3.8 T (from 120 mV to 200 mV) followed by a rapid increase from 3.8 T to 4.1 T (from 200 mV to 340 mV). Between 4.1 T and 5 T, a large fluctuation in the contact voltage drop is observed, which fluctuates from 340 mV to 600 mV repetitively. After disconnecting the plug and socket of the power connector, it was observed that the plastic housing has melted, as shown in Figure 10. Detaching the plug and the socket, melting traces are also visible on their surfaces.

In order to interpret the variation in contact voltage drop and the failure phenomena of power connectors under swept-sine vibration tests, the measured contact voltage drop was converted into estimated contact temperature using the classical method of Kohlrausch’s equation [26]. Frankly, the application scope of Kohlrausch’s equation is indeed subject to certain limitations. However, the intention in using this equation is to qualitatively understand temperature evolution at the contact interface, and the feasibility has been validated by our previous investigation [27]. Thus, the contact spot temperature T_m can be estimated as

$$T_m=\sqrt{{\displaystyle \frac{1}{4L}}{U}_c^2+T_0^2}$$

(5)

The estimated contact temperature variation (shown in Figure 9b) at the contact position is calculated with the obtained contact voltage drop. As stated in [28], 120 mV corresponds to the softening point of 180 °C of copper material, and 430 mV corresponds to the melting point of 1083 °C of copper material. The continuous increase in contact voltage drop reflects the progressive degradation of the conduction path, which enhances local Joule heating. Then, insufficient heat removal combined with reduced normal pressure accelerates this thermoelectric coupling effect, eventually causing interfacial softening and localized melting. Therefore, we speculate that the contact interface gradually evolves from the initial solid-state contact to the molten contact. In the later stage, multiple recurrent transitions between the soften state and the molten state were observed.

In order to better understand the degradation process of electrical contact performance of silver coating carrying a heavy-duty load current, the representative variation in contact voltage drop in each single swept-sine vibration is extracted and interpreted explicitly. As plotted in Figure 11a, the vibration amplitude is fixed before 0.2 T, and the contact voltage drop remains at the initial value of 71.6 mV despite the gradually increased vibration acceleration. From 10 Hz to the crossover frequency of 71.1 Hz, the contact voltage drop increases almost linearly to 78 mV. After that, the vibration acceleration reached 20 g, and the contact voltage drop reduced to 74.5 mV with the vibration amplitude decreasing gradually. Similarly, during the process of downward swept-sine from 500 Hz, the change in contact voltage drop is the reverse of the upward swept-sine process. This phenomenon basically conforms to the above-mentioned ECR characteristics. However, as shown in Figure 11b, when the vibration test time reached 1.89 T, that is, 1506 s, the on-state current dropped sharply from 60 A to 26.6 A and persisted for 7.06 ms. After that, the contact voltage drop showed an instantaneous jump to 2.63 mV and persisted for more than 0.2 s. This also leads to the contact voltage drop failing to reproduce the characteristics of symmetric variation within the vibration period from 1.5 T to 2.5 T.

As illustrated in Figure 9, the contact voltage drop shows a significant upward trend commencing from the 3rd swept-sine vibration cycle, increasing from the initial 74 mV to 240 mV. This directly results in a notable rise in heat generation within the contact region. Meanwhile, the instantaneous value of the contact voltage drop shows periodic fluctuations and exhibits a sharp drop at 2607 s, shown in Figure 12a. This can be attributed to the softening of the material in the electrical contact region. As expected, the softer the contact interface, the greater the variation amplitude of the contact area will be under vibration conditions. When the contact area increases to a certain extent, it will result in a smaller contact voltage drop and forms a new contact equilibrium state. As plotted in Figure 12b, as the contact voltage drop increases further, it can produce periodic fluctuations with a higher frequency. It is verified that the change in the contact voltage drop at this stage is significantly different from that observed in the first swept-frequency vibration cycle.

Figure 13 plots the typical instantaneous contact voltage drop of silver coating contact pairs in the melting status. As shown, the contact voltage drop still shows an overall fluctuating upward trend: the upward process is sometimes gradual and sometimes steep, while the downward process is characterized by sharp drops. It should be noted that the variation in the contact voltage drop has no obvious correlation with the frequency of external vibration. For the contact interface in a molten state, prolonged high temperatures can accelerate material oxidation. Thus, if the oxide generated in the interface molten pool has excessively high resistivity, it may cause an open circuit failure.

The surface morphology and elemental distribution of the failed plug component are further characterized using a scanning electron microscope (Sigma 300, ZEISS, Oberkochen, Germany) equipped with an energy-dispersive X-ray spectrometer (EDS). The quantitative comparison of elemental contents is listed in

Table 2. Comparison of weight percent of elements for different positions.

Element	I	II	III
Ag	98.06 wt%	13.34 wt%	7.34 wt%
Ni	0	39.13 wt%	2.52 wt%
Cu	0	28.47 wt%	74.22 wt%
O	1.94 wt%	19.06 wt%	15.92 wt%

. As shown in Figure 14, three individual wear scars on the plug exhibit approximately circular contours with obvious pitting, and the central zone of each wear scar contains multiple cracks, while the periphery displays layered accumulations of redeposited material. These morphological features correspond to the periodic melting and resolidification of the contact material, which occurs when the local contact temperature fluctuates around the melting point during the arc erosion stage on the copper substrate.

The EDS analysis reveals a clear compositional degradation from the unworn surface to the center of the worn region. In the unworn area, the surface is dominated by silver. However, in the worn regions, the silver and nickel contents decrease drastically, accompanied by a pronounced increase in copper and oxygen. At the wear edge, Ag drops to 13.34 wt%, while Ni and Cu become rich due to partial exposure of the underlying interlayer and substrate, together with the deposition of oxidized debris. Toward the crater center, Ag and Ni are nearly exhausted, whereas Cu exceeds 74.22 wt% and O rises to 15.92 wt%, indicating that the silver coating was completely removed and the copper substrate was oxidized. These compositional changes demonstrate that the electrical wear process caused progressive removal of the Ag–Ni coating, exposure of the Cu substrate, and subsequent oxidation and redeposition of molten material, leading to the layered morphology observed around the wear scar.

The cross profiles (shown in Figure 14a) obtained by a 3D optical profilometer (SRI7050, SSZEN, Shenzhen, China) are displayed in Figure 15. The surface profile along the Y-direction clearly exhibits three crater-like pits compared with the original reference line. Each pit corresponds to a wear scar formed by local material removal. Pronounced raised edges are observed on both sides of the pits, indicating material pile-up and transfer around the worn scars. These features suggest that under the operating conditions of sustained current-carrying vibration, plastic flow and molten material migration occurred in the contact zone, which lead to the generation of pits and the aggregation of edge accumulations.

Based on the variations in contact voltage drop and associated ECR as a function of vibration duration, surface morphology, and profiles of the fretted zone, the current-carrying performance degradation mechanism of the power connector under mechanical vibration is clarified in Figure 16. The occurred ECR trends and open circuit failure of power connectors were due to wear, metal melting, and oxidation behavior between contact pairs. That was also reported for tin-plated and gold-plated copper contacts in [29,30,31,32,33]. Initially, the excellent electrical and thermal conducting characteristics of silver guarantees the low and stable ECR and contact temperature rise. As fretting proceeds, wear debris from the silver plating is gradually generated between the contact surfaces, and their accumulation effect reduces the actual contact area. This also causes the ECR to exhibit characteristics of jitter variation and an overall increasing trend when the silver coating is worn out, leaving the substrate nickel and copper exposed to the air and forming the copper oxide easily in the air. The oxidation behavior substantially reduces the electrical conductivity of the interface and also generates a large amount of Joule heat when carrying a heavy-duty current. When the contact temperature reaches the melting point of the material, the wear debris will melt, and the molten state in the interfacial micro-region causes the ECR to decrease again. As the amount of wear debris and the intensification of oxidation increase, both the ECR and the contact temperature rise increase significantly. Finally, the fluctuation of the ECR attributed to the oxide debris along the wear track becomes extremely uneven. Once there are oxides with extremely high resistivity at the contact location, the circuit will exhibit an open state.

4. Conclusions

In this work, the fretting wear mechanisms and electrical contact degradation of power connectors were systematically examined through mechanical vibration experiments under heavy current loads. Within the tested vibration amplitude range of 0.5~2 mm, the average ECR increases with amplitude, and the transient ECR fluctuations exhibit a clear amplitude-dependent trend. When the vibration amplitude exceeds 2 mm, saturation-like behavior appears due to the displacement-limiting features of the connector structure. The load current, varied between 5~30 A, further intensifies the thermo-electrical coupling: a higher current promotes the formation of low-conductivity ablation scars and increases localized Joule heating, thereby accelerating the resistance growth. The sweep-frequency excitation from 5 Hz to 500 Hz successfully reproduces the complete degradation-to-failure process, in which progressive fretting wear, oxidation, thermal softening, and micro-scale melting collectively lead to electrical disconnection of the contact interface. Therefore, suppressing harmful vibration levels, enhancing heat dissipation, and employing more oxidation-resistant contact materials together with thicker protective coatings are recommended to improve the long-term durability of power connectors.