Abstract
This paper presents a study on the nonlinear vibrations in the impact-echo (IE) method for void flaw detection of solid structures. Linear theory has historically served as the foundational framework for non-destructive methods, including the IE method, particularly for estimating flaws in solids. This paper gives a comprehensive analysis of the nonlinear theory behind the IE method for detection of voids in solids such as concrete structures. The general equation of motion is presented for the flexural vibration of a void-defected solid with general nonlinear constitutive material properties, and then the simplified solutions for polynomial nonlinearity and hysteresis nonlinearity are derived comprehensively. The solutions of principal frequency and sub- and super-harmonics as well as the frequency of combined modes are elaborated, and the theoretical formula of resonant frequency shift with amplitude is derived. As conventional nonlinear IE methods have been conducted by only using a phenomenological model of linear shift in resonant frequency with amplitude, the proposed new frame of nonlinear vibration theory can be used to implement the IE method more comprehensively and accurately for void detection in solids.
1. Introduction
Traditionally, linear theory has been widely used to develop non-destructive testing (NDT) methods such as the IE method for estimating the flaw void in solids such as metal, plastics, composite, wood, rock, and concrete.
Taking concrete bridge structures as an example, proper NDT is a critical basis for maintenance, rehabilitation, or replacement of flawed bridge decks, and it therefore plays a critical role in the nation’s economy and the safety of the public. Defects such as voids, cracks, and delamination are usually caused by poor consolidation of concrete during construction that can eventually lead to failure of the structure. The detection of defects in concrete bridge decks is crucial for ensuring structural integrity and safety.
Researchers use a variety of NDT techniques to detect and identify concrete defects such as damage acoustic emission detection technology, IE detection technology, ultrasonic detection technology, infrared thermography detection technology, ground-penetrating radar detection technology, piezoelectric transducer detection technology, X-ray detection technology, etc. [1].
The IE method is a stress wave technique that serves as a principal tool for flaw detection in structural components such as bridge decks. The basic procedure of this method involves hitting the surface of the measured structure with a hammer to generate elastic stress waves and subsequently measuring the response using a nearby accelerometer. During the propagation of stress waves, reflections occur when significant void defects are encountered in the medium. The transient resonance caused by reflection changes the displacement of the surface of the structure to be measured, and then the signal generated by the resonance is received by the sensor near the impact point.
The principle of the IE is based on the waveform and frequency analysis. The recorded time-domain signal is converted into a frequency-domain function via a fast Fourier transform. The transformation results in a frequency–amplitude spectrum, which shows the amplitudes of various frequencies contained in the waveform. The frequency corresponds to the arrival of the P-wave, reflected from the void interface. The reflected frequency is referred to as the depth or thickness frequency f, and the depth of the void in solid h can be determined using the measured compression wave velocity and thickness frequency [2].
Solid void detection with the IE technique generally uses the approximate mathematical relationship between the peak frequency, the speed in the solid, and the depth of the void in the solid. When there is a discrete void located below the impact point, if the flaw is large enough, there will be nearly complete reflection of the P-waves by the void. Basic guidance on and examples of defect detection with IE, including the effect of flaw size and depth and the influence of the impactor type, are provided by [3,4,5,6,7,8].
In most applications for non-destructive testing of structures with materials of concrete, IE methods and impactive response methods primarily rely on linear vibration theory. The IE method involves generating short-duration stress waves in a material and then recording the reflections of these waves from internal flaws or external boundaries. Analyzing these reflections, often transformed into the frequency domain, allows the identification of flaws. This process assumes elastic wave propagation within a linear elastic material. At the low strain levels typically involved in IE testing, solid such as a concrete deck can be reasonably approximated as a linear elastic material. This means that stress is proportional to the strain, and the material returns to its original shape after the stress is removed. This assumption simplifies the analysis of wave propagation and reflection.
While linear vibration theory forms the foundation, it is important to acknowledge that it is a simplification. In cases of damage and dealing with solids like concrete at higher stress levels, nonlinear effects might become more significant [9,10].
When damage is present, such as microcracks and voids in concrete, the material behavior can significantly deviate from linear elastic behavior. These nonlinear effects can be observed in changes in wave velocity, resonance frequencies, or the presence of harmonics in the structural response. It is crucial to develop and explore nonlinear IE methods as a more sensitive approach to evaluate damage, by incorporating more complex analytical approaches to account for nonlinear behavior complexities. While IE methods are fundamentally based on linear vibration theory for analyzing wave propagation and reflections, the presence of material damage can introduce nonlinear behavior. This has led to the requirement to develop more advanced, nonlinear analysis techniques to provide a more sensitive assessment of material integrity, particularly for complex materials like concrete. Essentially, concrete material is nonlinear [11].
This paper presents a comprehensive analysis of the nonlinear vibration theory behind the IE method for detecting voids in solids such as concrete structures. The general equation of motion is presented for the flexural vibration of a void-defected solid with a general nonlinear constitutive relationship, and then the simplified solutions for polynomial nonlinearity and hysteresis nonlinearity are derived comprehensively. The principal frequency and sub- and super-harmonics as well as the frequencies of combined modes are elaborated, and the formula of amplitude-dependent natural frequency is derived. The research sheds light on the IE method for void detection in solids in the new frame of nonlinear vibration theory. The current nonlinear IE methods only rely on a phenomenological model of resonant frequency linear shift with amplitude. This paper presents nonlinear shift in resonant frequency with amplitude and multiple harmonics associated with resonant frequency, which can be used to identify the nonlinear vibration system more accurately.
2. Linear Vibration Theory in IE Method
2.1. Vibration Model of Solids with Void Damage
The IE method relies on generating transient stress waves by impacting the solid surface. These waves propagate through the material and are reflected by internal flaws such as voids. When a void is present in a solid, the stress waves reflect off its upper surface, creating a resonance within the layer of the solid between the impact point and the void. In the IE test of a solid with a void, the recorded frequency corresponds to the natural (or resonant) frequency of the part of the structure above the void. Solid structures with void damage can be modeled as shown in Figure 1 [12].
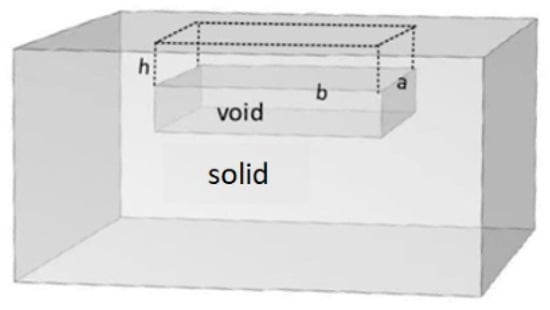
Figure 1.
Model of solid structure with void damage.
As illustrated in Figure 1, the void damage is modeled as a cuboid with length , width , and depth below the solid surface, whereas the solid above the void can be viewed as a plate of length , width , and thickness .
The vibration of the solid plate above the void is constrained by the surrounding solid materials, and the boundary condition can be like the elastic boundary. From the simply supported boundary to fixed boundaries, the boundary conditions could be varied. According to the vibration theory of thin plates, the formula for calculating the natural frequency of a simply supported thin plate on four sides is given as [13]
where is the bending stiffness of the thin plate, ρ is the material density, is the geometric thickness of the thin plate, a and b are the length and width of the plate, respectively, and m and n represent the modal order of the rectangular simply supported plate in its direction. For fixed constrained thin plates, the modification can be found in [14].
For the natural vibrations of the simply supported thick plate at all edges, the natural frequency is given as [15,16,17,18]
where and are the plate-specific mass per unit area and its moment of inertia, respectively, and is mass density. . is plate shear rigidity, , and is the shear coefficient.
2.2. Conventional IE Method for Solid Void Testing and Diagnosis
In the case of detection of voids/delamination/cracks inside a solid structure using the IE method, the model is shown in Figure 1, and the plate theory results have been applied. Following the traditional procedure of the IE method, the corresponding time-domain signal is transformed to the frequency domain via FFT [19]. After that, a significant peak in the spectrum is identified and correlated with the specific natural frequency of the structure ω, as given by Equation (1) or (2), the void thickness/depth resonances, f = ω/2π, relating to the solid plate above the planar void flaw. If the effective P-wave velocity, , of the solid structure is known, the depth of the void, , is obtained by using the following general formula:
in which K is a geometric correction factor depending on the geometry of the structure, β is the “Lamb wave” correction factor, and n is a constant factor depending on the acoustic impedances for the back wall which equals to 2 if surrounded by air, air-filled void. The dimensionless factor β was modified empirically to be 0.96 in order to match experimental observations in the case of concrete slabs. The Cp of the P-wave velocity is related to Young’s modulus E, Poisson’s ratio ν, and the structural density as follows:
The IE method could be interpreted as a frequency-domain resonance technique (vibration modal analysis). Many improvements can be found in related research [20,21,22].
3. Nonlinear Vibration Theory in IE Method
3.1. Conventional Nonlinear Resonance Acoustic Spectroscopy and Phenomenological Model
To assess the solid of complex materials for NDT, a series of studies have been conducted to capture the patterns of the measurement and identify key solid material states that influence the behavior. The nonlinear resonant acoustic spectroscopy (NRAS) test method has been established to measure solid material nonlinearity [23,24,25,26].
The NRAS method makes use of the linear resonance frequency shift and is based on typical observations of mesoscopic hysteretic materials. The technique focuses on the acoustic nonlinear (i.e., amplitude-dependent) response of one of the material’s resonance modes when driven at relatively small wave amplitudes. Early NRAS experiments applied specimens of plexiglass and sandstone as well as automobile engine components. NRAS has been used for nonlinearity characterization, which focuses on frequency shift detection and attenuation factor shift detection. The observed phenomenon of nonlinear resonance vibration is the shift in resonance frequency depending on the input amplitude. NRAS focuses on the use of specific types of nonlinearity features, usually generating larger strain on solid materials than linear IE methods.
The nonlinearity is determined from the strain-induced changes in material properties, such as frequency shift and velocity changes. The relative resonance frequency shift is related to the strain change as follows:
This states that the resonant frequency ratio is proportional to the strain level or acceleration amplitude rate , is the linear resonant frequency measured at a low strain level, and f is the frequency at a high strain level. In this equation, is frequency–strain nonlinearity coefficient and is the frequency–acceleration coefficient. In most experiments, the acceleration amplitude is used because vibration acceleration is easier to measure than the strain.
For specimens at higher damage levels, a larger decrease in resonance frequency has been observed with increasing acceleration amplitude. The NRAS method has been used in many applications [27,28,29,30,31,32,33,34,35,36,37,38,39].
3.2. Nonlinear Constitutive Relationship of Void Solid
As a popular solid, concrete is a nonlinear material with complex mesoscopic structures. The nonlinearity of concrete comes from the mesoscopic linkages among the cement, aggregates, and cracks. Cracks and microcracks in concrete will dramatically increase the concrete material’s nonlinearity. The presence of nonlinearity in concrete is observed in the hysteresis found in its stress–strain relationship and its discrete memory.
Solid materials such as concrete exhibit both classical and non-classical elastic nonlinearities, or polynomial nonlinearity and hysteresis nonlinearity, respectively. Classical nonlinearity is modeled by expressing the elastic modulus E as a polynomial function of strain ε. As documented in the literature, materials such as concrete also exhibit hysteretic behavior and end-point memory. One of the most widely used models including both classical and non-classical nonlinear behavior in the stress–strain constitutive relation is as follows [37,40,41,42]:
where E0 is the linear modulus, ε and are the strain and strain rate, respectively, β and δ are the quadratic and cubic nonlinear parameters, and α represents the hysteresis parameter.
For solids with a nonlinear modulus, the relationship between natural frequencies and harmonics in the spectrum becomes more complex. The natural frequencies may shift as the amplitude of vibration increases. The advanced analysis below rigorously examines the nonlinear vibrations of the plate—modeled over a solid void and featuring a nonlinear modulus—as shown in Figure 1.
3.3. Nonlinear Vibrations with Polynomial Nonlinearity
When the plate above the solid void comes to the free vibration, both polynomial and hysteretic nonlinearities can play a role. This section focuses on polynomial nonlinearities. Consider the plate model above void damage in a solid structure, as shown in Figure 1; the involved physical nonlinearities are described through polynomial nonlinearity laws.
By following [43,44,45,46,47,48,49], the system nonlinearities are modeled by the classic nonlinear plate theory. Then, the Novozhilov nonlinear plate model, commonly recognized as the finest classical plate model, reduces to the well-known von Karman nonlinear plate model. Dynamic local models are first built in the vicinity of a static configuration of interest. Galerkin’s method is then utilized to give rise to the approximation of the plate’s behavior in the form of a system of ordinary differential equations with quadratic and cubic nonlinearities corresponding to Equation (6),
where qn is generalized coordinates, and kni, knij, and knijl are known coefficients.
Consider the simplest case of Equation (7), a nonlinear oscillator with cubic nonlinearity, or the Duffing oscillator,
The solution can be derived by using the methods in [50]:
Consider another simplest case of Equation (7), a nonlinear oscillator with quadratic nonlinearity,
The solution can be figured out by using methods in [51,52]:
From the above simplified cases, we can see that the free responses of nonlinear oscillators with quadratic and cubic nonlinearities include the components of natural frequency and double and triple natural frequencies.
The free vibration of an oscillator with quadratic and cubic nonlinearities is characterized by their restoring force, which is not directly proportional to the displacement but includes quadratic and cubic terms. This leads to phenomena like amplitude-dependent natural frequency. For a nonlinear oscillator with both quadratic and cubic nonlinearities as well as higher order nonlinearities,
The amplitude-dependent natural frequency can be derived by using the methods in [53,54,55,56,57],
in which A is the response amplitude.
3.4. Nonlinear Vibrations with Hysteretic Nonlinearity
Studies have shown that non-classical nonlinearity is more dominant than the classical one in concrete when these materials contain microcracks [58,59,60].
Nonlinear dynamics of oscillators with hysteresis exhibit complex phenomena due to the system’s memory-dependent behavior. These phenomena include frequency response shifts, amplitude-dependent behavior, potential for bistability and chaos, etc. Hysteresis, a characteristic of materials where the output depends not only on the current input but also on past inputs, introduces significant nonlinearities into the system’s dynamics. In structure analysis, the stress–strain constitutive hysteresis relation in Equation (6) has been reshaped as varied models for convenience. The Bouc–Wen model is a widely used mathematical model for describing hysteresis in various applications. Another model, Caughey’s bilinear model, is used for analyzing the transient and steady-state response of hysteretic oscillators [61,62,63,64].
Most proposed hysteretic models can be classified into two categories: polygonal hysteretic models and smooth hysteretic models [65,66,67,68].
Polygonal hysteretic models refer to hysteretic models with piecewise linear behavior. In polygonal hysteretic models, every branch of the force displacement diagram follows a linear relationship, according to the time history response of the system. The simplest model of this category is the bilinear hysteretic model.
Smooth hysteretic models employ nonlinear formulations to capture the response of a system, which seem to better represent the continuous changes in the loading branches during yielding. Moreover, the total stiffness of smooth hysteretic models can be represented by an appropriate combination of component springs. The first smooth hysteretic model is known as the Bouc–Wen hysteretic model.
The bilinear model, the simplest polygonal model, is characterized by two linear segments and is simpler and computationally efficient in capturing basic complex hysteretic behaviors [69,70,71]. It provides a simplified yet effective way to account for the nonlinear, energy-dissipating nature of these materials under dynamic or cyclic loading conditions.
The bilinear oscillator model can be approximated by
Closed-form analytical solutions are of great significance in configuring the overall vibration characteristics. Because the nonlinearities in this problem cannot be assumed to be small, general analytical solutions using only conventional methods such as the perturbation method are not feasible. By using the discontinuous transformation method [72,73,74,75,76,77,78,79], the solution of the above model Equation (16) under the unit initial condition is derived as
in which , , , , and .
Equation (17) demonstrates that the system free response has the components of two natural frequencies and their sub-harmonics, super-harmonics, and combined harmonics.
4. Discussion
The solutions of Equations (9), (10), (12), (13) and (17) specify the existence of multiple harmonics in addition to natural frequency components in the nonlinear responses of concrete with a void. The multiple harmonics in the numerical/experimental studies of the IE test of concrete with a void, such as [36,41], can be attributed to this kind of nonlinear phenomenon.
The solution of Equation (15) specifies that in the nonlinear responses of concrete with a void, the natural frequency nonlinearly depends on amplitude. It is noted that the linearization of Equation (15) gives rise to Equation (5) which has been used as the only basis in conventional nonlinear IE methods [9,10,40].
The applications of nonlinear IE methods for the detection of concrete voids are related to many factors, such as impactor or hammer types and echo sensor types. There are some recent developments, such as detecting transport road cavities using passing-by vehicles as impactors and using microphones/noise or accelerometers/acceleration as echo sensors [80,81].
5. Conclusions
This paper presents a comprehensive study on nonlinear vibrations in the IE method for void flaw detection in solid structures.
The general equation of motion is presented for the flexural vibration of a void-flawed solid with a general nonlinear constitutive relationship, and then the theoretical solutions for polynomial nonlinearity and hysteresis nonlinearity are derived comprehensively. The solutions of principal natural frequencies and the sub- and super-harmonics of natural frequencies as well as the frequencies of combined modes of natural frequencies are elaborated. The formula of the amplitude-dependent natural frequency is derived, which gives rise to the conventional formula of the conventional nonlinear IE method/NRAS after linearization simplification.
To the best of the authors’ knowledge, this is a new attempt to comprehensively propose a nonlinear vibration theory in IE methods for estimation and prediction of solid voids. The current nonlinear IE method/NRAS only relies on a phenomenological model of resonant frequency linear shift with amplitude, which is a simplified case of the proposed general solution of resonant frequency shift with amplitude. Compared with the current nonlinear IE method/NRAS, this paper develops a new nonlinear framework, which can be used to search for and develop more accurate nonlinear IE methods.
Author Contributions
Conceptualization, D.S. and G.S.C.; methodology, D.S., Y.S. and G.S.C.; validation, W.Z., H.N. and Z.Y.; formal analysis, D.S., Y.S. and G.S.C.; investigation, W.Z., H.N. and Z.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
This is a pure theoretical analysis paper, so no numerical data is used or derived.
Conflicts of Interest
Author Dengyue Sun was employed by the company Sun Consult. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Zheng, Y.; Wang, S.; Zhang, P.; Xu, T.; Zhuo, J. Application of Nondestructive Testing Technology in Quality Evaluation of Plain Concrete and RC Structures in Bridge Engineering: A Review. Buildings 2022, 12, 843. [Google Scholar] [CrossRef]
- Liu, Y.; Xu, H.; Ma, X.; Wang, D.; Huang, X. Study on Impact–Echo Response of Concrete Column near the Edge: Principle of Impact–Echo Method. Appl. Sci. 2023, 13, 5590. [Google Scholar] [CrossRef]
- ASTM International. ASTM C1383-15: Standard Test Method for Measuring the P-Wave Speed and the Thickness of Concrete Plates Using the Impact-Echo Method; ASTM International: West Conshohocken, PA, USA, 2015. [Google Scholar] [CrossRef]
- ASTM International. ASTM C215-14: Standard Test Method for Fundamental Transverse, Longitudinal, and Torsional Resonant Frequencies of Concrete Specimens; ASTM International: West Conshohocken, PA, USA, 2014. [Google Scholar] [CrossRef]
- ACI Committee 228. ACI 228.2R-13: Report on Nondestructive Test Methods for Evaluation of Concrete in Structures; American Concrete Institute: Farmington Hills, MI, USA, 2013. [Google Scholar]
- Sajid, S.; Chouinard, L.; Carino, N. Condition Assessment of Concrete Plates Using Impulse-Response Test with Affinity Propagation and Homoscedasticity. Mech. Syst. Signal Process. 2022, 178, 109289. [Google Scholar] [CrossRef]
- Carino, N.J. The Impact-Echo Method: An Overview. Building and Fire Research Laboratory; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2001. [Google Scholar]
- Liu, J.; He, X.; He, Y.; Zhong, J.; Xie, J. Detecting the Defects in Concrete Components with Impact-Echo Method. In Proceedings of the Arch’13, Trogir-Split, Croatia, 2–4 October 2013; pp. 855–868. [Google Scholar]
- Jin, J.; Moreno, M.G.; Riviere, J.; Shokouhi, P. Impact-Based Nonlinear Acoustic Testing for Characterizing Distributed Damage in Concrete. J. Nondestruct. Eval. 2017, 36, 51. [Google Scholar] [CrossRef]
- Malone, C.; Sun, H.; Zhu, J. Nonlinear Impact-Echo Test for Quantitative Evaluation of ASR Damage in Concrete. J. Nondestruct. Eval. 2023, 42, 93. [Google Scholar] [CrossRef]
- Pressmair, N.; Brosch, F.; Hammerl, M.; Kromoser, B. Non-Linear Material Modelling Strategy for Conventional and High-Performance Concrete Assisted by Testing. Cem. Concr. Res. 2022, 161, 106933. [Google Scholar] [CrossRef]
- Ju, J.; Tian, X.; Zhao, W.; Yang, Y. Detection and Identification for Void of Concrete Structure by Air-Coupled Impact-Echo Method. Sensors 2023, 23, 6018. [Google Scholar] [CrossRef]
- Soedel, W. Vibrations of Shells and Plates, 3rd ed.; Marcel Dekker: New York, NY, USA; Taylor & Francis e-Library: Online, 2004. [Google Scholar]
- Mitchell, A.K.; Hazell, C.R. A Simple Frequency Formula for Clamped Rectangular Plates. J. Sound Vib. 1987, 118, 271–281. [Google Scholar] [CrossRef]
- Wang, C.M. Natural Frequencies Formula for Simply Supported Mindlin Plates. J. Vib. Acoust. 1994, 116, 536–540. [Google Scholar] [CrossRef]
- Liew, K.M.; Xiang, Y.; Kitipornchai, S. Research on Thick Plate Vibration: A Literature Survey. J. Sound Vib. 1995, 180, 163–176. [Google Scholar] [CrossRef]
- Xing, Y.; Liu, B. Characteristic Equations and Closed-Form Solution for Free Vibrations of Rectangular Mindlin Plates. Acta Mech. Solida Sin. 2009, 22, 125–136. [Google Scholar] [CrossRef]
- Senjanović, I.; Vladimir, N.; Tomić, M. An Advanced Theory of Moderately Thick Plate Vibrations. J. Sound Vib. 2013, 332, 1868–1880. [Google Scholar] [CrossRef]
- Sansalone, M.; Streett, W.B. Impact-Echo: Nondestructive Evaluation of Concrete and Masonry; Bullbrier Press: Jersey Shore, PA, USA, 1997. [Google Scholar]
- Dethof, F.; Keßler, S. Explaining Impact-Echo Geometry Effects Using Modal Analysis Theory and Numerical Simulations. NDT E Int. 2024, 143, 103035. [Google Scholar] [CrossRef]
- Cao, R.; Agrawal, A.K. Defect Detection of Concrete Structures Through Sounding Data Analytics. In Proceedings of the 29th International Conference on Structural Health Monitoring of Intelligent Infrastructure, St. Louis, MO, USA, 4–7 August 2019. [Google Scholar]
- Nowotarski, P.; Dubas, S.; Milwicz, R. Review of the Air-Coupled Impact-Echo Method for Non-Destructive Testing. IOP Conf. Ser. Mater. Sci. Eng. 2017, 245, 032098. [Google Scholar] [CrossRef]
- Van Den Abeele, K.E.A.; Carmeliet, J.; Ten Cate, J.A.; Johnson, P.A. Nonlinear Elastic Wave Spectroscopy (NEWS) Techniques to Discern Material Damage. Part I: Nonlinear Wave Modulation Spectroscopy (NWMS). J. Res. Nondestruct. Eval. 2000, 12, 17–30. [Google Scholar] [CrossRef]
- Van Den Abeele, K.E.A.; Carmeliet, J.; Ten Cate, J.A.; Johnson, P.A. Nonlinear Elastic Wave Spectroscopy (NEWS) Techniques to Discern Material Damage. Part II: Single-Mode Nonlinear Resonance Acoustic Spectroscopy. J. Res. Nondestruct. Eval. 2000, 12, 31–42. [Google Scholar] [CrossRef]
- Ten Cate, J.A.; Smith, E.; Byers, L.; Shankland, T. Slow Dynamics Experiments in Solids with Nonlinear Mesoscopic Elasticity. AIP Conf. Proc. 2000, 306, 303–306. [Google Scholar] [CrossRef]
- Bentahar, M.; El Aqra, H.; El Guerjouma, R.; Griffa, M.; Scalerandi, M. Hysteretic Elasticity in Damaged Concrete: Quantitative Analysis of Slow and Fast Dynamics. Phys. Rev. B 2006, 73, 014116. [Google Scholar] [CrossRef]
- Eiras, J.N.; Payan, C.; Rakotonarivo, S.; Garnier, V. Damage Detection and Localization from Linear and Nonlinear Global Vibration Features in Concrete Slabs Subjected to Localized Thermal Damage. Struct. Health Monit. 2020, 20, 567–579. [Google Scholar] [CrossRef]
- Veksler, N.D. Resonance Acoustic Spectroscopy; Springer Science & Business Media: Berlin, Germany, 2012; ISBN 3642847951/9783642847950. [Google Scholar]
- Bittner, J.A.; Popovics, J.S. Transient Nonlinear Vibration Characterization of Building Materials in Sequential Impact Scale Experiments. Front. Built Environ. 2022, 8, 949484. [Google Scholar] [CrossRef]
- Chen, J.; Kim, J.-Y.; Kurtis, K.E.; Jacobs, L.J. Theoretical and Experimental Study of the Nonlinear Resonance Vibration of Cementitious Materials with an Application to Damage Characterization. J. Acoust. Soc. Am. 2011, 130, 2728–2737. [Google Scholar] [CrossRef] [PubMed]
- Livingston, R.; McMorris, N.; Lijeron, C.; Made, C. Non-Linear Frequency Domain Techniques for Processing Impact Echo Signals for Distributed Damage in Concrete. In Proceedings of the 2nd International Conference on Non-Destructive Testing in Civil Engineering (NDT-CE), Nantes, France, 30 June–3 July 2009. [Google Scholar]
- Zheng, Y.; Maev, R.G.; Solodov, I.Y. Nonlinear Acoustic Applications for Material Characterization: A Review. Can. J. Phys. 1999, 77, 927–967. [Google Scholar] [CrossRef]
- Park, S.-J.; Yim, H.J.; Kwak, H.-G. Nonlinear Resonance Vibration Method to Estimate the Damage Level on Heat-Exposed Concrete. Fire Saf. J. 2014, 69, 36–42. [Google Scholar] [CrossRef]
- Kim, J.H.; Park, S.-J.; Yim, H.J. Nonlinear Resonance Vibration Assessment to Evaluate the Freezing and Thawing Resistance of Concrete. Materials 2019, 12, 325. [Google Scholar] [CrossRef] [PubMed]
- Payan, C.; Ulrich, T.J.; Bas, P.Y.L.; Saleh, T.; Guimaraes, M. Quantitative Linear and Nonlinear Resonance Inspection Techniques and Analysis for Material Characterization: Application to Concrete Thermal Damage. J. Acoust. Soc. Am. 2014, 136, 537–546. [Google Scholar] [CrossRef] [PubMed]
- Dahlena, U.; Ryden, N.; Jakobsson, A. Damage Identification in Concrete Using Impact Non-Linear Reverberation Spectroscopy. NDT E Int. 2015, 75, 15–25. [Google Scholar] [CrossRef]
- Benipal, G.; Singh, A.K. Constitutive modeling of concrete: An overview. Asian J. Civ. Eng. 2005, 6, 211–246. [Google Scholar]
- Spalvier, A.; Domenech, L.; Pérez, N.; Cetrangolo, G.P. Nonlinear-Elastic Characterization of Cement-Based Materials Under Uniaxial Stress: A Comparison Between Ultrasonic and Resonance Techniques. Constr. Build. Mater. 2022, 331, 127211. [Google Scholar] [CrossRef]
- Malone, C.; Zhu, J.; Hu, J.; Snyder, A.; Giannini, E. Evaluation of Alkali-Silica Reaction Damage in Concrete Using Linear and Nonlinear Resonance Techniques. Constr. Build. Mater. 2021, 303, 124538. [Google Scholar] [CrossRef]
- Hafiz, A.; Schumacher, T.; Raad, A. A Self-Referencing Non-Destructive Test Method to Detect Damage in Reinforced Concrete Bridge Decks Using Nonlinear Vibration Response Characteristics. Constr. Build. Mater. 2022, 318, 125924. [Google Scholar] [CrossRef]
- Dvořák, R.; Topolár, L. Effect of Hammer Type on Generated Mechanical Signals in Impact-Echo Testing. Materials 2021, 14, 606. [Google Scholar] [CrossRef] [PubMed]
- Guyer, R.A.; McCall, K.R.; Boitnott, G.N. Hysteresis, Discrete Memory, and Nonlinear Wave Propagation in Rock: A New Paradigm. Phys. Rev. Lett. 1995, 74, 3491–3494. [Google Scholar] [CrossRef]
- Breslavsky, I.; Amabili, M.; Legrand, M. Nonlinear Vibrations of Thin Hyperelastic Plates. J. Sound Vib. 2014, 333, 4668–4681. [Google Scholar] [CrossRef]
- Breslavsky, I.; Avramov, K. Two Modes Nonresonant Interaction for Rectangular Plate with Geometrical Nonlinearity. Nonlinear Dyn. 2012, 69, 285–294. [Google Scholar] [CrossRef]
- Amabili, M. Nonlinear Vibrations and Stability of Shells and Plates; Cambridge University Press: New York, NY, USA, 2008. [Google Scholar] [CrossRef]
- Sathyamoorthy, M. Nonlinear Vibration Analysis of Plates: A Review and Survey of Current Developments. Appl. Mech. Rev. 1987, 40, 1553–1561. [Google Scholar] [CrossRef]
- Breslavsky, I.D.; Amabili, M.; Legrand, M. Physically and Geometrically Non-Linear Vibrations of Thin Rectangular Plates. Int. J. Non-Linear Mech. 2014, 58, 30–40. [Google Scholar] [CrossRef]
- Hao, Y.X.; Chen, L.H.; Zhang, W.; Lei, J.G. Nonlinear Oscillations, Bifurcations and Chaos of Functionally Graded Materials Plate. J. Sound Vib. 2008, 312, 862–892. [Google Scholar] [CrossRef]
- Yang, J.H.; Liu, B.D. Nonlinear Dynamics Behaviors of a Composite Laminated Cantilevered Plate under Transverse Excitation. IOP Conf. Ser. Mater. Sci. Eng. 2018, 423, 012147. [Google Scholar] [CrossRef]
- Rand, R.H. Lecture Notes on Nonlinear Vibrations; Cornell University: Ithaca, NY, USA, 2012; Available online: https://ecommons.cornell.edu/handle/1813/28989 (accessed on 1 October 2025).
- Hu, H. Solution of a Quadratic Nonlinear Oscillator by the Method of Harmonic Balance. J. Sound Vib. 2006, 293, 462–468. [Google Scholar] [CrossRef]
- Mondal, M.M.H.; Molla, M.H.U.; Razzak, M.A.; Alam, M.S. A New Analytical Approach for Solving Quadratic Nonlinear Oscillators. Alex. Eng. J. 2017, 56, 629–634. [Google Scholar] [CrossRef][Green Version]
- Mickens, R.E. Oscillations in Planar Dynamic Systems; World Scientific: Singapore, 1996. [Google Scholar] [CrossRef]
- Liu, C.-S.; Kuo, C.-L.; Chang, C.-W. Linearized Harmonic Balance Method for Seeking the Periodic Vibrations of Second- and Third-Order Nonlinear Oscillators. Mathematics 2025, 13, 162. [Google Scholar] [CrossRef]
- Yusry, O.; El-Dib, A. A Review of the Frequency-Amplitude Formula for Nonlinear Oscillators and Its Advancements. J. Low Freq. Noise Vib. Act. Control 2024, 43, 1032–1064. [Google Scholar] [CrossRef]
- El-Dib, Y.O. Insightful and Comprehensive Formularization of Frequency–Amplitude Formula for Strong or Singular Nonlinear Oscillators. J. Low Freq. Noise Vib. Act. Control 2023, 42, 89–109. [Google Scholar] [CrossRef]
- He, J.H. On the Frequency–Amplitude Formulation for Nonlinear Oscillators with General Initial Conditions. Int. J. Appl. Comput. Math. 2021, 7, 111. [Google Scholar] [CrossRef]
- He, J.H. Homotopy Perturbation Technique. Comput. Methods Appl. Mech. Eng. 1999, 178, 257–262. [Google Scholar] [CrossRef]
- Kim, R.; Woo, U.; Shin, M.; Ahn, E.; Choi, H. Evaluation of self-healing in concrete using linear and nonlinear resonance spectroscopy. Constr. Build. Mater. 2022, 335, 127492. [Google Scholar] [CrossRef]
- Oh, S.; Kim, T.; Song, J. Bouc–Wen Class Models Considering Hysteresis Mechanism of RC Columns in Nonlinear Dynamic Analysis. Int. J. Non-Linear Mech. 2023, 148, 104263. [Google Scholar] [CrossRef]
- Ma, Y.; Wu, Z.; Cheng, X.; Sun, Z.; Chen, X. Parameter Identification of Hysteresis Model of Reinforced Concrete Columns Considering Shear Action. Structures 2023, 47, 93–104. [Google Scholar] [CrossRef]
- Cusatis, G. Strain-Rate Effects on Concrete Behavior. Int. J. Impact Eng. 2011, 38, 162–170. [Google Scholar] [CrossRef]
- Roesler, J.; Paulino, G.H.; Park, K.; Gaedicke, C. Concrete Fracture Prediction Using Bilinear Softening. Cem. Concr. Compos. 2007, 29, 300–312. [Google Scholar] [CrossRef]
- Zhang, P.; Wang, S.; He, L. Modeling and Simulation of the Hysteretic Behavior of Concrete Under Cyclic Tension–Compression Using the Smeared Crack Approach. Materials 2023, 16, 4442. [Google Scholar] [CrossRef]
- Balasubramanian, P.; Franchini, G.; Ferrari, G.; Painter, B.; Karazis, K.; Amabili, M. Nonlinear Vibrations of Beams with Bilinear Hysteresis at Supports: Interpretation of Experimental Results. J. Sound Vib. 2021, 499, 115998. [Google Scholar] [CrossRef]
- Xiao, J.; Pham, T.; Ding, T.; Wang, C. Polygonal Loop Model for Hysteretic Behaviour of Frame Structures with Recycled Aggregate Concrete. Eur. J. Environ. Civ. Eng. 2016, 20, 1083–1105. [Google Scholar] [CrossRef]
- Zhao, G.; Zhang, M.; Li, Y.; Li, D. The Hysteresis Performance and Restoring Force Model for Corroded Reinforced Concrete Frame Columns. J. Eng. 2016, 2016, 7615385. [Google Scholar] [CrossRef]
- Dai, K.; Yu, X.; Jiang, Z.; Wang, D.; Qian, K. Hysteretic Model for Corroded Reinforced Concrete Columns Retrofitted with FRP. Constr. Build. Mater. 2023, 380, 131207. [Google Scholar] [CrossRef]
- Sengupta, P.; Li, B. Hysteresis Modeling of Reinforced Concrete Structures: State of the Art. ACI Struct. J. 2017, 114, 25–38. [Google Scholar] [CrossRef]
- Tarawneh, A.N.; Majdalaweyh, S.A.; Mahasneh, B.Z. The Effect of Using Hysteresis Models (Bilinear and Modified Clough) on Seismic Demands of Single Degree of Freedom Systems. Am. J. Appl. Sci. 2016, 13, 913–923. [Google Scholar] [CrossRef]
- Attinger, R.; Kluegel, J.-U. A Model for the Hysteresis of Concrete to Describe the Cyclic Fatigue of Reinforced Concrete Structures During an Earthquake. In Proceedings of the 20th International Conference on Structural Mechanics in Reactor Technology (SMiRT 20), Espoo, Finland, 9–14 August 2009. Division V, Paper 1632. [Google Scholar]
- Shaw, S.W.; Holmes, P.J. A Periodically Forced Piecewise Linear Oscillator. J. Sound Vib. 1983, 90, 129–155. [Google Scholar] [CrossRef]
- Teich, M.C.; Keilson, S.E.; Khanna, S.M. Models of Nonlinear Vibration. II. Oscillator with Bilinear Stiffness. Acta Otolaryngol. 1989, 108, 249–256. [Google Scholar] [CrossRef]
- Kim, Y.B.; Noah, S.T. Stability and Bifurcation Analysis of Oscillators with Piecewise-Linear Characteristics: A General Approach. J. Appl. Mech. 1991, 58, 545–553. [Google Scholar] [CrossRef]
- Miles, R.N. Spectral Response of a Bilinear Oscillator. J. Sound Vib. 1993, 163, 319–326. [Google Scholar] [CrossRef]
- Natsiavas, S. On the Dynamics of Oscillators with Bi-Linear Damping and Stiffness. Int. J. Non-Linear Mech. 1990, 25, 535–554. [Google Scholar] [CrossRef]
- Pilipchuk, V.N. Analytical Study of Vibrating Systems with Strong Non-Linearities by Employing Saw-Tooth Time Transformation. J. Sound Vib. 1996, 192, 43–64. [Google Scholar] [CrossRef]
- Pilipchuk, V.N.; Vakakis, A.F.; Azeez, M.A.F. Study of a Class of Subharmonic Motions Using a Non-Smooth Temporal Transformation (NSTT). Phys. D Nonlinear Phenom. 1997, 100, 145–164. [Google Scholar] [CrossRef]
- Makris, N.; Black, C.J. Dimensional Analysis of Bilinear Oscillators under Pulse-Type Excitations. J. Eng. Mech. 2004, 130, 1019–1031. [Google Scholar] [CrossRef]
- Khan, D.; Burdzik, R. Measurement and Analysis of Transport Noise and Vibration: A Review of Techniques, Case Studies, and Future Directions. Measurement 2023, 220, 113354. [Google Scholar] [CrossRef]
- Burdzik, R.; Khan, D. An Overview of the Current State of Knowledge and Technology on Techniques and Procedures for Signal Processing, Analysis, and Accurate Inference for Transportation Noise and Vibration. Measurement 2025, 252, 117314. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).