Study on Vibration Control Systems for Spherical Water Tanks Under Earthquake Loads
Abstract
1. Introduction
2. Materials and Methods
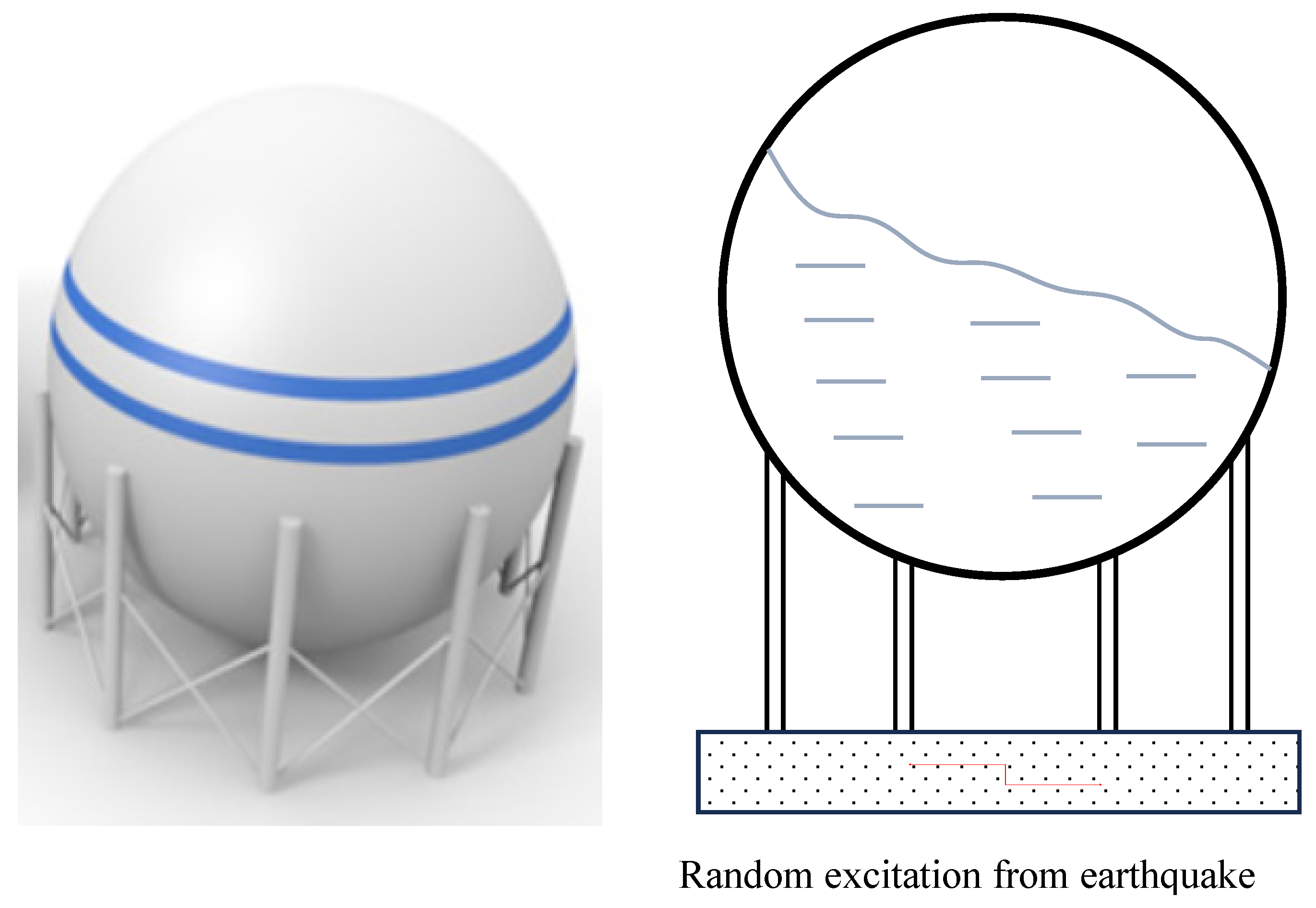
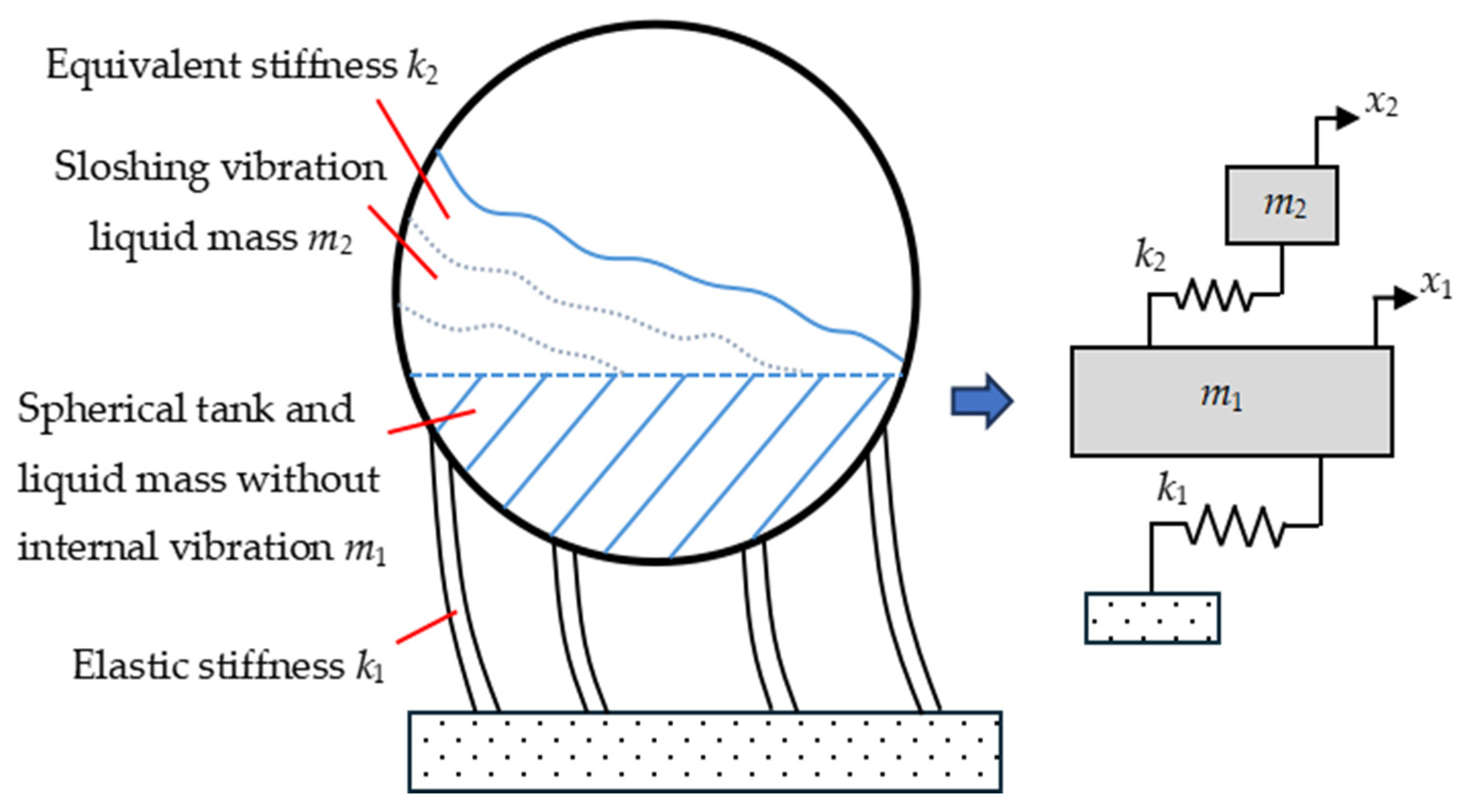
2.1. Natural Frequencies of a Spherical Water Tank
2.2. Vibration Control Device for a Spherical Water Tank
2.3. TMD Vibration Control Experiment Device for a Spherical Water Tank
2.4. Tuning of the TMD
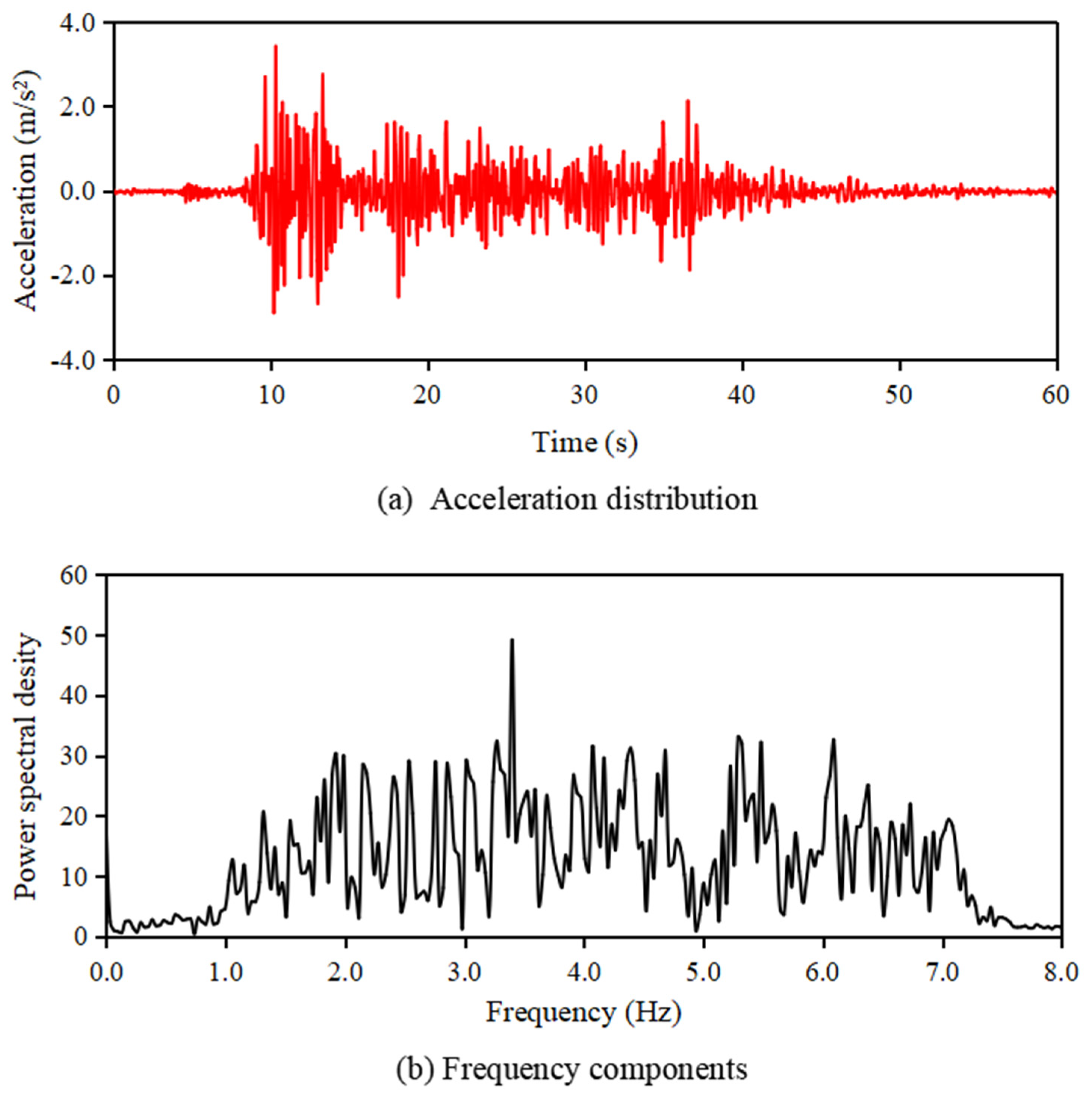
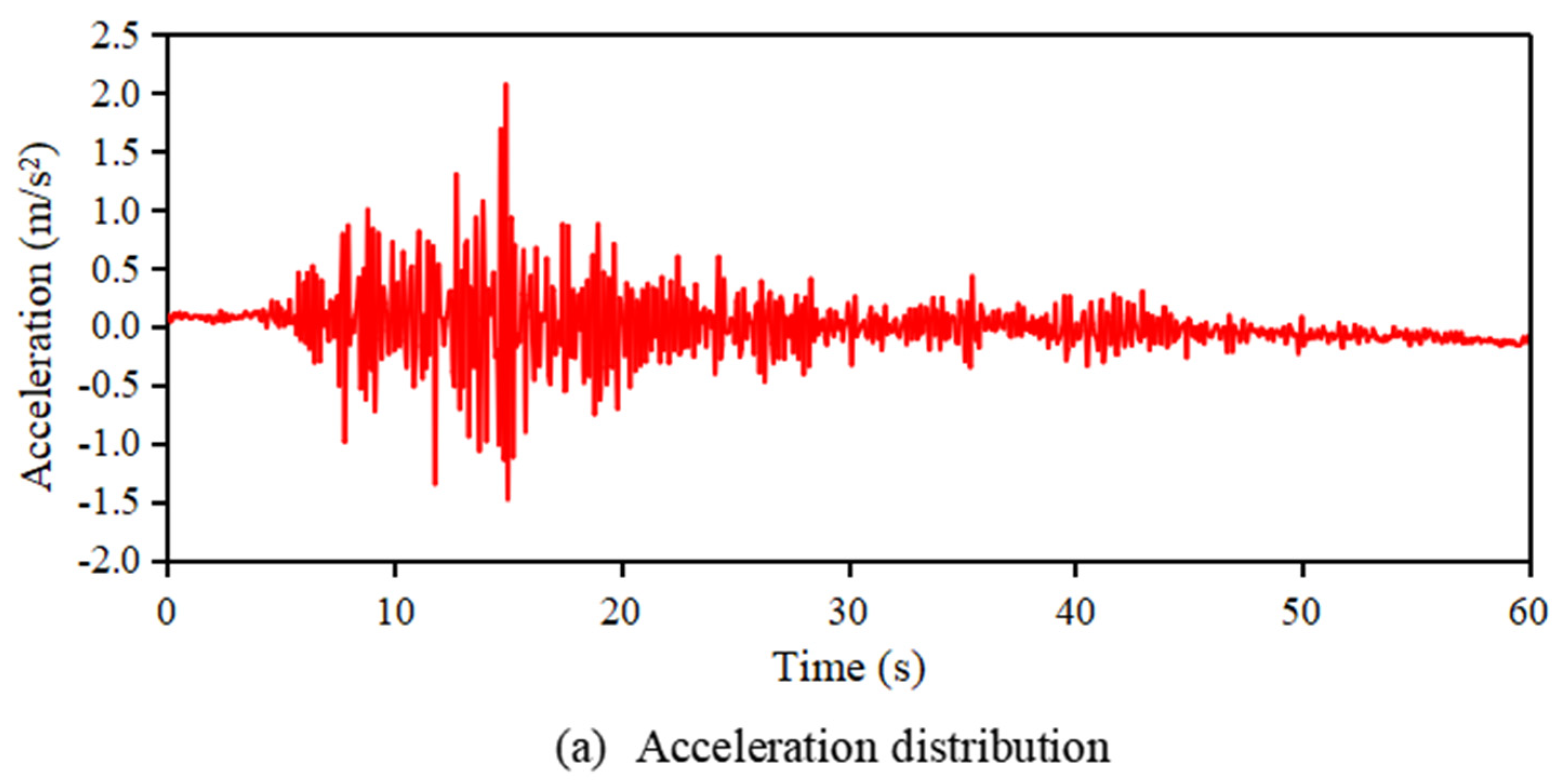
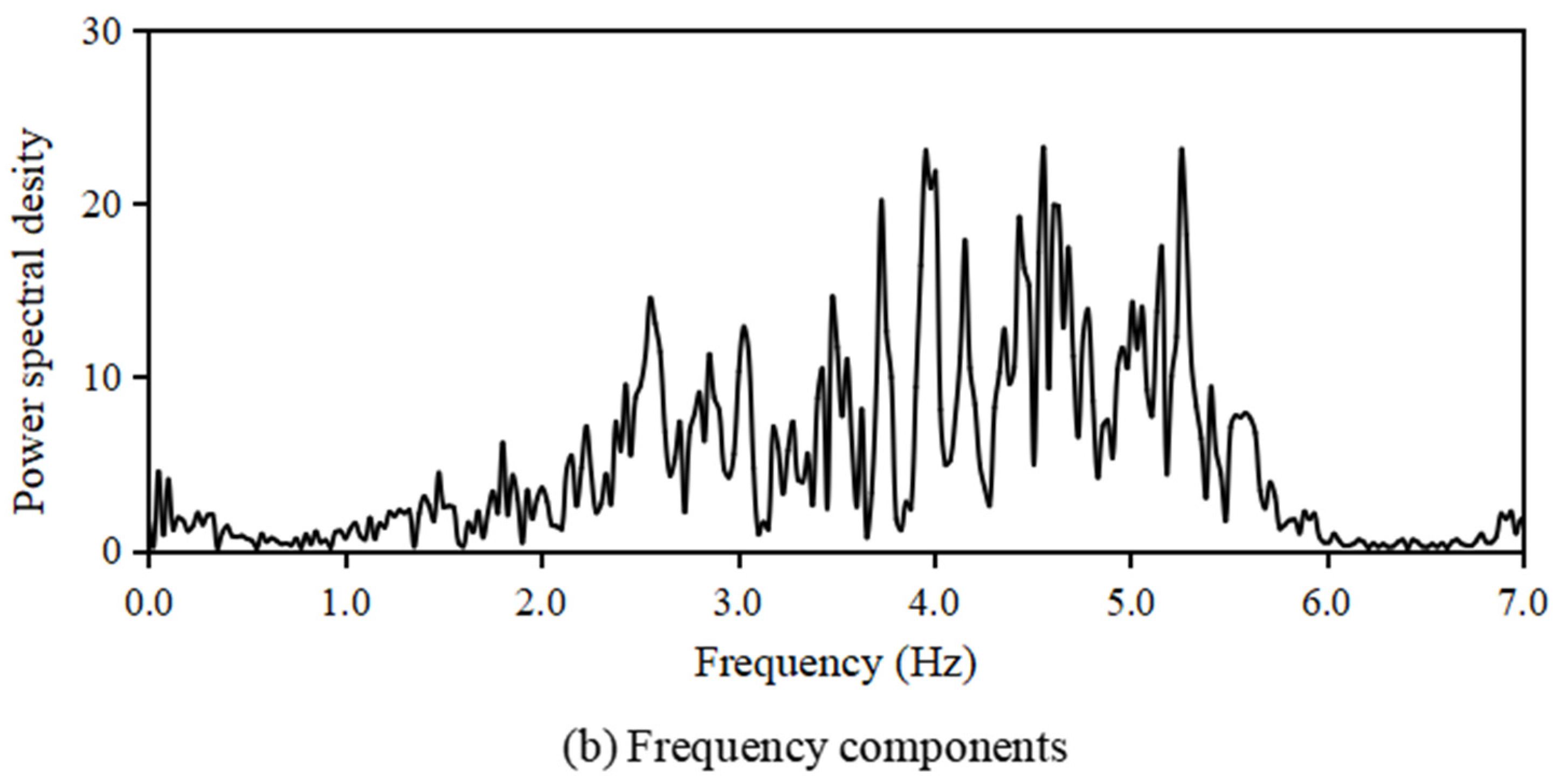
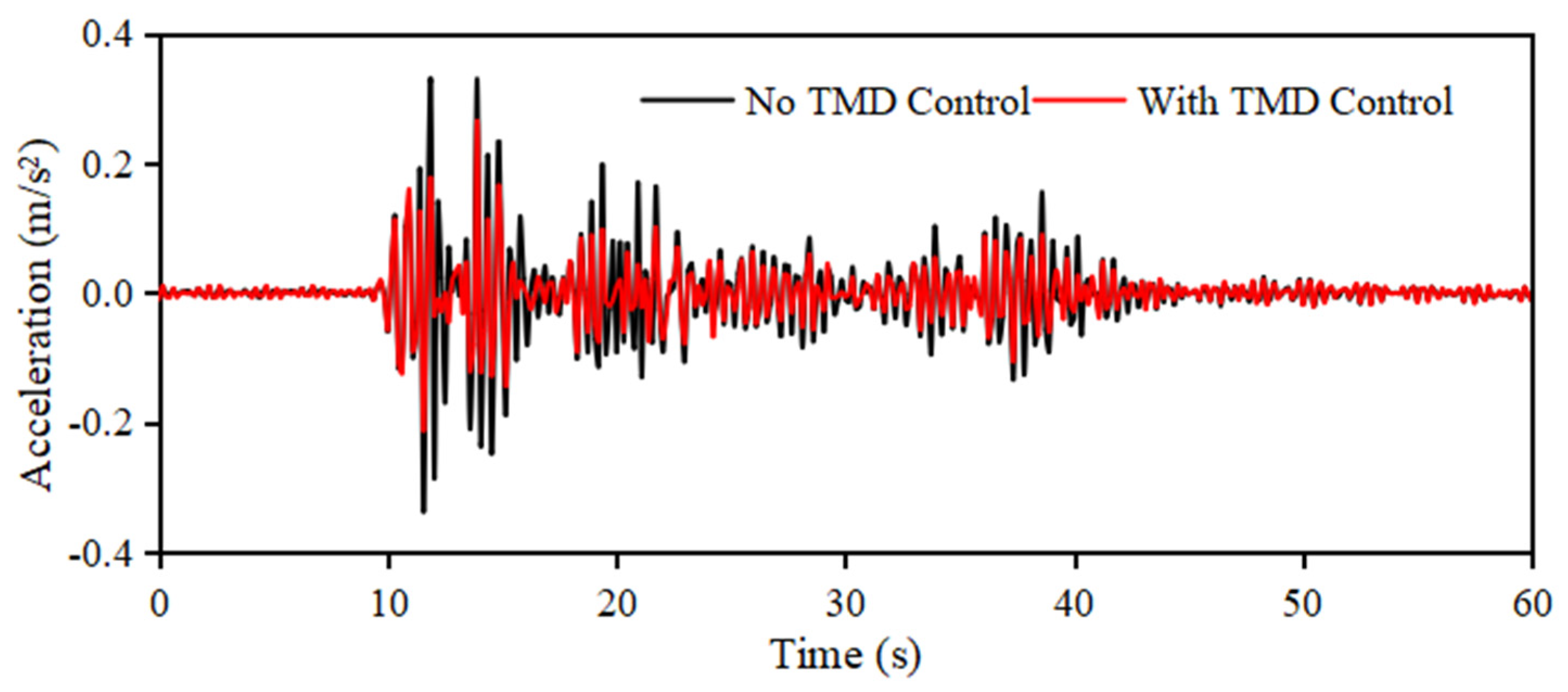
2.5. The Experimental Earthquake Excitation Signal
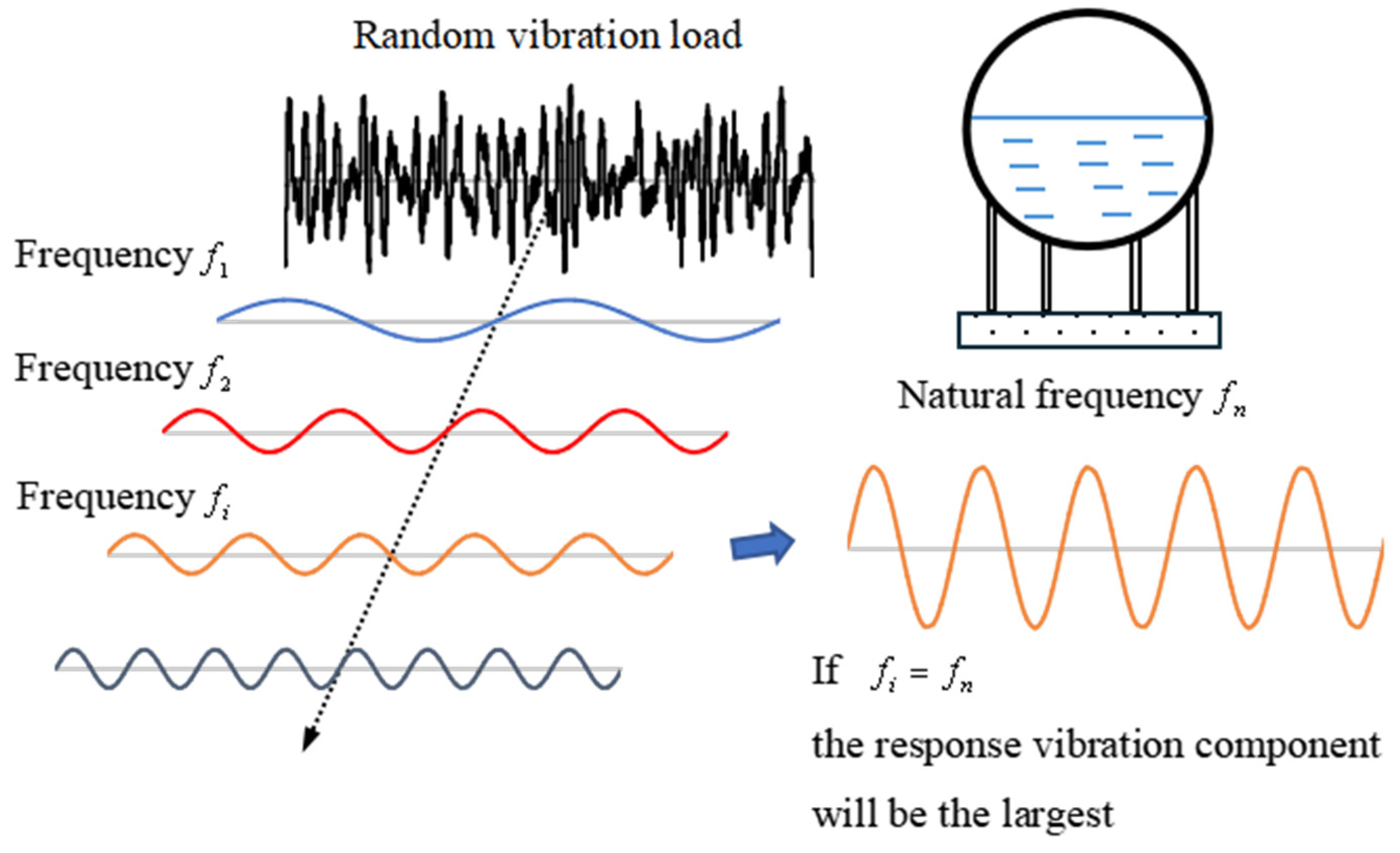
2.6. Quantitative Evaluation of Response Acceleration Due to Seismic Excitation
3. Results and Discussions
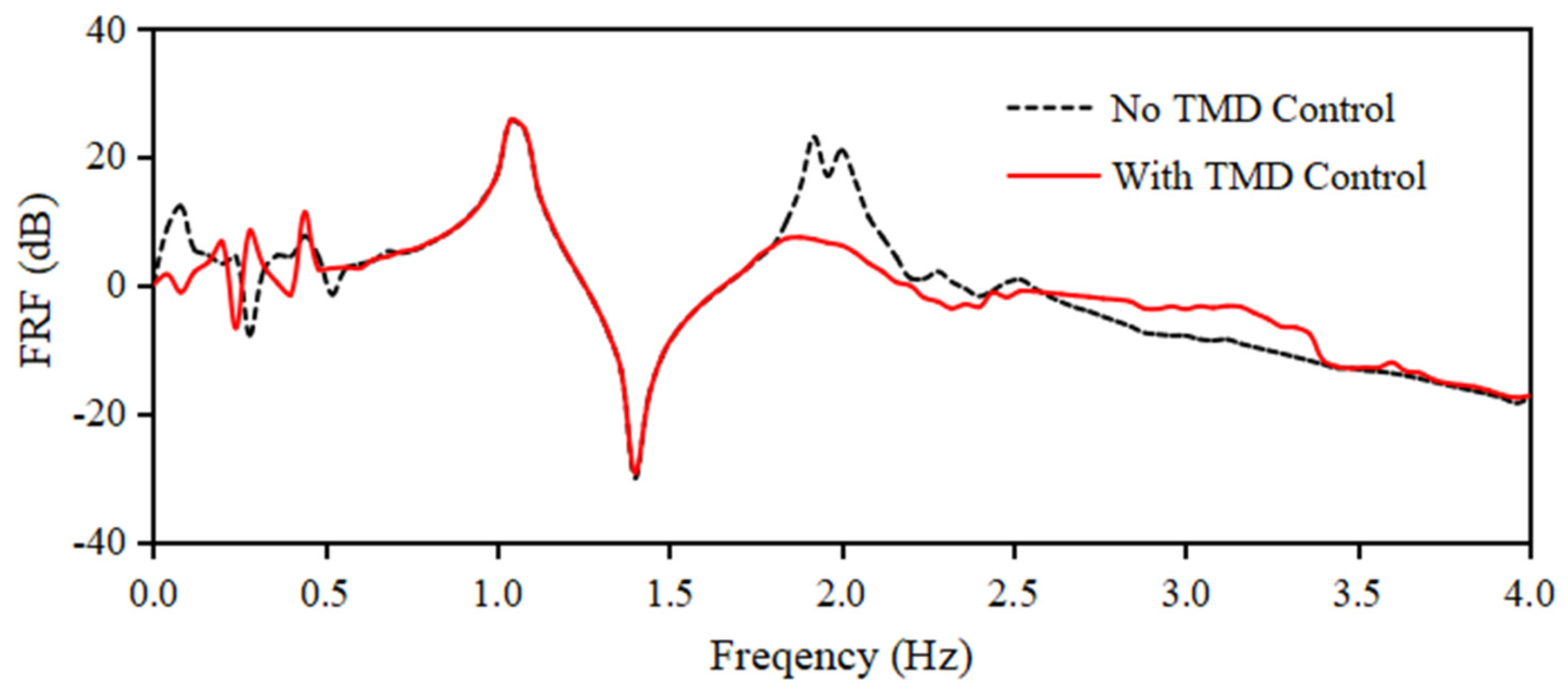
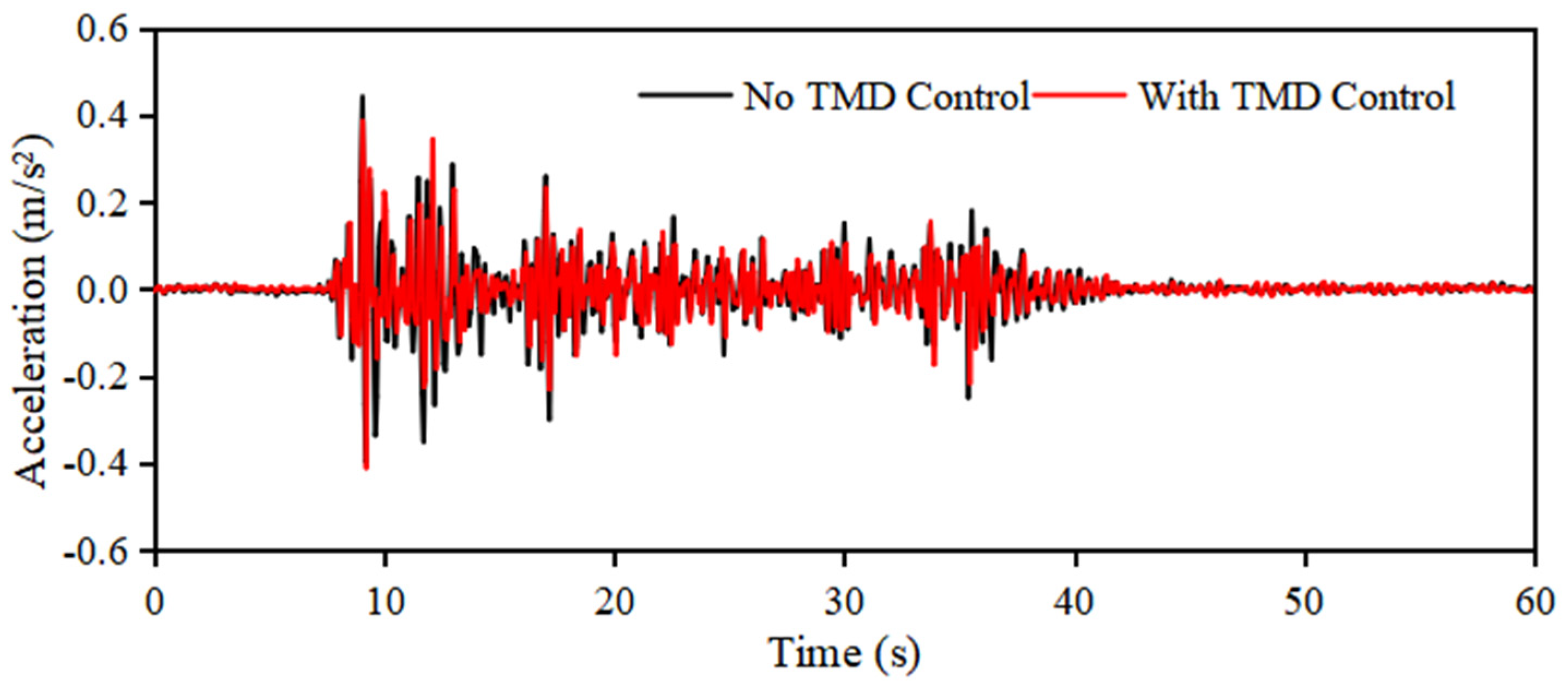
3.1. The Vibration Damping Effect of TMD
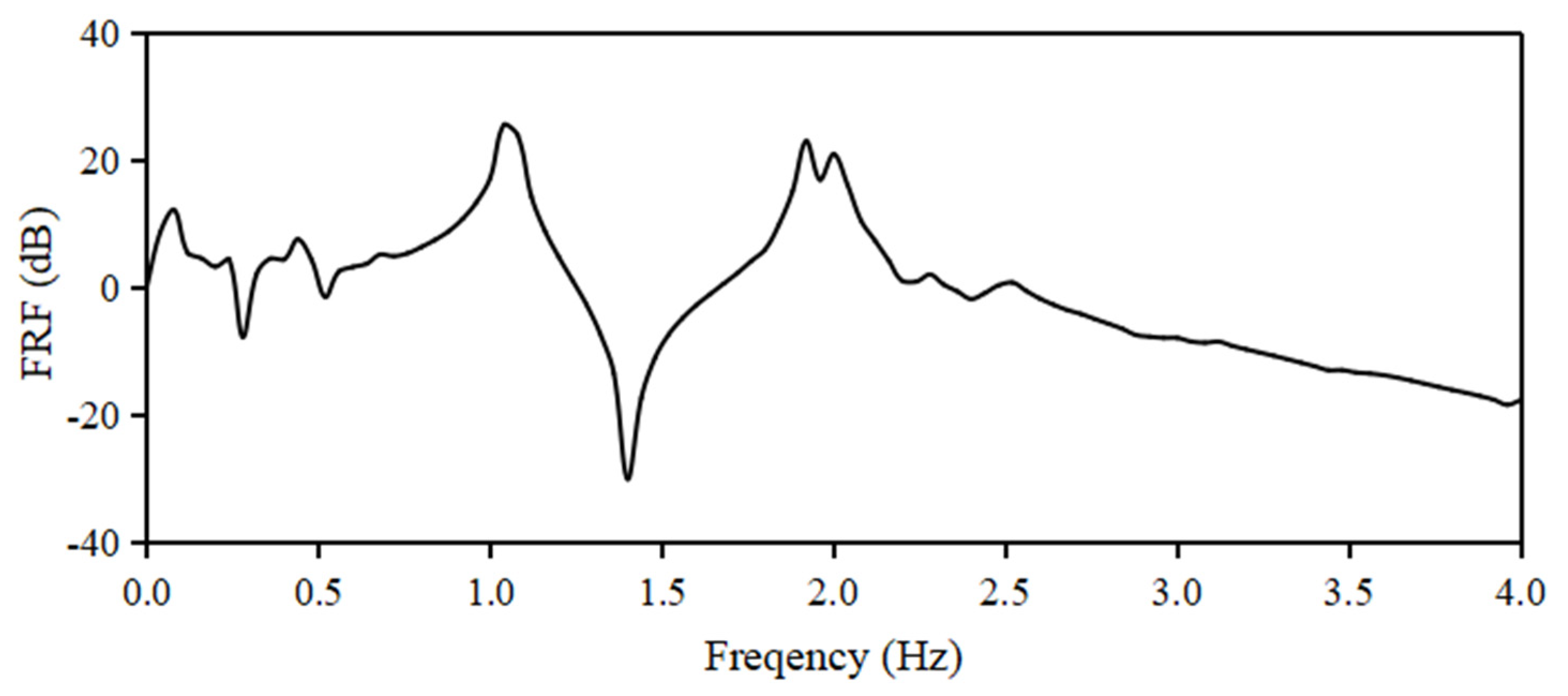
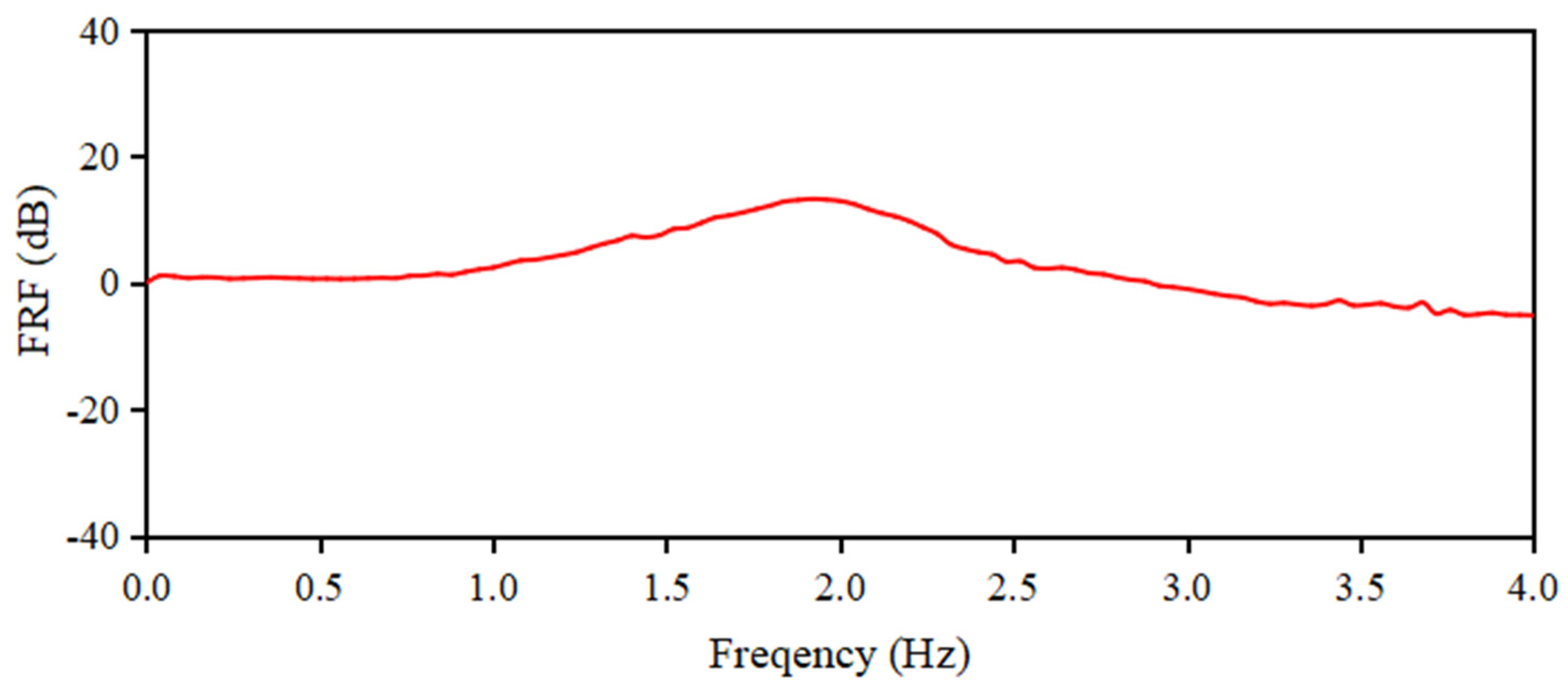
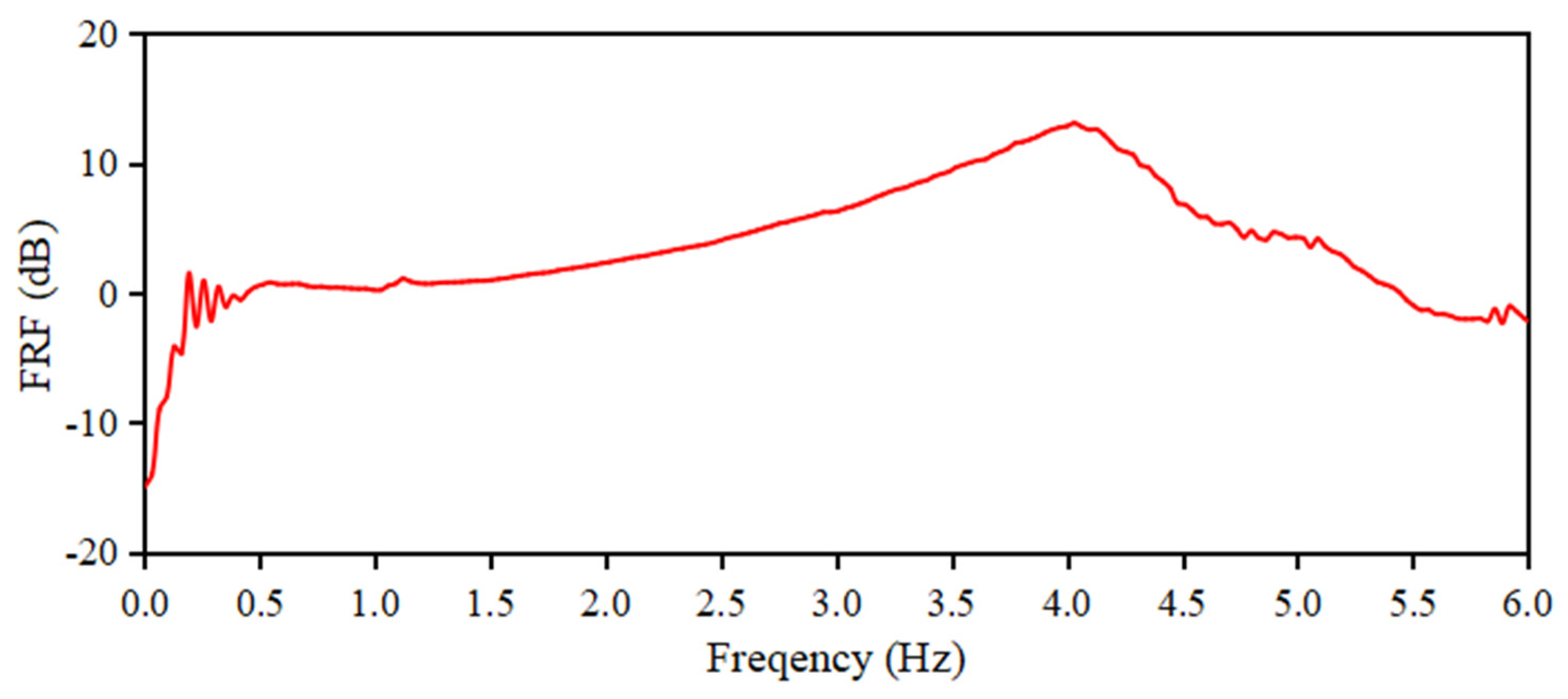
3.1.1. Natural Frequency Tuning for TMD
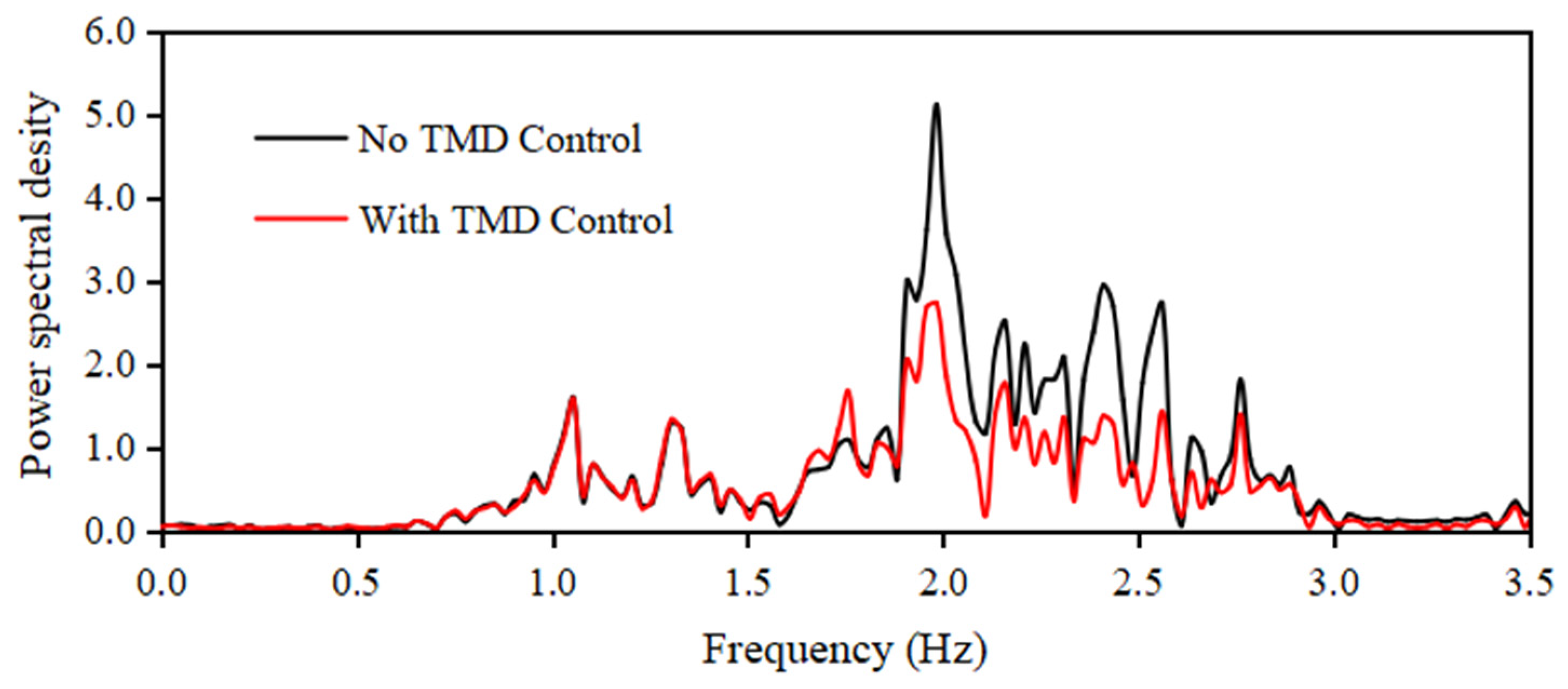
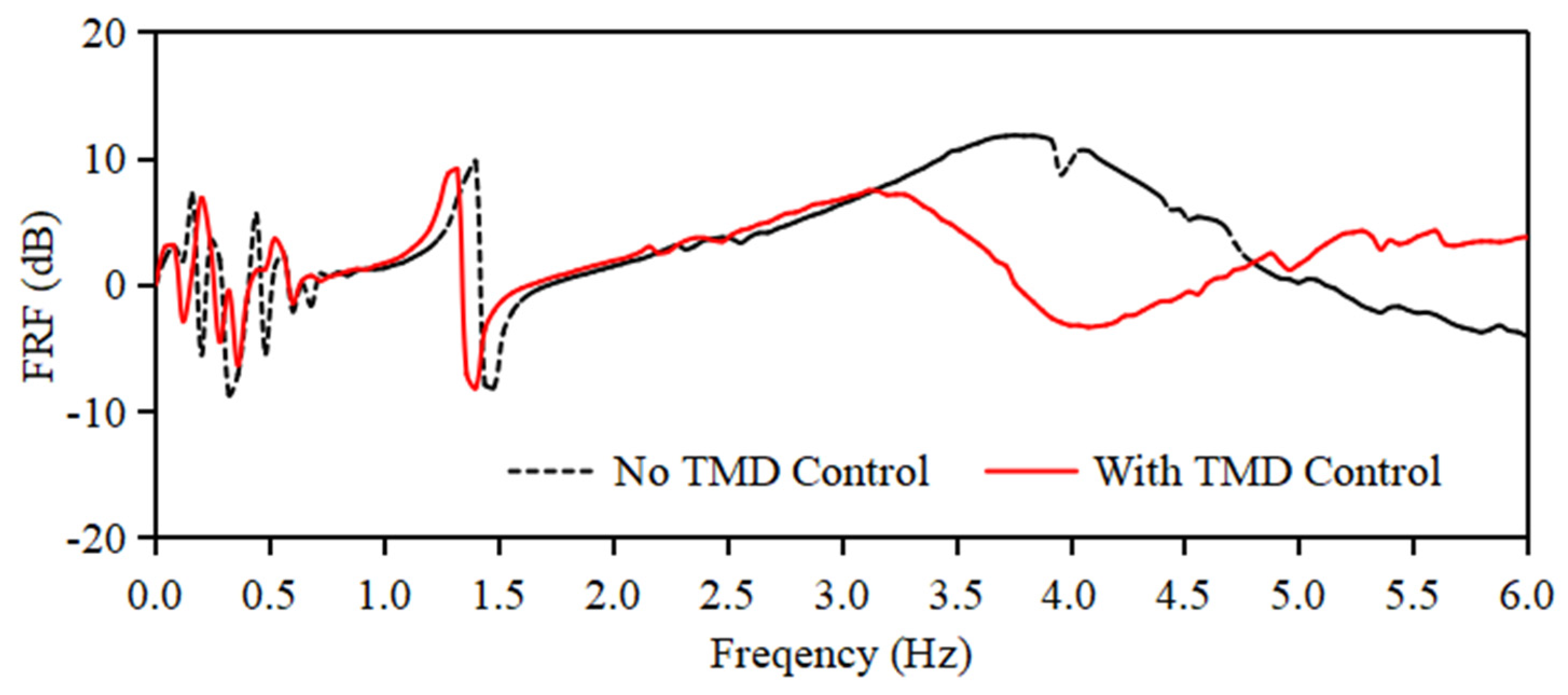
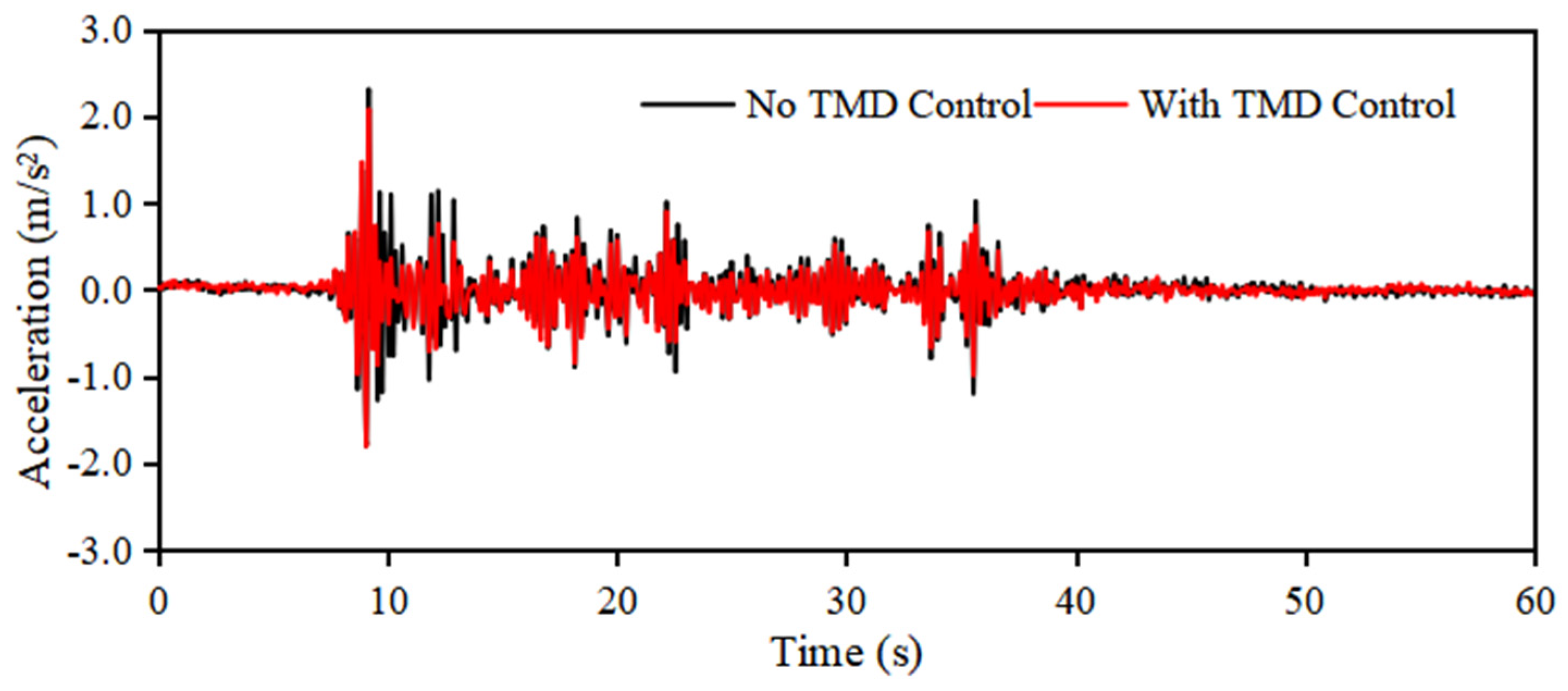
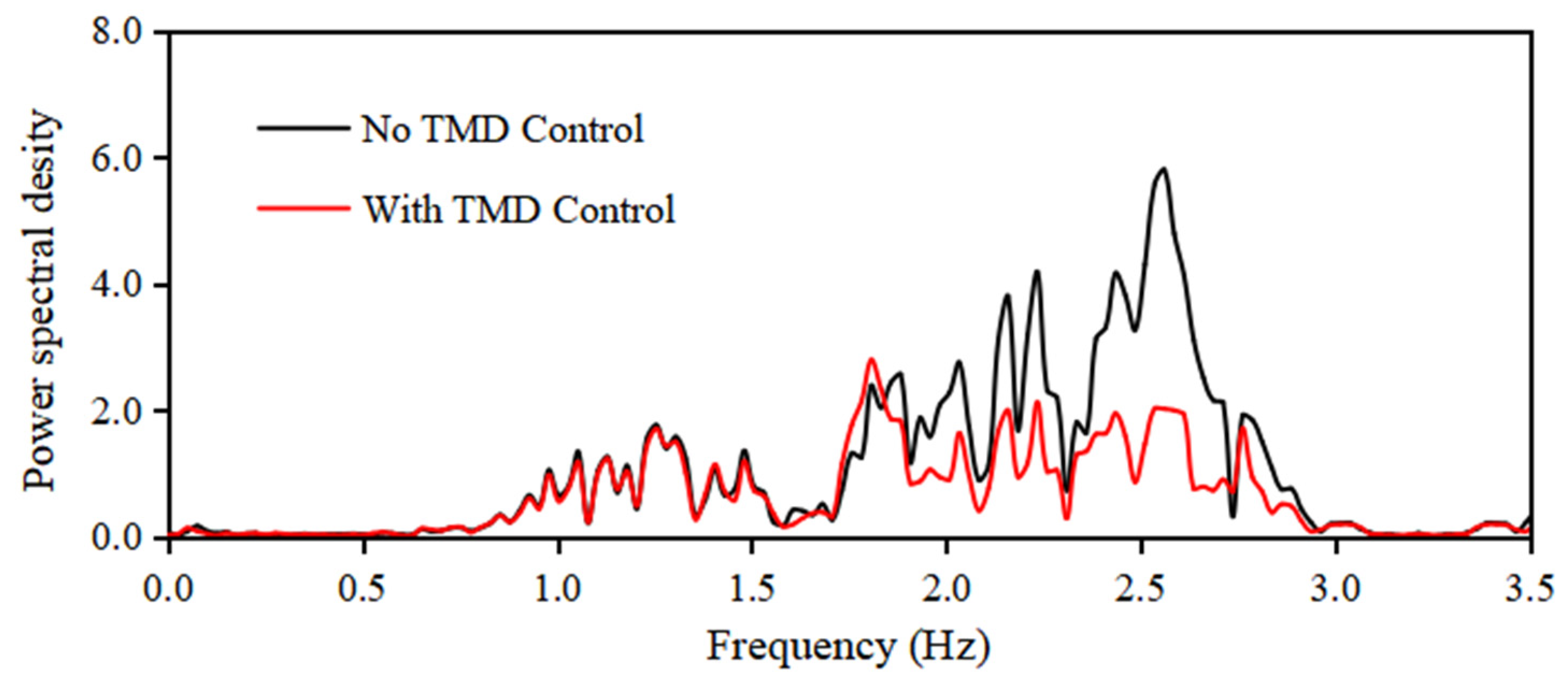
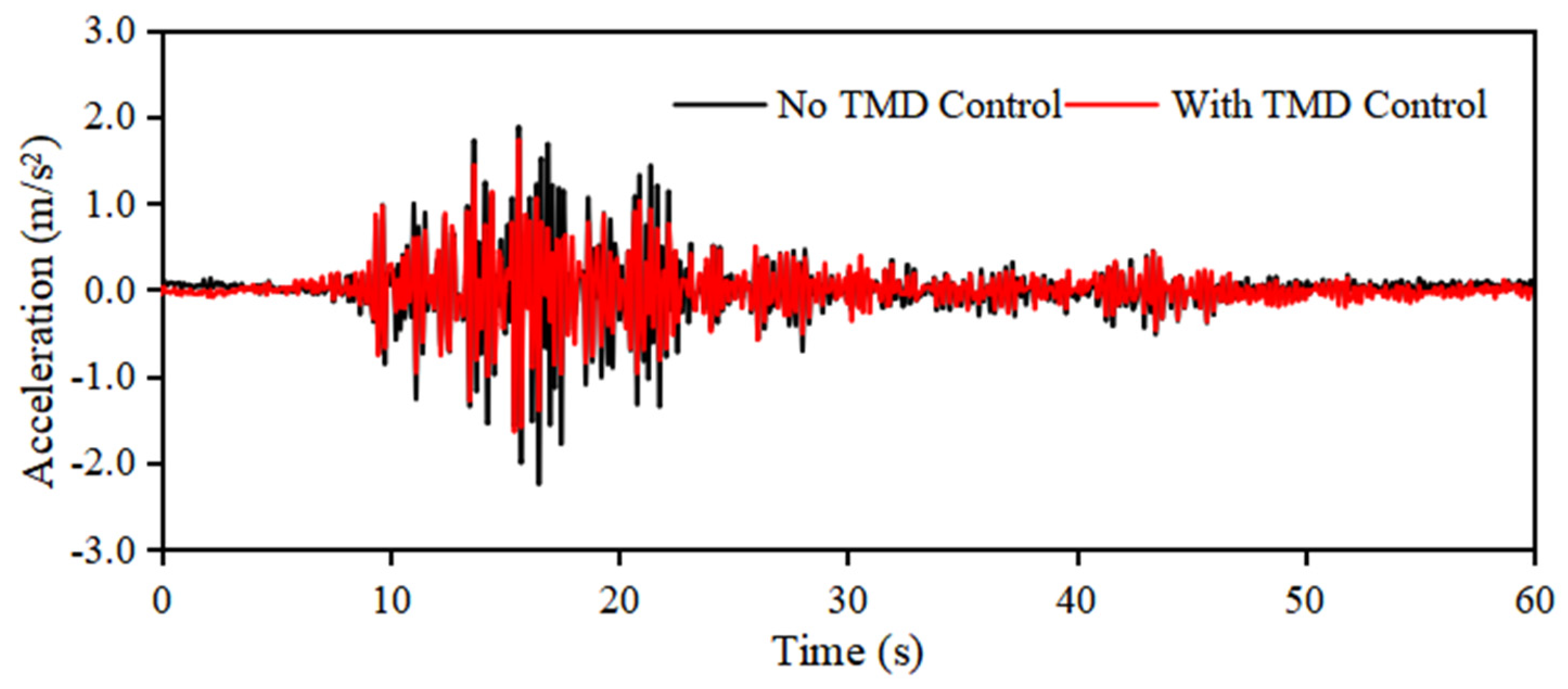
3.1.2. Vibration Control Performance of Spherical Water Tanks in a Seismic Environment
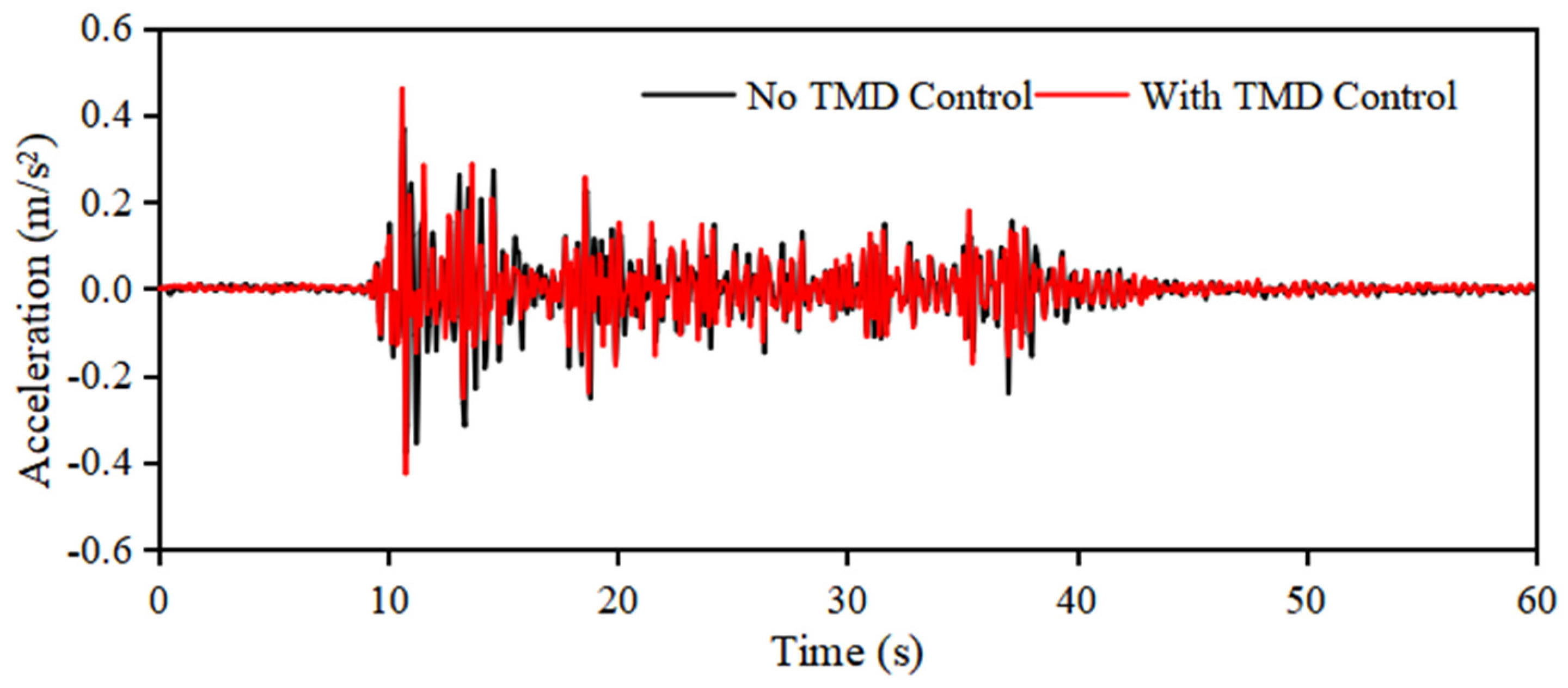
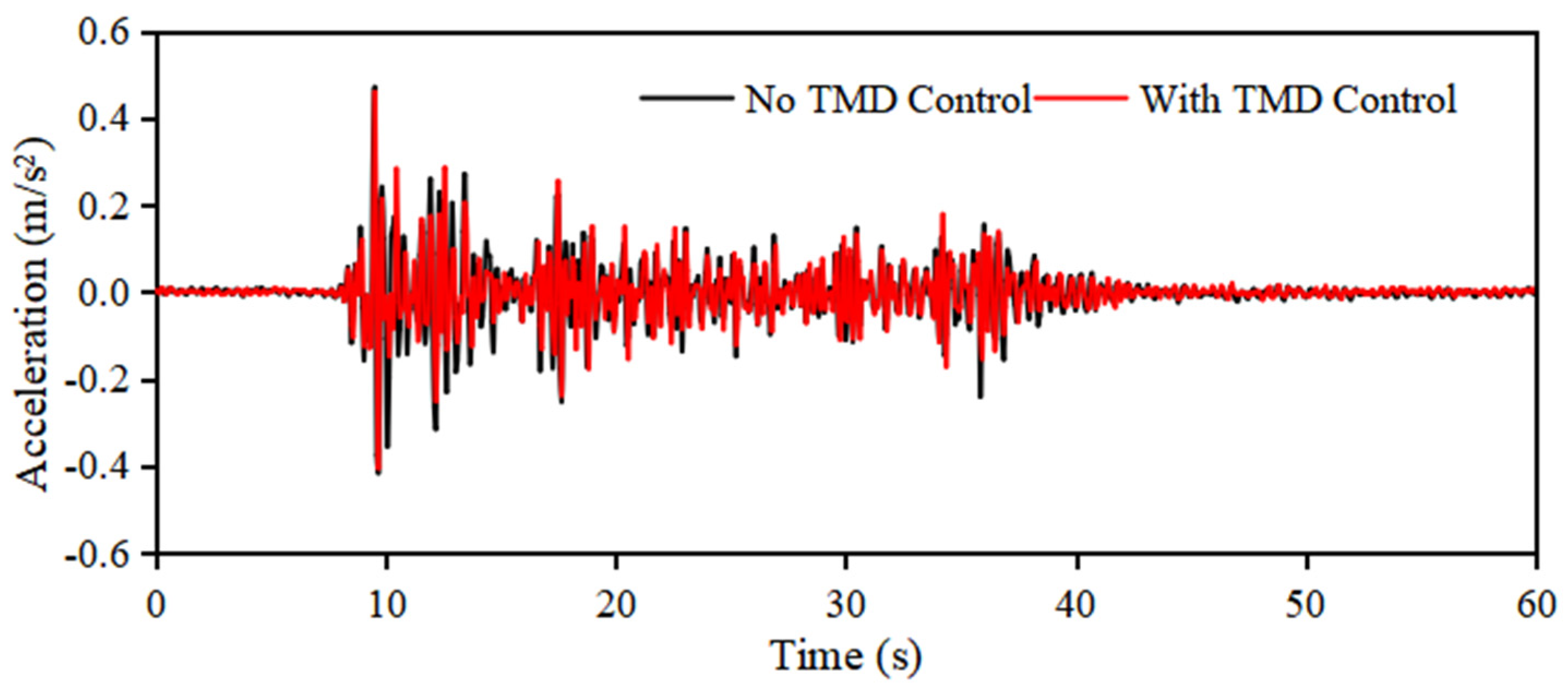
3.2. The Effect of Structural Conditions on the Spherical Water Tank
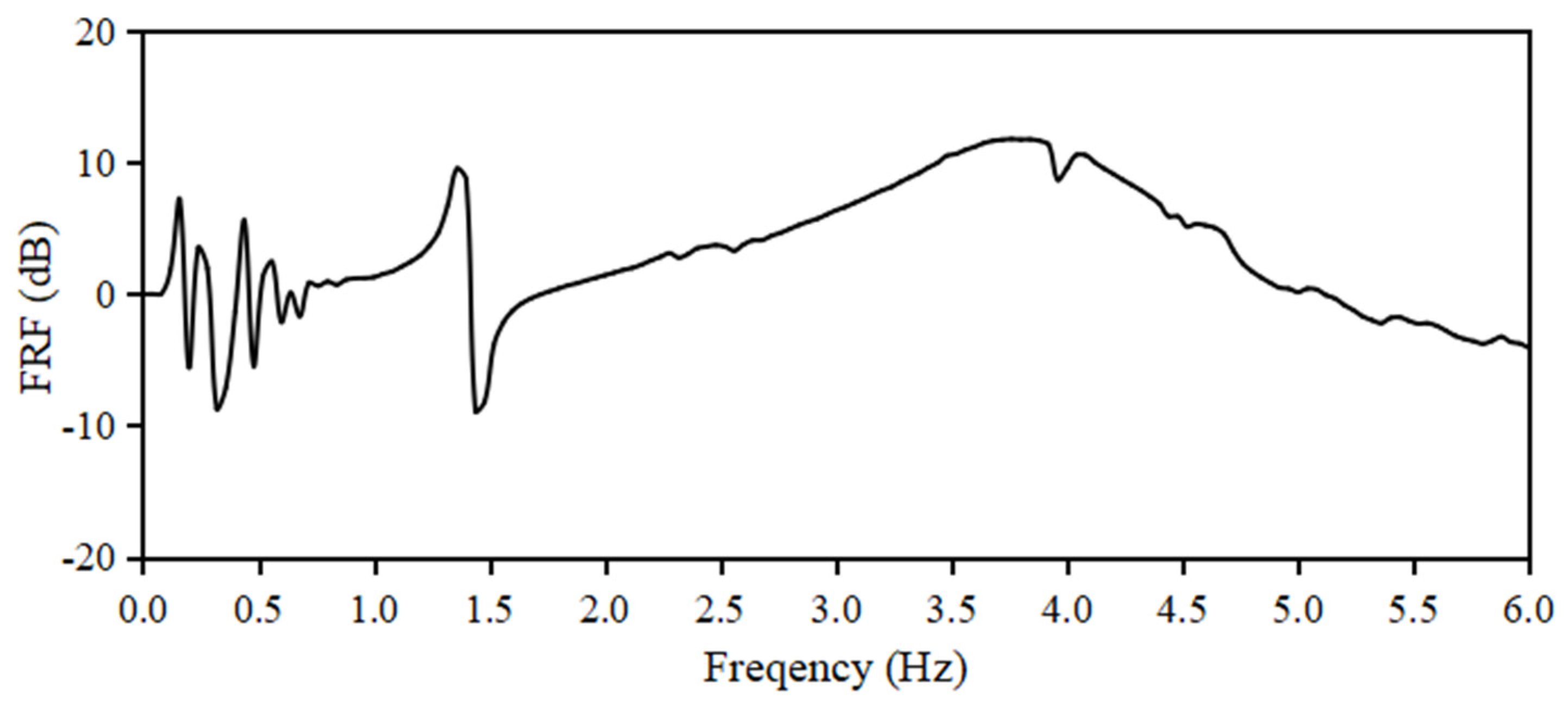
3.2.1. Natural Frequency Tuning for TMD
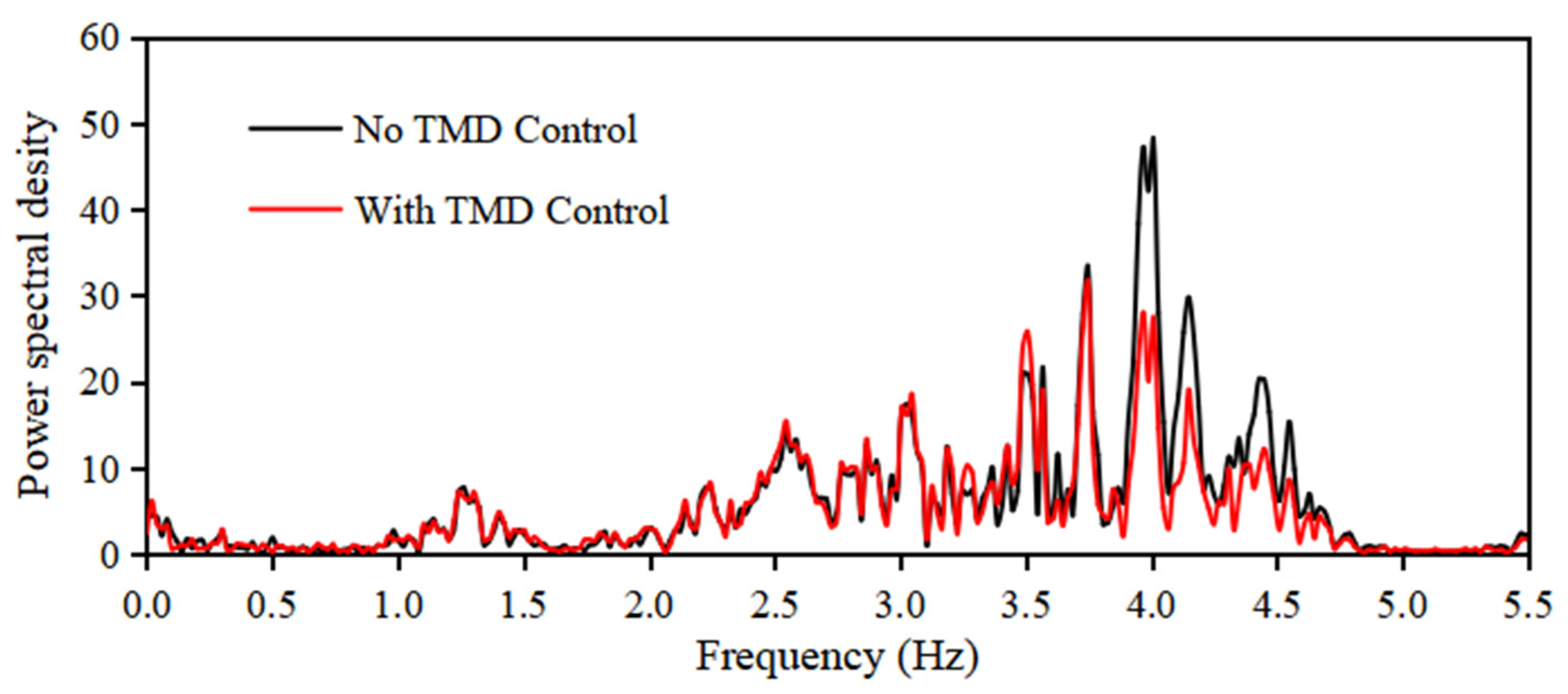
3.2.2. Vibration Control Performance of Spherical Water Tanks in a Seismic Environment
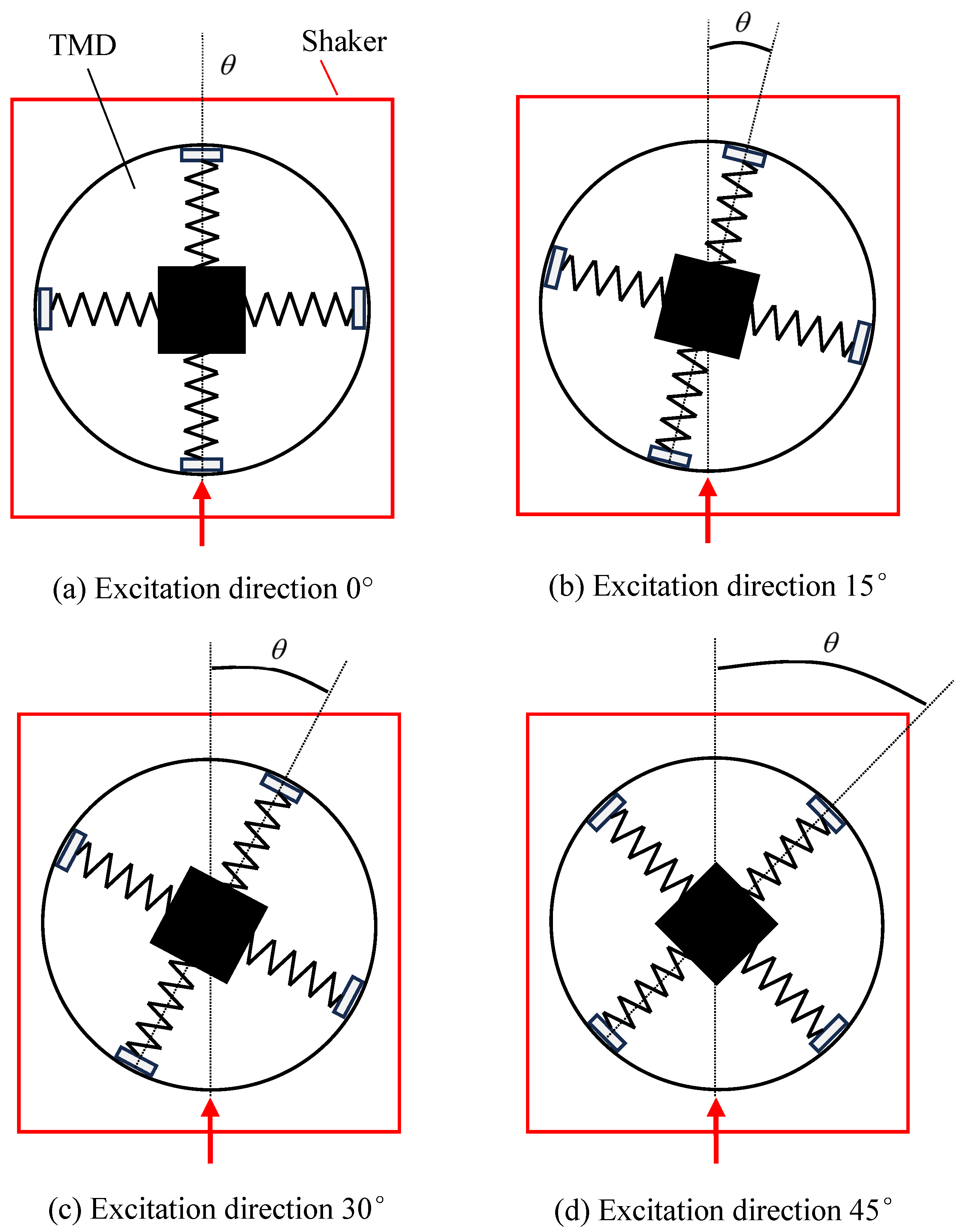
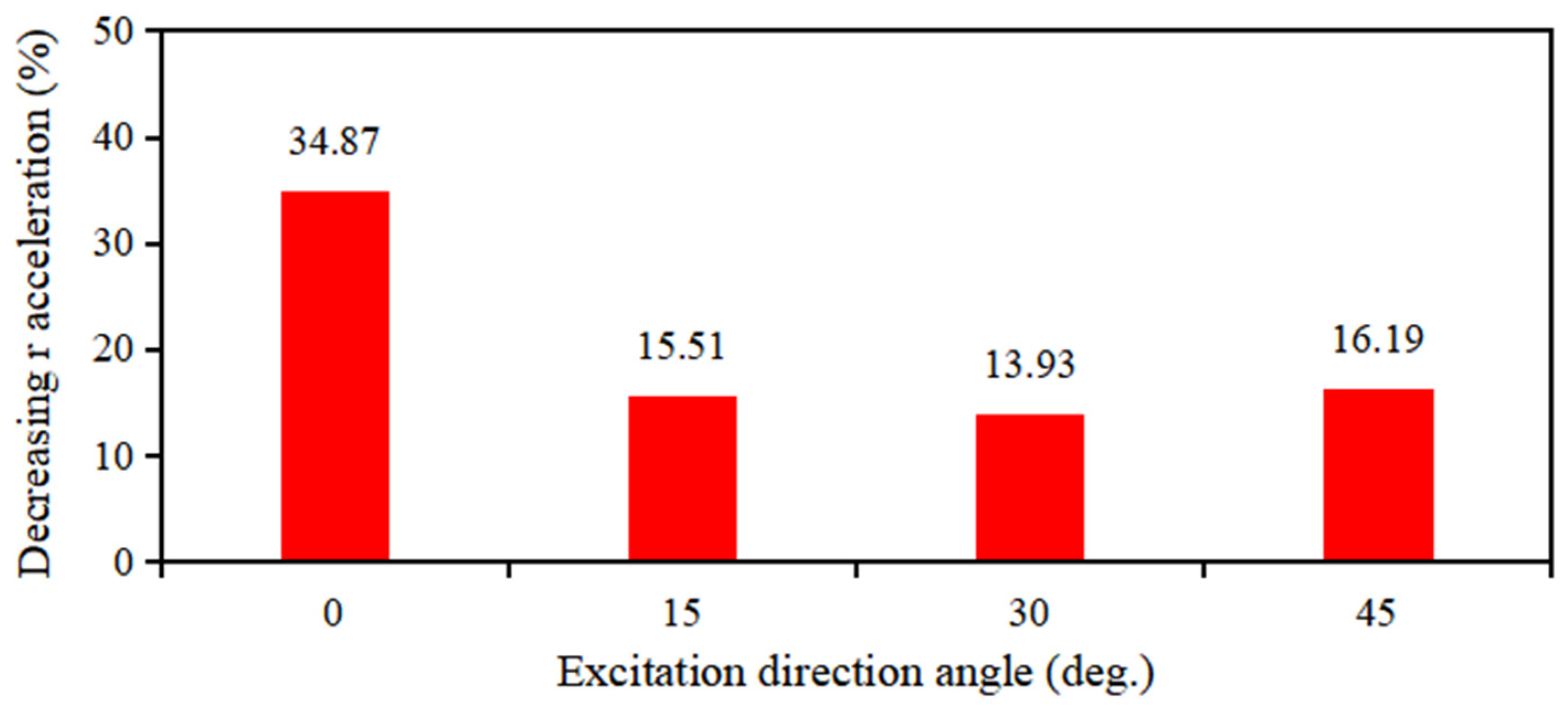
3.3. The Effect of Seismic Excitation Direction on Vibration Control Performance
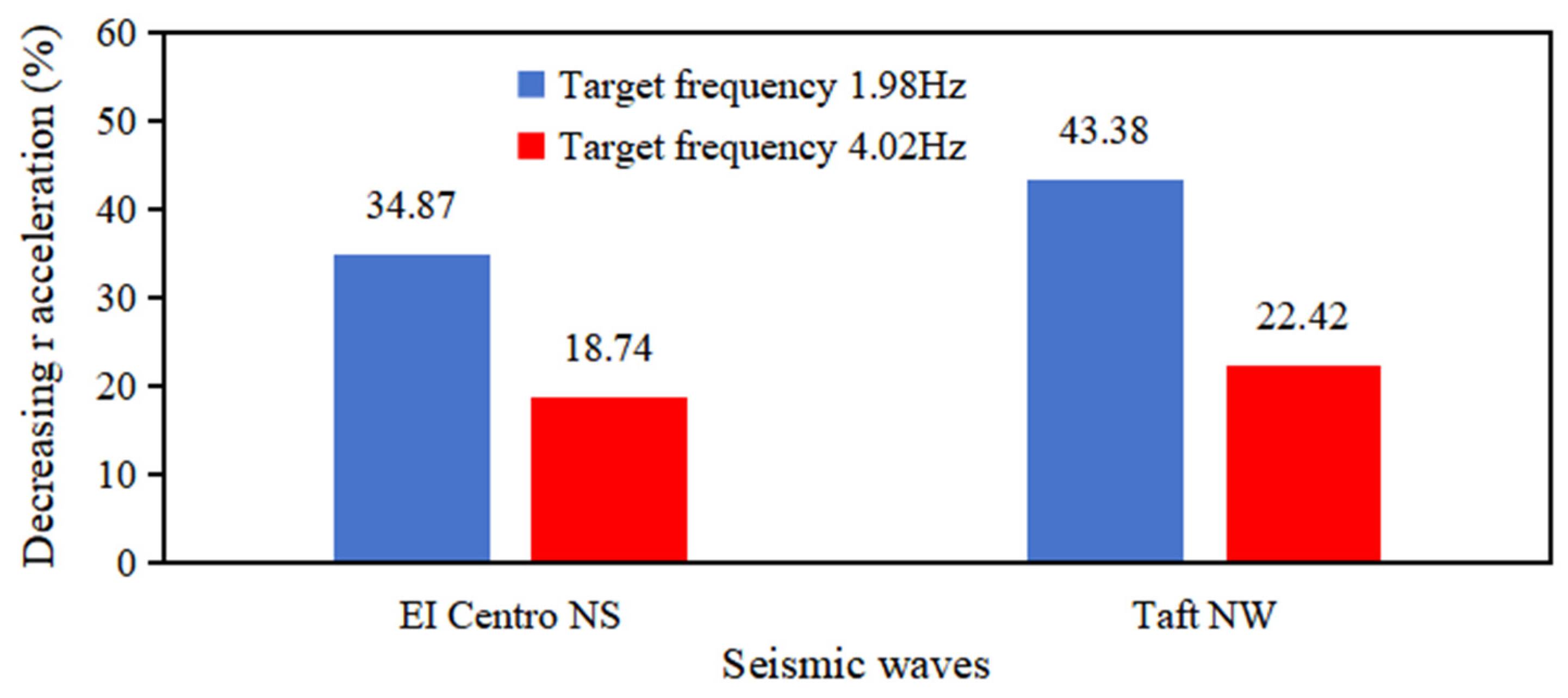
3.4. Effects on Vibration Control Performance from Different Seismic Waves
4. Conclusions
- (1)
- Vibration control effects can be ensured by matching the target frequency. It was experimentally confirmed that by adjusting the natural frequency of the TMD to match the natural frequency of the spherical water tank, a clear vibration control effect can be obtained.
- (2)
- It can flexibly respond to changes in the structural conditions of the spherical water tank. Even if the total mass of the spherical water tank or the rigidity of its supporting columns changes, causing fluctuations in its natural frequency, it was shown that sufficient vibration control effect can be maintained by adjusting the TMD.
- (3)
- As a result of verifying the vibration control effect against different seismic excitation directions, it was confirmed through experimental measurements that even when the excitation comes from directions other than the design direction of the vibration control system, the vibration control effect slightly decreases but still maintains an average effect of more than 15%.
- (4)
- To verify the vibration control effect against different seismic waves, shaking experiments using the EI Centro NS and Taft NW seismic waves were conducted. The results showed that, regardless of the type of seismic wave, the vibration control effect by the TMD was consistently exhibited at an average level of over 20%. As a future challenge, it is necessary to further examine the versatility of the TMD system, including seismic waves that have occurred around Japan.
- (5)
- When using the TMD, it was confirmed that the response acceleration is effectively reduced not only around the vibration control target frequency but also within the main frequency ranges of the seismic waves, indicating that the TMD possesses versatile vibration control effectiveness.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| TMD | Multidisciplinary Digital Publishing Institute |
| FEM | finite element methods |
References
- Fiore, A.; Demartino, C.; Greco, R.; Rago, C.; Sulpizio, C.; Vanzi, I. Seismic performance of spherical liquid storage tanks: A case study. Int. J. Adv. Struct. Eng. 2018, 10, 121–130. [Google Scholar] [CrossRef]
- Shibata, H. Survey Report on Earthquake Damage of Industrial Facilities in the World—Spherical Vessels and Cylindrical Vessels. Seisan Kenkyu 1974, 26, 259–264. [Google Scholar]
- Sakai, F. Studies on Seismic Design of Liquid Storage Tanks—Present and Future. J. JSCE 1985, 1985, 1–11. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Yamada, Y.; Iemura, H.; Noda, S.; Shimada, S. Characteristics of Relatively Long-period Ground Motions Estimated form Oil-sloshing in Huge Tanks and Earthquake Records. J. JSCE 1985, 1985, 471–480. [Google Scholar] [CrossRef][Green Version]
- Milovanovic, A.; Sedmak, A. Integrity Assessment of Ammonia Spherical Storage Tank. Procedia Struct. Integr. 2018, 13, 994–999. [Google Scholar] [CrossRef]
- Hashimoto, H. Future Trend and Topics of Liquid Sloshing. J. Soc. Mech. Eng. 1986, 89, 512–517. [Google Scholar] [CrossRef]
- Karamanos, S.A.; Patkas, L.A.; Platyrrachos, M.A. Sloshing Effects on the Seismic Design of Horizontal-Cylindrical and Spherical Industrial Vessels. J. Press. Vessel Technol. 2006, 128, 328–340. [Google Scholar] [CrossRef]
- Hata, R.; Arai, M.; Cheng, L. Nonlinear Sloshing inside a Spherical LNG Tank. In Conference Proceedings, the Japan Society of Naval Architects and Ocean Engineers; Japan Society of Naval Architects and Ocean Engineers: Tokyo, Japan, 2017; Volume 25, pp. 431–434. [Google Scholar] [CrossRef]
- Sakada, H.; Sakai, F. Sloshing Effects in Spherical Liquid Storage Tanks. High Press. Inst. Jpn. 1978, 16, 143–151. [Google Scholar] [CrossRef]
- Lu, Y.; Sun, J.; Sun, Z.; Cui, L.; Wang, Z. Basic Theory of Simplified Dynamic Model for Spherical Tank Considering Swinging Effect. J. Press. Vessel Technol. 2019, 141, 061202. [Google Scholar] [CrossRef]
- Utsumi, M. Vibration analysis of liquid in an asymmetric tank covered by a diaphragm. Mech. Eng. J. 2022, 9, 22-00022. [Google Scholar] [CrossRef]
- Utami, S.; Trimulyono, A.; Manik, P. Numerical Simulation of the Effect of Tank Shape on Sloshing Using Smoothed Partical Hydrodynamics. IOP Conf. Ser. Earth Environ. Sci. 2022, 1198, 012002. Available online: https://iopscience.iop.org/article/10.1088/1755-1315/1198/1/012002 (accessed on 1 April 2025). [CrossRef]
- Uddin, S.S. Seismic Analysis of Liquid Storage Tanks. Int. J. Adv. Trends Comput. Sci. Eng. 2013, 2, 357–362. [Google Scholar] [CrossRef]
- Koyama, K. Earthquake Response Analysis of Spherical Storage Tank. High Press. Inst. Jpn. 1979, 17, 121–129. [Google Scholar] [CrossRef]
- Chen, J.; Xian, Q.; Zhang, P. Seismic response analysis and damping method of spherical liquid storage tank. IOP Conf. Ser. Mater. Sci. Eng. 2019, 542, 012006. Available online: https://iopscience.iop.org/article/10.1088/1757-899X/542/1/012006 (accessed on 1 April 2025). [CrossRef]
- Singh, R.; Gupta, R.K. Seismic Analysis of Liquid Storage Tank. Trans. SMiRT 2011, 21, 197–201. [Google Scholar]
- Hasibuan, P.; Habibi, A.; Panjaitan, A.; Hasan, M.; Saidi, T. Stability Analysis of HSD Tank Against Dynamic Response. E3S Web Conf. 2024, 476, 01032. [Google Scholar] [CrossRef]
- Afkar, A.; Camari, M.N.; Paykani, A. Design and analysis of a spherical pressure vessel using finite element method. World J. Model. Simul. 2014, 10, 126–135. Available online: https://www.academia.edu/22301876/Design_and_analysis_of_a_spherical_pressure_vessel_using_finite_element_method (accessed on 1 April 2025).
- Malhotra, P.K.; Wenk, T.; Wieland, M. Simple Procedure for Seismic Analysis of Liquid-Storage Tanks. Struct. Eng. Int. 2000, 10, 197–201. [Google Scholar] [CrossRef]
- Yang, Z.; Shou, B.; Sun, L.; Wang, J. Earthquake Response Analysis of Spherical Tanks with Seismic Isolation. Procedia Eng. 2011, 14, 1879–1886. [Google Scholar] [CrossRef]
- Al-Khafaji, M.S.; Mohammed, A.S.; Salman, M.A. ANSYS-Based Structural Analysis Study of Elevated Spherical Tank Exposed to Earthquake. Eng. Technol. J. 2021, 39, 870–883. [Google Scholar] [CrossRef]
- Takiguchi, A. Stress Analysis of Spherical Tank by the Finite Element Method. High Press. Inst. Jpn. 1974, 12, 33–47. [Google Scholar] [CrossRef]
- Prakash, K.S.J.; Mastanaiah, T. Industrial Spherical pressure vessel design & analysis using FEA. Int. J. Comput. Eng. Res. 2014, 4, 32–35. Available online: https://www.academia.edu/9363907/Industrial_Spherical_pressure_vessel_design_and_analysis_using_FEA (accessed on 1 April 2025).
- Pappa, P.; Vasilikis, D.; Vazouras, P.; Karamanos, S.A. On the Seismic Behaviour and Design of Liquid Storage Tanks. In Proceedings of the Thematic Conference on Computational Methods in Structural Dynamics and Earthquake Engineering, Corfu, Greece, 25–28 May 2011; Available online: https://www.academia.edu/67336598/On_the_seismic_behaviour_and_design_of_liquid_storage_tanks (accessed on 1 April 2025).
- Drosos, G.C.; Dimas, A.A.; Karabalis, D.L. Discrete Models for Seismic Analysis of Liquid Storage Tanks of Arbitrary Shape and Fill Height. J. Press. Vessel. Technol. 2008, 130, 041801. [Google Scholar] [CrossRef]
- Sezen, H.; Livaoglu, R.; Dogangun, A. Dynamic analysis and seismic performance evaluation of above-ground liquid-containing tanks. Eng. Struct. 2008, 30, 794–803. [Google Scholar] [CrossRef]
- Sivy, M.; Musil, M. Design of the Spherical Liquid Storage Tanks for Earthquake Resistance. Ann. Fac. Eng. Hunedoara Int. J. Eng. 2018, 16, 121–126. Available online: https://annals.fih.upt.ro/pdf-full/2018/ANNALS-2018-1-19.pdf (accessed on 1 April 2025).
- Asodariya, D.B. Design And Analysis of Spherical Pressure Vessel As Per Manufacturing Aspect. Int. J. Sci. Adv. Res. Technol. (IJSART) 2022, 8, 59–66. Available online: https://ijsart.com/design-and-analysis-of-spherical-pressure-vessel-as-per-manufacturing-aspect-56795 (accessed on 1 April 2025).
- Oyelami, A.T.; Olusunle, S.O.O. Spherical Storage Tank Development Through Mathematical Modeling of Constituent Sections. Math. Model. Eng. Probl. 2019, 6, 467–473. [Google Scholar] [CrossRef]
- Jaiswa, O.R.; Rai, D.C.; Jain, S.K. Review of Seismic Codes on Liquid Containing Tanks. Earthq. Spectra 2007, 23, 239–260. [Google Scholar] [CrossRef]
- Martin, I.; Milos, M. Seismic Resistance of Storage Tanks Containing Liquid in Acc0rdance with Principles of Eurcode 8 Standard. J. Mech. Eng. 2016, 66, 79–88. [Google Scholar] [CrossRef]
- Higashi, K. Design of Normal Temperature Spherical Tank, Design of Low Temperature Spherical Tank. High Press. Inst. Jpn. 1998, 36, 31–40. [Google Scholar] [CrossRef]
- Wieschollek, M.; Kopp, M.; Hoffmeister, B.; Feldmann, M. Seismic Design of Spherical Liquid Storage Tanks. In Proceedings of the Thematic Conference on Computational Methods in Structural Dynamics and Earthquake Engineering, Corfu, Greece, 26–28 May 2011; Available online: https://congress.cimne.com/eccomas/proceedings/compdyn2011/compdyn2011_full/588.pdf (accessed on 1 April 2025).
- Kunieda, M.; Sakurai, H. Application of the Oil Damper to Spherical Tank in Earthquake-Resistant Design. Bull. JSME 1975, 18, 807–812. [Google Scholar] [CrossRef]
- Yamashita, K.; Tagawa, K. Development of a Seismic Damper to Spherical Tanks. High Press. Inst. Jpn. 1978, 16, 9–16. [Google Scholar] [CrossRef]
- Yamamoto, S.; Nagai, Y.; Kawata, E. An Earthquake Isolating and Vibration Absorbing Equipment for Spherical Tanks. High Press. Inst. Jpn. 1975, 13, 11–19. [Google Scholar] [CrossRef]
- Yoshida, Y.; Hamaguchi, M.; Taniguchi, T. Damping Control of Liquid Container on a Carrier with Dual Swing-Type Active Vibration Reducer. Trans. Jpn. Soc. Mech. Eng. 2008, 74, 2031–2037. [Google Scholar] [CrossRef]
- Nsieri, E.; Offir, Y.; Shohat, A. Seismic Retrofit of Exiting Spherical Tank using Non-Linear Viscous Dampers. In Proceedings of the Second European Conference on Earthquake Engineering and Seismology, Istanbul, Turkey, 25–29 August 2014; Available online: https://www.researchgate.net/profile/Yaron-Offir/publication/274389647_SEISMIC_RETROFIT_OF_EXITING_SPHERICAL_TANK_USING_NON-LINEAR_VISCOUS_DAMPERS/links/5808be3c08ae07cbaa56e763/SEISMIC-RETROFIT-OF-EXITING-SPHERICAL-TANK-USING-NON-LINEAR-VISCOUS-DAMPERS.pd (accessed on 1 April 2025).
- Drosos, J.C.; Tsinopoulos, S.V.; Karabalis, D.L. Seismic retrofit of spherical liquid storage tanks with energy dissipative devices. Soil Dyn. Earthq. Eng. 2019, 119, 158–169. [Google Scholar] [CrossRef]
- Shrimali, M.K.; Jangid, R.S. Seismic analysis of base-isolated liquid storage tanks. J. Sound Vib. 2004, 275, 59–75. [Google Scholar] [CrossRef]
- Ucar, Y.; Altan, M.F. Optimizing seismic performance: Integrating friction dampers into spherical liquid tanks. J. Sustain. Constr. Mater. Technol. 2024, 9, 294–304. [Google Scholar] [CrossRef]








Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zuo, J.; Guan, J.; Zhao, W.; Minagawa, K.; Zhao, X. Study on Vibration Control Systems for Spherical Water Tanks Under Earthquake Loads. Vibration 2025, 8, 41. https://doi.org/10.3390/vibration8030041
Zuo J, Guan J, Zhao W, Minagawa K, Zhao X. Study on Vibration Control Systems for Spherical Water Tanks Under Earthquake Loads. Vibration. 2025; 8(3):41. https://doi.org/10.3390/vibration8030041
Chicago/Turabian StyleZuo, Jingshun, Jingchao Guan, Wei Zhao, Keisuke Minagawa, and Xilu Zhao. 2025. "Study on Vibration Control Systems for Spherical Water Tanks Under Earthquake Loads" Vibration 8, no. 3: 41. https://doi.org/10.3390/vibration8030041
APA StyleZuo, J., Guan, J., Zhao, W., Minagawa, K., & Zhao, X. (2025). Study on Vibration Control Systems for Spherical Water Tanks Under Earthquake Loads. Vibration, 8(3), 41. https://doi.org/10.3390/vibration8030041





