Application of Homogenization Method in Free Vibration of Multi-Material Auxetic Metamaterials
Abstract
1. Introduction
2. Materials and Methods
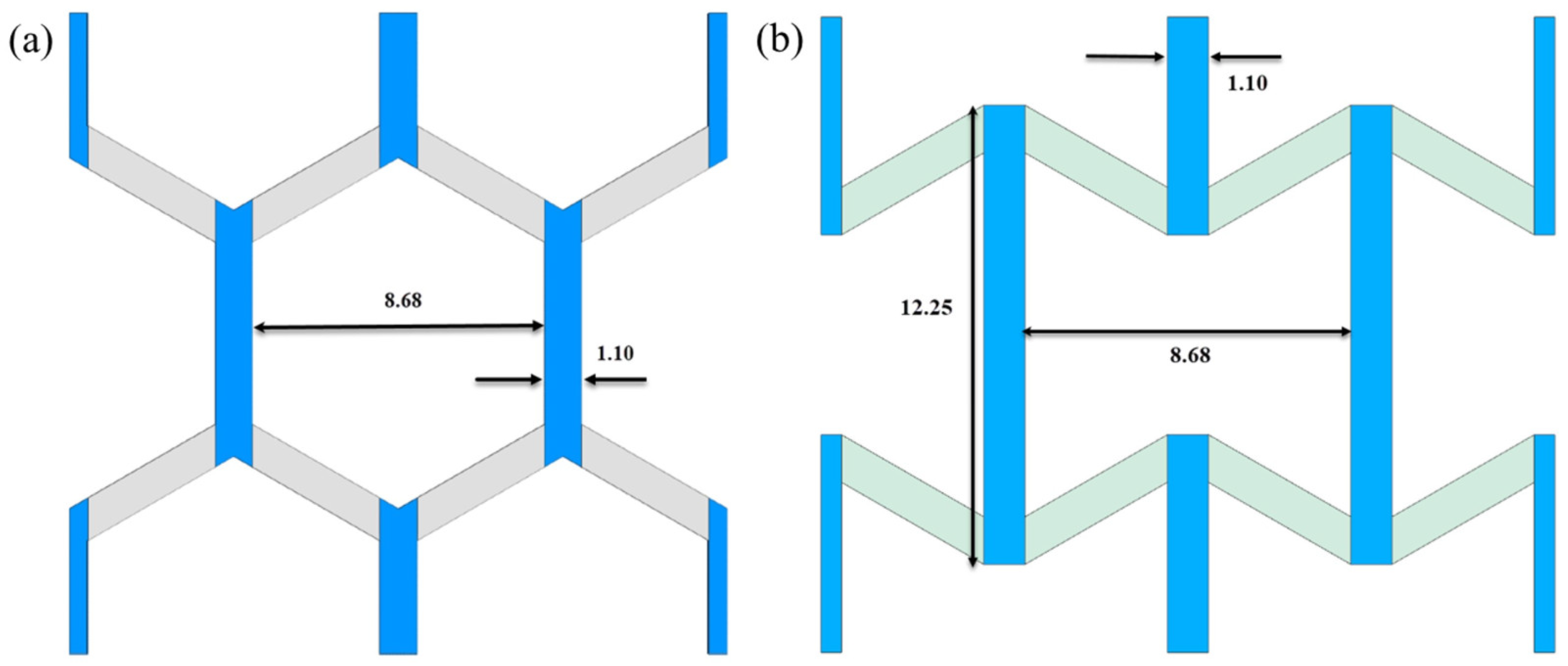
2.1. Unit Cell
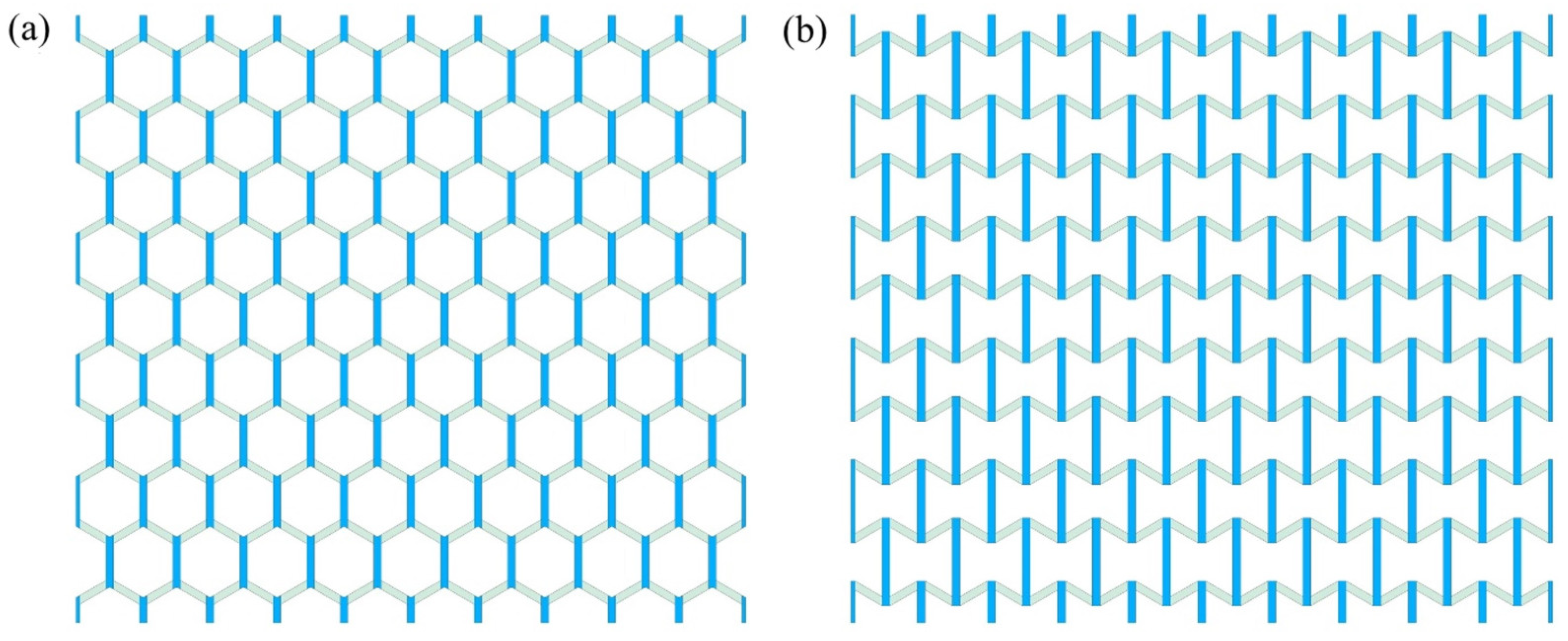
2.2. Multi-Material Lattice Structure
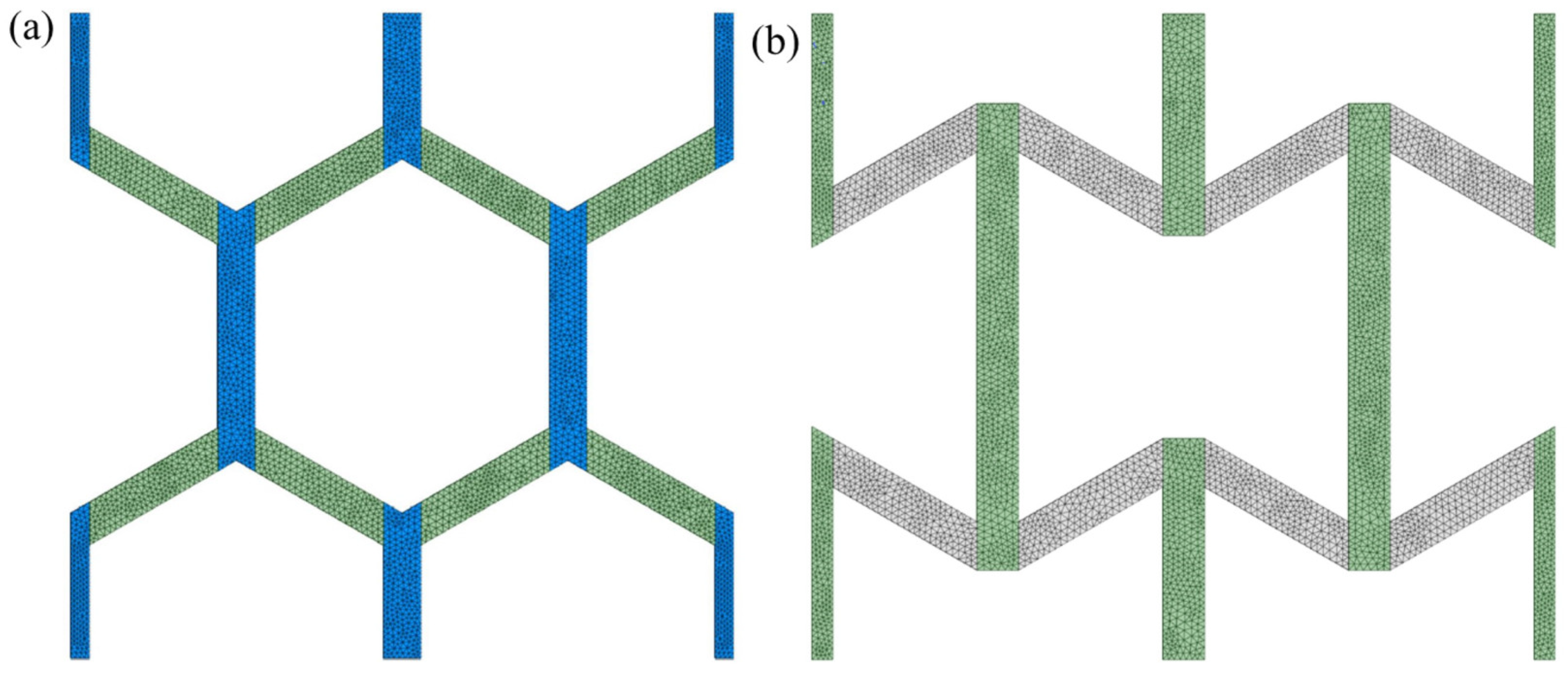
2.3. Finite Element Model
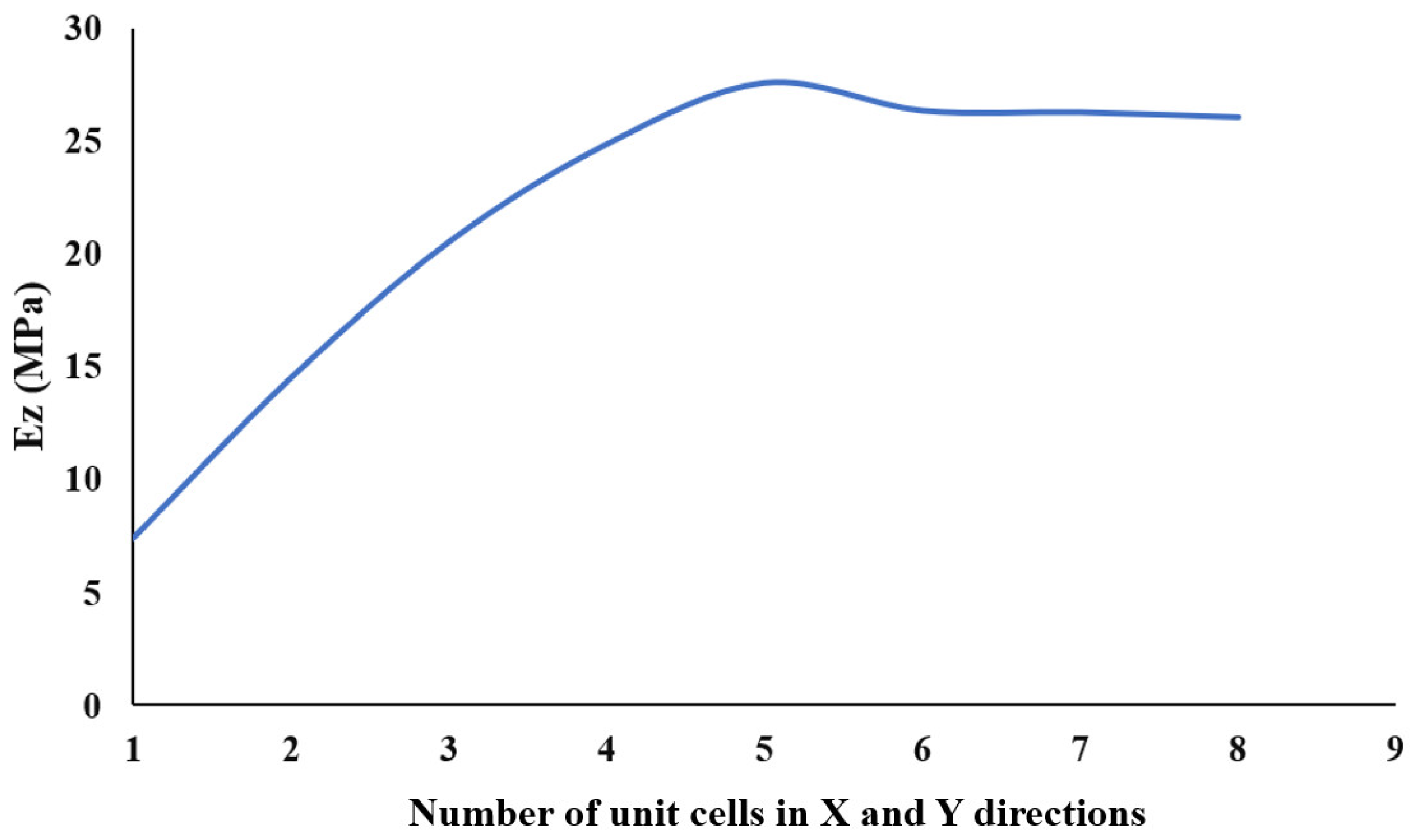
2.4. Mesh Convergence
2.5. Mode Correlation
3. Results and Discussion
3.1. Honeycomb Structures
3.2. Re-Entrant Structures
4. Conclusions
- It was numerically shown that homogenization can be successfully used in the modal analysis of multi-material honeycomb and re-entrant auxetic lattices without compromising the accuracy. There is a good agreement between the explicit and implicit mode shapes for both lattices.
- Regarding the natural frequency, the error ranges between the implicit and explicit models are 0.7–3.4% for the honeycomb structure and 1.2–6.5% for the re-entrant auxetic structure.
- The MAC number was found to be higher than 0.996, which is an indication of very high similarities between the explicit and implicit models.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hu, Q.; Zhang, X.; Zhang, J.; Lu, G.; Tse, K.M. A review on energy absorption performance of auxetic composites with fillings. Thin-Walled Struct. 2024, 205, 112348. [Google Scholar] [CrossRef]
- Jiang, D.; Thissen, H.; Hughes, T.C.; Yang, K.; Wilson, R.; Murphy, A.B.; Nguyen, V. Advances in additive manufacturing of auxetic structures for biomedical applications. Mater. Today Commun. 2024, 40, 110045. [Google Scholar] [CrossRef]
- Yin, H.; Zhang, W.; Zhu, L.; Meng, F.; Liu, J.; Wen, G. Review on lattice structures for energy absorption properties. Compos. Struct. 2023, 304, 116397. [Google Scholar] [CrossRef]
- Wu, Y.; Fang, J.; Wu, C.; Li, C.; Sun, G.; Li, Q. Additively manufactured materials and structures: A state-of-the-art review on their mechanical characteristics and energy absorption. Int. J. Mech. Sci. 2023, 246, 108102. [Google Scholar]
- Gomes, R.A.; de Oliveira, L.A.; Francisco, M.B.; Gomes, G.F. Tubular auxetic structures: A review. Thin-Walled Struct. 2023, 188, 110850. [Google Scholar] [CrossRef]
- Hou, W.; He, P.; Yang, Y.; Sang, L. Crashworthiness optimization of crash box with 3D-printed lattice structures. Int. J. Mech. Sci. 2023, 247, 108198. [Google Scholar] [CrossRef]
- Günaydın, K.; Gülcan, O.; Türkmen, H.S. Experimental and numerical crushing performance of crash boxes filled with re-entrant and anti-tetrachiral auxetic structures. Int. J. Crashworthiness 2023, 28, 649–663. [Google Scholar] [CrossRef]
- Gülcan, O.; Günaydın, K.; Tamer, A. The effect of geometrical parameters on blast resistance of sandwich panels—A review. Funct. Compos. Struct. 2023, 5, 022001. [Google Scholar] [CrossRef]
- Zhou, J.; Liu, H.; Dear, J.P.; Falzon, B.G.; Kazancı, Z. Comparison of different quasi-static loading conditions of additively manufactured composite hexagonal and auxetic cellular structures. Int. J. Mech. Sci. 2023, 244, 108054. [Google Scholar] [CrossRef]
- Günaydın, K.; Gülcan, O. Air blast response of sandwich structures with auxetic cores under in-plane and axial loadings. Res. Eng. Struct. Mater. 2023, 9, 617–630. [Google Scholar] [CrossRef]
- Günaydin, K.; Eren, Z.; Kazancı, Z.; Scarpa, F.; Grande, A.M.; Türkmen, H.S. In-plane compression behavior of anti-tetrachiral and re-entrant lattices. Smart Mater. Struct. 2019, 28, 115028. [Google Scholar] [CrossRef]
- Aktas, C.; Acar, E.; Güler, M.A.; Altın, M. An investigation of the crashworthiness performance and optimization of tetra-chiral and reentrant crash boxes. Mech. Based Des. Struct. Mach. 2022, 51, 6881–6904. [Google Scholar] [CrossRef]
- Lu, Q.; Qi, D.; Li, Y.; Xiao, D.; Wu, W. Impact energy absorption performances of ordinary and hierarchical chiral structures. Thin-Walled Struct. 2019, 140, 495–505. [Google Scholar]
- Simpson, J.; Kazancı, Z. Crushing investigation of crash boxes filled with honeycomb and re-entrant (auxetic) lattices. Thin-Walled Struct. 2020, 150, 106676. [Google Scholar] [CrossRef]
- Gülcan, O. Crashworthiness of laser powder bed fusion processed In718 auxetic metamaterials. J. Braz. Soc. Mech. Sci. Eng. 2024, 46, 414. [Google Scholar] [CrossRef]
- Ji, J.C.; Luo, Q.; Ye, K. Vibration control based metamaterials and origami structures: A state-of-the-art review. Mech. Syst. Signal Process. 2021, 161, 107945. [Google Scholar]
- Namazinia, N.; Alibeigloo, A.; Karimiasl, M. Free vibration and static analysis of sandwich composite plate with auxetic core and GPLRC facing sheets in hygrothermal environment. Forces Mech. 2024, 15, 100264. [Google Scholar] [CrossRef]
- Thang, P.T.; Kim, H.; Kim, C.; Jang, H.; Kim, T.; Kim, J. Free vibration analysis of barrel-shaped sandwich shells with auxetic honeycomb core using modified thick shell theory. Aerosp. Sci. Technol. 2024, 145, 108861. [Google Scholar]
- Liu, X.; Yang, J.; Li, S.; Fan, Y.; Yang, F.; Zhang, M.; Wu, L. Design, fabrication and vibration characteristics of a novel composite auxetic structure embedded with resonators. Mater. Today Commun. 2024, 41, 110420. [Google Scholar] [CrossRef]
- Shoaei, A.G.; Eipakchi, H.; Nasrekani, F.M. Auxetic honeycomb core layer effect on vibrations of annular plates based on shear deformation theory. Eng. Struct. 2024, 306, 117855. [Google Scholar] [CrossRef]
- Tran, H.; Vu, V.; Nguyen, V.; Tran, M. Free vibration and nonlinear dynamic response of sandwich plates with auxetic honeycomb core and piezoelectric face sheets. Thin-Walled Struct. 2023, 191, 111141. [Google Scholar] [CrossRef]
- Sarafraz, M.; Seidi, H.; Kakavand, F.; Viliani, N.S. Free vibration and buckling analyses of a rectangular sandwich plate with an auxetic honeycomb core and laminated three-phase polymer/GNP/fiber face sheets. Thin-Walled Struct. 2023, 183, 110331. [Google Scholar] [CrossRef]
- Mohandesi, N.; Talebitooti, M.; Fadaee, M. Mathematical modeling of free vibration of star-shaped auxetic rectangular plate. Arch. Appl. Mech. 2024, 94, 3455–3467. [Google Scholar] [CrossRef]
- Babuška, I. Homogenization and its application. Mathematical and computational problems. In Proceedings of the Third Symposium on the Numerical Solution of Partial Differential Equations, College Park, MD, USA, 19–24 May 1976. [Google Scholar]
- Bensoussan, A.; Lions, L.; Papanicolaou, G. Asymptotic analysis for periodic structures. In Studies in Mathematics and Its Application; North-Holland: Amsterdam, The Netherlands, 1978; Volume 5. [Google Scholar]
- Sanchez-Palencia, E. Homogenization method for the study of composite media. In Lecture Notes in Mathematics; Verhulst, F., Ed.; Springer: Berlin/Heidelberg, Germany, 1983; Volume 985. [Google Scholar]
- Blinowski, A.; Ostrowska-Maciejewska, J. On the elastic orthotropy. Arch. Mech. 1996, 48, 129–141. [Google Scholar]
- Zhang, G.; Khandelwal, K. Computational design of finite strain auxetic metamaterials via topology optimization and nonlinear homogenization. Comput. Methods Appl. Mech. Eng. 2019, 356, 490–527. [Google Scholar] [CrossRef]
- Mahapatra, B.P.; Sinha, V.; Maiti, D.K.; Jana, P. Active vibration suppression of tetrachiral auxetic core sandwich panel with CFRP skin: An RVE homogenization-assisted finite element approach. Eur. J. Mech. A/Solids 2024, 106, 105282. [Google Scholar] [CrossRef]
- Ge, L.; Jiang, W.; Zhang, Y.; Tu, S.-T. Analytical evaluation of the homogenized elastic constants of plate-fin structures. Int. J. Mech. Sci. 2017, 134, 51–62. [Google Scholar] [CrossRef]
- Ge, L.; Jiang, W.; Wang, Y.; Tu, S.-T. Creep-fatigue strength design of plate-fin heat exchanger by a homogeneous method. Int. J. Mech. Sci. 2018, 146–147, 221–233. [Google Scholar] [CrossRef]
- Dirrenberger, J.; Forest, S.; Jeulin, D.; Colin, C. Homogenization of periodic auxetic materials. Procedia Eng. 2011, 10, 1847–1852. [Google Scholar] [CrossRef]
- Reis, F.D.; Ganghoffer, J.F. Equivalent mechanical properties of auxetic lattices from discrete homogenization. Comput. Mater. Sci. 2012, 51, 314–321. [Google Scholar] [CrossRef]
- El Nady, K.; Reis, F.D.; Ganghoffer, J.F. Computation of the homogenized nonlinear elastic response of 2D and 3D auxetic structures based on micropolar continuum models. Compos. Struct. 2017, 170, 271–290. [Google Scholar] [CrossRef]
- Wang, T.; Wang, L.; Ma, Z.; Hulbert, G.M. Elastic analysis of auxetic cellular structure consisting of re-entrant hexagonal cells using a strain-based expansion homogenization method. Mater. Des. 2018, 160, 284–293. [Google Scholar] [CrossRef]
- Biswas, R.; Poh, L.H.; Shedbale, A.S. A micromorphic computational homogenization framework for auxetic tetra-chiral structures. J. Mech. Phys. Solids 2020, 135, 103801. [Google Scholar] [CrossRef]
- Zhang, M.; Zhong, Y.; Liu, X.; Liu, R. Applications of VAM-based homogenization model in free and forced vibrations of sandwich plates with bowtie-shaped auxetic core. Compos. Struct. 2023, 314, 116967. [Google Scholar] [CrossRef]
- Günaydın, K.; Türkmen, H.S. Common FDM 3D printing defects. In Proceedings of the International Congress on 3D Printing (Additive Manufacturing) Technologies and Digital Industry, Antalya, Turkey, 19–21 April 2018. [Google Scholar]
- Gülcan, O.; Günaydın, K.; Tamer, A. The state of the art of material jetting—A critical review. Polymers 2021, 13, 2829. [Google Scholar] [CrossRef] [PubMed]
- Günaydin, K.; Yavuz, A.; Tamer, A. Free vibration characteristics of multi-material lattice structures. Vibration 2023, 6, 82–101. [Google Scholar] [CrossRef]
- Li, D.; Dai, N.; Tang, Y.; Dong, G.; Zhao, Y.F. Design and optimization of graded cellular structures with triply periodic level surface-based topological shapes. ASME J. Mech. Des. 2019, 141, 071402. [Google Scholar] [CrossRef]
- Pastor, M.; Binda, M.; Harčarik, T. Modal Assurance Criterion. Procedia Eng. 2012, 48, 543–548. [Google Scholar] [CrossRef]
- Filippi, M.; Magliacano, D.; Petrolo, M.; Carrera, E. Variable-kinematics finite elements for propagation analyses of two-dimensional waveguides. In Proceedings of the 30th AIAA/CEAS Aeroacoustics Conference, Rome, Italy, 4–7 June 2024. [Google Scholar]
- Filippi, M.; Magliacano, D.; Petrolo, M.; Carrera, E. Wave propagation in prestressed structures with geometric nonlinearities through carrera unified formulation. In Proceedings of the 30th AIAA/CEAS Aeroacoustics Conference, Rome, Italy, 4–7 June 2024. [Google Scholar]

| Material | Tensile Modulus (GPa) | Tensile Strength (MPa) | Density (g/cm3) |
|---|---|---|---|
| Nylon | 1.7 | 51 | 1.1 |
| Onyx | 2.4 | 40 | 1.2 |
| Honeycomb | Re-entrant | |||
|---|---|---|---|---|
| Model Type | Explicit | Implicit | Explicit | Implicit |
| Mesh type | Quadrilateral | Quadrilateral | Quadrilateral | Quadrilateral |
| Number of nodes | 10,381,912 | 1,444,581 | 20,308,548 | 10,851,093 |
| Number of elements | 2,033,304 | 348,880 | 4,159,360 | 2,665,600 |
| Material | E1 | E2 | E3 | G12 | G23 | G13 | υ12 | υ23 | υ13 |
|---|---|---|---|---|---|---|---|---|---|
| Re-entrant | 0.027 | 0.022 | 0.316 | 0.001 | 0.035 | 0.039 | 0.868 | 0.025 | 0.035 |
| Honeycomb | 0.018 | 0.020 | 0.227 | 0.005 | 0.049 | 0.035 | 0.809 | 0.036 | 0.033 |
| Honeycomb Explicit | Honeycomb Implicit | ||
|---|---|---|---|
| 1st Mode MAC = 0.999 |  f = 568.29 Hz |  f = 587.43 Hz |  |
| 2nd Mode MAC = 0.998 | 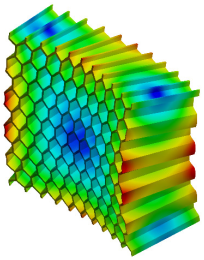 f = 779.85 Hz |  f = 798.82 Hz |  |
| 3rd Mode MAC = 0.998 | 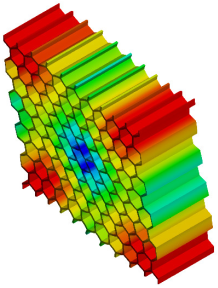 f = 1002.6 Hz | 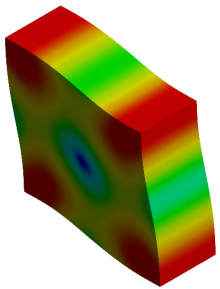 f = 1023.5 Hz |  |
| 4th Mode MAC = 0.996 | 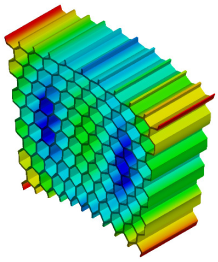 f = 1073.1 Hz |  f = 1105.4 Hz |  |
| 5th Mode MAC = 0.997 | 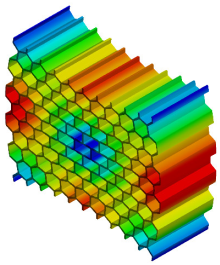 f = 1112.0 Hz |  f = 1119.5 Hz |  |
| 6th Mode MAC = 0.996 | 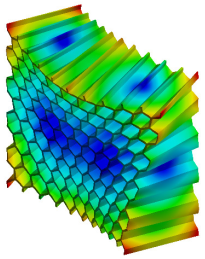 f = 1263.6 Hz |  f = 1295.5 Hz |  |
| Natural Frequencies (Hz) | |||
|---|---|---|---|
| Honeycomb Explicit | Honeycomb Implicit | Error (%) | |
| First mode | 568.29 | 587.43 | 3.4 |
| Second mode | 779.85 | 798.82 | 2.4 |
| Third mode | 1002.6 | 1023.5 | 2.1 |
| Fourth mode | 1073.1 | 1105.4 | 3.0 |
| Fifth mode | 1112.0 | 1119.5 | 0.7 |
| Sixth mode | 1263.6 | 1295.5 | 2.5 |
| Implicit | |||||||
|---|---|---|---|---|---|---|---|
| 587.4 | 798.8 | 1023.5 | 1105.4 | 1119.5 | 1295.5 | ||
| Explicit | 568.3 | 0.999 | 0 | 0 | 0 | 0 | 0 |
| 779.9 | 0 | 0.998 | 0 | 0 | 0 | 0 | |
| 1002.6 | 0 | 0 | 0.998 | 0 | 0 | 0 | |
| 1073.1 | 0 | 0 | 0 | 0.996 | 0 | 0 | |
| 1121.0 | 0 | 0 | 0 | 0 | 0.997 | 0 | |
| 1263.6 | 0 | 0 | 0 | 0 | 0 | 0.996 | |
| Re-Entrant Explicit | Re-Entrant Implicit | ||
|---|---|---|---|
| 1st Mode MAC = 0.999 | 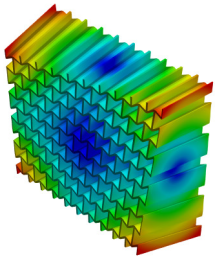 f = 267.8 Hz |  f = 273.8 Hz |  |
| 2nd Mode MAC = 0.999 | 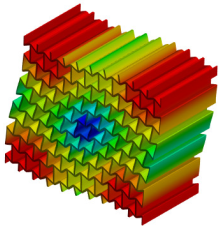 f = 448.3 Hz |  f = 453.8 Hz |  |
| 3rd Mode MAC = 0.997 | 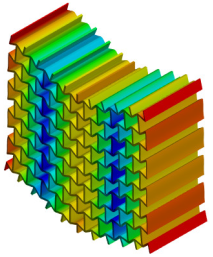 f = 596.4 Hz | 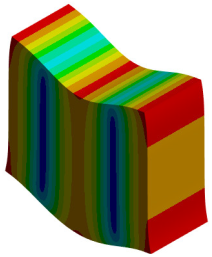 f = 606.2 Hz |  |
| 4th Mode MAC = 0.987 | 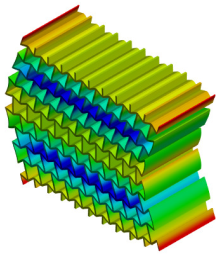 f = 665.5 Hz | 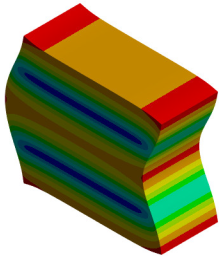 f = 708.8 Hz |  |
| 5th Mode MAC = 0.996 | 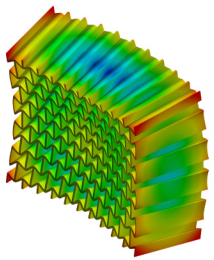 f = 785.0 Hz | 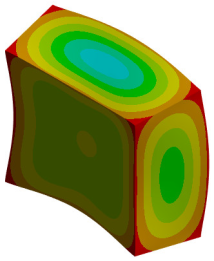 f = 798.1 Hz |  |
| 6th Mode MAC = 0.970 | 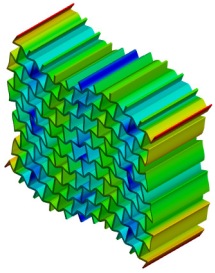 f = 919.3 Hz |  f = 938.2 Hz |  |
| Natural Frequencies (Hz) | |||
|---|---|---|---|
| Re-entrant Explicit | Re-entrant Implicit | Error (%) | |
| First mode | 267.8 | 273.8 | 2.2 |
| Second mode | 448.3 | 453.8 | 1.2 |
| Third mode | 596.4 | 606.2 | 1.6 |
| Fourth mode | 665.5 | 708.8 | 6.5 |
| Fifth mode | 785.0 | 798.1 | 1.7 |
| Sixth mode | 919.3 | 938.2 | 2.1 |
| Implicit | |||||||
|---|---|---|---|---|---|---|---|
| 273.8 | 453.8 | 606.2 | 708.8 | 798.1 | 938.2 | ||
| Explicit | 267.8 | 0.999 | 0 | 0 | 0 | 0 | 0 |
| 448.3 | 0 | 0.999 | 0 | 0 | 0 | 0 | |
| 596.4 | 0 | 0 | 0.997 | 0 | 0 | 0 | |
| 665.5 | 0 | 0 | 0 | 0.987 | 0 | 0 | |
| 785.0 | 0 | 0 | 0 | 0 | 0.996 | 0 | |
| 919.3 | 0 | 0 | 0 | 0 | 0 | 0.970 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gunaydin, K.; Gülcan, O.; Tamer, A. Application of Homogenization Method in Free Vibration of Multi-Material Auxetic Metamaterials. Vibration 2025, 8, 2. https://doi.org/10.3390/vibration8010002
Gunaydin K, Gülcan O, Tamer A. Application of Homogenization Method in Free Vibration of Multi-Material Auxetic Metamaterials. Vibration. 2025; 8(1):2. https://doi.org/10.3390/vibration8010002
Chicago/Turabian StyleGunaydin, Kadir, Orhan Gülcan, and Aykut Tamer. 2025. "Application of Homogenization Method in Free Vibration of Multi-Material Auxetic Metamaterials" Vibration 8, no. 1: 2. https://doi.org/10.3390/vibration8010002
APA StyleGunaydin, K., Gülcan, O., & Tamer, A. (2025). Application of Homogenization Method in Free Vibration of Multi-Material Auxetic Metamaterials. Vibration, 8(1), 2. https://doi.org/10.3390/vibration8010002








