Parameter Estimation of Nonlinear Structural Systems Using Bayesian Filtering Methods
Abstract
:1. Introduction
2. Modeling of Nonlinear Dynamical Systems and State-Space Identification Model
3. Parameter Estimation Using Nonlinear Bayesian Filtering
3.1. Extended Kalman Filter (EKF)
| Algorithm 1: EKF |
|
3.2. Unscented Kalman Filter (UKF)
| Algorithm 2: UKF |
|
3.3. Ensemble Kalman Filter (EnKF)
| Algorithm 3: EnKF |
|
3.4. Particle Filter (PF)
| Algorithm 4: PF with resampling |
|
4. Numerical Examples
4.1. Duffing Oscillator
4.2. Bouc–Wen Hysteretic Oscillator
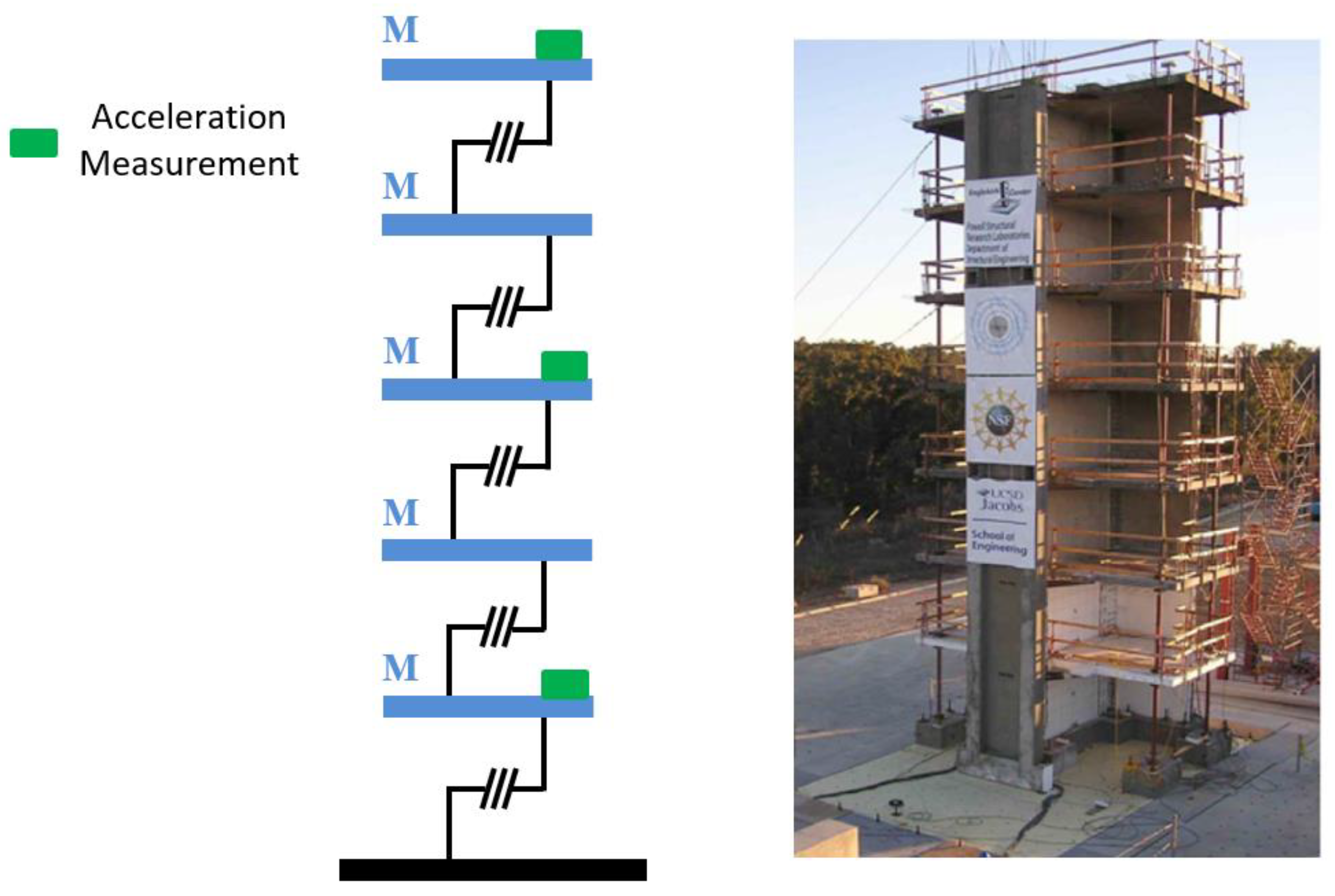
4.3. Bouc–Wen Hysteretic Chain System
5. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Grigoriu, M. Stochastic Systems: Uncertainty Quantification and Propagation; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Ljung, L. System Identification. In Signal Analysis and Prediction; Procházka, A., Uhlíř, J., Rayner, P.W.J., Kingsbury, N.G., Eds.; Birkhäuser Verlag: Basel, Switzerland, 1998. [Google Scholar]
- Maia, N.M.M.; Montalvão Silva e Silva, J.M. Theoretical and Experimental Modal Analysis; Wiley: Hoboken, NJ, USA, 1997. [Google Scholar]
- Kerschen, G.; Worden, K.; Vakakis, A.F.; Golinval, J.-C. Past, present and future of nonlinear system identification in structural dynamics. Mech. Syst. Signal Process. 2005, 20, 505–592. [Google Scholar] [CrossRef]
- Moaveni, B.; He, X.; Conte, J.P.; Restrepo, J.I. Damage identification study of a seven-story full-scale building slice tested on the UCSD-NEES shake table. Struct. Saf. 2010, 32, 347–356. [Google Scholar] [CrossRef]
- Ortiz, G.A.; Alvarez, D.A.; Bedoya-Ruíz, D. Identification of Bouc–Wen type models using multi-objective optimization algorithms. Comput. Struct. 2013, 114–115, 121–132. [Google Scholar] [CrossRef]
- Beck, J.L. Bayesian system identification based on probability logic. Struct. Control Health Monit. 2010, 17, 825–847. [Google Scholar] [CrossRef]
- Yuen, K.V.; Mu, H.Q. Real-time system identification: An algorithm for simultaneous model class selection and parametric identification. Comput.-Aided Civ. Infrastruct. Eng. 2015, 30, 785–801. [Google Scholar] [CrossRef]
- Behmanesh, I.; Moaveni, B.; Lombaert, G.; Papadimitriou, C. Hierarchical Bayesian model updating for structural identification. Mech. Syst. Signal Process. 2015, 64, 360–376. [Google Scholar] [CrossRef]
- Yuen, K.V.; Kuok, S.C.; Dong, L. Self-calibrating Bayesian real-time system identification. Comput.-Aided Civ. Infrastruct. Eng. 2019, 34, 806–821. [Google Scholar] [CrossRef]
- Jazwinski, A.H. Stochastic Processes and Filtering Theory; Courier Corporation: Chelmsford, MA, USA, 2007. [Google Scholar]
- Kalman, R.E. A New Approach to Linear Filtering and Prediction Problems. J. Basic Eng. 1960, 82, 35–45. [Google Scholar] [CrossRef]
- Simon, D. Optimal State Estimation: Kalman, H Infinity, and Nonlinear Approaches; John Wiley and Sons: Hoboken, NJ, USA, 2006. [Google Scholar]
- Julier, S.; Uhlmann, J. A new extension of the Kalman filter to nonlinear systems. In The Robotic Research Group Report; The University of Oxford: Oxford, UK, 1997. [Google Scholar]
- Evensen, G. The Ensemble Kalman Filter: Theoretical formulation and practical implementation. Ocean. Dyn. 2003, 53, 343–367. [Google Scholar] [CrossRef]
- Doucet, A.; Godsill, S.; Andrieu, C. On sequential Monte Carlo sampling methods for Bayesian filtering. Stat. Comput. 2000, 10, 197–208. [Google Scholar] [CrossRef]
- Corigliano, A.; Mariani, S. Parameter identification in explicit structural dynamics: Performance of the extended Kalman filter. Comput. Methods Appl. Mech. Eng. 2004, 193, 3807–3835. [Google Scholar] [CrossRef]
- Lin, J.W.; Betti, R. On-line identification and damage detection in non-linear structural systems using a variable forgetting factor approach. Earthq. Eng. Struct. Dyn. 2004, 33, 419–444. [Google Scholar] [CrossRef]
- Ghanem, R.; Ferro, G. Health monitoring for strongly non-linear systems using the Ensemble Kalman filter. Struct. Control Health Monit. 2005, 13, 245–259. [Google Scholar] [CrossRef]
- Ching, J.; Beck, J.; Porter, K.; Shaikhutdinov, R. Bayesian state estimation method for nonlinear systems and its application to recorded seismic response. ASCE J. Eng. Mech. 2006, 132, 396–410. [Google Scholar] [CrossRef]
- Yang, J.N.; Lin, S.; Huang, H.; Zhou, L. An adaptive extended Kalman filter for structural damage identification. Struct. Control Health Monit. 2006, 13, 849–867. [Google Scholar] [CrossRef]
- Namdeo, V.; Manohar, C. Nonlinear structural dynamical system identification using adaptive particle filters. J. Sound Vib. 2007, 306, 524–563. [Google Scholar] [CrossRef]
- Wu, M.; Smyth, A.W. Application of the unscented Kalman filter for real-time nonlinear structural system identification. Struct. Control Health Monit. 2007, 14, 971–990. [Google Scholar] [CrossRef]
- Chatzi, E.N.; Smyth, A.W. The unscented Kalman filter and particle filter methods for nonlinear structural system identification with non-collocated heterogeneous sensing. Struct. Control Health Monit. 2009, 16, 99–123. [Google Scholar] [CrossRef]
- Lourens, E.; Papadimitriou, C.; Gillijns, S.; Reynders, E.; De Roeck, G.; Lombaert, G. Joint input-response estimation for structural systems based on reduced-order models and vibration data from a limited number of sensors. Mech. Syst. Signal Process. 2012, 29, 310–327. [Google Scholar] [CrossRef]
- Xu, B.; He, J.; Rovekamp, R.; Dyke, S.J. Structural parameters and dynamic loading identification from incomplete measurements: Approach and validation. Mech. Syst. Signal Process. 2012, 28, 244–257. [Google Scholar] [CrossRef]
- Chatzis, M.; Chatzi, E.; Smyth, A. An experimental validation of time domain system identification methods with fusion of heterogeneous data. Earthq. Eng. Struct. Dyn. 2014, 44, 523–547. [Google Scholar] [CrossRef]
- Sun, H.; Betti, R. Simultaneous identification of structural parameters and dynamic input with incomplete output-only measurements. Struct. Control Health Monit. 2014, 21, 868–889. [Google Scholar] [CrossRef]
- Azam, S.E.; Chatzi, E.; Papadimitriou, C. A dual Kalman filter approach for state estimation via output-only acceleration measurements. Mech. Syst. Signal Process. 2015, 60, 866–886. [Google Scholar] [CrossRef]
- Khalil, M.; Sarkar, A.; Adhikari, S.; Poirel, D. The estimation of time-invariant parameters of noisy nonlinear oscillatory systems. J. Sound Vib. 2015, 344, 81–100. [Google Scholar] [CrossRef]
- Liu, L.; Su, Y.; Zhu, J.; Lei, Y. Data fusion based EKF-UI for real-time simultaneous identification of structural systems and unknown external inputs. Measurement 2016, 88, 456–467. [Google Scholar] [CrossRef]
- Maes, K.; Smyth, A.; De Roeck, G.; Lombaert, G. Joint input-state estimation in structural dynamics. Mech. Syst. Signal Process. 2016, 70–71, 445–466. [Google Scholar] [CrossRef]
- Yan, G.; Sun, H.; Büyüköztürk, O. Impact load identification for composite structures using Bayesian regularization and unscented Kalman filter. Struct. Control Health Monit. 2016, 24, e1910. [Google Scholar] [CrossRef]
- Erazo, K.; Nagarajaiah, S. An offline approach for output-only Bayesian identification of stochastic nonlinear systems using unscented Kalman filtering. J. Sound Vib. 2017, 397, 222–240. [Google Scholar] [CrossRef]
- Erazo, K.; Nagarajaiah, S. Bayesian structural identification of a hysteretic negative stiffness earthquake protection system using unscented Kalman filtering. Struct. Control Health Monit. 2018, 25, e2203. [Google Scholar] [CrossRef]
- Erazo, K.; Sen, D.; Nagarajaiah, S.; Sun, L. Vibration-based structural health monitoring under changing environmental conditions using Kalman filtering. Mech. Syst. Signal Process. 2018, 117, 1–15. [Google Scholar] [CrossRef]
- Lei, Y.; Xia, D.; Erazo, K.; Nagarajaiah, S. A novel unscented Kalman filter for recursive state-input-system identification of nonlinear systems. Mech. Syst. Signal Process. 2019, 127, 120–135. [Google Scholar] [CrossRef]
- Kammouh, O.; Gardoni, P.; Cimellaro, G.P. Probabilistic framework to evaluate the resilience of engineering systems using Bayesian and dynamic Bayesian networks. Reliab. Eng. Syst. Saf. 2020, 198, 106813. [Google Scholar] [CrossRef]
- Ierimonti, L.; Cavalagli, N.; Venanzi, I.; García-Macías, E.; Ubertini, F. A transfer Bayesian learning methodology for structural health monitoring of monumental structures. Eng. Struct. 2021, 247, 113089. [Google Scholar] [CrossRef]
- Diaz, M.; Charbonnel, P.; Chamoin, L. A new Kalman filter approach for structural parameter tracking: Application to the monitoring of damaging structures tested on shaking-tables. Mech. Syst. Signal Process. 2022, 182, 109529. [Google Scholar] [CrossRef]
- Yu, X.; Li, X.; Bai, Y. Evaluating maximum inter-story drift ratios of building structures using time-varying models and Bayesian filters. Soil Dyn. Earthq. Eng. 2022, 162, 107496. [Google Scholar] [CrossRef]
- Hu, L.; Bao, Y.; Sun, Z.; Meng, X.; Tang, C.; Zhang, D. Outlier Detection Based on Nelder-Mead Simplex Robust Kalman Filtering for Trustworthy Bridge Structural Health Monitoring. Remote Sens. 2023, 15, 2385. [Google Scholar] [CrossRef]
- Liu, W.; Lai, Z.; Bacsa, K.; Chatzi, E. Neural extended Kalman filters for learning and predicting dynamics of structural systems. Struct. Health Monit. 2023, 23, 1037–1052. [Google Scholar] [CrossRef]
- Erazo, K.; Di Matteo, A.; Spanos, P. Parameter Estimation of Stochastic Fractional Dynamic Systems Using Nonlinear Bayesian Filtering System Identification Methods. J. Eng. Mech. 2024, 150, 04023117. [Google Scholar] [CrossRef]
- Julier, S.; Uhlmann, J.; Durrant-Whyte, H.F. A new method for the nonlinear transformation of means and covariances in filters and estimators. IEEE Trans. Autom. Control. 2001, 45, 477–482. [Google Scholar] [CrossRef]
- Särkkä, S. Bayesian Filtering and Smoothing; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- Kudryashov, N.A. The generalized Duffing oscillator. Commun. Nonlinear Sci. Numer. Simul. 2021, 93, 105526. [Google Scholar] [CrossRef]
- Jerath, K.; Brennan, S.; Lagoa, C. Bridging the gap between sensor noise modeling and sensor characterization. Measurement 2018, 116, 350–366. [Google Scholar] [CrossRef]
- Ikhouane, F.; Rodellar, J. Systems with Hysteresis: Analysis, Identification and Control Using the Bouc-Wen Model; John Wiley & Sons: Hoboken, NJ, USA, 2007. [Google Scholar]
- Charalampakis, A.E.; Koumousis, V.K. Identification of Bouc–Wen hysteretic systems by a hybrid evolutionary algorithm. J. Sound Vib. 2008, 314, 571–585. [Google Scholar] [CrossRef]
- Worden, K.; Hensman, J. Parameter estimation and model selection for a class of hysteretic systems using Bayesian inference. Mech. Syst. Signal Process. 2012, 32, 153–169. [Google Scholar] [CrossRef]
- Omrani, R.; Hudson, R.E.; Taciroglu, E. Parametric identification of nondegrading hysteresis in a laterally and torsionally coupled building using an unscented Kalman filter. J. Eng. Mech. 2013, 139, 452–468. [Google Scholar] [CrossRef]
- Erazo, K.; Hernandez, E.M. State estimation in nonlinear structural systems. In Nonlinear Dynamics, Volume 2, Proceedings of the 32nd IMAC, A Conference and Exposition on Structural Dynamics, Orlando, FL, USA, 3–6 February 2014; Allen, M., Catbas, F.N., Foss, G., Kerschen, G., Mayes, R., Niezrecki, C., Rixen, D., Atamturktur, H.S., De Clerck, J., Allemang, R.J., et al., Eds.; Springer International Publishing: Berlin/Heidelberg, Germany, 2014; pp. 249–257. [Google Scholar]
- Erazo, K.; Hernandez, E.M. Uncertainty quantification of state estimation in nonlinear structural systems with application to seismic response in buildings. ASCE-ASME J. Risk Uncertain. Eng. Syst. Part A Civ. Eng. 2016, 2, B5015001. [Google Scholar] [CrossRef]
- Roohi, M.; Erazo, K.; Rosowsky, D.; Hernandez, E.M. An extended model-based observer for state estimation in nonlinear hysteretic structural systems. Mech. Syst. Signal Process. 2020, 146, 107015. [Google Scholar] [CrossRef]
- Panagiotou, M.; Restrepo, J.I.; Conte, J.P. Shake-table test of a full-scale 7-story building slice. Phase I: Rectangular wall. J. Struct. Eng. 2011, 137, 691–704. [Google Scholar] [CrossRef]
- Erazo, K.; Moaveni, B.; Nagarajaiah, S. Bayesian seismic strong-motion response and damage estimation with application to a full-scale seven story shear wall structure. Eng. Struct. 2019, 186, 146–160. [Google Scholar] [CrossRef]
- Chatzis, M.N.; Chatzi, E.N.; Smyth, A.W. On the observability and identifiability of nonlinear structural and mechanical systems. Struct. Control Health Monit. 2014, 22, 574–593. [Google Scholar] [CrossRef]
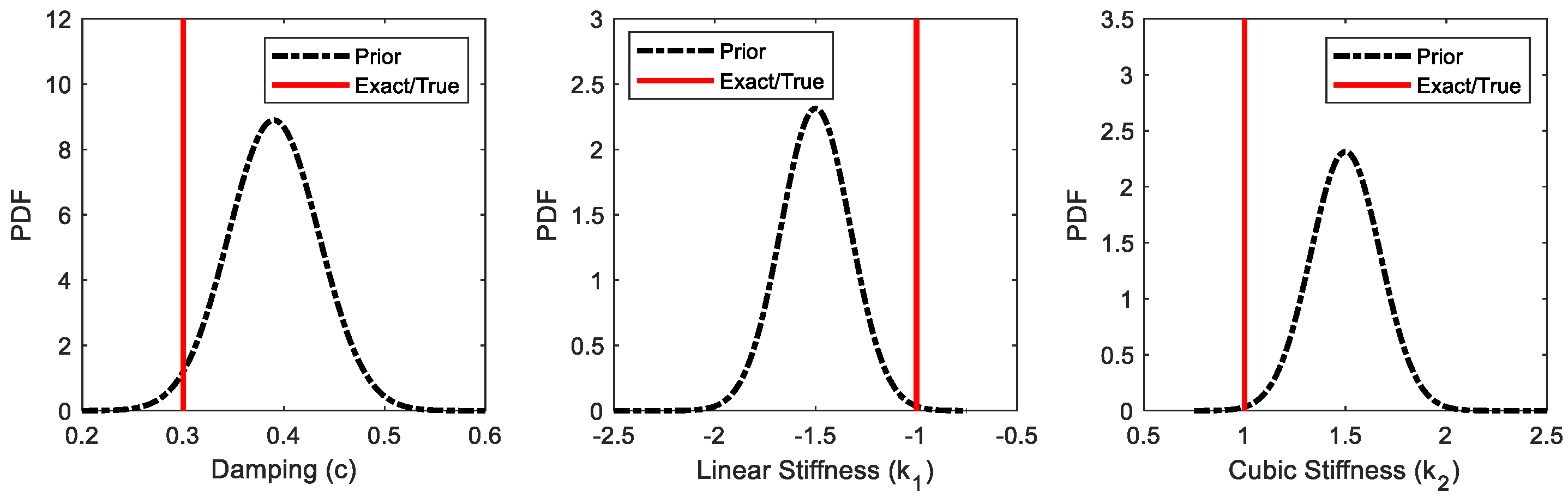
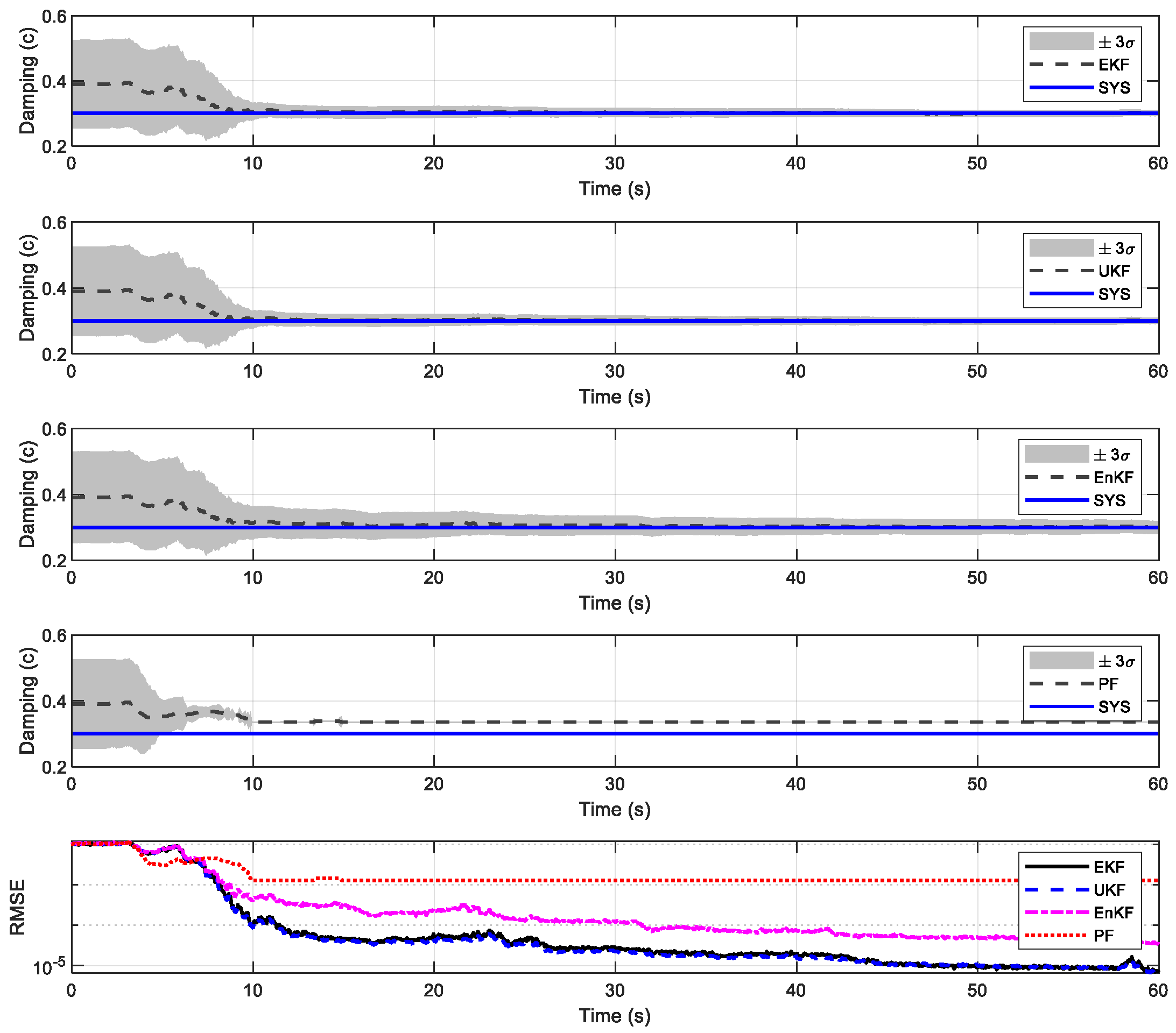

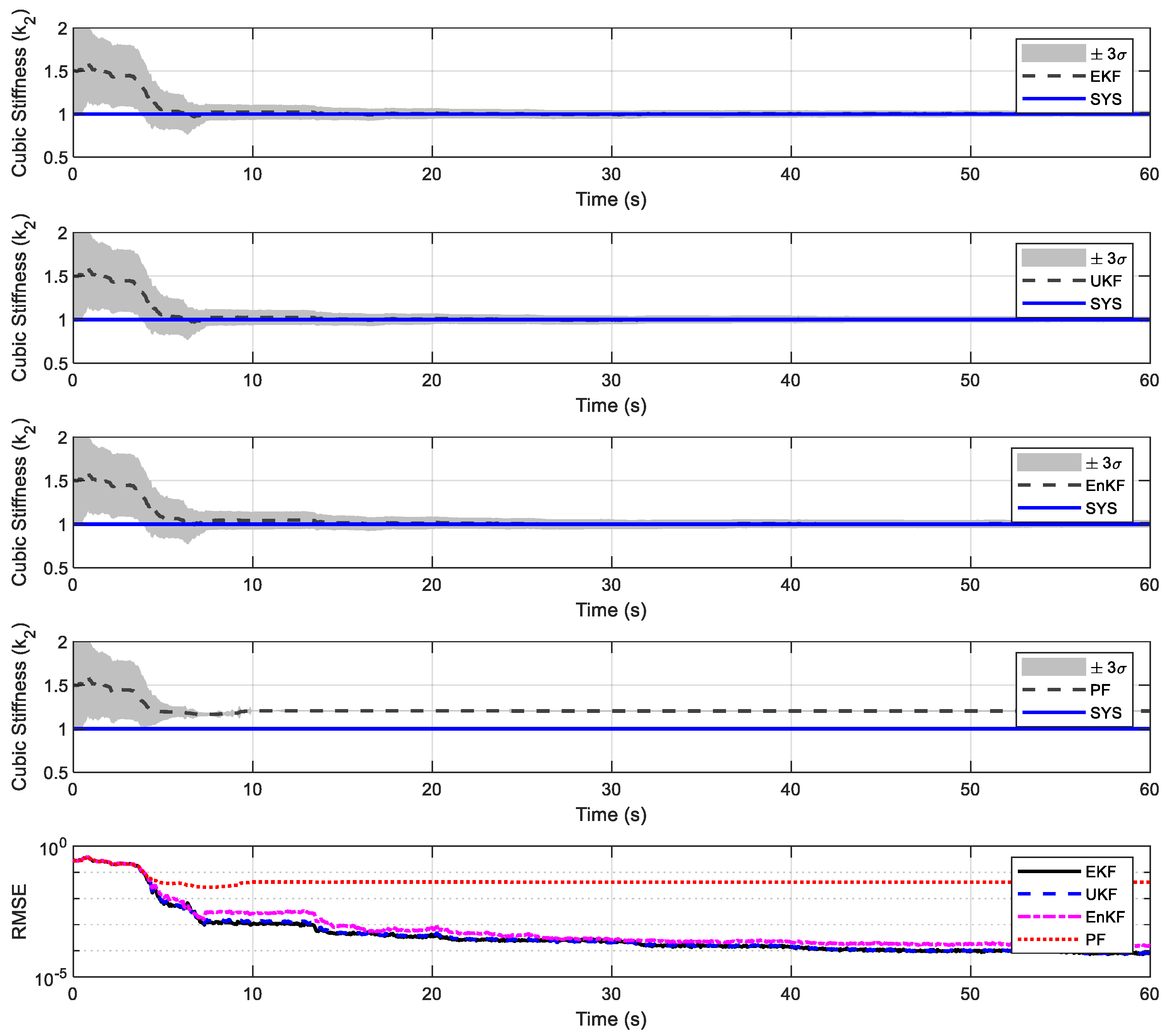
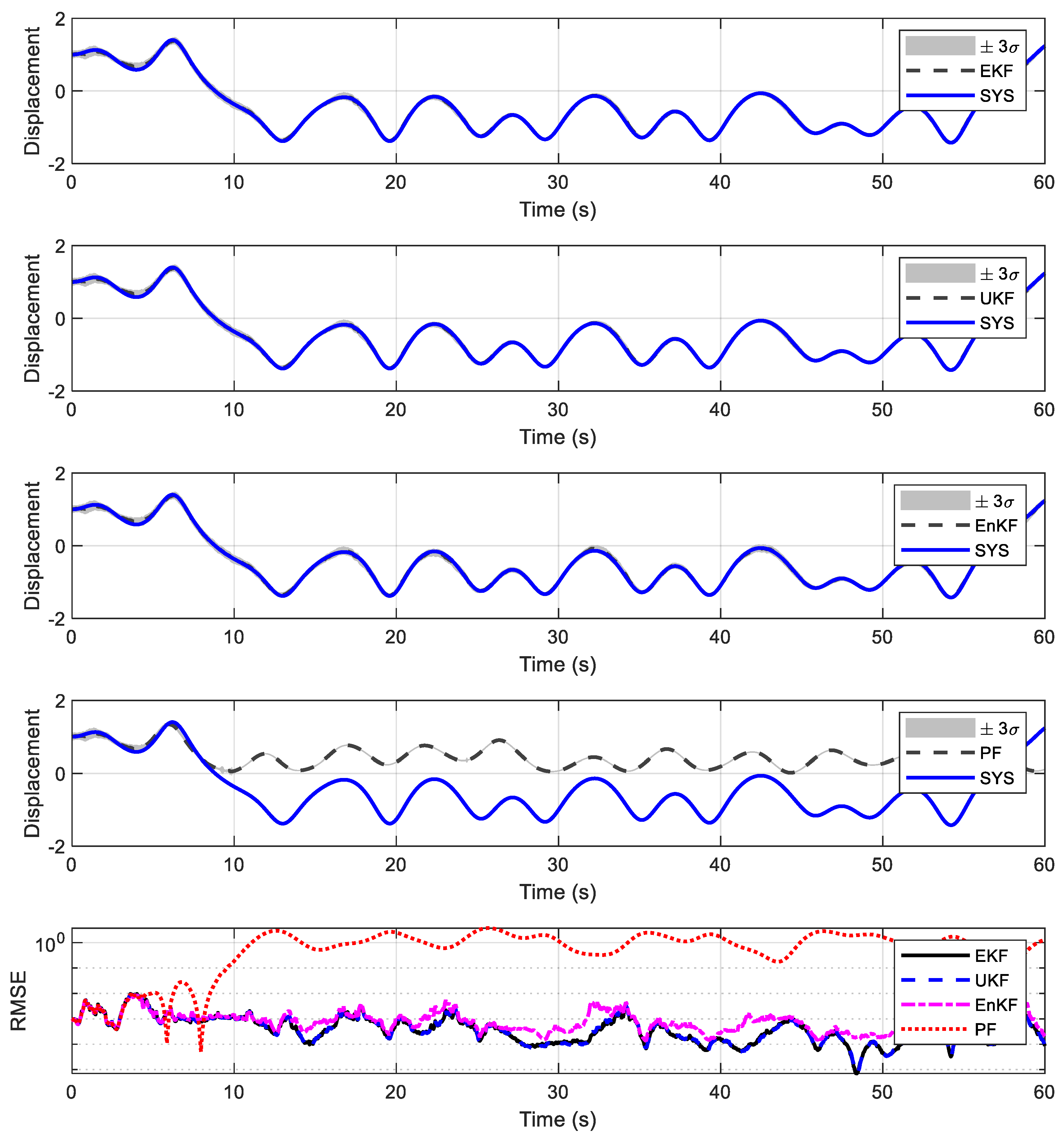

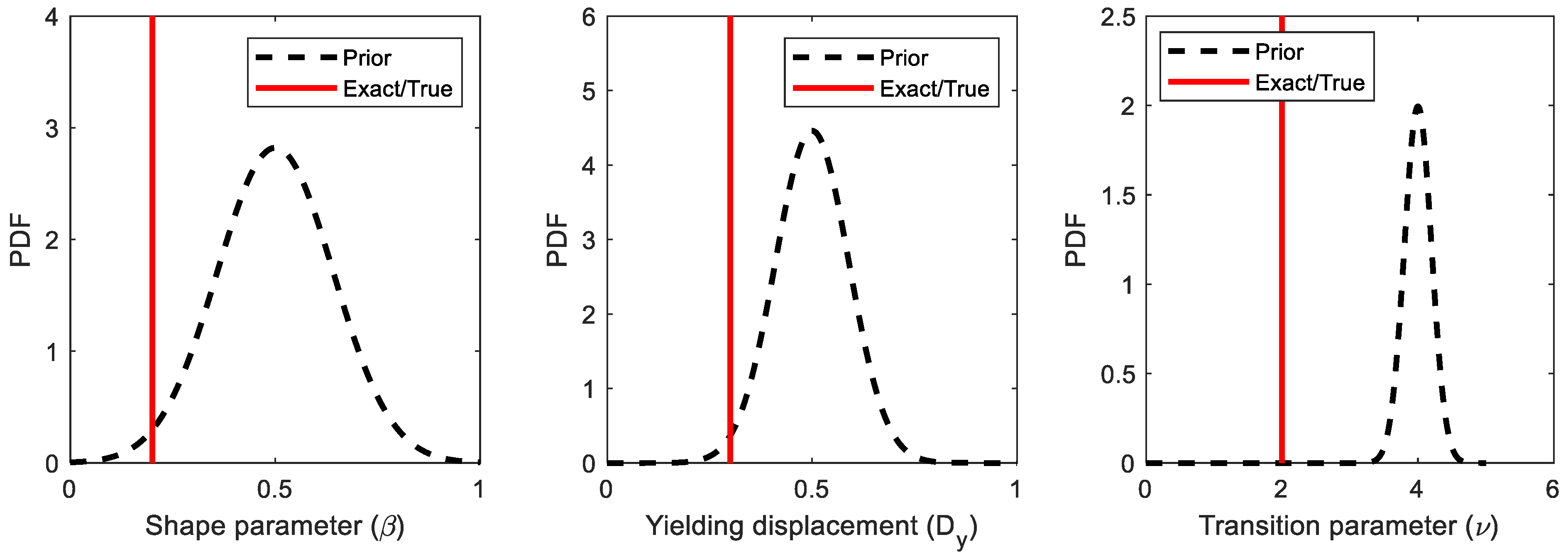
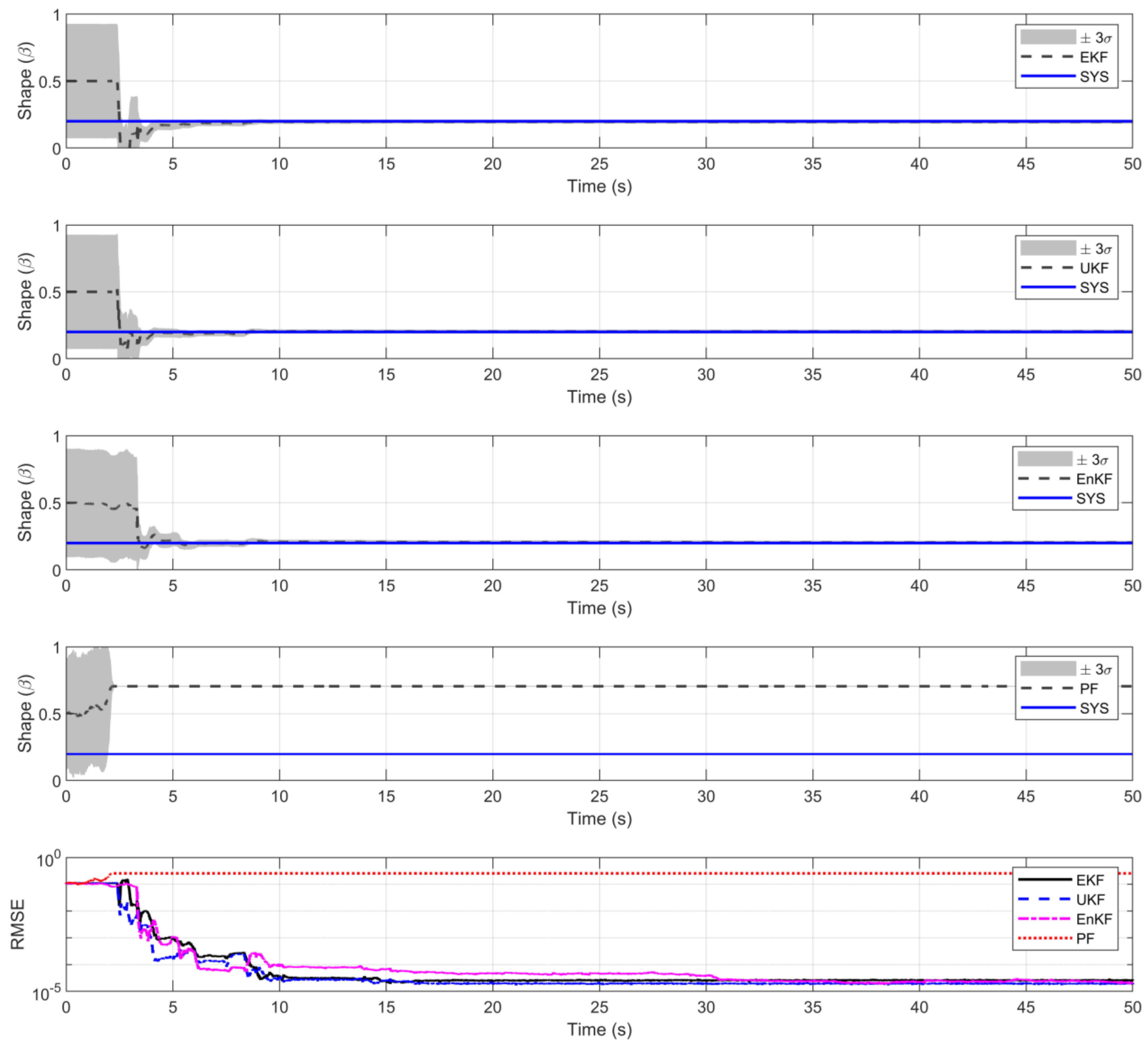
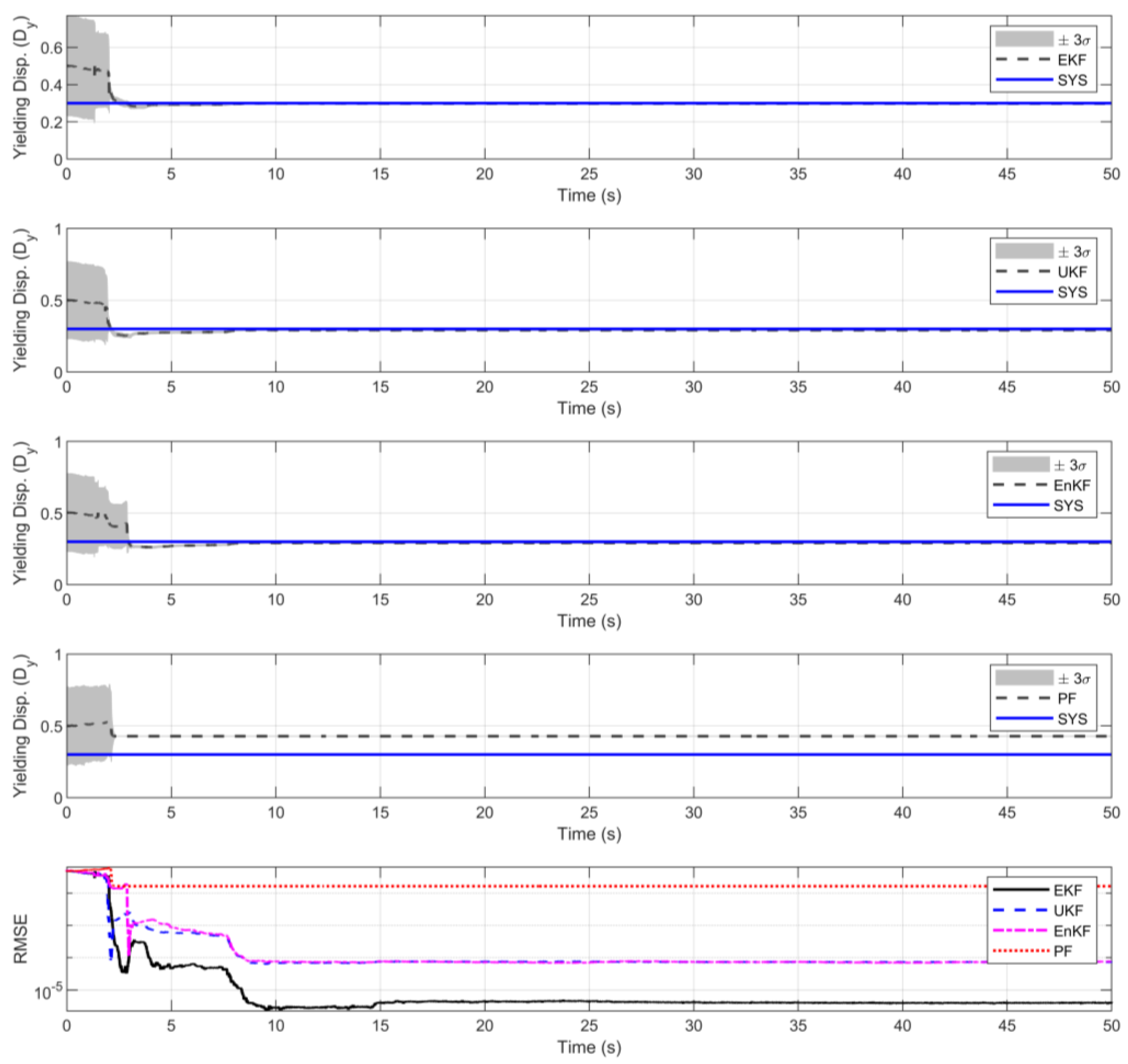

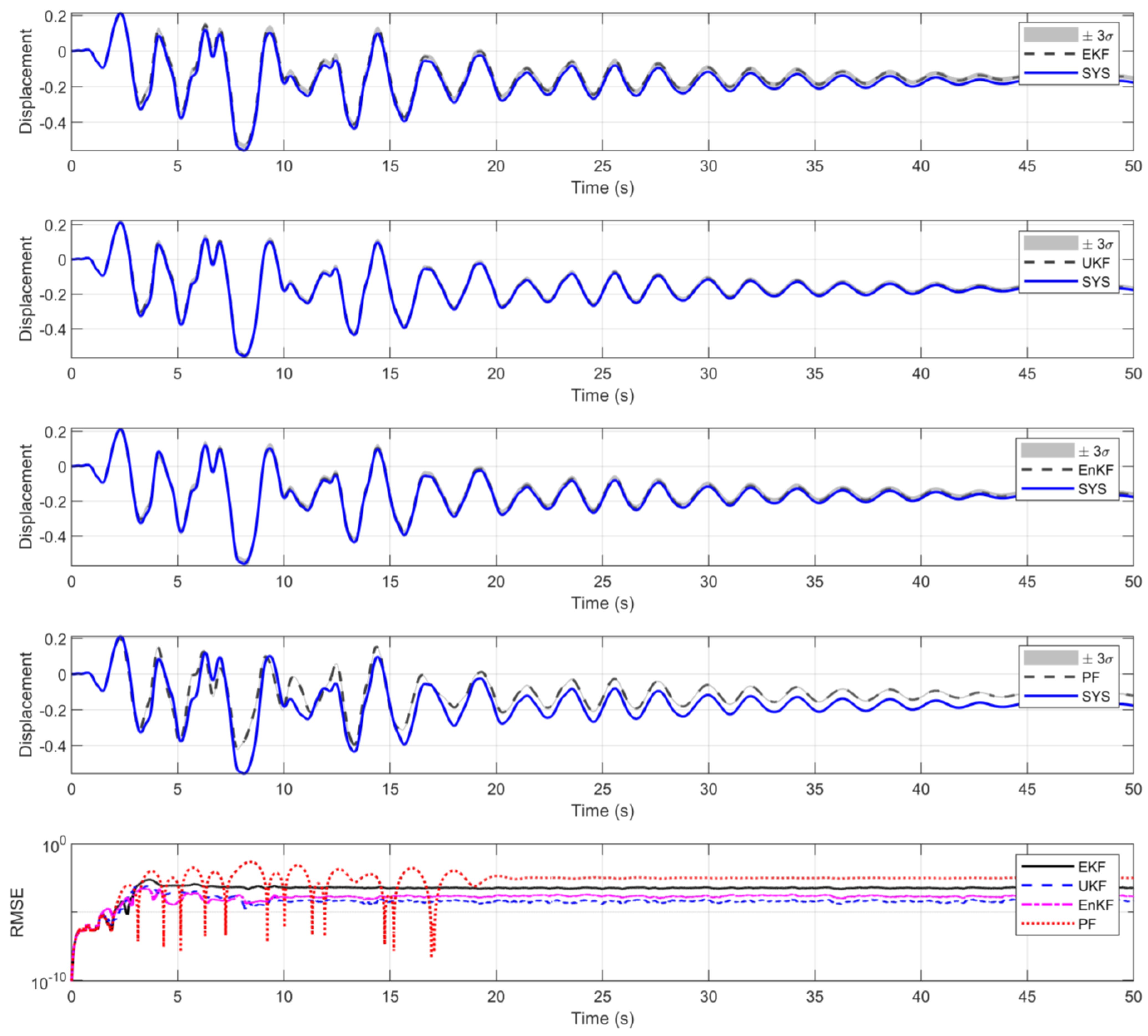
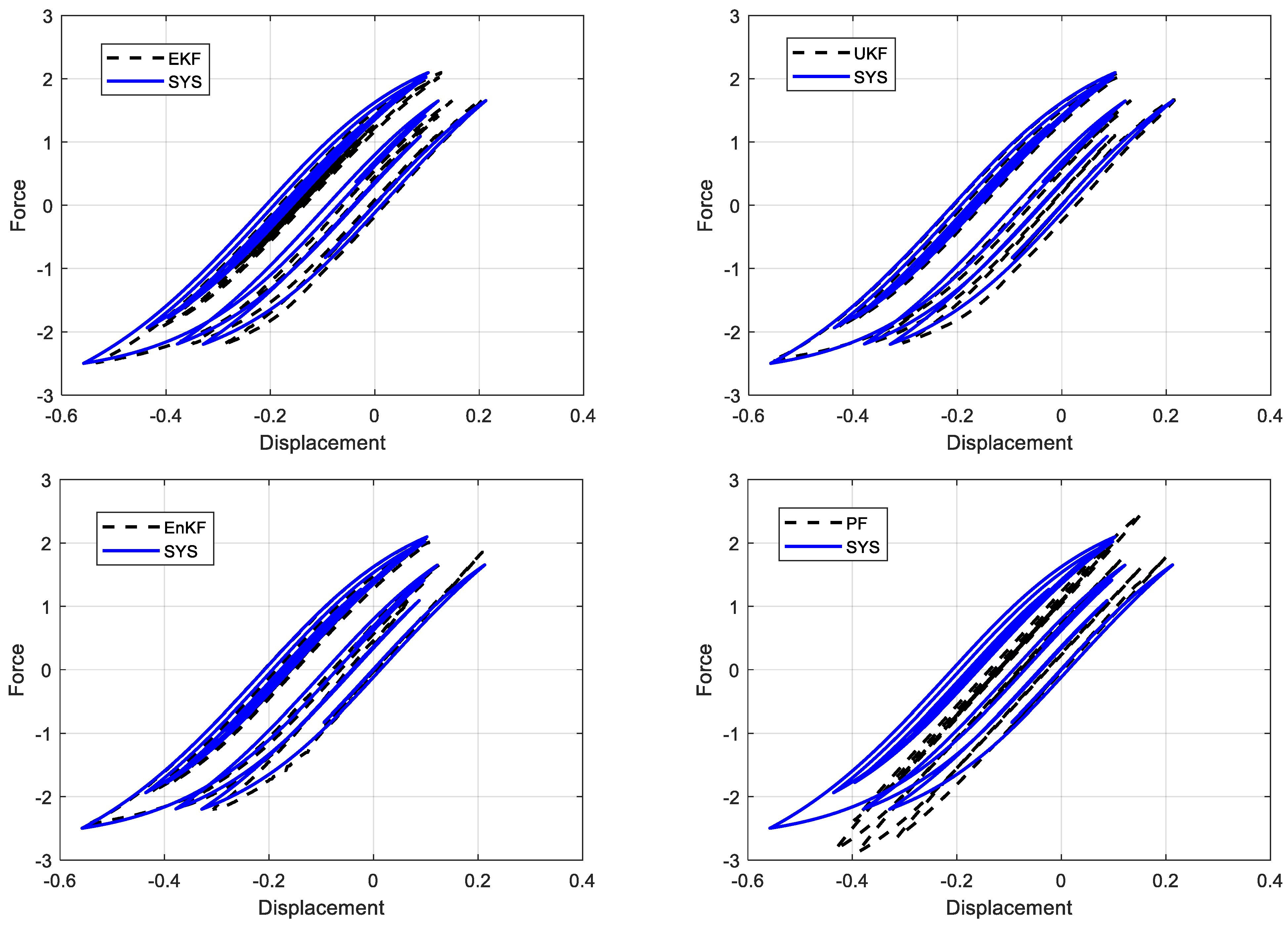
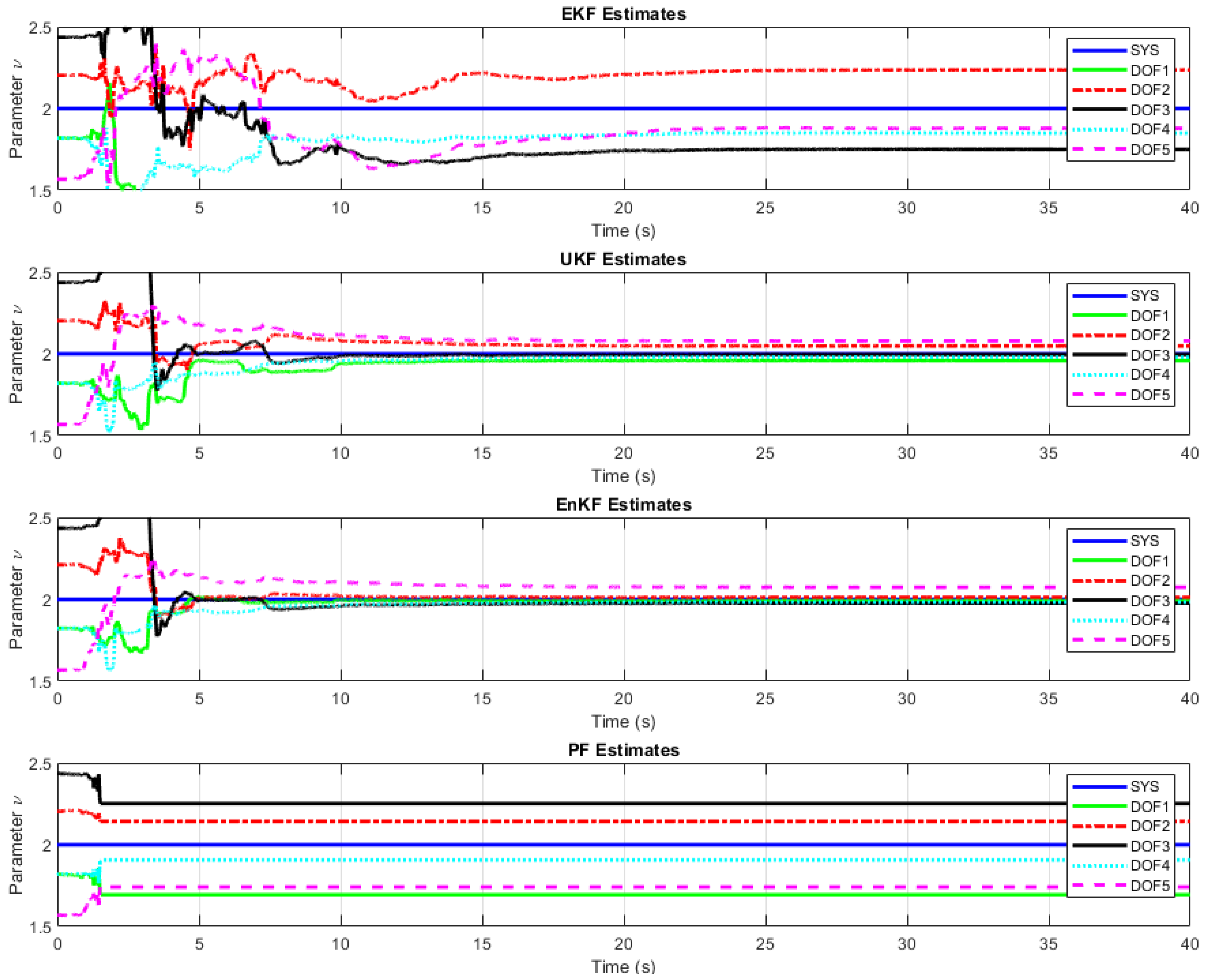
| EKF | |||
| UKF | |||
| EnKF | |||
| PF |
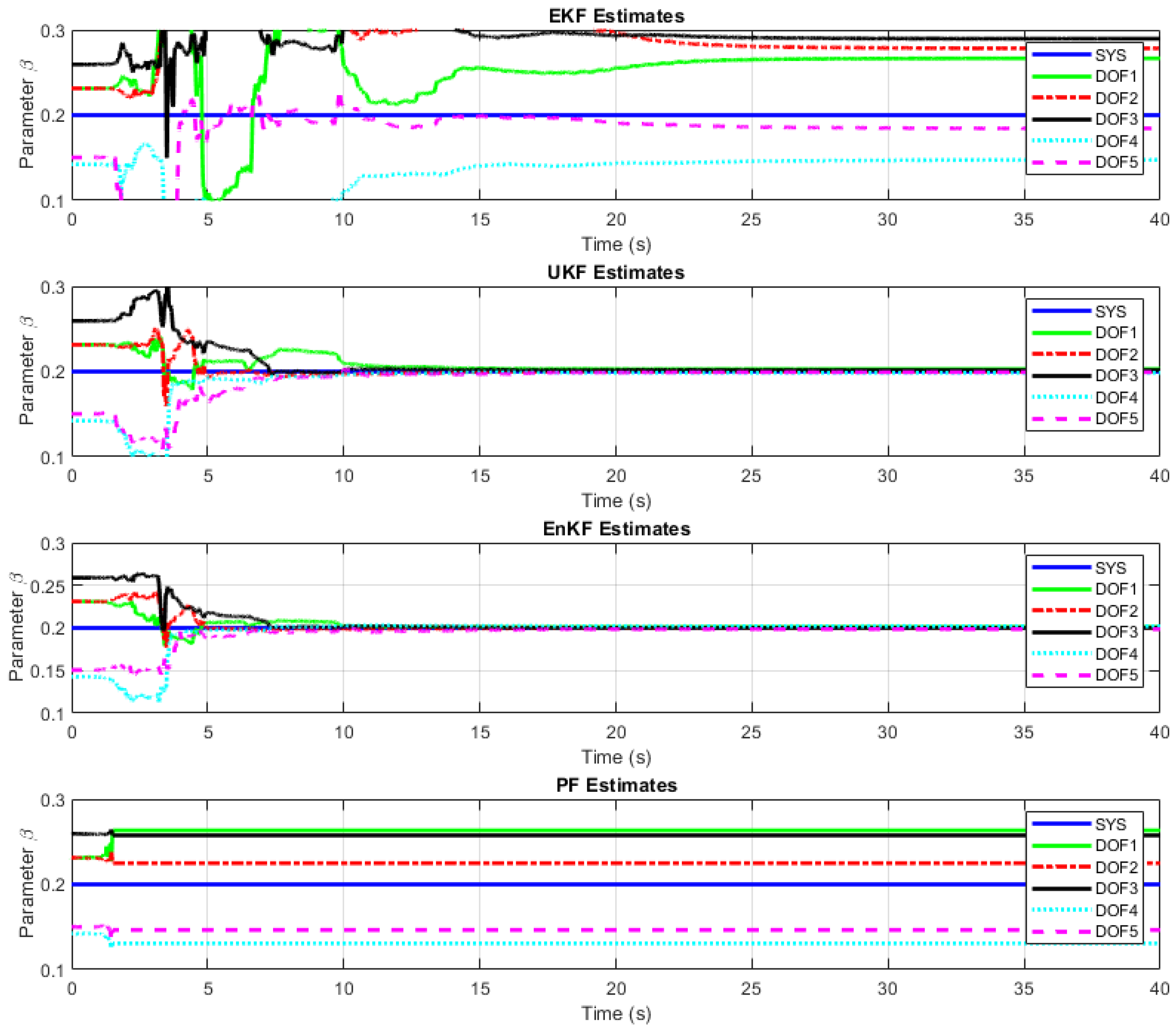
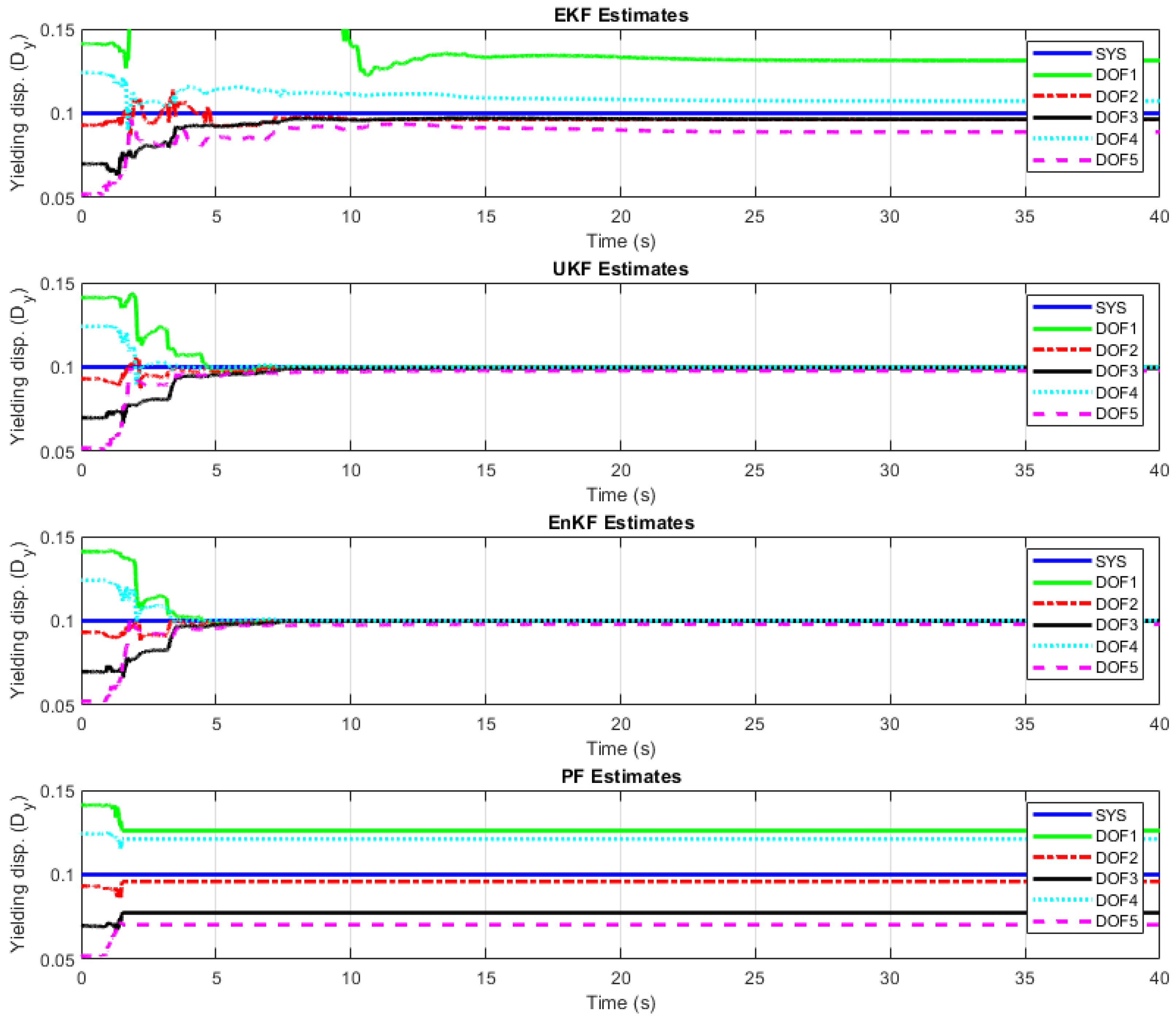
| EKF | |||
| UKF | |||
| EnKF | |||
| PF |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Erazo, K. Parameter Estimation of Nonlinear Structural Systems Using Bayesian Filtering Methods. Vibration 2025, 8, 1. https://doi.org/10.3390/vibration8010001
Erazo K. Parameter Estimation of Nonlinear Structural Systems Using Bayesian Filtering Methods. Vibration. 2025; 8(1):1. https://doi.org/10.3390/vibration8010001
Chicago/Turabian StyleErazo, Kalil. 2025. "Parameter Estimation of Nonlinear Structural Systems Using Bayesian Filtering Methods" Vibration 8, no. 1: 1. https://doi.org/10.3390/vibration8010001
APA StyleErazo, K. (2025). Parameter Estimation of Nonlinear Structural Systems Using Bayesian Filtering Methods. Vibration, 8(1), 1. https://doi.org/10.3390/vibration8010001






