Study on the Mechanism and Suppression of Harmonic Vibration of AMB-Rotor System
Abstract
1. Introduction
2. Analysis of Harmonic Vibration Mechanism
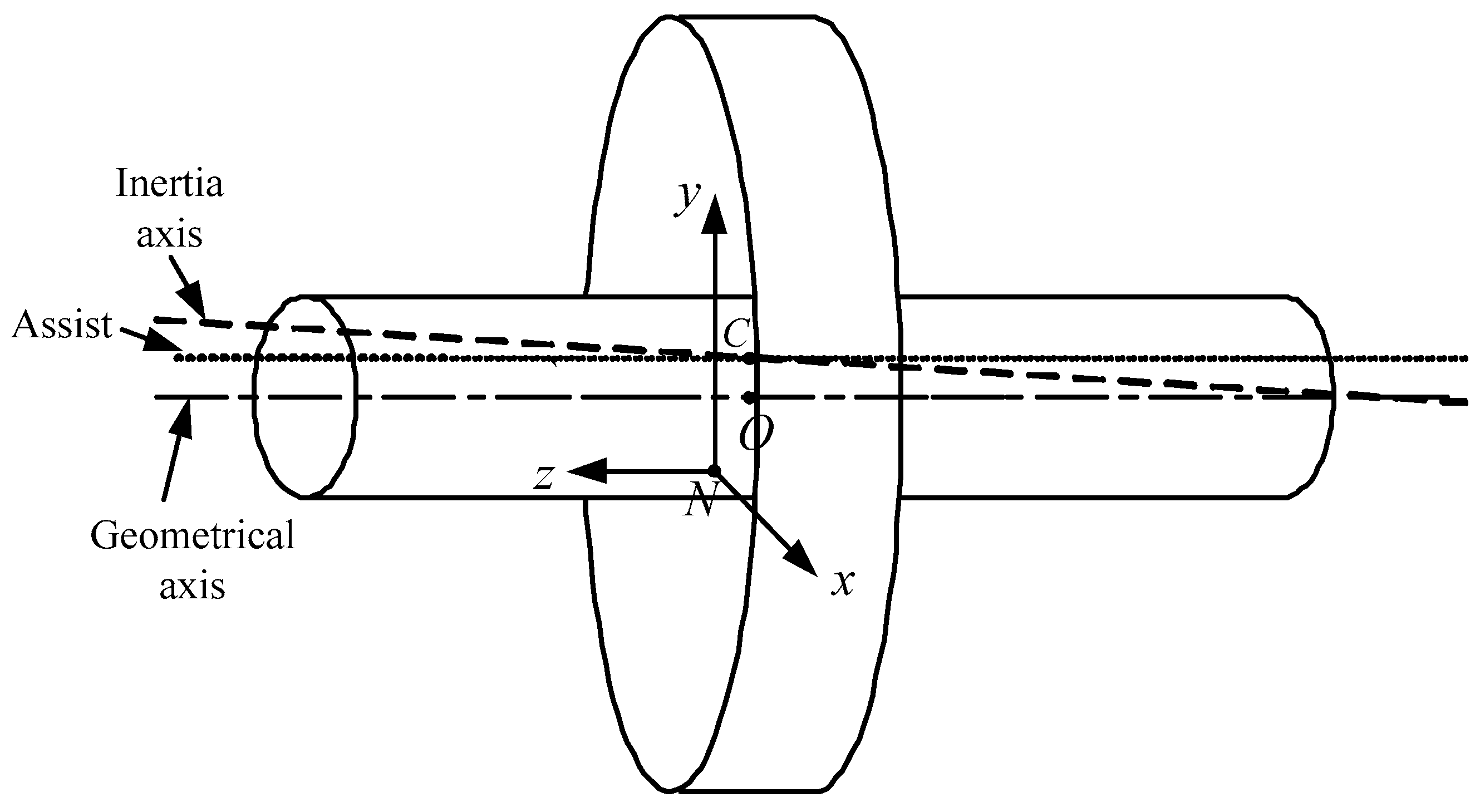
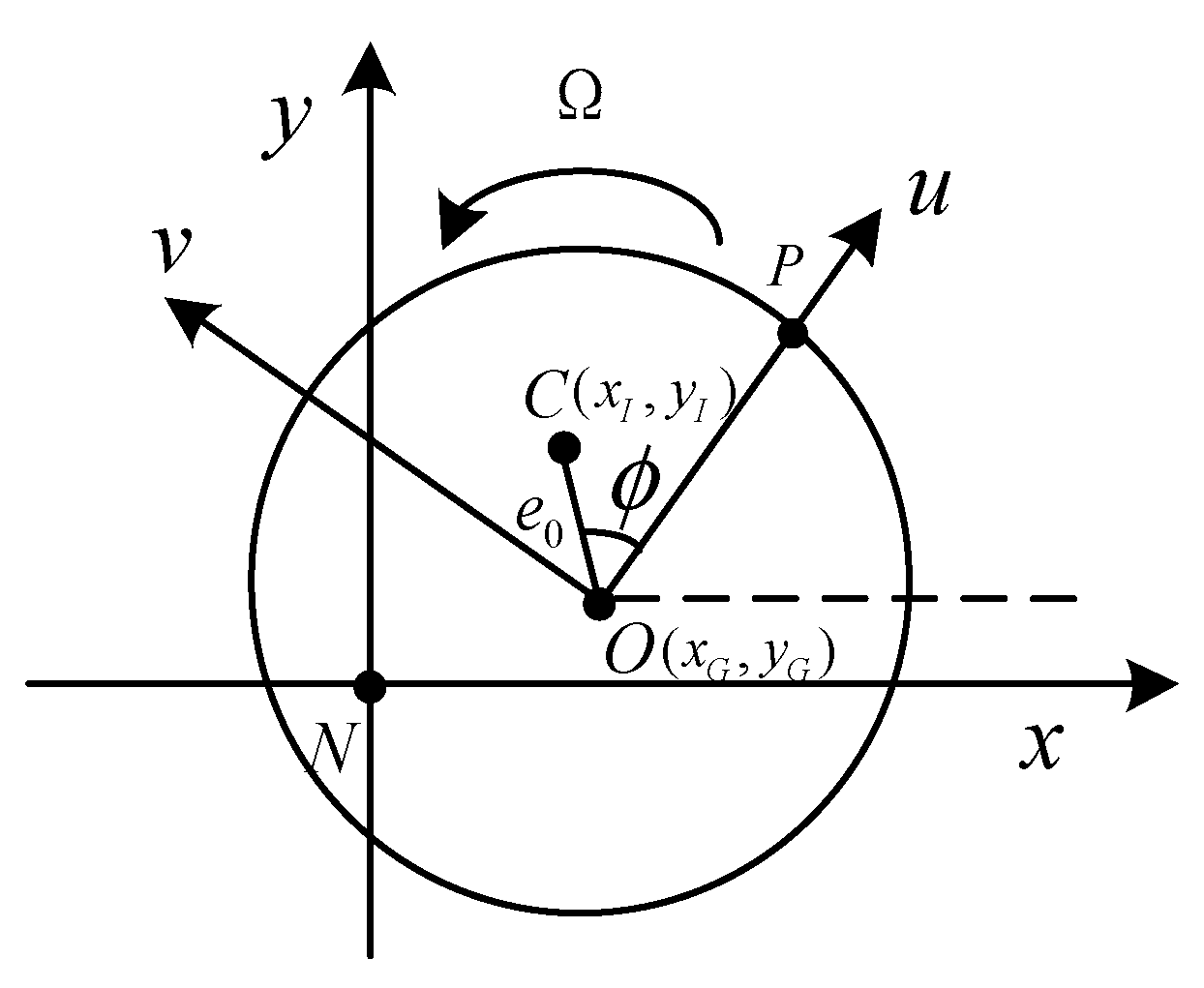
2.1. Mechanism Analysis of Unbalanced Vibration
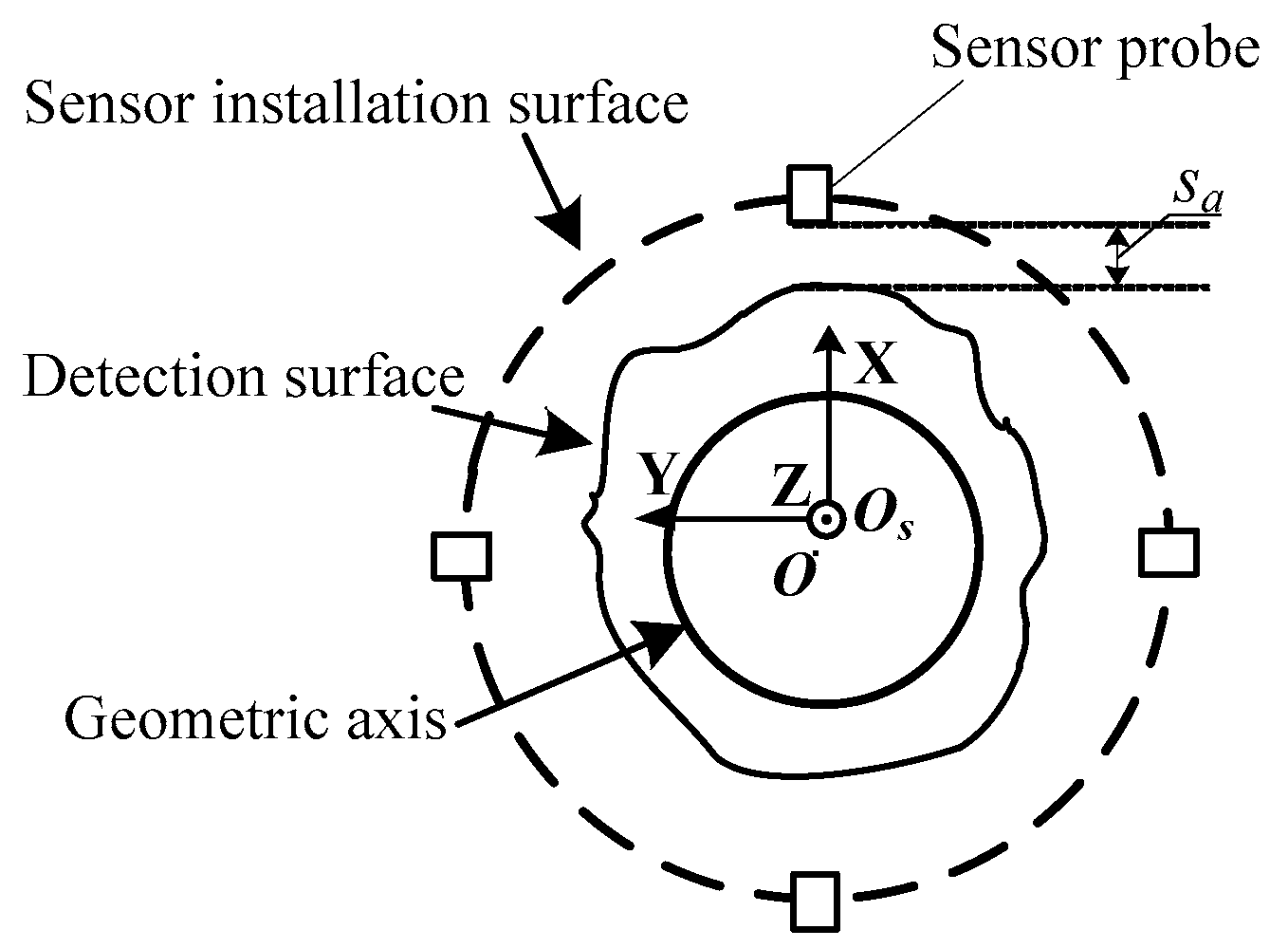
2.2. Mechanism Analysis of Harmonic Vibration
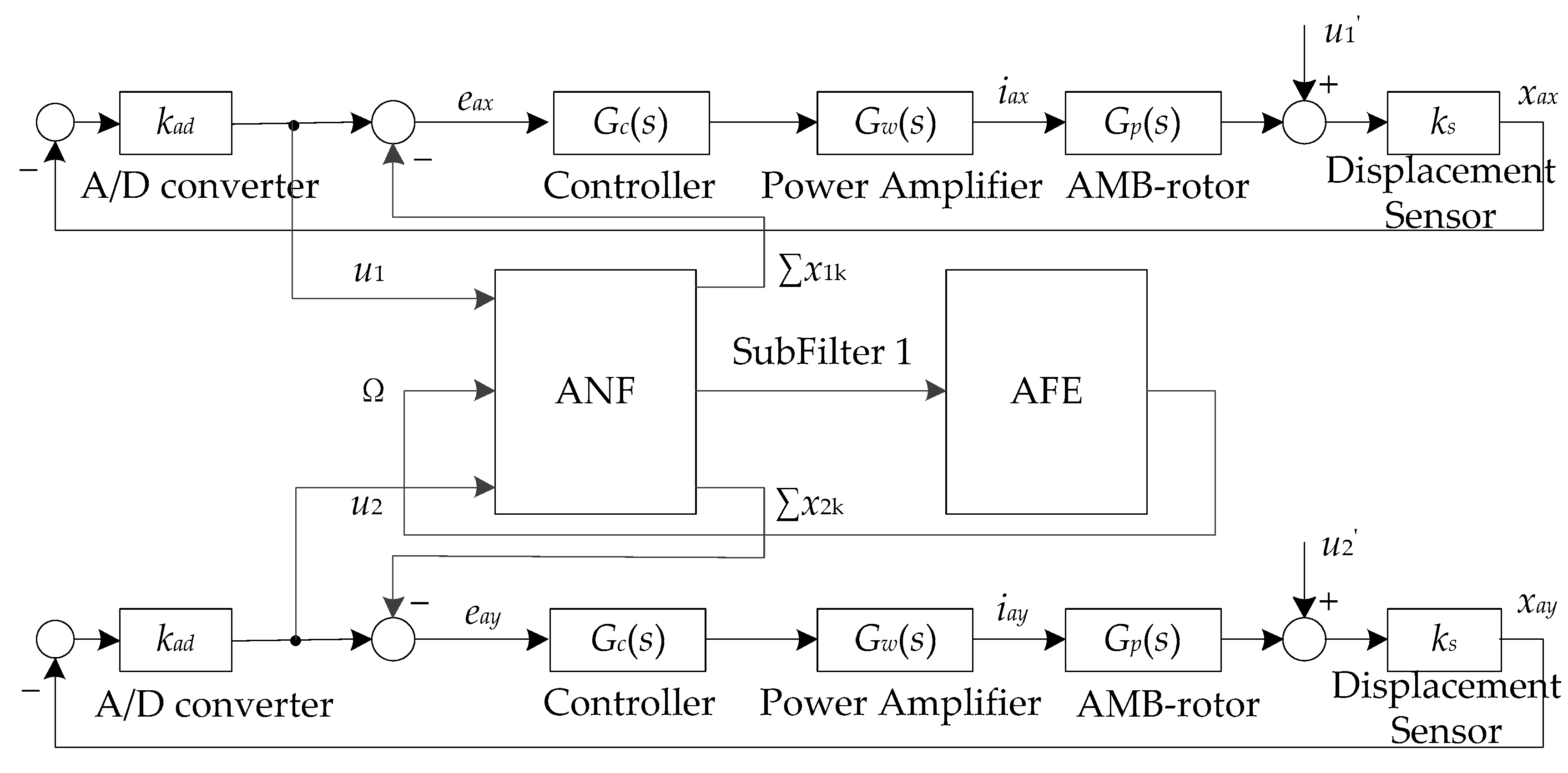
3. Suppression of Harmonic Current with Adaptive Frequency Estimation
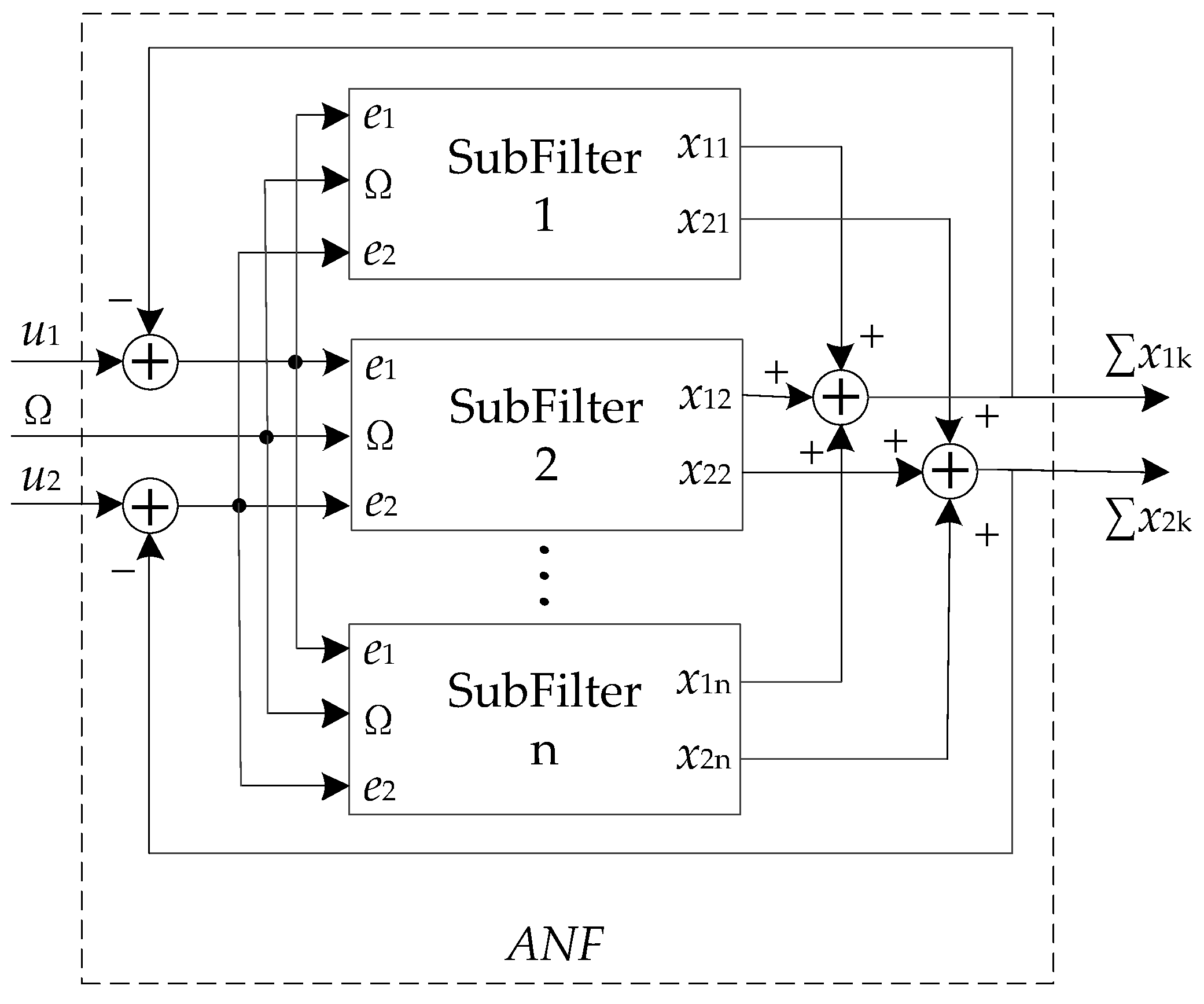
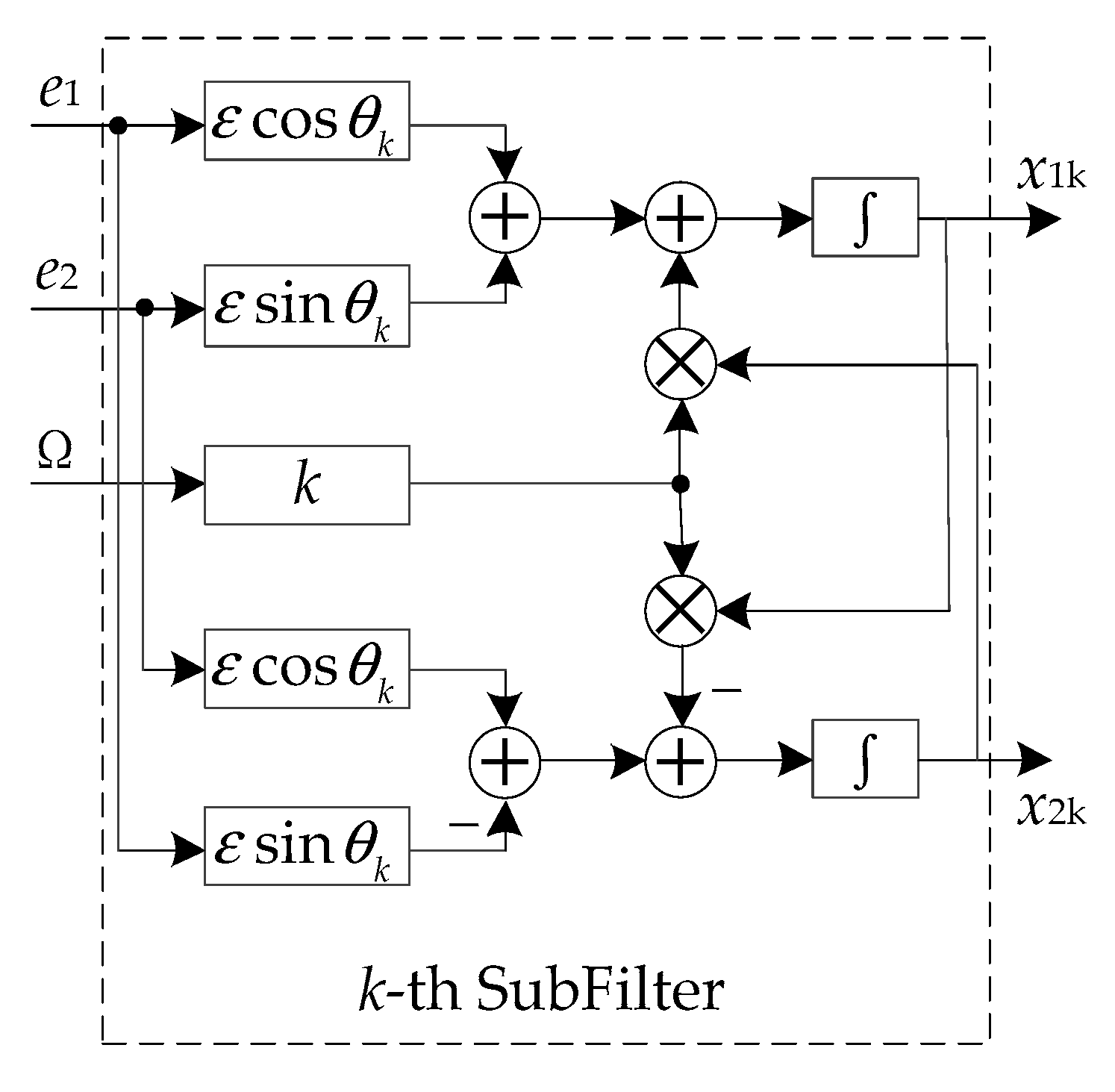
3.1. The Structure of Novel Adaptive Notch Filter for Harmonic Sinusoidal Signals
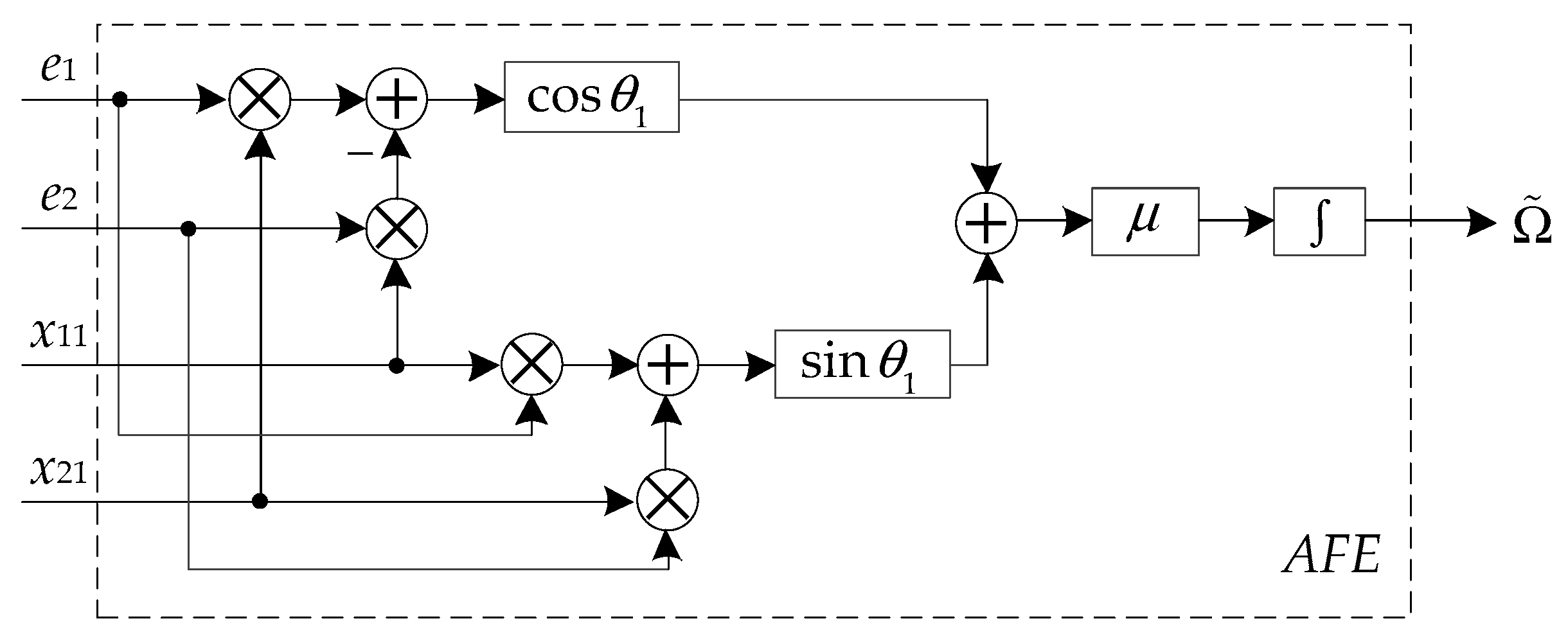
3.2. Adaptive Frequency Estimation
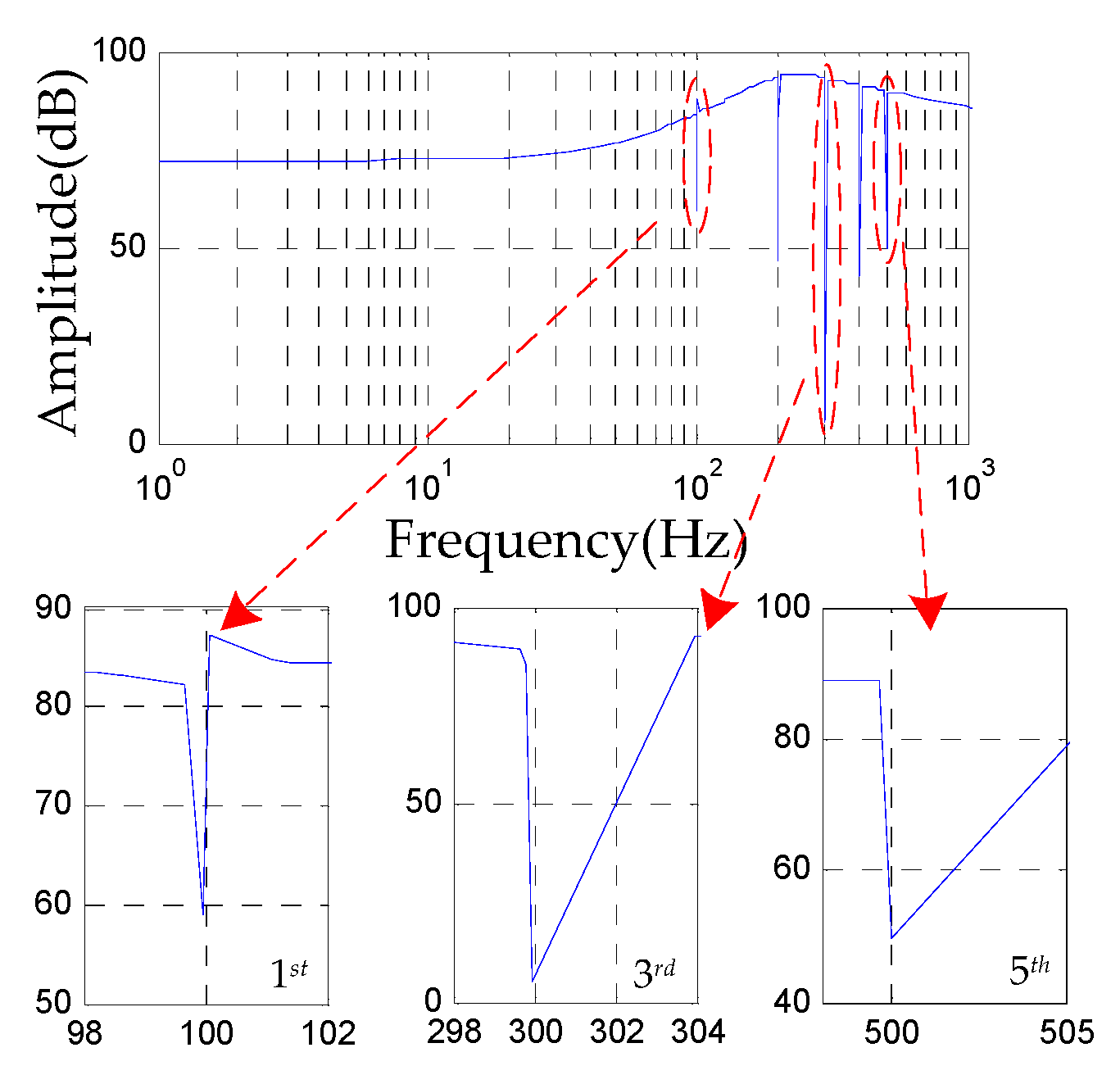
3.3. Analysis of Harmonic Current Suppression
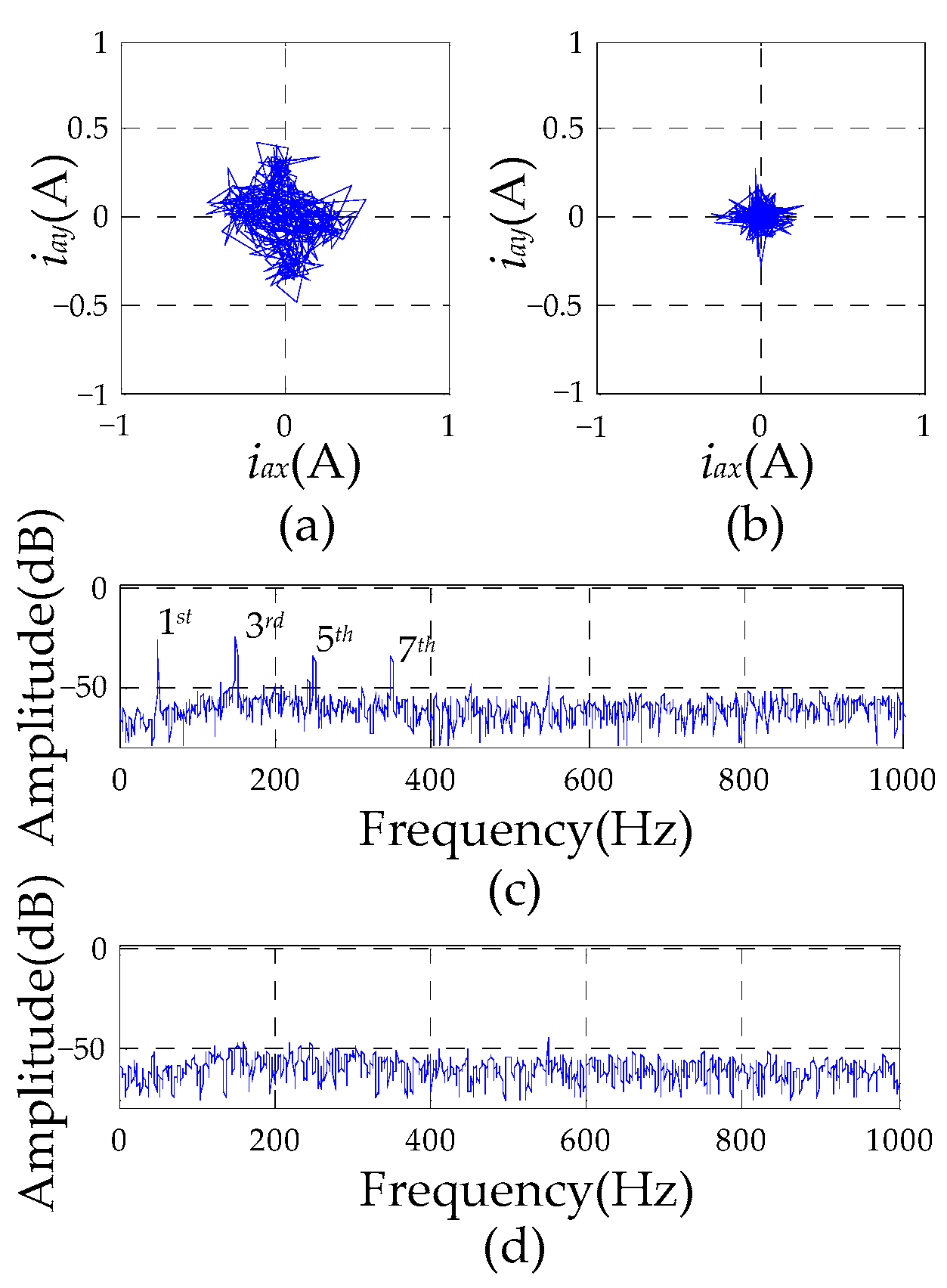
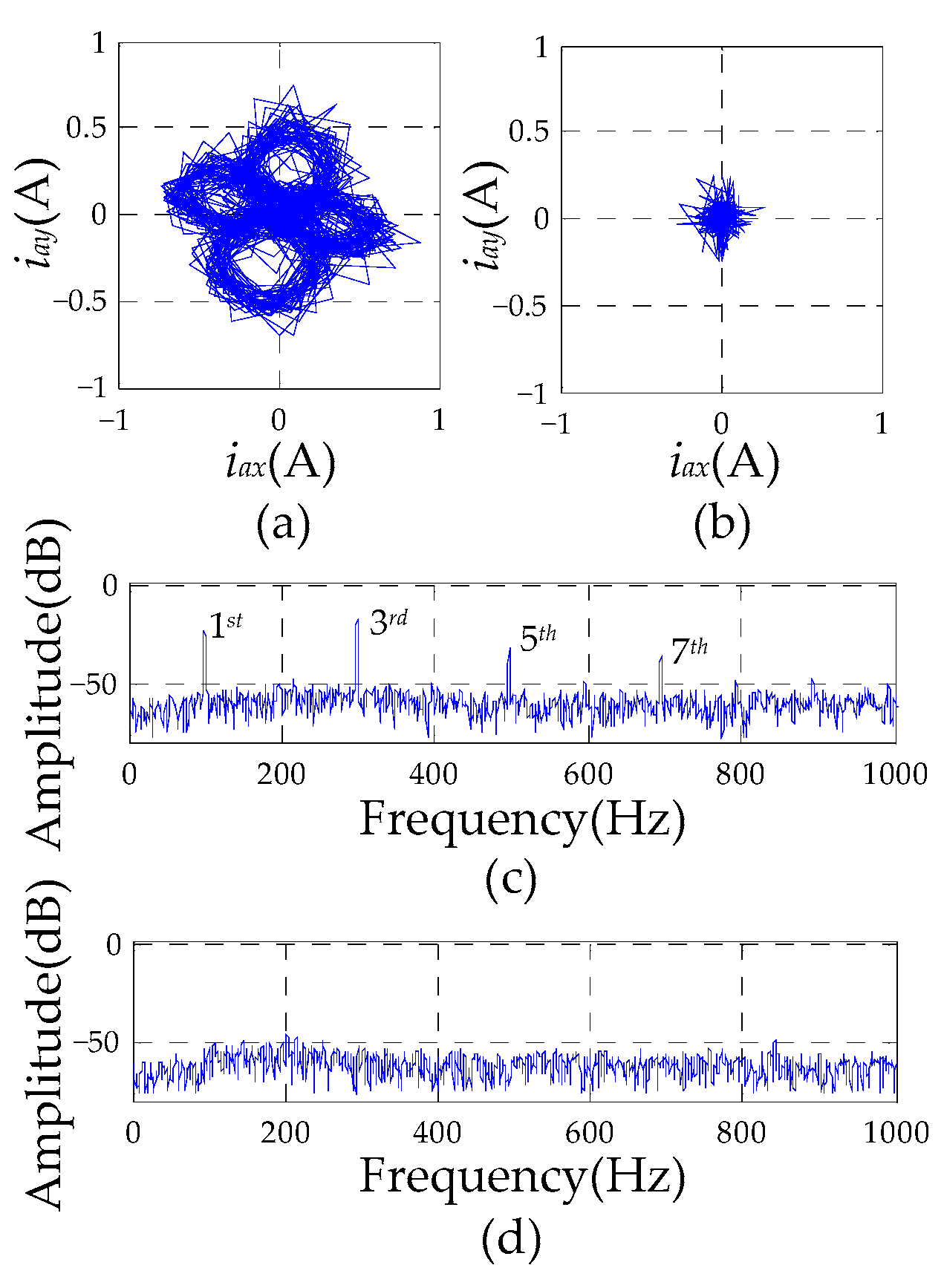
4. Results
4.1. Experimental System
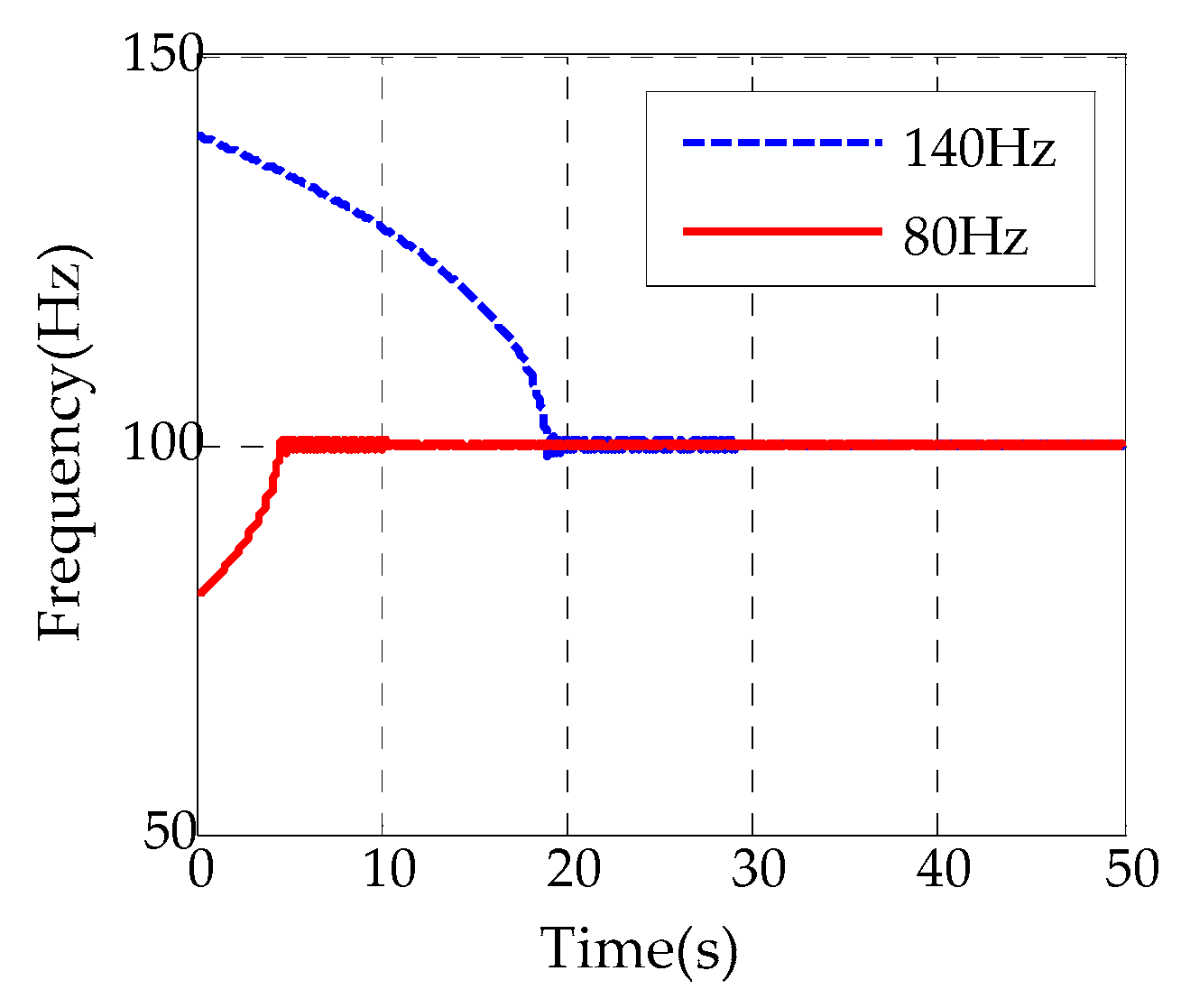
4.2. Simulation Results
4.3. Experimental Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Angeletti, F.; Gasbarri, P.; Sabatini, M. Optimal design and robust analysis of a net of active devices for micro-vibration control of an on-orbit large space antenna. Acta Astron. 2019, 164, 241–253. [Google Scholar] [CrossRef]
- Li, L.; Wang, L.; Yuan, L. Micro-vibration suppression methods and key technologies for high-precision space optical instruments. Acta Astron. 2021, 180, 417–428. [Google Scholar]
- Zhou, X.; Sun, J.; Li, H.; Lu, M.; Zeng, F. PMSM open-phase fault-tolerant control strategy based on four-leg inverter. IEEE Trans. Power Electron. 2020, 35, 2799–2808. [Google Scholar]
- Ji, J.C.; Leung, A.Y.T. Resonances of a non-linear s.d.o.f. system with two time-delays in linear feedback control. J. Sound Vib. 2002, 253, 985–1000. [Google Scholar]
- Ji, J.C.; Hansen, C.H. Non-linear oscillations of a rotor in active magnetic bearings. J. Sound Vib. 2001, 240, 599–612. [Google Scholar] [CrossRef]
- Sun, J.; Zhao, J.; Wang, K. Online surge detection method based on axial displacement sensor of MSCC. IEEE Sens. J. 2019, 19, 6029–6036. [Google Scholar] [CrossRef]
- Tang, J.; Peng, Z.; Liu, B. Control of rotor’s vernier-gimballing for a magnetically suspended flywheel. IEEE Trans. Ind. Electron. 2017, 64, 2972–2981. [Google Scholar]
- Huang, L.; Wu, Z.; Wang, K. Indirect measurement of rotor dynamic imbalance for control moment gyroscopes via gimbal disturbance observer. Sensors 2018, 18, 1873. [Google Scholar] [CrossRef]
- Serdar, H.; Ozcelik, Z. Design of laboratory dynamic balancing device and investigation of vibrations of rotating bodies. Eng. Technol. Appl. Sci. Res. 2021, 6, 9–21. [Google Scholar]
- Li, J.; Liu, G.; Zheng, S.; Cui, P. Micro-jitter control of magnetically suspended control moment gyro using adaptive LMS algorithm. IEEE/ASME Trans. Mech. 2022, 27, 327–335. [Google Scholar] [CrossRef]
- Zheng, S.; Chen, Q.; Ren, H. Active balancing control of AMB-rotor systems using a phase-shift notch filter connected in parallel mode. IEEE Trans. Ind. Electron. 2016, 63, 3777–3785. [Google Scholar]
- Jiang, K.; Zhu, C.; Tang, M. A uniform control method for imbalance compensation and automation balancing in active magnetic bearing-rotor systems. J. Dyn. Sys. Meas. Con. 2012, 134, 021006–021019. [Google Scholar]
- Li, J.; Liu, G.; Cui, P. Suppression of harmonic vibration in AMB-Rotor systems using double-input adaptive frequency estimator. IEEE Trans. Ind. Electron. 2021, 69, 2986–2995. [Google Scholar] [CrossRef]
- Kim, C.; Lee, C. In situ runout identification in active magnetic bearing system by extended influence coefficient method. IEEE/ASME Trans. Mech. 1997, 2, 51–57. [Google Scholar]
- Setiawan, J.D.; Mukherjee, R.; Maslen, E.H. Adaptive compensation of sensor runout for magnetic bearings with uncertain parameters: Theory and experiments. J. Dyn. Sys. Meas. Con. 2001, 123, 211–218. [Google Scholar] [CrossRef]
- Cai, K.; Deng, Z.; Peng, C. Suppression of harmonic vibration in magnetically suspended centrifugal compressor using zero-phase odd-harmonic repetitive controller. IEEE Trans. Ind. Electron. 2020, 67, 7789–7797. [Google Scholar] [CrossRef]
- Cui, P.; Li, W.; Zhou, X. Multi-order repetitive controller for harmonic current suppression in magnetically suspended rotor system. J. Vib. Con. 2020, 27, 2657–2668. [Google Scholar]
- Li, J.; Liu, G.; Cui, P.; Zheng, S. An improved resonant controller for AMB-rotor system subject to displacement harmonic disturbance. IEEE Trans. Power Electron. 2022, 37, 5235–5244. [Google Scholar] [CrossRef]
- Zhou, K.; Lu, W.; Yang, Y. Harmonic control: A natural way to bridge resonant control and repetitive control. In Proceedings of the American Control Conference, Washington, DC, USA, 17–19 June 2013; pp. 3189–3193. [Google Scholar]
- Peng, C.; Zhou, Q. Direct vibration force suppression for magnetically suspended motor based on synchronous rotating frame transformation. IEEE Access 2019, 7, 37639–37649. [Google Scholar]
- Cui, P.; Du, L.; Zhou, X. Harmonic vibration control of MSCMG based on multi-synchronous rotating frame transformation. IEEE Trans. Ind. Electron. 2022, 69, 1717–1727. [Google Scholar] [CrossRef]
- Liu, G.; Li, J.; Zheng, S.; Chen, Q.; Liu, H. Suppression of synchronous current using double input improved adaptive notch filter algorithm. IEEE Trans. Ind. Electron. 2020, 67, 8599–8607. [Google Scholar] [CrossRef]






| Parameter | Value | Parameter | Value |
|---|---|---|---|
| m | 16.7 kg | kP | 4.7 |
| ki | 600 N·A−1 | kI | 2.5 |
| kx | 2.4 × 106 N·m−1 | kD | 0.001725 |
| R | 2.3 Ω | Tf | 0.000225 |
| L | 20 mH | kad | 1365 |
| kamp | 0.8 | ks | 8333 |
| kico | 6.4 | kc | 0.495 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Q.; Li, J. Study on the Mechanism and Suppression of Harmonic Vibration of AMB-Rotor System. Vibration 2024, 7, 83-97. https://doi.org/10.3390/vibration7010005
Chen Q, Li J. Study on the Mechanism and Suppression of Harmonic Vibration of AMB-Rotor System. Vibration. 2024; 7(1):83-97. https://doi.org/10.3390/vibration7010005
Chicago/Turabian StyleChen, Qi, and Jinlei Li. 2024. "Study on the Mechanism and Suppression of Harmonic Vibration of AMB-Rotor System" Vibration 7, no. 1: 83-97. https://doi.org/10.3390/vibration7010005
APA StyleChen, Q., & Li, J. (2024). Study on the Mechanism and Suppression of Harmonic Vibration of AMB-Rotor System. Vibration, 7(1), 83-97. https://doi.org/10.3390/vibration7010005







