Free-Vibration Analysis for Truncated Uflyand–Mindlin Plate Models: An Alternative Theoretical Formulation

Abstract

Plates are flat structural elements whose thickness is small in relation to the size of the surface. Their use may include engine foundations, reinforced concrete bridge elements or parts of various floating structures. Consequently, knowledge of their mechanical behavior under static and dynamic loads is of primary importance in engineering applications and of interest from a structural point of view. As a result, numerous works existing in the literature have investigated the mechanical properties of plates using various plate models, such as Reissner’s theory, Levinson’s theory, Kirchhoff’s theory and Mindlin’s theory, and their static and dynamic behavior has been examined. In the present paper the truncated Uflyand–Mindlin plate equation is proposed. According to Uflyand–Mindlin theory, an alternative theoretical formulation is presented for the free-vibration analysis of plates, and the equations of motion and the general corresponding boundary conditions are derived. This paper develops the truncated Uflyand–Mindlin plate equation, i.e., without the fourth-order derivative, by means of the direct method and variational formulation. The first-order shear deformable plate theory developed by Elishakoff, which takes into account rotational inertia and shear deformation and does not include a fourth-order time derivative, is variationally derived here. This derivation complements that performed by Mindlin some 70 years ago. The innovative aspect of the suggested strategy is that variational and direct methods for studying plate dynamics are analogous. Finding the third equation of the reduced Uflyand–Mindlin equations, the accompanying boundary conditions and their mathematical resemblance are the goals of the presented formulations. In order to solve the dynamic equilibrium problem of a truncated Uflyand–Mindlin equation via a variational formulation, it is demonstrated that the differential equations and the corresponding boundary conditions have the same form as those found using the direct technique. This paper successfully completes this task. Finally, in order to validate the effectiveness and correctness of the proposed procedure, a numerical example of the case of a plate simply supported at all four ends is proposed.

1. Introduction

Since Gustav Robert Kirchhoff proposed his theory [1,2,3], Claude-Louis Navier [4] and Eric Reissner [5] have elaborated several calculation theories with the objective of widening the field of application of plates. According to [4], Kirchhoff’s plate theory is one of the most commonly used theories for thin plates. It is based on two ideas: (1) that plate mid-plane elements do not elongate during small plate deflections under lateral load, and (2) that lines initially perpendicular to the plate mid-plane remain straight during bending and normal to the deflected plate mid-plane. These presumptions are very close to the notion of plane cross-sections that is currently used in the basic theory of plate bending. Kirchhoff found the right formulation for the potential energy of a bent plate using his two conditions. The principle of virtual work asserts that for any virtual displacements, the work performed by the load q spread over the plate must equal the increase in the plate’s potential energy. Kirchhoff then applied this principle to obtain the differential equation of bending. Additionally, he demonstrated that there are only two boundary conditions, not three as Poisson assumed.

The refining effects of shear deformation in a static setting were apparently introduced by Basset [6], Reissner [7,8,9], Bolle [10] and Hencky [11]. The first researcher to develop dynamic equations of plates with rotary inertia and shear deformation was Uflyand [12] using the dynamic equilibrium equations. Mindlin [13,14,15] derived the same equations variationally. Thus, the development of refined plate equations followed a similar fate to their classical counterpart a century ago: first, the equations were derived, and then, they were formulated variationally. Whereas alternative names for this theory are possible, like the refined theory of plates or first-order shear deformable plate theory, we prefer—in order to emphasize the original developers—to dub it the Uflyand–Mindlin plate theory. An analogous avenue was chosen by Wojnar in [16,17], Rossikhin and Shitikova in [18,19] and Loktev in [20]. A review of Uflyand–Mindlin theory is given in the recent monograph of Elishakoff [21].

The original Uflyand–Mindlin equations, just like the Timoshenko–Ehrenfest equations for beams, contain the fourth-order time derivative. Elishakoff in [22] suggested neglecting this term to arrive at a simplified equation. Elishakoff [21] refers to the resulting equation as the truncated Uflyand–Mindlin equation. It is important to point out that the truncated Timoshenko–Ehrenfest beam model was provided by Elishakoff et al. [23] and by Erbaş et al. [24]. Likewise, the validation of the truncated plate theory was furnished, independently of Elishakoff [22], by Goldenveiser et al. [25] and Kaplunov et al. [26]. In particular, higher-order theories for shells and plates are proposed in the studies by Goldenveizer et al. [25] and Kaplunov et al. [26]. Here, modified transverse and tangential inertia operators take the place of the conventional inertia terms. It is common knowledge that higher-order theories make studying vibrations and waves in plates and shells easier because they increase the application limits of 2D theories without adding to the number of partial modes in the solution. The lack of finer boundary conditions with the same level of approximation is the sole issue.

In the present paper, the truncated Uflyand–Mindlin plate equation is proposed. According to Uflyand–Mindlin theory, an alternative theoretical formulation for the free-vibration analysis of plates is presented, and the equations of motion and the general corresponding boundary conditions are derived. This paper develops the truncated Uflyand–Mindlin plate equation, i.e., without the fourth-order derivative, by means of the direct method and variational formulation. Variational derivation is the basis for finite element formulation and application, as was shown by Falsone et al. [27,28]. In [27], the authors propose a new FE approach for the dynamic analysis of the Mindlin plate. The model is based on the Mindlin equations that are consistent and do not include the higher-order time derivative contribution. In [28], a novel class of shape polynomials is proposed in order to reduce the inconsistency of the higher-order spectra, and the interdependent shape polynomials for the Timoshenko beam model are determined. In addition, many finite element formulations for the Mindlin plate have been developed and incorporated into commercial FEM software. In the literature, there are finite element formulations associated with the original Uflyand–Mindlin equations (Häggblad and Bathe, [29], Brezzi et al. [30], Dolbow et al. [31]).

The innovative aspect of the suggested strategy is that variational and direct methods for studying plate dynamics are analogous. Finding the third equation of the reduced Uflyand–Mindlin equations, the accompanying boundary conditions and their mathematical resemblance are the goals of the presented formulations. In order to solve the dynamic equilibrium problem of a truncated Uflyand–Mindlin variational formulation, it is demonstrated that the differential equations and the corresponding boundary conditions have the same form as those found using the direct technique. To emphasize this, the truncated set $\mathsf{\Omega }$ equation is much simpler than original Uflyand–Mindlin equation. Moreover, it is desirable to have a variational formulation that leads to truncated equations, for example, for possible use within FEM. This paper accomplishes exactly this task. Finally, in order to validate the effectiveness and correctness of the proposed procedure, a numerical example of the case of a plate simply supported at all four ends is proposed. The authors are well aware that Levy plates and other combinations of boundary conditions can also be considered. The purpose, however, of this paper is to show the novelty of a proposed analytical approach to dynamic plate analysis. A single, simple numerical example has, in fact, been presented because the leaning plate is amply supported by data and results from the literature, thus allowing validation of the correctness of the procedure proposed in the present research.

The suggested strategy is unusual in that it provides a flawless comparison between variational and direct methods for the dynamic analysis of plates. The proposed formulations attempt to discover the truncated Uflyand–Mindlin equations and the accompanying boundary conditions. Their mathematical closeness is established by employing the two separate approaches. It is shown that the differential equations and matching boundary conditions that are utilized in the variational formulation of the dynamic problem of a truncated Uflyand–Mindlin equation have the same form as the solution found using the direct technique. Since the suggested theory is variationally consistent, the identical governing equation and boundary conditions are reached using the variational technique as well as the direct geometric approach. This paper fills a vacuum in the literature by providing the precise variational theory for this “truncated plate”. To the best of the authors’ knowledge, no analytical formulation has been proposed for this shortened model in any of the literature.

2. Mathematical Model

2.1. Pioneering and Modern Plate Studies

Plates are a type of flat structural element where the thickness is relatively minimal compared to the surface area. They can be used for engine foundations, sections of floating constructions or components of reinforced concrete bridges. Consequently, knowledge of their mechanical behavior becomes of fundamental importance and interest from a structural point of view. As result, an extensive study of the mechanical properties of plates was conducted and their static and dynamic behavior was examined using several plate models, such as Reissner theory [5,7], Shimpi refined theory [32], Reddy theory [33], Levinson theory [34], Kirchhoff theory [3,35], Mindlin theory [13,14,15,36], etc. The earliest works are those of Reissner [8] and Mindlin [13], in which it is assumed that the plate cross-section remains flat but not perpendicular to the mean plate surface. In Mindlin’s theory, two cross-sectional rotation angles and plate deflection are the unknown variables in a system of three differential equations of motion. The most fundamental and widely applied theory of plates is the Kirchhoff plate theory, often known as the conventional small deflection theory of thin plates. Despite the obvious mathematical simplicity of the governing equations, it has been found to produce satisfactory results for thin plates. However, the theory has a number of drawbacks that have prompted the development of other plate theories, including the Reissner, Mindlin, Reddy, Levinson and Shimpi refined plate theories. In particular, in [32], a variationally consistent hypothesis is provided. Also, it is demonstrated that, in many ways, it is quite comparable to traditional plate theory and does not call for a shear correction factor. In [33], a higher-order plate shear deformation theory that takes the von Karman strains into account is developed, and exact solutions for simply supported plates are produced using the linear theory. The outcomes are compared to the exact solutions of the three-dimensional elasticity theory.

In this study, a unique formulation of the Uflyand–Mindlin plate theory that takes into consideration shear deformation and rotating inertia is developed. It is established that the Uflyand–Mindlin theory can be compared to the Timoshenko–Ehrenfest theory for beams, which includes shear deformation in the flexural analysis of beams. As Grigolyuk and Selezov [37] mention, “the dynamic equations of the plates were apparently first obtained by Franciscus Gehring [38]. His derivation was included by Gustav Kirchhoff in his 30th lecture on mathematical physics [39]. More late exposition of the problem is available in the book by Paul Germain [40]”. The Uflyand–Mindlin plate theory, also referred to as the first-order shear deformation plate theory, is the most basic plate theory to account for transverse shear strains.

2.2. Direct Method

In this section, using the direct method, the equilibrium of the plate element is presented.

Consider a thick rectangular plate whose dimensions are as follows: length a, width b and uniform thickness h. It is further assumed that the plate consists of an isotropic and homogeneous material. Assuming the Cartesian coordinate system $(x,y,z)$, as shown in Figure 1, the transverse displacement in a Mindlin plate of uniform thickness h is denoted as w with respect to abscissa z, where z represents the spatial coordinate along the beam and the $xy$-plane coincides with the geometrical mid-plane of the undeformed plate.

In Figure 2a,b, ${\mathsf{\Psi }}_x$ and ${\mathsf{\Psi }}_y$ indicate the angles of rotation of a normal line due to the bending of the plate with respect to the x and y axes, respectively.

Applying the formulation of the Mindlin plate equations, for the plate under consideration, the displacements along the x, y and z directions are assumed as follows:

$$\begin{array}{cc}\hfill & u_x=z{\mathsf{\Psi }}_x\hfill \\ \hfill & u_y=z{\mathsf{\Psi }}_y\hfill \\ \hfill & u_z=w\hfill \end{array}$$

(1)

where $w(x,y,t)$ is the transverse deflection of a point on the middle plane (i.e., $z=0$). Adopting the Kirchhoff–Love assumption, the displacement functions are as follows:

$$\begin{array}{cc}\hfill & {\overline{u}}_x=-z\frac{\mathsf{\partial }w}{\mathsf{\partial }x}\hfill \\ \hfill & {\overline{u}}_y=-z\frac{\mathsf{\partial }w}{\mathsf{\partial }y}\hfill \\ \hfill & {\overline{u}}_z=w\hfill \end{array}$$

(2)

In both theories, where the displacement field equations are decoupled, the effect of in-plane displacement is ignored and studied independently. Also, our focus here is solely on the flexural–shear case, the inextensibility of a transverse normal can be removed by assuming that the transverse deflection varies through the thickness.

Based upon Equation (1) and for a small-displacement assumption, the kinematics relations are given by the following equations:

$$\begin{array}{cc}\hfill & {ϵ}_{xx}=z\frac{\mathsf{\partial }{\mathsf{\Psi }}_x}{\mathsf{\partial }x}\hfill \\ \hfill & {ϵ}_{yy}=z\frac{\mathsf{\partial }{\mathsf{\Psi }}_y}{\mathsf{\partial }y}\hfill \\ \hfill & {ϵ}_{xy}=\frac{1}{2}z\left(\frac{\mathsf{\partial }{\mathsf{\Psi }}_x}{\mathsf{\partial }y}+\frac{\mathsf{\partial }{\mathsf{\Psi }}_y}{\mathsf{\partial }x}\right)\hfill \\ \hfill & {ϵ}_{xz}=\frac{1}{2}\left(\frac{\mathsf{\partial }w}{\mathsf{\partial }x}+{\mathsf{\Psi }}_x\right)\hfill \\ \hfill & {ϵ}_{yz}=\frac{1}{2}\left(\frac{\mathsf{\partial }w}{\mathsf{\partial }y}+{\mathsf{\Psi }}_y\right)\hfill \end{array}$$

(3)

where ${ϵ}_{xx}$, ${ϵ}_{yy}$ and ${ϵ}_{xy}$, ${ϵ}_{xz}$, ${ϵ}_{yz}$ represent normal strains and shear strains, respectively.

For homogeneous isotropic materials, the following stress–strain relations apply:

$$\begin{array}{cc}\hfill & {\sigma }_{xx}=\frac{\mathrm{E}}{\left(1-{\nu }^2\right)}\left({ϵ}_{xx}+\nu {ϵ}_{yy}\right)=\frac{\mathrm{E}}{\left(1-{\nu }^2\right)}\left(z\frac{\mathsf{\partial }{\mathsf{\Psi }}_x}{\mathsf{\partial }x}+\nu z\frac{\mathsf{\partial }{\mathsf{\Psi }}_y}{\mathsf{\partial }y}\right)\hfill \\ \hfill & {\sigma }_{yy}=\frac{\mathrm{E}}{\left(1-{\nu }^2\right)}\left({ϵ}_{yy}+\nu {ϵ}_{xx}\right)=\frac{\mathrm{E}}{\left(1-{\nu }^2\right)}\left(z\frac{\mathsf{\partial }{\mathsf{\Psi }}_y}{\mathsf{\partial }y}+\nu z\frac{\mathsf{\partial }{\mathsf{\Psi }}_x}{\mathsf{\partial }x}\right)\hfill \\ \hfill & {\tau }_{xy}=2\mathrm{G}{ϵ}_{xy}=\frac{\mathrm{E}z}{2(1+\nu )}\left(\frac{\mathsf{\partial }{\mathsf{\Psi }}_x}{\mathsf{\partial }y}+\frac{\mathsf{\partial }{\mathsf{\Psi }}_y}{\mathsf{\partial }x}\right)\hfill \\ \hfill & {\tau }_{xz}=2\mathrm{G}{ϵ}_{xz}=\frac{\mathrm{E}}{2(1+\nu )}\left(\frac{\mathsf{\partial }w}{\mathsf{\partial }x}+{\mathsf{\Psi }}_x\right)\hfill \\ \hfill & {\tau }_{yz}=2\mathrm{G}{ϵ}_{xz}=\frac{\mathrm{E}}{2(1+\nu )}\left(\frac{\mathsf{\partial }w}{\mathsf{\partial }y}+{\mathsf{\Psi }}_y\right)\hfill \end{array}$$

(4)

where ${\sigma }_{xx}$, ${\sigma }_{yy}$ and ${\tau }_{xy}$, ${\tau }_{xz}$, ${\tau }_{yz}$ are normal stresses and shear stresses, respectively. E is also Young’s modulus of elasticity, $\nu$ is Poisson’s coefficient and G is the shear modulus. In the usual plane stress, ${\sigma }_{zz}=0$ is assumed.

The following integrals across the thickness of the plate are used to determine the internal forces that result, such as bending moments, twisting moments and shear forces:

$$\begin{array}{cc}\hfill & {\mathrm{M}}_x={\int }_{-h/2}^{h/2}{\sigma }_{xx}zdz={\int }_{-h/2}^{h/2}\frac{\mathrm{E}{z}^2}{\left(1-{\nu }^2\right)}\left(\frac{\mathsf{\partial }{\mathsf{\Psi }}_x}{\mathsf{\partial }x}+\nu \frac{\mathsf{\partial }{\mathsf{\Psi }}_y}{\mathsf{\partial }y}\right)dz=D\left(\frac{\mathsf{\partial }{\mathsf{\Psi }}_x}{\mathsf{\partial }x}+\nu \frac{\mathsf{\partial }{\mathsf{\Psi }}_y}{\mathsf{\partial }y}\right)\hfill \\ \hfill & {\mathrm{M}}_y={\int }_{-h/2}^{h/2}{\sigma }_{yy}zdz={\int }_{-h/2}^{h/2}\frac{\mathrm{E}{z}^2}{\left(1-{\nu }^2\right)}\left(\frac{\mathsf{\partial }{\mathsf{\Psi }}_y}{\mathsf{\partial }y}+\nu \frac{\mathsf{\partial }{\mathsf{\Psi }}_x}{\mathsf{\partial }x}\right)dz=D\left(\frac{\mathsf{\partial }{\mathsf{\Psi }}_y}{\mathsf{\partial }y}+\nu \frac{\mathsf{\partial }{\mathsf{\Psi }}_x}{\mathsf{\partial }x}\right)\hfill \\ \hfill & {\mathrm{M}}_{xy}={\int }_{-h/2}^{h/2}{\tau }_{xy}zdz={\int }_{-h/2}^{h/2}\frac{\mathrm{E}{z}^2}{2(1+\nu )}\left(\frac{\mathsf{\partial }{\mathsf{\Psi }}_x}{\mathsf{\partial }y}+\frac{\mathsf{\partial }{\mathsf{\Psi }}_y}{\mathsf{\partial }x}\right)dz=\frac{D(1-\nu )}{2}\left(\frac{\mathsf{\partial }{\mathsf{\Psi }}_x}{\mathsf{\partial }y}+\frac{\mathsf{\partial }{\mathsf{\Psi }}_y}{\mathsf{\partial }x}\right)\hfill \\ \hfill & {\mathrm{V}}_x={\int }_{-h/2}^{h/2}{\tau }_{xz}dz={\int }_{-h/2}^{h/2}\frac{\mathrm{E}}{2(1+\nu )}\left(\frac{\mathsf{\partial }w}{\mathsf{\partial }x}+{\mathsf{\Psi }}_x\right)dz=\kappa \mathrm{G}h\left(\frac{\mathsf{\partial }w}{\mathsf{\partial }x}+{\mathsf{\Psi }}_x\right)\hfill \\ \hfill & {\mathrm{V}}_y={\int }_{-h/2}^{h/2}{\tau }_{yz}dz={\int }_{-h/2}^{h/2}\frac{\mathrm{E}}{2(1+\nu )}\left(\frac{\mathsf{\partial }w}{\mathsf{\partial }y}+{\mathsf{\Psi }}_y\right)dz=\kappa \mathrm{G}h\left(\frac{\mathsf{\partial }w}{\mathsf{\partial }y}+{\mathsf{\Psi }}_y\right)\hfill \end{array}$$

(5)

where D = $\frac{\mathrm{E}{h}^3}{12\left(1-{\nu }^2\right)}$ is the plate’s flexural rigidity and $\kappa$ is the shear correction factor, which depends not only on the geometric parameters, but also on the boundary conditions and loading of the plate. The shear correction factor is introduced in Mindlin theory to rectify the disparity between the distribution of transverse shear forces that are really seen and those that are calculated via the use of kinematic relations.

Also, assuming the plate is described as a Cauchy continuum, the governing partial differential equations of dynamic equilibrium are given by

$$\begin{array}{cc}\hfill & \frac{\mathsf{\partial }{\sigma }_{xx}}{\mathsf{\partial }x}+\frac{\mathsf{\partial }{\tau }_{yx}}{\mathsf{\partial }y}+\frac{\mathsf{\partial }{\tau }_{zx}}{\mathsf{\partial }z}-\rho \frac{{\mathsf{\partial }}^2{\overline{u}}_x}{\mathsf{\partial }{t}^2}=0\hfill \\ \hfill & \frac{\mathsf{\partial }{\tau }_{yx}}{\mathsf{\partial }x}+\frac{\mathsf{\partial }{\sigma }_{yy}}{\mathsf{\partial }y}+\frac{\mathsf{\partial }{\tau }_{zy}}{\mathsf{\partial }z}-\rho \frac{{\mathsf{\partial }}^2{\overline{u}}_y}{\mathsf{\partial }{t}^2}=0\hfill \\ \hfill & \frac{\mathsf{\partial }{\tau }_{zx}}{\mathsf{\partial }x}+\frac{\mathsf{\partial }{\tau }_{zy}}{\mathsf{\partial }y}+\frac{\mathsf{\partial }{\sigma }_{zz}}{\mathsf{\partial }z}-\rho \frac{{\mathsf{\partial }}^2{\overline{u}}_z}{\mathsf{\partial }{t}^2}=0\hfill \end{array}$$

(6)

where t is the time variable and $\rho$ is the mass density.

As can be easily seen in Equation (6), the truncated Uflyand–Mindlin plate formulation is characterized by introducing in the inertia forces the displacement relations, as defined in the Kirchhoff–Love theory. By using Equation (5), multiplication by z and integration over the thickness of the plate leads to the following system of three equations:

$$\begin{array}{cc}\hfill & \frac{\mathsf{\partial }{\mathrm{M}}_x}{\mathsf{\partial }x}+\frac{\mathsf{\partial }{\mathrm{M}}_{yx}}{\mathsf{\partial }y}-{\mathrm{V}}_x+\frac{\rho h^3}{12}\frac{{\mathsf{\partial }}^{2}w}{\mathsf{\partial }x\mathsf{\partial }{t}^2}=0\hfill \\ \hfill & \frac{\mathsf{\partial }{\mathrm{M}}_{yx}}{\mathsf{\partial }x}+\frac{\mathsf{\partial }{\mathrm{M}}_y}{\mathsf{\partial }y}-{\mathrm{V}}_y+\frac{\rho h^3}{12}\frac{{\mathsf{\partial }}^{2}w}{\mathsf{\partial }y\mathsf{\partial }{t}^2}=0\hfill \\ \hfill & \frac{\mathsf{\partial }{\mathrm{V}}_x}{\mathsf{\partial }x}+\frac{\mathsf{\partial }{\mathrm{V}}_y}{\mathsf{\partial }y}-\rho h\frac{{\mathsf{\partial }}^{2}w}{\mathsf{\partial }{t}^2}=0\hfill \end{array}$$

(7)

where ${\mathrm{V}}_x$ and ${\mathrm{V}}_y$ are the transverse shear forces, which can be obtained by integrating the stresses through the thickness of the plate. Also, the boundary conditions ${\tau }_{xz}(z=\pm \frac{h}{2})$ = ${\tau }_{yz}(z=\pm \frac{h}{2})=0$ and ${\sigma }_{zz}(z=\pm \frac{h}{2})=0$ are used.

Substituting Equation (5) into Equation (7), the equations of motion become

$$\frac{D}{2}\left[(1-\nu ){\nabla }^2{\mathsf{\Psi }}_x+(1+\nu )\left(\frac{{\mathsf{\partial }}^2{\mathsf{\Psi }}_x}{\mathsf{\partial }{x}^2}+\frac{{\mathsf{\partial }}^2{\mathsf{\Psi }}_y}{\mathsf{\partial }y\mathsf{\partial }x}\right)\right]-\kappa \mathrm{G}h\left({\mathsf{\Psi }}_x+\frac{\mathsf{\partial }w}{\mathsf{\partial }x}\right)+\frac{\rho h^3}{12}\left(\frac{{\mathsf{\partial }}^{3}w}{\mathsf{\partial }{t}^2\mathsf{\partial }x}\right)=0$$

(8)

$$\frac{D}{2}\left[(1-\nu ){\nabla }^2{\mathsf{\Psi }}_y+(1+\nu )\left(\frac{{\mathsf{\partial }}^2{\mathsf{\Psi }}_x}{\mathsf{\partial }x\mathsf{\partial }y}+\frac{{\mathsf{\partial }}^2{\mathsf{\Psi }}_y}{\mathsf{\partial }{y}^2}\right)\right]-\kappa \mathrm{G}h\left({\mathsf{\Psi }}_y+\frac{\mathsf{\partial }w}{\mathsf{\partial }y}\right)+\frac{\rho h^3}{12}\left(\frac{{\mathsf{\partial }}^{3}w}{\mathsf{\partial }{t}^2\mathsf{\partial }y}\right)=0$$

(9)

$$\kappa \mathrm{G}h\left[{\nabla }^{2}w+\left(\frac{\mathsf{\partial }{\mathsf{\Psi }}_x}{\mathsf{\partial }x}+\frac{\mathsf{\partial }{\mathsf{\Psi }}_y}{\mathsf{\partial }y}\right)\right]-\rho h\left(\frac{{\mathsf{\partial }}^{2}w}{\mathsf{\partial }{t}^2}\right)=0$$

(10)

where ${\nabla }^2$ is the Laplace operator.

2.3. Variational Formulation

The original (i.e., non-truncated) Uflyand–Mindlin plate model was obtained as a variational formulation in [22], where the Hamilton principle was used to explore the mechanical behavior of the plates using two different methods. The first approach presents the variational derivation of the original Uflyand–Mindlin equations as given in Mindlin’s paper [13], while the second approach presents the equations of the Uflyand–Mindlin theory based on slope inertia.

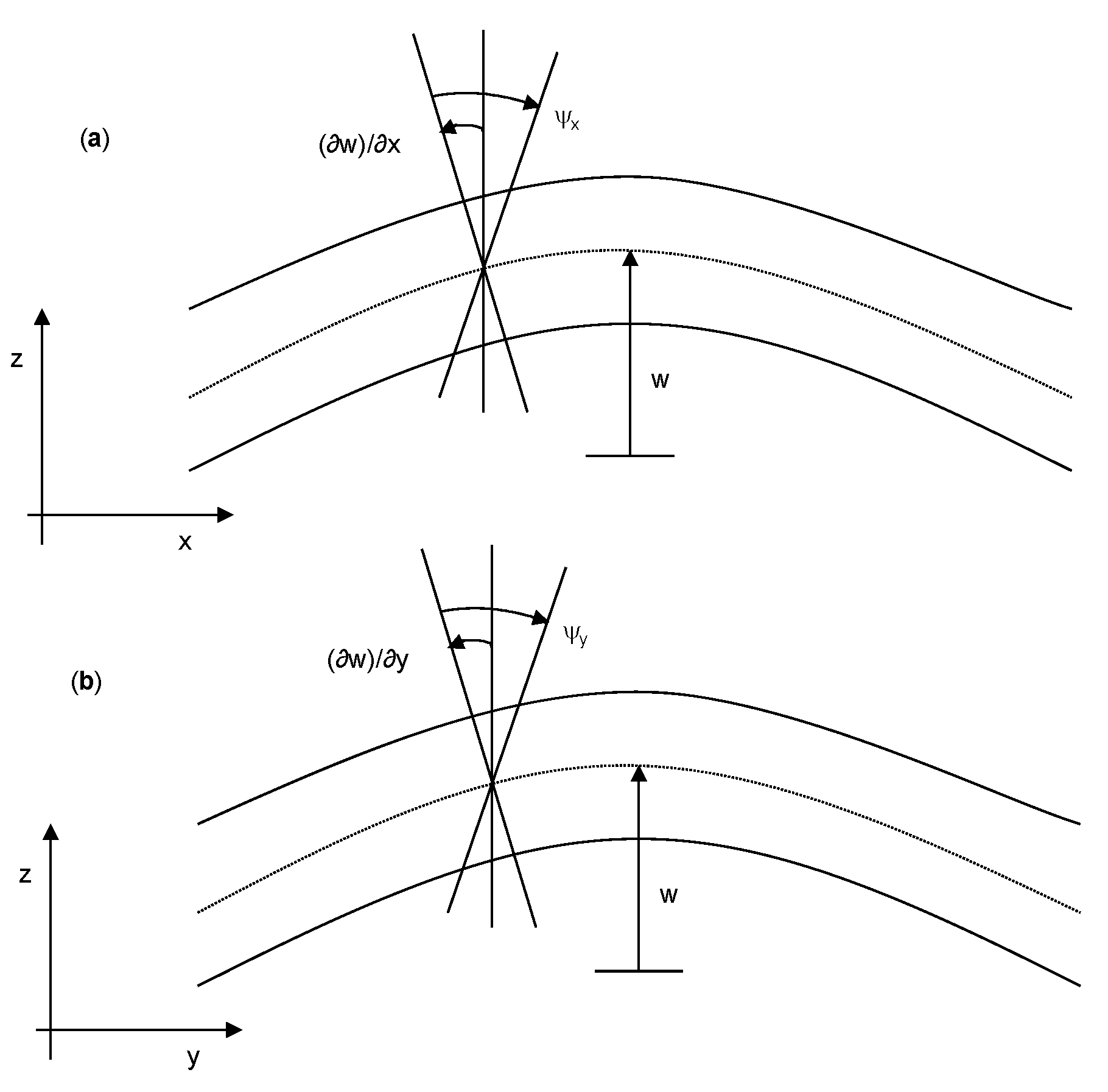
2.4. Original Uflyand–Mindlin Theory (Model I)

In the original Uflyand–Mindlin theory, the kinetic and strain energies assume the following form:

$$T=\frac{1}{2}\int {\int }_{\mathsf{\Omega }}\rho h{\left(\frac{\mathsf{\partial }w}{\mathsf{\partial }t}\right)}^2+\frac{\rho h^3}{12}\left[{\left(\frac{\mathsf{\partial }{\mathsf{\Psi }}_x}{\mathsf{\partial }t}\right)}^2+{\left(\frac{\mathsf{\partial }{\mathsf{\Psi }}_y}{\mathsf{\partial }t}\right)}^2\right]dxdy$$

(11)

$$\begin{array}{cc}\hfill L_e=& \frac{1}{2}\int {\int }_{\mathsf{\Omega }}(D\left[{\left(\frac{\mathsf{\partial }{\mathsf{\Psi }}_x}{\mathsf{\partial }x}+\frac{\mathsf{\partial }{\mathsf{\Psi }}_y}{\mathsf{\partial }y}\right)}^2-2(1-\nu )\left(\frac{\mathsf{\partial }{\mathsf{\Psi }}_x}{\mathsf{\partial }x}\frac{\mathsf{\partial }{\mathsf{\Psi }}_y}{\mathsf{\partial }y}-\frac{1}{4}{\left(\frac{\mathsf{\partial }{\mathsf{\Psi }}_x}{\mathsf{\partial }y}+\frac{\mathsf{\partial }{\mathsf{\Psi }}_y}{\mathsf{\partial }x}\right)}^2\right)\right]+\hfill \\ & \kappa \mathrm{G}h\left[{\left(\frac{\mathsf{\partial }w}{\mathsf{\partial }x}+{\mathsf{\Psi }}_x\right)}^2+{\left(\frac{\mathsf{\partial }w}{\mathsf{\partial }y}+{\mathsf{\Psi }}_y\right)}^2\right])dxdy\hfill \end{array}$$

(12)

where $\mathsf{\Omega }$ is the domain occupied by the middle plane of the plate.

2.5. Uflyand–Mindlin Plate Model Based on Slope Inertia (Model II)

Based on slope inertia [35], the Uflyand–Mindlin plate model’s kinetic and strain energies are calculated as follows:

$$T=\frac{1}{2}\int {\int }_{\mathsf{\Omega }}\rho h{\left(\frac{\mathsf{\partial }w}{\mathsf{\partial }t}\right)}^2+\frac{\rho h^3}{12}\left[{\left(\frac{{\mathsf{\partial }}^{2}w}{\mathsf{\partial }t\mathsf{\partial }x}\right)}^2+{\left(\frac{{\mathsf{\partial }}^{2}w}{\mathsf{\partial }t\mathsf{\partial }y}\right)}^2\right]dxdy$$

(13)

and

$$\begin{array}{cc}\hfill L_e=& \frac{1}{2}\int {\int }_{\mathsf{\Omega }}(D\left[{\left(\frac{\mathsf{\partial }{\mathsf{\Psi }}_x}{\mathsf{\partial }x}+\frac{\mathsf{\partial }{\mathsf{\Psi }}_y}{\mathsf{\partial }y}\right)}^2-2(1-\nu )\left(\frac{\mathsf{\partial }{\mathsf{\Psi }}_x}{\mathsf{\partial }x}\frac{\mathsf{\partial }{\mathsf{\Psi }}_y}{\mathsf{\partial }y}-\frac{1}{4}{\left(\frac{\mathsf{\partial }{\mathsf{\Psi }}_x}{\mathsf{\partial }y}+\frac{\mathsf{\partial }{\mathsf{\Psi }}_y}{\mathsf{\partial }x}\right)}^2\right)\right]\hfill \\ & +\kappa \mathrm{G}h\left[{\left(\frac{\mathsf{\partial }w}{\mathsf{\partial }x}+{\mathsf{\Psi }}_x\right)}^2+{\left(\frac{\mathsf{\partial }w}{\mathsf{\partial }y}+{\mathsf{\Psi }}_y\right)}^2\right])dxdy\hfill \end{array}$$

(14)

It should be note that the expressions in square brackets can be associated with inertia connected to the slopes $\frac{\mathsf{\partial }w}{\mathsf{\partial }x}$ and $\frac{\mathsf{\partial }w}{\mathsf{\partial }y}$.

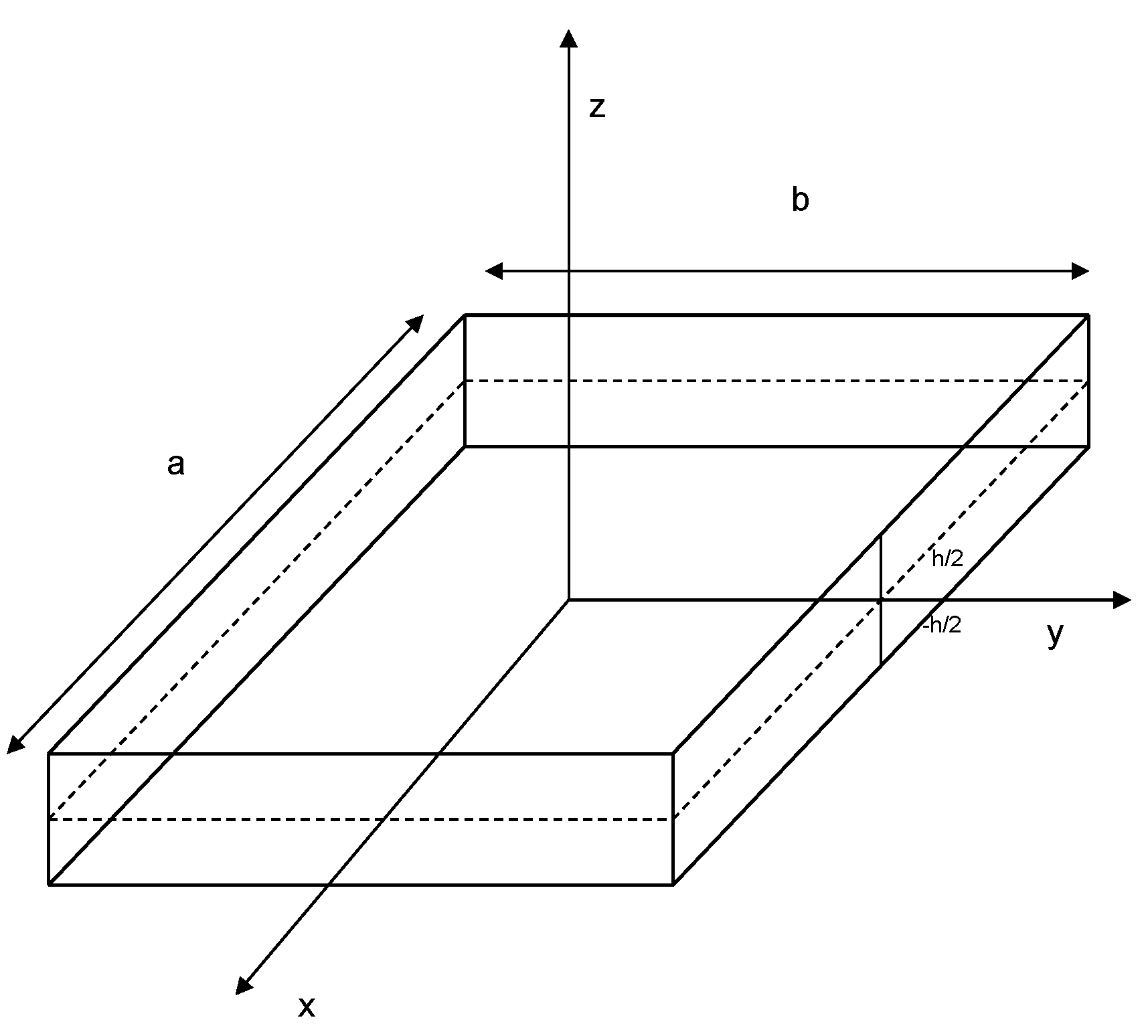
2.6. Truncated Uflyand–Mindlin Plate Model (Model III)

In the truncated Uflyand–Mindlin plate model case, the kinetic and strain energy take on the following forms:

$$T=\frac{1}{2}\int {\int }_{\mathsf{\Omega }}\rho h{\left(\frac{\mathsf{\partial }w}{\mathsf{\partial }t}\right)}^{2}dxdy$$

(15)

and

$$\begin{array}{cc}\hfill & L_e=\hfill \\ \hfill & \frac{1}{2}\int {\int }_{\mathsf{\Omega }}(D\left[{\left(\frac{\mathsf{\partial }{\mathsf{\Psi }}_x}{\mathsf{\partial }x}+\frac{\mathsf{\partial }{\mathsf{\Psi }}_y}{\mathsf{\partial }y}\right)}^2-2(1-\nu )\left(\frac{\mathsf{\partial }{\mathsf{\Psi }}_x}{\mathsf{\partial }x}\frac{\mathsf{\partial }{\mathsf{\Psi }}_y}{\mathsf{\partial }y}-\frac{1}{4}{\left(\frac{\mathsf{\partial }{\mathsf{\Psi }}_x}{\mathsf{\partial }y}+\frac{\mathsf{\partial }{\mathsf{\Psi }}_y}{\mathsf{\partial }x}\right)}^2\right)\right]\hfill \\ & +\kappa \mathrm{G}h\left[{\left(\frac{\mathsf{\partial }w}{\mathsf{\partial }x}+{\mathsf{\Psi }}_x\right)}^2+{\left(\frac{\mathsf{\partial }w}{\mathsf{\partial }y}+{\mathsf{\Psi }}_y\right)}^2\right])dxdy\hfill \end{array}$$

(16)

It is worth mentioning that the Kirchhoff–Love plate theory can be retrieved by setting ${\mathsf{\Psi }}_x$ = $-\left(\frac{\mathsf{\partial }w}{\mathsf{\partial }x}\right)$ and ${\mathsf{\Psi }}_y$ = $-\left(\frac{\mathsf{\partial }w}{\mathsf{\partial }y}\right)$.

Also, let us define the potential energy P as the inertial rotational forces, which depend only on bending rotation, work for the total corresponding rotations ${\mathsf{\Psi }}_x$ and ${\mathsf{\Psi }}_y$ and a changed sign:

$$\begin{array}{c}\hfill P=-\int {\int }_{\mathsf{\Omega }}\frac{\rho h^3}{12}\left(\frac{{\mathsf{\partial }}^{3}w}{\mathsf{\partial }{t}^2\mathsf{\partial }x}{\mathsf{\Psi }}_x+\frac{{\mathsf{\partial }}^{3}w}{\mathsf{\partial }{t}^2\mathsf{\partial }y}{\mathsf{\Psi }}_y\right)dxdy\end{array}$$

(17)

The equations of the motions and corresponding boundary conditions relating to the first two theories are reported in [41].

In what follows, the truncated Uflyand–Mindlin plate model is developed.

According to Hamilton’s principle,

$$\begin{array}{cc}\hfill & {\int }_{t_1}^{t_2}\delta \mathrm{L}\mathrm{dt}=0\hfill \end{array}$$

(18)

where the Lagrangian L is given by

$$\begin{array}{cc}\hfill & L=T-L_e-P=\hfill \\ \hfill & \frac{1}{2}\int {\int }_{\mathsf{\Omega }}(\rho h{\left(\frac{\mathsf{\partial }w}{\mathsf{\partial }t}\right)}^2-D\left[{\left(\frac{\mathsf{\partial }{\mathsf{\Psi }}_x}{\mathsf{\partial }x}+\frac{\mathsf{\partial }{\mathsf{\Psi }}_y}{\mathsf{\partial }y}\right)}^2-2(1-\nu )\left(\frac{\mathsf{\partial }{\mathsf{\Psi }}_x}{\mathsf{\partial }x}\frac{\mathsf{\partial }{\mathsf{\Psi }}_y}{\mathsf{\partial }y}-\frac{1}{4}{\left(\frac{\mathsf{\partial }{\mathsf{\Psi }}_x}{\mathsf{\partial }y}+\frac{\mathsf{\partial }{\mathsf{\Psi }}_y}{\mathsf{\partial }x}\right)}^2\right)\right]+\hfill \\ \hfill & -\kappa \mathrm{G}h\left[{\left(\frac{\mathsf{\partial }w}{\mathsf{\partial }x}+{\mathsf{\Psi }}_x\right)}^2+{\left(\frac{\mathsf{\partial }w}{\mathsf{\partial }y}+{\mathsf{\Psi }}_y\right)}^2\right])dxdy+\int {\int }_{\mathsf{\Omega }}\frac{\rho h^3}{12}\left(\frac{{\mathsf{\partial }}^{3}w}{\mathsf{\partial }{t}^2\mathsf{\partial }x}{\mathsf{\Psi }}_x+\frac{{\mathsf{\partial }}^{3}w}{\mathsf{\partial }{t}^2\mathsf{\partial }y}{\mathsf{\Psi }}_y\right)dxdy\hfill \end{array}$$

(19)

The first variation of the Lagrangian function can be easily calculated as

$$\begin{array}{cc}\hfill & {\int }_{t_1}^{t_2}\delta \mathrm{L}\mathrm{dt}={\int }_{t_1}^{t_2}\int {\int }_{\mathsf{\Omega }}(\rho h\frac{\mathsf{\partial }w}{\mathsf{\partial }t}\frac{\mathsf{\partial }\delta w}{\mathsf{\partial }t}\hfill \\ \hfill & -D\left(\frac{\mathsf{\partial }{\mathsf{\Psi }}_x}{\mathsf{\partial }x}\frac{\mathsf{\partial }\delta {\mathsf{\Psi }}_x}{\mathsf{\partial }x}+\frac{\mathsf{\partial }{\mathsf{\Psi }}_y}{\mathsf{\partial }y}\frac{\mathsf{\partial }\delta {\mathsf{\Psi }}_y}{\mathsf{\partial }y}+\nu \frac{\mathsf{\partial }{\mathsf{\Psi }}_y}{\mathsf{\partial }y}\frac{\mathsf{\partial }\delta {\mathsf{\Psi }}_x}{\mathsf{\partial }x}+\nu \frac{\mathsf{\partial }{\mathsf{\Psi }}_x}{\mathsf{\partial }x}\frac{\mathsf{\partial }\delta {\mathsf{\Psi }}_y}{\mathsf{\partial }y}\right)\hfill \\ \hfill & -D\frac{(1-\nu )}{2}\left(\frac{\mathsf{\partial }{\mathsf{\Psi }}_x}{\mathsf{\partial }y}\frac{\mathsf{\partial }\delta {\mathsf{\Psi }}_x}{\mathsf{\partial }y}+\frac{\mathsf{\partial }{\mathsf{\Psi }}_y}{\mathsf{\partial }x}\frac{\mathsf{\partial }\delta {\mathsf{\Psi }}_y}{\mathsf{\partial }x}+\frac{\mathsf{\partial }{\mathsf{\Psi }}_x}{\mathsf{\partial }y}\frac{\mathsf{\partial }\delta {\mathsf{\Psi }}_y}{\mathsf{\partial }x}+\frac{\mathsf{\partial }{\mathsf{\Psi }}_y}{\mathsf{\partial }x}\frac{\mathsf{\partial }\delta {\mathsf{\Psi }}_x}{\mathsf{\partial }y}\right)\hfill \\ \hfill & -\kappa \mathrm{G}h\left(\frac{\mathsf{\partial }w}{\mathsf{\partial }x}\frac{\mathsf{\partial }\delta w}{\mathsf{\partial }x}+{\mathsf{\Psi }}_x\delta {\mathsf{\Psi }}_x+\frac{\mathsf{\partial }w}{\mathsf{\partial }x}\delta {\mathsf{\Psi }}_x+{\mathsf{\Psi }}_x\frac{\mathsf{\partial }\delta w}{\mathsf{\partial }x}\right)\hfill \\ \hfill & -\kappa \mathrm{G}h\left(\frac{\mathsf{\partial }w}{\mathsf{\partial }y}\frac{\mathsf{\partial }\delta w}{\mathsf{\partial }y}+{\mathsf{\Psi }}_y\delta {\mathsf{\Psi }}_y+\frac{\mathsf{\partial }w}{\mathsf{\partial }y}\delta {\mathsf{\Psi }}_y+{\mathsf{\Psi }}_y\frac{\mathsf{\partial }\delta w}{\mathsf{\partial }y}\right)\hfill \\ \hfill & +\frac{\rho h^3}{12}\left(\frac{{\mathsf{\partial }}^{3}w}{\mathsf{\partial }{t}^2\mathsf{\partial }x}\delta {\mathsf{\Psi }}_x+\frac{{\mathsf{\partial }}^{2}w}{\mathsf{\partial }{t}^2\mathsf{\partial }y}\delta {\mathsf{\Psi }}_y\right))dxdydt\hfill \end{array}$$

(20)

where the inertial rotational forces $\frac{\rho h^3}{12}\frac{{\mathsf{\partial }}^{3}w}{\mathsf{\partial }{t}^2\mathsf{\partial }x}$ and $\frac{\rho h^3}{12}\frac{{\mathsf{\partial }}^{3}w}{\mathsf{\partial }{t}^2\mathsf{\partial }y}$ should be considered constants.

By performing the integration in parts and substituting their results in Equation (20), one obtains

$$\begin{array}{cc}\hfill & {\int }_{t_1}^{t_2}\delta \mathrm{L}\mathrm{dt}={\int }_{t_1}^{t_2}\int {\int }_{\mathsf{\Omega }}(-\rho h\frac{{\mathsf{\partial }}^{2}w}{\mathsf{\partial }{t}^2}\delta w+\hfill \\ \hfill & D\left(\frac{{\mathsf{\partial }}^2{\mathsf{\Psi }}_x}{\mathsf{\partial }{x}^2}\delta {\mathsf{\Psi }}_x+\frac{{\mathsf{\partial }}^2{\mathsf{\Psi }}_y}{\mathsf{\partial }{y}^2}\delta {\mathsf{\Psi }}_y+\nu \frac{{\mathsf{\partial }}^2{\mathsf{\Psi }}_y}{\mathsf{\partial }y\mathsf{\partial }x}\delta {\mathsf{\Psi }}_x+\nu \frac{{\mathsf{\partial }}^2{\mathsf{\Psi }}_x}{\mathsf{\partial }x\mathsf{\partial }y}\delta {\mathsf{\Psi }}_y\right)+\hfill \\ \hfill & D\frac{(1-\nu )}{2}\left(\frac{{\mathsf{\partial }}^2{\mathsf{\Psi }}_x}{\mathsf{\partial }{y}^2}\delta {\mathsf{\Psi }}_x+\frac{{\mathsf{\partial }}^2{\mathsf{\Psi }}_y}{\mathsf{\partial }{x}^2}\delta {\mathsf{\Psi }}_y+\frac{{\mathsf{\partial }}^2{\mathsf{\Psi }}_x}{\mathsf{\partial }x\mathsf{\partial }y}\delta {\mathsf{\Psi }}_y+\frac{{\mathsf{\partial }}^2{\mathsf{\Psi }}_y}{\mathsf{\partial }x\mathsf{\partial }y}\delta {\mathsf{\Psi }}_x\right)+\hfill \\ \hfill & \kappa \mathrm{G}h\left(\frac{{\mathsf{\partial }}^{2}w}{\mathsf{\partial }{x}^2}\delta w-{\mathsf{\Psi }}_x\delta {\mathsf{\Psi }}_x-\frac{\mathsf{\partial }w}{\mathsf{\partial }x}\delta {\mathsf{\Psi }}_x+\frac{\mathsf{\partial }{\mathsf{\Psi }}_x}{\mathsf{\partial }x}\delta w\right)+\hfill \\ \hfill & \kappa \mathrm{G}h\left(\frac{{\mathsf{\partial }}^{2}w}{\mathsf{\partial }{y}^2}\delta w-{\mathsf{\Psi }}_y\delta {\mathsf{\Psi }}_y-\frac{\mathsf{\partial }w}{\mathsf{\partial }y}\delta {\mathsf{\Psi }}_y+\frac{\mathsf{\partial }{\mathsf{\Psi }}_y}{\mathsf{\partial }y}\delta w\right)+\hfill \\ \hfill & \frac{\rho h^3}{12}\left(\frac{{\mathsf{\partial }}^{3}w}{\mathsf{\partial }{t}^2\mathsf{\partial }x}\delta {\mathsf{\Psi }}_x+\frac{{\mathsf{\partial }}^{3}w}{\mathsf{\partial }{t}^2\mathsf{\partial }y}\delta {\mathsf{\Psi }}_y\right))dxdydt+\hfill \\ \hfill & {\int }_{t_1}^{t_2}\{{\oint }_{\mathsf{\Gamma }}D\left(-\frac{\mathsf{\partial }{\mathsf{\Psi }}_x}{\mathsf{\partial }x}\delta {\mathsf{\Psi }}_{x}dy+\frac{\mathsf{\partial }{\mathsf{\Psi }}_y}{\mathsf{\partial }y}\delta {\mathsf{\Psi }}_{y}dx-\nu \frac{\mathsf{\partial }{\mathsf{\Psi }}_y}{\mathsf{\partial }y}\delta {\mathsf{\Psi }}_{x}dy+\nu \frac{\mathsf{\partial }{\mathsf{\Psi }}_x}{\mathsf{\partial }x}\delta {\mathsf{\Psi }}_{y}dx\right)+\hfill \\ \hfill & D\frac{(1-\nu )}{2}\left(\frac{\mathsf{\partial }{\mathsf{\Psi }}_x}{\mathsf{\partial }y}\delta {\mathsf{\Psi }}_{x}dx+\frac{\mathsf{\partial }{\mathsf{\Psi }}_y}{\mathsf{\partial }x}\delta {\mathsf{\Psi }}_{x}dx-\frac{\mathsf{\partial }{\mathsf{\Psi }}_x}{\mathsf{\partial }y}\delta {\mathsf{\Psi }}_{y}dy-\frac{\mathsf{\partial }{\mathsf{\Psi }}_y}{\mathsf{\partial }x}\delta {\mathsf{\Psi }}_{y}dy\right)+\hfill \\ \hfill & \kappa \mathrm{G}h\left(\frac{\mathsf{\partial }w}{\mathsf{\partial }x}\delta wdy-\frac{\mathsf{\partial }w}{\mathsf{\partial }y}\delta wdx+{\mathsf{\Psi }}_x\delta wdy-{\mathsf{\Psi }}_y\delta wdx\right)\}dt=0\hfill \end{array}$$

(21)

Grouping the terms of Equation (21), one obtains

$$\begin{array}{cc}\hfill & {\int }_{t_1}^{t_2}\{\int {\int }_{\mathsf{\Omega }}[D\left(\frac{{\mathsf{\partial }}^2{\mathsf{\Psi }}_x}{\mathsf{\partial }{x}^2}+\nu \frac{{\mathsf{\partial }}^2{\mathsf{\Psi }}_y}{\mathsf{\partial }y\mathsf{\partial }x}\right)+D\frac{(1-\nu )}{2}\left(\frac{{\mathsf{\partial }}^2{\mathsf{\Psi }}_x}{\mathsf{\partial }{y}^2}+\frac{{\mathsf{\partial }}^2{\mathsf{\Psi }}_y}{\mathsf{\partial }x\mathsf{\partial }y}\right)\hfill \\ \hfill & -\kappa \mathrm{G}h\left({\mathsf{\Psi }}_x+\frac{\mathsf{\partial }w}{\mathsf{\partial }x}\right)+\frac{\rho h^3}{12}\frac{{\mathsf{\partial }}^{3}w}{\mathsf{\partial }{t}^2\mathsf{\partial }x}]\delta {\mathsf{\Psi }}_{x}dxdy+\hfill \\ \hfill & \int {\int }_{\mathsf{\Omega }}[D\left(\frac{{\mathsf{\partial }}^2{\mathsf{\Psi }}_y}{\mathsf{\partial }{y}^2}+\nu \frac{{\mathsf{\partial }}^2{\mathsf{\Psi }}_x}{\mathsf{\partial }x\mathsf{\partial }y}\right)+D\frac{(1-\nu )}{2}\left(\frac{{\mathsf{\partial }}^2{\mathsf{\Psi }}_y}{\mathsf{\partial }{x}^2}+\frac{{\mathsf{\partial }}^2{\mathsf{\Psi }}_x}{\mathsf{\partial }x\mathsf{\partial }y}\right)+\hfill \\ \hfill & -\kappa \mathrm{G}h\left({\mathsf{\Psi }}_y+\frac{\mathsf{\partial }w}{\mathsf{\partial }y}\right)+\frac{\rho h^3}{12}\frac{{\mathsf{\partial }}^{3}w}{\mathsf{\partial }{t}^2\mathsf{\partial }y}]\delta {\mathsf{\Psi }}_{y}dxdy+\hfill \\ \hfill & \int {\int }_{\mathsf{\Omega }}\left[-\rho h\frac{{\mathsf{\partial }}^{2}w}{\mathsf{\partial }{t}^2}+\kappa \mathrm{G}h\left(\frac{{\mathsf{\partial }}^{2}w}{\mathsf{\partial }{x}^2}+\frac{\mathsf{\partial }{\mathsf{\Psi }}_x}{\mathsf{\partial }x}+\frac{{\mathsf{\partial }}^{2}w}{\mathsf{\partial }{y}^2}+\frac{\mathsf{\partial }{\mathsf{\Psi }}_y}{\mathsf{\partial }y}\right)\right]\delta wdxdy\left\}\right\}dt+\hfill \\ \hfill & -{\int }_{t_1}^{t_2}\{{\oint }_{\mathsf{\Gamma }}\left(D\left(\frac{\mathsf{\partial }{\mathsf{\Psi }}_x}{\mathsf{\partial }x}dy+\nu \frac{\mathsf{\partial }{\mathsf{\Psi }}_y}{\mathsf{\partial }y}dy\right)-D\frac{(1-\nu )}{2}\left(\frac{\mathsf{\partial }{\mathsf{\Psi }}_x}{\mathsf{\partial }y}dx+\frac{\mathsf{\partial }{\mathsf{\Psi }}_y}{\mathsf{\partial }x}dx\right)\right)\delta {\mathsf{\Psi }}_x+\hfill \\ \hfill & \left(-D\left(\frac{\mathsf{\partial }{\mathsf{\Psi }}_y}{\mathsf{\partial }y}dx+\nu \frac{\mathsf{\partial }{\mathsf{\Psi }}_x}{\mathsf{\partial }x}dx\right)+D\frac{(1-\nu )}{2}\left(\frac{\mathsf{\partial }{\mathsf{\Psi }}_y}{\mathsf{\partial }x}dy+\frac{\mathsf{\partial }{\mathsf{\Psi }}_x}{\mathsf{\partial }y}dy\right)\right)\delta {\mathsf{\Psi }}_y+\hfill \\ \hfill & \kappa \mathrm{G}h\left(\frac{\mathsf{\partial }w}{\mathsf{\partial }x}dy-\frac{\mathsf{\partial }w}{\mathsf{\partial }y}dx+{\mathsf{\Psi }}_{x}dy-{\mathsf{\Psi }}_{y}dx\right)\delta w\}\mathrm{dt}=0\hfill \end{array}$$

(22)

The equations of motion are given by

$$\begin{array}{cc}\hfill & D\left(\frac{{\mathsf{\partial }}^2{\mathsf{\Psi }}_x}{\mathsf{\partial }{x}^2}+\nu \frac{{\mathsf{\partial }}^2{\mathsf{\Psi }}_y}{\mathsf{\partial }y\mathsf{\partial }x}\right)+D\frac{(1-\nu )}{2}\left(\frac{{\mathsf{\partial }}^2{\mathsf{\Psi }}_x}{\mathsf{\partial }{y}^2}+\frac{{\mathsf{\partial }}^2{\mathsf{\Psi }}_y}{\mathsf{\partial }x\mathsf{\partial }y}\right)+\hfill \\ \hfill & -\kappa \mathrm{G}h\left({\mathsf{\Psi }}_x+\frac{\mathsf{\partial }w}{\mathsf{\partial }x}\right)+\frac{\rho h^3}{12}\frac{{\mathsf{\partial }}^{3}w}{\mathsf{\partial }{t}^2\mathsf{\partial }x}=0\hfill \end{array}$$

(23)

$$\begin{array}{cc}\hfill & D\left(\frac{{\mathsf{\partial }}^2{\mathsf{\Psi }}_y}{\mathsf{\partial }{y}^2}+\nu \frac{{\mathsf{\partial }}^2{\mathsf{\Psi }}_x}{\mathsf{\partial }x\mathsf{\partial }y}\right)+D\frac{(1-\nu )}{2}\left(\frac{{\mathsf{\partial }}^2{\mathsf{\Psi }}_y}{\mathsf{\partial }{x}^2}+\frac{{\mathsf{\partial }}^2{\mathsf{\Psi }}_x}{\mathsf{\partial }x\mathsf{\partial }y}\right)+\hfill \\ \hfill & -\kappa \mathrm{G}h\left({\mathsf{\Psi }}_y+\frac{\mathsf{\partial }w}{\mathsf{\partial }y}\right)+\frac{\rho h^3}{12}\frac{{\mathsf{\partial }}^{3}w}{\mathsf{\partial }{t}^2\mathsf{\partial }y}=0\hfill \end{array}$$

(24)

$$\kappa \mathrm{G}h\left(\frac{{\mathsf{\partial }}^{2}w}{\mathsf{\partial }{x}^2}+\frac{\mathsf{\partial }{\mathsf{\Psi }}_x}{\mathsf{\partial }x}+\frac{{\mathsf{\partial }}^{2}w}{\mathsf{\partial }{y}^2}+\frac{\mathsf{\partial }{\mathsf{\Psi }}_y}{\mathsf{\partial }y}\right)-\rho h\frac{{\mathsf{\partial }}^{2}w}{\mathsf{\partial }{t}^2}=0$$

(25)

together with the following general boundary conditions:

$${\oint }_{\mathsf{\Gamma }}\left\{D\left(\frac{\mathsf{\partial }{\mathsf{\Psi }}_x}{\mathsf{\partial }x}dy+\nu \frac{\mathsf{\partial }{\mathsf{\Psi }}_y}{\mathsf{\partial }y}dy\right)-D\frac{(1-\nu )}{2}\left(\frac{\mathsf{\partial }{\mathsf{\Psi }}_x}{\mathsf{\partial }y}dx+\frac{\mathsf{\partial }{\mathsf{\Psi }}_y}{\mathsf{\partial }x}dx\right)\right\}\delta {\mathsf{\Psi }}_x=0$$

(26)

$${\oint }_{\mathsf{\Gamma }}\left\{-D\left(\frac{\mathsf{\partial }{\mathsf{\Psi }}_y}{\mathsf{\partial }y}dx+\nu \frac{\mathsf{\partial }{\mathsf{\Psi }}_x}{\mathsf{\partial }x}dx\right)+D\frac{(1-\nu )}{2}\left(\frac{\mathsf{\partial }{\mathsf{\Psi }}_y}{\mathsf{\partial }x}dy+\frac{\mathsf{\partial }{\mathsf{\Psi }}_x}{\mathsf{\partial }y}dy\right)\right\}\delta {\mathsf{\Psi }}_y=0$$

(27)

$${\oint }_{\mathsf{\Gamma }}\left\{-\kappa \mathrm{G}h\left(\frac{\mathsf{\partial }w}{\mathsf{\partial }y}dx+{\mathsf{\Psi }}_{y}dx\right)+\kappa \mathrm{G}h\left(\frac{\mathsf{\partial }w}{\mathsf{\partial }x}dy+{\mathsf{\Psi }}_{x}dy\right)\right\}\delta w=0$$

(28)

The following equations define the boundary conditions of the rectangular plate for edges parallel to the x-axis:

$$\begin{array}{c}\hfill D\left(\frac{\mathsf{\partial }{\mathsf{\Psi }}_x}{\mathsf{\partial }x}+\nu \frac{\mathsf{\partial }{\mathsf{\Psi }}_y}{\mathsf{\partial }y}\right)=0\mathrm{or}{\mathsf{\Psi }}_x\\ \hfill D\frac{(1-\nu )}{2}\left(\frac{\mathsf{\partial }{\mathsf{\Psi }}_x}{\mathsf{\partial }y}+\frac{\mathsf{\partial }{\mathsf{\Psi }}_y}{\mathsf{\partial }x}\right)=0\mathrm{or}{\mathsf{\Psi }}_y\\ \hfill \kappa \mathrm{G}h\left(\frac{\mathsf{\partial }w}{\mathsf{\partial }y}+{\mathsf{\Psi }}_y\right)=0\mathrm{or}w\end{array}$$

(29)

Finally, the boundary conditions of the rectangular plate for the edges parallel to the y- axis, are given by

$$\begin{array}{c}\hfill D\left(\frac{\mathsf{\partial }{\mathsf{\Psi }}_y}{\mathsf{\partial }y}+\nu \frac{\mathsf{\partial }{\mathsf{\Psi }}_x}{\mathsf{\partial }x}\right)=0\mathrm{or}{\mathsf{\Psi }}_y\\ \hfill D\frac{(1-\nu )}{2}\left(\frac{\mathsf{\partial }{\mathsf{\Psi }}_x}{\mathsf{\partial }y}+\frac{\mathsf{\partial }{\mathsf{\Psi }}_y}{\mathsf{\partial }x}\right)=0\mathrm{or}{\mathsf{\Psi }}_x\\ \hfill \kappa \mathrm{G}h\left(\frac{\mathsf{\partial }w}{\mathsf{\partial }x}+{\mathsf{\Psi }}_x\right)=0\mathrm{or}w\end{array}$$

(30)

The governing differential Equations (23)–(25) assume the following expression as a result of some algebraic operations:

$$\frac{D}{2}\left[(1-\nu ){\nabla }^2{\mathsf{\Psi }}_x+(1+\nu )\left(\frac{{\mathsf{\partial }}^2{\mathsf{\Psi }}_x}{\mathsf{\partial }{x}^2}+\frac{{\mathsf{\partial }}^2{\mathsf{\Psi }}_y}{\mathsf{\partial }y\mathsf{\partial }x}\right)\right]-\kappa \mathrm{G}h\left({\mathsf{\Psi }}_x+\frac{\mathsf{\partial }w}{\mathsf{\partial }x}\right)+\frac{\rho h^3}{12}\frac{{\mathsf{\partial }}^{3}w}{\mathsf{\partial }{t}^2\mathsf{\partial }x}=0$$

(31)

$$\frac{D}{2}\left[(1-\nu ){\nabla }^2{\mathsf{\Psi }}_y+(1+\nu )\left(\frac{{\mathsf{\partial }}^2{\mathsf{\Psi }}_x}{\mathsf{\partial }x\mathsf{\partial }y}+\frac{{\mathsf{\partial }}^2{\mathsf{\Psi }}_y}{\mathsf{\partial }{y}^2}\right)\right]-\kappa \mathrm{G}h\left({\mathsf{\Psi }}_y+\frac{\mathsf{\partial }w}{\mathsf{\partial }y}\right)+\frac{\rho h^3}{12}\frac{{\mathsf{\partial }}^{3}w}{\mathsf{\partial }{t}^2\mathsf{\partial }y}=0$$

(32)

$$\kappa \mathrm{G}h\left({\nabla }^{2}w+\mathsf{\Phi }\right)=\rho h\frac{{\mathsf{\partial }}^{2}w}{\mathsf{\partial }{t}^2}$$

(33)

Setting

$$\mathsf{\Phi }=\frac{\mathsf{\partial }{\mathsf{\Psi }}_x}{\mathsf{\partial }x}+\frac{\mathsf{\partial }{\mathsf{\Psi }}_y}{\mathsf{\partial }y}$$

(34)

followed by differentiating Equation (31) with respect to x and Equation (32) with respect to y, and adding the obtained expressions, one obtains

$$D\left(\frac{{\mathsf{\partial }}^2\mathsf{\Phi }}{\mathsf{\partial }{x}^2}+\frac{{\mathsf{\partial }}^2\mathsf{\Phi }}{\mathsf{\partial }{y}^2}\right)-\kappa \mathrm{G}h\left({\nabla }^{2}w+\mathsf{\Phi }\right)+\frac{\rho h^3}{12}\frac{{\mathsf{\partial }}^2{\nabla }^{2}w}{\mathsf{\partial }{t}^2}=0$$

(35)

According to Equation (33),

$$\mathsf{\Phi }=-{\nabla }^{2}w+\frac{\rho }{\kappa G}\frac{{\mathsf{\partial }}^{2}w}{\mathsf{\partial }{t}^2}$$

(36)

Deriving Equation (36) with respect to x and y, respectively, and substituting this equation in Equation (35), one obtains the following expressions:

$$D{\nabla }^{4}w+\rho h\frac{{\mathsf{\partial }}^{2}w}{\mathsf{\partial }{t}^2}-\frac{\rho h^3}{12}\left(1+\frac{12}{h^3}\frac{D}{\kappa G}\right)\frac{{\mathsf{\partial }}^2}{\mathsf{\partial }{t}^2}{\nabla }^{2}w=0$$

(37)

together with the general boundary conditions Equations (29)–(32). Equation (37) denotes the truncated simpler governing equation, as deduced in [42]. This result corresponds to the one obtained in [42], in which the authors—Hache et al.—obtain an expression of the dynamic equation of the plate that differs for two reasons from the original equation proposed by Uflyand–Mindlin. The main difference from the original Uflyand–Mindlin equation is that the fourth-order time derivative, which is characteristic of the original Uflyand–Mindlin plate theory, does not appear in the treatment presented in [42], in the sense that the Authors neglect this term. The main difference between the treatment developed in the present paper and the work in [42] is that, by applying the variational approach to derive the equations of dynamic plate equilibrium, the fourth-order time derivative does not appear.

2.7. Transformation of Governing Differential Equations

Dealing with uncoupled equations makes it easier to solve the three coupled partial differential Equations (23)–(25). Setting

$$\overline{\mathsf{\Phi }}=\frac{\mathsf{\partial }{\mathsf{\Psi }}_x}{\mathsf{\partial }y}-\frac{\mathsf{\partial }{\mathsf{\Psi }}_y}{\mathsf{\partial }x}$$

(38)

and simplifying Equations (23) and (24) and differentiating with respect to y and x, respectively, one obtains

$$\begin{array}{cc}\hfill & D\frac{{\mathsf{\partial }}^2}{\mathsf{\partial }x\mathsf{\partial }y}\left(\frac{\mathsf{\partial }{\mathsf{\Psi }}_x}{\mathsf{\partial }x}+\frac{\mathsf{\partial }{\mathsf{\Psi }}_y}{\mathsf{\partial }y}\right)+\frac{D}{2}(1-\nu )\frac{{\mathsf{\partial }}^2}{\mathsf{\partial }{y}^2}\left(\frac{\mathsf{\partial }{\mathsf{\Psi }}_x}{\mathsf{\partial }y}-\frac{\mathsf{\partial }{\mathsf{\Psi }}_y}{\mathsf{\partial }x}\right)+\hfill \\ \hfill & -\kappa \mathrm{G}h\left(\frac{\mathsf{\partial }{\mathsf{\Psi }}_x}{\mathsf{\partial }y}+\frac{{\mathsf{\partial }}^{2}w}{\mathsf{\partial }x\mathsf{\partial }y}\right)+\frac{\rho h^3}{12}\left(\frac{{\mathsf{\partial }}^{4}w}{\mathsf{\partial }{t}^2\mathsf{\partial }x\mathsf{\partial }y}\right)=0\hfill \end{array}$$

(39)

$$\begin{array}{cc}\hfill & D\frac{{\mathsf{\partial }}^2}{\mathsf{\partial }y\mathsf{\partial }x}\left(\frac{\mathsf{\partial }{\mathsf{\Psi }}_x}{\mathsf{\partial }x}+\frac{\mathsf{\partial }{\mathsf{\Psi }}_y}{\mathsf{\partial }y}\right)-\frac{D}{2}(1-\nu )\frac{{\mathsf{\partial }}^2}{\mathsf{\partial }{x}^2}\left(\frac{\mathsf{\partial }{\mathsf{\Psi }}_x}{\mathsf{\partial }y}-\frac{\mathsf{\partial }{\mathsf{\Psi }}_y}{\mathsf{\partial }x}\right)+\hfill \\ \hfill & -\kappa \mathrm{G}h\left(\frac{\mathsf{\partial }{\mathsf{\Psi }}_y}{\mathsf{\partial }x}+\frac{{\mathsf{\partial }}^{2}w}{\mathsf{\partial }y\mathsf{\partial }x}\right)+\frac{\rho h^3}{12}\left(\frac{{\mathsf{\partial }}^{4}w}{\mathsf{\partial }{t}^2\mathsf{\partial }y\mathsf{\partial }x}\right)=0\hfill \end{array}$$

(40)

Subtracting Equation (40) from (39), one obtains

$$+\frac{D}{2}(1-\nu ){\nabla }^2\overline{\mathsf{\Phi }}-\kappa \mathrm{G}h\overline{\mathsf{\Phi }}=0$$

(41)

which, with Equation (37), leads to a system of two uncoupled differential equations.

By means Equations (23)–(25), the rotations ${\mathsf{\Psi }}_x$ and ${\mathsf{\Psi }}_y$ can be expressed through quantities $\overline{\mathsf{\Phi }}$ and w. From simplified Equations (23) and (24), the cross-section rotations ${\mathsf{\Psi }}_x$ and ${\mathsf{\Psi }}_y$ are obtained, respectively:

$$\begin{array}{cc}\hfill & \kappa \mathrm{G}h{\mathsf{\Psi }}_x=D\frac{\mathsf{\partial }}{\mathsf{\partial }x}\left(\frac{\mathsf{\partial }{\mathsf{\Psi }}_x}{\mathsf{\partial }x}+\frac{\mathsf{\partial }{\mathsf{\Psi }}_y}{\mathsf{\partial }y}\right)+\frac{D}{2}(1-\nu )\frac{\mathsf{\partial }}{\mathsf{\partial }y}\left(\frac{\mathsf{\partial }{\mathsf{\Psi }}_x}{\mathsf{\partial }y}-\frac{\mathsf{\partial }{\mathsf{\Psi }}_y}{\mathsf{\partial }x}\right)+\hfill \\ \hfill & \frac{\rho h^3}{12}\left(\frac{{\mathsf{\partial }}^{3}w}{\mathsf{\partial }{t}^2\mathsf{\partial }x}\right)-\kappa \mathrm{G}h\left(\frac{\mathsf{\partial }w}{\mathsf{\partial }x}\right)\hfill \end{array}$$

(42)

$$\begin{array}{cc}\hfill & \kappa \mathrm{G}h{\mathsf{\Psi }}_y=D\frac{\mathsf{\partial }}{\mathsf{\partial }y}\left(\frac{\mathsf{\partial }{\mathsf{\Psi }}_x}{\mathsf{\partial }x}+\frac{\mathsf{\partial }{\mathsf{\Psi }}_y}{\mathsf{\partial }y}\right)+\frac{D}{2}(1-\nu )\frac{\mathsf{\partial }}{\mathsf{\partial }x}\left(\frac{\mathsf{\partial }{\mathsf{\Psi }}_x}{\mathsf{\partial }y}-\frac{\mathsf{\partial }{\mathsf{\Psi }}_y}{\mathsf{\partial }x}\right)+\hfill \\ \hfill & \frac{\rho h^3}{12}\left(\frac{{\mathsf{\partial }}^{3}w}{\mathsf{\partial }{t}^2\mathsf{\partial }y}\right)-\kappa \mathrm{G}h\left(\frac{\mathsf{\partial }w}{\mathsf{\partial }y}\right)\hfill \end{array}$$

(43)

Using Equation (25), the following relation is obtained:

$$\left(\frac{\mathsf{\partial }{\mathsf{\Psi }}_x}{\mathsf{\partial }x}+\frac{\mathsf{\partial }{\mathsf{\Psi }}_y}{\mathsf{\partial }y}\right)=+\frac{\rho h}{\kappa \mathrm{G}h}\left(\frac{{\mathsf{\partial }}^{2}w}{\mathsf{\partial }{t}^2}\right)-\left(\frac{{\mathsf{\partial }}^{2}w}{\mathsf{\partial }{x}^2}+\frac{{\mathsf{\partial }}^{2}w}{\mathsf{\partial }{y}^2}\right)$$

(44)

which, inserted in Equations (43)–(44), leads to

$$\begin{array}{cc}\hfill & \kappa \mathrm{G}h{\mathsf{\Psi }}_x=D\frac{\mathsf{\partial }}{\mathsf{\partial }x}\left(\frac{\rho h}{\kappa \mathrm{G}h}\left(\frac{{\mathsf{\partial }}^{2}w}{\mathsf{\partial }{t}^2}\right)-{\nabla }^{2}w\right)-\kappa \mathrm{G}h\frac{\mathsf{\partial }w}{\mathsf{\partial }x}+\hfill \\ \hfill & +\frac{D}{2}(1-\nu )\frac{\mathsf{\partial }\overline{\mathsf{\Phi }}}{\mathsf{\partial }y}+\frac{\rho h^3}{12}\left(\frac{{\mathsf{\partial }}^{3}w}{\mathsf{\partial }{t}^2\mathsf{\partial }x}\right)\hfill \end{array}$$

(45)

$$\begin{array}{cc}\hfill & \kappa \mathrm{G}h{\mathsf{\Psi }}_y=D\frac{\mathsf{\partial }}{\mathsf{\partial }y}\left(\frac{\rho h}{\kappa \mathrm{G}h}\left(\frac{{\mathsf{\partial }}^{2}w}{\mathsf{\partial }{t}^2}\right)-{\nabla }^{2}w\right)-\kappa \mathrm{G}h\frac{\mathsf{\partial }w}{\mathsf{\partial }y}+\hfill \\ \hfill & +\frac{D}{2}(1-\nu )\frac{\mathsf{\partial }\overline{\mathsf{\Phi }}}{\mathsf{\partial }x}+\frac{\rho h^3}{12}\left(\frac{{\mathsf{\partial }}^{3}w}{\mathsf{\partial }{t}^2\mathsf{\partial }y}\right)\hfill \end{array}$$

(46)

It is also seen that the cross-section rotations ${\mathsf{\Psi }}_x$ and ${\mathsf{\Psi }}_y$ are given by means of w and $\overline{\mathsf{\Phi }}$.

3. Numerical Comparison and Discussion

In order to validate the effectiveness and correctness of the proposed procedure, a numerical example is proposed in the following section in the case of a plate simply supported at all four ends.

Numerical computations are performed through software developed in Mathematics language [43] and use the same geometrical features as Reference [42], which will be used throughout this section.

In what follows, the theoretical formulation of a rectangular plate with four edges that are simply supported is given.

3.1. Theoretical Formulation of a Rectangular Plate with Four Edges That Are Simply Supported

Consider a rectangular plate with four edges that are simply supported and set the following dimensionless quantities:

$${\lambda }^2=\frac{{\omega }^2{b}^4\rho h}{D};\beta =\frac{E}{G\left(1-{\nu }^2\right)};\xi =\frac{x}{a};\eta =\frac{y}{b};\chi =\frac{a}{b};\overline{h}=\frac{h}{a}$$

(47)

To find a solution to the system of differential equations describing the dynamic behavior of rectangular plates, we look for periodic solutions of the form:

$$w(x,y,t)=\overline{w}(x,y)e^{i\omega t}$$

(48)

where $\omega$ is the frequency of natural vibration. Accordingly, Equation (37) becomes

$$D\left(\frac{{\mathsf{\partial }}^4\overline{w}}{\mathsf{\partial }{x}^4}+\frac{{\mathsf{\partial }}^4\overline{w}}{\mathsf{\partial }{y}^4}+2\frac{{\mathsf{\partial }}^4\overline{w}}{\mathsf{\partial }{x}^2\mathsf{\partial }{y}^2}\right)+\frac{\rho h^3{\omega }^2}{12}\left(1+\frac{12}{h^3}\frac{D}{\kappa G}\right)\left(\frac{{\mathsf{\partial }}^2\overline{w}}{\mathsf{\partial }{x}^2}+\frac{{\mathsf{\partial }}^2\overline{w}}{\mathsf{\partial }{y}^2}\right)-{\omega }^2\rho h\overline{w}=0$$

(49)

Re-scaling Equation (49) with respect to Equation (47), we have

$$\left(\frac{{\mathsf{\partial }}^4\overline{w}}{\mathsf{\partial }{\xi }^4}+\frac{{\chi }^4{\mathsf{\partial }}^4\overline{w}}{\mathsf{\partial }{\eta }^4}+\frac{2{\chi }^2{\mathsf{\partial }}^4\overline{w}}{\mathsf{\partial }{\xi }^2\mathsf{\partial }{\eta }^2}\right)+\frac{{\lambda }^2{\overline{h}}^2{\chi }^4}{12}\left(1+\frac{\beta }{\kappa }\right)\left(\frac{{\mathsf{\partial }}^2\overline{w}}{\mathsf{\partial }{\xi }^2}+\frac{{\chi }^2{\mathsf{\partial }}^2\overline{w}}{\mathsf{\partial }{\eta }^2}\right)-{\lambda }^2{\chi }^4\overline{w}=0$$

(50)

Taking into account the boundary conditions, the solution is constructed primarily on the basis of the well-known classical Navier procedure [44] as

$$\stackrel{-}{w}(x,y)=asin\left(n\pi \eta \right)sin\left(m\pi \xi \right)$$

(51)

where m and n are the numbers of half-waves in the x and y direction, respectively.

Equation (51) substituted into Equation (50) leads to the following form of the dynamic equations of rectangular plates with all edges simply supported:

$${\pi }^4{\left({\left(\chi n\right)}^2+m^2\right)}^2-\frac{{\lambda }^2{\overline{h}}^2{\pi }^2{\chi }^4}{12}\left(1+\frac{\beta }{\kappa }\right)\left(m^2+{\chi }^2{n}^2\right)-{\lambda }^2{\chi }^4=0$$

(52)

whose solution is provided by

$$\lambda =\frac{{\pi }^2\left(m^2+n^2{\chi }^2\right)}{{\chi }^2\sqrt{\left(1+\frac{{\overline{h}}^2{\pi }^2}{12}\left(1+\frac{\beta }{\kappa }\right)\left(m^2+n^2{\chi }^2\right)\right)}}$$

(53)

Equation (53) coincides with Equation (47) obtained from Hache et al. in [42], obtained by the authors by setting ${\gamma }_2$ = 0 (see [42]).

The authors are well aware that Levy plates and other combinations of boundary conditions can also be considered. The purpose, however, of this paper is to show the novelty of a proposed analytical approach to dynamic plate analysis. A single, simple numerical example has, in fact, been presented because the leaning plate is amply supported by data and results from the literature, thus allowing validation of the correctness of the procedure proposed in the present research.

3.2. Numerical Example for a Rectangular Plate with Four Edges That Are Simply Supported

In the present research, frequencies were not compared with the various models and those obtained in the literature using numerical approaches. Complete numerical data for the first natural frequencies of all three variants for each of the six possible combinations of boundary conditions are available in [42].

In this section, the example of a rectangular plate with all four edges simply supported is offered in order to show the effectiveness of the proposed procedure. Assuming aspect ratios equal to 1 (square plate) and 2, a Poisson ratio equal to $0.3$ and a shear factor $\kappa$ equal to $0.86667$, and considering three values of thickness ratios of $\overline{h}$ = 0.01, 0.1, and 0.2, the first ten non-dimensional natural frequencies of SSSS of the truncated Uflyand–Mindlin plate theory are calculated. It is worth noting that, for an isotropic plate, the shear correction factor $\kappa$ depends on Poisson’s ratio $\nu$ and it may vary from $\kappa$ equal to $0.76$, for $\nu$ equal to zero, to $\kappa$ equal to $0.91$, for $\nu$ equal to $0.5$. It can be shown that the shear correction factor is given by a cubic equation by applying Mindlin’s suggestion to equate the angular frequency of the first antisymmetric mode of thickness–shear vibration according to the exact three-dimensional theory to the corresponding frequency according to his theory, as Wang et al. in [45] demonstrate.

The values obtained are shown in

Table 1. First ten non-dimensional natural frequencies of SSSS considering truncated Uflyand–Mindlin plate theory for different aspect and thickness ratios.

$\mathit{\chi }$	$\overline{\mathit{h}}$ = 0.01	$\overline{\mathit{h}}$ = 0.1	$\overline{\mathit{h}}$ = 0.2
1	19.732	19.077	17.429
	49.304	45.492	37.773
	78.845	69.715	54.089
	98.522	84.838	63.529
	128.011	106.207	76.167
	167.282	132.613	90.953
	177.091	138.889	94.363
	196.698	151.092	100.901
	245.657	179.788	115.879
	255.439	185.249	118.678
2	12.326	11.373	9.443
	19.711	17.429	13.522
	32.003	26.552	19.042
	41.820	33.153	22.738
	49.175	37.773	25.225
	61.414	44.947	28.969
	71.191	50.285	31.687
	78.514	54.089	33.596
	90.703	60.098	36.575
	98.006	63.529	38.261

.

As can be seen from Table 1, the results obtained coincide perfectly with those obtained by Hache et al. (see Table 2 in [42]). The excellent agreement of the present with the existing results validates the accuracy of the calculations and the theoretical procedure developed in this paper. Also, the influence of the thickness ratio $\overline{h}$ on the dimensionless natural frequency is established by taking the aspect ratio constant $\chi$ and varying h from 0.01 to 0.2. As can easily be seen in Table 1, when keeping the aspect ratio value constant, as the thickness ratios increases, the dimensionless free frequencies decrease. Finally, the values obtained for the first ten dimensionless natural frequencies allow the following considerations to be made:

-

When the aspect ratio increases, the natural frequencies decrease;

-

When the thickness ratio increases, the free frequencies increase.

4. Conclusions

In the present paper, the truncated Uflyand–Mindlin plate equation, i.e., without the fourth-order derivative, by means of the direct method and variational formulation, is proposed. According to Uflyand–Mindlin theory, an alternative theoretical formulation for the free-vibration analysis of plates is presented, and the equations of motion and the general corresponding boundary conditions are derived.

In a time of broadening scientific frontiers, new knowledge must eventually be organized and analyzed logically, claims Rosenfeld [46]. Kirchhoff was the leading physicist of the nineteenth century, whose temperament was most appropriate for this job. In all of his work, he used a straightforward, direct approach and basic concepts while aiming for clarity and rigor in the quantitative expression of experience. His way of thinking is evident in both his contributions that have direct applications (such as the principles of electrical networks) and those that have broad ramifications (such as the spectral analysis method).

In this paper, the ideas of Kirchhoff [4] and Mindlin [13,14,15] are applied for the truncated version of refined plate equations. The innovative aspect of the suggested strategy is that variational and direct methods for studying plate dynamics are analogous. Finding the third equation of the reduced Uflyand–Mindlin equations, the accompanying boundary conditions and their mathematical resemblance are the goals of the presented formulations. In order to solve the dynamic equilibrium problem of a truncated Uflyand–Mindlin equation via a variational formulation, it is demonstrated that the differential equations and the corresponding boundary conditions have the same form as those found using the direct technique.

The fourth-order derivative in the original Uflyand–Mindlin equations constitutes the correction of the shear deformation term by the rotary inertia effect. Physically, it is understood that such a “correction of the correction” must be of a small and negligible effect. The variational derivation exposed in this paper shows that the neglect of the fourth-order derivative is variationally justified. The omission of the fourth derivative is justified, since it can play an essential role only in the vicinity of the wavefront; however, in this zone, the Mindlin–Uflyand equations appear to be of questionable validity. On the other hand, Shamrovskii’s [47] equations appear to correctly describe the solution in the vicinity of the wavefront. Interested readers can also consult the paper by Andrianov and Awrejcewicz [48]. Finally, in order to validate the effectiveness and correctness of the proposed procedure, a numerical example of the case of a plate simply supported at all four ends is proposed. The values obtained show excellent agreement with the existing ones, which confirms the validity of the proposed procedure.

Mindlin’s theory certainly dates back many years. The objective of this paper is to fill the theoretical gap present in the treatment of the dynamic analysis of plates and even before that of beams. The suggested method is new in that it provides a flawless comparison between variational and direct methods for the dynamic analysis of plates. The purpose of the suggested formulations is to identify the shortened Uflyand–Mindlin equations, the associated boundary conditions and the mathematical similarities between them using the two distinct methods. It is shown that the differential equations and matching boundary conditions that are utilized in the variational formulation of the dynamic problem of a truncated Uflyand–Mindlin equation have the same form as the solution found using the direct technique. Since the suggested theory is variationally consistent, the identical governing equation and boundary conditions are reached by the variational technique as well as the direct geometric approach. This work fills a vacuum in the literature by providing the precise variational theory for this “truncated plate”. To the best of the authors’ knowledge, an analytical formulation has not been found for this shortened model in any of the literature.

Subsequent developments of the proposed theory are works in progress. In particular, the approach presented here will be extended for the dynamic analysis of composite plates, nanoplates and FGMs, but also shells and membranes, which will be the subject of future works.