FEM Investigation of the Air Resonance in a Cretan Lyra
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Methods
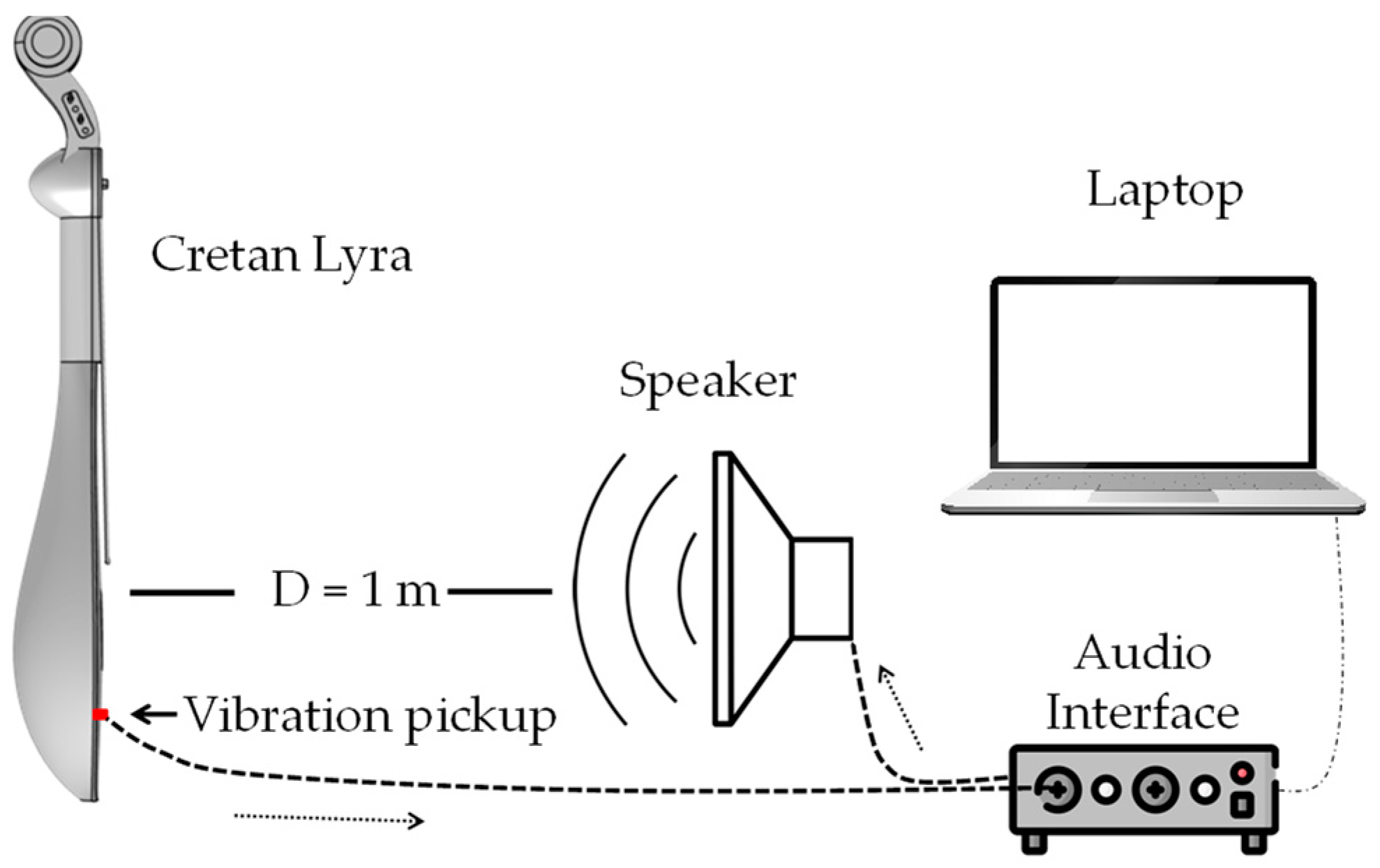
2.2.1. Acoustic Measurements
2.2.2. FEM Acoustic Modeling
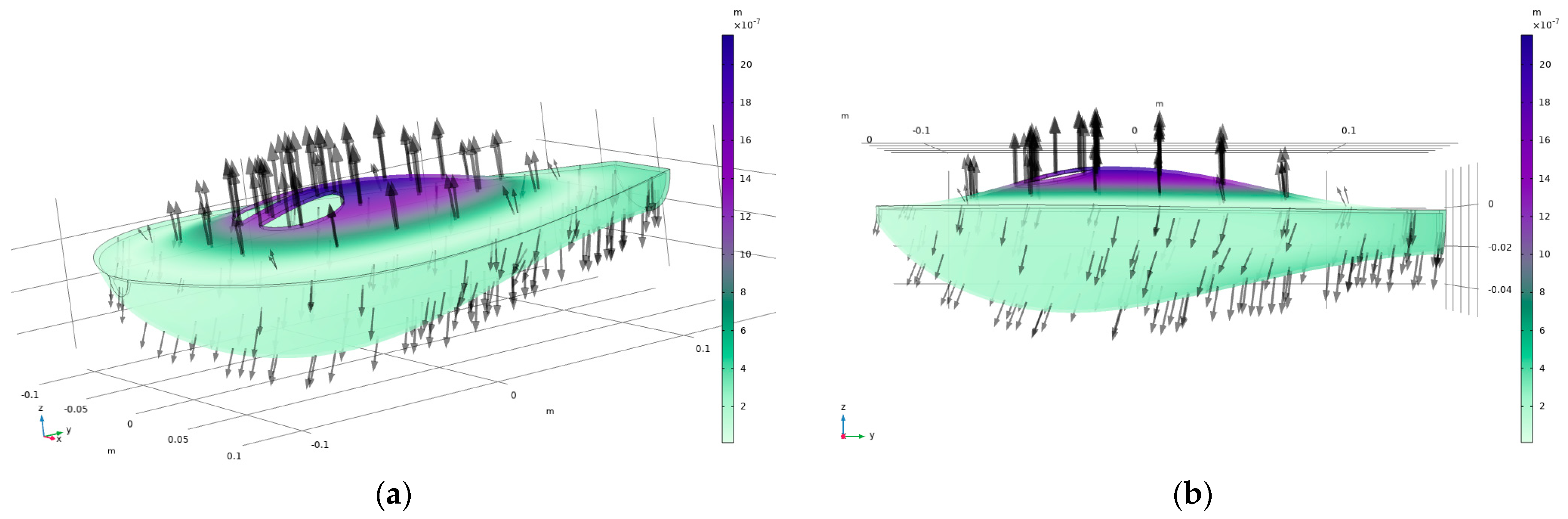
FEM Acoustic Modeling: Acoustic–Structure Interaction
FEM Acoustic Modeling: Rigid Body
3. Results
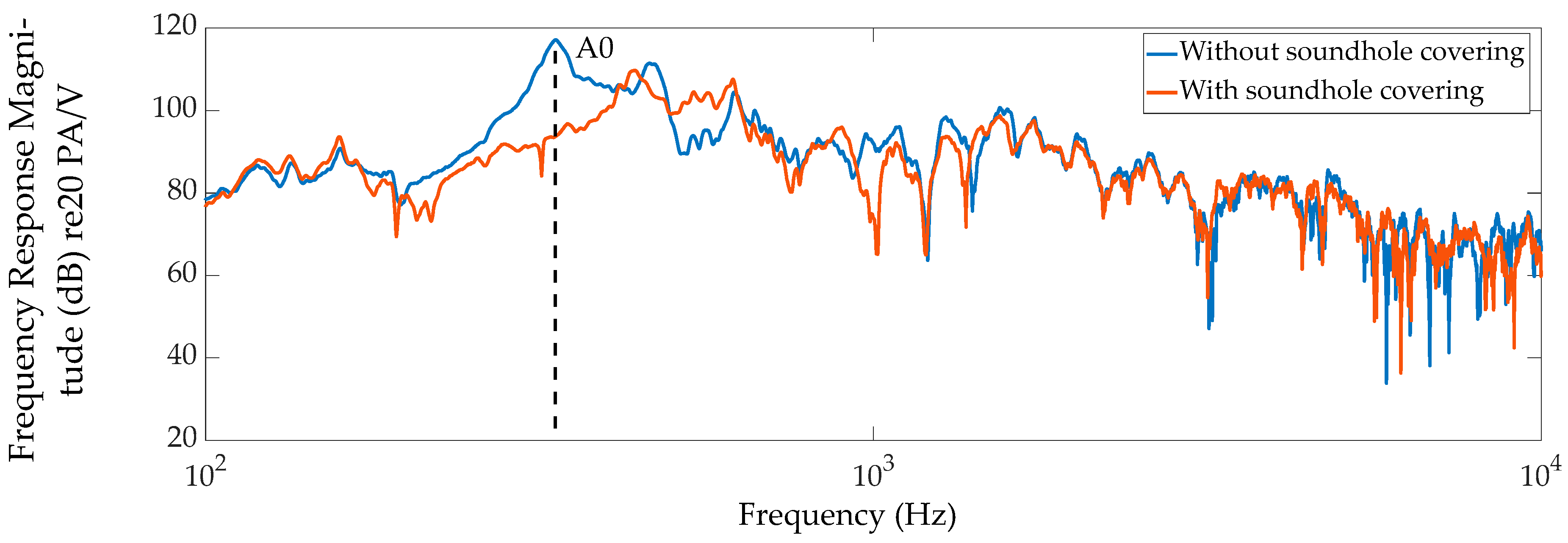
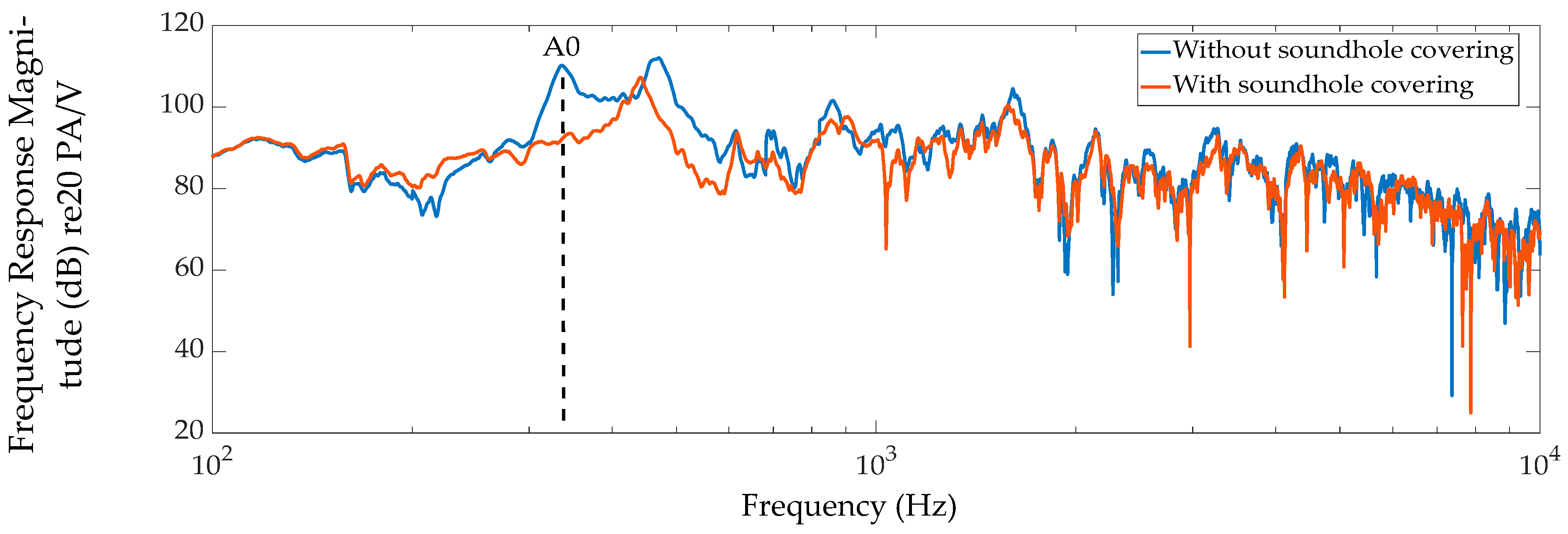
3.1. Acoustic Measurements
3.2. Acoustic Modeling
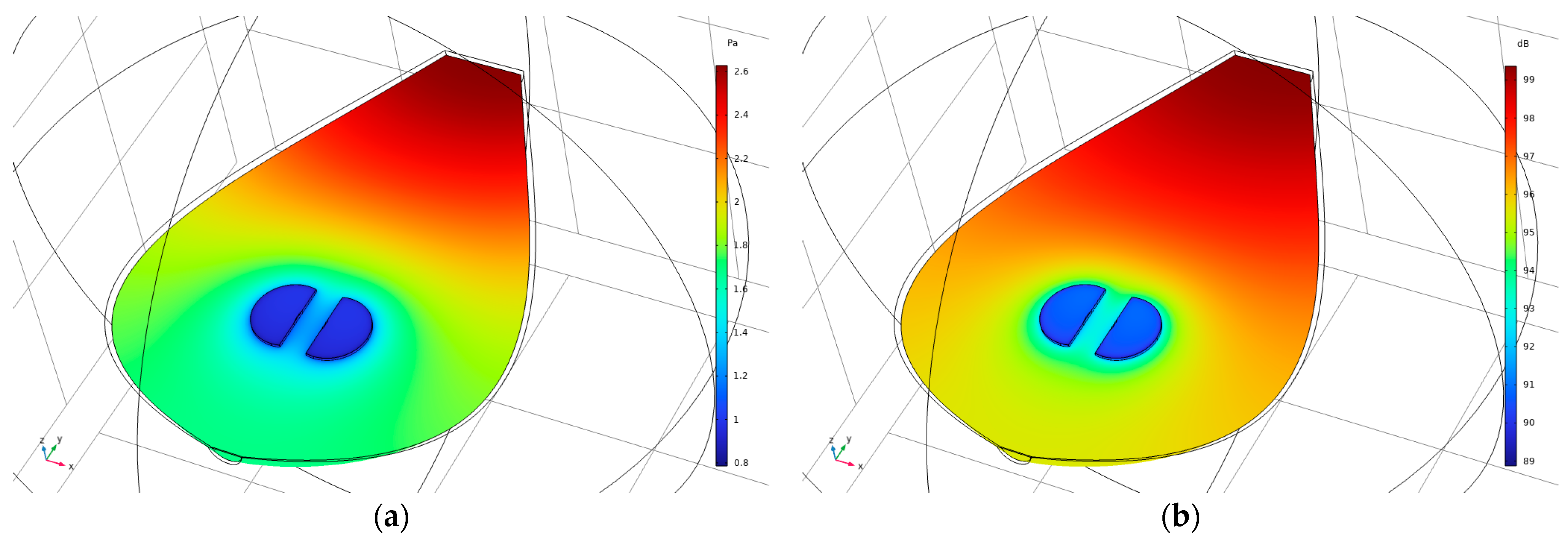
3.2.1. Acoustic–Structure Interaction
3.2.2. Rigid Body
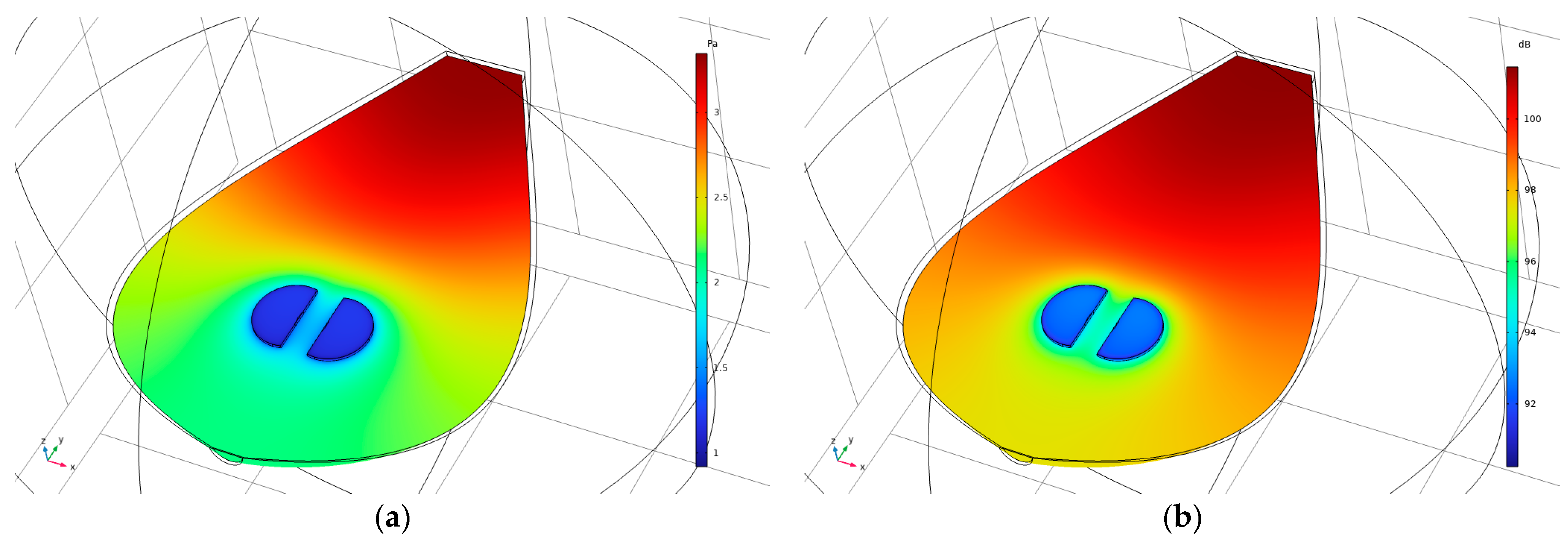
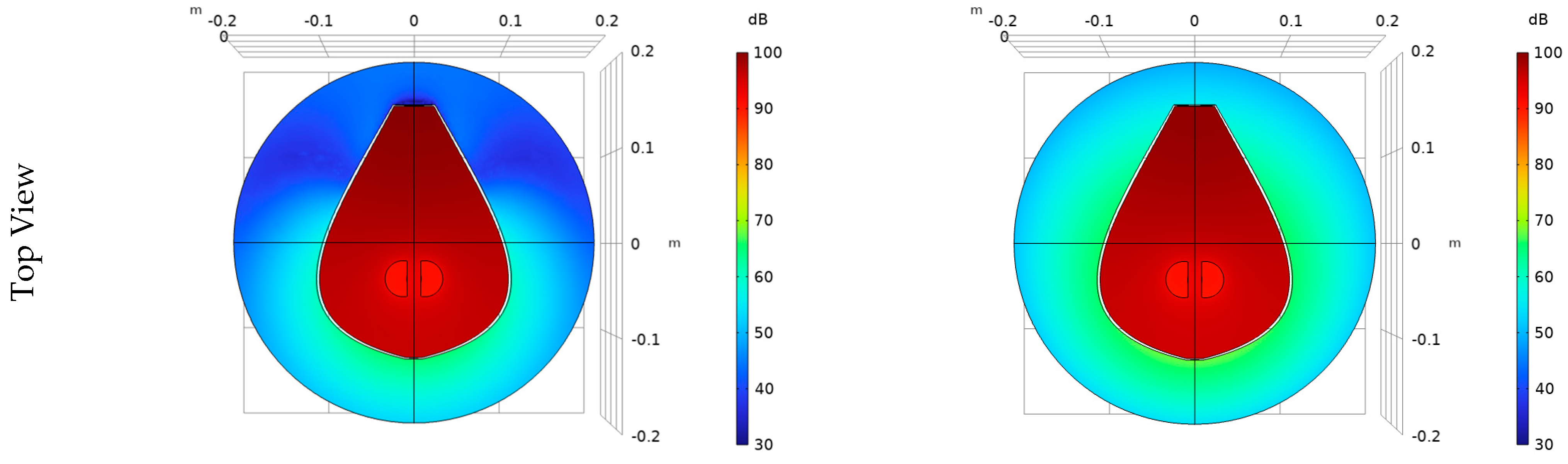
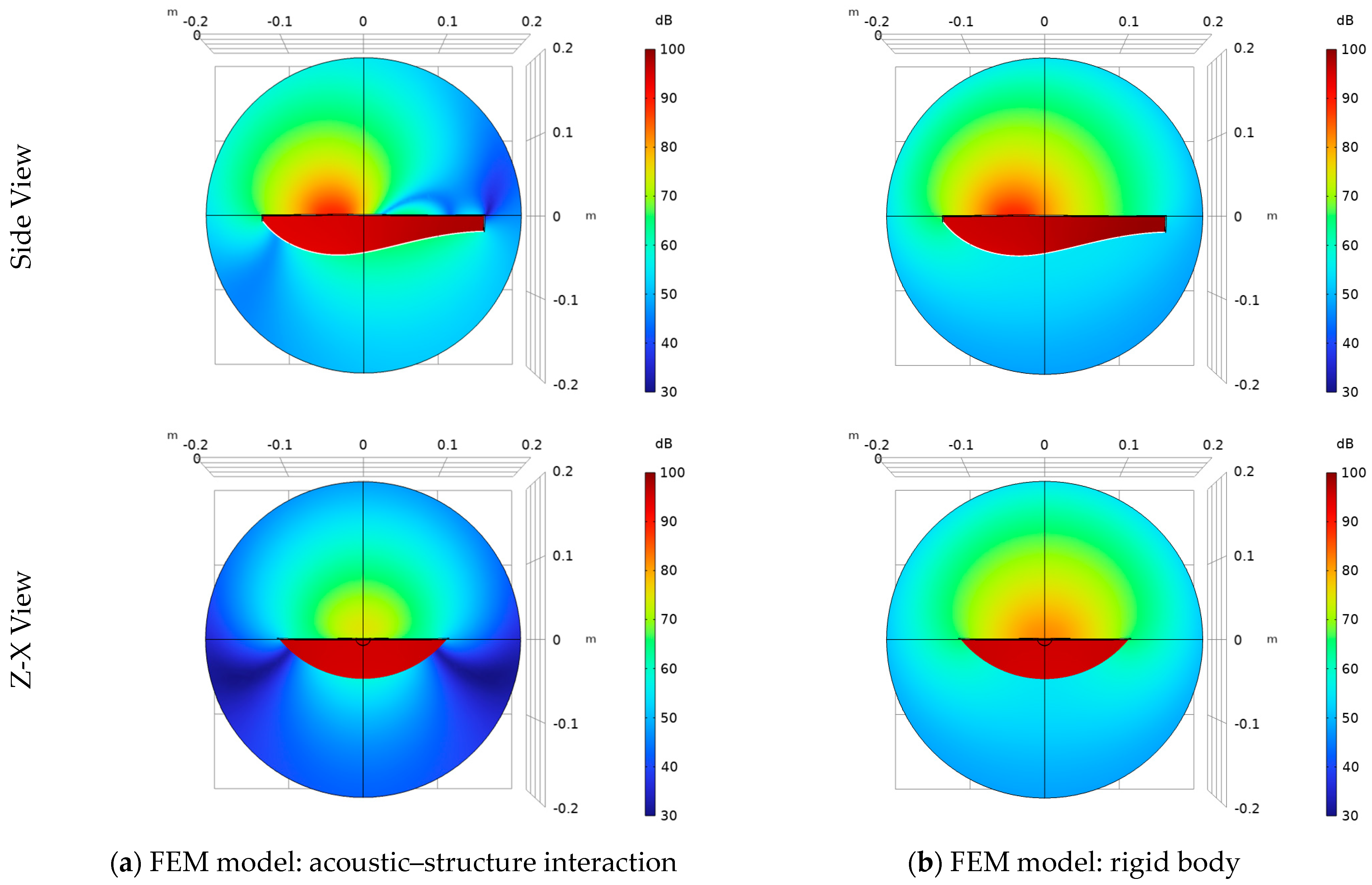
3.2.3. Comparison of SPL Distribution around the Cretan Lyra (Acoustic–Structure Interaction and Rigid Body)
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Dimensions | a | b | c | d | e | f | h | j |
|---|---|---|---|---|---|---|---|---|
| mm | 279 | 208 | 46 | 23 | 19 | 46 | 19 | 56 |
| Measurement Positions | A | B |
|---|---|---|
| (x, y, z) (mm, mm, mm) | (50, 57, 6) | (41, 51, −46) |
Appendix B
| Speed of Sound (m/s) | Density (kg/m3) | Direction | Young’s Modulus (N/mm2) | Plane | Shear Modulus (N/mm2) | Poisson’s Ratio |
|---|---|---|---|---|---|---|
| 4458 | 550 | L | 7920 | LR | 1036 | 0.55 |
| T | 677 | LT | 888 | 0.59 | ||
| R | 1069 | RT | 286 | 0.59 |
| Speed of Sound (m/s) | Density (kg/m3) | Young’s Modulus (N/mm2) | Shear Modulus (N/mm2) | Poisson’s Ratio |
|---|---|---|---|---|
| 3130 | 647 | 6300 | 1785 | 0.37 |
Appendix C

References
- Pavlopoulou, A. Musical Tradition and Change on the Island of Crete; Goldsmiths, University of London: London, UK, 2012. [Google Scholar]
- Dawe, K. Symbolic and social transformation in the lute cultures of Crete: Music, technology and the body in a Mediterranean society. Yearb. Tradit. Music 2005, 37, 58–68. [Google Scholar] [CrossRef]
- Hnaraki, M. Cretan Music: Unraveling Ariadne’s Thread; Kerkyra Publications: Attica, Greece, 2007. [Google Scholar]
- Dawe, K. Lyres and the body politic: Studying musical instruments in the Cretan musical landscape. Pop. Music. Soc. 2003, 26, 263–283. [Google Scholar] [CrossRef]
- Martin, A.R.; Mihalka, M. Music around the World: A Global Encyclopedia [3 volumes]: A Global Encyclopedia; ABC-CLIO: Santa Barbara, CA, USA, 2020. [Google Scholar]
- Fay, R. Ways of Understanding: Ethnomusicology and the Cretan Lyra; The University of Manchester: Manchester, UK, 2011. [Google Scholar]
- Cremer, L. The Physics of Violin. MA. 1984. Available online: https://philpapers.org/rec/CRETPO-11 (accessed on 1 August 2023).
- Bader, R.; Hansen, U. Acoustical analysis and modeling of musical instruments using modern signal processing methods. In Handbook of Signal Processing in Acoustics; Springer: New York, NY, USA, 2008; pp. 219–247. [Google Scholar]
- Sakai, S.; Samejima, T. Vibro-acoustic analysis of cellos using the finite and boundary element methods and its application to studies on the effects of endpin properties. Acoust. Sci. Technol. 2023, 44, 259–268. [Google Scholar] [CrossRef]
- Bilbao, S.; Hamilton, B.; Harrison, R.; Torin, A. Finite-difference schemes in musical acoustics: A tutorial. In Springer Handbook of Systematic Musicology; Springer: Berlin/Heidelberg, Germany, 2018; pp. 349–384. [Google Scholar] [CrossRef]
- Bader, R. Nonlinearities and Synchronization in Musical Acoustics and Music Psychology; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013; Volume 2. [Google Scholar]
- Papadakis, N.M.; Stavroulakis, G.E. Time domain finite element method for the calculation of impulse response of enclosed spaces. Room acoustics application. Mech. Hear. Protein Percept. 12th Int. Workshop Mech. Hear. 2015, 1703, 100002. [Google Scholar] [CrossRef]
- Papadakis, N.M.; Stavroulakis, G.E. Finite Element Method for the Estimation of Insertion Loss of Noise Barriers: Comparison with Various Formulae (2D). Urban Sci. 2020, 4, 77. [Google Scholar] [CrossRef]
- Ballou, G. Handbook for Sound Engineers; Taylor & Francis: Abingdon, UK, 2013; p. 228. [Google Scholar]
- Bakarezos, M.; Gymnopoulos, S.; Brezas, S.; Orfanos, Y.; Maravelakis, E.; Papadopoulos, C.; Tatarakis, M.; Antoniadis, A.; Papadogiannis, N. Vibration analysis of the top plates of traditional greek string musical instruments. In Proceedings of the 13th International Congress on Sound and Vibration, Vienna, Austria, 2–6 July 2006; pp. 4939–4946. [Google Scholar]
- Fletcher, N.H.; Rossing, T.D. The Physics of Musical Instruments; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Wolfe, J. Helmholtz Resonance. Available online: https://newt.phys.unsw.edu.au/jw/Helmholtz.html (accessed on 22 July 2023).
- Le Carrou, J.-L.; Gautier, F.; Foltête, E. Experimental study of A0 and T1 modes of the concert harp. J. Acoust. Soc. Am. 2007, 121, 559–567. [Google Scholar] [CrossRef]
- Woodhouse, J. The acoustics of a plucked harp string. J. Sound Vib. 2022, 523, 116669. [Google Scholar] [CrossRef]
- Bucur, V.; Bucur, V. Material Properties and the Modes of Vibration of the Concert Harp Soundboard. In Handbook of Materials for String Musical Instruments; Springer: Berlin/Heidelberg, Germany, 2016; pp. 249–282. [Google Scholar]
- Nia, H.T.; Jain, A.D.; Liu, Y.; Alam, M.-R.; Barnas, R.; Makris, N.C. The evolution of air resonance power efficiency in the violin and its ancestors. Proc. R. Soc. A Math. Phys. Eng. Sci. 2015, 471, 20140905. [Google Scholar] [CrossRef]
- Gonzalez, S.; Salvi, D.; Baeza, D.; Antonacci, F.; Sarti, A. A data-driven approach to violin making. Sci. Rep. 2021, 11, 9455. [Google Scholar] [CrossRef]
- Rossing, T.D. The Science of String Instruments; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Gough, C.E. A violin shell model: Vibrational modes and acoustics. J. Acoust. Soc. Am. 2015, 137, 1210–1225. [Google Scholar] [CrossRef]
- Bissinger, G. Structural acoustics of good and bad violins. J. Acoust. Soc. Am. 2008, 124, 1764–1773. [Google Scholar] [CrossRef] [PubMed]
- Güntekin, E.; Yılmaz Aydın, T.; Aydın, M. Elastic constants of Calabrian pine and cedar. In Proceedings of the International Forestry Symposium, Kastamonu, Türkiye, 7–10 December 2016; pp. 645–649. [Google Scholar]
- Yoshikawa, S. Acoustical classification of woods for string instruments. J. Acoust. Soc. Am. 2007, 122, 568–573. [Google Scholar] [CrossRef] [PubMed]
- French, R.M. Acoustic Guitar Design; Springer: Berlin/Heidelberg, Germany, 2022. [Google Scholar]
- Jansson, E.V. Acoustical properties of complex cavities. Prediction and measurements of resonance properties of violin-shaped and guitar-shaped cavities. Acta Acust. United Acust. 1977, 37, 211–221. [Google Scholar]
- Hutchins, C.M. A study of the cavity resonances of a violin and their effects on its tone and playing qualities. J. Acoust. Soc. Am. 1990, 87, 392–397. [Google Scholar] [CrossRef]
- Farina, A.; Langhoff, A.; Tronchin, L. Acoustic characterisation of “virtual” musical instruments: Using MLS technique on ancient violins. J. New Music Res. 1998, 27, 359–379. [Google Scholar] [CrossRef]
- Morset, L.H. A low-cost PC-based tool for violin acoustics measurements. Catgut Acoust. Soc. (CAS) J. 2001, 4, 45. [Google Scholar]
- Papadakis, N.M.; Antoniadou, S.; Stavroulakis, G.E. Effects of Varying Levels of Background Noise on Room Acoustic Parameters, Measured with ESS and MLS Methods. Acoustics 2023, 5, 563–574. [Google Scholar] [CrossRef]
- Farina, A. Simultaneous measurement of impulse response and distortion with a swept-sine technique. In Proceedings of the 108th Audio Engineering Society Convention, Paris, France, 21–24 October 2000. [Google Scholar]
- Papadakis, N.M.; Stavroulakis, G.E. Review of Acoustic Sources Alternatives to a Dodecahedron Speaker. Appl. Sci. 2019, 9, 3705. [Google Scholar] [CrossRef]
- Papadakis, N.M.; Stavroulakis, G.E. Low Cost Omnidirectional Sound Source Utilizing a Common Directional Loudspeaker for Impulse Response Measurements. Appl. Sci. 2018, 8, 1703. [Google Scholar] [CrossRef]
- Papadakis, N.M.; Stavroulakis, G.E. Handclap for Acoustic Measurements: Optimal Application and Limitations. Acoustics 2020, 2, 224–245. [Google Scholar] [CrossRef]
- de Vos, R.; Papadakis, N.M.; Stavroulakis, G.E. Improved Source Characteristics of a Handclap for Acoustic Measurements: Utilization of a Leather Glove. Acoustics 2020, 2, 803–811. [Google Scholar] [CrossRef]
- Chaigne, A.; Kergomard, J. Acoustics of Musical Instruments; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Zienkiewicz, O. Coupled Vibrations of a Structure Submerged in a Compressible Fluid. In Proceedings of the Symposium on Finite Element Techniques Held at the University of Stuttgart. 1969. Available online: https://cir.nii.ac.jp/crid/1570291224816730880 (accessed on 1 August 2023).
- Sigrist, J.-F. Fluid-Structure Interaction: An Introduction to Finite Element Coupling; John Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Hatami, M. Weighted Residual Methods: Principles, Modifications and Applications; Academic Press: Cambridge, MA, USA, 2017. [Google Scholar]
- Elejabarrieta, M.; Santamaria, C.; Ezcurra, A. Air cavity modes in the resonance box of the guitar: The effect of the sound hole. J. Sound Vib. 2002, 252, 584. [Google Scholar] [CrossRef]
- Ezcurra, A.; Elejabarrieta, M.; Santamaria, C. Fluid–structure coupling in the guitar box: Numerical and experimental comparative study. Appl. Acoust. 2005, 66, 411–425. [Google Scholar] [CrossRef]
- Papadakis, N.M.; Stavroulakis, G.E. FEM Investigation of a Multi-Neck Helmholtz Resonator. Appl. Sci. 2023, 13, 10610. [Google Scholar] [CrossRef]
- Li, L.; Liu, Y.; Zhang, F.; Sun, Z. Several explanations on the theoretical formula of Helmholtz resonator. Adv. Eng. Softw. 2017, 114, 361–371. [Google Scholar] [CrossRef]
- Christensen, O.; Vistisen, B.B. Simple model for low-frequency guitar function. J. Acoust. Soc. Am. 1980, 68, 758–766. [Google Scholar] [CrossRef]
- Güntekin, E.; Niemz, P. Prediction of Young’s Modulus in Three Orthotropic Directions for Some Important Turkish Wood Species Using Ultrasound. In Proceedings of the 19th International Nondestructive Testing and Evaluation of Wood Symposium, Rio de Janeiro, Brazil, 22–25 September 2015. [Google Scholar]
- Rossing, T.D.; Rossing, T.D. Springer Handbook of Acoustics; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Bishop, L.; Goebl, W. Music and movement: Musical instruments and performers. The Routledge Companion to Music Cognition; Routledge: New York, NY, USA, 2017. [Google Scholar]
- Papadakis, N.M.; Zantzas, A.; Lafazanis, K.; Stavroulakis, G.E. Influence of Color on Loudness Perception of Household Appliances: Case of a coffee maker. Designs 2022, 6, 101. [Google Scholar] [CrossRef]
- Thoret, E.; Caramiaux, B.; Depalle, P.; Mcadams, S. Learning metrics on spectrotemporal modulations reveals the perception of musical instrument timbre. Nat. Hum. Behav. 2021, 5, 369–377. [Google Scholar] [CrossRef]


| FEM Modeling | |||
|---|---|---|---|
| Acoustic Measurements | Acoustic–structure Interaction | Rigid Body | |
| A0 (Hz) | 336.2 | 348.8 | 382.6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Papadakis, N.M.; Nikolidakis, N.; Stavroulakis, G.E. FEM Investigation of the Air Resonance in a Cretan Lyra. Vibration 2023, 6, 945-959. https://doi.org/10.3390/vibration6040056
Papadakis NM, Nikolidakis N, Stavroulakis GE. FEM Investigation of the Air Resonance in a Cretan Lyra. Vibration. 2023; 6(4):945-959. https://doi.org/10.3390/vibration6040056
Chicago/Turabian StylePapadakis, Nikolaos M., Nikolaos Nikolidakis, and Georgios E. Stavroulakis. 2023. "FEM Investigation of the Air Resonance in a Cretan Lyra" Vibration 6, no. 4: 945-959. https://doi.org/10.3390/vibration6040056
APA StylePapadakis, N. M., Nikolidakis, N., & Stavroulakis, G. E. (2023). FEM Investigation of the Air Resonance in a Cretan Lyra. Vibration, 6(4), 945-959. https://doi.org/10.3390/vibration6040056








