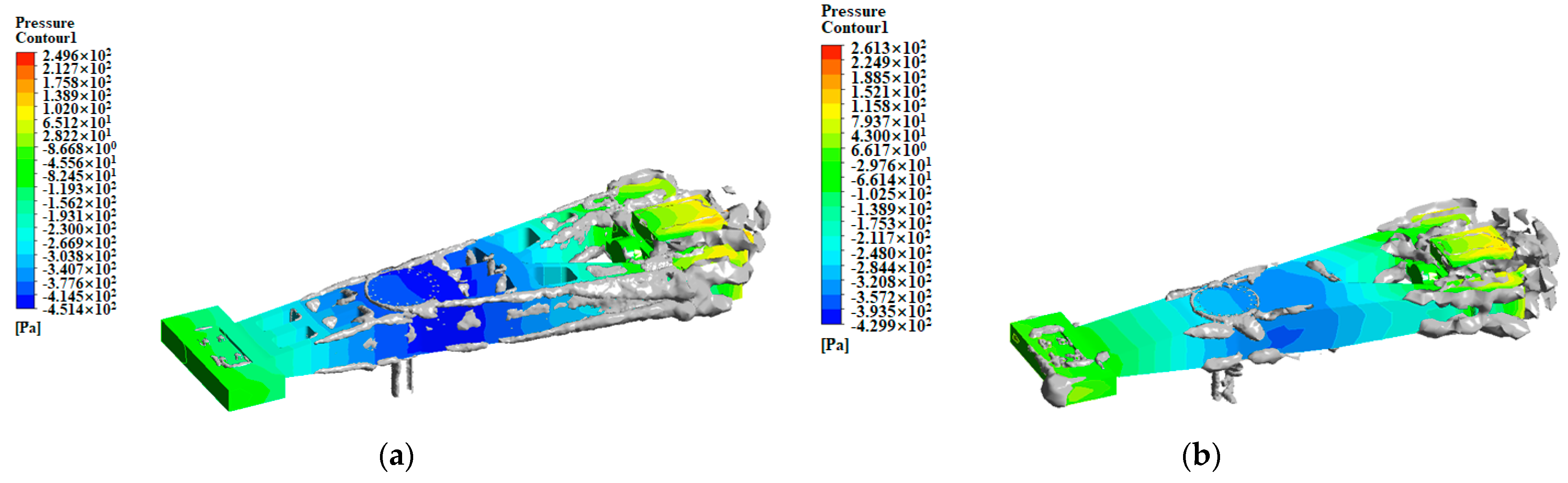
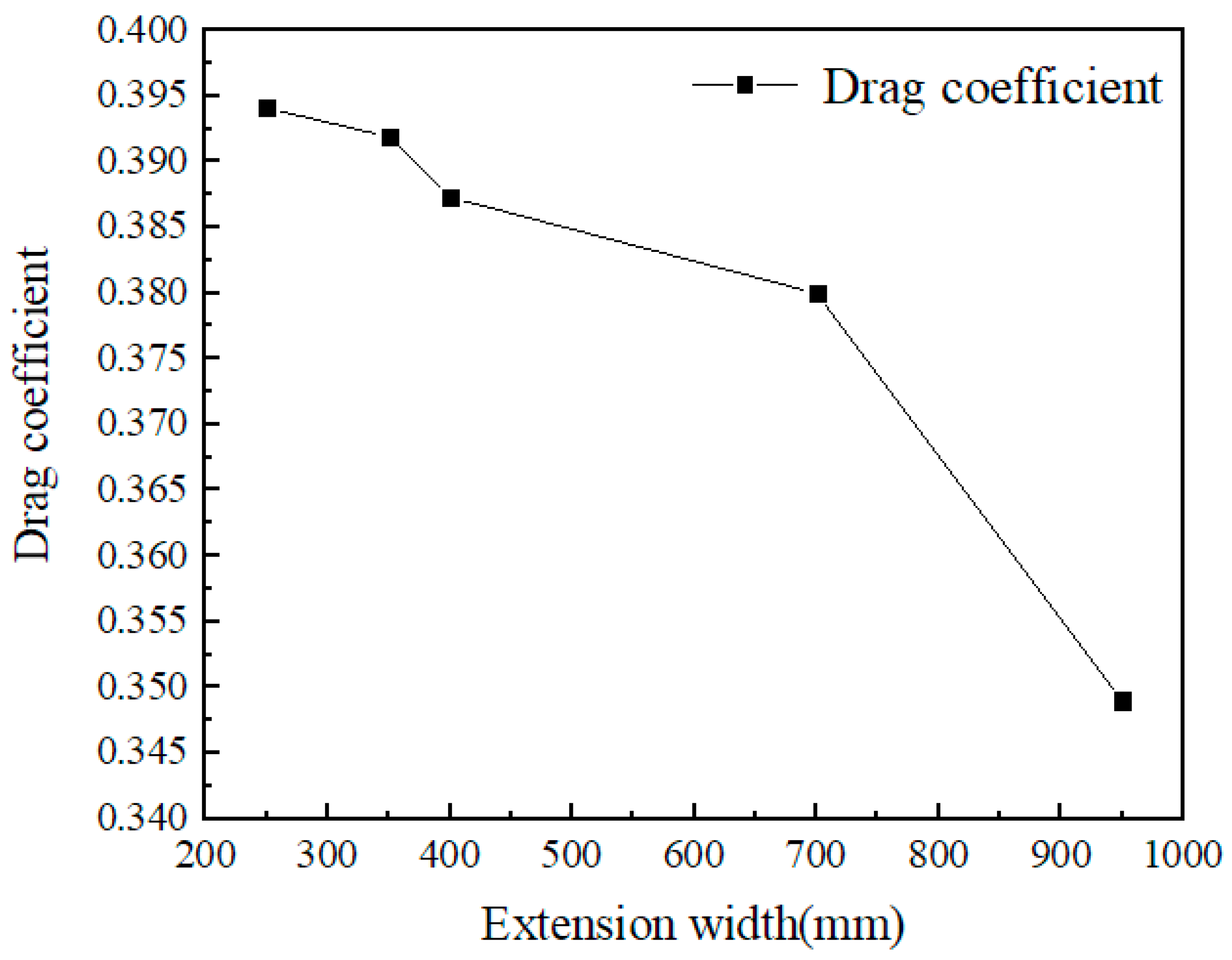
3.1. Vibration of the Test Centrifuge
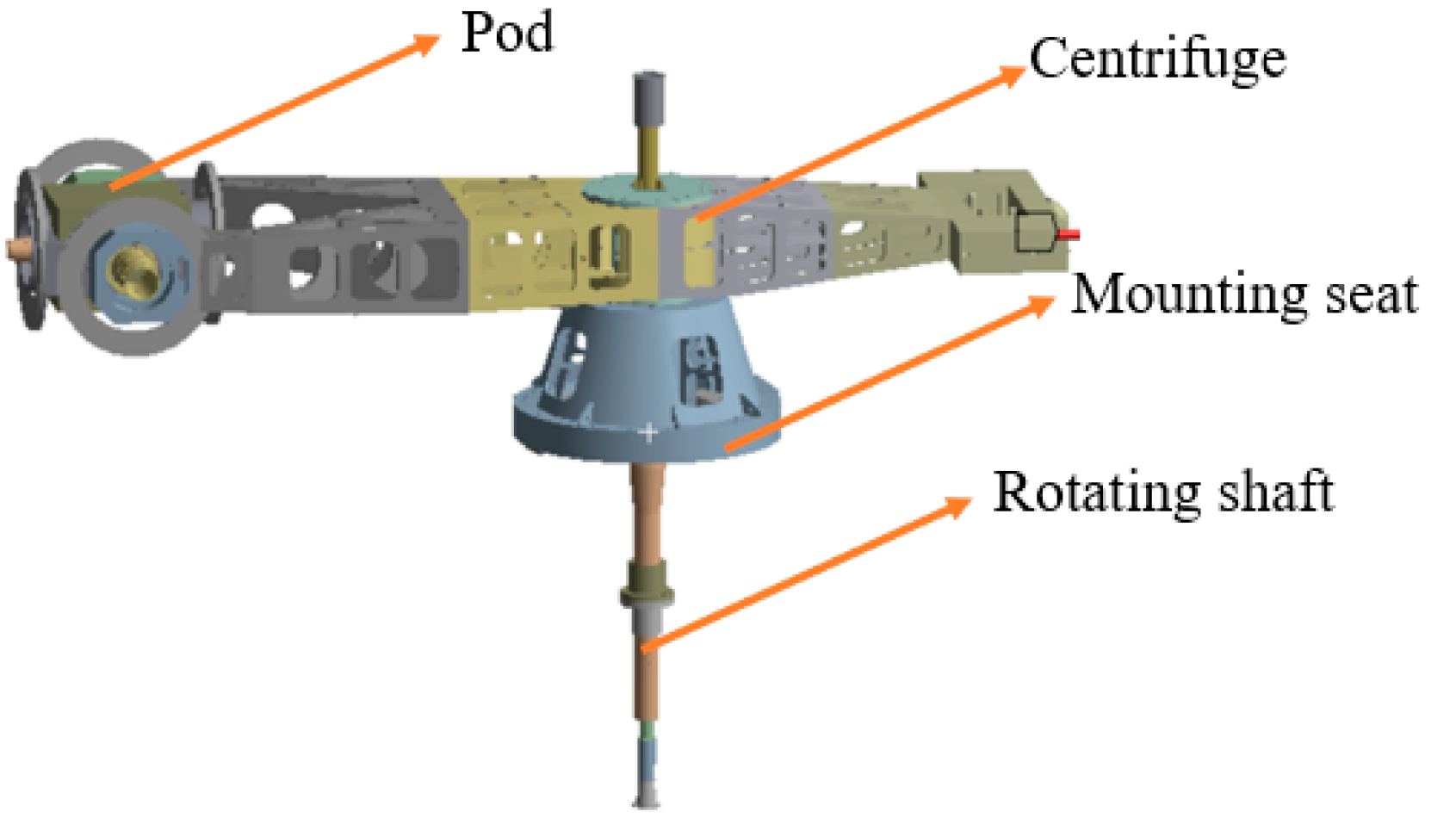
During the operation of the test centrifuge, the vibration at the mounting seat comes from the imbalance of the whole machine, the external vibration at the pod, and the vibration at the bearing. The vibration problem of the centrifuge has a great influence on the performance of the centrifuge. It is necessary to control the vibration value of the mounting seat within a reasonable range to minimize the vibration and provide the necessary technical basis for the good operation of the centrifuge. In order to ensure the safety and stability of the centrifuge, it is necessary to control the vibration at the mounting seat within the safety line.
There are many reasons for the imbalance of equipment in rotating machinery. The imbalance will make the rotating shaft bear excessive bending and torsion, which will lead to instability. In order to solve the above problems, it is necessary to identify and eliminate the imbalance of equipment [
22,
23,
24]. The FEM model is shown in
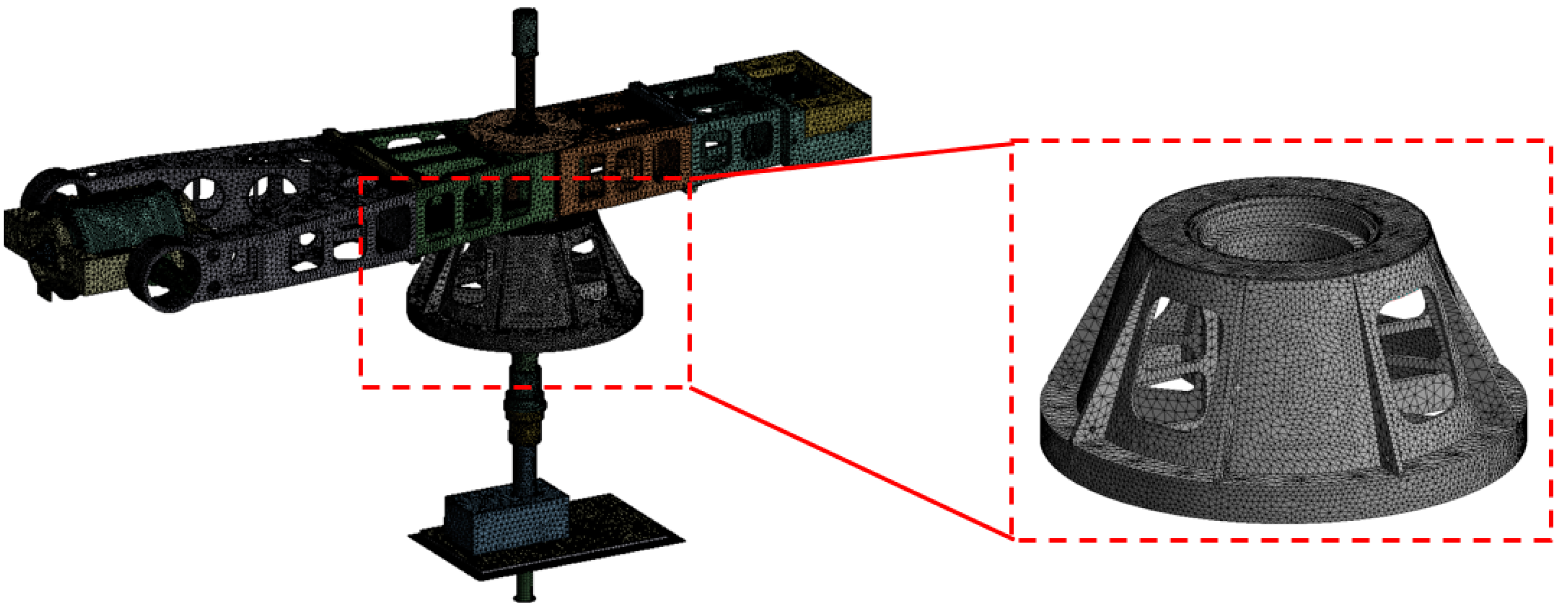
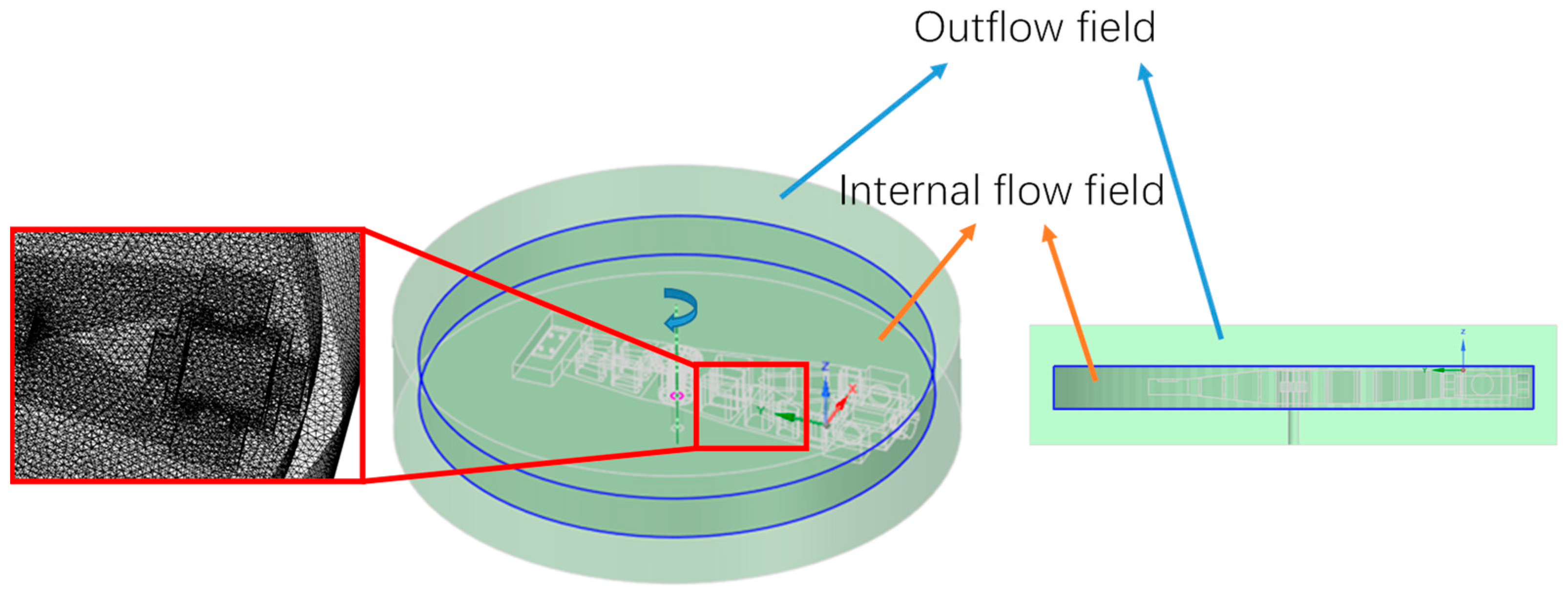
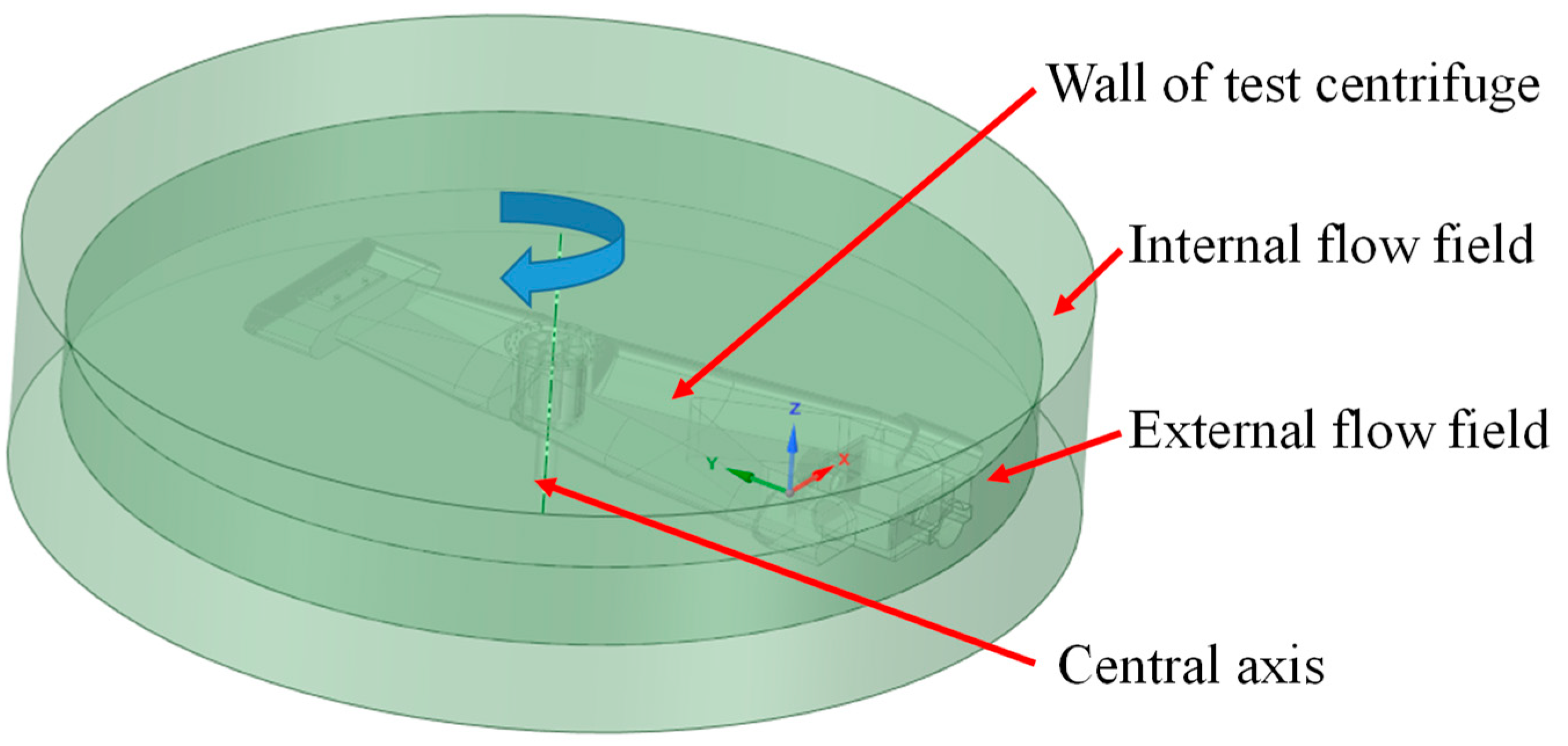
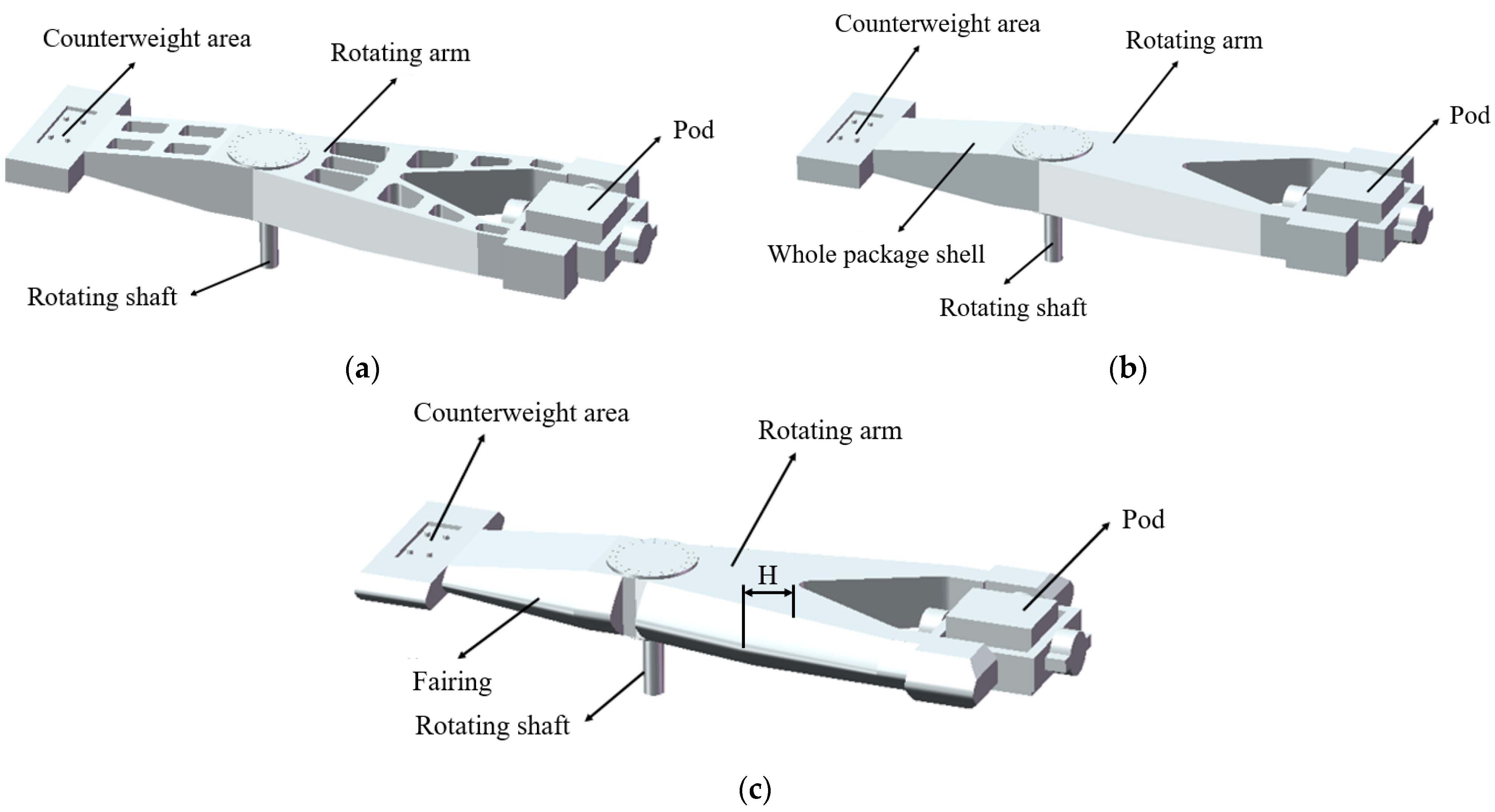
Figure 3, using a tetrahedral mesh. The number of elements is 1.44 million. The first load is the G40 dynamic unbalance.
In the Equation [
25],
M is the rotating arm mass,
G is the unbalanced precision grade,
r is the correction radius,
n is the working rotating speed of the centrifuge, and
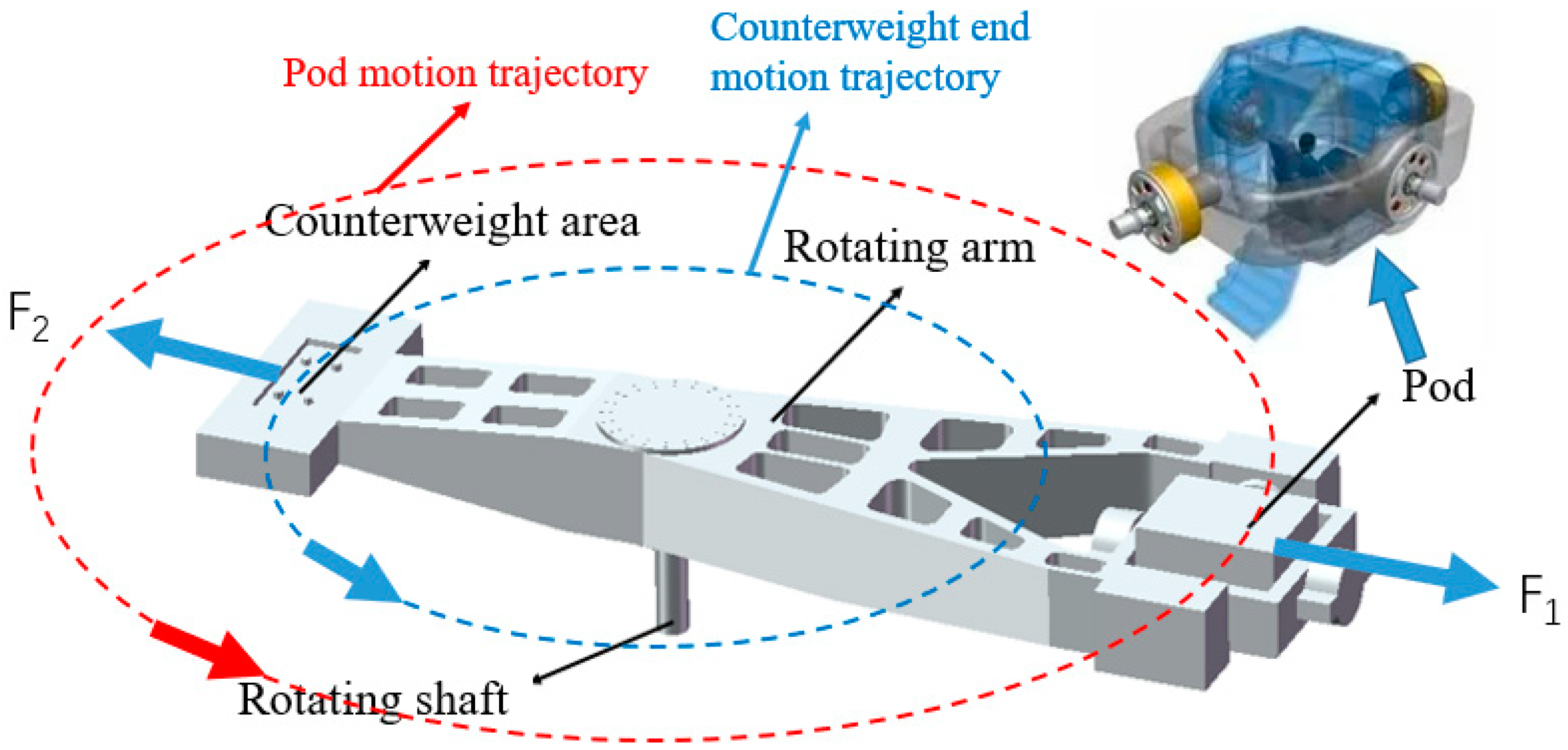
m is the unbalanced qualified quantity. The dynamic unbalance was simulated by applying force on the counterweight end face. According to Equation (1) [
25], the dynamic unbalance
G was 40, and the centrifuge speed was 38 r/min. It was calculated that the counterweight end should apply 200 kg of weight. According to Equation (2), it was calculated that a force of 19,077 N should be applied along the
Y-axis direction at the counterweight end, as shown in
Figure 4a. According to the spindle speed of 38 r/min, the harmonic response analysis frequency was 0~0.6333 Hz. The second load was the external vibration of the test piece in the pod, and its value was 1 g.
The acceleration excitation was converted into force by Equation (3). According to the mass of the test piece in the external vibration pod, the calculated excitation size was 7840 N. Therefore, the force was applied in all directions of the test piece, as shown in
Figure 4b. According to the test piece speed in 2400–17,000 r/min, the harmonic response analysis frequency was 40~290 Hz.
The last one is the bearing vibration. The excessive clearance of the bearing itself and the interaction between the bearings in the rotating machinery will cause an excessive vibration response of the equipment. To solve the problems, the appropriate bearing should be selected in the design [
26,
27,
28]. In order to simulate the vibration excitation of the bearing, the excitation force generated by the residual unbalanced mass was applied at the upper and lower spindle bearings, that is, a force of 19,077 N along the angular bisector of the X and Y axes, as shown in
Figure 4c. The bearing characteristic frequencies of radial bearing and thrust bearing were calculated, including the frequency
fbpfi of the rolling element passing through the inner ring, the rotation frequency
fbsf of the rolling element, and selecting the maximum value as the harmonic response analysis frequency to simulate the bearing excitation. According to Equations (4)–(6), the frequency of the rolling part passing through the inner ring and the rotation frequency of the rolling part were calculated.
In these equations,
D is the bearing pitch diameter,
Di is the bearing inner ring raceway diameter,
Do is the bearing outer ring raceway diameter,
d is the rolling element diameter,
α is the rolling element contact angle,
Z is the number of rollers, and
fi is the rotation frequency of the inner ring around the center of the circle. The radial bearing parameters and thrust bearing parameters are shown in
Table 1. The frequency of the rolling element of the radial bearing through the inner ring was calculated to be 11.57 Hz by Equation (5), and the frequency of the rolling element of the radial bearing through the inner ring was calculated to be 12.74 Hz. The rolling element rotation frequency of the radial bearing was calculated to be 4.16 Hz by Equation (6), and the rolling element rotation frequency of the radial bearing was calculated to be 5.33 Hz.
3.2. Harmonic Response Analysis Results
The rotational speed of the test centrifuge was 38 r/min. Three excitations of unbalance, external vibration, and bearing vibration were applied in the harmonic response analysis. At present, the centrifuge is still under design. In order to ensure sufficient safety margin, the vibration response of the support seat was linearly superimposed to analyze the maximum vibration response of the support seat. The static analysis adopted harmonic response analysis. The mesh is generated by the mesh module. The constraint setting in the analysis corresponded to the actual situation. A total of 1 fixed constraint, nine spring connections, and eight bearing connections were applied. Radial bearing stiffness K
1 and thrust bearing stiffness K
2 were calculated according to Equation (7) [
29].
In this Equation, K is the bearing stiffness, Z is the number of rollers, β is the contact angle of the roller, l is the effective length of the roller, d3 is the diameter of the roller, and R is the radial load.
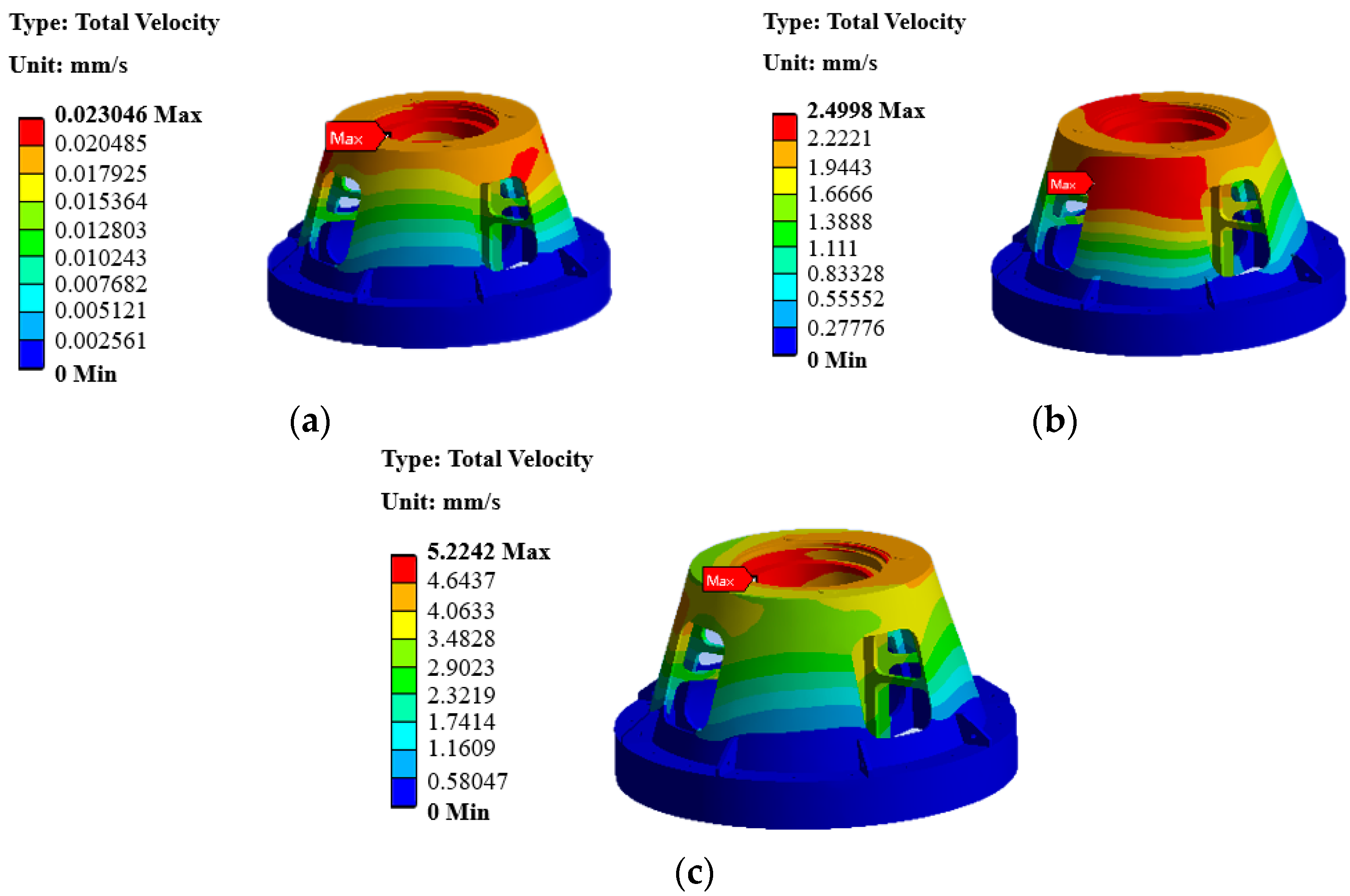
The first one is the vibration response under unbalanced excitation. According to the spindle rotating speed, 0~0.6333 Hz was set to simulate the harmonic response analysis frequency of G40 dynamic unbalance. The force was 19,077 N along the Y axis. As shown in
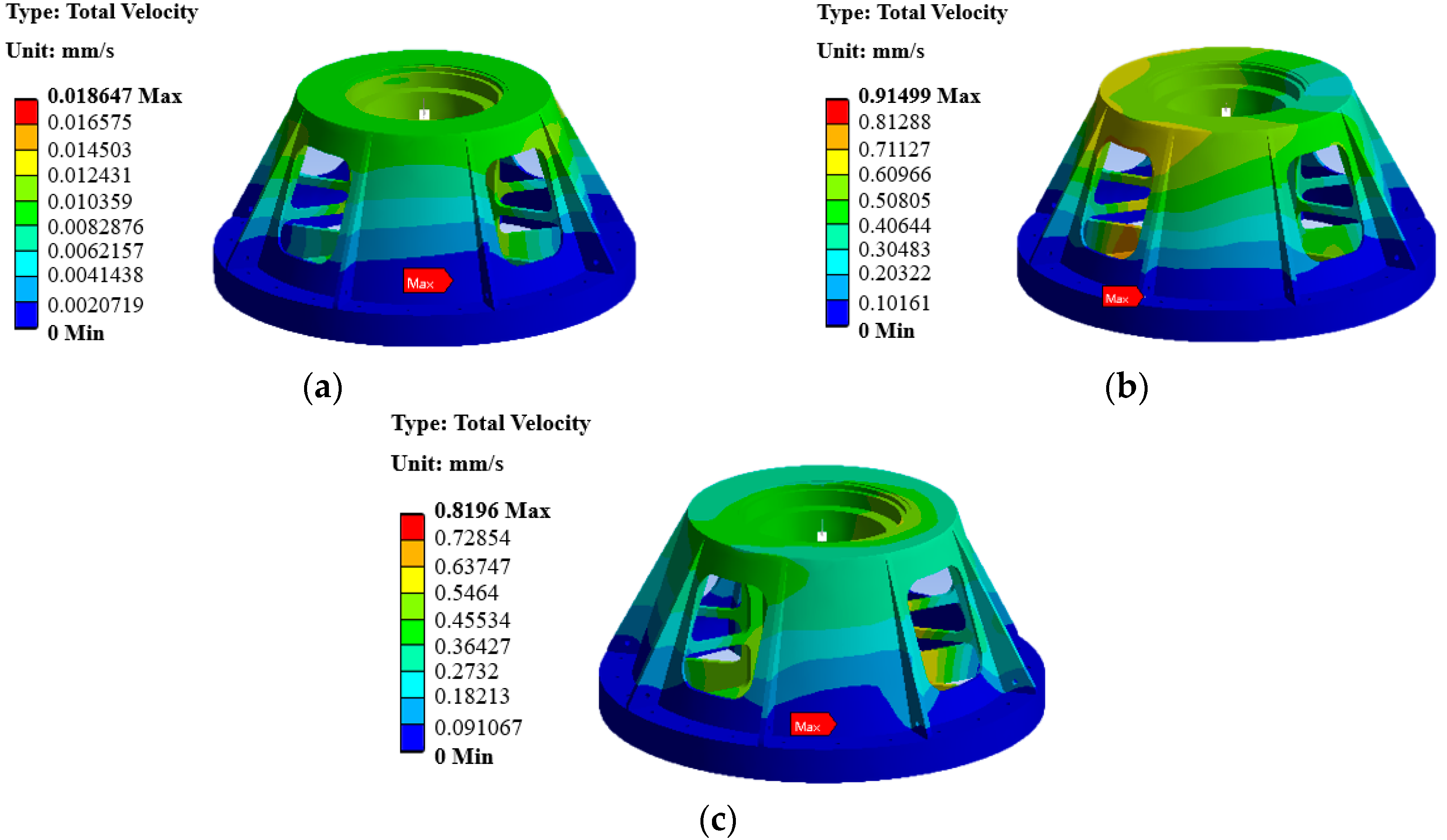
Figure 5a, the maximum vibration velocity response of the mounting seat under unbalanced excitation was 0.023 mm/s. The second one is the vibration response of the test piece in the pod under external vibration excitation. According to the rotational speed of the test piece, the harmonic response analysis frequency of the external vibration was set to 40~290 Hz. The force applied to the bottom of the test piece was 7840 N along the vertical direction, the radial direction of the centrifuge, and the tangential negative direction of the centrifuge. As shown in
Figure 5b, the maximum vibration velocity response of the mounting seat was 2.4998 mm/s under the external vibration excitation. The last one is the vibration response of bearing under vibration. The harmonic response analysis frequency was 0~22 Hz to simulate the harmonic response analysis frequency of the bearing vibration. The force was set to 13,500 N along the X and Y axes. As shown in
Figure 5c, the maximum vibration velocity response of the mounting seat under bearing vibration excitation was 5.2242 mm/s.
According to the analysis results, the maximum vibration velocity response of the mounting seat was 7.747 mm/s under the combined action of external vibration excitation, unbalanced excitation, and bearing vibration excitation. The specific data are shown in
Figure 6 and
Table 2.