Analysis of the Axial Vibration of Non-Uniform and Functionally Graded Rods via an Analytical-Based Numerical Approach
Abstract
1. Introduction
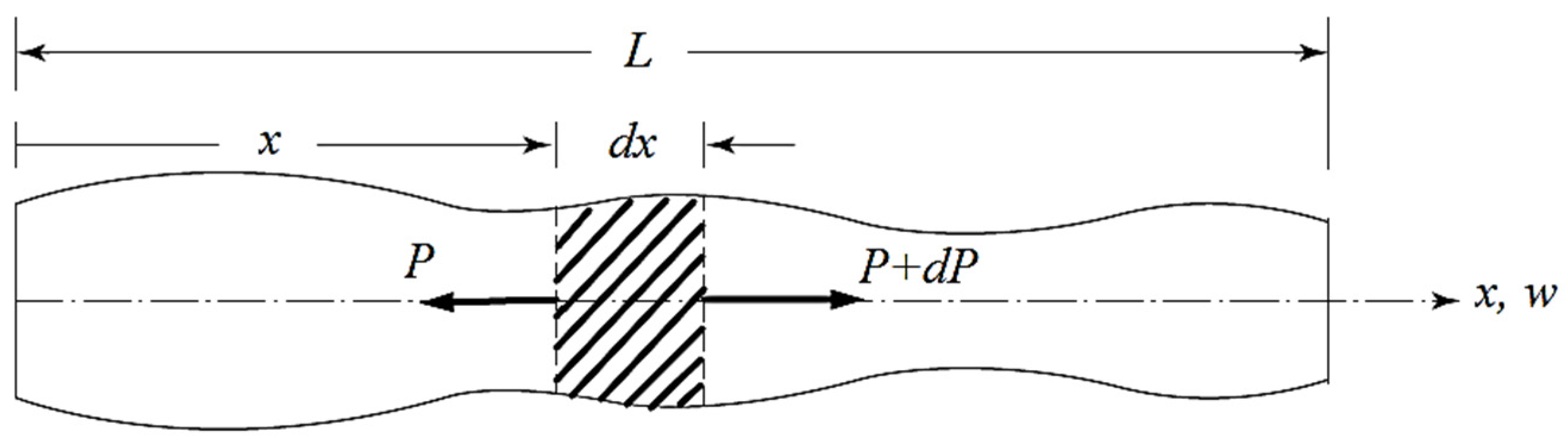
2. Axial Vibration of Rods
3. The Method
3.1. ADM
3.2. VIM
3.3. Subdomain-Based Numerical Solution Approach
4. Numerical Results
4.1. Case 1
4.2. Case 2
4.3. Case 3
4.4. Case 4
4.5. Case 5
4.6. Case 6
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Raman, V.M. On analytical solutions of vibrations of rods with variable cross sections. Appl. Math. Model. 1983, 7, 356–361. [Google Scholar] [CrossRef]
- Eisenberger, M. Exact longitudinal vibration frequencies of a variable cross-section rod. Appl. Acoust. 1991, 34, 123–130. [Google Scholar] [CrossRef]
- Abrate, S. Vibration of nonuniform rods and beams. J. Sound Vib. 1995, 185, 703–716. [Google Scholar] [CrossRef]
- Bapat, C.N. Vibration of rods with uniformly tapered sections. J. Sound Vib. 1995, 185, 185–189. [Google Scholar] [CrossRef]
- Kumar, B.M.; Sujith, R.I. Exact solutions for the longitudinal vibration of non-uniform rods. J. Sound Vib. 1997, 207, 721–729. [Google Scholar] [CrossRef]
- Li, Q.S. Exact solutions for free longitudinal vibrations of non-uniform rods. J. Sound Vib. 2000, 234, 1–19. [Google Scholar] [CrossRef]
- Li, Q.S. Exact solutions for free longitudinal vibration of stepped non-uniform rods. Appl. Acoust. 2000, 60, 13–28. [Google Scholar] [CrossRef]
- Zeng, H.; Bert, C.W. Vibration analysis of a tapered bar by differential transformation. J. Sound Vib. 2001, 242, 737–739. [Google Scholar] [CrossRef]
- Raj, A.; Sujith, R.I. Closed-form solutions for the free longitudinal vibration of inhomogeneous rods. J. Sound Vib. 2005, 283, 1015–1030. [Google Scholar] [CrossRef]
- Elishakoff, I. Eigenvalues of Inhomogeneous Structures: Unusual Closed-Form Solutions; CRC Press: Boca Raton, FL, USA, 2005. [Google Scholar]
- Al Kaisy, A.M.A.; Esmaeel, R.A.; Nassar, M.M. Application of the differential quadrature method in the longitudinal vibration of non-uniform rods. Eng. Mech. 2007, 14, 303–310. [Google Scholar]
- Provatidis, C.G. Free vibration analysis of elastic rods using global collocation. Arch. Appl. Mech. 2008, 78, 241–250. [Google Scholar] [CrossRef]
- Calio, I.; Elishakoff, I. Exponential solution for a longitudinally vibrating inhomogeneous rod. J. Mech. Mater. Struct. 2009, 4, 1251–1259. [Google Scholar] [CrossRef][Green Version]
- Arndt, M.; Machado, R.D.; Scremin, A. An adaptive generalized finite element method applied to free vibration analysis of straight bars and trusses. J. Sound Vib. 2010, 329, 659–672. [Google Scholar] [CrossRef]
- Inaudi, J.A.; Matusevich, A.E. Domain-partition power series in vibration analysis of variable-cross-section rods. J. Sound Vib. 2010, 329, 4534–4549. [Google Scholar] [CrossRef]
- Guo, S.Q.; Yang, S.P. Free longitudinal vibrations of non-uniform rods. Sci. China Technol. Sci. 2011, 54, 2735–2745. [Google Scholar] [CrossRef]
- Yardimoglu, B.; Aydin, L. Exact longitudinal vibration characteristics of rods with variable cross-sections. Shock Vib. 2011, 18, 555–562. [Google Scholar] [CrossRef][Green Version]
- Shahba, A.; Attarnejad, R.; Hajilar, S. Free vibration and stability of axially functionally graded tapered Euler-Bernoulli beams. Shock Vib. 2011, 18, 683–696. [Google Scholar] [CrossRef]
- Shahba, A.; Rajasekaran, S. Free vibration and stability of tapered Euler-Bernoulli beams made of axially functionally graded materials. Appl. Math. Model. 2012, 36, 3094–3111. [Google Scholar] [CrossRef]
- Shahba, A.; Attarnejad, R.; Hajilar, S. A Mechanical-Based Solution for Axially Functionally Graded Tapered Euler-Bernoulli Beams. Mech. Adv. Mater. Struct. 2013, 20, 696–707. [Google Scholar] [CrossRef]
- Gan, C.; Wei, Y.; Yang, S. Longitudinal wave propagation in a rod with variable cross-section. J. Sound Vib. 2014, 333, 434–445. [Google Scholar] [CrossRef]
- Hong, M.; Parl, I.; Lee, U. Dynamics and waves characteristics of the FGM axial bars by using spectral element method. Compos. Struct. 2014, 107, 585–593. [Google Scholar] [CrossRef]
- Shokrollahi, M.; Nejad, A.Z.B. Numerical Analysis of Free Longitudinal Vibration of Nonuniform Rods: Discrete Singular Convolution Approach. J. Eng. Mech. 2014, 140, 06014007. [Google Scholar] [CrossRef]
- Guo, S.; Yang, S. Longitudinal vibrations of arbitrary non-uniform rods. Acta Mech. Solida Sin. 2015, 28, 187–199. [Google Scholar] [CrossRef]
- Shali, S.; Nagaraja, S.R.; Jafarali, P. Vibration of non-uniform rod using Differential Transform Method. IOP Conf. Ser. Mater. Sci. Eng. 2017, 225, 012027. [Google Scholar] [CrossRef]
- Šalinića, S.; Obradović, A.; Tomović, A. Free vibration analysis of axially functionally graded tapered, stepped, and continuously segmented rods and beams. Compos. B. Eng. 2018, 150, 135–143. [Google Scholar] [CrossRef]
- Celebi, K.; Yarimpapuc, D.; Baran, T. Forced vibration analysis of inhomogeneous rods with non-uniform cross-section. J. Eng. Res. 2018, 6, 189–202. [Google Scholar]
- Pillutla, S.H.; Gopinathan, S.; Yerikalapudy, V.R. Free longitudinal vibrations of functionally graded tapered axial bars by pseudospectral method. J. Vibroeng. 2018, 20, 2137–2150. [Google Scholar] [CrossRef]
- Jedrysiak, J. Vibrations of microstructured beams with axial force. Vib. Phys. Syst. 2020, 31, 2020208. [Google Scholar] [CrossRef]
- Jedrysiak, J. Theoretical tolerance modelling of dynamics and stability for axially functionally graded (AFG) beams. Materials 2023, 16, 2096. [Google Scholar] [CrossRef]
- Zhou, J.K. Differential Transformation and Its Application for Electrical Circuits; Huazhong University Press: Wuhan, China, 1986. (In Chinese) [Google Scholar]
- He, J.-H. Variational iteration method—A kind of non-linear analytical technique: Some examples. Int. J. Non-Linear Mech. 1999, 34, 699–708. [Google Scholar] [CrossRef]
- Adomian, G. Solving Frontier Problems of Physics: The Decomposition Method; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1994. [Google Scholar]
- He, J.-H. Homotopy perturbation method: A new nonlinear analytical technique. Appl. Math. Comput. 2003, 135, 73–79. [Google Scholar] [CrossRef]
- Liao, S.J. The Proposed Homotopy Analysis Technique for the Solution of Nonlinear Problems. Ph.D. Thesis, Shanghai Jiao Tong University, Shanghai, China, 1992. [Google Scholar]
- Marinca, V.; Herisanu, N.; Marinca, B. Optimal Auxiliary Functions Method for Nonlinear Dynamical Systems; Springer: Cham, Switzerland, 2021. [Google Scholar]
- Den Hartog, J.P. Mechanical Vibrations; Dover Publications: Mineola, NY, USA, 1985. [Google Scholar]
- Yardimoglu, B. Exact solutions for the longitudinal vibration of non-uniform rods [J. Sound Vib.207(1997)721–729]. J. Sound Vib. 2010, 329, 4107. [Google Scholar] [CrossRef]
- Bahrami, A. Comments on “Exact solutions for the longitudinal vibration of non-uniform rods [J. Sound Vib. 1997, 207, 721–729]”. J. Sound Vib. 2019, 442, 843–844. [Google Scholar] [CrossRef]
- Kelly, S.G. Mechanical Vibrations: Theory and Applications; Cengage Learning: Boston, MA, USA, 2012. [Google Scholar]
- Rao, S.S. Mechanical Vibrations, 6th ed.; Pearson: London, UK, 2017. [Google Scholar]

| [2] First Five Frequencies | ||||
|---|---|---|---|---|
| ADM | VIM | ADM | VIM | |
| 1.79466 | 1.79466 | 1.79410 | 1.79410 | 1.79401 |
| 4.80205 | 4.80205 | 4.80211 | 4.80211 | 4.80206 |
| 7.91027 | 7.91027 | 7.90899 | 7.90899 | 7.90896 |
| 11.05688 | 11.05688 | 11.03511 | 11.03511 | 11.03509 |
| 14.25171 | 14.25171 | 14.16801 | 14.16801 | 14.16799 |
| [2] First Five Frequencies | ||||
|---|---|---|---|---|
| ADM | VIM | ADM | VIM | |
| 1.97035 | 1.97035 | 1.97011 | 1.97011 | 1.97090 |
| 4.82192 | 4.82192 | 4.82058 | 4.82058 | 4.82076 |
| 7.91805 | 7.91805 | 7.91813 | 7.91813 | 7.91820 |
| 11.05315 | 11.05315 | 11.04139 | 11.04139 | 11.04144 |
| 14.23085 | 14.23085 | 14.17282 | 14.17282 | 14.17284 |
| This Study | [2] First Five Frequencies | ||
|---|---|---|---|
| 1.79410 | 1.79403 | 1.79401 | 1.79401 |
| 4.80211 | 4.80207 | 4.80206 | 4.80206 |
| 7.90899 | 7.90897 | 7.90896 | 7.90896 |
| 11.03511 | 11.03510 | 11.03510 | 11.03509 |
| 14.16801 | 14.16799 | 14.16799 | 14.16799 |
| [2] First Five Frequencies | ||||
|---|---|---|---|---|
| ADM | VIM | ADM | VIM | |
| 1.97078 | 1.97088 | 1.97090 | 1.97090 | 1.97078 |
| 4.82071 | 4.82075 | 4.82076 | 4.82076 | 4.82071 |
| 7.91818 | 7.91820 | 7.91820 | 7.91820 | 7.91818 |
| 11.04143 | 11.04144 | 11.04144 | 11.04144 | 11.04143 |
| 14.17283 | 14.17284 | 14.17284 | 14.17284 | 14.17283 |
| Mode | ||||||
|---|---|---|---|---|---|---|
| This Study n = 20 | This Study n = 100 | [40] | This Study n = 20 | This Study n = 100 | [40] | |
| 1 | 3.286029 | 3.286007 | 3.285998 | 3.474486 | 3.474339 | 3.474339 |
| 2 | 6.360710 | 6.360678 | 6.360671 | 6.480282 | 6.480034 | 6.480028 |
| 3 | 9.477253 | 9.477196 | 9.477180 | 9.561781 | 9.561370 | 9.561367 |
| 4 | 12.606002 | 12.605890 | 12.605802 | 12.671048 | 12.670362 | 12.670323 |
| 5 | 15.739881 | 15.739656 | 15.739648 | 15.792900 | 15.791752 | 15.791747 |
| 6 | 18.876445 | 18.876002 | 18.874533 | 18.921558 | 18.919655 | 18.919130 |
| Mode | ||||||
|---|---|---|---|---|---|---|
| This Study n = 20 | This Study n = 100 | [40] | This Study n = 20 | This Study n = 100 | [40] | |
| 1 | 0.824911 | 0.824969 | 0.824971 | 0.526525 | 0.526686 | 0.526694 |
| 2 | 4.600469 | 4.600454 | 4.600454 | 4.689503 | 4.689332 | 4.689329 |
| 3 | 7.789132 | 7.789097 | 7.789096 | 7.849000 | 7.848697 | 7.848695 |
| 4 | 10.949734 | 10.949659 | 10.949659 | 10.994129 | 10.993612 | 10.993610 |
| 5 | 14.101746 | 14.101592 | 14.101591 | 14.137111 | 14.136237 | 14.136235 |
| 6 | 17.250022 | 17.249709 | 17.249708 | 17.279715 | 17.278249 | 17.278247 |
| Mode | ||||||
|---|---|---|---|---|---|---|
| This Study n = 20 | This Study n = 100 | [40] | This Study n = 20 | This Study n = 100 | [40] | |
| 1 | 3.555887 | 3.555792 | 3.555788 | 4.041829 | 4.041340 | 4.041322 |
| 2 | 6.513149 | 6.513070 | 6.513068 | 6.857766 | 6.857191 | 6.857173 |
| 3 | 9.581360 | 9.581272 | 9.581270 | 9.830658 | 9.830000 | 9.829986 |
| 4 | 12.684744 | 12.684610 | 12.684608 | 12.877428 | 12.876563 | 12.876551 |
| 5 | 15.803120 | 15.802878 | 15.802877 | 15.959733 | 15.958463 | 15.958453 |
| 6 | 18.929253 | 18.928799 | 18.928798 | 19.061341 | 19.059368 | 19.059359 |
| Mode | ||||||
|---|---|---|---|---|---|---|
| This Study n = 20 | This Study n = 100 | [40] | This Study n = 20 | This Study n = 100 | [40] | |
| 1 | 2.978151 | 2.978187 | 2.978189 | 2.422827 | 2.422601 | 2.422727 |
| 2 | 6.203079 | 6.203097 | 6.203097 | 5.955421 | 5.956256 | 5.956376 |
| 3 | 9.371565 | 9.371576 | 9.371576 | 9.210152 | 9.210008 | 9.210127 |
| 4 | 12.526513 | 12.526518 | 12.526519 | 12.407305 | 12.406080 | 12.406195 |
| 5 | 15.676103 | 15.676100 | 15.676100 | 15.582357 | 15.580012 | 15.580119 |
| 6 | 18.823033 | 18.823011 | 18.823011 | 18.746557 | 18.743054 | 18.743152 |
| Mode | ||||||
|---|---|---|---|---|---|---|
| This Study n = 20 | This Study n = 100 | [40] | This Study n = 20 | This Study n = 100 | [40] | |
| 1 | 1.517623 | 1.517637 | 1.517638 | 2.149426 | 2.148593 | 2.148560 |
| 2 | 4.702142 | 4.702145 | 4.702145 | 5.539852 | 5.535922 | 5.535762 |
| 3 | 7.848310 | 7.848311 | 7.848311 | 8.639936 | 8.633093 | 8.632812 |
| 4 | 10.991621 | 10.991621 | 10.991620 | 11.703833 | 11.695014 | 11.694640 |
| 5 | 14.134128 | 14.134123 | 14.134120 | 14.767991 | 14.758288 | 14.757860 |
| 6 | 17.276297 | 17.276824 | 17.276280 | 17.840719 | 17.831054 | 17.830600 |
| Mode | ||||||
|---|---|---|---|---|---|---|
| This Study n = 20 | This Study n = 100 | [40] | This Study n = 20 | This Study n = 100 | [40] | |
| 1 | 3.309109 | 3.309071 | 3.309070 | 4.212406 | 4.209714 | 4.209604 |
| 2 | 6.375233 | 6.37509 | 6.375209 | 7.265756 | 7.260092 | 7.259860 |
| 3 | 9.487380 | 9.487363 | 9.487363 | 10.291902 | 10.283836 | 10.283498 |
| 4 | 12.613663 | 12.613649 | 12.613648 | 13.327822 | 13.318388 | 13.317980 |
| 5 | 15.745930 | 15.745914 | 15.745913 | 16.379162 | 16.369366 | 16.368917 |
| 6 | 18.881271 | 18.881240 | 18.881240 | 19.445177 | 19.435801 | 19.435335 |
| Mode | ||||||
|---|---|---|---|---|---|---|
| This Study n = 100 | Kummer Function [16] | This Study n = 100 | Kummer Function [16] | This Study n = 100 | Kummer Function [16] | |
| 1 | 3.231130281 | 3.231130281 | 3.339335867 | 3.339335867 | 3.603139793 | 3.603139793 |
| 2 | 6.329186675 | 6.329186675 | 6.387440255 | 6.387440254 | 6.539562685 | 6.539562675 |
| 3 | 9.455600357 | 9.455600357 | 9.494964059 | 9.494964058 | 9.598980448 | 9.598980427 |
| 4 | 12.58952819 | 12.58952819 | 12.61919022 | 12.61919022 | 12.69788674 | 12.69788671 |
| Mode | ||||||
|---|---|---|---|---|---|---|
| Fixed–Free | Free–Free | Fixed–Free | Free–Free | Fixed–Free | Free–Free | |
| 1 | 1.414214 | 3.072491 | 1.263693 | 3.025089 | 0.985886 | 2.997101 |
| 2 | 4.667369 | 6.249688 | 4.638712 | 6.228916 | 4.631731 | 6.226225 |
| 3 | 7.827282 | 9.402573 | 7.810922 | 9.389054 | 7.809608 | 9.388313 |
| 4 | 10.976564 | 12.549750 | 10.965036 | 12.539695 | 10.964576 | 12.539391 |
| 5 | 14.122401 | 15.694679 | 14.113484 | 15.686666 | 14.113271 | 15.686512 |
| Mode | ||||||||
|---|---|---|---|---|---|---|---|---|
| This Study | [17] | This Study | [17] | This Study | [17] | This Study | [17] | |
| 1 | 3.033656 | 3.033658 | 2.926834 | 2.926836 | 2.821242 | 2.821246 | 2.716998 | 2.717003 |
| 2 | 6.228474 | 6.228475 | 6.178606 | 6.178607 | 6.133694 | 6.133696 | 6.093837 | 6.093840 |
| 3 | 9.388171 | 9.388171 | 9.355383 | 9.355384 | 9.326455 | 9.326456 | 9.301423 | 9.301424 |
| 4 | 12.538877 | 12.538877 | 12.514409 | 12.514409 | 12.492984 | 12.492985 | 12.474620 | 12.474621 |
| 5 | 15.685953 | 15.685954 | 15.666425 | 15.666425 | 15.649387 | 15.649387 | 15.634848 | 15.634849 |
| 6 | 18.831208 | 18.831208 | 18.814954 | 18.814955 | 18.800802 | 18.800803 | 18.788757 | 18.788757 |
| Mode | ||||||||
|---|---|---|---|---|---|---|---|---|
| This Study | [17] | This Study | [17] | This Study | [17] | This Study | [17] | |
| 1 | 1.568123 | 1.568123 | 1.560154 | 1.560155 | 1.547041 | 1.547041 | 1.529022 | 1.529023 |
| 2 | 4.715830 | 4.715830 | 4.726103 | 4.726102 | 4.743064 | 4.743064 | 4.766485 | 4.766484 |
| 3 | 7.856372 | 7.856372 | 7.863537 | 7.863537 | 7.875459 | 7.875459 | 7.892109 | 7.892108 |
| 4 | 10.997350 | 10.997350 | 11.002678 | 11.002678 | 11.011552 | 11.011552 | 11.023968 | 11.023967 |
| 5 | 14.138571 | 14.138571 | 14.142783 | 14.142783 | 14.149801 | 14.149801 | 14.159624 | 14.159624 |
| 6 | 17.279918 | 17.279918 | 17.283392 | 17.283392 | 17.289183 | 17.289183 | 17.297288 | 17.297288 |
| Mode | ||||||||
|---|---|---|---|---|---|---|---|---|
| This Study | [17] | This Study | [17] | This Study | [17] | This Study | [17] | |
| 1 | 3.250524 | 3.250523 | 3.360331 | 3.360328 | 3.470895 | 3.470891 | 3.582098 | 3.582093 |
| 2 | 6.342611 | 6.342610 | 6.406607 | 6.406605 | 6.475018 | 6.475015 | 6.547679 | 6.547675 |
| 3 | 9.465160 | 9.465160 | 9.509270 | 9.509269 | 9.557058 | 9.557056 | 9.608469 | 9.608466 |
| 4 | 12.596871 | 12.596870 | 12.630356 | 12.630355 | 12.666807 | 12.666805 | 12.706199 | 12.706197 |
| 5 | 15.732444 | 15.732444 | 15.759386 | 15.759385 | 15.788776 | 15.788777 | 15.820607 | 15.820605 |
| 6 | 18.869994 | 18.869993 | 18.892515 | 18.892514 | 18.917112 | 18.917113 | 18.943782 | 18.943781 |
| ch | cb | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| [19] | [28] | This Study | [19] | [28] | This Study | [19] | [28] | This Study | ||
| 0.0 | 0.0 | 2.8760 | - | 2.875963 | 5.7627 | - | 5.762720 | 8.6453 | - | 8.645279 |
| 0.2 | 2.8631 | - | 2.863124 | 5.7562 | - | 5.756197 | 8.6409 | - | 8.640920 | |
| 0.4 | 2.8415 | - | 2.841461 | 5.7453 | - | 5.745320 | 8.6337 | - | 8.633663 | |
| 0.6 | 2.8023 | - | 2.802335 | 5.7251 | - | 5.725108 | 8.6201 | - | 8.620077 | |
| 0.8 | 2.7192 | - | 2.719200 | 5.6767 | - | 5.676634 | 8.5860 | - | 8.586022 | |
| 0.2 | 0.2 | 2.8539 | 2.853926 | 2.853922 | 5.7515 | 5.751501 | 5.751493 | 8.6378 | 8.637841 | 8.637772 |
| 0.4 | 2.8369 | 2.836936 | 2.836933 | 5.7430 | 5.742957 | 5.742966 | 8.6321 | 8.632147 | 8.632078 | |
| 0.6 | 2.8042 | 2.804223 | 2.804218 | 5.7260 | 5.726023 | 5.726014 | 8.6207 | 8.620747 | 8.620682 | |
| 0.8 | 2.7311 | 2.731119 | 2.731107 | 5.6829 | 5.682885 | 5.682900 | 8.5903 | 8.590337 | 8.590280 | |
| 0.4 | 0.4 | 2.8260 | 2.825973 | 2.825970 | 5.7375 | 5.737498 | 5.737489 | 8.6284 | 8.628504 | 8.628435 |
| 0.6 | 2.8016 | 2.801561 | 2.801557 | 5.7249 | 5.724929 | 5.724920 | 8.6200 | 8.620056 | 8.619992 | |
| 0.8 | 2.7415 | 2.741519 | 2.741508 | 5.6892 | 5.689170 | 5.689156 | 8.5947 | 8.594748 | 8.594692 | |
| 0.6 | 0.6 | 2.7886 | 2.788644 | 2.788640 | 5.7188 | 5.718775 | 5.718765 | 8.6160 | 8.615999 | 8.615940 |
| 0.8 | 2.7468 | 2.746813 | 2.746803 | 5.6942 | 5.694204 | 5.694192 | 8.5986 | 8.598631 | 8.598578 | |
| 0.8 | 0.8 | 2.7340 | 2.734041 | 2.734030 | 5.6901 | 5.690056 | 5.690056 | 8.5965 | 8.596521 | 8.596473 |
| ch | cb | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| [19] | [28] | This Study | [19] | [28] | This Study | [19] | [28] | This Study | ||
| 0.0 | 0.0 | 1.1901 | - | 1.190121 | 4.2549 | - | 4.254908 | 7.1650 | - | 7.165005 |
| 0.2 | 1.2503 | - | 1.250273 | 4.2683 | - | 4.268343 | 7.1728 | - | 7.172861 | |
| 0.4 | 1.3293 | - | 1.329260 | 4.2903 | - | 4.290291 | 7.1859 | - | 7.185878 | |
| 0.6 | 1.4400 | - | 1.440031 | 4.3333 | - | 4.333294 | 7.2123 | - | 7.212325 | |
| 0.8 | 1.6129 | - | 1.612889 | 4.4444 | - | 4.444389 | 7.2891 | - | 7.289126 | |
| 0.2 | 0.2 | 1.3119 | 1.311936 | 1.311941 | 4.2841 | 4.284133 | 4.284152 | 7.1821 | 7.181803 | 7.182161 |
| 0.4 | 1.3928 | 1.392789 | 1.392794 | 4.3090 | 4.309044 | 4.309063 | 7.1970 | 7.196715 | 7.197021 | |
| 0.6 | 1.5059 | 1.505925 | 1.505931 | 4.3559 | 4.355943 | 4.355962 | 7.2260 | 7.225773 | 7.225995 | |
| 0.8 | 1.6818 | 1.681840 | 1.681836 | 4.4726 | 4.472646 | 4.472622 | 7.3068 | 7.306703 | 7.306799 | |
| 0.4 | 0.4 | 1.4759 | 1.475871 | 1.475877 | 4.3377 | 4.337722 | 4.337740 | 7.2143 | 7.214022 | 7.214275 |
| 0.6 | 1.5917 | 1.591695 | 1.591701 | 4.3897 | 4.389690 | 4.389708 | 7.2466 | 7.246450 | 7.246626 | |
| 0.8 | 1.7706 | 1.770668 | 1.770663 | 4.5138 | 4.513827 | 4.513801 | 7.3329 | 7.332918 | 7.332981 | |
| 0.6 | 0.6 | 1.7104 | 1.710443 | 1.710450 | 4.4487 | 4.448671 | 4.448690 | 7.2839 | 7.283791 | 7.283910 |
| 0.8 | 1.8918 | 1.891820 | 1.891814 | 4.5832 | 4.583282 | 4.583249 | 7.3787 | 7.378728 | 7.378747 | |
| 0.8 | 0.8 | 2.0723 | 2.072303 | 2.072286 | 4.7328 | 4.732920 | 4.732813 | 7.4888 | 7.488952 | 7.488819 |
| ch | cb | Fixed–Fixed Rod | Fixed–Free Rod | ||||
|---|---|---|---|---|---|---|---|
| 0.0 | 0.0 | 11.527389 | 14.409395 | 17.291364 | 10.058501 | 12.946776 | 15.832722 |
| 0.2 | 11.524117 | 14.406776 | 17.289181 | 10.064076 | 12.951100 | 15.836256 | |
| 0.4 | 11.518673 | 14.402421 | 17.285552 | 10.073349 | 12.958304 | 15.842147 | |
| 0.6 | 11.508451 | 14.394231 | 17.278720 | 10.092388 | 12.973163 | 15.854326 | |
| 0.8 | 11.482303 | 14.373052 | 17.260943 | 10.150175 | 13.019219 | 15.892511 | |
| 0.2 | 0.2 | 11.521753 | 14.404884 | 17.287604 | 10.070687 | 12.956231 | 15.840450 |
| 0.4 | 11.517481 | 14.401466 | 17.284756 | 10.081286 | 12.964471 | 15.847190 | |
| 0.6 | 11.508906 | 14.394595 | 17.279024 | 10.102171 | 12.980778 | 15.860559 | |
| 0.8 | 11.485529 | 14.375646 | 17.263112 | 10.162984 | 13.029246 | 15.900742 | |
| 0.4 | 0.4 | 11.514750 | 14.399282 | 17.282936 | 10.093623 | 12.974071 | 15.855046 |
| 0.6 | 11.508399 | 14.394194 | 17.278692 | 10.116990 | 12.992331 | 15.870023 | |
| 0.8 | 11.488913 | 14.378385 | 17.265409 | 10.182042 | 13.044192 | 15.913024 | |
| 0.6 | 0.6 | 11.505375 | 14.391780 | 17.276683 | 10.144039 | 13.013508 | 15.887408 |
| 0.8 | 11.492002 | 14.380928 | 17.267564 | 10.215716 | 13.070717 | 15.934868 | |
| 0.8 | 0.8 | 11.490668 | 14.379970 | 17.266821 | 10.300149 | 13.138517 | 15.991278 |
| ch | cb | ||||||
|---|---|---|---|---|---|---|---|
| 0.0 | 0.0 | 2.946681 | 5.794961 | 8.666278 | 11.543029 | 14.421883 | 17.301774 |
| 0.2 | 2.934015 | 5.788683 | 8.662112 | 11.539910 | 14.419390 | 17.299698 | |
| 0.4 | 2.933673 | 5.788820 | 8.662252 | 11.540028 | 14.419489 | 17.299782 | |
| 0.6 | 2.962114 | 5.805445 | 8.673717 | 11.548734 | 14.426494 | 17.305639 | |
| 0.8 | 3.068501 | 5.880639 | 8.729109 | 11.592045 | 14.461882 | 17.335486 | |
| 0.2 | 0.2 | 2.924899 | 5.784214 | 8.659156 | 11.537699 | 14.417624 | 17.298227 |
| 0.4 | 2.929150 | 5.786684 | 8.660854 | 11.538987 | 14.418659 | 17.299092 | |
| 0.6 | 2.963729 | 5.806550 | 8.674503 | 11.549336 | 14.426982 | 17.306047 | |
| 0.8 | 3.078513 | 5.886890 | 8.733501 | 11.595402 | 14.464592 | 17.337756 | |
| 0.4 | 0.4 | 2.939281 | 5.792205 | 8.664600 | 11.541814 | 14.420927 | 17.300985 |
| 0.6 | 2.981602 | 5.816379 | 8.681183 | 11.554380 | 14.431030 | 17.309426 | |
| 0.8 | 3.106649 | 5.903695 | 8.745184 | 11.604301 | 14.471763 | 17.343756 | |
| 0.6 | 0.6 | 3.033852 | 5.846773 | 8.702104 | 11.570253 | 14.443796 | 17.320096 |
| 0.8 | 3.171214 | 5.944370 | 8.773819 | 11.626209 | 14.489453 | 17.358572 | |
| 0.8 | 0.8 | 3.320973 | 6.058919 | 8.859947 | 11.693961 | 14.544927 | 17.405400 |
| c | Mode | Fixed–Fixed Rod | Fixed–Free Rod | ||||
|---|---|---|---|---|---|---|---|
| [20] | [28] | This Study n = 20 | [20] | [28] | This Study n = 20 | ||
| 0.1 | 1 | 3.1757 | 3.172409 | 3.172409 | 1.2988 | 1.2985 | 1.298593 |
| 2 | 6.3247 | 6.298648 | 6.298648 | 4.6478 | 4.637424 | 4.637424 | |
| 3 | 9.5228 | 9.435093 | 9.435095 | 7.8592 | 7.809505 | 7.809506 | |
| 0.3 | 1 | 3.1514 | 3.148153 | 3.148153 | 1.3722 | 1.371958 | 1.371958 |
| 2 | 6.3123 | 6.286365 | 6.286365 | 4.6656 | 4.655118 | 4.655118 | |
| 3 | 9.5144 | 9.426885 | 9.426885 | 7.8698 | 7.819942 | 7.819942 | |
| 0.5 | 1 | 3.1120 | 3.108831 | 3.108818 | 1.4710 | 1.470676 | 1.470698 |
| 2 | 6.2916 | 6.265918 | 6.265911 | 4.6983 | 4.687528 | 4.687538 | |
| 3 | 9.5005 | 9.413135 | 9.413131 | 7.8899 | 7.83957 | 7.839577 | |
| 0.8 | 1 | 2.9780 | 2.975221 | 2.974925 | 1.7168 | 1.716251 | 1.716528 |
| 2 | 6.2113 | 6.186568 | 6.186339 | 4.8486 | 4.836778 | 4.837135 | |
| 3 | 9.4427 | 9.357079 | 9.356909 | 7.9958 | 7.9433464 | 7.943773 | |
| c | ||||||
|---|---|---|---|---|---|---|
| 0.1 | 3.172409 | 6.298648 | 9.435093 | 12.574109 | 15.714154 | 18.854715 |
| 0.3 | 3.148154 | 6.286366 | 9.426885 | 12.567948 | 15.709223 | 18.850605 |
| 0.5 | 3.108831 | 6.265918 | 9.413135 | 12.557602 | 15.700935 | 18.843693 |
| 0.7 | 3.037652 | 6.225862 | 9.385513 | 12.536596 | 15.684013 | 18.829536 |
| 0.9 | 2.865805 | 6.107338 | 9.294870 | 12.463441 | 15.622847 | 18.777080 |
| c | ||||||
|---|---|---|---|---|---|---|
| 0.1 | 1.298593 | 4.637424 | 7.809505 | 10.963902 | 14.112563 | 17.258642 |
| 0.3 | 1.371958 | 4.655118 | 7.819942 | 10.971323 | 14.118324 | 17.263351 |
| 0.5 | 1.470678 | 4.687529 | 7.839571 | 10.985386 | 14.129277 | 17.272319 |
| 0.7 | 1.614399 | 4.760055 | 7.886977 | 11.020261 | 14.156765 | 17.294968 |
| 0.9 | 1.853356 | 4.987153 | 8.076173 | 11.177288 | 14.289295 | 17.408893 |
| C | ||||||
|---|---|---|---|---|---|---|
| 0.1 | 3.174157 | 6.299530 | 9.435682 | 12.574551 | 15.714508 | 18.855010 |
| 0.3 | 3.168121 | 6.296532 | 9.433687 | 12.573055 | 15.713312 | 18.854014 |
| 0.5 | 3.182758 | 6.304872 | 9.439404 | 12.577387 | 15.716794 | 18.856923 |
| 0.7 | 3.246929 | 6.346320 | 9.468966 | 12.600161 | 15.735255 | 18.872421 |
| 0.9 | 3.458060 | 6.538647 | 9.630470 | 12.736129 | 15.851494 | 18.973406 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kondakcı, K.; Coşkun, S.B. Analysis of the Axial Vibration of Non-Uniform and Functionally Graded Rods via an Analytical-Based Numerical Approach. Vibration 2023, 6, 876-894. https://doi.org/10.3390/vibration6040052
Kondakcı K, Coşkun SB. Analysis of the Axial Vibration of Non-Uniform and Functionally Graded Rods via an Analytical-Based Numerical Approach. Vibration. 2023; 6(4):876-894. https://doi.org/10.3390/vibration6040052
Chicago/Turabian StyleKondakcı, Koray, and Safa Bozkurt Coşkun. 2023. "Analysis of the Axial Vibration of Non-Uniform and Functionally Graded Rods via an Analytical-Based Numerical Approach" Vibration 6, no. 4: 876-894. https://doi.org/10.3390/vibration6040052
APA StyleKondakcı, K., & Coşkun, S. B. (2023). Analysis of the Axial Vibration of Non-Uniform and Functionally Graded Rods via an Analytical-Based Numerical Approach. Vibration, 6(4), 876-894. https://doi.org/10.3390/vibration6040052





