Abstract
Vibration-based damage detection is a range of methods that utilizes the dynamic response of a structure to evaluate its condition and detect damage. It is an important approach for structural health monitoring and has drawn much attention from researchers. While multiple reviews have been published focusing on different aspects of this field, there has not been a study specifically examining the recent development across the range of methods, including natural frequency, mode shape, modal curvature, modal strain energy, and modal flexibility-based damage detection methods. This paper aims to fill this gap by reviewing the recent application of these methods in civil structures, including beams, plates, trusses, frames, and composite structural members. The merits and limitations of each method are discussed, and research opportunities are presented. This broader review also provides an opportunity for critical comparison across this range of methods. While predominantly reviewing experiment-based studies, this review also considers some numerical studies that may motivate further research.
1. Introduction
The safety and serviceability of structures can be adversely affected by the loss of structural integrity due to gradual aging and deterioration or shock events such as earthquakes and hurricanes. Such circumstances demand that any structural damage should be detected at the earliest possible stage to avoid catastrophic incidents. Structural Health Monitoring (SHM) is oriented toward this mission.
Detecting the occurrence of damages, identifying their locations, and determining their severities are the three steps involved in damage assessment. These steps can be facilitated through different types of non-destructive testing (NDT) [1], such as visual inspection, digital image correlation, ultrasound, acoustic emission, magnetic field, eddy current, thermography, and radiography tests, to name a few. However, typically, these experimental techniques are local methods (as shown in Figure 1) [2], only able to inspect a limited region at once; hence, several measurements must be taken to inspect a structure or for inspection focused on specific regions. Such NDT techniques also require that the portion of the structure being inspected is readily accessible [3,4,5]. The need for quantitative global damage detection without prior knowledge of damage location has prompted the development of two global methods. One is based on the measurement of static deflections [6,7,8], and the other is to examine changes in vibration characteristics of structures, i.e., vibration-based damage detection methods, as shown in Figure 1. In the vibration-based method, damage detection can be fulfilled by examining changes in measured vibration response, where the modal parameters (natural frequencies, mode shapes, and modal damping) are functions of the physical properties (mass, damping, and stiffness) of a structure [9]. Therefore, changes in structural properties will result in changes in modal properties, which can either be detected absolutely or more often with reference to an undamaged state.
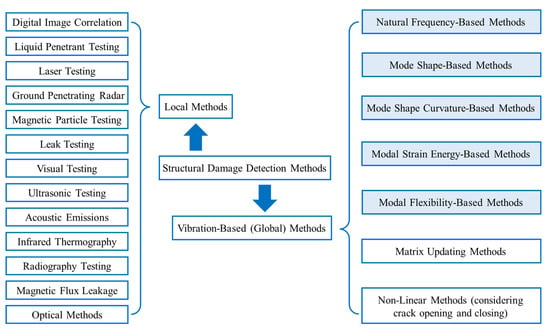
Figure 1.
The categorization of structural damage detection methods.
Vibration-based damage detection has received considerable attention, and an array of methods have been proposed in the past decades, ranging from those based on changes in modal parameters to those incorporating signal processing, model updating, and optimization algorithms. Doebling et al. [9] gave an overview of damage detection methods based on changes in basic modal properties (e.g., natural frequencies, mode shapes, and modal damping ratios) up to 1998. A review of subsequent literature reveals that most of the summarized issues in [9], such as the dependence on prior test data and linear structural models, the number and location of measurement sensors, and the sensitivity to small flaws, have not yet been addressed and are still with the subject of ongoing research across the community.
In 2008, a review focusing on the identification of double/multiple cracks in beams, rotors, and pipes was provided by Sekhar [10]. The effects of multiple cracks on the frequency, mode shape, and stability of rotors were summarized. For the multi-crack situation where crack variables increase, the crack-induced effect on dynamic response is dominated by the largest crack. Thus, the author suggested that to successfully detect cracks of various severity, the use of advanced signal processing techniques, for instance, the wavelet transform and the Hilbert–Huang transform, should be considered. While advanced signal processing is not a core focus of the current review, the literature covering recent applications is incorporated where relevant.
In 2009, based on structural dynamic changes and linear and/or non-linear vibrational measurements, a review focusing on civil engineering structures and rotating machineries was given by Sinou [11]. Some topics of interest for future research were listed concerning crack models (open, breathing, and propagating cracks), the effect of changes in damping, temperature effects, uncertainties caused by ambient conditions or by evolutions of boundary conditions, modeling errors, and uncertainties in numerical analysis. Linear vibrational experiment-based methods will be emphasized in this review.
In 2011, a review of vibration-based damage identification methods was performed by Fan and Qiao [12]. The methods were classified into four categories, namely, natural frequency-based, mode shape-based, modal curvature-based, and combined methods based on both frequencies and mode shapes. A comparative study based on finite element (FE) modeling was performed under varying conditions (single/multiple damages, large-area damage, measurement noise, and sensor spacing) to demonstrate the merits and shortcomings of each of the four methods. It was concluded that: (a) the quantification of damage severity was still in a less mature stage compared to damage localization; (b) reliable damage identification methods for 2D plates were not well developed, and signal processing techniques such as 2D wavelet transform could be a powerful tool. Relevant recent damage identification methods for metallic and composite plates will be discussed in this review. In 2015, a review specifically based on wavelet analysis of modal curvatures for composite structures was performed by Katunin [13]. The influence of various factors such as measurement apparatus, measurement noise, wavelet functions, damage location, sampling distance, and boundary effects was discussed.
Recently, Avci et al. [2] reviewed the application of machine learning and deep learning in vibration-based damage detection. Perhaps the most intriguing feature of machine learning-based methods is that, with the help of fast-developing computing power and sensing technology, the method can be devised in a straightforward manner, i.e., focusing on feature extraction and feature classification. However, the application of the machine learning-based method still shows a case-by-case pattern because it is difficult to find a set of universal feature classifiers that is suitable for any type of civil structure and for all kinds of damage scenarios. Moreover, reference vibration data from the undamaged structure as well as the data measured under several structural damage scenarios, is still essential when training the algorithm, while for a given civil structure, a full set of data containing pre and post-damage cases is rarely available. Although the machine learning-based method is an alternative to the traditional method, both methods suffer from similar limitations, including the necessity of reference data, the difficulty in finding a universal method that works for multiple types of structures, and the influence of environmental factors.
In the present study, the authors aim to provide the current state of the literature on vibration-based damage detection methods in civil structures such as beams, trusses, frames, plates, composite beams, laminated composite plates, etc. The five reviewed methods are highlighted in Figure 1, which are natural frequency, mode shape, modal curvature, modal strain energy, and modal flexibility-based damage detection methods. Compared with previous literature reviews that focus on different aspects of damage detection, this review examines the pros and cons of the above vibrational signature-based methods. This is achieved by investigating the selection of damage index, the design of a methodology, and the experimental or numerical verification. Therefore, this review predominantly investigates recent experiment-based studies. However, some numerical studies that may motivate further research are also considered. It is anticipated that this review will provide researchers with some reference information in terms of damage index, damage sensitivity, method complexity, and experiment design when contriving vibrational signature-based methodologies for damage detection. This review does not deal with practical implementation aspects such as designing the monitoring system, sensor placement, sensor validation, and sensor failure (interested readers are referred to the review of Worden and Dulieu-Barton [14]). Furthermore, the ‘crack’ termed in this study mostly represents an open, non-propagating edge crack, in contrast to a breathing crack that will repetitively open and close depending on the amplitude of vibration [15,16]. The equations of motion of the system become non-linear when a breathing crack model is employed, and a numerical method must be adopted as there is currently no exact solution to these equations [17,18].
The remainder of the article is organized as follows. Section 2 to Section 5 review the current state of the art of the above-mentioned five types of methods. For each method, recent developments are reviewed, followed by a discussion commenting on its characteristics, pros and cons, and potential research opportunities. The comments on mode shape and modal curvature-based methods are merged and presented together in Section 3.3 due to the close relevance between these two types of methods. The article ends with some concluding remarks and research prospects in Section 6.
2. Methods Based on Natural Frequency
2.1. Review
Natural frequency is a global dynamic parameter that normally contains limited spatial information of damage. Thus, an auxiliary mass has been used to draw spatial information from a frequency shift [19]. Zhang et al. [20] presented the frequency shift surface method, which was essentially roving an auxiliary mass on a plate and measuring the frequency with the mass at different positions. The damage was modeled as a local thickness reduction. The advantages of using the frequency shift surface are that, firstly, the frequency shift surface is related to the mode shape squared; thus, it contains spatial information of damage. Secondly, frequency measurement is usually easier and less susceptible to noise compared with mode shape measurement. In the experiment, a steel plate with a central thickness reduction was tested. The steel plate was supported by sponges to approximate free boundary conditions (see Figure 2a). A 0.3 kg accelerometer was considered as the auxiliary mass. The damage was identified using the fundamental frequency shift surface. An observation of this approach is that if the plate is large, more measurement points would be required to maintain the same spatial resolution, and the experiment could be time-consuming.

Figure 2.
The application of auxiliary mass: (a) the experiment in [20] and (b) the experiment in [21].
Subsequently, a similar method was applied to a damaged steel cylindrical shell [21]. By changing the location of the auxiliary mass around the circumference of the cylindrical shell (see Figure 2b), the frequency shift curve was obtained, and the lowest trough on the curve indicated the damage location. In the experiment, thickness reduction was made on the inner surface of the shell. It is interesting to observe the difference between the lowest trough and other troughs on the frequency shift curve for each damage case in Figure 3. When the area of thickness reduction was large, the frequency difference was 2.97 Hz. However, when the area of damage was small and did not cross the trajectory of the mass, the frequency difference was 0.81 Hz. The frequency difference could be even smaller if the damage were not severe. The methods in [20,21] deserve further study to see how the frequency curves behave when there are multiple damages. Moreover, whether the presence of measurable frequency shifts implies that the damage is already too severe or if the structure is amenable to repair is a question that has not been addressed.
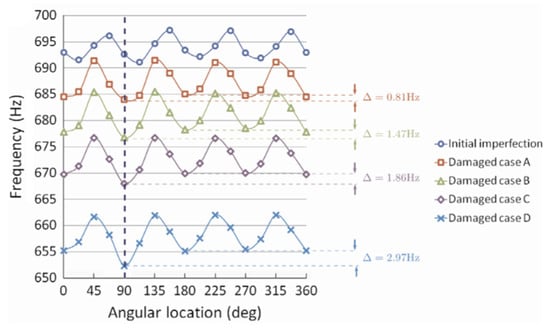
Figure 3.
The +2nd frequency shift curves for the undamaged cylindrical shell with an initial imperfection and different damaged cases [21].
The auxiliary mass approach has also been applied in more complex structures. For example, by extending the frequency shift curve method presented in [21], Lie et al. [22] used the frequency shift caused by an auxiliary mass to detect a sharp slot in a compressed natural gas (CNG) cylinder (see Figure 4a). Cao et al. [23] simplified a parked vehicle-bridge system as a beam carrying a mass block (see Figure 4b). The frequency of the beam-mass system varied when placing the mass block at different positions before and after damage, and the frequency change was used to locate damages. The relationship between the frequency change and damage severity was established via FEM analysis and curve fitting. It is worth mentioning that in [23], the damage severity was of a bending stiffness loss of 15% or 20% in the numerical study. In the experiment, the damage severity was approximately 25%. Although the damage was located and its severity quantified, whether this methodology works for minor damage was not reported. For a practical structure, a damage severity of 25% may have already jeopardized its serviceability. This again indicates the necessity of a direct comparison between measurable damage-induced frequency change and structural integrity, which has been neglected in past research. Wang et al. [24] applied an auxiliary mass on a railway track model (Figure 4c) to detect damaged supports under the railway track, such as loose or missing fasteners and damaged ballast. The method was shown to be effective, especially when detecting a missing fastener or severely damaged ballast.

Figure 4.
The experiments in [22,23,24]: (a) the CNG cylinder containing a crack [22], (b) the experimental set-up in [23], (c) the experimental set-up in [24].
When an auxiliary mass is used, it is crucial to measure the frequency shift accurately. However, the frequency change caused by either the damage or the auxiliary mass can be small and difficult to capture or may be masked by measurement errors. For example, for a crack with a normalized severity (i.e., normalized crack length or normalized crack depth) of 10% or below, the magnitude of natural frequency change tends to be small, especially for the first two modes, posing a challenge to the natural frequency measurement if environmental effects are also considered [25,26,27,28,29]. It would be difficult to distinguish between a small natural frequency change and measurement noise.
Wavelet transform has been introduced to natural frequency-based crack detection to alleviate the above issue. Zhong and Oyadiji [30] processed the frequency data of a beam carrying an auxiliary mass using stationary wavelet transform (SWT). The application of SWT involved two steps. Firstly, natural frequency curves were decomposed into approximation coefficients and detail coefficients, where the approximate coefficients were the high-scale, low-frequency components, and the detail coefficients were the low-scale, high-frequency components of the frequency signal. Secondly, the detail coefficients were thresholded to reduce noise. After these two steps, a new coefficient was obtained as the crack indicator, and the crack location could be determined by peaks in the curves of the new coefficient. An experiment was conducted on a cracked simply supported aluminum beam carrying a 4 kg auxiliary mass (see Figure 5a). The length of the beam was 2.4 m, and the spatial probing interval of the mass was 0.05 m; thus, 49 sampling points were needed. A challenge in this study is the determination of adequate sampling points. If sampling points are insufficient, the obtained natural frequency curve may not contain the information of cracks. If, on the other hand, the scale of the tested structure is relatively large, a dense measurement grid is required, and the number of sampling points can be considerable, which limits the application of this method in practical situations. In this situation, how to optimize the sampling interval [31] to minimize the effects of measurement noise requires further research.

Figure 5.
The application of auxiliary mass: (a) the experimental set-up in [30] and (b) the experimental set-up in [32].
In [30], SWT was applied to the curve of frequency versus mass location; thus, the local perturbation caused by a crack was revealed, and the crack was located. However, the theoretical basis of the application of the frequency curve in damage detection was not well established. Later, based on the eigenvalue problem and the assumption that a defect induces local perturbation in modal response, Yang and Oyadiji [32] demonstrated the relationship between the frequency curve, the roving mass, the mode shapes of the intact beam, and the local mode shape perturbation caused by damage. It was shown that the roving mass magnified the effect of local mode shape perturbation. After applying a discrete wavelet transform to the curve of frequency versus mass location, it could be seen that the approximation coefficients were the smooth terms that were dependent on the linear combination of the mode shapes of the intact beam, while the local mode shape perturbation contributed to detail coefficients. Thus, the detail coefficients contained high-order oscillations caused by damage and could be extracted and used for damage detection. Compared with [30], where only the wavelet detailed coefficients of individual modes were used, the responses from multiple modes were accumulated by superposing the absolute detailed coefficients from each mode, highlighting the existence of damage. To model the internal damage detection in multi-layer structures, the debonding was simulated using node separation at pre-defined locations, and the effect of inter lamina contact was ignored in the FE model. An experiment was conducted in [32] on a clamped-clamped two-layer bonded aluminum beam, as shown in Figure 5b. Two layers of aluminum were bonded using high-strength epoxy adhesive. The internal defect was modeled as interfacial debonding where the adhesive was not applied. The location of the debonding was detected, but the accuracy of size evaluation was influenced by random effects. It is worth noting that the size of the debonding may not be the same as the expected size in Figure 5b, as the adhesive may flow when the bond is formed. In a practical application, accurate size estimation may require the superposition of frequency data from a sufficient number of modes to suppress random effects, which means a large number of sampling points would be necessary to obtain accurate frequency curves of high-order modes. Comparable to the limitation of [30], this would be the major drawback of the method in [32].
The effect of the translational inertia of an auxiliary mass is considered in theoretical derivations in [20,21,22,23,24,30,32], while the effect of rotary inertia is ignored. Cannizzaro et al. [33] analytically proved that as a roving body with mass and rotary inertia passes a crack, the natural frequencies of a beam would generally change abruptly. Based on this, they also presented an explicit closed-form solution of the governing equation of a multi-cracked Euler–Bernoulli beam carrying a roving body. Similarly, Ilanko et al. [34] analyzed the frequency changes as a roving body passed a crack on a plate using the Rayleigh–Ritz Method for various boundary conditions. A sudden frequency shift was obtained as the roving body with rotary inertia crossed a partial crack or with translational inertia only when crossing a complete (through-thickness) crack. This can be a simplified model for crack detection in a bridge, which is to identify points where sudden frequency shifts occur as a vehicle moves on the bridge; thus, the crack locations can be obtained. Experimental verification is needed to examine the feasibility of the method in [33,34]. Massless rotational springs were used to model the crack, and the evaluation of crack severity (i.e., spring stiffness) remains a challenge.
As damage detection is a typical inverse problem, some optimization algorithms (such as the fuzzy inference system [35], the genetic algorithm [36,37], and the clonal selection algorithm [38]) have been utilized to solve it. Zhang et al. [39] used a surrogate-assisted generic algorithm to locate delamination in a composite laminated plate. This surrogate-assisted generic algorithm is essentially an artificial neural network (ANN)-aided optimization algorithm that takes the five parameters describing the size and location of the delamination as input and a single frequency shift as output. In the FE model, a pair of contact elements were added between the mating surfaces of the delaminated area, thus allowing neither penetration nor separation between the sub-laminates. In their experiment, the delamination in the composite plate was ‘simulated’ by embedding double layers of 25 µm thick Teflon release films at predetermined locations, which was only an approximation of how real delamination may respond. Oliver et al. [40] employed two ANN algorithms fed with frequency shifts to identify delamination in composite laminate plates. The delamination was modeled by an element with stiffness reduction. Considering the experiment results in [39], the experimental verification for [40] can be challenging. The mismatch between the simulation and the real delamination can lead to wrong predictions. For the above optimization algorithms, the optimal solution is searched for in the full domain, which inevitably increases computation time with the risk of being trapped in the local optimum. Dahak et al. [41] presented a method for detecting the zone containing a concentrated crack instead of precisely locating the crack. Thus, the search space in the inverse method can be considerably reduced. It is a possible way to improve the efficiency of crack detection methods incorporating optimization algorithms.
After identifying the damage location, quantifying the damage severity is still challenging. Some researchers strive to separate the effect of damage severity and the effect of damage location. De Los Rios et al. [42] found an interesting property of the characteristic equation of a cracked beam using the determinant of the dynamic stiffness matrix. It was noted that the crack severity and crack location parameters are separated explicitly in known terms, one with the characteristic equation of the uncracked beam and the other with the characteristic equation of the beam with a hinge at the location of the crack. Using this property, for known crack location, the severity of the crack can be determined by frequency measurement as the determinant of the dynamic stiffness matrix is a linear function of crack severity. Labib et al. [43] proposed a method for locating a single crack in a frame using natural frequency degradations. They assumed a linear relationship between frequency changes and crack severity (represented by the stiffness of a rotational spring) when the dimensionless crack depth (i.e., crack depth/cross-sectional height) is below 0.4. It was then possible to eliminate the severity factor through statistical processes and perform the numerical search for the crack location. Natural frequencies were calculated as a benchmark when the crack was placed at discretized positions. For this method, the natural frequencies of the corresponding intact structure were required. Both [42] and [43] employed the dynamic stiffness method which is suitable for deriving analytical solutions. A similar application on frames using the dynamic stiffness method can be found in [44], where the effect of damage severity and the effect of damage location were not separated but were expressed in one function. For a known frequency, each possible damage location maps to a damage severity; hence, the damage can be uniquely identified by showing the point of intersection between three curves (i.e., three natural frequencies).
Apart from beams and frames, arches represent an important engineering structural typology that is frequently used to construct bridges [45]. Some researchers have endeavored to apply frequency-based damage detection to arches [46]. For example, the methodology in [44] was modified and applied to a double-hinged parabolic arch in [47], where the numerical model was developed using FEM instead of the dynamic stiffness method. Greco et al. [48] presented a damage model considering a reduction in the volume of a segment of an arch. The dynamic stiffness matrix of the damaged segment was integrated into the global dynamic stiffness matrix, and exact eigen-properties of the damaged spatial arch were calculated. Genetic algorithms were used to retrieve the global optima for two objective functions, namely, considering frequency measurements only and considering both frequency and mode shape. It was found that the involvement of mode shape data can be helpful in avoiding symmetry in the identified damage configurations. Giordano et al. [49] conducted a series of pseudo-static loading-unloading cycles to masonry arches to progressively induce damage. In this process, they used a damage index evaluating frequency shifts between progressive displacement scenarios to detect the damage and assess the global stiffness degradation. Although the damage index is not able to localize the damage, it can follow the stiffness loss of the arch during progressive damage and hence set the threshold beyond which reinforcement interventions are necessary.
Frequency-based damage detection has also been considered a promising technique for the health monitoring of concrete members. When the damage in a concrete member is not obvious or difficult to quantify (e.g., some hidden defects after shock events), frequency-based FE model updating is a possible approach to localizing the damage. To model the damage in concrete-encased composite column-beam connections after an earthquake, Nasery et al. [50] conducted a cyclic loading test on four samples with different connections (as shown in Figure 6a). Concrete failure and some welding damages can be observed after the loading test (see Figure 6b). Natural frequencies were measured through ambient vibration tests for 15 min, considering the 0–100 Hz frequency range. For the FE model updating, the first and fourth modes were taken as references. The modulus of elasticity, density, the spring stiffness at the boundary, and the moment of inertia of beam and encased column cross-sections were updated. To localize the damage, the percentage change of updated parameters is plotted (as shown in Figure 7), and those parameters showing high percentage changes indicated the most significant changes in the FE model, based on which the damaged regions could be identified. Overall, this study explores the possibility of damage detection in a practical scenario using FE model updating. Although the damage is artificially introduced, it is close to real damage and hence makes damage localization more difficult compared with detecting open cracks in many controlled experiments. The idea of using the rate of change of updated parameters during model updating to localize the damaged zone warrants further research.

Figure 6.
Concrete-encased composite column-beam connections [50]: (a) four different connections and (b) damaged samples after cyclic loading test.
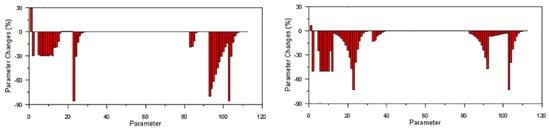
Figure 7.
The percentage change of updated parameters [50].
2.2. Comments
Based on the above literature survey, some comments are made as follows:
- (1)
- An advantage of the natural frequency-based approach is the global nature of natural frequency. It is a good indicator of the overall mass and stiffness of a structure. This characteristic, on the other hand, may render the natural frequency weakly sensitive to minor damage because minor damage tends to be a local phenomenon. Methods incorporating signal processing techniques, e.g., wavelet transform, are proposed to deal with this weak sensitivity [30,32]; however, new challenges, such as how to optimize the sampling interval [31], require further research.
- (2)
- A combination of different damages may lead to identical frequency changes [51]. For unique identification of damage location, there are a few promising ways to include the spatial information of damage in frequency responses. For example, an auxiliary mass with or without rotary inertia can be attached to the structure [20,21,22,23,24,30,32,33,34]. In this case, the mass acts as a probe, and the spatial information of damage is contained in the curve of frequency versus mass location. This helps to separate the location effect from the severity effect.
- (3)
- To date, most natural frequency-based damage detection methods are verified by successfully detecting cracks of moderate size (e.g., with dimensionless crack depth between 0.2 and 0.5 for skeletal structures) as the resulting frequency changes are easier to capture. Taking the frequency change as input data, the feasibility of the crack detection method can be tested. Nevertheless, a question that remains unaddressed is the direct comparison between the crack severity reaching the initiation of crack propagation or leading to brittle fracture and the crack severity causing a measurable frequency change. If the former severity is reached before the latter, frequency-based crack detection would be risky. If, on the other hand, the crack already causes measurable frequency drops in the first few modes before it jeopardizes the safety of a structure, then there may be some safety margin where frequency-based crack detection can be executed. Overall, with this issue being unsolved, even when cracks of moderate size are detected successfully in a controlled experimental condition, it is debatable whether the presented crack detection method is feasible in practical situations. To make a direct comparison, fracture toughness in fracture mechanics would be an important parameter to determine the critical state of crack propagation or brittle fracture.
- (4)
- The damage-induced frequency changes may be veiled by the frequency changes due to other factors such as the effects of ambient conditions (e.g., temperature, humidity, wind, rainfall, etc.), operating loads, and possible evolution of boundary conditions. It has been reported in [25,26,27,28] that the frequency variation due to such environmental and operational factors is usually of the order of 5–10% but can exceed this. Currently, most successful frequency-based damage detection methods are verified only under controlled laboratory conditions rather than exposed to variations in environmental or operational effects. In practical applications, damage-induced frequency changes should, as a minimum, be expected to exceed 5% to detect the damage with confidence.
- (5)
- Quantifying the damage severity is still a challenging task, and to date, there are few simple and robust methods. The method comparing the frequency response of damaged structures with ‘baseline information’ that contains different damage scenarios exhibits its viability in numerical simulations and laboratory environments. However, a large amount of calculation, either through the finite element analysis or in an analytical manner, is necessary to obtain the ‘baseline information,’ which may render this method impractical when using it in complex structures. One possible way to reduce the computation is to roughly estimate the damage location ranges, then accurately localize the damage and quantify the severity. For example, the method in [41] can be used to preliminarily narrow down the ranges where the crack may be located, and then other methods based on pattern recognition or global optimization can be employed to search for the optimal solution (i.e., the damage location) within the prescribed spans. Once the damage location is found, the severity of the damage can be evaluated in the second step by trial and error to find the severity that gives results matching experimental measurements.
3. Methods Based on Mode Shapes and Their Derivatives
3.1. Review of Mode Shape-Based Damage Detection Methods
Natural frequencies alone can only indicate the presence of damage but cannot pinpoint its location (except in cases where a roving inertial interrogator is used); by contrast, the spatial information of damage can be found in mode shapes. However, damage-induced changes in mode shapes can be subtle (unless the damage is severe), and the damage cannot be easily identified. Therefore, several indices have been proposed as correlation indices between two sets of modal data, for example, the modal assurance criterion (MAC) [52], the coordinate modal assurance criterion (COMAC) [53], the coordinate modal error function (COMEF) [54], etc. These criteria provide the evaluation of consistency between mode shapes (i.e., mode shapes of the intact structure and damaged structure); thus, damage can be identified where discrepancy happens. They are not the validity or orthogonality check. A review of various criteria was provided by Allemang [55], stating that the modal assurance criterion, as a simple statistical concept, could be very powerful when used correctly but misleading when used improperly. More specifically, the misuse of the modal assurance criterion resulted from five issues, namely, incomplete modal vector measurement, the occurrence of complex-valued modal vectors, the dominance of erroneous data in modal vectors (wild points), a limited number of degrees of freedom in the modal space, and the zero-padding for elements of modal vectors when modal vectors are exported from one computational environment to another. Therefore, the abovementioned modal correlation indices require accurate measurement of mode shapes, and damage-induced local perturbations may be consumed and lost in the computation, which involves all degrees of freedom.
The wavelet transform can be employed to identify local perturbations in the original signal. The wavelet coefficient curves show oscillations, ridges, or peaks when a discontinuity or a sudden change occurs. Thus, mode shapes can be processed by wavelet transform, and damage-induced discontinuities can be shown on curves of wavelet coefficients. The study of Solís et al. [56] confirmed the effect caused by a stationary roving mass (as in [30]); namely, both the noise immunity and the damage sensitivity were improved in the presence of a roving mass. Contrary to [30], the continuous wavelet transform (CWT) analysis was performed on the difference between the mode shapes of the healthy and damaged beams. Reference noise-free mode shapes were obtained by implementing the smoothed spline interpolation to experimental mode shapes. By comparing experimental mode shapes with the reference noise-free mode shapes, the level of noise for each mode was estimated by the signal-to-noise ratio. Thus, the less noisy mode shapes could be emphasized. The experimental set-up in [56] is shown in Figure 8. The roving mass was 5% or 10% of the total mass of the beam. Three crack depths were used, namely, 10%, 20%, and 50% of the height of the beam. The saw-cut crack was located in the middle of two adjacent measuring points. It is worth noting that to accurately evaluate experimental mode shapes, thirty-two accelerometers were distributed evenly across the beam, which might require a significant amount of signal processing.
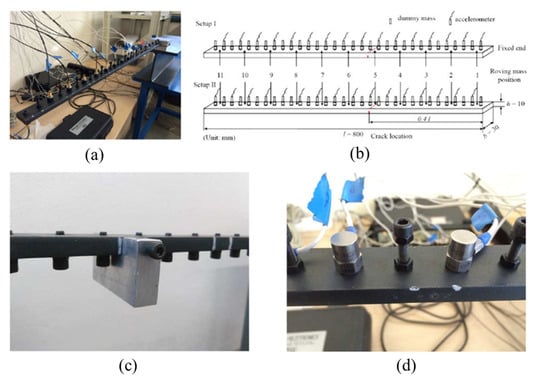
Figure 8.
The experimental set-up in [56]: (a) the experimental set-up, (b) the scheme of the tested beam, (c) the roving mass, (d) the accelerometer and the dummy accelerometer masses.
The authors of [56] demonstrated that the less noisy mode shape (mode 2 in this experiment) provided a more reliable result for damage detection (see Figure 9, and the crack is at 0.4 L). However, local peak values of the wavelet coefficient due to noise can be observed at different measuring points (as indicated by the bright stripes in Figure 9), and they can easily mask the perturbations caused by a small crack. When locating a small crack, using the summation of wavelet coefficients of all mode shapes (without proper selection beforehand based on sensitivity) may not be advisable because the noise effects from all mode shapes could potentially accumulate and further mask the crack.
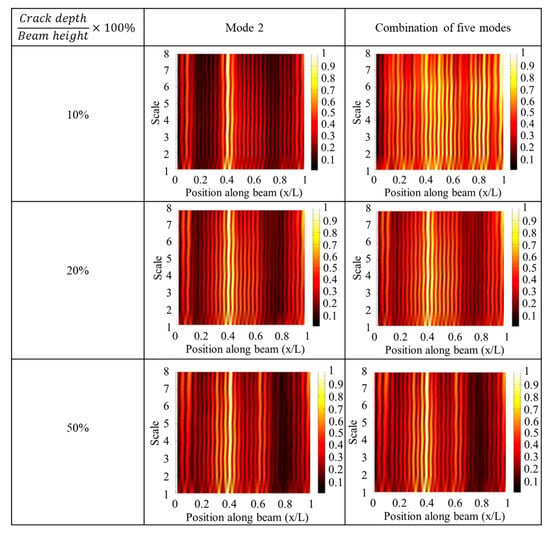
Figure 9.
The summation of normalized weighted wavelet coefficients (the crack location is 0.4 L) [56].
A demanding task when using mode shape-based damage detection is to minimize the noise in mode shape measurement. This is paramount if wavelet transform is incorporated. It was mentioned earlier that sampling intervals should be optimized to enhance the damage sensitivity. Zhong and Oyadiji [57] observed that when the CWT was used, the accuracy of crack localization degraded as the sampling distance increased. Thus, they adopted a cubic spline interpolation as an over-sampling technique for the sparsely measured mode shape data, and the accuracy for localizing a small crack (for the dimensionless crack depth of less than 0.05) was improved. Sampling interval sensitivity analysis was conducted in subsequent research [58]. The relation between the maximum values of the SWT detail coefficient and sampling intervals was obtained via a fifth-order polynomial fitting method; thus, the sampling interval sensitivity was quantified. Both the methods for damage localization in [57,58] require that the mode shapes are symmetric or antisymmetric, which means the structure, including its boundary conditions, should be symmetric.
Sparsely measured data may not contain enough information about damage while measuring data in a dense manner may be unnecessary. Therefore, some researchers investigated the effect of down-sampling [59,60]. The aim was to establish the minimum sampling intervals on the condition that small cracks could be localized successfully. For example, in the context of mode shape-based damage detection incorporating the CWT, a parametric study was provided by Montanari et al. [61] to investigate the impact of sampling intervals with factors such as the padding method, the level of noise, the type of mother wavelet, and the crack configuration. The crack was modeled using a massless rotational spring. The results showed that when high-order mode shapes were used, more measurement points were needed. A parameter named the pseudo-frequency was found. The pseudo-frequency is a function of the sampling interval, the center frequency of the mother wavelet, and the scale parameter of the mother wavelet. They found that as long as the optimal value of the pseudo-frequency could be achieved, down-sampling densely measured data could reduce the costs of damage detection without affecting performances. It should be noted that this study proves the possibility of applying down-sampling without affecting the results of damage localization. For practical applications, especially for damage detection in large-scale structures, ensuring enough measuring points is still important. This down-sampling technique can be used as a tool to verify the accuracy of detection results.
Some researchers [62,63] have concluded that, compared with mode shape, derivatives of mode shape, such as slope and curvature, are more sensitive to the presence and location of the crack and make good candidates for damage detection. For example, Whalen [63] investigated the sensitivity of the second, third, and fourth derivatives of mode shape to various damage-related parameters (mass loss, stiffness loss, and damage radius scale). Both stiffness loss and mass loss were considered in the damage model. It was shown that in the context of transverse vibrations of a beam-like structure, all higher-order derivatives of the mode shape exhibited strong damage localization and sensitivity properties. Lower modes were demonstrated to be the best choices to evaluate modal changes, as higher modes were less sensitive to damage radius while more sensitive to mass loss, overall rendering lower levels of modal change. The author of [63] acknowledged that the fourth-order derivative of the mode shape could not be obtained from direct measurements; instead, it must be calculated numerically, which would inevitably introduce errors.
In light of the abovementioned advantages of high-order derivatives of mode shape, it is necessary to review the recent development of damage detection methods based on the derivatives of mode shape. As the second derivative of mode shape (i.e., modal curvature) is extensively studied by researchers, damage detection methods based on modal curvature are reviewed in the next subsection.
3.2. Review of Modal Curvature-Based Damage Detection Methods
Generally, it is considered possible to locate the damage by the largest absolute difference between modal curvature-based functions calculated from both damaged and healthy states of a structure. Ručevskis et al. [64] presented a method using the modal curvature square obtained from only the damaged state of a beam. They used the average of the sum of modal curvature squares from each mode to diminish the influence of measurement noise, and modal curvature squares were shown to be capable of damage localization. However, the scale of the mill-cut damage in the experiment was large, i.e., the depth of damage was between 54% and 66% of the thickness of the beam, and the width of damage was 4% or 6.7% of the total length of the beam. Apart from edge cracks aligned perpendicular to the axis of the beam, horizontal cracks can also be detected without modal data of the corresponding undamaged beam [65]. This is potentially useful in composite beams due to the analogy between the horizontal crack in uniform beams and the delamination in laminated beams.
Measurement noise is known to induce local perturbations to mode shapes, leading to crests in modal curvature. It is possible to mistakenly identify these crests as local damages, whereas the real damages may be obscured, which leads to false alarms or missed detections. To improve the robustness against noise and to ameliorate the sensitivity to multiple damages, Cao et al. [66] explored the application of modal curvature with the synergy between two signal processing tools, namely, the wavelet transform (WT) and the Teager energy operator (TEO). Given the prominent feature of the TEO being the identification of local singularities and the salient advantage of the WT being denoising, the proposed synergistic regime aimed to combine the complementary merits of both. Subsequently, Cao et al. [67] proposed the complex wavelet modal curvature, in which the complex wavelet was derived from the Gabor wavelet. Experiments were conducted on a single-crack aluminum beam and a multi-crack carbon-fiber-reinforced polymer (CFRP) composite beam consisting of five layers. From the experimental results in [66,67], the susceptibility of conventional modal curvature to noise can be alleviated by incorporating noise suppression techniques. However, this may be achieved at the cost of losing sensitivity to small cracks because a small perturbation in modal curvature may be induced by either noise or a small crack. An advantage of [66,67] is that multiple damages can be identified without baseline information, which shows the prospect of the combined utilization of modal curvature and signal processing techniques.
It is a demanding task to juggle noise suppression and the identification of small damages, factors with conflicting requirements, because the sensitivity to small damages may also lead to noise susceptibility. Apart from signal processing, suppressing the noise caused by the numerical differentiation has also been considered [68,69]. Yang et al. [70] adopted a Fourier spectral-based method as an alternative to the central difference method to increase the precision when estimating modal curvature. In addition to the noise amplification caused by the numerical differentiation, the authors of [70] stated that the approximation of mode shapes (assuming polynomials in estimation instead of trigonometric functions as expressed in the modes) also adds to the error. By contrast, the approximation functions in the Fourier spectral method were trigonometric functions, and the mode shape was synthesized via trigonometric interpolation. Quaranta et al. [71] compared damage indices based on numerically obtained modal curvatures. The modal curvature was calculated using the central difference method, cubic spline interpolation, a modified Savitzky–Golay filter, and cubic smoothing spline, respectively. The modified Savitzky–Golay filter and the cubic smoothing spline method were demonstrated to be superior to the central difference method regarding the robustness against measurement errors.
It is worth recalling that modal curvature can be obtained either by numerical calculation from modal displacements or by direct measurement of strain [72,73], which is proportional to the curvature of an Euler–Bernoulli beam. The latter approach has been used by Lestari et al. in [74], where they used surface-bonded piezoelectric sensors (PVDF films) to directly acquire the modal curvature of composite beams. Thus, the computing errors arising when calculating modal curvatures from mode shapes identified from measured lateral acceleration, velocity, or displacement signals were circumvented. Hsu et al. [75] utilized long-gauge fiber Bragg grating (FBG) strain sensors to obtain the modal curvature of a thin plate without a numerical differentiation procedure. The damage was simulated through changes in stiffness caused by attaching stiffened aluminum plates. Macro-strain mode shapes were identified directly from dynamic vibration signals measured by the FBG sensors mounted on the plate.
As previously mentioned, damage detection techniques based on natural frequencies are commonly formulated as a type of inverse problem that is often ill-conditioned; namely, even by leaving symmetrical positions aside, cracks in two sets of different locations can cause identical frequency changes [76]. However, a study by Capecchi et al. [77] shows that the inclusion of modal curvature could help remove the indeterminacy due to the symmetry of a structure. They proposed an objective function that minimizes the difference between numerical and experimental response quantities (i.e., natural frequency and modal displacement). Taking advantage of the localized feature of modal curvature, the difference in modal curvature was introduced as a penalty term to enhance the global minimum and accelerate convergence. The method was verified on a pinned parabolic arch with a notch-type crack. The crack depth ratio ranged from 12.5% to 50%. Seven accelerometers were equally spaced along the arch. The results indicated that the penalized objective function performed more robustly than the common objective function, minimizing frequency difference only. Although coordinating multiple modal parameters within one objective function might require additional efforts in data processing, ref. [77] shows the potential of the combined use of modal parameters.
Narrow damage can induce a localized and abrupt change in modal curvature that may otherwise be undetected if insufficient sensors are used in experiments. Ciambella et al. [59] investigated the minimum number of measurement points that allow the damaged area to be accurately identified. The use of a reduced number of sensors was enabled through a filtering procedure acting on the variation of modal curvatures. It was shown that the variation between modal curvatures of the damaged and undamaged beams alone could not provide meaningful results when the number of sampling points was limited. In contrast, the properly filtered variations of modal curvature were demonstrated to be competent for damage localization (when noise is not considered). This could be explained by [60,78], where the damage was represented via a smooth stiffness variation function (or, in the authors’ terms, damage shape) that is non-zero only in the damaged region. According to the analytical approximation, modal damage shape is related to modal curvature variation, some measured quantities, and some spurious terms. These spurious terms, relevant to the width of damage and the position of damage with respect to the position of measurement points, contribute to multiple peaks outside the damaged area in the graph of modal damage shape (see Figure 10). In the experiment, modal curvature was measured directly through the time history of strains on the surface of the beam. It was found that, in the absence of a measurement point within the damaged region, the modal curvature variation should be filtered to eliminate the influence of those spurious terms, thereby avoiding the misdetection of damage.
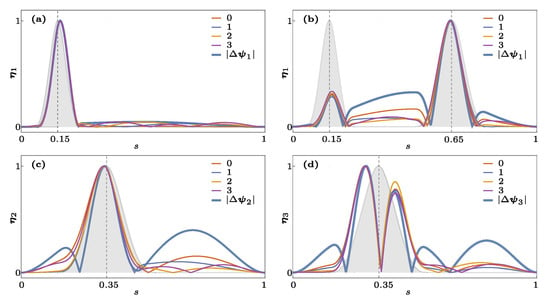
Figure 10.
Modal damage shapes reconstructed from the analytical approximation for an increasing number of terms in the series [60] for (a) the first mode and a damage located at 0.15 and width 0.1; (b) first mode and two damages at 0.15 and 0.65 with widths 0.2 and 0.3, respectively; (c,d) second and third modes and damage at 0.35 and width 0.4. Grey areas represent the actual damage shape . Continuous lines represent the absolute values of modal curvature variation (thick blue line) and approximated modal damage shape, respectively.
The 2D modal curvature has been used to detect non-uniform damage in metal plates [79,80]. Analogous to the method proposed in [66], the TEO-WT modal curvature of a plate was taken as the damage index in [79]. The FE model of the plate consists of two layers, and a through-thickness crack was introduced to the first layer. In the experiment, an X-shape notch was made on an aluminum plate (see Figure 11) under completely free boundary conditions, practically achieved by hanging the plate with two strings. The thickness of the plate was 4 mm, and the depth of the notch was 1.2 mm. Thus, the notch only caused insignificant variation in natural frequencies. By using the TEO-WT modal curvature, the damage was identified successfully. However, to avoid the influence of abnormal wavelet coefficients caused by boundary distortion, the wavelet coefficients around boundaries were discarded, which means only the grey area, as shown in Figure 11, was analyzed. Thus, the method was not capable of identifying any damage near boundaries.
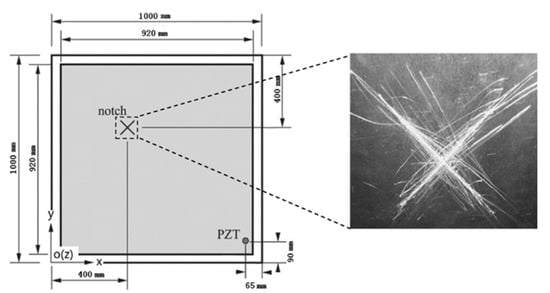
Figure 11.
The X-shape damage in [79].
The problem of boundary distortion can be avoided by using the difference between the damaged and undamaged mode shapes. Abdulkareem et al. [81] employed the 2D CWT to decompose the mode shape difference. The singular peaks in wavelet coefficients near the support resulted from the sudden increase in stiffness due to the support. By considering the mode shape difference, the sudden change in stiffness around the support could be canceled out. Thus, it was possible to identify the damage near the boundary. In the FE model, the damage was modeled by local thickness reduction. In the experiment, a fully clamped steel plate was studied (see Figure 12). Damages were introduced to the middle, the top, and the corner of the plate, respectively. The damaged area was approximately 0.5% of the plate area, and the damage was manufactured by milling off 62.5% of the plate thickness. Using the wavelet coefficients of the difference of the first mode shape, the damaged areas were identified with reasonable accuracy.

Figure 12.
A fully clamped steel plate with middle damage [81].
Apart from metal plates, various methods were devised using 2D modal curvature to identify delamination, cracks, and cut-outs in composite plates. Xu et al. [82] conducted an experimental study to detect delamination in carbon fiber-reinforced polymer (CFRP) laminated plates based on the integration of complex wavelet and 2D modal curvature. In the FE model, the small delamination was modeled by inserting a non-thickness interface between the second and third plies; on the non-thickness interface, the coincident nodes in adjacent but separated elements were distributed. The CFRP plate consisted of four plies, and the delamination was manufactured by inserting a 50 µm thick rectangular Teflon sheet between the second and third plies when the laminated plate was fabricated. The delaminated area was 0.09% of the total area. Although the delamination was successfully identified under noisy conditions, it should be noted that a high-order mode was necessary.
Composite laminates with cutouts are usually found in complex structural designs such as aircraft windows. Damage may occur around the cutout due to severe stress concentration or local buckling. To identify such damages, an experimental study was conducted by Zhou et al. [83], where the 2D modal curvature processed by CWT was taken as the damage index. They considered multiple high-order modes simultaneously and summed the damage index of each mode. Essentially, more fluctuations in a high-order mode shape would be beneficial to reducing the influence of damage location. Thus, it was possible to quantify the damage according to the magnitude of the total damage index. In the FE model, the concentrated damage was simulated by the reduction in the modulus of elasticity. The method was applied to a unidirectional fiber-reinforced composite laminate with a circular cutout, as shown in Figure 13a. The vibration data were captured using a scanning laser vibrometer, with the distance between scanning points being 3 mm. It can be seen from Figure 13b that both damage locations (A and C) were identified, and the damage severity could be roughly estimated, which was confirmed by conventional ultrasound testing. This study [83] explored the possibility of damage quantification using modal curvature without baseline information, which is rarely touched upon in the literature, especially for composite laminates with cut-outs. However, a few limitations also exist. Firstly, a high-order mode is a vague definition. If the order is not high enough, the total damage index may still be susceptible to damage location. If the order is too high, too many coupling modes may be involved, and the result of damage severity evaluation would be affected. Secondly, it is possible to compare the damage severity qualitatively among various damages, but recognizing the damage severity quantitatively (e.g., expressed as the percentage of stiffness) remains a challenge and may need to employ NDT techniques.
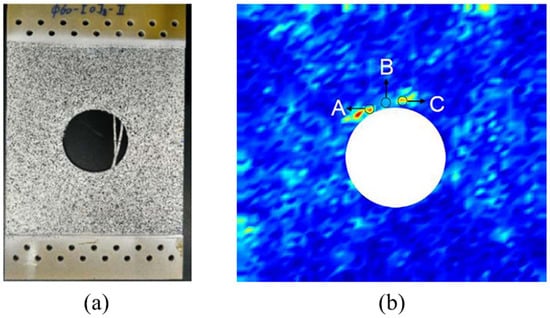
Figure 13.
The experiment in [83]: (a) the specimen and (b) experimental damage index result.
3.3. Comments
Based on the above literature survey, some comments are made as follows:
- (1)
- As natural frequencies represent the global dynamic characteristics of a structure, in general, their measurement alone may not be sufficient to draw spatial information on the damage. Measurement of mode shapes and their derivatives may be more useful. However, mode shape-based methods tend to be very sensitive to measurement inaccuracy, which may obscure damage-induced perturbations. Moreover, a large number of measurement points are required to estimate a detailed mode shape or a high-order mode shape when using MAC and other relevant assurance criteria in damage detection, which inevitably increases the duration of the measurement. The accessibility of measurement points could also pose problems. These factors place limitations on the practical application of the mode shape-based method.
- (2)
- Since mode shape is not sensitive enough to minor damage, many damage indices defined by modal curvature have been proposed in the literature. Modal curvature is commonly computed by numerical differentiation, which amplifies the errors in measurements. This is particularly worse when modal curvature is obtained from a densely-measured mode shape. To address these problems, generally, four approaches are employed, namely, reducing noise [64,66,67], filtering or smoothing [59,60,71], reducing measurement points [59,61], and measuring modal curvature directly [74,75]. For damage detection using modal curvature only, three ways are known to alleviate noise effects, i.e., optimal sampling interval [31,61], signal processing [66,80,81], and multi-resolution analysis [65,68]. Nevertheless, the opinion held by several researchers that reducing noise cannot essentially solve the problem caused by the inherent flaw of the numerical difference [71] is valid as the causes of deviations are entirely independent. Similarly, reducing measurement points (down-sampling) is not always a reasonable choice as it may increase the lower bound of the detectable damage severity, which impairs the identification of minor damage.
- (3)
- Combining the wavelet transform and modal curvature helps to focus on damage effects, and small damage in a plate can be identified in the laboratory environment using a scanning laser vibrometer [79,80,82,83]. This is more advantageous compared with natural frequency-based methods. In addition, there is no specific requirement for the shape of damage. The damage can be through-thickness damage or a thickness reduction. The depth of the damage can be constant or non-uniform [80]. However, the minimum detectable damage can be directly affected by noise, and the damage near boundaries cannot be identified owing to the boundary distortion issue when using wavelet transform signal processing.
- (4)
- When wavelet signal processing is applied, one way to avoid boundary distortion and identify the boundary damage simultaneously is to use baseline information. For example, some damage indices are proposed based on mode shape difference [81] and the curvature difference of operational deformation shapes [84]. By using these indices, the effect of a sudden change in stiffness near boundaries is canceled; hence, boundary distortion is circumvented. Nevertheless, this is achieved at the sacrifice of an advantage of wavelet signal processing, i.e., baseline information free. The benefit is that, normally, high-order mode shapes are not essential when baseline information is available. This is in sharp contrast to the situation where baseline information is unavailable. In those situations, the necessary order of mode shape may exceed ten to ensure the successful identification of small damages [69,79,82].
4. Methods Based on Modal Strain Energy
4.1. Review
Modal strain energy is directly related to modal curvature in beams. This feature also applies to plates. Therefore, the modal strain energy-based method shares common advantages and drawbacks with the modal curvature-based method, and some researchers regard it as a special case of the modal curvature-based method [12]. Normally, the modal strain energy employed in damage detection is based on discretized elements rather than the entire structure. Thus, by checking the modal strain energy-based damage index element by element, damage can be localized where an unusual change in damage index is shown after the damage occurs.
Many modal strain energy-based damage detection methods show a two-stage feature; namely, the damage is localized in the first stage through a damage index derived from modal strain energy, and then the damage severity is estimated in the following stage using optimization algorithms. For example, Pal and Banerjee [85] processed measured mode shapes using wavelet transform and obtained a damage index based on the modal strain energy calculated in the wavelet domain. Probable damage locations were indicated by the peaks in the curve of the damage index. In the second stage, the stiffness reduction at probable damage locations was taken as the updated variable, and the objective function was minimized by particle swarm optimization. It should be noted that in the numerical and experimental results, some false peaks were present in the curve of the damage index even though the damage was severe. In addition, when the effect of noise was significant, the number of false peaks tended to increase. Khatir et al. [86] proposed a two-stage method where local frequency changes and modal strain energy were used to derive a damage location indicator, and a teaching-learning-based optimization algorithm was utilized to evaluate damage severity. The damage index in [86] was the same as that in [85]. Although the damage indices derived from modal strain energy are similar in many studies, different techniques are utilized in the second stage, e.g., Jaya algorithm [87], finite element (FE) model updating [88], genetic algorithm [89,90], differential evolution algorithm [91], etc. Apart from beam and truss, these two-stage methods have been applied to thin plates [87,88] and composite plates [90,91]. However, although the dimension of search space in the second stage is substantially reduced by approximately localizing the damage, an obvious disadvantage is that if the true damage location is not correctly identified in the first stage, there is no remedial measure in the second stage and the damage would remain unidentified throughout. The study conducted by Xu et al. [92] is an attempt to address this issue. They proposed an iterative approach where the two stages were conducted alternately. Through cyclic iterations, the predicted damage locations and damage severities were mutually calibrated; thus, false positive indications of damage could be gradually suppressed. By embedding an element activation operation into the iterative process, false negative indications could be activated and retested. This method is an improvement to the traditional two-stage method, but some experiments are needed to verify its efficacy. It is possible that the convergence rate is slow when damage is minor or when noise is pronounced (in either case, the number of false positive/negative indications may increase, which extends computation time).
A mode storing the maximum modal strain energy provides more accurate results for damage detection [93], and this mode does not have to be the first mode. Therefore, selecting the modes that are most indicative of the damage is important. Wu et al. [94] presented a procedure for selecting sensitive modes. The modes that significantly contribute to the modal strain energy changes (before and after the damage occurrence) of an element were regarded as the sensitive modes of that element. The sensitive mode of an element was defined according to (a) the magnitude of normalized elemental modal strain energy of the intact structure and (b) the noise immunity of the element. The proposed modal strain energy-based damage indicator was the average normalized modal strain energy changes of the selected sensitive modes. In the numerical model, the damage was simulated by reducing the modulus of elasticity of damaged elements. The proposed damage localization indicator was numerically proven to be more robust than traditional indicators utilizing the first several modes together.
Methods based on the changes in elemental modal strain energy have shown reasonable accuracy in damage localization, while their performance in quantifying damage severity is poor. Striving to address this issue, some researchers proposed methods based on cross-modal strain energy [95,96]. Here, ‘cross’ means that compared with the expression of the traditional modal strain energy term, the expression of the defined cross-modal strain energy is similar, except that the modal vectors are replaced by the th modal vector from the undamaged structure and the th modal vector from the damaged structure. A review of modal strain energy-based methods was conducted by Wang and Xu [97] with a comparative study on a 3D off-shore platform structure. They classified the methods into four categories, namely, damage index method (e.g., [98,99]), modal strain energy change method (e.g., [94]), cross-modal strain energy method (e.g., [95]), and other methods. The pros and cons of four typical damage detection algorithms were demonstrated via the comparative study, and slight superiority to other algorithms was exhibited for the modal strain energy decomposition method in the first category.
Modal strain energy-based damage detection method has also been applied to inhomogeneous materials such as functionally graded materials [100] and laminated composite plates [90]. In [100], the elemental modal strain energy change after the damage occurred was taken as the damage index. The influence of noise level, damage extent, the order of mode shape, and the gradient index of the material were investigated. However, as the damage was considered as a stiffness reduction in an element, whether this method is feasible in experiments requires further research. In [90], the delamination in composite plates was detected. The genetic algorithm was applied to FE model updating, and the parameters of damage were updated. The proposed objective function in the genetic algorithm was based on natural frequency and weighted strain energy; thus, the sensitivity of elemental strain energy to damage location could be fully utilized.
Experimental studies employing modal strain energy-based damage index are often found in frame models or offshore platform scale models [101,102,103]. Damage detection under varying environmental and operational conditions has also been researched. Xu et al. [104] considered temperature variations and proposed a method based on residual modal strain energy. To eliminate the influence of temperature variations on damage localization, principal component analysis was applied to measured mode shapes. Through principal component analysis, a set of observations of possibly correlated variables could be converted into a set of values of linearly uncorrelated variables. By projecting the measured data to the principal component space, temperature effects and damage were accounted for using different principal components; thus, temperature effects and damage were decoupled. Changes in mode shapes due to temperature variations were then subtracted from measured mode shapes, leading to residual mode shapes. The method was verified through the numerical model of a 3D off-shore platform. Multiple damages were clearly localized. Overall, the results in [104] indirectly reflect the efficacy of the modal strain energy decomposition method [97,98], which is more suitable for damage localization in 3D skeletal structures by considering the modal strain energy in both transverse and axial directions. It should be noted that uniform temperature distribution was assumed in [104], and other sources of noise were not considered.
4.2. Comments
Some important points that emerge from the above review of modal strain energy-based methods follow:
- (1)
- In most modal strain energy-based methods, modal strain energy is checked element by element. The advantage is that damage can be localized within an element (if disregarding false alarms), and the accuracy can be guaranteed (if the element size is reasonable). The disadvantage is that the number of elements increases for complex structures, and more degrees of freedom are involved. Modal strain energy in multiple degrees of freedom should be considered to ensure that no false-negative alarms occur. Therefore, most studies are focusing on beams, planar frames, and 3D frames. For 3D frames, the modal strain energy decomposition method is necessary.
- (2)
- The performance of modal strain energy-based methods in damage quantification is generally unsatisfactory. Optimization algorithms or FE model updating are often utilized to estimate damage severity. Thus, many modal strain energy-based damage detection methods exhibit a two-stage feature, i.e., damage location is determined in the first stage, and damage severity is evaluated in the second stage. This is a common characteristic of many vibration-based damage detection methods, but it is more obvious when modal strain energy is used. A false-positive alarm in the first stage may lead to error in the second stage, and a false-negative alarm in the first stage cannot be corrected afterward. Thus, the iterative two-stage method (e.g., [92]), where the two stages are conducted alternately, deserves further research.
- (3)
- As modal strain energy is evaluated in an elementwise manner, modal strain energy-based methods fit the finite element method (FEM) well. In many numerical studies using the FEM, the damage is considered by introducing elemental stiffness reduction. Although many damage indices are proven reliable in numerical studies, simulated and experimental results may differ significantly. This is because cracks or corrosion in practical applications may not exactly map to the general stiffness degradation of an element. Apart from numerical studies, more experimental studies are needed to assess and, if possible, improve the reliability of modal strain energy-based methods for practical applications.
- (4)
- The presence of the false-positive alarm remains a major challenge. Normally, it is assumed that the effect of damage is constrained within a certain element and other elements are intact. However, the actual effect of damage usually distributes unevenly in a certain area instead of being concentrated. Thus, false-positive alarms could happen near the damage. Wei et al. [88] presented a method for reducing false-positive alarms, but at the cost that the magnitude of the damage index was holistically suppressed. It means the number of false-negative alarms may increase if the damage is minor and the signal contains noise. Overall, the problem of false alarms calls for further research.
5. Methods Based on Modal Flexibility
5.1. Review
The dynamically measured modal flexibility matrix has been employed in damage detection. Damage results in a flexibility increase in elements near the damage, especially in the corresponding diagonal terms of the modal flexibility matrix. Pandey and Biswas [105] took the absolute change in the modal flexibility matrix as the damage index. The stiffness matrix can be expressed as
where is the mass normalized mode shape, is the natural frequency matrix given by . The flexibility matrix is the inverse of the stiffness matrix , and it can be written as
where is the number of modes and () represents the th mode shape. The maximum variation observed in the column of the modal flexibility matrix after damage occurs corresponds to the damage location. The flexibility matrix converges rapidly with increasing frequency; thus, it can be easily and accurately estimated from a few of the low-order modes. The minor contribution of high-order modes to modal flexibility can also be observed from the inversely proportional relationship between the flexibility and the squares of natural frequencies in Equation (2). In [105], the damage was modeled by a reduction of the modulus of elasticity in the damaged element, and the damage severity was related to the extent of the reduction. An experiment was conducted on a wide-flange steel beam with a splice at the mid-span. Damage was represented by opening bolts from the splice plates. The first two modes were used to estimate the modal flexibility. It is worth mentioning that the magnitude of the modal flexibility change was very small (around 10−11) if the damage (i.e., stiffness reduction) was not severe.
Many modal flexibility-based methods involve optimization algorithms. These methods normally show a two-stage feature. In the first stage, a damage index is proposed based on modal flexibility, and subsequently, an objective function is formulated in which the global extremum solution represents the damage location. In the second stage, various optimization algorithms are utilized to find the global extremum solution in the search space. The challenge in the second stage is typically to avoid being trapped in local optima while accelerating the convergence. There is usually a trade-off between finding global optima and boosting convergence speed by, for instance, iteratively reducing search space. Hosseinzadeh et al. [106] presented an objective function based on the modal assurance criterion and modal flexibility matrix. The novelty of this objective function was to search the geometrical correlation between the vector of a monitored damaged structure and the vector of an analytical model with unknown damage severity. Both vectors were composed of diagonal terms of modal flexibility matrices. In the second stage, the conventional particle swarm optimization algorithm was modified by considering the experiences of all kinds of particles (eligible particles and bad particles) when searching the solution domain; thus, premature convergence could be avoided. Dinh-Cong et al. [107] presented an objective function based on the Frobenius norm of modal flexibility change matrix. In the second stage, the differential evolution algorithm was modified by enhancing the balance of global and local searches in each generation. To be specific, the variables corresponding to healthy elements were gradually eliminated after several generations to reduce the dimension of search space, thereby accelerating the convergence. Ahmadi-Nedushan and Fathnejat [108] introduced a new damage index based on modal flexibility and modal strain energy. The modal strain energy of each element was normalized by the diagonal terms of the modal flexibility matrix. The normalization was performed because of the two characteristics of modal flexibility matrix: modal flexibility matrix can be estimated using merely the first few modes; modal flexibility matrix is a diagonal matrix. Thus, the normalization made it possible to improve the performance of modal strain energy by using a smaller number of modes. A modified teaching-learning-based optimization algorithm was employed in the second stage. Results showed that the new damage index resulted in a smaller search domain of the optimization algorithm. It should be noted that in the numerical models of [106,107,108], the damage was modeled by stiffness reduction in the damaged element, and mass reduction was not considered.
Modal flexibility-based methods have been compared with other methods by some researchers. Wang et al. [109] applied FE model updating to a cracked three-story frame. The damage was modeled by stiffness reduction, and elemental stiffness parameters were updated. Based on the same set of data, two objective functions were proposed. One objective function was a weighted function of mode shape residues and natural frequency, and the other was the modal flexibility residue. The advantage of the former objective function was that different weights could be assigned to natural frequencies and mode shapes; thus, the measurement accuracy could be considered. In comparison, this cannot be achieved in the modal flexibility-based objective function. In both objective functions, the uncertainties in the measured modal data were assumed as independent, normally distributed random variables with zero means and specific covariance. It was found that the introduction of different weights in the first objective function made the modal parameter-based method outperform its counterpart. Measured mode shapes usually contain larger noise than measured frequencies. Introducing different weights can be a feasible way to suppress noise effects. However, it may be difficult to determine suitable weights, and some case-dependent trial calculations are necessary.
Altunisik et al. [110] compared a modal curvature-based method with a modal flexibility-based method. A crack was modeled using a local flexibility matrix in the analytical model based on the transfer matrix method. Crack detection in multi-cracked steel cantilever beams with circular-hollow cross-sections and box cross-sections was carried out through changes in modal curvature and modal flexibility. Because there were only six measurement points, the cracks could not be localized precisely every time. In terms of detecting multiple cracks regardless of their depths, the modal curvature-based method performed better than the modal flexibility-based method. However, when the number of measurement points was limited, the modal flexibility-based method would be a better option. However, one should bear in mind that in the presence of cracks with different severity, the modal flexibility-based method tends to be less sensitive to smaller cracks. This was also observed by Kahya et al. [111] when comparing the application of two damage indices, i.e., the absolute changes in modal curvature and the modal flexibility after damage occurred, in laminated composite beams with multiple edge cracks.
To identify multiple damages and enhance noise immunity, data fusion techniques were considered by some researchers. Data fusion techniques combine data from multiple information sources to improve accuracy and robustness. In [112], for example, mode shapes of the damaged and undamaged states were regarded as information sources, and local decisions were made through the relative change of modal flexibility at each element and subsequently fused. In contrast to using the relative change alone, multiple damages could be identified more clearly when data fusion was used. However, the situation where multiple damages with distinct severity are present is not studied. Previous studies (e.g., [110,111]) have shown that the effect of severe damage may be dominant and consequently obscures minor damages. Further research is needed to determine whether data fusion techniques can tackle this issue.
Unlike the data fusion technique that accumulates a shared characteristic from multiple information sources, the statistical pattern recognition method aims to identify a certain damage pattern from a large amount of data. For example, Entezami et al. [113] proposed a hybrid method combining modal flexibility and clustering analysis. Clustering is a statistical tool for dividing data into clusters based on similarity. The discrepancy between the modal flexibility matrices of the damaged and undamaged states of a structure was taken as the damage-sensitive feature. The advantage of [113] is good noise immunity. It was shown that when the noise level increased from 0% to 10%, the variation in the Frobenius norms of clustering outputs was negligible. However, to make the damage signature pronounced, a huge amount of data is processed when using statistical pattern recognition methods, such as the clustering method.
The in-situ application of modal flexibility-based damage detection is scarce. Schommer et al. [29] conducted in-situ dynamic testing on a new concrete bridge and a retired prestressed concrete bridge in Luxembourg. The influence of temperature on frequencies and modal flexibility matrices of the new bridge was investigated. Before demolishing the retired bridge, artificial damages were introduced in multiple steps, and the variation in frequencies and modal flexibility matrices was studied. Artificial damages were made by cutting tendons and subsequently inducing cracks using mass loading of 250 tons. In the dynamic test, both bridges were excited by an excitation force of 2.5 kN from an unbalanced mass exciter. Figure 14 shows that the temperature in summer can lead to a frequency drop as large as 15.5% for the first bending frequency of the new bridge, which is consistent with the description in [25,26,27,28]. Figure 15 shows the influence of temperature on the modal flexibility matrix based on the first two modes of the new bridge. As the temperature changes, a global shift can be observed in diagonal terms. According to the authors’ explanation, the temperature effect may be due to the thermal sensitivity of the thick asphalt layer and the elastomeric bearing pads of supports.
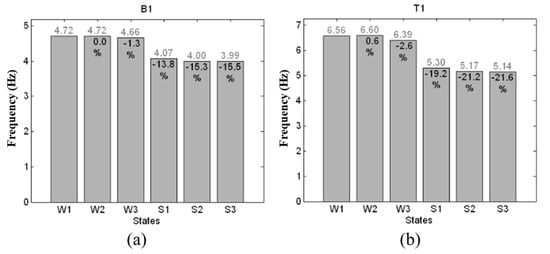
Figure 14.
Natural frequencies identified in summer (denoted by S1, S2, and S3) and winter (denoted by W1, W2, and W3) [29]: (a) bending mode B1 and (b) torsional mode T1.
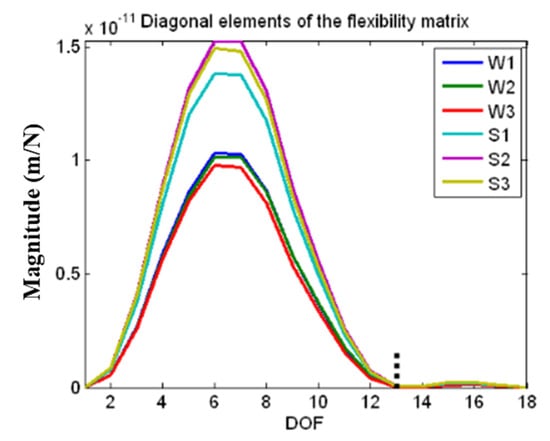
Figure 15.
The diagonal terms of the flexibility matrix in summer and winter [29].
The variation of natural frequencies as the damage develops is shown in Figure 16. Comparing Figure 16 with Figure 14, the magnitude of frequency drop caused by damage is similar to that caused by temperature change, which indicates the importance of maintaining a roughly constant temperature during the measurement. Figure 17 shows the variation of diagonal terms in the modal flexibility matrix that is based on the measurement of seven modes. The damage on the first cutting line located at the mid-span could be identified, whereas the damage on the second cutting line located above the intermediate support was not detected due to the low absolute flexibility or the high stiffness. Overall, ref. [29] demonstrates that the type of support and the damage location have a considerable influence on modal flexibility-based damage detection. The modal flexibility change is often very small, especially when the damage location is far from the region with high modal curvature. Therefore, it can be challenging to make correct interpretations when measurement noise and temperature effects interfere.
Figure 16.
Natural frequencies of the retired bridge under different damage states [29]: (a) bending mode B1 and (b) torsional mode T2.
Figure 17.
The diagonal terms of the flexibility matrix of the retired bridge [29]: (a) diagonal terms and (b) the relative percentage difference of diagonal terms.
5.2. Comments
Based on the above literature survey, some comments are made as follows:
- (1)
- The greatest strength of the modal flexibility-based damage index is that modal flexibility converges rapidly with increasing natural frequency. Thus, the modal flexibility matrix can be properly estimated by using the first few modes. This is beneficial because, normally, only a limited number of modes can be measured in a practical structure. However, most of the damage indices are based on modal flexibility change, which means baseline information is indispensable. This is the most obvious limitation of modal flexibility-based methods. Baseline information is obtained from the FE model of the intact structure in many studies, whereas baseline information is not always available for a practical structure.
- (2)
- Modal flexibility is a function of both natural frequencies and mode shapes. It inherits the noise immunity of natural frequency as well as the spatial information from mode shape, which makes it a sensitive parameter to damage location. However, it is difficult to formulate an explicit relationship between modal flexibility and damage severity. Thus, the modal flexibility-based damage index is not a good candidate for severity estimation.
- (3)
- Data-driven techniques (e.g., data fusion, clustering, big data analytics, etc.) seem promising when dealing with some challenging situations where, for example, multiple damages are present or modal data contain considerable noise. Although multi-damage scenarios are considered in the above literature, it is still unknown whether the proposed methods are applicable for identifying closely spaced damages. Moreover, when there are multiple damages with distinct severity, the performance of those methods seems not satisfactory. It is shown in [112] that compared with using the relative change of modal flexibility alone, multiple damages can be identified more clearly when data fusion is employed. For the heavily noise-polluted modal data, ref. [113] shows that the clustering approach has stable performance. Overall, hybrid methods combining data-driven techniques or statistical pattern recognition deserve further research.
6. Concluding Remarks and Future Recommendations
This study provides an overview of vibration-based damage detection with emphasis on the application of natural frequency, mode shape, modal curvature, modal strain energy, and modal flexibility-based damage detection methods in civil structures. The current state of the art is given for each type of method, followed by some comments on characteristics, pros and cons, and potential research opportunities. In this section, the main findings from this literature review are briefly summarized, and areas where further research is indicated are addressed.
Summarizing the reviewed literature and extracting the main features of most studies, a schematic of the general methodology of vibration-based damage detection is presented in Figure 18. From START to END, each possible route represents a possible methodology; thus, the flow chart implies numerous possibilities: whether they are baseline-free or baseline-dependent; one-stage, two-stage, or even multi-stage; advanced signal processing-assisted or FE model-involved, etc.
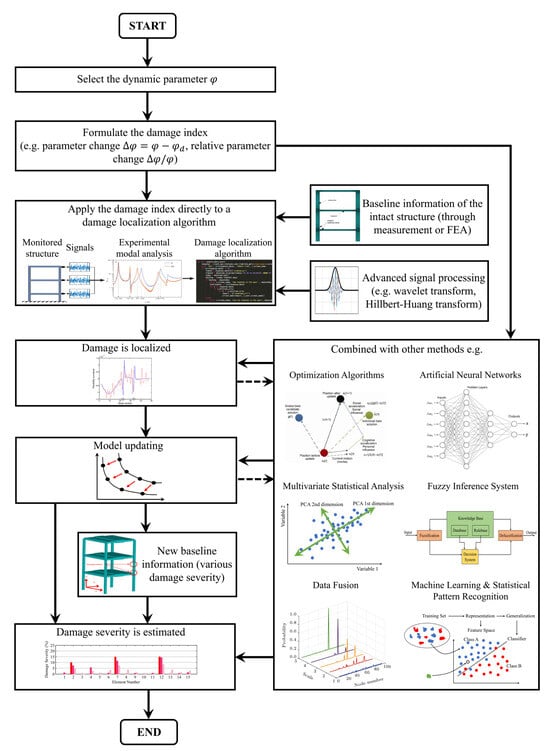
Figure 18.
A schematic of the general methodology of vibration-based damage detection.
The characteristics of the five vibrational signature-based damage detection methods discussed above are briefly outlined in Figure 19. The efficacy of natural frequency-based methods has been verified only under laboratory conditions by some researchers, and the artificial damages used are of significant magnitude. In contrast, they may serve the purpose of proof of concept, their feasibility for practical damage detection when the damage is small enough to be repaired, or their applicability in the presence of multiple damages has not been verified. Although the natural frequency-based method may be easy to implement, it is advisable to supplement it with other methods, for example, methods based on mode shape or methods considering an auxiliary mass, to take advantage of its global nature while circumventing its inherent drawbacks.
Figure 19.
The summary of comments.
Based on mode shape and its derivatives, such as modal curvature, extensive research has been conducted on various methodologies. Even though measurement noise emerges as a crucial factor determining the reliability of these methodologies, the sensitivity to minor damage is highlighted in their application. However, problems relevant to measurement error propagation and amplification still pose a challenge for methods based on mode shape derivatives. Compared with natural frequency-based methods, the mode shape and modal curvature-based methods have an increased demand for measurement equipment. However, with the increasing availability of high precision and quasi-continuous modern measurement techniques (such as scanning laser vibrometers, piezoelectric sensors, fiber optic sensors, and smart wireless sensors), the mode shape and modal curvature-based methods are likely to receive considerable attention as potential solutions for damage detection.
Modal strain energy and modal flexibility are good candidates for damage localization. However, due to the approximation adopted in the calculation of modal strain energy, the accuracy for damage severity estimation based on modal strain energy is inadequate. Moreover, to date, no explicit mathematical relationship has been derived between modal flexibility and damage severity. Considering these issues, combining the modal strain energy or modal flexibility matrix with other supplementary methods is common, and damage localization and severity estimation can be solved successively in a two-stage or multi-stage manner (as shown in Figure 18).
From the reviewed literature, the authors believe the following lines of research will be beneficial in turning theory into practical implementation.
- (1)
- Damage-induced changes in dynamic parameters such as natural frequency, mode shape, modal curvature, etc., have been used as indices in damage detection. However, the changes in parameters relevant to structural integrity, such as levels of stress and displacement, have been ignored. For example, damage-induced changes in stress fields have not been fully utilized in vibration-based damage detection. When the damage severity varies, natural frequency, displacement, and stress levels may change to different extents. This then raises a question of whether the damage that causes a small change in natural frequency, which is difficult to distinguish from measurement noise based on existing technologies, can cause stress levels that are significant enough to warrant remedial action. If this is not the case, then frequency measurement based on current technology can still be a good indicator of damage that should trigger inspection and repair. Thus, a direct comparison between the crack severity threatening structural integrity and the crack severity causing a measurable frequency change is necessary.
- (2)
- An auxiliary system affiliating to a damaged beam and plate has been used for damage detection. For example, a stationary roving mass is utilized to enhance the effect of a crack on the dynamics of a cracked beam and provide additional spatial information about the crack [19,30]. A roving mass with or without rotary inertia has been used for crack detection in beams, plates, and cylindrical shells [20,21,33,34] without any knowledge of the theoretical model and irrespective of the crack severity. However, its practical application is yet to be explored. Firstly, further research is required to determine whether the measured frequency change is higher than the change caused by measurement noise in practical situations. Secondly, the fact that the rotary inertia does not act at a point would make the theoretical frequency jump in [33,34] simply a steep change, which will raise the difficulty to discern the frequency change, and advanced signal processing techniques such as wavelet transform may be needed. A potential application of this method may be the use of traffic or a dedicated vehicle to test the integrity of a bridge or monitor the health of a bridge. This would also mean further research is needed to consider not only the effect of a roving body but also the effect of a moving body, in which factors such as the velocity of the vehicle need to be considered.
Author Contributions
Conceptualization, S.I. and X.S.; methodology, S.I. and X.S.; software, X.S.; validation, X.S.; formal analysis, X.S., S.I., Y.M. and R.C.T.; investigation, X.S.; resources, S.I., Y.M. and R.C.T.; data curation, X.S.; writing—original draft preparation, X.S.; writing—review and editing, S.I., Y.M. and R.C.T.; visualization, X.S.; supervision, S.I., Y.M. and R.C.T.; project administration, S.I., Y.M. and R.C.T.; funding acquisition, S.I., Y.M. and R.C.T.. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Hellier, C. Handbook of Nondestructive Evaluation, 2nd ed.; McGraw Hill Professional: New York, NY, USA, 2013. [Google Scholar]
- Avci, O.; Abdeljaber, O.; Kiranyaz, S.; Hussein, M.; Gabbouj, M.; Inman, D.J. A review of vibration-based damage detection in civil structures: From traditional methods to Machine Learning and Deep Learning applications. Mech. Syst. Signal Proc. 2021, 147, 107077. [Google Scholar] [CrossRef]
- Wang, Z.; Ong, K. Autoregressive coefficients based Hotelling’s T2 control chart for structural health monitoring. Comput. Struct. 2008, 86, 1918–1935. [Google Scholar] [CrossRef]
- Teughels, A.; Maeck, J.; De Roeck, G. Damage assessment by FE model updating using damage functions. Comput. Struct. 2002, 80, 1869–1879. [Google Scholar] [CrossRef]
- Rytter, A. Vibrational Based Inspection of Civil Engineering Structures. Ph.D. Thesis, Department of Building Technology and Structural Engineering, Aalborg University, Aalborg, Denmark, 1993. [Google Scholar]
- Caddemi, S.; Calio, I.; Cannizzaro, F.; Morassi, A. A procedure for the identification of multiple cracks on beams and frames by static measurements. Struct. Control Health Monit. 2018, 25, e2194. [Google Scholar] [CrossRef]
- Buda, G.; Caddemi, S. Identification of concentrated damages in Euler-Bernoulli beams under static loads. J. Eng. Mech. 2007, 133, 942–956. [Google Scholar] [CrossRef]
- Waldmann-Diederich, D.; Erdenebat, D. Potential of the Deformation Area Difference (DAD)-Method for Condition Assessment of Bridge Structures. In Proceedings of the SMAR 2019—5th International Conference on Smart Monitoring, Assessment and Rehabilitation of Civil Structures, Potsdam, Germany, 27–29 August 2019. [Google Scholar]
- Doebling, S.W.; Farrar, C.R.; Prime, M.B. A summary review of vibration-based damage identification methods. Shock Vib. Dig. 1998, 30, 91–105. [Google Scholar] [CrossRef]
- Sekhar, A.S. Multiple cracks effects and identification. Mech. Syst. Signal Proc. 2008, 22, 845–878. [Google Scholar] [CrossRef]
- Sinou, J.J. A review of damage detection and health monitoring of mechanical systems from changes in the measurement of linear and non-linear vibrations. In Mechanical Vibrations: Measurement, Effects and Control; Sapri, R.C., Ed.; Nova Science Publishers, Inc.: New York, NY, USA, 2009; pp. 643–702. [Google Scholar]
- Fan, W.; Qiao, P. Vibration-based damage identification methods: A review and comparative study. Struct. Health Monit. 2011, 10, 83–111. [Google Scholar] [CrossRef]
- Katunin, A. Nondestructive damage assessment of composite structures based on wavelet analysis of modal curvatures: State-of-the-art review and description of wavelet-based damage assessment benchmark. Shock Vib. 2015, 2015, 735219. [Google Scholar] [CrossRef]
- Worden, K.; Dulieu-Barton, J.M. An Overview of Intelligent Fault Detection in Systems and Structures. Struct. Health Monit. 2016, 3, 85–98. [Google Scholar] [CrossRef]
- Bovsunovsky, A.; Surace, C. Non-linearities in the vibrations of elastic structures with a closing crack: A state of the art review. Mech. Syst. Signal Proc. 2015, 62–63, 129–148. [Google Scholar] [CrossRef]
- Giannini, O.; Casini, P.; Vestroni, F. Nonlinear harmonic identification of breathing cracks in beams. Comput. Struct. 2013, 129, 166–177. [Google Scholar] [CrossRef]
- Caddemi, S.; Caliò, I.; Marletta, M. The dynamic non-linear behaviour of beams with closing cracks. In Proceedings of the AIMETA 2009 XIX Congresso di Meccanica Teorica ed Applicata, Ancona, Italy, 14–17 September 2009. [Google Scholar]
- Kisa, M.; Brandon, J. The effects of closure of cracks on the dynamics of a cracked cantilever beam. J. Sound Vibr. 2000, 238, 1–18. [Google Scholar] [CrossRef]
- Zhong, S.; Oyadiji, S.O. Analytical predictions of natural frequencies of cracked simply supported beams with a stationary roving mass. J. Sound Vibr. 2008, 311, 328–352. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, L.; Lie, S.T.; Xiang, Z. Damage detection in plates structures based on frequency shift surface curvature. J. Sound Vibr. 2013, 332, 6665–6684. [Google Scholar] [CrossRef]
- Zhang, Y.; Lie, S.T.; Xiang, Z.; Lu, Q. A frequency shift curve based damage detection method for cylindrical shell structures. J. Sound Vibr. 2014, 333, 1671–1683. [Google Scholar] [CrossRef]
- Lie, S.; Zhang, Y.; Wang, L. Damage detection in compressed natural gas (CNG) cylinders based on auxiliary mass induced frequency shift. Exp. Mech. 2015, 55, 487–498. [Google Scholar] [CrossRef]
- Cao, L.; He, W.-Y.; Ren, W.-X. Damage localization and quantification for beam bridges based on frequency variation of parked vehicle-bridge systems. Structures 2021, 31, 357–368. [Google Scholar] [CrossRef]
- Wang, L.; Zhang, Y.; Lie, S.T. Detection of damaged supports under railway track based on frequency shift. J. Sound Vibr. 2017, 392, 142–153. [Google Scholar] [CrossRef]
- Liu, C.; DeWolf, J.T. Effect of temperature on modal variability of a curved concrete bridge under ambient loads. J. Struct. Eng. 2007, 133, 1742–1751. [Google Scholar] [CrossRef]
- Xia, Y.; Hao, H.; Zanardo, G.; Deeks, A. Long term vibration monitoring of an RC slab: Temperature and humidity effect. Eng. Struct. 2006, 28, 441–452. [Google Scholar] [CrossRef]
- Sohn, H. Effects of environmental and operational variability on structural health monitoring. Philos. Trans. A Math. Phys. Eng. Sci. 2007, 365, 539–560. [Google Scholar] [CrossRef]
- Peeters, B.; De Roeck, G. One-year monitoring of the Z24-Bridge: Environmental effects versus damage events. Earthq. Eng. Struct. Dyn. 2001, 30, 149–171. [Google Scholar] [CrossRef]
- Schommer, S.; Mahowald, J.; Nguyen, V.H.; Waldmann, D.; Maas, S.; Zürbes, A.; De Roeck, G. Health monitoring based on dynamic flexibility matrix: Theoretical models versus in-situ tests. Engineering 2017, 9, 37–67. [Google Scholar] [CrossRef]
- Zhong, S.; Oyadiji, S.O. Identification of cracks in beams with auxiliary mass spatial probing by stationary wavelet transform. J. Vib. Acoust. 2008, 130, 041001. [Google Scholar] [CrossRef]
- Sazonov, E.; Klinkhachorn, P. Optimal spatial sampling interval for damage detection by curvature or strain energy mode shapes. J. Sound Vibr. 2005, 285, 783–801. [Google Scholar] [CrossRef]
- Yang, C.; Oyadiji, S.O. Damage detection using modal frequency curve and squared residual wavelet coefficients-based damage indicator. Mech. Syst. Signal Proc. 2017, 83, 385–405. [Google Scholar] [CrossRef]
- Cannizzaro, F.; De Los Rios, J.; Caddemi, S.; Caliò, I.; Ilanko, S. On the use of a roving body with rotary inertia to locate cracks in beams. J. Sound Vibr. 2018, 425, 275–300. [Google Scholar] [CrossRef]
- Ilanko, S.; Mochida, Y.; De Los Rois, J. Vibration Analysis of Cracked Structures as a Roving Body Passes a Crack Using the Rayleigh-Ritz Method. EPI Int. J. Eng. 2018, 1, 30–34. [Google Scholar] [CrossRef][Green Version]
- Behera, S.; Parhi, D.; Das, H. Numerical, experimental and fuzzy logic applications for investigation of crack location and crack depth estimation in a free-free aluminum beam. Vib. Phys. Syst. 2018, 29, 2018019. [Google Scholar]
- Agarwalla, D.K.; Khan, A.S.; Sahoo, S.K. Application of Genetic Fuzzy System for Damage Identification in Cantilever Beam Structure. Procedia Eng. 2016, 144, 215–225. [Google Scholar] [CrossRef]
- Gomes, G.F.; Mendéz, Y.A.D.; da Cunha, S.S.; Ancelotti, A.C. A numerical–experimental study for structural damage detection in CFRP plates using remote vibration measurements. J. Civ. Struct. Health Monit. 2018, 8, 33–47. [Google Scholar] [CrossRef]
- Sahu, S.; Kumar, P.B.; Parhi, D.R. Intelligent hybrid fuzzy logic system for damage detection of beam-like structural elements. J. Theor. Appl. Mech. 2017, 55, 509–521. [Google Scholar] [CrossRef]
- Zhang, Z.; He, M.; Liu, A.; Singh, H.K.; Ramakrishnan, K.R.; Hui, D.; Shankar, K.; Morozov, E.V. Vibration-based assessment of delaminations in FRP composite plates. Compos. Part B Eng. 2018, 144, 254–266. [Google Scholar] [CrossRef]
- Oliver, G.A.; Ancelotti, A.C.; Gomes, G.F. Neural network-based damage identification in composite laminated plates using frequency shifts. Neural Comput. Appl. 2021, 33, 3183–3194. [Google Scholar] [CrossRef]
- Dahak, M.; Touat, N.; Benseddiq, N. On the classification of normalized natural frequencies for damage detection in cantilever beam. J. Sound Vibr. 2017, 402, 70–84. [Google Scholar] [CrossRef]
- De Los Rios, J.; Ilanko, S.; Kennedy, D. Decoupling severity and location from cracked beams. In Proceedings of the 23rd International Congress on Sound and Vibration, Athens, Greece, 10–14 July 2016. [Google Scholar]
- Labib, A.; Kennedy, D.; Featherston, C.A. Crack localisation in frames using natural frequency degradations. Comput. Struct. 2015, 157, 51–59. [Google Scholar] [CrossRef]
- Greco, A.; Pau, A. Damage identification in Euler frames. Comput. Struct. 2012, 92–93, 328–336. [Google Scholar] [CrossRef]
- Yang, J.; Huang, L.; Tong, K.; Tang, Q.; Li, H.; Cai, H.; Xin, J. A Review on Damage Monitoring and Identification Methods for Arch Bridges. Buildings 2023, 13, 1975. [Google Scholar] [CrossRef]
- Caliò, I.; Greco, A.; D’Urso, D. Structural models for the evaluation of eigen-properties in damaged spatial arches: A critical appraisal. Arch. Appl. Mech. 2016, 86, 1853–1867. [Google Scholar] [CrossRef]
- Pau, A.; Greco, A.; Vestroni, F. Numerical and experimental detection of concentrated damage in a parabolic arch by measured frequency variations. J. Vib. Control 2011, 17, 605–614. [Google Scholar] [CrossRef]
- Greco, A.; D’Urso, D.; Cannizzaro, F.; Pluchino, A. Damage identification on spatial Timoshenko arches by means of genetic algorithms. Mech. Syst. Signal Proc. 2018, 105, 51–67. [Google Scholar] [CrossRef]
- Giordano, E.; Mendes, N.; Masciotta, M.G.; Clementi, F.; Sadeghi, N.H.; Silva, R.A.; Oliveira, D.V. Expeditious damage index for arched structures based on dynamic identification testing. Constr. Build. Mater. 2020, 265, 120236. [Google Scholar] [CrossRef]
- Nasery, M.M.; Hüsem, M.; Okur, F.Y.; Altunışık, A.C.; Nasery, M.E. Model updating-based automated damage detection of concrete-encased composite column-beam connections. Struct. Control. Health Monit. 2020, 27, e2600. [Google Scholar] [CrossRef]
- Morassi, A.; Rollo, M. Identification of two cracks in a simply supported beam from minimal frequency measurements. J. Vib. Control 2001, 7, 729–739. [Google Scholar] [CrossRef]
- Allemang, R.J.; Brown, D.L. A correlation coefficient for modal vector analysis. In Proceedings of the 1st International Modal Analysis Conference, Orlando, FL, USA, 8–10 November 1982. [Google Scholar]
- Lieven, N.; Ewins, D. Spatial correlation of mode shapes, the coordinate modal assurance criterion (COMAC). In Proceedings of the Sixth International Modal Analysis Conference, Kissimmee, FL, USA, 1–4 February 1988. [Google Scholar]
- Catbas, F.; Aktan, A.; Allemang, R.; Brown, D. A correlation function for spatial locations of scaled mode shapes-(comef). In Society for Experimental Mechanics, Inc., Proceedings of the 16th International Modal Analysis Conference, Santa Barabara, CA, USA, 2–5 February 1998; ACS Publications: Washington, DC, USA, 1998. [Google Scholar]
- Allemang, R.J. The modal assurance criterion–twenty years of use and abuse. Sound Vib. 2003, 37, 14–23. [Google Scholar]
- Solís, M.; Ma, Q.; Galvín, P. Damage detection in beams from modal and wavelet analysis using a stationary roving mass and noise estimation. Strain 2018, 54, e12266. [Google Scholar] [CrossRef]
- Zhong, S.; Oyadiji, S.O. Detection of cracks in simply-supported beams by continuous wavelet transform of reconstructed modal data. Comput. Struct. 2011, 89, 127–148. [Google Scholar] [CrossRef]
- Zhong, S.; Oyadiji, S.O. Sampling interval sensitivity analysis for crack detection by stationary wavelet transform. Struct. Control. Health Monit. 2013, 20, 45–69. [Google Scholar] [CrossRef]
- Ciambella, J.; Pau, A.; Vestroni, F. Effective filtering of modal curvatures for damage identification in beams. Procedia Eng. 2017, 199, 1876–1881. [Google Scholar] [CrossRef]
- Ciambella, J.; Pau, A.; Vestroni, F. Modal curvature-based damage localization in weakly damaged continuous beams. Mech. Syst. Signal Proc. 2019, 121, 171–182. [Google Scholar] [CrossRef]
- Montanari, L.; Spagnoli, A.; Basu, B.; Broderick, B. On the effect of spatial sampling in damage detection of cracked beams by continuous wavelet transform. J. Sound Vibr. 2015, 345, 233–249. [Google Scholar] [CrossRef]
- De Silva, W.; Lewangamage, C.; Jayasinghe, M. Detection and estimation of damage in framed structures using modal data. In Proceedings of the 2019 Moratuwa Engineering Research Conference (MERCon), Moratuwa, Sri Lanka, 3–5 July 2019. [Google Scholar]
- Whalen, T.M. The behavior of higher order mode shape derivatives in damaged, beam-like structures. J. Sound Vibr. 2008, 309, 426–464. [Google Scholar] [CrossRef]
- Ručevskis, S.; Wesolowski, M.; Chate, A. Vibration-based damage detection in a beam structure with multiple damage locations. Aviation 2009, 13, 61–71. [Google Scholar] [CrossRef]
- Xu, Y.; Zhu, W.; Liu, J.; Shao, Y. Identification of embedded horizontal cracks in beams using measured mode shapes. J. Sound Vibr. 2014, 333, 6273–6294. [Google Scholar] [CrossRef]
- Cao, M.; Radzieński, M.; Xu, W.; Ostachowicz, W. Identification of multiple damage in beams based on robust curvature mode shapes. Mech. Syst. Signal Proc. 2014, 46, 468–480. [Google Scholar] [CrossRef]
- Cao, M.-S.; Xu, W.; Ren, W.-X.; Ostachowicz, W.; Sha, G.-G.; Pan, L.-X. A concept of complex-wavelet modal curvature for detecting multiple cracks in beams under noisy conditions. Mech. Syst. Signal Proc. 2016, 76, 555–575. [Google Scholar] [CrossRef]
- Cao, M.; Qiao, P. Novel Laplacian scheme and multiresolution modal curvatures for structural damage identification. Mech. Syst. Signal Proc. 2009, 23, 1223–1242. [Google Scholar] [CrossRef]
- Cao, S.; Ouyang, H.; Cheng, L. Baseline-free multidamage identification in plate-like structures by using multiscale approach and low-rank modelling. Struct. Control. Health Monit. 2019, 26, e2293. [Google Scholar] [CrossRef]
- Yang, Z.-B.; Radzienski, M.; Kudela, P.; Ostachowicz, W. Fourier spectral-based modal curvature analysis and its application to damage detection in beams. Mech. Syst. Signal Proc. 2017, 84, 763–781. [Google Scholar] [CrossRef]
- Quaranta, G.; Carboni, B.; Lacarbonara, W. Damage detection by modal curvatures: Numerical issues. J. Vib. Control 2016, 22, 1913–1927. [Google Scholar] [CrossRef]
- Anastasopoulos, D.; De Smedt, M.; Vandewalle, L.; De Roeck, G.; Reynders, E.P.B. Damage identification using modal strains identified from operational fiber-optic Bragg grating data. Struct. Health Monit. 2018, 17, 1441–1459. [Google Scholar] [CrossRef]
- dos Santos, F.M.; Peeters, B.; Lau, J.; Desmet, W.; Goes, L. An overview of experimental strain-based modal analysis methods. In Proceedings of the 26th International Conference on Noise and Vibration Engineering (ISMA2014), Leuven, Belgium, 15–17 September 2014. [Google Scholar]
- Lestari, W.; Qiao, P.; Hanagud, S. Curvature mode shape-based damage assessment of carbon/epoxy composite beams. J. Intell. Mater. Syst. Struct. 2007, 18, 189–208. [Google Scholar] [CrossRef]
- Hsu, T.Y.; Shih, Y.C.; Pham, Q.V. Damage detection of a thin plate using modal curvature via macrostrain measurement. Earthq. Eng. Eng. Vib. 2019, 18, 409–424. [Google Scholar] [CrossRef]
- Rubio, L.; Fernández-Sáez, J.; Morassi, A. Identification of two cracks with different severity in beams and rods from minimal frequency data. J. Vib. Control 2016, 22, 3102–3117. [Google Scholar] [CrossRef]
- Capecchi, D.; Ciambella, J.; Pau, A.; Vestroni, F. Damage identification in a parabolic arch by means of natural frequencies, modal shapes and curvatures. Meccanica 2016, 51, 2847–2859. [Google Scholar] [CrossRef]
- Ciambella, J.; Vestroni, F. The use of modal curvatures for damage localization in beam-type structures. J. Sound Vibr. 2015, 340, 126–137. [Google Scholar] [CrossRef]
- Xu, W.; Cao, M.; Ostachowicz, W.; Radzieński, M.; Xia, N. Two-dimensional curvature mode shape method based on wavelets and Teager energy for damage detection in plates. J. Sound Vibr. 2015, 347, 266–278. [Google Scholar] [CrossRef]
- Xu, W.; Ding, K.; Liu, J.; Cao, M.; Radzieński, M.; Ostachowicz, W. Non-uniform crack identification in plate-like structures using wavelet 2D modal curvature under noisy conditions. Mech. Syst. Signal Proc. 2019, 126, 469–489. [Google Scholar] [CrossRef]
- Abdulkareem, M.; Bakhary, N.; Vafaei, M.; Noor, N.M.; Mohamed, R.N. Application of two-dimensional wavelet transform to detect damage in steel plate structures. Measurement 2019, 146, 912–923. [Google Scholar] [CrossRef]
- Xu, W.; Cao, M.; Li, X.; Radzieński, M.; Ostachowicz, W.; Bai, R. Delamination monitoring in CFRP laminated plates under noisy conditions using complex-wavelet 2D curvature mode shapes. Smart Mater. Struct. 2017, 26, 104008. [Google Scholar] [CrossRef]
- Zhou, J.; Li, Z.; Chen, J. Damage identification method based on continuous wavelet transform and mode shapes for composite laminates with cutouts. Compos. Struct. 2018, 191, 12–23. [Google Scholar] [CrossRef]
- Chen, D.-M.; Xu, Y.F.; Zhu, W.D. A Comprehensive Study on Detection of Hidden Delamination Damage in a Composite Plate Using Curvatures of Operating Deflection Shapes. J. Nondestruct. Eval. 2019, 38, 54. [Google Scholar] [CrossRef]
- Pal, J.; Banerjee, S. A combined modal strain energy and particle swarm optimization for health monitoring of structures. J. Civ. Struct. Health Monit. 2015, 5, 353–363. [Google Scholar] [CrossRef]
- Khatir, S.; Wahab, M.A.; Boutchicha, D.; Khatir, T. Structural health monitoring using modal strain energy damage indicator coupled with teaching-learning-based optimization algorithm and isogoemetric analysis. J. Sound Vibr. 2019, 448, 230–246. [Google Scholar] [CrossRef]
- Dinh-Cong, D.; Vo-Duy, T.; Ho-Huu, V.; Nguyen-Thoi, T. Damage assessment in plate-like structures using a two-stage method based on modal strain energy change and Jaya algorithm. Inverse Probl. Sci. Eng. 2019, 27, 166–189. [Google Scholar] [CrossRef]
- Wei, Z.; Liu, J.; Lu, Z. Damage identification in plates based on the ratio of modal strain energy change and sensitivity analysis. Inverse Probl. Sci. Eng. 2016, 24, 265–283. [Google Scholar] [CrossRef]
- Ghasemi, M.R.; Nobahari, M.; Shabakhty, N. Enhanced optimization-based structural damage detection method using modal strain energy and modal frequencies. Eng. Comput. 2018, 34, 637–647. [Google Scholar] [CrossRef]
- Ashory, M.-R.; Ghasemi-Ghalebahman, A.; Kokabi, M.-J. An efficient modal strain energy-based damage detection for laminated composite plates. Adv. Compos. Mater. 2018, 27, 147–162. [Google Scholar] [CrossRef]
- Vo-Duy, T.; Ho-Huu, V.; Dang-Trung, H.; Nguyen-Thoi, T. A two-step approach for damage detection in laminated composite structures using modal strain energy method and an improved differential evolution algorithm. Compos. Struct. 2016, 147, 42–53. [Google Scholar] [CrossRef]
- Xu, M.; Wang, S.; Jiang, Y. Iterative two-stage approach for identifying structural damage by combining the modal strain energy decomposition method with the multiobjective particle swarm optimization algorithm. Struct. Control. Health Monit. 2019, 26, e2301. [Google Scholar] [CrossRef]
- Doebling, S.W.; Hemez, F.M.; Peterson, L.D.; Farhat, C. Improved damage location accuracy using strain energy-based mode selection criteria. AIAA J. 1997, 35, 693–699. [Google Scholar] [CrossRef][Green Version]
- Wu, X.; Xia, J.; Zhu, X. Finding Damage Localizations of a Planar Truss Using Modal Strain Energy Change. Adv. Civ. Eng. 2019, 2019, 3040682. [Google Scholar] [CrossRef]
- Asgarian, B.; Amiri, M.; Ghafooripour, A. Damage detection in jacket type offshore platforms using modal strain energy. Struct. Eng. Mech. 2009, 33, 325–337. [Google Scholar] [CrossRef]
- Fan, Q. A Two-Step Damage Identification Based on Cross-Model Modal Strain Energy and Simultaneous Optimization. IOP Conf. Ser. Earth Environ. Sci. 2021, 643, 012145. [Google Scholar] [CrossRef]
- Wang, S.; Xu, M. Modal strain energy-based structural damage identification: A review and comparative study. Struct. Eng. Int. 2019, 29, 234–248. [Google Scholar] [CrossRef]
- Li, H.; Yang, H.; Hu, S.-L.J. Modal strain energy decomposition method for damage localization in 3D frame structures. J. Eng. Mech. 2006, 132, 941–951. [Google Scholar] [CrossRef]
- Stubbs, N.; Kim, J.-T. Damage localization in structures without baseline modal parameters. AIAA J. 1996, 34, 1644–1649. [Google Scholar] [CrossRef]
- Yang, D.; Kang, C.; Hu, Z.; Ye, B.; Xiang, P. On the study of element modal strain energy sensitivity for damage detection of functionally graded beams. Compos. Struct. 2019, 224, 110989. [Google Scholar] [CrossRef]
- Li, Y.; Wang, S.; Zhang, M.; Zheng, C. An improved modal strain energy method for damage detection in offshore platform structures. J. Mar. Sci. Appl. 2016, 15, 182–192. [Google Scholar] [CrossRef]
- Samaei, S.; Hassanabad, M.G.; Ghahfarrokhi, M.A.; Ketabdari, M. Numerical and experimental investigation of damage in environmentally-sensitive civil structures using modal strain energy (case study: LPG wharf). Int. J. Environ. Sci. Technol. 2021, 18, 1939–1952. [Google Scholar] [CrossRef]
- Khosravan, A.; Asgarian, B.; Shokrgozar, H.R. Improved Modal Strain Energy Decomposition Method for damage detection of offshore platforms using data of sensors above the water level. Ocean Eng. 2021, 219, 108337. [Google Scholar] [CrossRef]
- Xu, M.; Wang, S.; Li, H. A residual strain energy based damage localisation method for offshore platforms under environmental variations. Ships Offshore Struct. 2019, 14, 747–754. [Google Scholar] [CrossRef]
- Pandey, A.; Biswas, M. Damage detection in structures using changes in flexibility. J. Sound Vibr. 1994, 169, 3–17. [Google Scholar] [CrossRef]
- Hosseinzadeh, A.Z.; Amiri, G.G.; Razzaghi, S.S.; Koo, K.; Sung, S.-H. Structural damage detection using sparse sensors installation by optimization procedure based on the modal flexibility matrix. J. Sound Vibr. 2016, 381, 65–82. [Google Scholar] [CrossRef]
- Dinh-Cong, D.; Vo-Duy, T.; Ho-Huu, V.; Dang-Trung, H.; Nguyen-Thoi, T. An efficient multi-stage optimization approach for damage detection in plate structures. Adv. Eng. Softw. 2017, 112, 76–87. [Google Scholar] [CrossRef]
- Ahmadi-Nedushan, B.; Fathnejat, H. A modified teaching–learning optimization algorithm for structural damage detection using a novel damage index based on modal flexibility and strain energy under environmental variations. Eng. Comput. 2020, 38, 847–874. [Google Scholar] [CrossRef]
- Wang, X.; Zhou, X.; Xia, Y.; Weng, S. Comparisons between modal-parameter-based and flexibility-based damage identification methods. Adv. Struct. Eng. 2013, 16, 1611–1619. [Google Scholar] [CrossRef]
- Altunışık, A.C.; Okur, F.Y.; Karaca, S.; Kahya, V. Vibration-based damage detection in beam structures with multiple cracks: Modal curvature vs. modal flexibility methods. Nondestruct. Test. Eval. 2019, 34, 33–53. [Google Scholar] [CrossRef]
- Kahya, V.; Karaca, S.; Okur, F.Y.; Altunışık, A.C.; Aslan, M. Damage localization in laminated composite beams with multiple edge cracks based on vibration measurements. Iran. J. Sci. Technol. Trans. Civ. Eng. 2021, 45, 75–87. [Google Scholar] [CrossRef]
- Grande, E.; Imbimbo, M. A multi-stage approach for damage detection in structural systems based on flexibility. Mech. Syst. Signal Proc. 2016, 76, 455–475. [Google Scholar] [CrossRef]
- Entezami, A.; Sarmadi, H.; Razavi, B.S. An innovative hybrid strategy for structural health monitoring by modal flexibility and clustering methods. J. Civ. Struct. Health Monit. 2020, 10, 845–859. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).