Abstract
This paper provides an initial investigation of quadruped rotary galloping gait patterns using data from racing greyhounds as they navigate their way around a constant radius bend. This study reviewed actual race data collected over a five month period from 2986 racing greyhounds. Using numerical dynamics modelling and value range analysis important factors were identified and analysed. By cleaning and synthesising simple X and Y data and also processing data for accuracy greyhound motion path dynamics results were produced for analysis. The results show that the galloping path greyhounds took going into the bend was different from the path coming out of the bend. It also shows that more than 50% of the greyhounds naturally optimised their path for a longer transition while minimising jerk when entering and exiting the bend. This research verified that individual greyhounds naturally chose different path transition lengths for accommodating their dynamic conditions. Finally, it was found that the greyhound galloping path dynamics state is less intense during the second half of the bend.
1. Introduction
During greyhound racing, multiple greyhounds race each other while chasing an artificial ‘non animal’ lure. In competing for speed with other greyhounds they enter the bend at high speed and attempt to maintain this speed inside the bend. Greyhounds galloping within the bend have dynamic aspects which control greyhound motion and their safety. The forces each greyhound experiences within the bend are generally higher than what they experience on the straight due to the presence of centrifugal force. Usherwood and Wilson [1] in a seminal study on greyhound running in tight bends, the peak force increase was more than 50% on each leg. Related research on thoroughbreds was published by Pfau et al. [2] on the centre-of-mass (CoM) movement and mechanical energy fluctuation during gallop locomotion in thoroughbred racehorses. Also, the gait of the greyhound inside the bend has to cope with the track camber profile. With humans, it was found that step frequency is different between left steps and right steps indicating changing of gait dynamics inside the bend [3]. It has also been shown that the turning radius affects both step length and step frequency for bend runners [4]. In rotary galloping quadrupeds like greyhounds the bend galloping conditions such as gait posture and related motion state outcome are not clearly understood or researched. In previous research stride frequency of greyhounds showed no significant difference between the straight and bend run [5,6,7]. Also, the stride frequency of the greyhound is far more stable with the increasing speed compared to cheetah [8]. This gives some hints about greyhound galloping dynamics that the energy state of galloping gait is varied in some forms other than stride frequency during change in speed. In related research, it was also observed that stride length was considerably lower for greyhounds inside the bend [9]. Nevertheless, the greyhound path trajectory motion outcome inside the bend is not clearly understood as it has not previously been investigated due to a lack of resources and data. Without looking into the major kinetic modification factors that affect greyhound gait the resulting greyhound motion patterns and trends can still be independently analysed and studied for greyhound bend galloping conditions. Preliminary study of different greyhound track path shapes following as defined by the lure affected greyhounds in their heading yaw rate [10]. There are design concerns for greyhound oval-shaped race track designs where the greyhound galloping conditions and motion patterns are highly dependent on race track variables such as track camber, bend radius and the transition length between the straight and bend to minimise the forces acting on the greyhound [11,12]. Also, in one research on the greyhound racing industry, the author feels protection of the greyhounds in racing can be done through establishing care-orientated and dog-focused practices within the industry [13]. One such example is the research done on establishing the probable best location and nature of protecting padding for greyhound racing through research, testing and industry collaboration [14].
When a greyhound navigates its way around the bend with a non-optimum motion path it will inevitably be forced to undertake a sharp motion which increases the chance of a limit state shock load, vibration and jerk [15] on the greyhound musculoskeletal system, because the g-force experienced can vary significantly in a short period of time when there is a rapid change in the force support platform and environment. The aerodynamic effects can also be considered for bodies moving through the air quickly when there is an abrupt change in motion. As greyhounds move very fast during racing they make sweeping changes in their direction of movement to avoid collisions or also to take the lead. Minor changes in bodies to adjust balance such as moving their tail or to reduce fatigue such as changing their lead paw. Greyhounds undergo aerodynamic pressure changes, the specific effect of which is not known during racing. As in every other bio-mechanical system, a greyhound’s musculoskeletal system can only sustain a certain level of strain and stress. Thus a proper understanding of what leads to massive straining is essential for safe galloping around a bend. By analysing and understanding greyhound galloping motion trends inside the bend predictions can be made as to which motion actions from the greyhound are precursors to unsafe bend galloping conditions.
In the previous study analysis of greyhound path dynamics demonstrated that centrifugal acceleration and vector sum of planner acceleration decrease inside the bend with the maximum acceleration occurring at the entrance [16]. However, in that study greyhound data were not tailored for looking into the motion of individual greyhound galloping condition patterns but rather the overall picture of greyhound dynamics drawn from average values. Motion prediction and pattern matching techniques that can be found from analysing galloping gait conditions and mapping them into the data are essential steps for modelling galloping motion more precisely inside the bend. Especially, it can be assumed that bend galloping conditions would require some forms of transition for going into and coming out of the bend and also for making smooth motions inside the bend when there is a need for optimising smoothness of movements. The effect of transition can be seen clearly where the nature of the transition can greatly influence the transition end radius and the jerk experienced during the transition [17]. It was noted in the research that greyhounds followed a gradual curvature transition even in the absence of track transition path [17]. Thus, transitions and centrifugal jerks are highly salient predictive factors from bend galloping motion conditions. In human sports, sprinting in curvilinear motion or bend running occurs more frequently than linear motion although it has not received much attention from sports scientists [18]. It has been noted that curve sprinting puts unique motor demands on the human musculoskeletal structure in comparison to linear sprinting thus requiring a separate performance measurement technique [18].
In this research, the greyhound galloping curve or bend performance is analysed by looking into the formation of bend transitions and patterns of greyhound motion relevant to outcomes.
2. Greyhound Motion Inside the Bend
Many greyhound racing tracks around the world are built using oval shapes. Thus the shapes of tracks present both bend and straight sections for a particular race distance. The bend found in a track can be as small as a 45 m radius of turn. The greyhound, with rotary galloping which is the fastest gait observed in land animals, a gait shared with the cheetah, can reach a speed of more than 20 m/s. As a greyhound races through different sections of the track including bend and straight sections, it goes through different phases of dynamic conditions and instinctively makes adjustments for these conditions. For instance, when galloping around the bend the greyhound has to deal with the centrifugal force that increases its effective weight. The camber inside the bend is usually raised to provide better support for greyhounds dealing with this centrifugal force but also can affect greyhound rotary galloping and other conditions. A motion across the camber inside the bend by the greyhound would be felt as changing transient loading on the greyhound’s feet. Severe injuries to the tarsus can be debilitating. Lowering the dynamic forces experienced by the greyhound reduces the probability of these severe injuries. There is little known about how a greyhound would adjust to changing dynamic conditions inside the bend and whether greyhounds follow a particular rule or direction when dealing with the changes they face. From a dynamics point of view greyhounds naturally optimise their path inside the bend to achieve optimal balance. As a general rule, they are pushing their bodies and the track surface to the the limit state and any deviation in a balanced trajectory has a high probability of inducing instability. The greyhound faces challenges inside the bend dealing with the random and dynamic changes imposed by closely-packed greyhounds all vying for the lead as they hustle and bustle for the lead position while still keeping their balance.
3. Safety Measures for Greyhound Motion Inside the Bend
When galloping within the bend a greyhound needs to change its direction constantly and in a consistent manner. This is a precise manoeuvre for a greyhound as in the galloping phase a greyhound increases its stride frequency to more than 3.5 strides/second where balancing and coordination to accommodate changing direction can be critical. Moreover, the double-flight phase of their rotary gallop means that the relatively short stance time in the fully extended gait (>5 m) creates a moment in the horizontal plane between their CoM and front paws. The greyhounds manage their weight distribution by keeping CoM low in the vertical plane and aligned with the track path while also maintaining the timing of their limb movements to maintain stability and prevent falling over. Other aspects that affect greyhound dynamics during racing for millisecond decision-making are the greyhound’s track familiarity, ability to make decisions in the presence of other greyhounds and perception of track turn curvature.
To aid greyhounds in navigating the bends, racing tracks are constructed with engineered safety elements that enable greyhounds to have additional support during galloping. One such element is deciding the exact camber profile needed inside the bend for centrifugal force support. Tracks are also designed with transition curves although these are not found in all tracks. Greyhounds go through rigorous training with these track features and get used to managing their gait accordingly.
The greyhound track camber is limited primarily by the ability of the track curators to maintain a safe and consistent running surface. Unlike a velodrome where the track surface is solid and consistent, the greyhound track surface is a mixture of rounded sand and clay particles bound together by water throughout the vertical profile of the racing surface. For optimum greyhound safety, the track surface needs to be consistent in both longitudinally and radially so it provides the greyhounds with certainty. Longitudinal consistency is required from stride to stride as they gallop around the track while radial consistency is required when they change their radius overtaking another greyhound.
If the camber is increased beyond approximately 10% the track surface can deteriorate rapidly due to riverlets when additional water is applied to maintain an optimum vertical water profile. A secondary physical safety consideration is minimising the rapid change in track surface camber when accommodating starting boxes on a bend.
Currently there is not enough data evidence to fully understand greyhound galloping gait locomotion buildup and formation type according to race, bend and track feature conditions. This is especially true for biomechanical and physiological factors that play an essential role in greyhound galloping dynamics inside the bend. Likewise, by understanding the greyhound galloping pattern and corresponding path-taking patterns inside the bend, safety measures for greyhound galloping conditions can be improved overall.
4. Quantifying Greyhound Galloping State Inside the Bend
Greyhound galloping conditions inside the bend can be inferred from kinematics and kinetics. The state variables such as greyhound speed and radius of turn are representative of greyhound motion inside the bend. Greyhound galloping state can be quantified by measuring these state variables and also by looking at state variable ratios for change and their effects on the greyhound. Speed inside the bend directly affects the centrifugal force experienced by the greyhound where a lower magnitude is preferable to a higher. Similarly, for greyhound instantaneous radius of turn a higher value is preferable to a lower. In Table 1 it can be seen that the galloping greyhound turning radius over speed ratio results in a high value when the greyhound galloping condition is improved inside the bend.

Table 1.
Greyhound turning radius over speed ratio.
As races are conducted anticlockwise, the final yaw inside the bend is also anticlockwise. A momentary change of direction relative to track path inside the bend can be considered either clockwise or anticlockwise. For instance, Figure 1 shows that in stride #2 greyhound direction change is counterclockwise relative to stride #1. Whereas, for a possible stride #3 it is clockwise relative to track path. In terms of the ratio of turning radius over speed relative counterclockwise is indicative of a slower greyhound path where a greyhound is relaxed in comparison to relative clockwise motion indicative of a faster greyhound path.
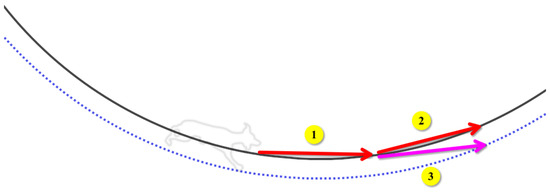
Figure 1.
Greyhound direction changes inside the bend.
5. Material and Methods
Based on the theoretical calculations of greyhound path following dynamics, it was expected and presumed that greyhounds formed some level of smooth trajectory for their path dynamics to minimise jerk and vibration levels. As in research, it describes an associative strategy which explains relationships between variables and tries to answer the nature of different variables [19]. In this research data from the greyhound path following worked as a bridge to close the gap between theoretical calculations and observational study. The design of the research methodology and procedure is largely based on the inherent understanding of greyhound theoretical dynamics and measurement system accuracy. The result generation was aimed towards descriptive strategy primary dynamics variables.
5.1. Collecting Greyhound Galloping Motion Data
Data from greyhound motion coordinates have been collected from greyhound racing from three oval tracks of similar dimensions and shapes.Tracks dimensions and the respective number of greyhounds from each track are shown in (Table 2). Using a proprietary location triangulation solution greyhound relative spatial XY coordinates data have been collected for races over a five month period in 2023. The data collection system ran at more than 30 spatial locations samples per second which gave greyhound motion coordinates around the bend. The data were later processed for accuracy and anomalies before extracting the greyhound galloping motion state inside the bends from the tracks.

Table 2.
Oval tracks dimensions and greyhound data sample size.
In the races the first track bend is located approximately between a 70 ± 10 m and 230 ± 20 m distance from the greyhound starting boxes. So the data are processed for this distance region only. All the greyhound starting boxes started on the straight section of the track before going into the first bend. Usually, at a race meeting, there are eight boxes or eight greyhounds participating in a race. However, there were also some races which did not have eight boxes starts. For the data processing, only races with more than six box starts were considered as this would give a better view of greyhound dynamic conditions with other competing greyhounds. This gave data from a sample size of 2986 greyhounds. Only the first bend from the race start was considered as this is the bend where greyhounds reach peak speed and most race injuries apparently also occur more frequently in the first bend. For path transition calculation, a transition starts when path turning radius is under 500 m radius and ended when it approaches the turning radius of the constant radius bend.
5.2. Taking Anomalies in the Data into Consideration
Due to the nature and the construct of the data collection system, there were various levels of noise in the location coordinates data containing X and Y coordinates. This noise arose from various reasons such as signal interference from various sources, precision thresholds of the system creating data duplicates for two different timestamps instead of two unique data points and communication cutting at various points in time. These are considered in the post processing of the location coordinates data to extract the overall dynamic condition of the galloping state to an acceptable threshold for the research. A modified moving filter was applied to the X and Y coordinates of greyhound location data which was deemed essential to remove high frequency noise. The same rule was applied to the greyhound state variables calculation results such as speed and radius of turning for removing low frequency noise.
5.3. Result Generation Process
Figure 2 depicts a diagram of steps taken for arriving at the results from greyhound data. In the data processing stage, greyhound XY coordinates data were resampled to the stride frequency of the greyhound which was calculated to be around 3.5 Hz. Resampling of data to stride frequency formatted coordinates data to behave like greyhound galloping stride motion condition data. This process also removed some of the random noise responsible for unstabilised state variables data. A window filter was applied to the resampled XY data as shown in the diagram. This filter removed high frequency noise from the data as this noise made greyhound location prediction from XY data jittery. After computing the state variables such as instantaneous speed and turning radius feature extraction algorithms were applied to sort the data. The algorithms checked for data anomalies such as sudden spikes in the calculated greyhound state variables and replaced them with predictable greyhound dynamics interpolated data. The sorting algorithms also fixed state variables data when greyhound motion occurred in a random manner such as turning steep left and right again in subsequent strides as this is less likely to occur due to the constraints of physical law. A window filter using algorithmic data sorting was applied to remove low frequency noise. Figure 3 shows the result of algorithmic sorting to turning radius state variable for a greyhound compared to moving average and no sorting applied.
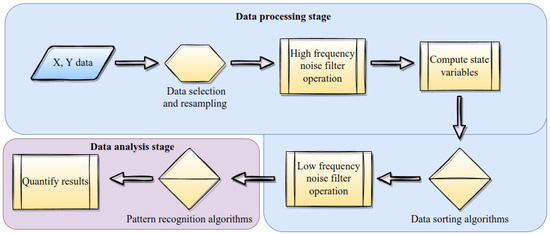
Figure 2.
Data analysis procedure from the raw greyhound data.
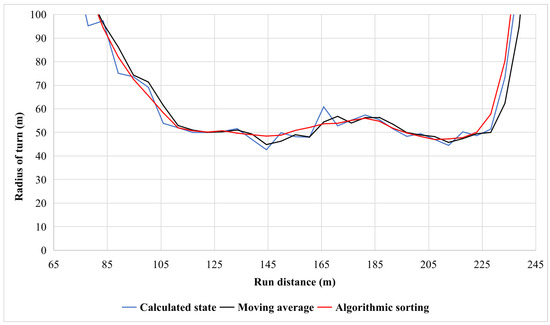
Figure 3.
Designed algorithms that remove data spree from greyhound state variable data profile.
For state variables data analysis, designed algorithms were utilised for identifying greyhound galloping motion transition points (TPs). Transition points are the locations where greyhound motion changes from a straight to a transition path towards the bend, a transition path to a constant radius bend for going into the bend, a bend to a transition path towards the straight and a transition path to a straight when coming out of the bend. There were four TPs for navigating around the bend from the straight starts. The algorithms looked into the stability of the greyhound turning radius to track TPs from state variables. After recognising TPs it was easy to calculate greyhound transition paths for going into and coming out of the bend. The algorithms also extracted all the local maxima and minima for the bend state variables data. The algorithms repeated the process for all the greyhound data. Figure 4 shows the result of the algorithm extracting local maxima and minima as pointed out by red circles from the ratio of the states turning radius over speed inside the bend run.
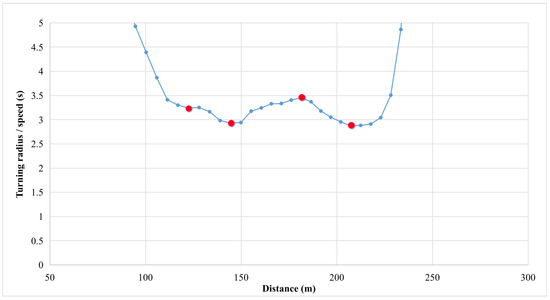
Figure 4.
Designed algorithm that captures local maxima and minima from a state variable data profile.
6. Results
6.1. Greyhound Galloping Motion Transitions for the Bend
Figure 5 and Figure 6 depict the greyhound galloping condition for the bend by looking into how the greyhounds enter and exit the first bend. The histogram plots show the percentage of greyhounds and their corresponding transition lengths. As greyhounds come into contact with the bend from the straight section of the track and also move from bend to straight the greyhounds make a gradual transition from the straight to the constant radius bend as depicted in the histograms. This motion transition is measured in the distance travelled during this phase. A longer transition is usually related to less jerk (m/s) in comparison to a shorter transition.
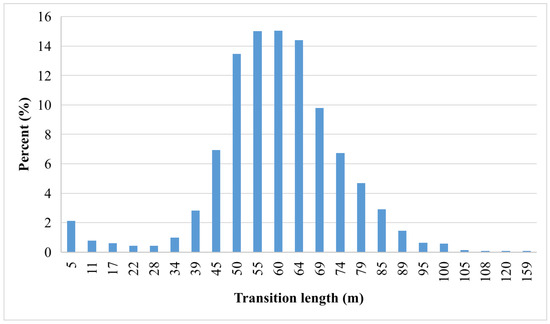
Figure 5.
Histogram of greyhound motion transitions versus percent of the entire 2986 greyhounds entering the bend from the straight section of the track.
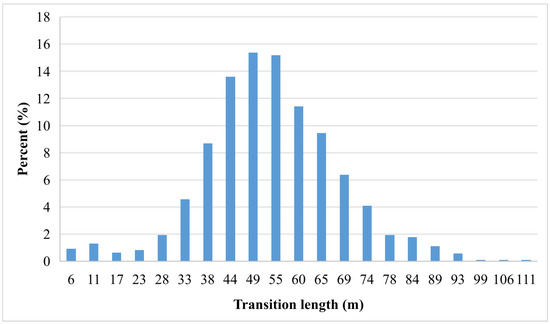
Figure 6.
Histogram of greyhound motion transitions versus percent of the entire 2986 greyhounds exiting the bend into the straight section of the track.
Figure 7 and Figure 8 depict greyhound transition standard deviation values from the curvature rate of each transition for entering and exiting the bend respectively. The standard deviation of curvature rate shows smoothness or perfectness of greyhound transition in comparison to a standard Euler spiral transition. In a Euler spiral transition the standard deviation of the curvature rate is zero as the curvature changes gradually with the distance. Thus, the standard deviation of the curvature rate was used for verifying the accuracy of the greyhound data models used for transition length calculations.
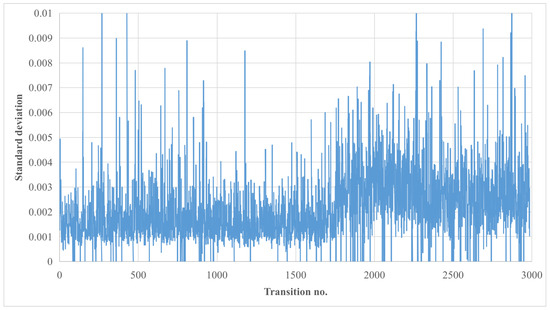
Figure 7.
Standard deviation plot of curvature rate per stride for greyhounds entering the bend transition for the entire 2986 greyhound population.
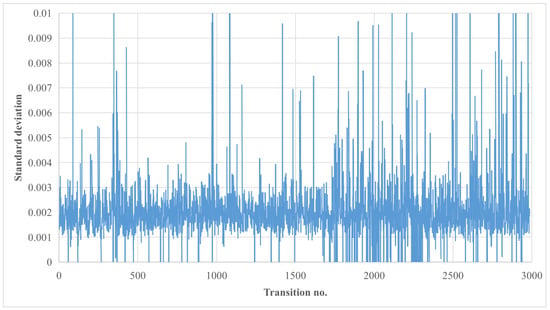
Figure 8.
Standard deviation plot of curvature rate per stride for greyhounds exiting the bend transition for the entire 2986 greyhound population.
Table 3 and Table 4 show the comparison of greyhound starting box and corresponding major transition length groups for going into and coming out of the bend where the number of greyhounds is greater than 13. The presented data in both tables show that each starting box has a different number of greyhounds for the similar and unique level of transition lengths.

Table 3.
Greyhound transition length groups and corresponding greyhound numbers for entering the bend, where: TL = transition length (m); and N = numbers of greyhounds.

Table 4.
Greyhound transition length groups and corresponding greyhound numbers for exiting the bend, where: TL = transition length (m); and N = numbers of greyhounds.
6.2. Greyhound Galloping Energy State Tendency Inside the Bend
Figure 9 illustrates a plot of local maxima and minima points of greyhound state variable ratio turning radius over speed for inside the bend. From the 2986 greyhound starts, there were 14,775 points where each point measuring either high or low dynamic condition experienced by the greyhound. The plot also depicts an exponential trend-line showing the trend in the data points.
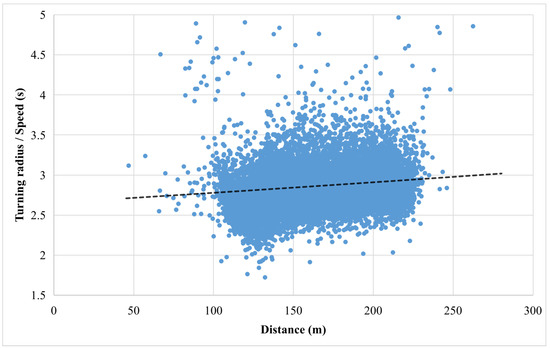
Figure 9.
The plot of local maxima and minima points of greyhound state variable ratio turning radius over speed inside the bend and trend line comprising 14,775 points from the total greyhound population.
7. Discussion
As can be seen from Figure 5 and Figure 6, greyhounds made various transition paths for going into and coming out of the track bend. Without considering the straight section of the track these transitions roughly emulate Euler transitions as their curvature is linearly changing as found by the pattern matching algorithm. For horses, it was found that duty factor an important measure in gait was affected by the centripetal acceleration where it was shown that there was a decreasing relationship with increasing centripetal acceleration [20]. Thus, for the greyhounds it would be also an important validating measure to consider and find out duty factor of greyhound in the changing centripetal acceleration as it happens during the transition paths. For going into the bend the four major transition groups were 50 m, 55 m, 60 m and 64 m length transitions where more than 57% of greyhounds took these transition paths for entering the bend. Roughly 7% of greyhounds chose a 45 m transition. Very few greyhounds chose transitions between 10 m and 35 m. It should be understood that these transitions under 20 m represent high jerk values. At the same time, small transitions also could influence the mechanical energy of the galloping gait as the greyhound would need to work harder with every stride to quickly transition into a smaller turning radius. In a study of mechanical energy for horses fluctuation of mechanical energy was observed during the stride cycle showing an energy rise prior to and throughout hind foot contact [2]. Now, if the greyhound suddenly changes its direction from a 1000 m radius to 51 m radius turn in one stride the centrifugal jerk value would be greater than 20 m/s. This is assuming the greyhound was moving with a speed greater than 19 m/s. More than 24% of all greyhounds made a long transition of 65 m representing a low jerk path for these greyhounds. Very few greyhounds took transitions greater than 85 m in length. For coming out of the bend the three major transition groups were 44 m, 49 m and 55 m length transitions where more than 44% of greyhounds took these transition paths for leaving the bend. More than 8% of greyhounds chose a 38 m transition whereas small groups of greyhounds took transitions under a 35 m length. For long transitions, 27% of greyhounds utilised transitions greater than 60 m. Finally, small groups of greyhounds went with transitions greater than 70 m. A detailed view of greyhound transitions relating to each starting box of eight race starts can be seen from the Table 3 and Table 4.
As can be seen from the table for entering the bend, starting box one greyhounds which were closest to the track inside edge took the shortest transitions among all the starting boxes. On the other hand, no such pattern can be found for the greyhounds coming out of the bend.
It is evident from the analysis that, the major groups of greyhounds that entered the bend took longer transitions compared to the major groups of greyhounds that exited the bend. As can be seen from the transition length plots, the lowest of the groups for entering the bend was the 50 m transition group whereas the lowest of the groups for leaving the bend was the 44 m transition group. With these levels of motion transitions the greyhounds were experiencing jerk values between 2.9 m/s and 3.3 m/s for entering and leaving the bend respectively. It should be noted that when entering the bend greyhound speed was higher compared to leaving the bend. So, it seems that the greyhounds balanced the force of jerk and related rigid body vibration according to their speed. A greyhound’s musculoskeletal system can not be considered a purely rigid body as such as there are shock absorption capabilities and other damping capabilities within the body to minimise the vibration level. The rigid part of the musculoskeletal system can definitely be affected by the jerk and related vibration which can disorient greyhound gait and galloping balance. Likewise, the weak portion of the musculoskeletal system can be greatly affected from the jerk level experienced by the greyhound. For smaller transition groups a larger percentage of greyhounds took transitions below 40 m for exiting the bend compared entering the bend. Also, the transitions between 10 m and 25 m were the lowest occurring transitions where each transition group represented under one percent to around one percent of greyhounds.
As can be seen from Figure 7 and Figure 8 the standard deviation of curvature rate from one stride to the next stride was under 0.01 averaging at around 0.002 for all the 2987 greyhound transitions for both entering and exiting the bend. This shows that the transitions that all the greyhounds closely conformed to Euler transition types having zero standard deviation. Furthermore, by following a close to linearly variable curvature the greyhounds managed their rigid body vibration to a minimal level acceptable to their musculoskeletal system. Since the tracks on which greyhounds were galloping were sandy loam surfaces the level of torsional and shear friction provided to the paw can be directly co-related to the level of curvature rate variation the greyhound managed to maintain. A different type of track surface might provide the greyhound with finer control of curvature rate variation reducing the rigid body vibration and jerk level.
As shown in Figure 9, the greyhound dynamic state of lowest and highest turning radius points for inside bend intermediate transitions there was an upward trend in the dynamic state of the greyhounds. The covariance of local maxima and minima points was 496 where at the beginning of the bend the greyhound state variable ratio was under 2.8 s and at the end of the bend, it was above 3.0 s. This indicates the low or relaxed dynamic condition for the second half of the bend compared to the first half of the bend.
8. Conclusions and Future Work
The research presented in this paper provides valuable and significant insights into greyhound bend galloping motion conditions by optimally processing and analysing greyhound racing data containing planner XY locations from three different tracks and from 2986 greyhounds. The results presented provide a highly detailed view of the straight to bend transition paths taken by galloping greyhounds when navigating their way around the bend. By investigating the greyhound dynamic state variables ratio it was shown that the greyhound’s galloping lateral dynamics condition was less intense as it moved past the second half of the bend. Moreover, with the help of curvature rate analysis, it was shown that greyhound galloping transition run paths were smooth having very low standard deviations just under 0.01 for entering into and exiting the bend. Both the path transition levels and curvature rate of greyhound galloping show that greyhounds minimised their motion vibration source such as jerks in their gait.
One limitation of this study was of alignment of the sensor outputs that gathered XY locations data. The transmitting sensors gave relative XY data instead of one-to-one matching to track layout survey data. Also, in the data noise levels were time-varying. In the data processing, relative analysis was conducted and also clean data was picked from the data poll to minimise data variations due to sensor output formats.
Future research of a similar nature considering different and broader aspects of bend galloping conditions can be carried out to develop a better understanding of bend galloping motion path conditions. With the availability of new and more precise data sets and a proper understanding of raw data mapping to real-world dynamics, it can be said that the future of quadruped bend motion dynamics research is promising.
Author Contributions
Conceptualization, D.E. and I.H.; methodology, I.H.; software, I.H.; validation, I.H.; formal analysis, I.H.; investigation, D.E. and I.H.; resources, D.E., I.H. and C.B.; data curation, C.B. and I.H.; writing—original draft preparation, I.H. and D.E.; writing—review and editing, D.E. and I.H.; visualization, I.H.; supervision, D.E.; project administration, D.E.; funding acquisition, D.E. All authors have read and agreed to the published version of the manuscript.
Funding
This research was internally funded by the University of Technology Sydney.
Acknowledgments
The authors would like to thank Greyhound Racing Victoria for access to the greyhound racing data. In particular the authors thank Glenn Fish for his invaluable assistance. They also acknowledge the ongoing assistance provided by Brook Racing and Sporting Technology.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| CoM | centre of mass |
| Jerk | centrifugal changing in acceleration (m/s) |
| g-force | force measured as a ratio to gravity |
| GRV | Greyhound Racing Victoria |
| TPs | transition points |
| XY | relative X and Y coordinates |
References
- Usherwood, J.R.; Wilson, A.M. No force limit on greyhound sprint speed. Nature 2005, 438, 753–754. [Google Scholar] [CrossRef] [PubMed]
- Pfau, T.; Witte, T.H.; Wilson, A.M. Centre of mass movement and mechanical energy fluctuation during gallop locomotion in the thoroughbred racehorse. J. Exp. Biol. 2006, 209, 3742–3757. [Google Scholar] [CrossRef] [PubMed]
- Churchill, S.M.; Salo, A.I.; Trewartha, G. The effect of the bend on technique and performance during maximal effort sprinting. Sports Biomech. 2015, 14, 106–121. [Google Scholar] [CrossRef] [PubMed]
- Churchill, S.M.; Trewartha, G.; Salo, A.I. Bend sprinting performance: New insights into the effect of running lane. Sports Biomech. 2018, 18, 437–447. [Google Scholar] [CrossRef] [PubMed]
- Hayati, H.; Eager, D.; Jusufi, A.; Brown, T. A study of rapid tetrapod running and turning dynamics utilizing inertial measurement units in greyhound sprinting. In Proceedings of the ASME-IDETC/CIE29017, American Society of Mechanical Engineers, Cleveland, OH, USA, 6–9 August 2017. [Google Scholar]
- Hayati, H.; Walker, P.; Mahdavi, F.; Stephenson, R.; Brown, T.; Eager, D. A comparative study of rapid quadrupedal sprinting and turning dynamics on different terrains and conditions: Racing greyhounds galloping dynamics. In Proceedings of the IMECE2018, American Society of Mechanical Engineers, Pittsburgh, PA, USA, 9–15 November 2018. [Google Scholar]
- Hayati, H.; Mahdavi, F.; Eager, D. Analysis of agile canine gait characteristics using accelerometry. Sensors 2019, 19, 4379. [Google Scholar] [CrossRef] [PubMed]
- Hudson, P.E.; Corr, S.A.; Wilson, A.M. High speed galloping in the cheetah (Acinonyx jubatus) and the racing greyhound (Canis familiaris): Spatio-temporal and kinetic characteristics. J. Exp. Biol. 2012, 215, 2425–2434. [Google Scholar] [CrossRef] [PubMed]
- Hayati, H.; Eager, D.; Jusufi, A.; Brown, T. Stride length as a speed indicator in fast quadrupeds. In Proceedings of the International Society of Biomechanics (ISB 2017), Brisbane, Australia, 23–27 July 2017. [Google Scholar]
- Mahdavi, F.; Hossain, M.I.; Hayati, H.; Eager, D.; Kennedy, P. Track shape, resulting dynamics and injury rates of greyhounds. In Proceedings of the ASME International Mechanical Engineering Congress and Exposition, American Society of Mechanical Engineers, Pittsburgh, Pennsylvania, USA, 9–15 November 2018; Volume 52187, p. V013T05A018. [Google Scholar]
- Hayati, H.; Eager, D.; Stevenson, R.; Brown, T.; Arnott, E. The impact of track related parameters on catastrophic injury rate of racing greyhounds. In Proceedings of the 9th Australian Congress on Applied Mechanics ACAM9, Sydney, Australia, 27–29 November 2017. [Google Scholar]
- Hayati, H.; Eager, D.; Peham, C.; Qi, Y. Dynamic behaviour of high performance of sand surfaces used in the sports industry. Vibration 2020, 3, 410–424. [Google Scholar] [CrossRef]
- Groizard, J. Greyhounds and racing industry participants: A Look at the new south Wales greyhound racing community. Anim. Stud. J. 2019, 8, 133–157. [Google Scholar]
- Eager, D.; Zhou, S.; Hossain, I.; Ishac, K.; Halkon, B. Research on impact attenuation characteristics of greyhound racing track padding for injury prevention. Vibration 2022, 5, 497–512. [Google Scholar] [CrossRef]
- Hayati, H.; Eager, D.; Pendrill, A.M.; Alberg, H. Jerk within the context of science and engineering—A systematic review. Vibration 2020, 3, 371–409. [Google Scholar] [CrossRef]
- Eager, D.; Hossain, I.; Ishac, K.; Robins, S. Analysis of racing greyhound path following dynamics using a tracking system. Animals 2021, 11, 2687. [Google Scholar] [CrossRef]
- Hossain, M.I.; Eager, D.; Walker, P.D. Greyhound racing ideal trajectory path generation for straight to bend based on jerk rate minimization. Sci. Rep. 2020, 10, 7088. [Google Scholar] [CrossRef] [PubMed]
- Fílter, A.; Olivares, J.; Santalla, A.; Nakamura, F.Y.; Loturco, I.; Requena, B. New curve sprint test for soccer players: Reliability and relationship with linear sprint. J. Sport. Sci. 2020, 38, 1320–1325. [Google Scholar] [CrossRef] [PubMed]
- Ato, M.; Lopez, J.J.; Benavente, A. A classification system for research designs in psychology. Anales de Psicología 2013, 29, 1038–1059. [Google Scholar]
- Parkes, R.S.; Pfau, T.; Weller, R.; Witte, T.H. The effect of curve running on distal limb kinematics in the thoroughbred racehorse. PLoS ONE 2020, 15, e0244105. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).