1. Introduction
Several passive control systems have been used in past studies to attenuate vibrations of structures and machines. Particle dampers belong in these systems, and their attractiveness [
1,
2,
3,
4,
5,
6,
7,
8,
9,
10,
11,
12,
13,
14,
15,
16] is based on their simplicity, low cost, and effectiveness in reducing the dynamic response of mechanical systems and machines. Lately, their use has been extended in the civil engineering area [
17].
Particle dampers can have different forms. They can consist of free-moving particles either inside a container attached to a structure or inside cavities at specific parts of the structure. They can attenuate the response of structures due to momentum transfer and energy absorption during collisions of the particles with the walls of the container and among themselves. Their performance is influenced by the mass ratio (the mass of particles with respect to the mass of the primary system), the amplitude and frequency content of the excitation signal, the size of the container, and the material of the particles.
The container usually consists of a single compartment or is divided into equally sized compartments. Papalou [
18] divided the container in two unequal size compartments in order to reduce the effect of the level of the excitation on the effectiveness of the particle damper. A small and a large compartment were used with filling area ratios (FARs) in the range of 50–70% to attenuate the response of structures. The FAR was defined for a single layer of particles as the total area the particles occupy considered as squares (with sides equal to the diameter of the particles) divided by the area of the compartment. It was found that for structures with low natural frequencies (in the typical range of mid- to high-level buildings) equipped with particle dampers having either equally sized compartments with FARs of 50–60% or unequally sized compartments (a small and a large one) with FARs in the range of 50–70%, can reduce considerably the response of structures for a wide range of excitation levels.
Inspired from previous research, it was decided to assess whether using more than two compartments of unequal size (where there will be at least one large compartment where the particles have a lot of space to move, a compartment with medium space, and one with small space) will further improve the performance of the damper. A particle damper with four compartments of unequal size was used with filling area ratios in the 40–70% range. The performance of a particle damper with this particular configuration was examined in reducing dynamic vibrations. Initially, a small symmetric single-story structure including the container (primary system) without the moving particles was excited by random excitation, considering different levels of intensity. In the next step, the particles were placed inside the compartments and the structure was excited with the same excitations. The results of the two sets of experiments were compared. In addition, earthquake excitation signals were used to verify the previous results. The results were compared with those obtained using a single damper with two equally and two unequally sized compartments.
As mentioned previously, several parameters influence the behavior of particle dampers. The focus of this investigation was on the layout of the container considering four unequally sized compartments properly selected in order to minimize the effect of the amplitude of the excitation. For this reason, the mass ratio, the size, and the material of the particles remained constant through all the experiments.
2. Experimental Setup and Testing
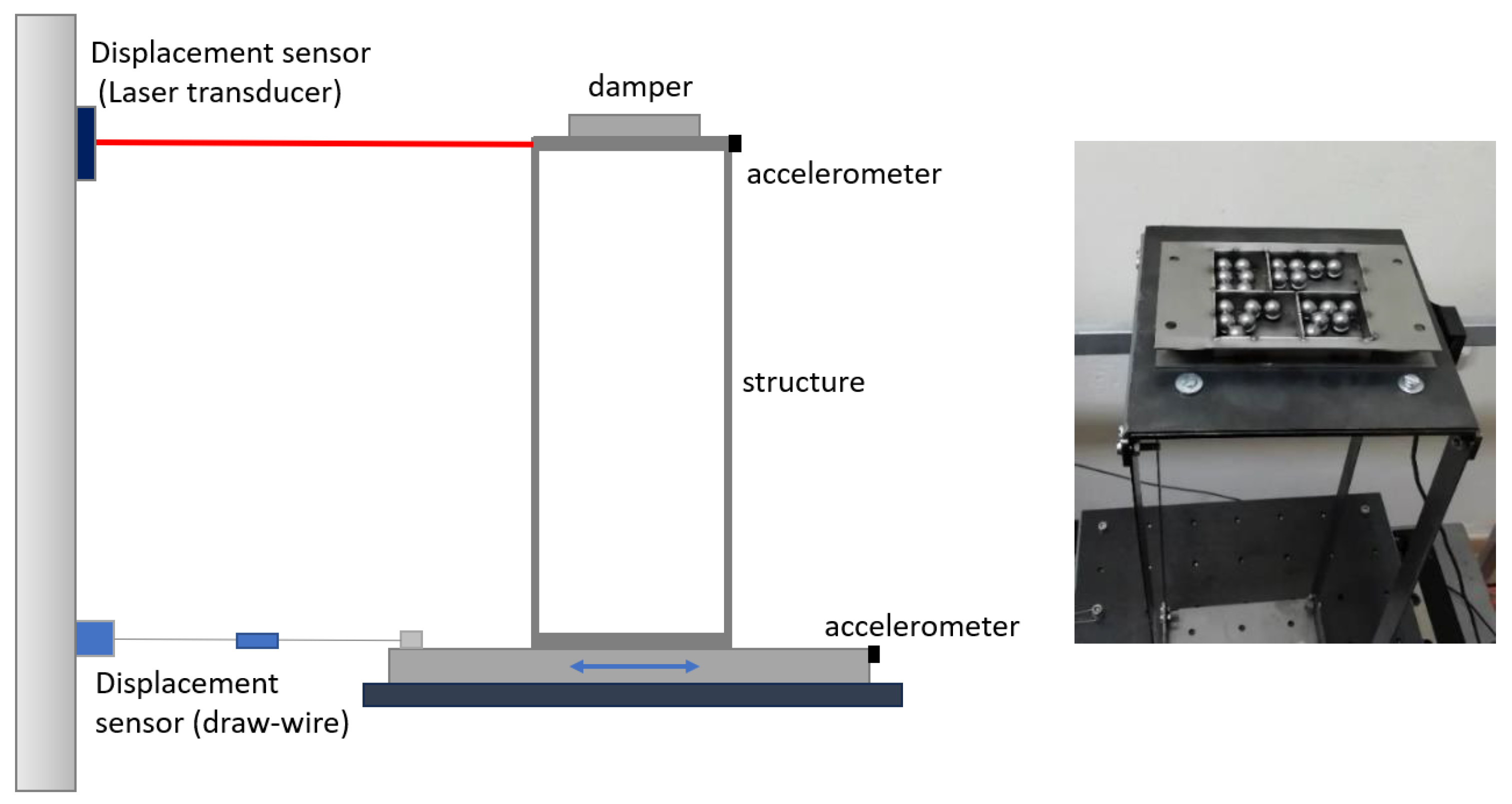
The experimental setup included a single-story steel structure, a multi-compartment particle damper, a shake table, instruments to measure the motion of the base and of the structure, a data acquisition system, and a computer to control the process.
The structure consisted of four columns of the same dimensions which were attached on two steel plates (
Figure 1). An additional mass was added on the top plate to reduce the natural frequency of the structure. The bottom plate was mounted on a uniaxial shake table. The vibrating mass was 1.5 kg, the natural frequency was 2.3 Hz, and the damping ratio was approximately 2%.
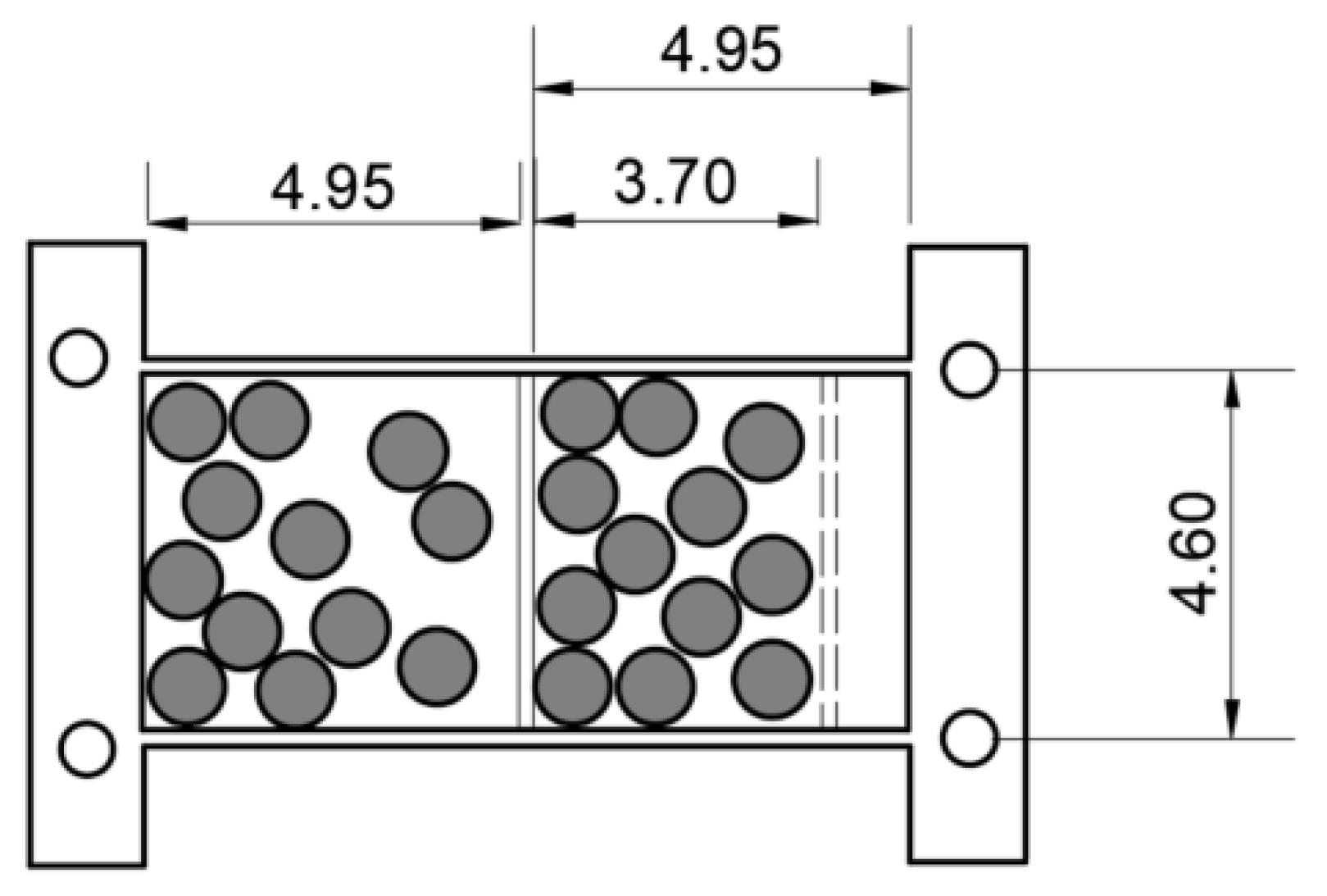
The particle damper, which consisted of four-unequal in size compartments, was attached to the top plate of the structure (
Figure 1). The FAR values that were used were approximately 40%, 50%, 60%, and 70%.
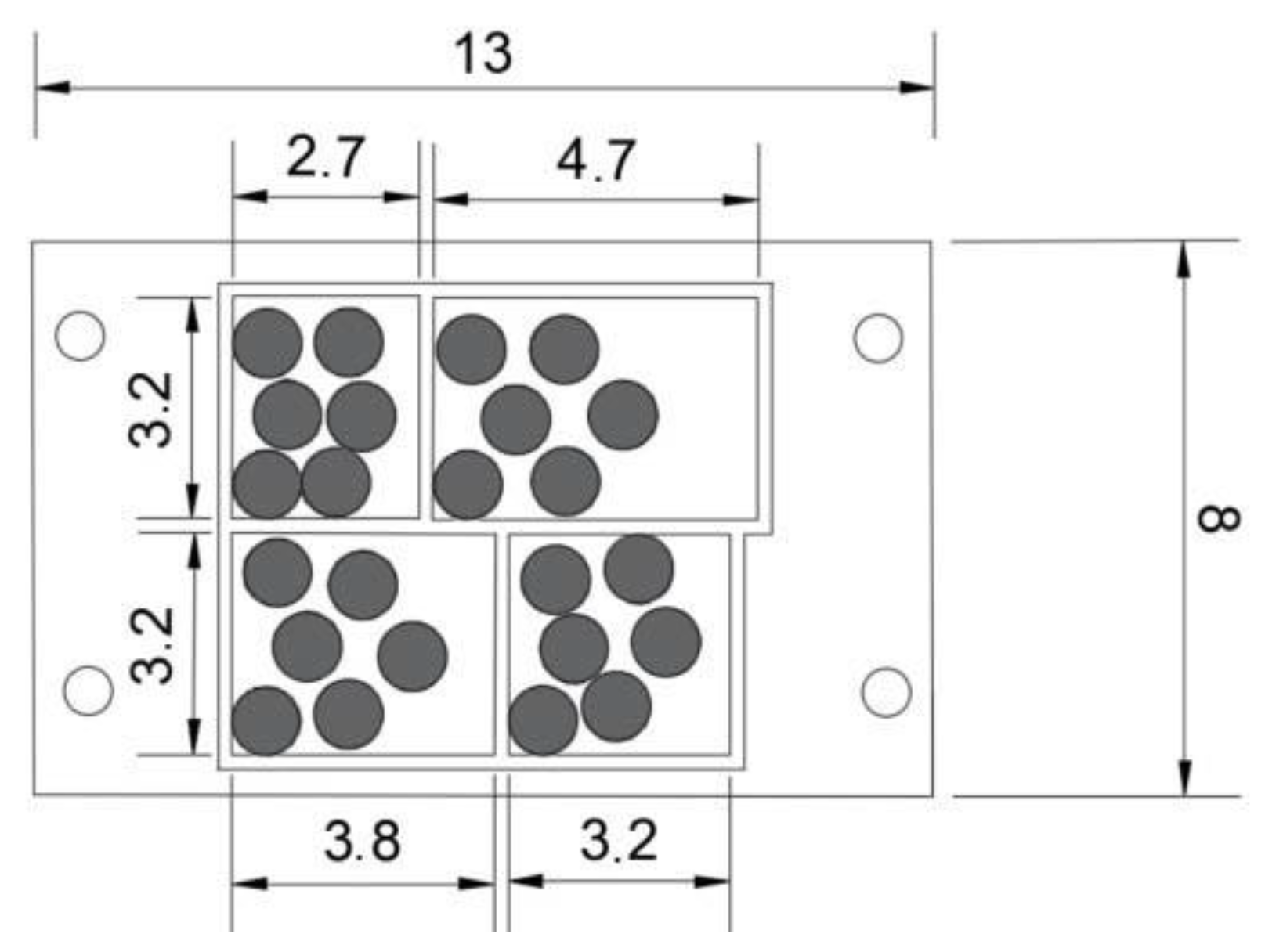
Figure 2 presents the size of each compartment. Twenty-four steel spherical particles of 1 cm in diameter were used, producing a mass ratio (mass of particles to the mass of the structure) equal to 6.6%. The particles were equally divided and placed in each of the four compartments without any order. The number of particles and their size were selected in order to obtain the aforementioned FAR values, creating a single layer of particles which is recommended for structures with low natural frequency (Papalou 2018).
The motion of the structure was measured by a laser transducer and an accelerometer, while the motion of the base was measured by a draw-wire sensor and an accelerometer (
Figure 1). A random signal, with frequency band from 0 to 10 Hz, with increasing intensity was used as an excitation signal (
Figure 3). Five levels of excitation were used. The larger value (EL V) was 3 times higher than the smaller value (EL I). The rest of the levels were 1.5, 2, and 2.5 times higher than the smaller one.
In the first set of experiments, the response of the structure was measured without the damper operating (without the particles). Subsequently, the particles were placed inside the compartments and the tests were repeated.
The performance of the four-compartment damper was compared with the performance of a damper having two unequally sized compartments with FAR values of 52% and 70% and with a damper having two equal compartments with FARs equal to 52%. The same number of particles were equally divided in the two compartments. Lastly, the effectiveness of the four-compartment damper was examined with additional tests using earthquake excitations.
3. System Response
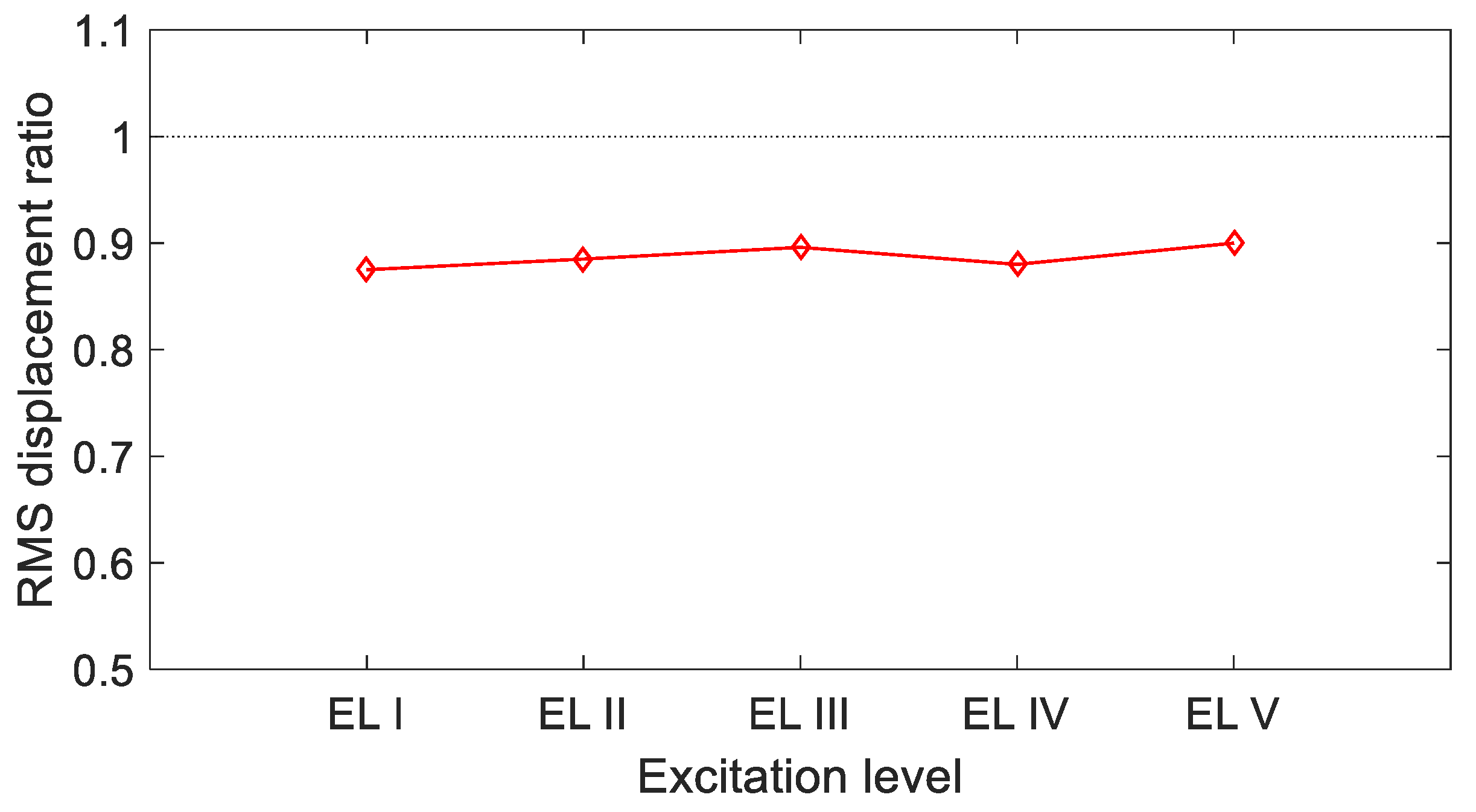
In the first set of experiments, the primary system without the particles was excited by a random signal with varying intensity. The root mean square (RMS) of the relative displacement was calculated with respect to the base (RMS displacement ratio). In the next set of experiments, the tests were repeated with the particles inside the compartments of the damper. A comparison of the results is presented in
Figure 4. The results were normalized with the response of the primary system (without the particles). Therefore, if the response is higher or lower than 1 (black dashed line in Figures), then an increase or a decrease in the response with the damper operating occurs, respectively. The damper had a consistent performance, decreasing the response of the structure by approximately 13%. The influence of the excitation level was minimal.
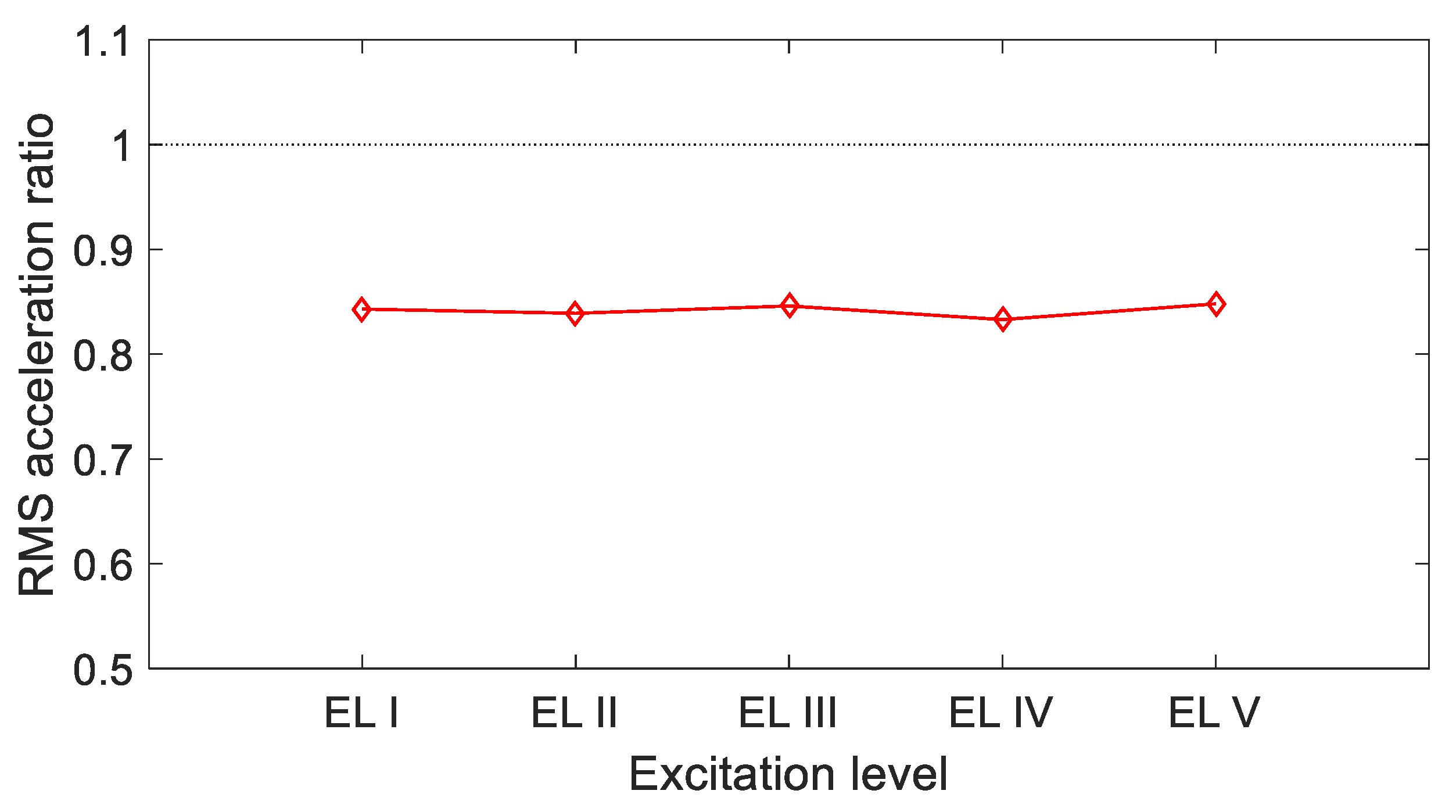
Similar behavior was observed for the response acceleration. The RMS acceleration ratio is smaller, with the damper operating reaching reduction levels up to 17% (
Figure 5). The amplitude level of the excitation did not play an important role. The different size compartments offer this benefit since each compartment can be considered as a separate particle damper, contributing more to the attenuation of the response at a specific level of excitation, giving a more consistent performance. In the small compartments (especially at high levels of excitation), the particles all moved together in the direction of excitation, with the front row hitting the two sides perpendicular to the direction of the excitation. In the larger compartments, the particles moved more freely and in all directions.
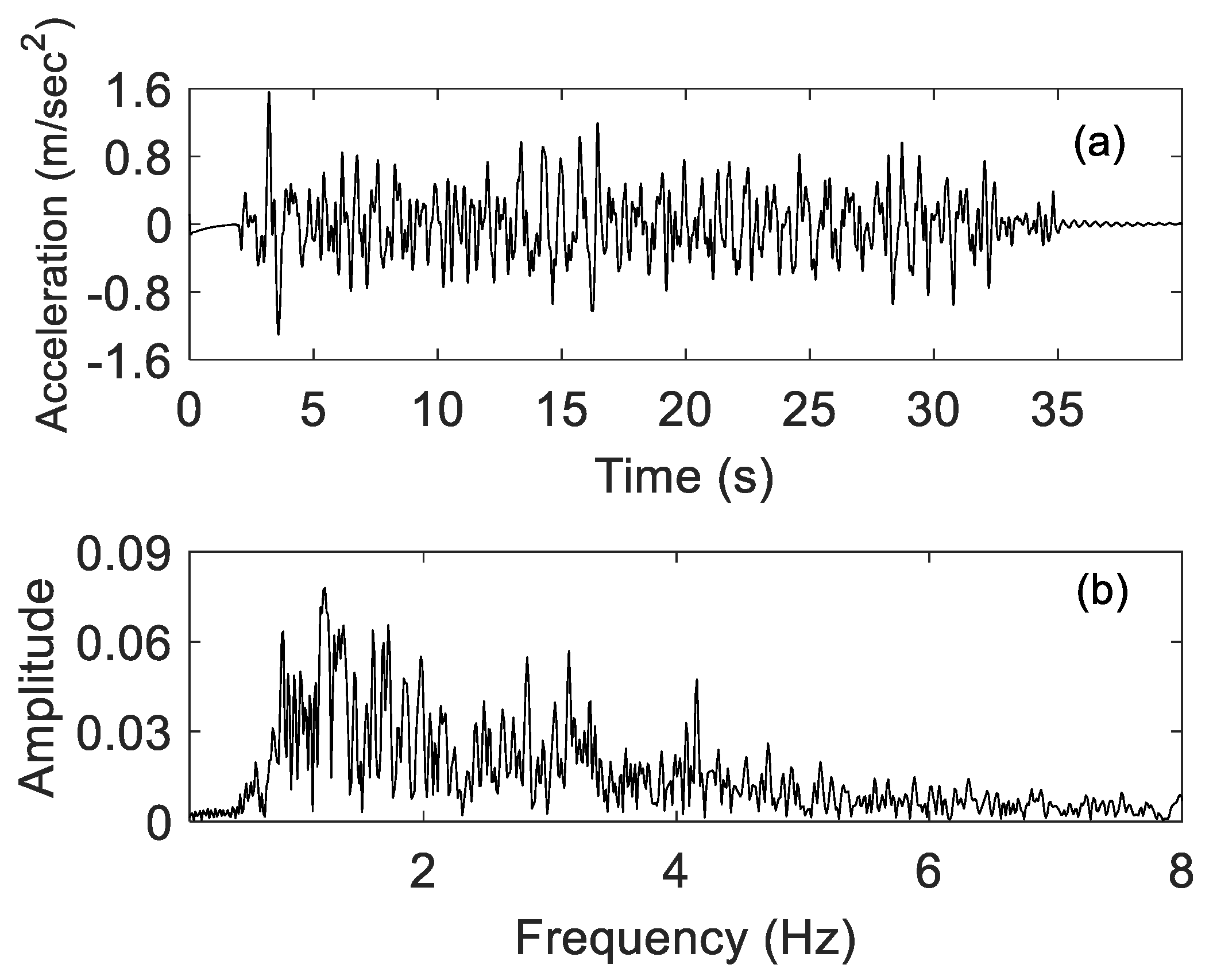
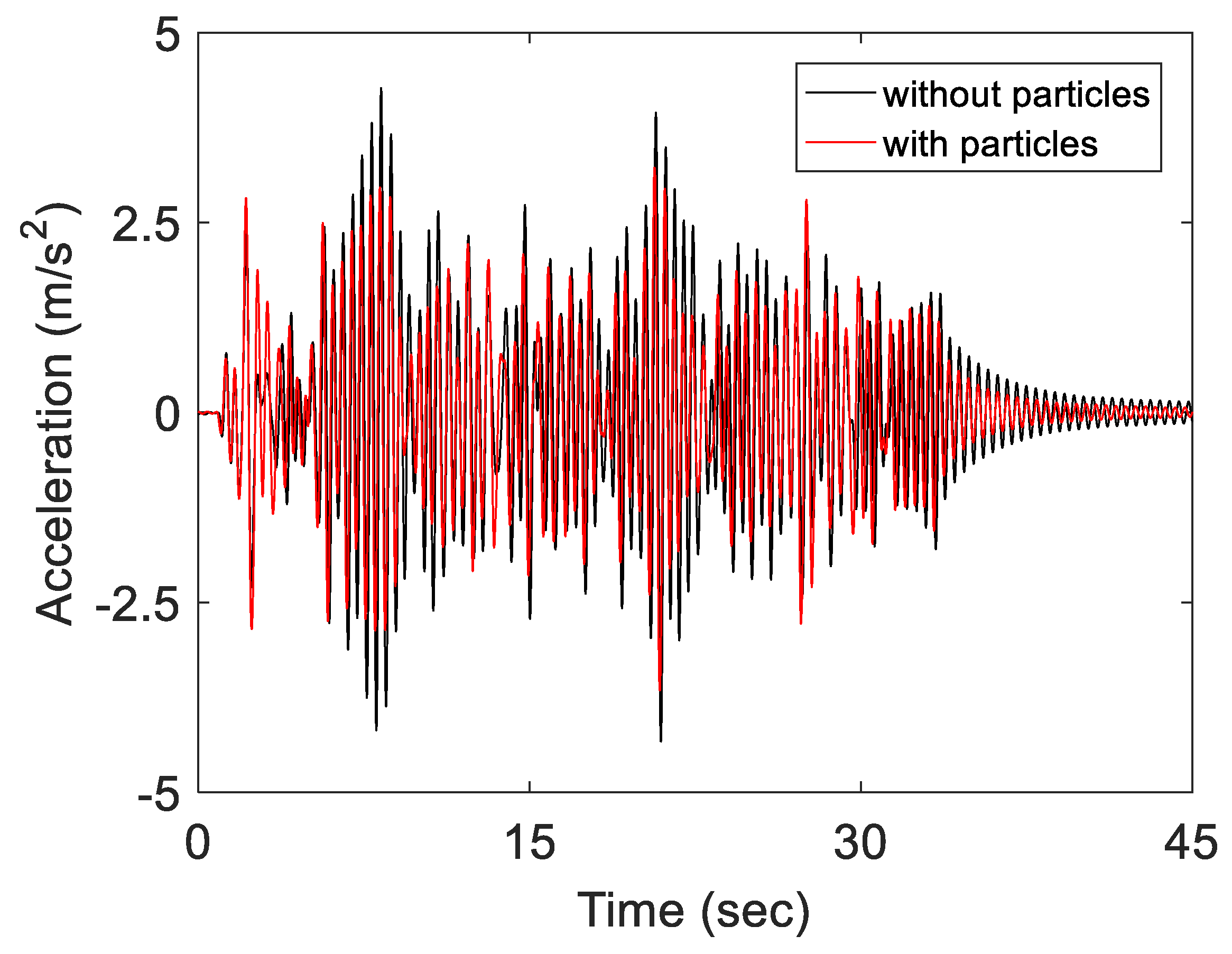
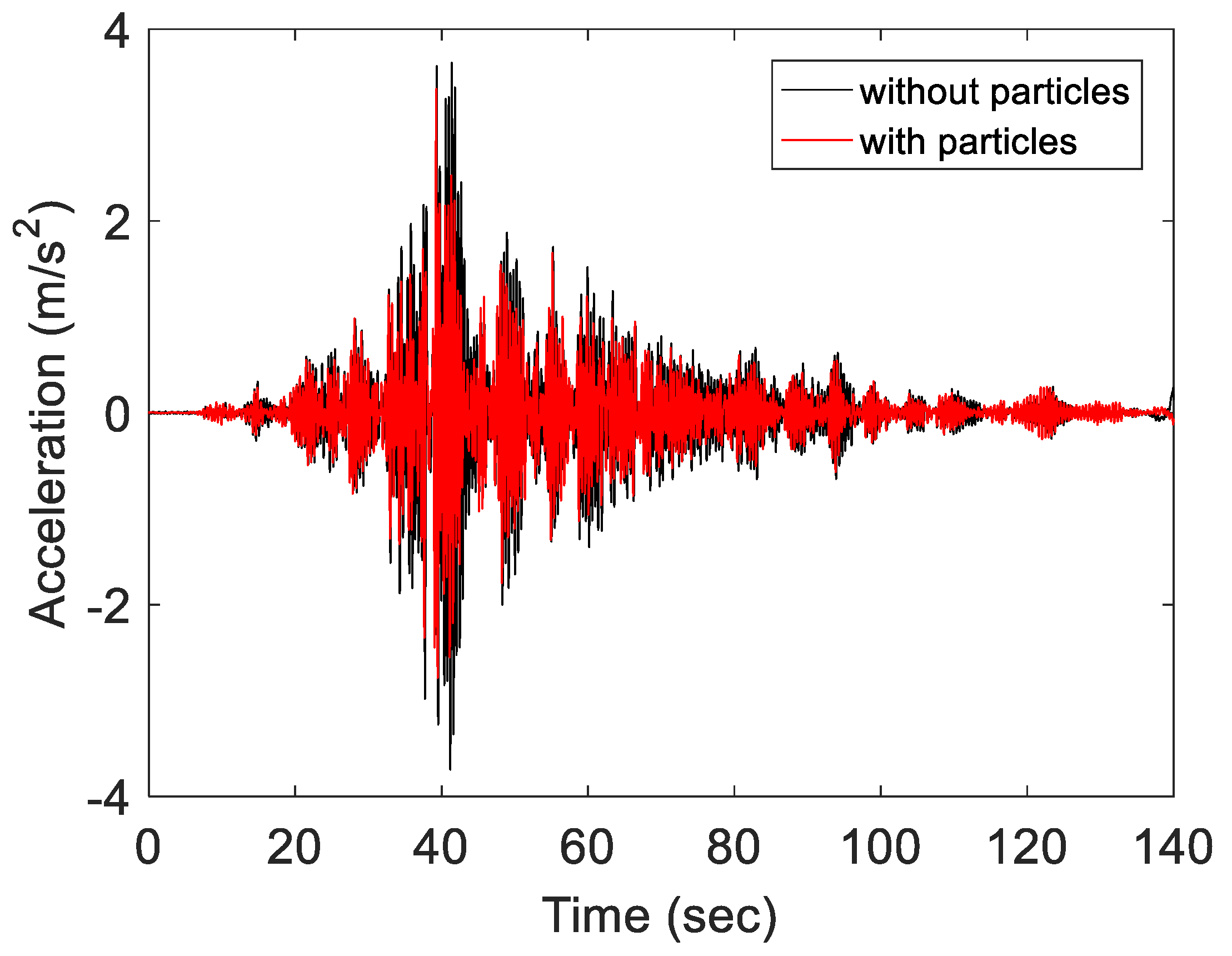
A representative time history of the response acceleration for the two sets of experiments (without and with the particles) is presented in
Figure 6 for the final level of excitation (EL V). At the beginning of the excitation, the response of the structure was not reduced, even though the damper was active. Reduction in the response occurred after the first few seconds when the motion of the structure and the impacts (between the particles and the walls of the container) increased. Considerable reduction in the response occurred when the excitation ended; the structure vibrated freely before it comes to rest.
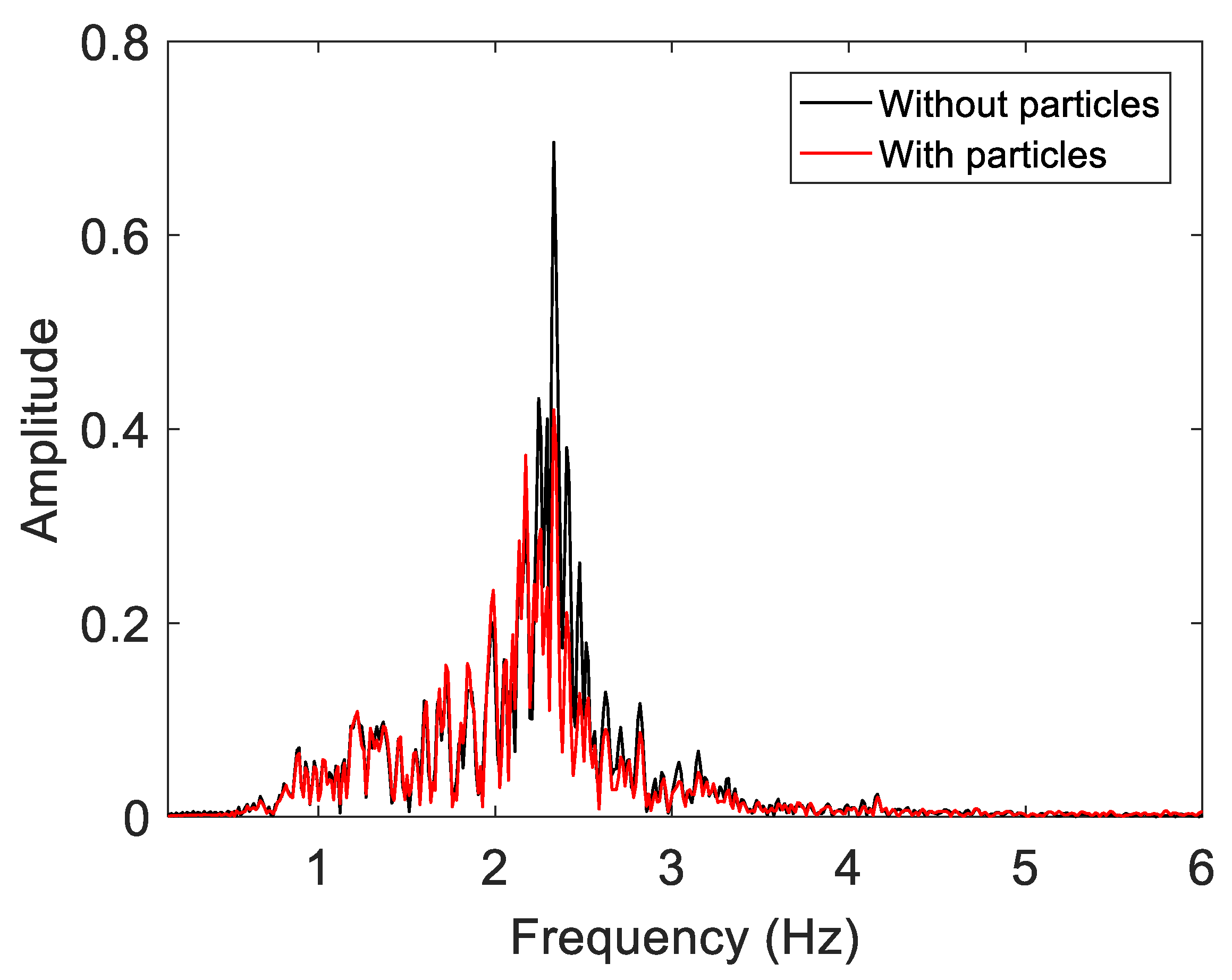
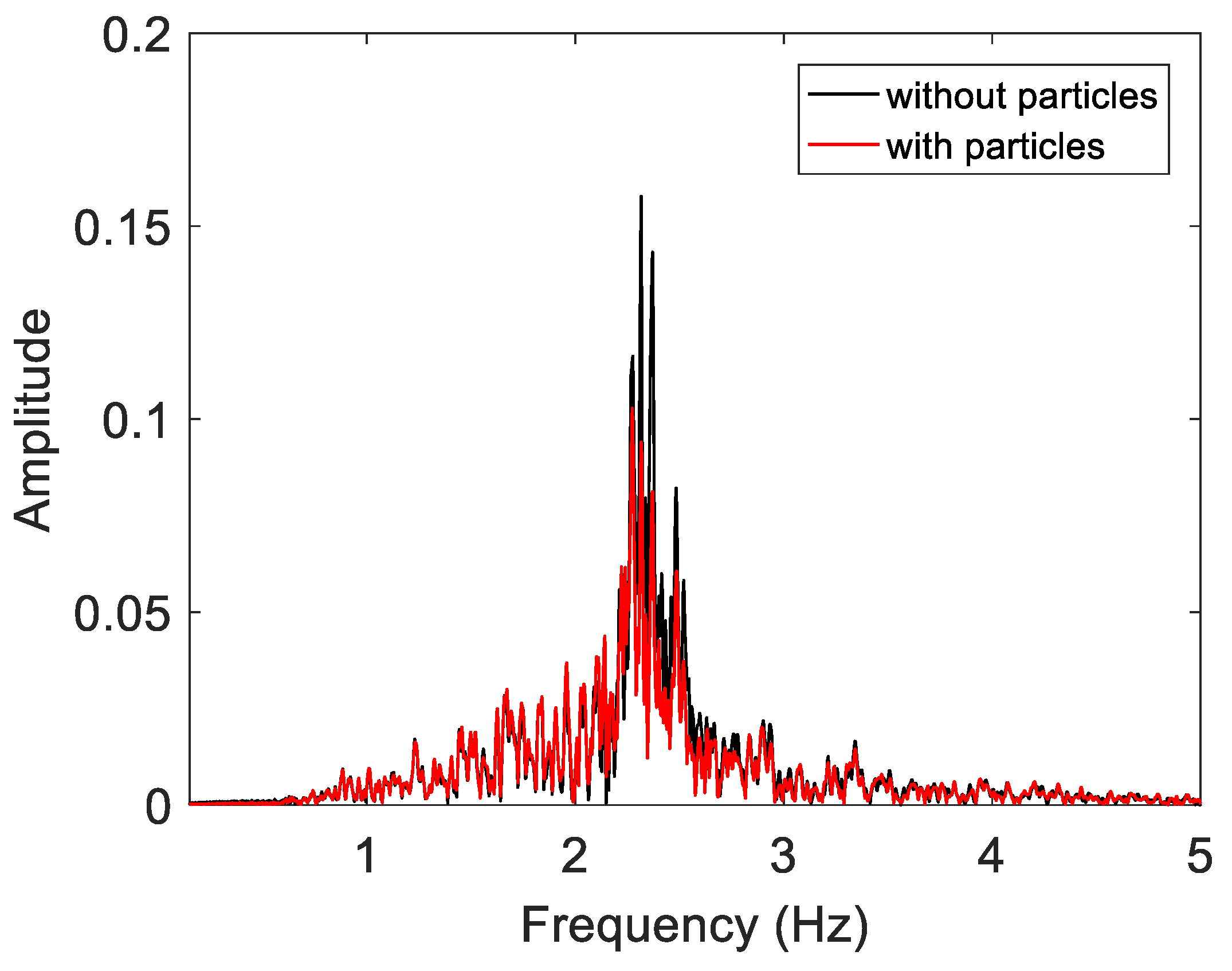
The frequency spectrum of the acceleration of the structure is presented in
Figure 7. The black curve, which corresponds to the response of the structure without the particles, peaked at the natural frequency of the system. A large reduction in the amplitude occurred with the addition of the free moving particles at the natural frequency of the structure.
The motion of the primary system (without the particles) can be expressed by the following equation:
where
m is the mass,
k the stiffness,
c is the damping coefficient,
is the relative acceleration,
is the relative velocity,
u is the relative displacement of the system with respect to the base, and
is the base acceleration. Equation (1) can be written as:
where
is the absolute acceleration of the structure and
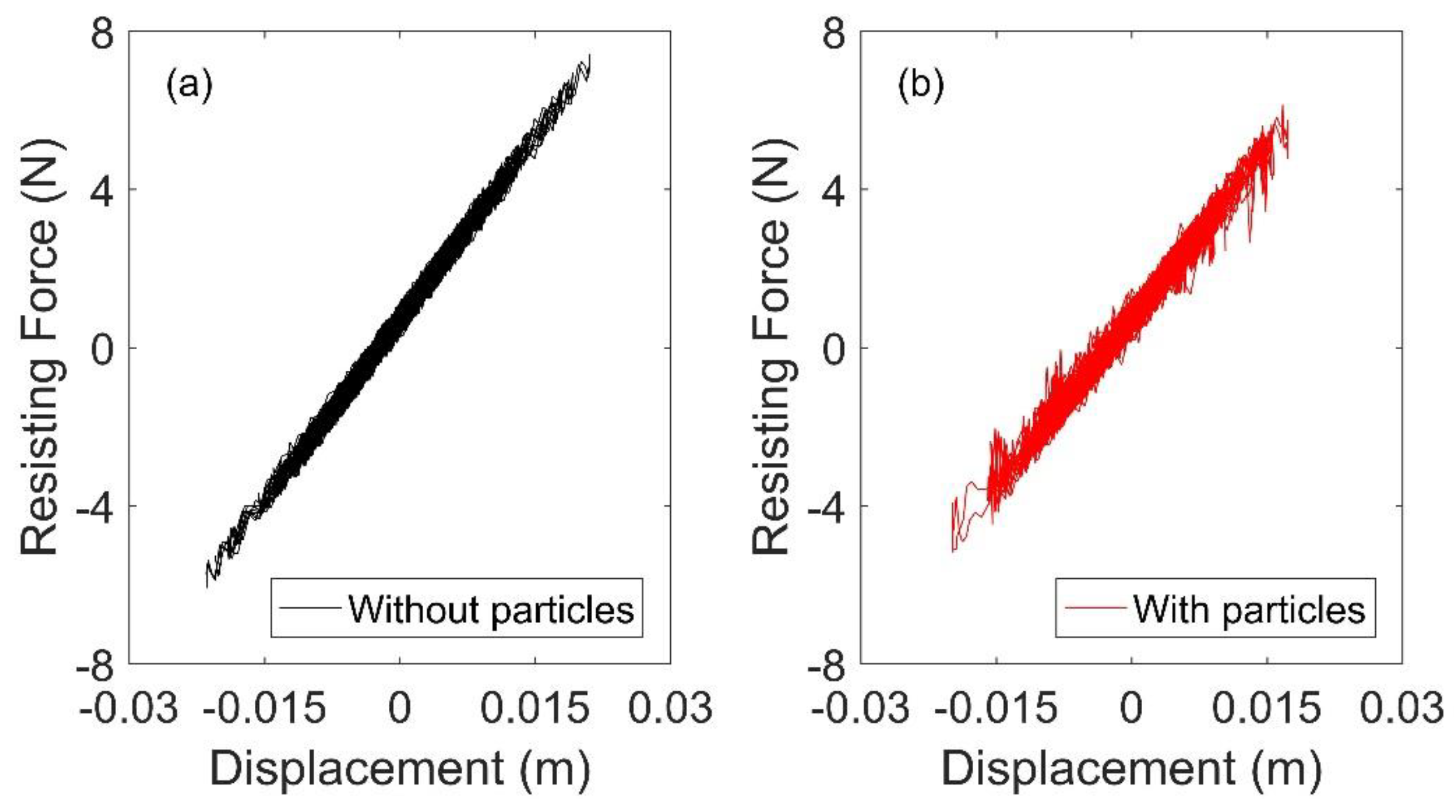
represents the resisting force. Plotting the resisting force versus the displacement, an indication of the energy absorbed during the vibration of the structure can be obtained (
Figure 8a). When the particles were added, an additional force (
Fd) resisted the motion of the structure (Equation (3)), increasing the absorbed energy, and reducing the displacement (
Figure 8b).
Fd is the contact force of the container with the particles in the direction of the motion of the structure.
The performance of the four-compartment damper was compared with the performance of a two-compartment damper. The two-compartment damper had, in the first set of experiments, two unequally sized compartments with FARs of 52% and 70%, and in the second set two equally sized compartments with FARs of 52% (
Figure 9). The total mass of the primary system remained the same. The twenty-four particles were divided equally and placed inside each compartment.
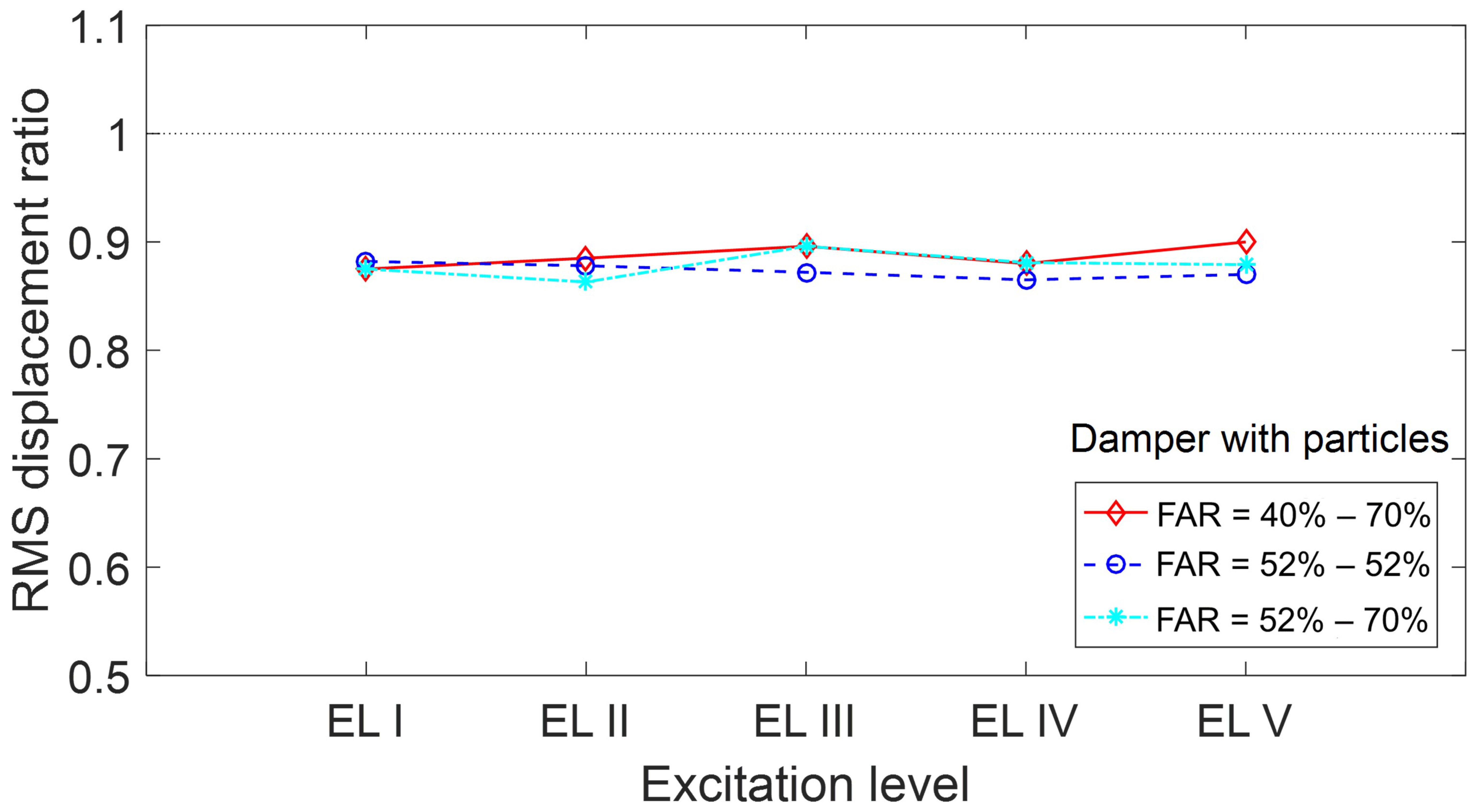
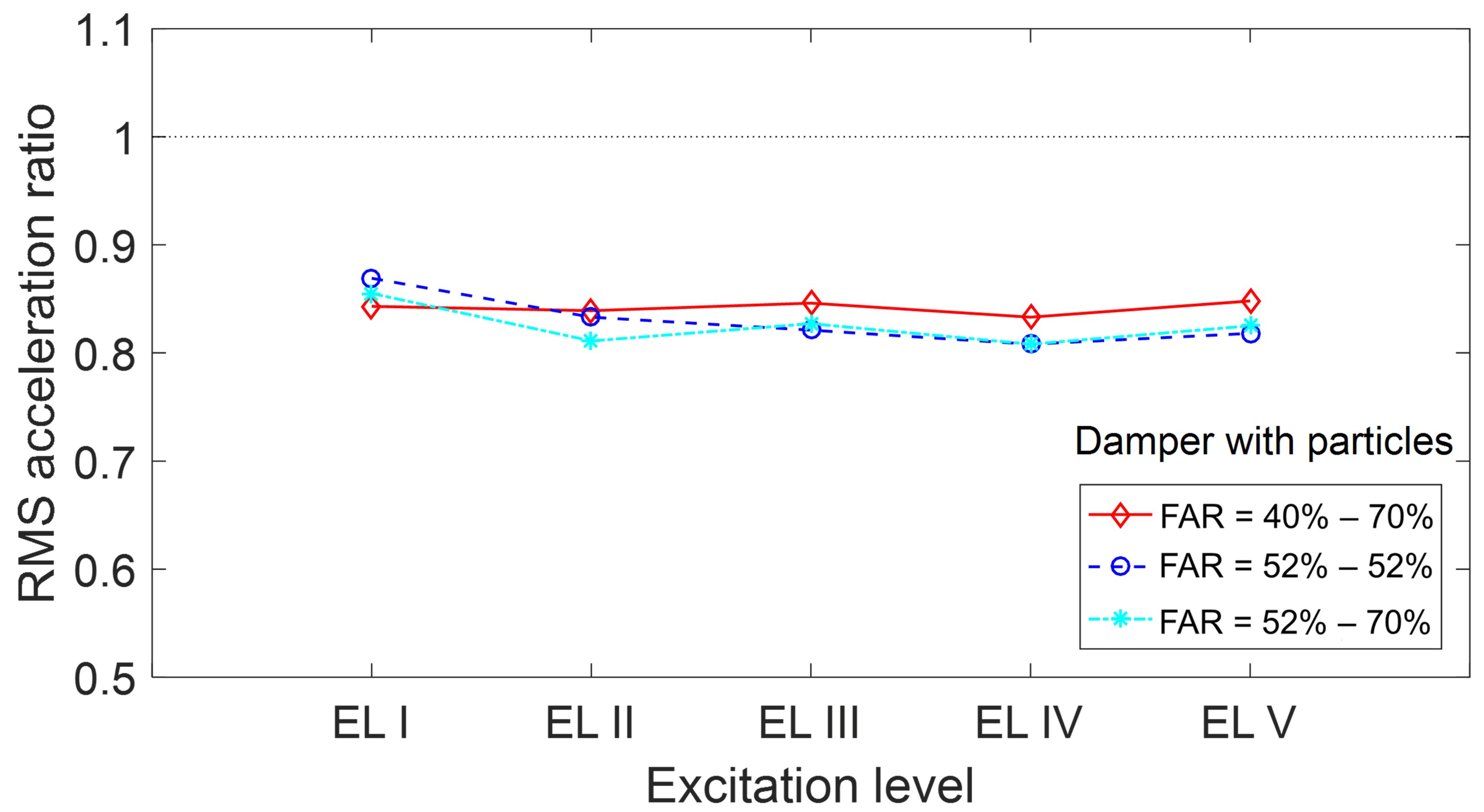
The RMS displacement ratio and acceleration ratio for different intensity levels are presented in
Figure 10 and
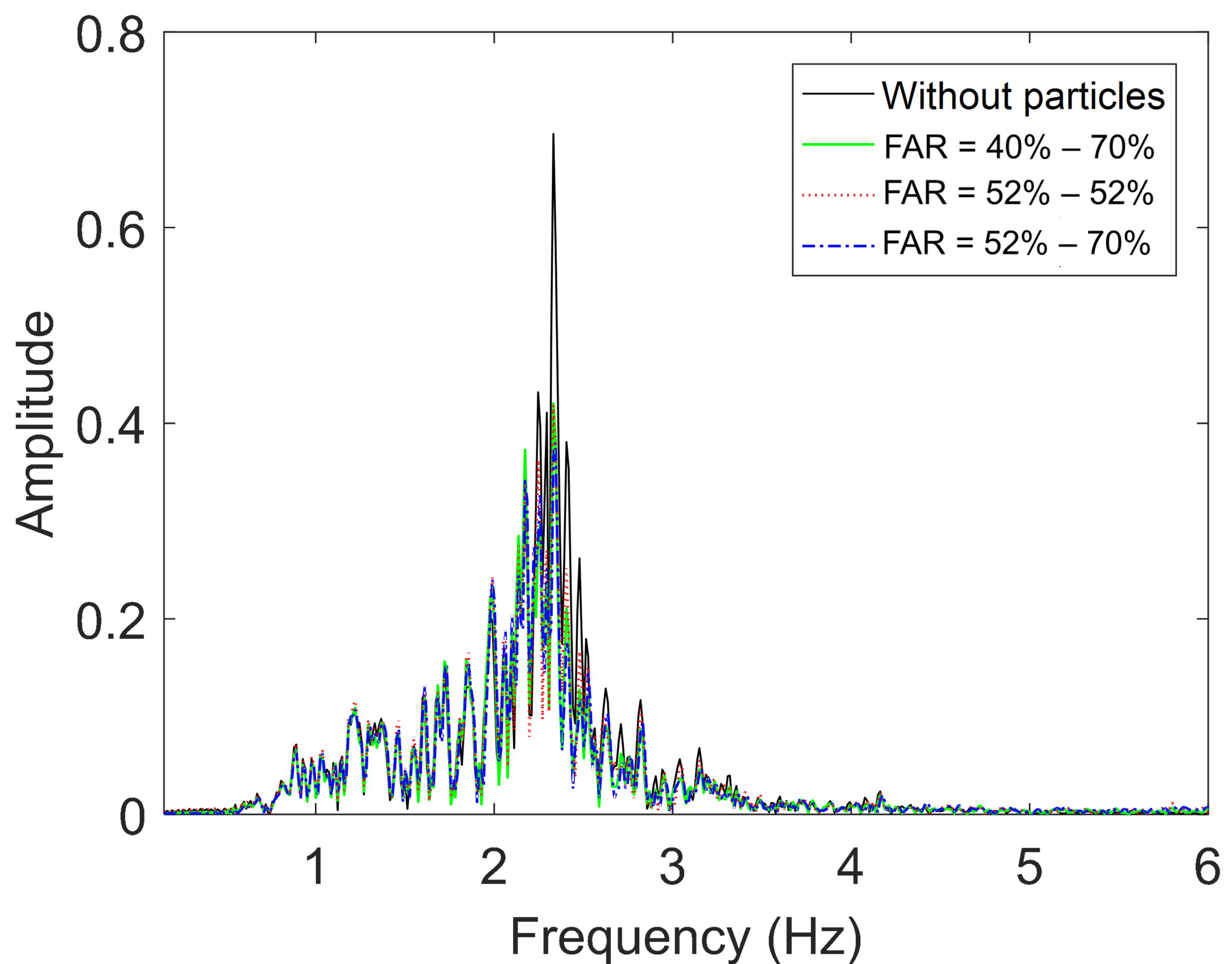
Figure 11, respectively. The RMS displacement ratio was similar for the four and two-compartment dampers with differences no more than 3%. Similar observations can be made for the RMS acceleration ratio. The performance of the particle damper with the four unequal compartments behaved equally well in all excitations. The two-compartment damper was slightly less effective in the low level of excitation. The performance of the four unequal compartment dampers with FARs ranging from 40% to 70% demonstrated similar performance to the two unequally and equally sized compartments, with FARs of 52–70% and 52–52%, respectively. Comparison of the performance of the four-compartment damper with the performance of the two-compartment damper in the frequency domain is presented in
Figure 12. The frequency spectrum of the response acceleration when the damper was operating is similar for the three cases examined.
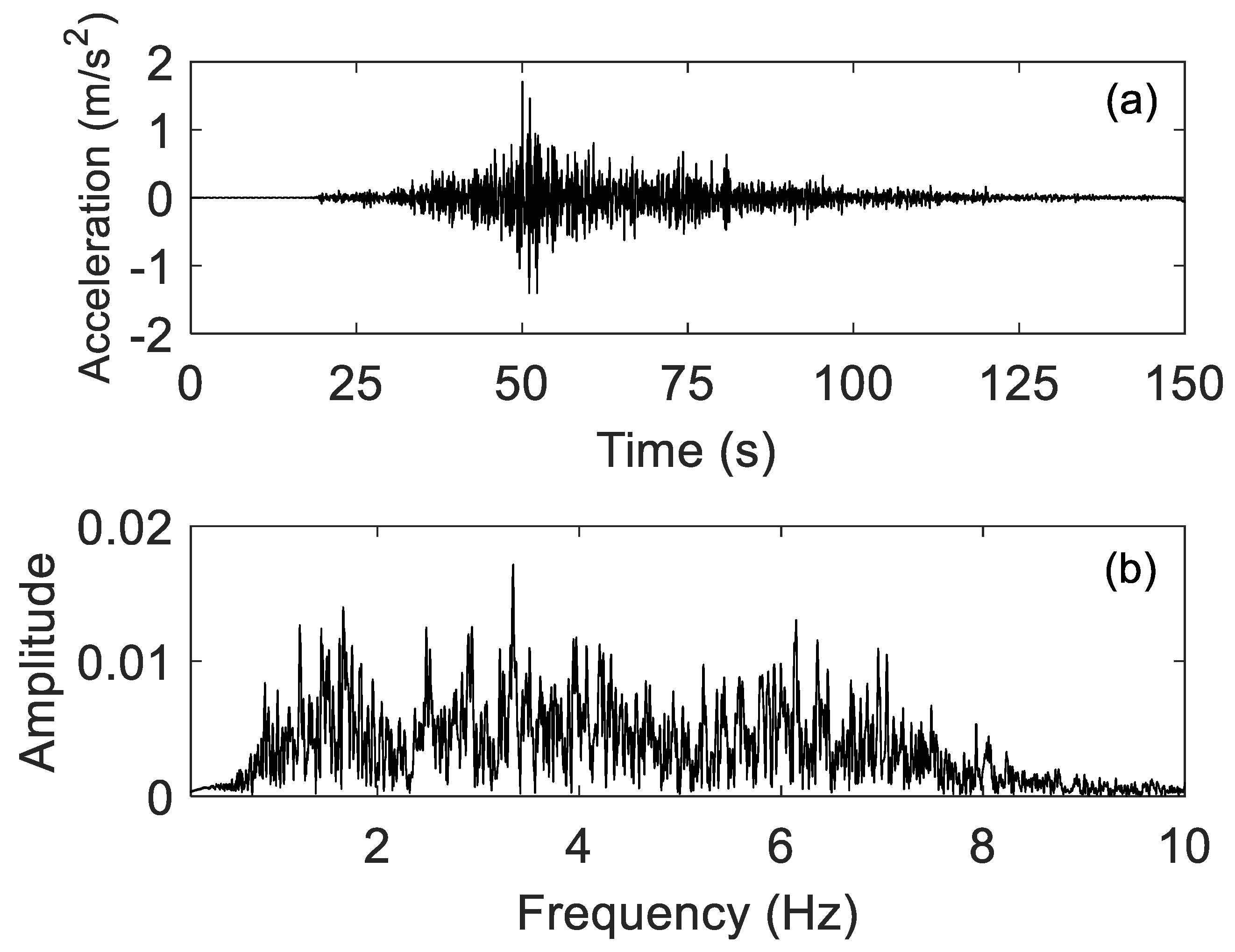
The performance of the four-compartment particle damper was also examined for earthquake excitations. The time history and frequency spectrum of a representative earthquake signal is presented in
Figure 13. This signal contains frequencies from 0 to 8 Hz and includes the natural frequency of the system. The effectiveness of the damper in attenuating earthquake signals was determined by comparing the response of the structure with and without the damper operating (
Figure 14 and
Figure 15), keeping the level of excitation constant. Reduction in the response was observed through most of the time history of the acceleration, except for the first few seconds. In addition, the amplitude of the frequency spectrum of the acceleration was much smaller, verifying the efficiency of the four-compartment damper.
4. Conclusions
A new form of a particle damper was examined, consisting of four unequally sized compartments. The damper was mounted on a small metal structure with low natural frequency that was excited by random earthquake signals. Equal numbers of particles were placed inside the four compartments, achieving filling area ratios (FARs) of 40% to 70%. It was found that the damper was effective in reducing the dynamic response of the structure, achieving attenuation up to 20% for a mass ratio close to 7%. The four compartments with filling area ratios from 40% to 70% made the damper versatile, accommodating a wide range of excitation levels.
The performance of the four-compartment damper was compared with the performance of dampers with two compartments of equal or unequal size. The filling area ratios of the selected two-compartment dampers (FAR = 52%, 70% and FAR = 52%, 52%) have been proven in past research (Papalou 2022) to give good attenuation levels. It was found that the four-compartment damper was equally good in reducing the displacement of the structure independently of the level of excitation. Therefore, even though the four-compartment damper was not proven to be superior from the two-compartment damper for the cases that were compared, it is safe to select this particular layout knowing that, independently of the intensity of the excitation, there will be a reduction of the response.