Numerical Approach to Optimize the Dynamic Behaviour of Structures Considering Structural Durability

Abstract

In the design of lightweight structures, both the dynamics and durability must be taken into account. In this paper, a methodology for the combined optimization of structural dynamics, lightweight design, and lifetime with discrete vibration engineering measures is developed and discussed using a demonstration structure. A two-sided welded bending beam is excited at the centre and optimal parameters for tuned mass dampers (TMD) are searched, satisfying the requirements for the dynamic behaviour, the overall mass, and the lifetime of the weldings. It is shown that the combination of a reduced order model with the implementation of the structural stress approach at critical welds enables an efficient evaluation of certain design concepts in the time domain. Using this approach, multi-criterial optimization methods are used to identify the best set of parameters of the TMD to reduce the structural vibrations and enhance the durability.

1. Introduction

In various industrial sectors, such as mechanical engineering, cranes, intra-logistics, automotive, and agricultural engineering, the requirements on the vibration behaviour of components and structures are constantly increasing since it affects performance, comfort, and noise emission. At the same time, products must be optimized in terms of lightweight design to save resources during production and operation while they still have to satisfy various other requirements. For example, the overall stiffness or the maximum allowable deflection needs to be considered or sufficient, static and cyclic strength needs to be verified, and in some cases also the crash-worthiness needs to be addressed.

The optimization of such dynamically loaded structures is usually decoupled according to the state of the art. However, such a recursive approach may lead to many design cycles. All mechanical properties, e.g., structural dynamics and fatigue, are closely linked and interdependent. Those relations can be seen as a typical multidisciplinary optimization (MDO) problem. MDO is evolving with the growing complexity of modern engineering problems. It involves different engineering domains to evaluate interactions within a coupled optimization problem. Traditional design and domain optimization mainly focus on optimal properties on component level and engineering sub-domains. As complexity increases due to progress, even more interactions need to be considered. In addition, lightweight structures are not just a hot topic, they are state-of-the-art. However, with the goal of achieving the lightest possible structures, dynamic problems are steadily increasing. This can correlate with reduced durability. Thus, structural dynamics should be addressed together with fatigue investigations to enhance structural durability and system reliability. MDO is well established, theoretically covered, and, for different types of problems, investigated, e.g., [1,2,3]. Structural optimization with fatigue constraints can also be found, e.g., [4,5]. However, just a few contributions are known which address structural dynamic fatigue correlation in terms of vibration engineering for lightweight structures and none of them deals with parameter optimization of vibrational measures.

Zeiler demonstrated in [6] the correlation between structural dynamics and fatigue performance in an automotive design optimization task using fatigue analysis and sensitivity derivatives in the context of a MDO. Häusler and Albers provided a workflow in [7] for optimization of the shape of a hole in a dynamically loaded plate and included a fatigue analysis. The process involves a multi-body simulation whose results were applied to a finite element model as excitation in the time domain. The location of the inner nodes of the hole were the optimization design points and could be moved according to the stress distribution. A commercial software was then used for damage estimation. Miao et al. [8] presented a multidisciplinary fatigue optimization method and evaluated them on structural lightweight design of a railway carbody, including a fatigue assessment. The multibody structure is first investigated numerically, starting with a multibody simulation and afterwards evaluating the stress in a FE environment. They also compared numerical and experimental results and concluded that MDO in terms of structural dynamics and fatigue can improve lightweight design. Han et al. [9] propose a methodology for structural topology optimization with stress minimization considering non-linear continuum damage. Chen et al. [10] presented topology optimization methods with the penalization of elemental damage to achieve lightweight design by simultaneously restricting the maximal damage. Faes et al. [11] show a reliability-based design optimization, taking into account uncertainties. Martins et al. [12] provide a survey on different methods in multidisciplinary design optimization and classified them. They indicated that benchmarking of different approaches is difficult—which leads to the approach of evolving a process by starting the optimization procedure with a low order model. Additionally, they stated that large-scale problems in MDO have only slow convergence. Here, reduced order models can provide a benefit. For obtaining less computational effort in multidisciplinary design optimization problems, Meng et al. [13] used a surrogate model for uncertainty evaluations in MDO. Their investigations were made on a turbine blade considering aerodynamic performance and structural reliability. They concluded that uncertainty investigation of this coupled problem can be investigated more efficient using an MDO approach. An interesting multidisciplinary design optimization approach for a gear transmission is presented by Mahiddini et al. [14] with an analytical formulation based on product reliability and economic aspects like product costs and customer preference. However, aspects of dynamic behaviour and lightweight design are not addressed in that work.

Moreover, all these works do not focus on the durability of welds especially. Therefore, the aim of this work is to present a method for evaluating and optimizing both the structural dynamics and the durability of a lightweight structure with critical welds in the same computational environment via the use of vibration measures.

2. Materials and Methods

2.1. Modelling of Dynamic System Behaviour

Modelling and simulation of dynamic systems are fundamental steps in a product development process. In the mathematical description of these systems, balance equations for energies, masses, and momentum can be derived with the help of basic physical laws. This usually leads to ordinary differential equations (ODE). The ODEs are usually generated by analytical or numerical methods and can be solved by various algorithms. The general approach to the computational solution of higher order ODEs involves the transformation to first order ODE systems. This increases the dimension of the system matrices in proportion to the number of derivatives.

In structural mechanics, the representation form of a second-order system has proven to be useful, since the assignment of the system matrices to the physical properties of the structure is unambiguous. The second-order system of equations can be represented as a linear descriptor system or generalized control system (1).

$$\begin{array}{cc}\hfill \mathbf{M}\ddot{\mathbf{u}}\left(t\right)+\mathbf{B}\dot{\mathbf{u}}\left(t\right)+\mathbf{C}\mathbf{u}\left(t\right)& ={\mathbf{B}}^{in}\mathbf{f}\left(t\right)\hfill \end{array}$$

(1)

$$\begin{array}{ccccccccccccccccccc}& & & & & & & & & & & & & & & & & \hfill \mathbf{y}\left(t\right)& ={\mathbf{B}}_1^{out}\mathbf{u}\left(t\right)+{\mathbf{B}}_2^{out}\dot{\mathbf{u}}\left(t\right)\hfill \end{array}$$

(2)

Here, $t\in {\mathbb{R}}^{+}$ is the time variable and the vector functions $\mathbf{u}:\mathbb{R}\to {\mathbb{R}}^n$, $\mathbf{f}:\mathbb{R}\to {\mathbb{R}}^k$, and $\mathbf{y}:\mathbb{R}\to {\mathbb{R}}^l$ describe the internal states, the inputs, and the outputs of the system. The system order n represents the dimension of the system matrices. The number of inputs or outputs is denoted by k and l. In structural systems, the real matrices $\mathbf{M}$, $\mathbf{B}$, $\mathbf{C}\in {\mathbb{R}}^{n\times n}$ represent the mass, damping, and stiffness matrices, respectively. For systems with regular mass matrix $\mathbf{M}$, Equation (1) corresponds to a second order ODE system.

In practice, ODE systems with a huge amount of degrees of freedom (DOF) often arise in the modelling of dynamic systems. In particular, this applies to numerical discretization methods, e.g., Finite Element Method (FEM), and reduces the attractiveness for optimization tasks or time domain simulations. Models with approximately the same accuracy and considerably greater computational efficiency are often generated by model order reduction (MOR) methods. The reduced order models (ROM) are then available for efficient analysis or optimization tasks. For further details about numerical modelling, especially FEM and the implementation, the reader is referred to the literature (e.g., [15,16]).

2.1.1. Model Order Reduction Methods

A large part of the currently established MOR techniques are projective methods, where the output system of order n is projected into a subspace of order r. The prerequisites for this are that the dynamics between input and output of the dynamical system are preserved in a defined time or frequency range and that the methods are numerically stable and efficient. Basically, the methods are distinguished with respect to the system behaviour to be considered. The majority of the developed algorithms assume linear and time-invariant systems.

In structural dynamics, the modal methods for MOR are among the most frequently used approaches, since they enable a suitable approximation of the dynamic behaviour. The basic idea of all modal methods is the transformation of physical coordinates into the modal coordinate space. For this purpose, the eigenvectors of the FE model are calculated by solving the eigenvalue problem and are combined in the modal matrix. The transformation is then based on this same modal matrix and the calculated deformations of the overall structure arise from the superposition of eigenvectors. This procedure is called modal synthesis or modal superposition [17]. For systems with linear independent eigenvectors and nonzero eigenvalues, the modal stiffness and modal mass matrices are diagonal. Thus, the equations of the system in modal space are decoupled, i.e., the transfer function of the overall system corresponds to the superposition of the transfer functions of decoupled single-mass oscillators.

In the modal coordinate reduction the modal superposition is combined with modal truncation. With the FE model, a reduced amount of eigenvectors is calculated and the modal matrix is thus built from a reduced modal base. Since a transformation matrix with a limited number of dynamic eigenmodes is used for this MOR, the static behaviour of the ROM may exhibit an error [18], which corresponds to the static residuals of the modes not considered.

2.1.2. Modal Approach

In modal truncation, the ODE system (1) is transformed into generalized or modal coordinates. The transformation rule is

$$\mathbf{u}\left(t\right)=\mathrm{\Phi }\mathbf{w}\left(t\right)$$

(3)

with the modal matrix $\mathrm{\Phi }$ and the vector of modal degrees of freedom $\mathbf{w}\left(t\right)$. The time dependent representation is omitted in the following in favour of better readability.

By solving the generalized eigenvalue problem

$$\mathbf{C}{\mathrm{\Phi }}_i={\lambda }_i\mathbf{M}{\mathrm{\Phi }}_i$$

(4)

with the system matrices from Equation (1) and the eigenvalues ${\lambda }_i$, the modal matrix $\mathrm{\Phi }=[{\mathrm{\Phi }}_1,\dots ,{\mathrm{\Phi }}_n]$ is calculated. Using this matrix as a projection matrix, a system of n decoupled differential equations is obtained:

$${\mathrm{\Phi }}^T\mathbf{M}\mathrm{\Phi }\ddot{\mathbf{w}}+{\mathrm{\Phi }}^T\mathbf{B}\mathrm{\Phi }\dot{\mathbf{w}}+{\mathrm{\Phi }}^T\mathbf{C}\mathrm{\Phi }\mathbf{w}={\mathrm{\Phi }}^T{\mathbf{B}}^{in}\mathbf{f}$$

(5)

If the eigenvectors are mass-normalized and the damping matrix is approximated by a linear combination of the stiffness and mass matrices, the following equation

$$\mathbf{I}\ddot{\mathbf{w}}+\mathrm{diag}\left(2\vartheta {\omega }_0\right)\dot{\mathbf{w}}+\mathrm{diag}\left({\omega }_0^2\right)\mathbf{w}={\mathrm{\Phi }}^T{\mathbf{B}}^{in}\mathbf{f}$$

(6)

with the global damping $\vartheta$ and the natural frequencies ${\omega }_0$ applies. Equations (5) and (6) describe the full model of dimension n with correspondingly many eigenvectors.

Since the system matrices are now diagonal and contain parameters to n decoupled equations, rows and columns of the modal transformed matrices associated to an eigenvalue can be truncated. The reduced modal basis ${\mathrm{\Phi }}_r\in {\mathbb{R}}^{n\times r}$ is described only by the first r eigenmodes. Using the reduced modal basis as transformation matrix, the physical degrees of freedom

$$\mathbf{u}={\mathrm{\Phi }}_r\overline{\mathbf{w}}+ϵ$$

(7)

are approximated with an approximation error $ϵ$ that depends on the selected number of eigenmodes r. Based on Equation (1), the system description is derived with $r\ll n$ decoupled differential equations

$$\begin{array}{cc}\hfill \overline{\mathbf{M}}\ddot{\overline{\mathbf{w}}}+\overline{\mathbf{B}}\dot{\overline{\mathbf{w}}}+\overline{\mathbf{C}}\overline{\mathbf{w}}& ={\mathrm{\Phi }}_r^T{\mathbf{B}}^{in}\mathbf{f}\hfill \end{array}$$

(8)

$$\begin{array}{cc}\hfill \mathbf{y}& ={\overline{\mathbf{B}}}_1^{out}\mathbf{w}+{\overline{\mathbf{B}}}_2^{out}\dot{\mathbf{w}}\hfill \end{array}$$

(9)

with the reduced system matrices

$$\begin{array}{cc}\hfill \overline{\mathbf{M}}& ={\mathrm{\Phi }}_r^T\mathbf{M}{\mathrm{\Phi }}_r,\hfill \end{array}$$

(10)

$$\begin{array}{cc}\hfill \overline{\mathbf{B}}& ={\mathrm{\Phi }}_r^T\mathbf{B}{\mathrm{\Phi }}_r,\hfill \end{array}$$

(11)

$$\begin{array}{cc}\hfill \overline{\mathbf{C}}& ={\mathrm{\Phi }}_r^T\mathbf{C}{\mathrm{\Phi }}_r\in {\mathbb{R}}^{r\times r}\hfill \end{array}$$

(12)

and

$$\overline{\mathbf{w}}\in {\mathbb{R}}^r.$$

(13)

2.1.3. System Formulation

Since each modal deformation corresponds to a modal stress state [19], the output matrix ${\overline{\mathbf{B}}}_1^{out}$ can also be extended to stresses. The idea is based on the fundamental equation

$$\sum _{j=1}^n{\sigma }_j{w}_j=\sigma$$

(14)

with modal stresses ${\sigma }_j$ in the particular mode j and the total stress $\sigma$. The modal coordinates $w_j$ correspond to a weighting factor describing the influence of an individual modal stress to the total stress. Compared to the modal reduced model (Section 2.1.2) the nodal stresses are used instead of eigenvectors to build the output matrix. For the back transformation from modal to physical stress values, the following transformation matrix is used.

$${\mathrm{\Phi }}_{\sigma }=[{\sigma }_1,\dots ,{\sigma }_r]$$

(15)

This results in the final system representation according to Equations (8) and (9) with the extended output matrix

$${\overline{\mathbf{B}}}_1^{out}=\left. [\begin{array}{c}{\mathrm{\Phi }}_r\\ {\mathrm{\Phi }}_{\sigma }\end{array}\right]$$

(16)

in which the stress states are now calculated in addition to the deformation states.

2.2. Fatigue Strength Assessment

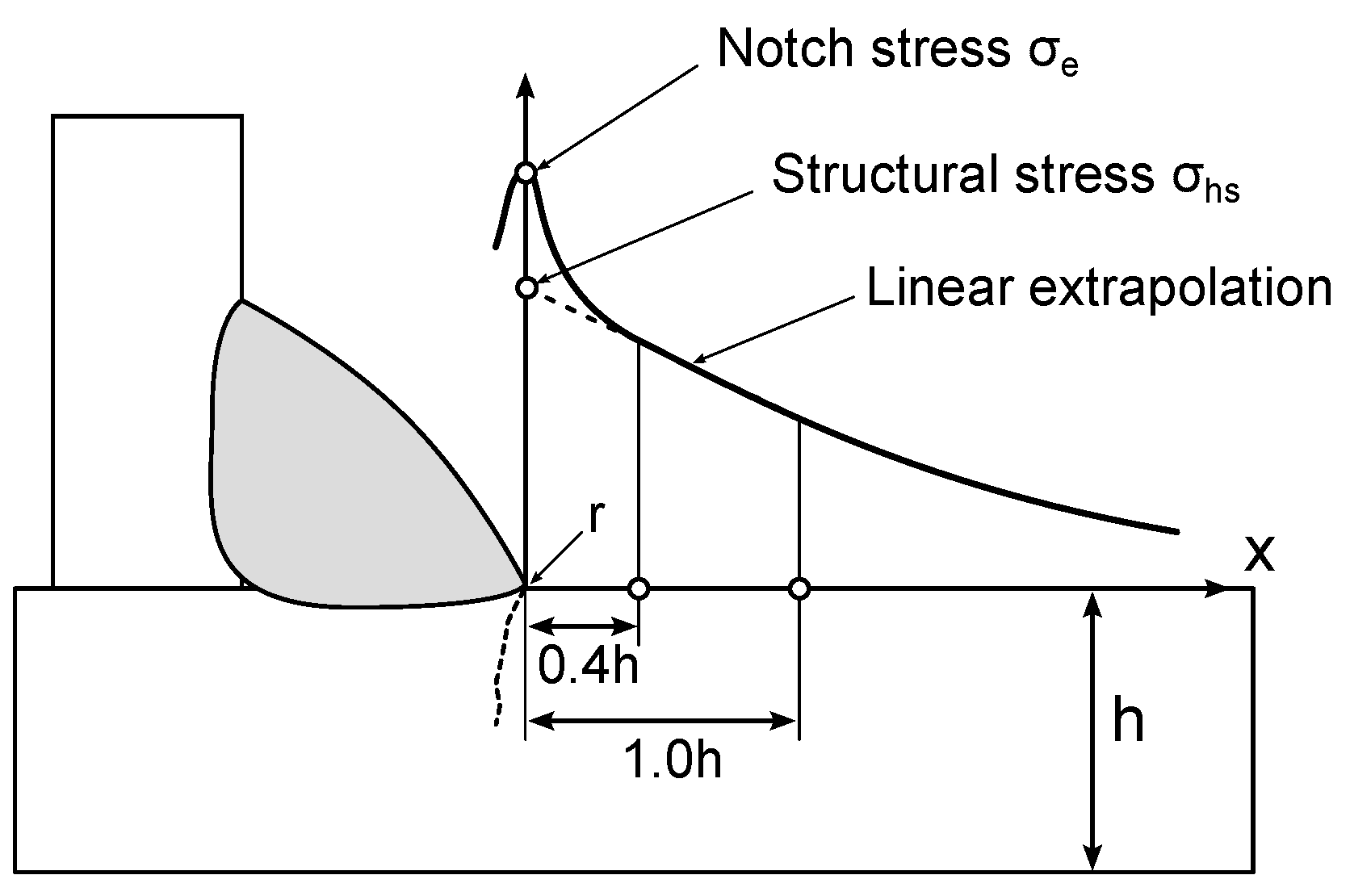
2.2.1. Linear-Elastic Approaches

In a fatigue assessment, linear elastically calculated stresses ${\sigma }^S$ in the structure are compared to endurable stresses ${\sigma }^R$ that depend on the material strength. For constant amplitude loading, the fatigue life N, representing the endurable number of cycles until a fracture is expected, can be calculated by the equation of the S–N curve

$$N=N^R{\left(\frac{{\sigma }^R}{{\sigma }^S}\right)}^k$$

(17)

where k is the slope of the S–N curve and $N^R$ is the number of endurable cycles for the stress $S^R$.

In case of dynamically loaded structures, not a constant but a variable stress amplitude is expected. With an appropriate cycle-counting algorithm, e.g., such as described in ASTM E1049-85 [20], different stress cycles $n_i$ with individual amplitudes ${\sigma }_{a,i}^S$ and mean values ${\sigma }_{m,i}^S$ can be extracted. The damaging effect of these cycles be assessed by a linear damage accumulation

$$D=\sum _i{D}_i=\sum _i{n}_i/N_i$$

(18)

in which the damaging effect of each counted cycle is evaluated against the endurable cycles $N_i=$ for a given stress amplitude and mean stress using Equation (17). The approach is visualized in Figure 1, where $\mathrm{\Delta }\sigma$ is the stress used for the evaluation, e.g., noth stress ${\sigma }_e$, hot-spot stress ${\sigma }_{hs}$. According to IIW [21], the slope $k^{*}$ of the S–N curve in the very high cycle regime ($N>N_k$) is decreased to:

$$k^{*}=2k-1.$$

(19)

In Figure 1, $\mathrm{\Delta }\sigma$ is the stress used for evaluation, e.g., hot-spot stress $\mathrm{\Delta }{\sigma }_{hs}$ or notch stress $\mathrm{\Delta }{\sigma }_e$. Further information on the assessment of variable amplitudes can be found in [22].

Furthermore, additional influencing factors, such as mean stresses, stress gradients, or roughness need to be taken into account [23]. These factors are used to decrease or increase the endurable fatigue strength by shifting the S–N curve up or down. The slope k of the S–N curve is typically set constant.

2.2.2. Application for Welded Joints

Various approaches are available for the fatigue assessment of structures with welded components [24]. The ones most often used are linear–elastic approaches, such as the nominal stress, the structural stress or the notch stress approach [21].

For a numerical assessment of a large and complex structure, the structural stress approach [25] is commonly used. A structural stress is used for the evaluation that is extracted by an extrapolation of the surface stress to the failure critical weld toe [21]. Stresses at two locations are used for the evaluation that have the distance of $0.4·h$ and $1.0·h$ from the weld toe, where h is the material thickness, as shown in Figure 2. An extrapolation to the weld toe

$${\sigma }_{hs}=1.66·\sigma (x=0.4·h)-0.67·\sigma (x=1.0·h)$$

(20)

leads to the so-called hot-spot stress ${\sigma }_{hs}$.

The derived acting structural stresses can directly be evaluated against the S–N curve.

For the structural stress approach an endurable stress range of $\mathrm{\Delta }{\sigma }_{hs}^R$ = 100 MPa at $N^R=2\times {10}^6$ cycles can be used [21]. The slope for welded joints under stresses normal to the weld in as-welded condition depends on the sheet thickness. For thick ($h\le 7$ mm) welded sheets a slope of $k=3$ and for thin sheets h > 7 mm a slope of $k=5$ is recommended [26]. The knee point of the S–N curve is typically expected to be located at $N_k={10}^7$ cycles.

Compared to other local approaches, such as the effective notch stress approach [21], the structural stress approach has the advantage that stresses at only two locations need to be evaluated. Of course, for real-world structures this evaluation has to be conducted for every relevant cross section. So, depending on the complexity, hundreds, or even thousands, of locations need to be considered.

2.3. Application Model

For the application of the proposed approach, a simple demonstrator is chosen. The geometry is inspired by a field sprayer which is typically used on tractors for, e.g., nutrient distribution, see Figure 3 and Figure 4. This low complexity model allows a perceivable interpretation of the results. For point masses were added to the structure in order to obtain low resonance frequencies while keeping the overall length at 1 m, considering a possible realization as lab demonstrator. The model is symmetric, while each side is distributed into three sections of different thicknesses. Construction steel material properties are considered ($E=210 \mathrm{GPa}$ and $\nu =0.3$). Additional specifications are noted in

Table 1. Additional model specifications.

Section	Length	Width	Thickness	Add. Mass	Base Stiff.
	m	m	m	kg	N/m
Outer	0.20	0.07	2 × 10−3	0.5	-
Inner	0.25	0.07	4 × 10−3	0.5	-
Mid	0.10	0.07	10 × 10−3	-	1 × 10−8

. The transition regions due to the thickness change represent the welds $w_1$ and $w_2$, which are the focus of the following investigations. At this stage of process development, only two input locations for measures are considered per side. For the optimization of the dynamic behaviour of the structure, passive mass-stiffness-damping ($m_T$, $k_t$, ${\vartheta }_T$) absorber (tuned-mass-damper (TMD)) are included. Since the positions are fixed, the parameters of the TMD are of interest instead of the optimal positioning. The design space of each parameter is defined in Section 3.1.2.

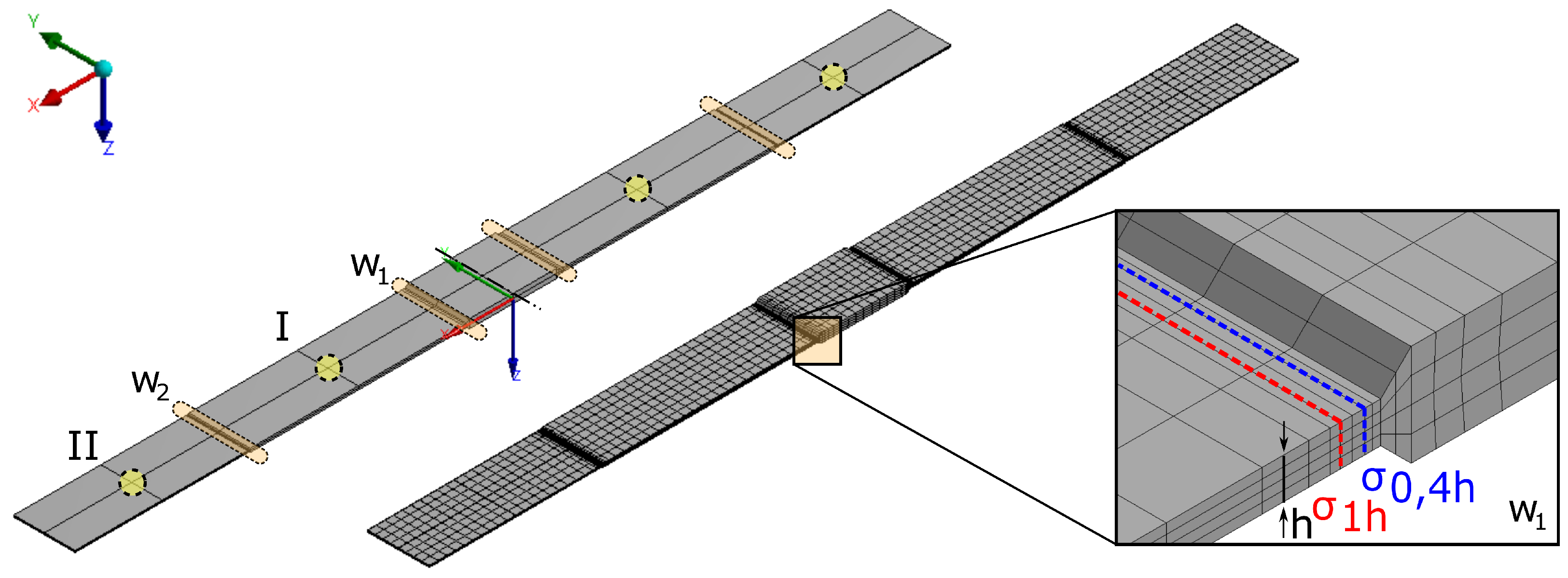
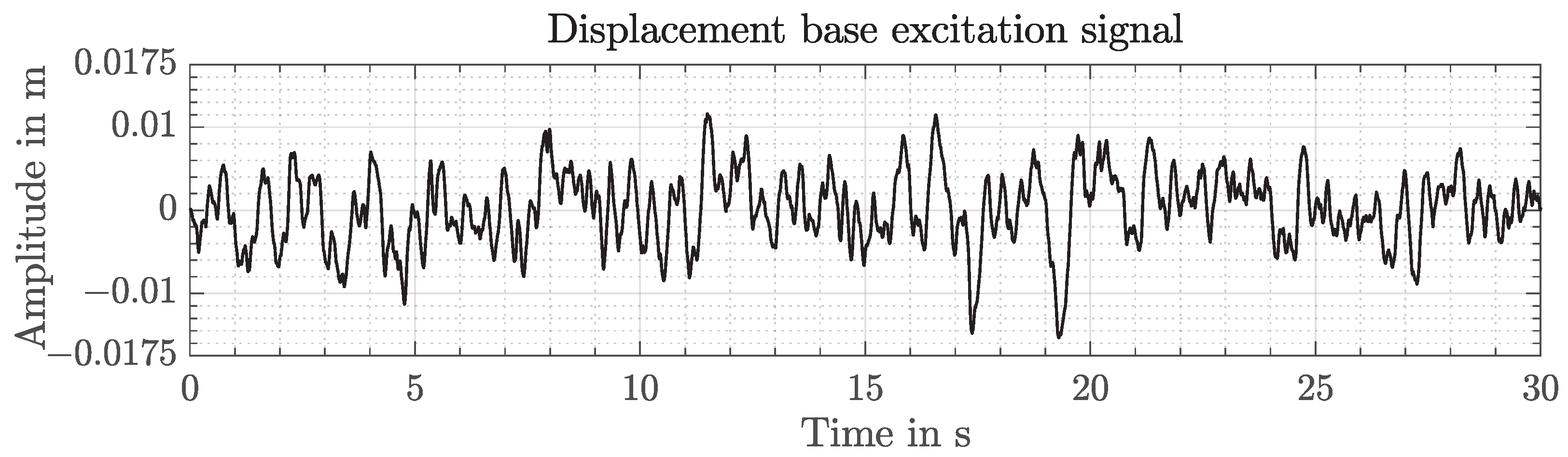
2.3.1. Finite-Element Model

Figure 4 shows the FE model of the demonstrator. The model was built using the Software ANSYS [27]. The discretization of the model is based on a second-order approach with hexahedron elements. The specifications of the mesh at the welds are designed after recommendations in [21], as discussed in Section 2.2.2. The model consists of 4640 elements, 24,191 nodes, and 71,352 degrees of freedom. The outer and the inner sections are loaded with an additional mass which is equally distributed (weighted Multi-Point Constraint (MPC) interpolation (RBE3)) to all corresponding nodes of the area. The displacement of the middle section is constrained in the symmetry plane ($x=0$ and $y=0$), excluding the z-direction. No other displacement boundary conditions have been applied. As an excitation, a displacement base excitation $z_{in}\left(t\right)$ is chosen. It is considered that the fixing is achieved by a stiff spring support, thus a spring with a longitudinal stiffness of $k_L=1 \times {10}^{-8} \mathrm{N}/\mathrm{m}$ is implemented. The excitation is equal for all nodes of the lower surface of the middle area using a MPC resulting in one global excitation point, which is connected to the spring $k_L$.

At this point, no physical measurement data of a ground profile exists, so the input signal is synthetically constructed, as shown in Figure 5. The frequency content is dominated by low-frequency behaviour, representing, e.g., a farmland ground.

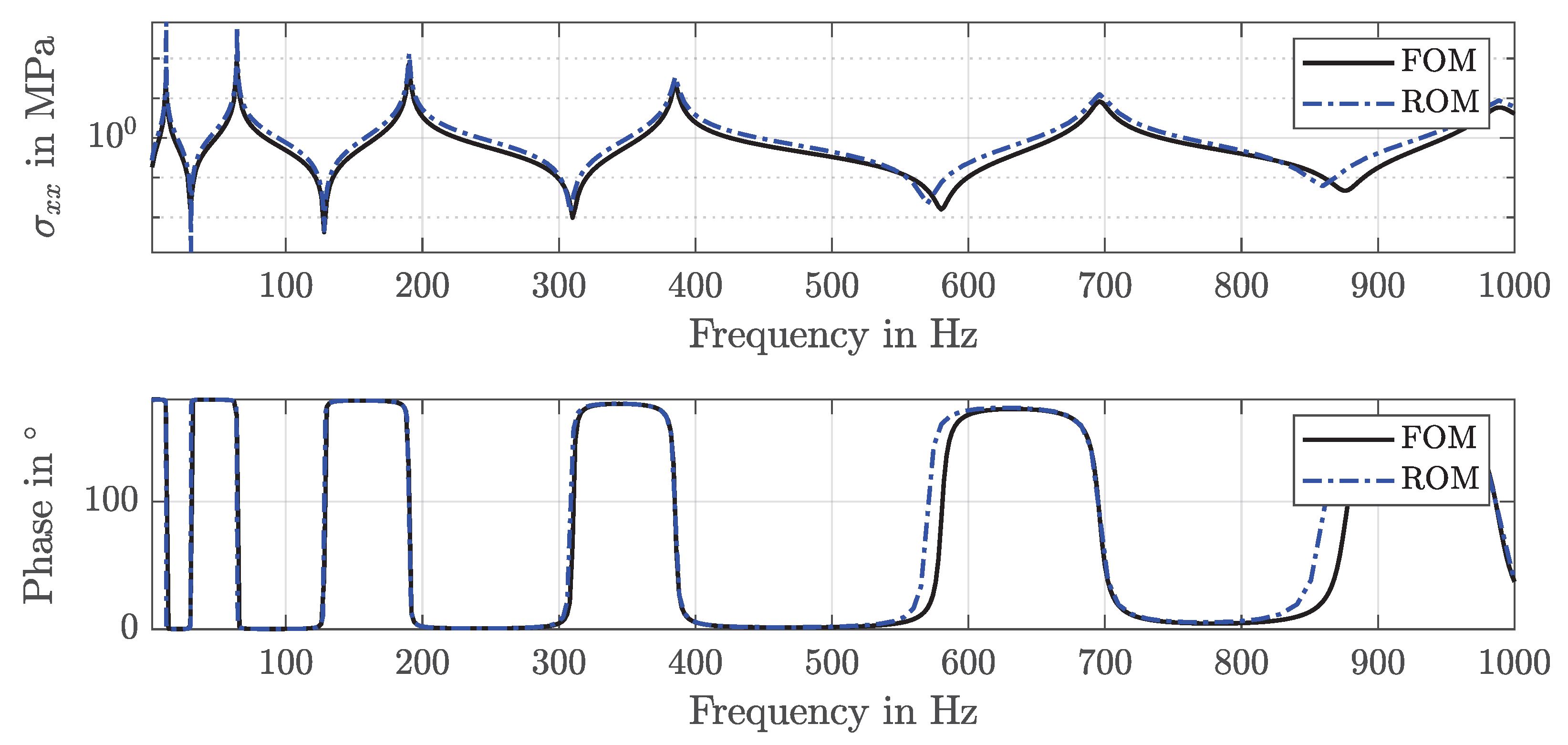
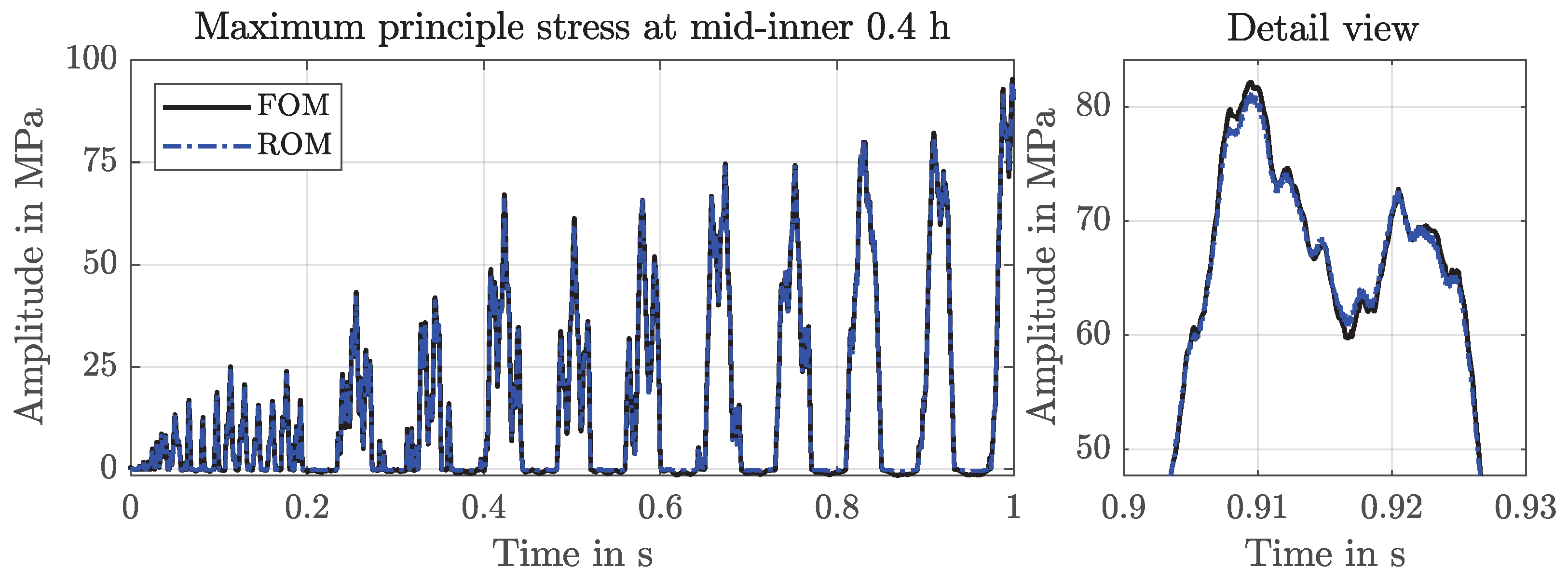
2.3.2. Verification

To verify that the results of the ROM are valid, a verification the FE solution is computed using ANSYS. For this aim, a full transient simulation is conducted, which represents the FOM. While the FOM is solved using an implicit scheme, the ROM is solved with an explicit fourth-order Runge–Kutta algorithm [28] using MATLAB/SIMULINK software environment [29]. For comparison, $1 \mathrm{s}$ of the shown base excitation signal is taken into account. The FE FOM simulation, as well as the ROM system simulation are performed with a time step size of $t_s=1 \times {10}^{-4} \mathrm{s}$, which ensures numerically stable solutions covering the resonance of the stiff spring (stability condition only for ROM). The ROM is established after the description in Section 2.1.2. The used eigenvectors are obtained from a modal analysis using ANSYS. The results, here the modal eigenvectors (displacements) and the modal stresses, are extracted and organized as a state-space representation, as described in Section 2.1.3. This first order system of linear equations can be evaluated in the time domain. This is equal to a modal superposition transient analysis composed of modal states. If the displacements $\mathit{u}$ of the ROM are comparable to the displacements of the FOM ${\mathit{u}}_{\mathrm{ref}}$, then the stress states are also valid $\sigma \approx {\sigma }_{\mathrm{ref}}$. This can be derived from the usual isotropic stress–strain relationship following Equation (21). The stress tensor $\sigma$ depends on the strain tensor $\epsilon$, as well as the material tensor $\mathcal{C}$, and is calculated by the Frobenius inner product.

$$\sigma ={〈\mathcal{C},\epsilon 〉}_F$$

(21)

The strains are the derivatives of the calculated displacements. The fourth order material tensor depends on the material description. In case of linear–elastic, isotropic behaviour, it is symmetric with 36 components while 12 entries are non-zero elements which depend on only two of three parameters ($E,G,\nu$), see, e.g., [30,31].

As a criterion for the amount of modes to consider, the effective mass is investigated [32]. The applied displacement excitation is fully one-dimensional, thus only the fraction in the direction of the excitation is relevant. It has been detected that the first 16 (modal) eigenvectors are necessary to achieve a valid ROM stress result compared to the FOM solution. This amount of eigenmodes mobilize 98.8% of the total mass in z-direction (cumulative mass fraction in z-direction). Taking more eigenmodes into account does not lead to any further relevant change—they only enlarge the model size. This amount can be further reduced by neglecting all modes in this range without any contribution to the effective masses in z-direction. The total number of modes then is reduced to 10. Since a modal approach is used, the ROM consists of the modal eigenvectors. These are computed using the FOM, so there is no mismatch between the eigenvectors for the points of interest.

To ensure that the ROM is able to approximate FOM results a verification stage is necessary. The easiest and computationally most efficient way is to compare frequency domain data. Figure 6 shows this for a normal stress transfer function at one exemplary welding position up to $1000 \mathrm{H}\mathrm{z}$ for magnitude and phase response. It can be seen that both solutions are very well comparable, only slight differences occur in the higher frequency domain. However, the following investigations are made within the time domain, thus a time domain verification is also completed. Figure 7 shows the results of the FOM and the ROM for the maximum principle stress at the weld, denoting the transition from the middle to the inner section, excited by the base excitation input signal shown in Figure 5. The shown $1\mathrm{s}$ cutout verifies the ROM solution since the characteristics, as well as the amplitudes, are very well comparable. The ROM can therefore be used in the optimization process, presented in the following chapter. Again, slight differences are visible but comparing the simulation times after

Table 2. Comparison of computing times for simulation of $T_{sim}=1 \mathrm{s}$ with $t_s={1\times 10}^{-4} \mathrm{s}$. FOM solved with ANSYS. ROM solved with MATLAB/SIMULINK. ANSYS used 16 cores in distributed memory parallel mode. MATLAB used four cores in shared memory parallel mode. Before the ROM solution, a modal analysis must be performed once with ANSYS, which takes $9 \mathrm{s}$. The solvable system formulation must also be established once and takes $23 \mathrm{s}$. The required time per iteration is the last denoted time specification ($+2 \mathrm{s}$). In addition, the computing time for $T_{sim}=30 \mathrm{s}$ using the ROM (=ROM $30 \mathrm{s}$) is noted in the last column to underline the ROM advantage.

Type	FOM 1 s	ROM ANSYS 1 s	ROM 1 s	ROM 30 s
Time	$1907\mathrm{s}$	$812\mathrm{s}$	$9\mathrm{s}+23\mathrm{s}+2\mathrm{s}$	$9\mathrm{s}+23\mathrm{s}+19\mathrm{s}$

, the advantage is predominant; the FOM takes roughly half an hour (1907 s) to solve a single design point, optimization procedures are not expedient—only the ROM enables this kind of procedure. The overall process then includes parameter optimization using the ROM and concludes with a final verification solution using the discovered optimal parameters with the FOM.

3. Results and Discussion

3.1. Optimization

The overall goal of the optimization process is to find a set of parameters that minimizes both the dynamic amplitudes and the damage values of the critical welds with a minimum expense of additional mass. Since these demands are in conflict with each other and cannot be minimized at the same time, the optimization problem can be seen as a MDO task from a mathematical point of view, which can be denoted as a multi-criterial optimization since several criteria are considered. However, to gain a good understanding of the problem, the system is initially analysed in the three dimensions structural dynamics, durability and lightweight design independently.

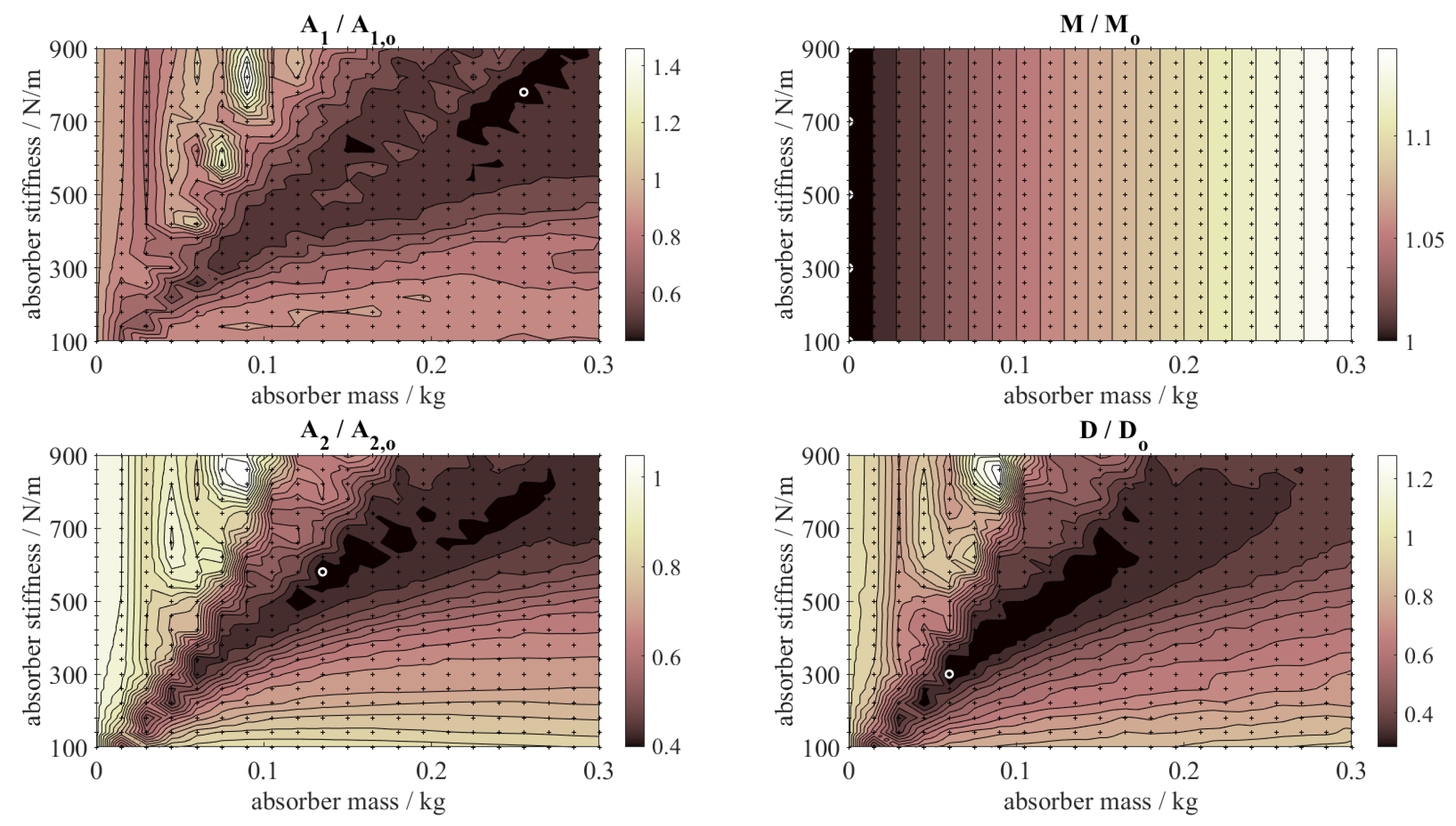
3.1.1. Mono-Criterial Optimization

Input for the damage accumulation are the counted hot-spot stress ranges $\mathrm{\Delta }{\sigma }_{hs,i}$ using ASTM 1049-85 based on the simulated stress-time course and the design S–N curve with ${\sigma }^R$ = 100 MPa and the slopes $k=3$ and $k^{*}=5$. The damage D is evaluated with the linear damage accumulation.

Four values are defined to asses each parameter set: $A_1$ is the maximum displacement range (peak to peak) at the outer tip within the given time frame, $A_2$ is the mean displacement at the same point, M is the overall mass and D is the damage value of the most critical weld, that is the maximum of all damage values $d_i$. The equations for each value is given in (22) to (25) with u denoting the difference in displacement in z-direction (Equation (26)).

$$\begin{array}{ccc}\hfill A_1& =& max\left(u\right(t\left)\right)-min\left(u\right(t\left)\right)\hfill \end{array}$$

(22)

$$\begin{array}{ccc}\hfill A_2& =& \mathrm{mean}\left(\right|u\left(t\right)-\mathrm{mean}\left(u\right(t\left)\right)\left|\right)\hfill \end{array}$$

(23)

$$\begin{array}{ccc}\hfill M& =& m_0+2m_T\hfill \end{array}$$

(24)

$$\begin{array}{ccc}\hfill D& =& max\left(d_i\right)\hfill \end{array}$$

(25)

$$\begin{array}{ccc}\hfill u\left(t\right)& =& z_{out}\left(t\right)-z_{in}\left(t\right)\hfill \end{array}$$

(26)

The calculation of $A_1$ and $A_2$ according to Equations (22) and (23) is visualized in Figure 8 for exemplary time data of u and a simulation time of 5 s.

Since each value should be as low as possible, various optimization algorithms can be used to find optimal design parameters in a given design space. However, for a simple structure as this a full factorial parameter variation can be performed with reasonable computational effort. This typically gives a good understanding of the problem and allows an illustrative 2D visualization in the case of only two design variables. Therefore, the simulation model was run 21 × 21 = 441 times, while the absorber mass $m_T$ was varied from 0 to 0.300 kg in steps of 0.015 kg and the absorber stiffness $k_T$ was varied from 100 N/m to 900 N/m in steps of 40 N/m. The damping ratio ${\vartheta }_T$ was kept constant at 3%, which is a realistic average value for vibration absorbers with elastomer-based damping.

Figure 9 shows the relative values for $A_1$, $A_2$, M, and D for the full factorial parameter variation (relative to the corresponding values of the initial system, denoted as $A_{1,o}$, $A_{2,o}$, $M_o$, and $D_o$). The optimal value is marked in each case and given in

Table 3. Results of the mono-criterial optimization gained by full factorial calculation (21 × 21 evaluations).

Goal	${\mathit{m}}_{\mathit{T}}$	${\mathit{k}}_{\mathit{T}}$	${\mathit{f}}_{\mathit{T}}$	${\mathit{A}}_1/{\mathit{A}}_{1,\mathit{o}}$	${\mathit{A}}_2/{\mathit{A}}_{2,\mathit{o}}$	$\mathit{M}/{\mathit{M}}_{\mathit{o}}$	$\mathit{D}/{\mathit{D}}_{\mathit{o}}$
	kg	N/m	Hz
$A_1$	0.255	780	8.85	0.4297	0.4176	1.1275	0.3688
$A_2$	0.135	580	10.50	0.5224	0.3959	1.0675	0.2930
M	0.000	-	-	1.0000	1.0000	1.0000	1.0000
D	0.060	300	10.98	0.6242	0.4340	1.0300	0.2843

, together with the corresponding design parameters mass $m_T$, stiffness $k_T$, and the related undamped eigenfrequency of the absorber $f_T$.

As observed, the single parameter optimization leads to very different optimal design parameters. The value $A_1$ can be reduced most effectively with an absorber mass of 0.255 kg tuned to 8.85 Hz, while the mean displacement $A_2$ is lowest for an absorber mass of 0.135 kg tuned to 10.5 Hz. The best lightweight design has no absorber at all, and for the most durable design an absorber mass of 0.060 kg tuned to 10.98 Hz is needed. Interestingly, the design parameter set for the best dynamics differs from the one for the best durability, which underlines that evaluating the damage of the structure together with its dynamic behaviour is essential.

With the results shown in Figure 9 the engineer can choose a proper set of design parameters, taking into account the specific boundary conditions and requirements of the application, and see, at a glance, the implications of a certain design regarding dynamics, durability, and lightweight design.

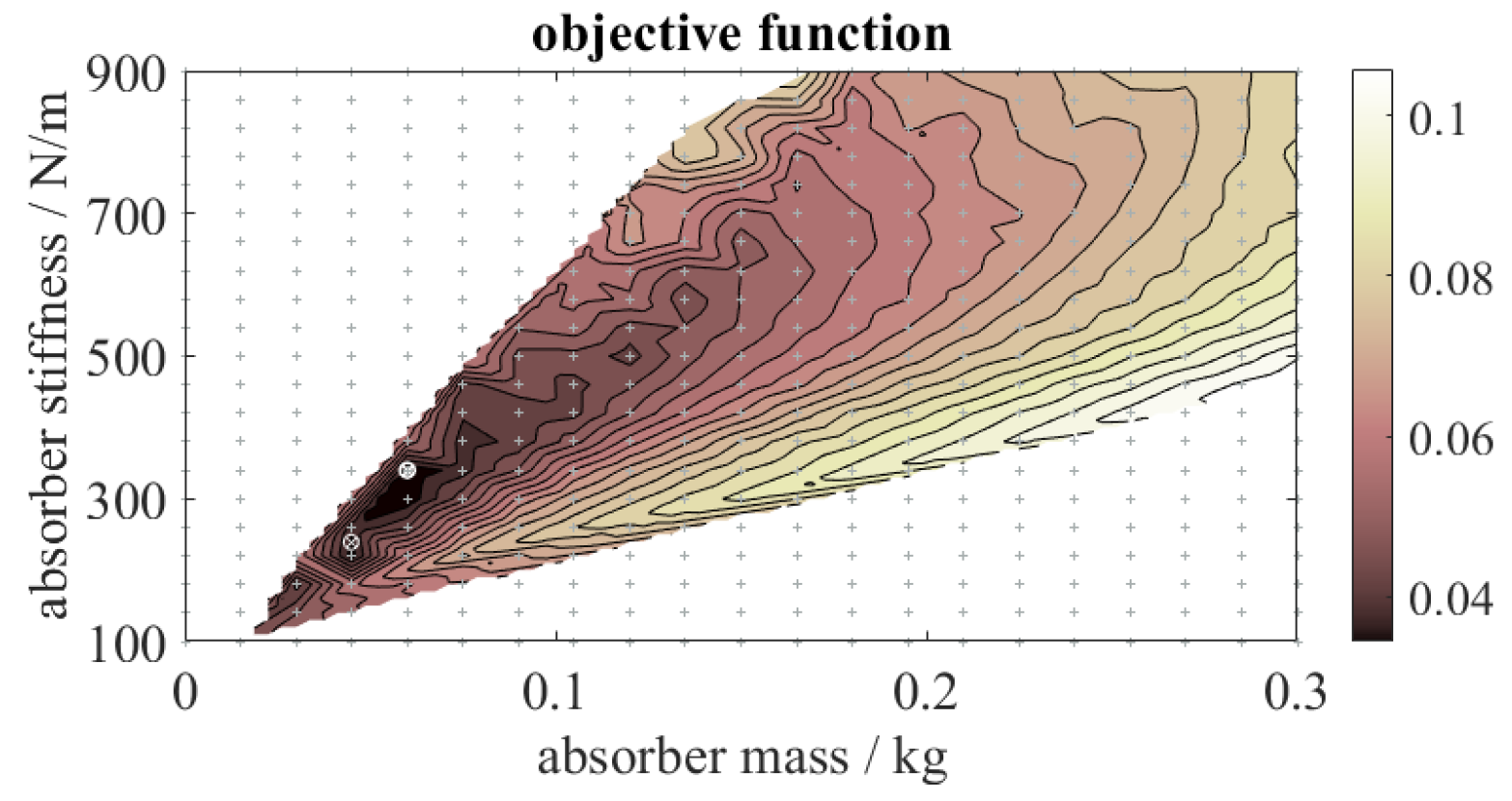
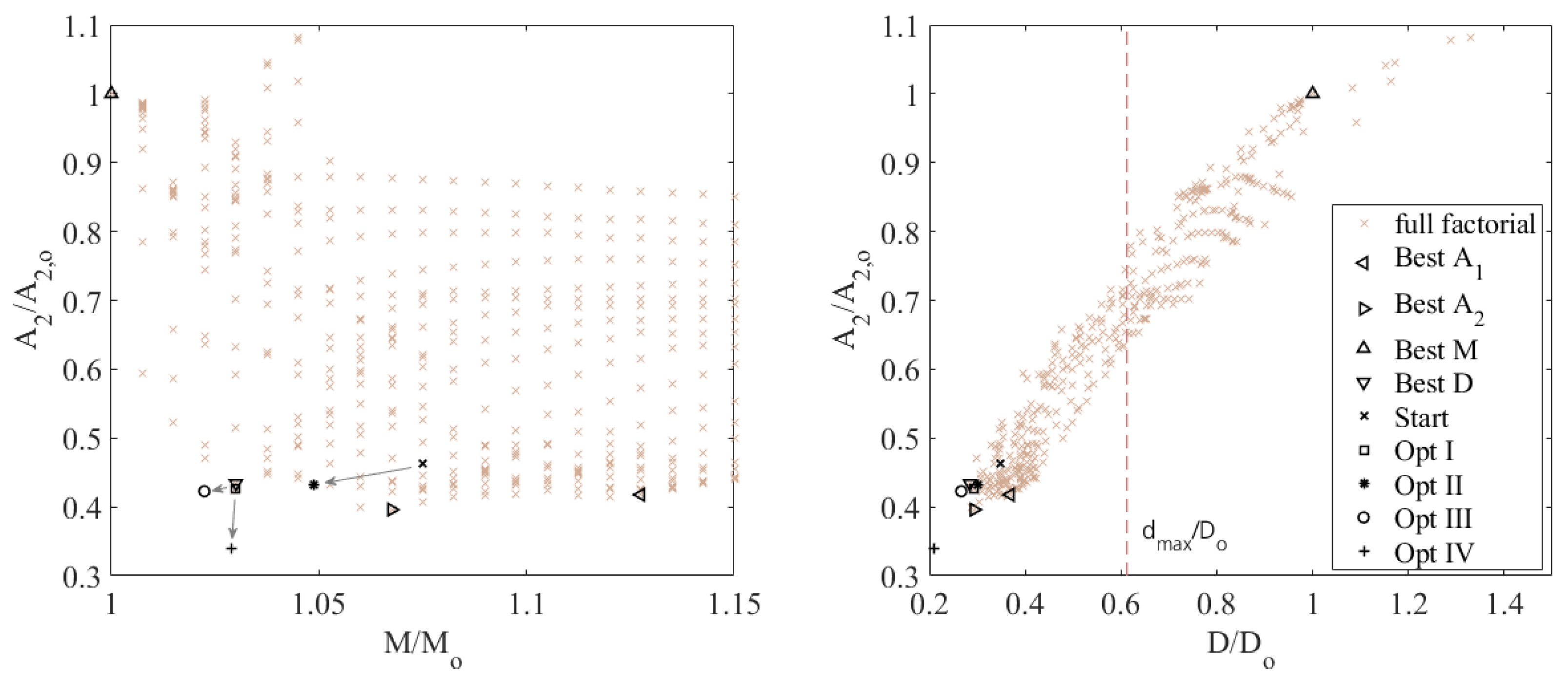
3.1.2. Multi-Criterial Optimization

For multi-criterial optimization problems in the engineering context many different techniques are known and described in the literature [33,34,35].

Here, the most straight forward approach with weighting functions for each target value and an arithmetic summation of all four components is chosen, which mathematically reduces the problem to the mono-criterial optimization of a cost function. The corresponding equations are given in Equations (27)–(30).

For the maximum displacement difference $A_1$ a step function is chosen to guarantee that a certain threshold value $A_{1,max}$ is never exceeded, which may result from practical considerations in the application ((27), with H denoting the Heaviside step function). For the mean displacement $A_2$, a quadratic weighting function is chosen with the optimization parameter $\zeta$. This accounts for the assumption that the vibration of the system should be as low as possible at all times for a good performance (Equation (28)). For the overall mass M, a linear weighting function is chosen with the optimization parameter $\xi$, assuming that any additional mass is seen as disadvantageous in the application (Equation (29)). For the damage D, again a step function is chosen with a threshold value $d_{max}$, taking into account that in many engineering problems a minimum lifetime must be guaranteed, but no further requirements regarding lifetime are made (Equation (29)). The formulation of these weighting functions and the specification of the parameters can be adjusted to each individual application scenario considering further requirements and boundary conditions of the system.

$$\begin{array}{ccc}\hfill S_{A1}& =& \mathrm{H}(A_1-A_{1,max})\hfill \end{array}$$

(27)

$$\begin{array}{ccc}\hfill S_{A2}& =& \zeta {\left(A_2\right)}^2\hfill \end{array}$$

(28)

$$\begin{array}{ccc}\hfill S_M& =& \xi (M-m_0)\hfill \end{array}$$

(29)

$$\begin{array}{ccc}\hfill S_D& =& \mathrm{H}(D-d_{max})\hfill \end{array}$$

(30)

The summation of the weighting functions results in the overall cost function S (31) that needs to be minimized.

$$S=S_{A1}+S_{A2}+S_M+S_D$$

(31)

The optimization parameters for this example are set to $A_{1,max}=30$ mm, $\zeta =0.005$ 1/mm², $\xi =0.1$ 1/kg and $d_{max}$ = 0.001 as an initial guess. The determination of suitable values is not focused on here as the emphasis is on the methodology. Therefore, the values in this context were chosen exemplary. In practice, engineering expertise, experience, and economic considerations and design restrictions will be used in determining the values. The consideration of individual example cases or a pairwise comparison can also be helpful here. Since full factorial data are available, the goal function S can easily be visualized and the minimum value identified. The surface plot of S is shown in Figure 10. The white areas are invalid regions because the cost function is above 1. The parameters of the minimum are given in the first row of

Table 4. Results of the multi-criterial optimization based on the cost function S with different optimization methods: I: full factorial search (2 variable parameters), II: fminsearch (2 variable parameters, start values $m_T$ = 0.150 kg, $k_T$ = 500 N/m), III: fminsearch (2 variable parameters, start values $m_T$ = 0.06 kg, $k_T$ = 340 N/m), IV: fminsearch (3 variable parameters, start values $m_T$ = 0.06 kg, $k_T$ = 340 N/m, ${\vartheta }_T$ = 3%).

Method	${\mathit{m}}_{\mathit{T}}$	${\mathit{k}}_{\mathit{T}}$	${\mathit{\vartheta }}_{\mathit{T}}$	${\mathit{f}}_{\mathit{T}}$	S	Numb.
	kg	N/m	%	Hz	-	Eval.
I	0.0600	340.0	3.0	11.98	0.03443	441
II	0.0976	412.0	3.0	10.34	0.04260	44
III	0.0448	239.2	3.0	11.63	0.03096	485
IV	0.0581	300.4	5.9	11.44	0.02582	485

.

A standard optimization algorithm is used to find an optimum of S. In this case, the function fminsearch of Matlab is implemented, which is based on the simplex search method of Lagarias et al. [36]. Upper and lower limits are additionally implemented and the algorithm was confined to a maximum of 44 evaluations, that is 10% of the number of evaluations of the full factorial simulation. Using the central point of the design space as initial guess ($m_T$ = 0.150 kg, $k_T$ = 500 N/m), the algorithm yields a result that is worse compared to the minimum found by the full-factorial search. This is due to the fact that the function S is not very smooth and the algorithm is susceptible to become caught in local minima. Therefore, the minimum found by the full-factorial search was used as initial guess for another optimization run, yielding now an improved design point. The values of these two optimization runs are given in the second and third row of Table 4 and

Table 5. Mono-criterial values of the results of the multi-criterial optimization based on the cost function S with different optimization methods: I—full factorial search (2 variable parameters); II—fminsearch (2 variable parameters, start values $m_T$ = 0.150 kg, $k_T$ = 500 N/m); III—fminsearch (2 variable parameters, start values $m_T$ = 0.06 kg, $k_T$ = 340 N/m); and IV—fminsearch (3 variable parameters, start values $m_T$ = 0.06 kg, $k_T$ = 340 N/m, ${\vartheta }_T$ = 3%).

Method	${\mathit{A}}_1/{\mathit{A}}_{1,\mathit{o}}$	${\mathit{A}}_2/{\mathit{A}}_{2,\mathit{o}}$	$\mathit{M}/{\mathit{M}}_{\mathit{o}}$	$\mathit{D}/{\mathit{D}}_{\mathit{o}}$
I	0.6309	0.4267	1.0300	0.2925
II	0.5424	0.4329	1.0488	0.3009
III	0.5568	0.4227	1.0224	0.2666
IV	0.4670	0.3398	1.0291	0.2090

.

In the optimization runs, the damping ratio has been kept constant at 3%. Finally, an optimization run with the damping ratio as free design variable (within 0.5 and 6%, accounting for practical limitations) is performed, starting from the same design point as before. The results of this optimization process are given in the last row of Table 4 and Table 5.

Finally, all optimization results obtained in this study are visualized in Figure 11 in the three dimensional solution space regarding structural dynamics (in terms of mean displacement $A_2$), lightweight design (in terms of overall mass M) and durability (in terms of damage D). On the left side, the conflict of goals between overall mass and displacement reduction can be seen. Up to an additional mass of 7% an increasing displacement reduction is possible with higher masses, clearly showing a typical Pareto frontier for these objectives with the optimum found by method I being part of the front line. The Pareto frontier is defined as the sum of all solutions for which any improvement in one objective can only take place if at least one other objective worsens [37]. The quick optimization run, starting from the centre of the design space (method II), does not reach the Pareto frontier. However, the successive optimization runs starting from the best full factorial value (method III and IV) exceed the Pareto frontier. On the right side, the relationship between displacement reduction and lifetime increase is comprehensible. By and large, a reduction in mean displacement corresponds with the reduction in the damage value; however, this is not true in general as, for some cases, a displacement reduction can also mean a reduction in durability. The dashed line indicates the threshold $d_{max}$.

The results of this simple example show the challenges of multi-criterial optimization. As it can be seen, the full factorial analysis gives a good understanding of the problem and is recommended if the required simulation capacity is available. A pure gradient-based optimization with an arbitrary starting point runs the risk of ending in an unfavourable local minimum due to the complexity of the cost function and should be used with care. A combination of a coarse full-factorial search with a limited number of design parameters and a subsequent gradient-based optimization starting from a previously found minimum can yield satisfactory results with justifiable numerical effort. However, more complex search algorithms that are designed to search for global minima like particle swarm, surrogate, or pattern search are also possible options [38]. As can be seen, numerical optimization processes need many evaluations and can rapidly become time-consuming for complicated structures in the time domain. In these cases, an evaluation of both the structural dynamics and the durability is recommended in the frequency domain, which is typically accompanied by a loss in accuracy in assessment [39], but which will lead to better optimization results within a limited computation time.

4. Conclusions

In this paper, a numerical approach for optimizing lightweight structures that are subjected to dynamic loads has been presented. This simulative approach takes into account both the structural dynamics and the lifetime assessment of the most critical welds. The focus has been on the method itself, which has been presented and discussed by means of a simple structure with parameterized absorbers. For this aim, we demonstrated how to establish a numerical valid reduced order model for stress evaluation in time from a full order model and what advantages can be achieved. Furthermore, a general optimization process was handled and specific results for mono-criteria and multi-criteria optimization approaches were presented.

From the investigations, the following main conclusions can be drawn:

• Numerically efficient assessment of dynamically loaded structures with critical welds is possible using reduced order model methods and structural stress approach;
• For a limited number of design variables, a full factorial simulation helps to understand the system and identify conflicting objectives between different criteria;
• If a single cost function is defined combining the different objectives, a careful selection of the optimization algorithm and start values is recommended in order to avoid trusting optimization results arising from local minima;
• Moreover, the robustness of the optimum should be analysed with respect to the optimization parameters. In case of doubt, a robust, less good design point is preferable to an optimal but very sensitive design point.

Current and future work is focused on applying this method to more practical structures and also to integrate techniques of parametric model order reduction in order to consider a variation of, e.g., sheet thicknesses. Moreover, more sophisticated multi-criterial optimization algorithms will be used which can also address and analyse the robustness of the identified optimal design points. Beyond this, a more holistic approach will be developed to simplify the initialization and optimization procedure for easy and safe industrial handling.