Vibration Characteristics of Flexible Steel Plate on Proposed Magnetic Levitation System Using Gravity
Abstract
1. Introduction
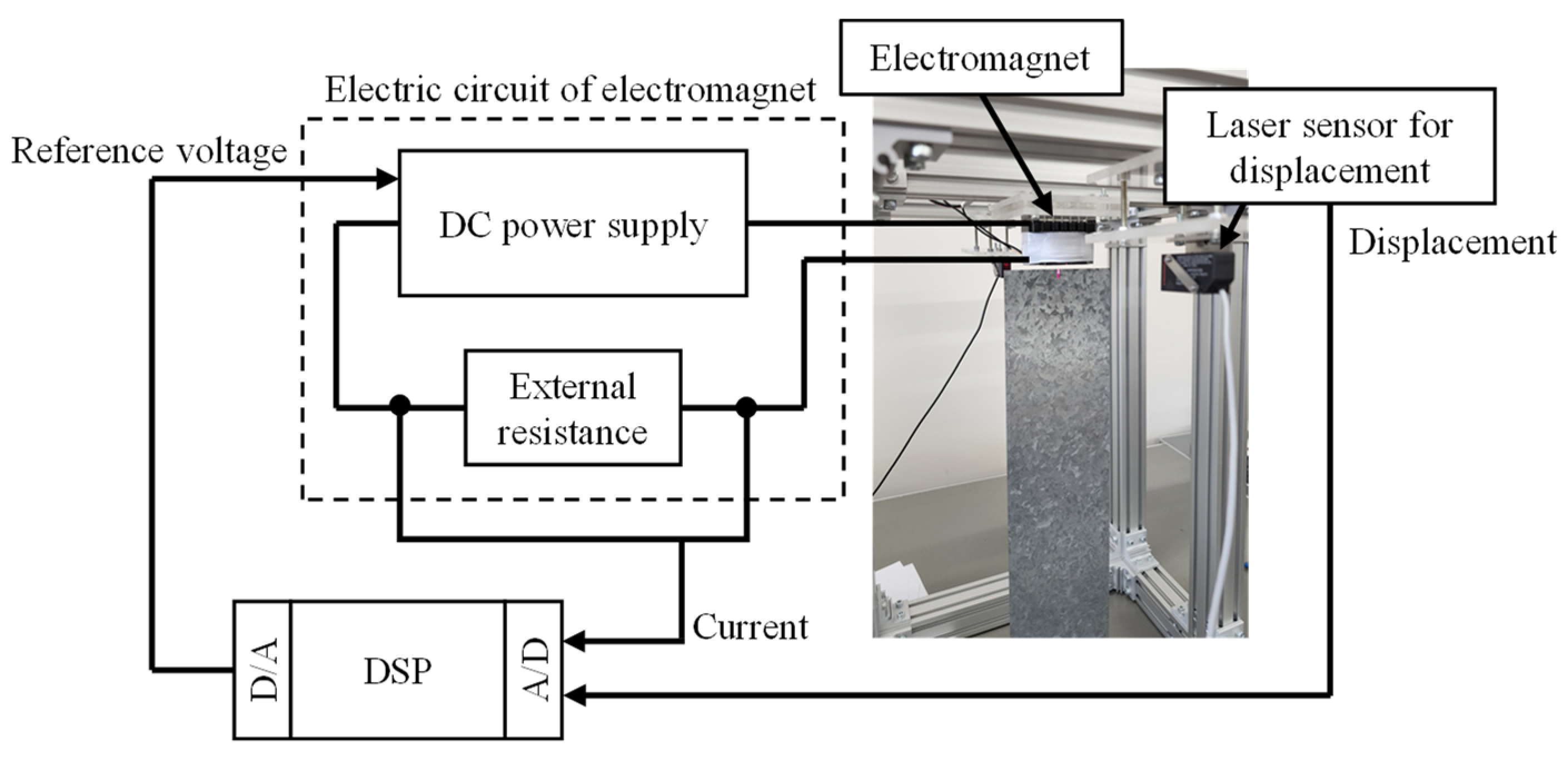
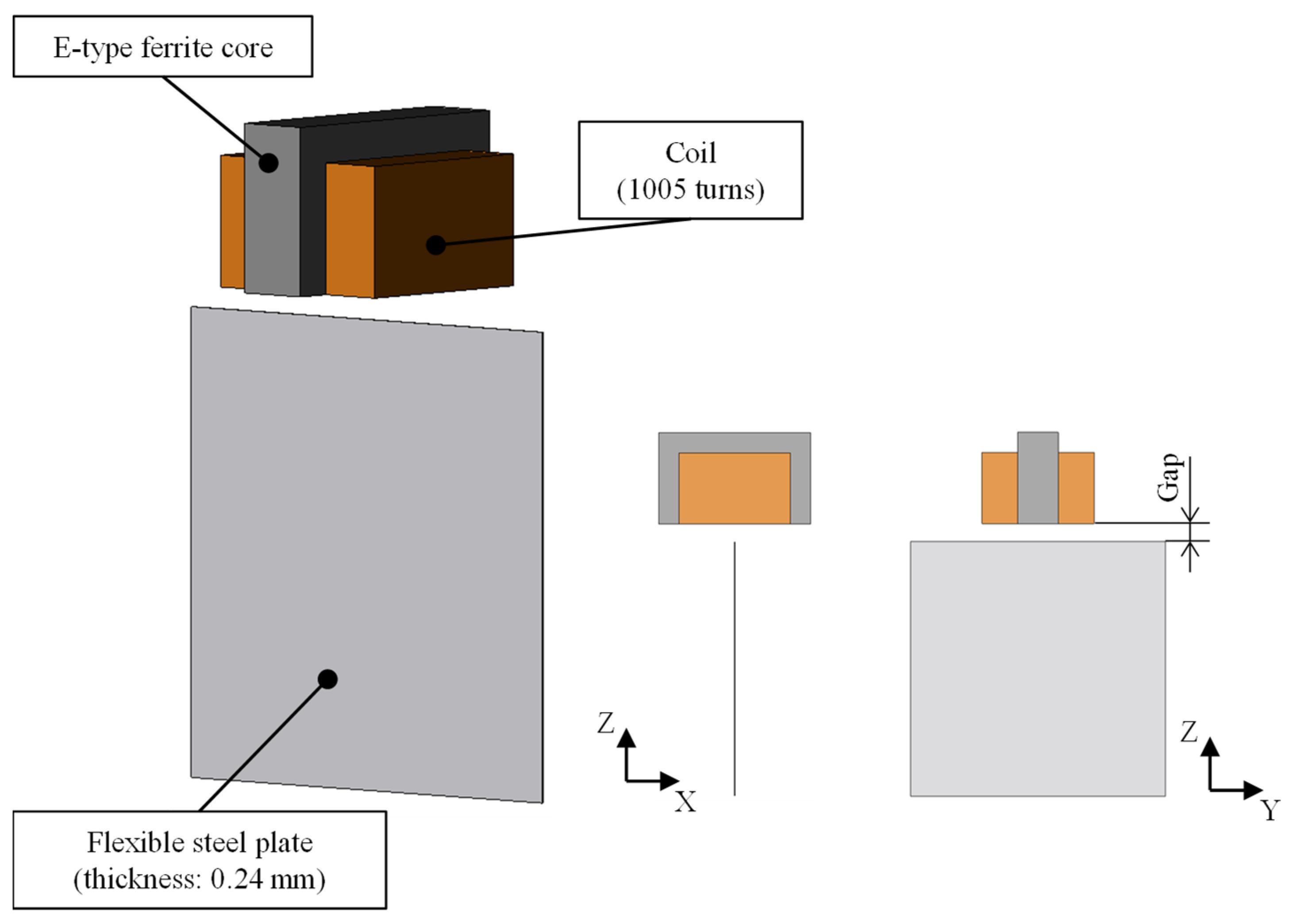
2. Proposed Magnetic Levitation System for Flexible Steel Plate
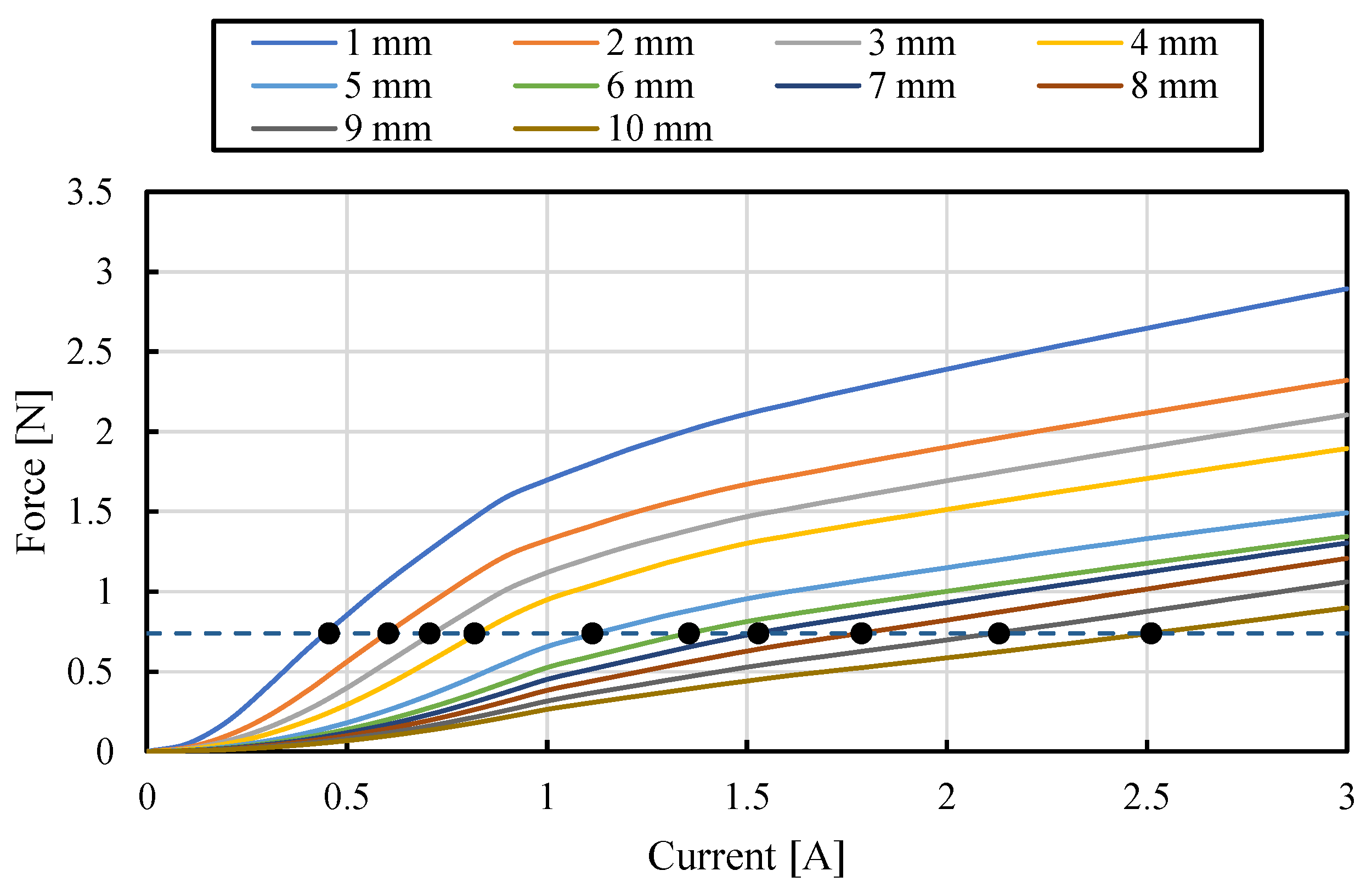
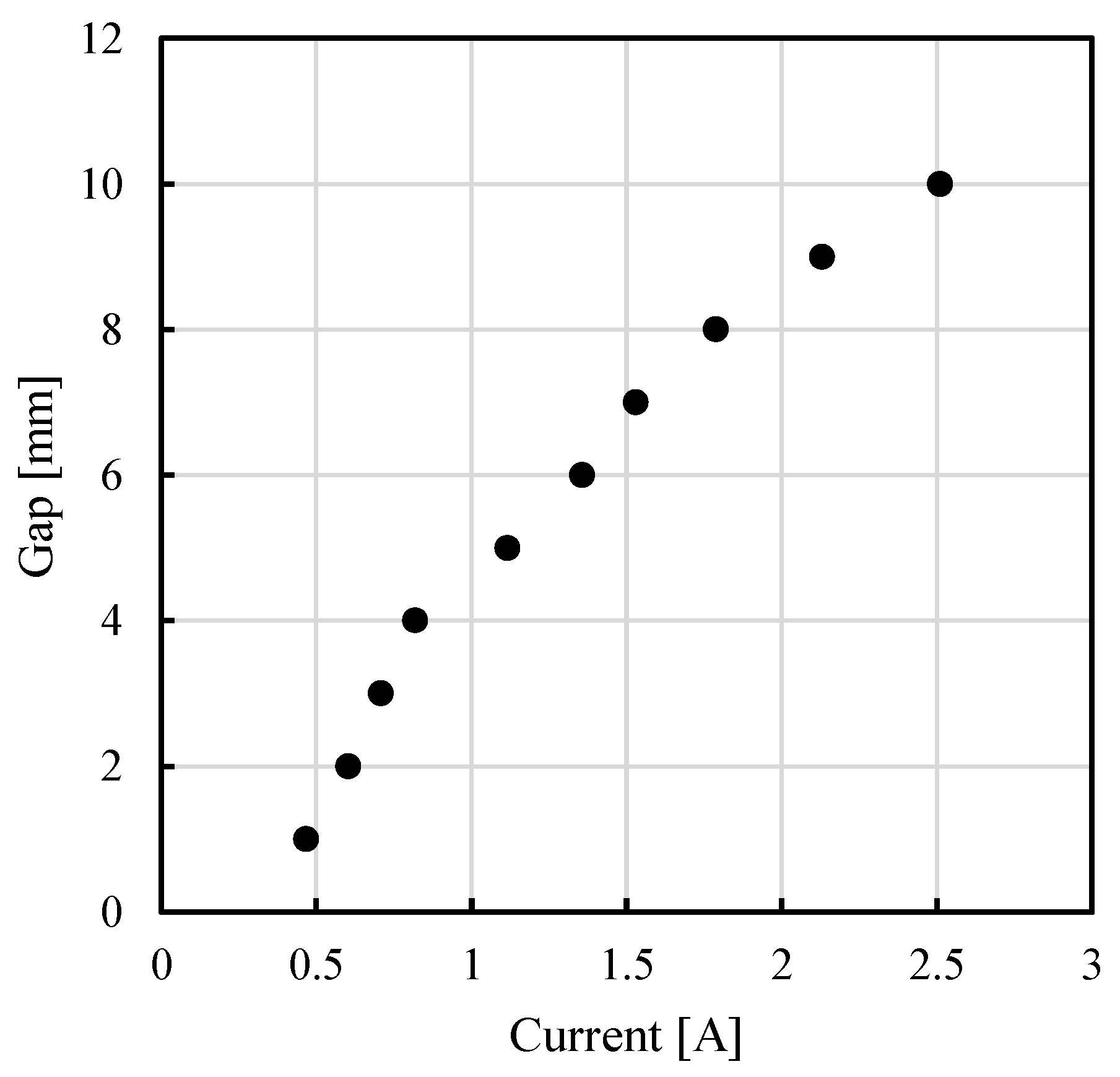
3. Attractive Force of Proposed Magnetic Levitation System
4. Control System for Levitating Flexible Steel Plate
5. Vibration Characteristics of a Levitating Flexible Steel Plate
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Murakami, I.; Zhao, Y.; Tashiro, T. Stabilization of a Magnetic Repulsive Levitation Flywheel System Using a High-Efficiency Superconducting Magnetic Bearing. Actuators 2022, 11, 180. [Google Scholar] [CrossRef]
- Stettinger, G.; Benedikt, M.; Horn, M.; Zehetner, J.; Giebenhain, C. Control of a magnetic levitation system with communication imperfections: A model-based coupling approach. Control Eng. Pract. 2017, 58, 161. [Google Scholar] [CrossRef]
- Xu, F.; Zhang, K.; Xu, X. Development of Magnetically Levitated Rotary Table for Repetitive Trajectory Tracking. Sensors 2022, 22, 4270. [Google Scholar] [CrossRef]
- Dalwadi, N.; Deb, D.; Muyeen, S.M. A Reference Model Assisted Adaptive Control Structure for Maglev Transportation System. Electronics 2021, 10, 332. [Google Scholar] [CrossRef]
- Ismail, L.S.; Lupu, C.; Alshareefi, H. Design of Adaptive-RST Controller for Nonlinear Magnetic Levitation System Using Multiple Zone-Model Approach in Real-Time Experimentation. Appl. Syst. Innov. 2022, 5, 93. [Google Scholar] [CrossRef]
- Belmonte, L.M.; Segura, E.; Fernández-Caballero, A.; Somolinos, J.A.; Morales, R. Generalised Proportional Integral Control for Magnetic Levitation Systems Using a Tangent Linearisation Approach. Mathematics 2021, 9, 1424. [Google Scholar] [CrossRef]
- Gopi, R.S.; Srinivasan, S.; Panneerselvam, K.; Teekaraman, Y.; Kuppusamy, R.; Urooj, S. Enhanced Model Reference Adaptive Control Scheme for Tracking Control of Magnetic Levitation System. Energies 2021, 14, 1455. [Google Scholar] [CrossRef]
- Hayashiya, H.; Ohsaki, H.; Masada, E. A combined lift and propulsion system of a steel plate by transverse flux linear induction motors. IEEE Trans. Magn. 1999, 35, 4019. [Google Scholar] [CrossRef]
- Ohji, T.; Shinkai, T.; Amei, K.; Sakui, M. Application of Lorentz force to a magnetic levitation system for a non-magnetic thin plate. J. Mater. Process. Technol. 2007, 181, 40. [Google Scholar] [CrossRef]
- Odajima, Y.; Takada, Y.; Oikawa, I.; Nakagawa, T. Construction and levitation guidance experiment of magnetic levitation system without gap sensors using inductance model of thin steel plates. Electr. Eng. Jpn. 2019, 206, 32. [Google Scholar] [CrossRef]
- Arita, Y.; Ota, K.; Oikawa, I.; Nakagawa, T. A proposal of magnetic levitation system without using sideslip-sensors and actuators in guidance control. In Proceedings of the 20th International Conference on Electrical Machines and Systems, Sydney, Australia, 11–14 August 2017; Volume 20, p. 1. [Google Scholar] [CrossRef]
- Liu, C.T.; Yang, Y.Y.; Lin, S.Y. On-line realizations of dynamic gap detection and control for levitated industrial steel plate conveyance system. In Proceedings of the IEEE Industry Applications Society Annual Meeting, Las Vegas, NV, USA, 7–11 October 2012. [Google Scholar] [CrossRef]
- Liu, C.T.; Yang, Y.Y.; Lin, S.Y. Development of an Automatic Online Gap-Detection Scheme for Levitated Industrial Steel-Plate Conveyance System. IEEE Trans. Ind. Appl. 2008, 44, 517. [Google Scholar] [CrossRef]
- Kundu, J.; Sengupta, M. Design, analysis, fabrication, control and comparative study of two different-shaped plate levitation prototypes. Sādhanā 2020, 45, 53. [Google Scholar] [CrossRef]
- Guney, O.F.; Bozkurt, A.F.; Erkan, K. Centralized gap clearance control for maglev based steel-plate conveyance system. Adv. Electr. Comput. Eng. 2017, 17, 101. [Google Scholar] [CrossRef]
- Choi, J.S.; Baek, Y.S. Magnetically-Levitated Steel-Plate Conveyance System Using Electromagnets and a Linear Induction Motor. IEEE Trans. Magn. 2008, 44, 4171. [Google Scholar] [CrossRef]
- Matsumoto, S.; Arai, Y.; Nakagawa, T. Noncontact Levitation and Conveyance Characteristics of a Very Thin Steel Plate Magnetically Levitated by a LIM-Driven Cart. IEEE Trans. Magn. 2014, 50, 8600304. [Google Scholar] [CrossRef]
- Namerikawa, T.; Mizutani, D.; Robust, H. DIA Control of Levitated Steel Plates. IEEJ Trans. Ind. Appl. 2006, 126, 1319. [Google Scholar] [CrossRef]
- Hasegawa, S.; Oshinoya, Y.; Ishibashi, K. Consideration on Elastic Vibration Control of a Magnetically Levitated Thin Steel Plate Using Sliding Mode Control. JSME Int. J. Ser. C Mech. Syst. Mach. Elem. Manuf. 2006, 49, 983. [Google Scholar] [CrossRef]
- Ogawa, K.; Miyazaki, R.; Uchida, Y.; Kobayashi, I.; Kuroda, J.; Uchino, D.; Ikeda, K.; Kato, T.; Endo, A.; Narita, T.; et al. Experimental Consideration on Suppression Effect of Elastic Vibration in Electromagnetic Levitation System for Flexible Thin Steel Plate with Curvature. Vibration 2022, 5, 817–828. [Google Scholar] [CrossRef]
- Takada, Y.; Kimura, T.; Nakagawa, T. Influence of Inductance Properties on a Magnetic Levitation for Thin-Steel Plates. IEEE Trans. Magn. 2017, 53, 2500705. [Google Scholar] [CrossRef]
- Suzuki, O.; Nagashima, D.; Nishimura, K.; Nakagawa, T. Magnetic Levitation Control by Considering the Twisting Mode of a 0.18 mm Thick Steel Plate. IEEE Trans. Magn. 2015, 51, 8600304. [Google Scholar] [CrossRef]
- Ogawa, K.; Funada, K.; Narita, T.; Kato, H. Vibration suppression effect in an electromagnetic levitation system for flexible steel plate: Experimental consideration on levitation performance using sliding mode control. In Proceedings of the International Conference on Motion and Vibration Control, Toki Messe, Niigata, 8–11 September 2020; p. 10112. [Google Scholar] [CrossRef]
- Ogawa, K.; Tada, M.; Narita, T.; Kato, H. Electromagnetic Levitation Control for Bending Flexible Steel Plate: Experimental Consideration on Disturbance Cancellation Control. Actuators 2018, 7, 43. [Google Scholar] [CrossRef]
- Ito, Y.; Oda, Y.; Kato, T.; Liu, X.; Endo, A.; Ikeda, K.; Narita, T.; Kato, H. Basic study on effect of transport acceleration in electromagnetic levitation system for thin steel plate. Int. J. Appl. Electromagn. Mech. 2020, 64, 597. [Google Scholar] [CrossRef]
- Ito, Y.; Oda, Y.; Narita, T.; Kato, H. Effect of Optimal Placement of Permanent Magnets on the Electromagnetic Force in the Horizontal Direction. Actuators 2018, 7, 54. [Google Scholar] [CrossRef]
- Narita, T.; Oda, Y.; Ito, Y.; Kato, H. A basic study on levitation characteristics of metal foil by edge-supported electromagnetic levitation system. Int. J. Appl. Electromagn. Mech. 2020, 64, 1191. [Google Scholar] [CrossRef]
- Narita, T.; Kida, M.; Suzuki, T.; Kato, H. Study on Electromagnetic Levitation System for Ultrathin Flexible Steel Plate Using Magnetic Field from Horizontal Direction. J. Magn. Soc. Jpn. 2017, 41, 14. [Google Scholar] [CrossRef]
- Narita, T.; Oda, Y.; Ito, Y.; Okuno, K.; Kato, H. Positioning Control for Flexible Steel Plate Using Facing Electromagnetic Actuator: Fundamental Consideration on Support Characteristic of Electromagnetic Actuator. In Proceedings of the 16th International Conference on New Actuators, Bremen, Germany, 25–27 June 2018; p. 344. [Google Scholar]
- Oda, Y.; Ito, Y.; Okuno, K.; Kida, M.; Suzuki, T.; Narita, T.; Kato, H.; Moriyama, H. A Study on Edge Supported Electromagnetic Levitation System: Fundamental Consideration on Levitation Performance of Thin Steel Plate. In Proceedings of the International Power Electronics Conference, Niigata, Japan, 20–24 May 2018; p. 2324. [Google Scholar] [CrossRef]
- Oda, Y.; Kida, M.; Suzuki, T.; Narita, T.; Kato, H.; Moriyama, H. Basic study on edge supported electromagnetic levitation system for flexible steel plate. Int. J. Appl. Electromagn. Mech. 2019, 59, 985. [Google Scholar] [CrossRef]
- Oda, Y.; Ito, Y.; Okuno, K.; Kida, M.; Suzuki, T.; Endo, A.; Narita, T.; Kato, H.; Moriyama, H. Evaluation on Edge-supported Magnetic Levitation Apparatus for Thin Steel Plates. J. Magn. Soc. Jpn. 2019, 43, 11. [Google Scholar] [CrossRef]



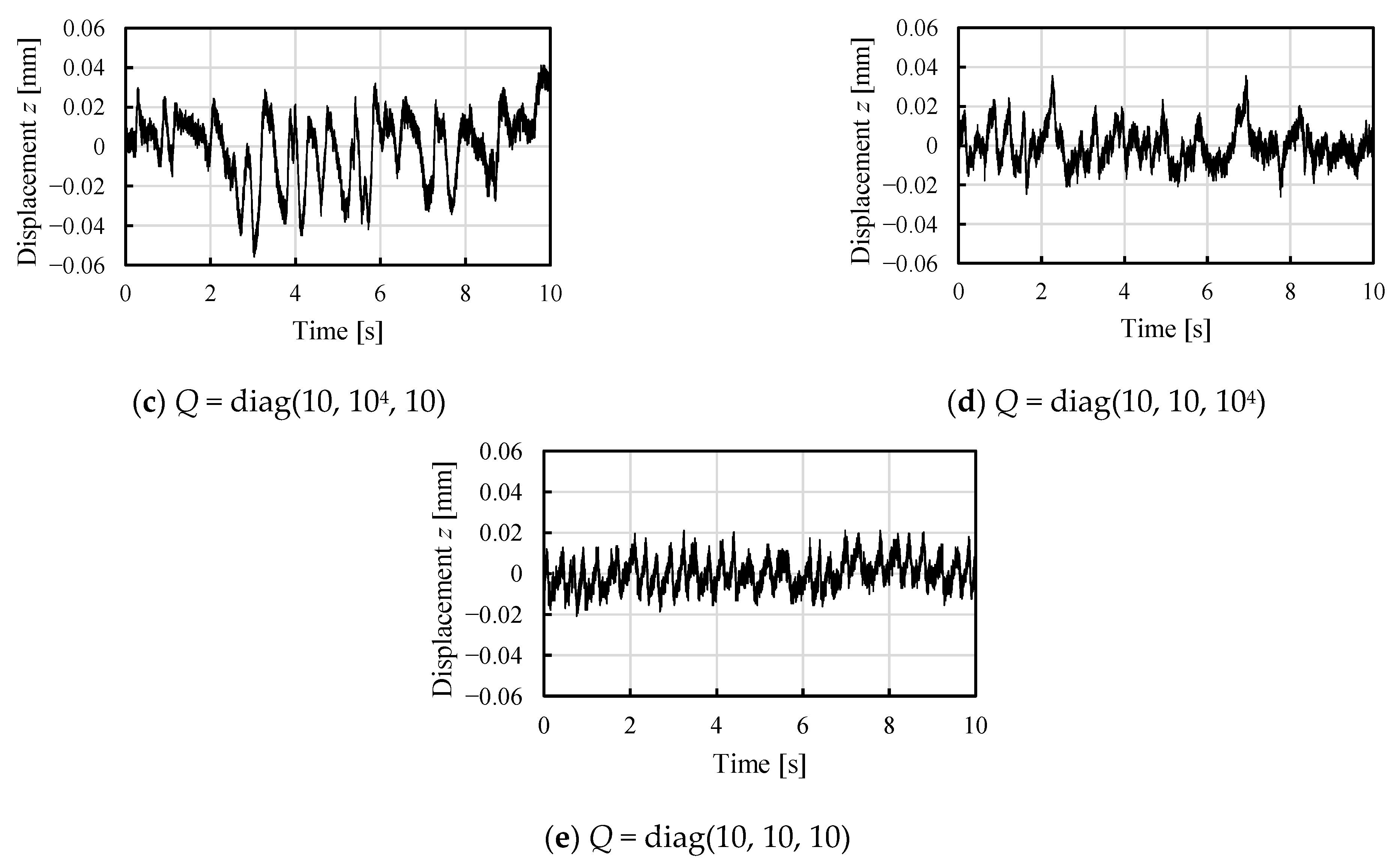
| No. | Weighting Factor Q = Diag(q1, q2, q3) (q1: For Displacement z, q2: For Velocity dz/dt, q3: For Current i) |
|---|---|
| (a) | Q = diag(109, 10, 10) |
| (b) | Q = diag(104, 10, 10) |
| (c) | Q = diag(10, 104, 10) |
| (d) | Q = diag(10, 10, 104) |
| (e) | Q = diag(10, 10, 10) |
| Type | Gap [mm] |
|---|---|
| Analytical | 5.94 |
| Experimental | 5.75 |
| Weighting Coefficient Q | Standard Deviations of Displacement z [mm] | |
|---|---|---|
| (a) | Q = diag(109, 10, 10) | 0.0033 |
| (b) | Q = diag(104, 10, 10) | 0.0117 |
| (c) | Q = diag(10, 104, 10) | 0.0255 |
| (d) | Q = diag(10, 10, 104) | 0.0129 |
| (e) | Q = diag(10, 10, 10) | 0.0083 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Endo, A.; Itoyama, R.; Kuroda, J.; Uchino, D.; Ogawa, K.; Ikeda, K.; Kato, T.; Narita, T.; Kato, H. Vibration Characteristics of Flexible Steel Plate on Proposed Magnetic Levitation System Using Gravity. Vibration 2022, 5, 936-945. https://doi.org/10.3390/vibration5040054
Endo A, Itoyama R, Kuroda J, Uchino D, Ogawa K, Ikeda K, Kato T, Narita T, Kato H. Vibration Characteristics of Flexible Steel Plate on Proposed Magnetic Levitation System Using Gravity. Vibration. 2022; 5(4):936-945. https://doi.org/10.3390/vibration5040054
Chicago/Turabian StyleEndo, Ayato, Rintaro Itoyama, Jumpei Kuroda, Daigo Uchino, Kazuki Ogawa, Keigo Ikeda, Taro Kato, Takayoshi Narita, and Hideaki Kato. 2022. "Vibration Characteristics of Flexible Steel Plate on Proposed Magnetic Levitation System Using Gravity" Vibration 5, no. 4: 936-945. https://doi.org/10.3390/vibration5040054
APA StyleEndo, A., Itoyama, R., Kuroda, J., Uchino, D., Ogawa, K., Ikeda, K., Kato, T., Narita, T., & Kato, H. (2022). Vibration Characteristics of Flexible Steel Plate on Proposed Magnetic Levitation System Using Gravity. Vibration, 5(4), 936-945. https://doi.org/10.3390/vibration5040054






