Co-Simulation-Based Verification of Torsional Vibration Protection of Electric-Driven Railway Vehicle Wheelsets

Abstract

Torsional vibration is an oscillation phenomenon occurring at driven railway vehicle wheelsets. As the resulting dynamic stresses can be significantly larger than the maximum static motor torque, axle and press fit are at risk of failure. To prevent dangerous vibration events and with these, press fit and axle from failure, traction drive manufactures nowadays used to implement vibration suppression algorithms in drive controls. In this paper, the effectiveness of such suppression algorithms is analyzed. Furthermore, as a pilot survey, we analyze to what extend traction controls influence the excitation of torsional vibration.

1. Introduction

The oscillation phenomenon torsional vibration has been known since the 1980s when the first three-phase drives with traction controls for a high force utilisation were developed. Torsional vibration was found to be a self-excited oscillation of the wheelset, which cannot actively be damped by an appropriately designed traction control. Therefore, in the following decades, torsional vibration was tolerated as no further safety concerns appeared. This changed in 2010, when wheel twists were found on traction vehicles [1]. The cause of these twists was investigated in measurements, and torsional vibration was found to result in exceeding the maximum transferable torque between wheel and axle.

Subsequently, research was undertaken to predict the highest dynamic torque resulting from torsional vibration. Railway vehicle manufacturers wanted to consider it in the design phase and enable appropriate dimensioning of a new wheelset. No suitable prediction method could be developed. However, several approaches have been published to simulate torsional vibration. Some of these models aim to predict maximum dynamic torque as described before whereas others are used to investigate the vibration phenomenon itself. A summary of these approaches is given in the following.

Yu and Breuer [2] and Weinhardt [3] tried to predict the maximum dynamic torque with empirical or semi-empirical methods. These models could not be transferred to other traction drive-wheelset configurations but to those they are based on. In a similar way, Szolc [4], Schneider [5] and Saur [6,7,8] used analytical simulation methods to predict maximum dynamic torque. However for these models no validation on measurements is documented.

Further investigations on the physics of torsional vibration have been performed by Liu et al. [9], Xu et al. [10], Konowrocki and Szolc [4], Meierhofer et al. [11] and Fridrichovsky and Sulc [12]. First investigations on the physics of torsional vibrations have already been documented by Körner [13], Schwartz [14] and Buscher [15] in the 1980s. These investigations lack to provide dependencies between the amplitude of torsional vibration and the physical conditions under which they appear.

Finally, such dependencies were discovered in measurements documented in a study by Trimpe and Salander [16]. These dependencies are further investigated in simulations published in Trimpe et al. [17]. These simulations consider the traction control as a relevant influence for the development of torsional vibration. As the traction control used in Trimpe et al. [17] does not feature any torsional vibration suppression methods as documented in Abouzeid et al. [18], the influence of such suppression methods is investigated in this article. Basing on this, the novelty of the article at hand is firstly to introduce a simulation procedure enabling realistic simulation of torsional vibration. Here, realistic simulation especially means the implementation of vibration excitation by changing wheel–rail conditions. Secondly, the article at hand shall validate the effectiveness of a torsional vibration protection implementation.

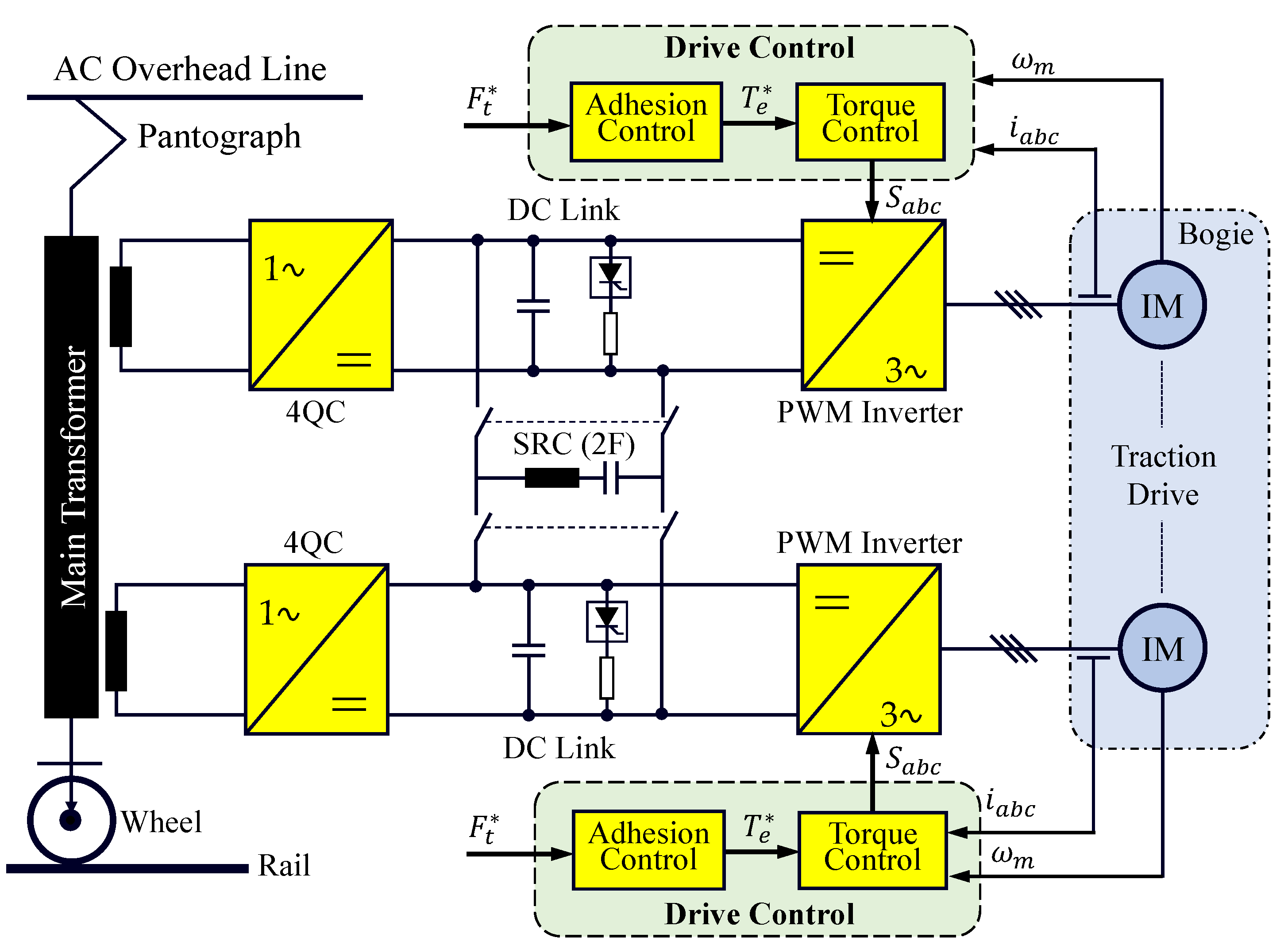
2. System Description

In this section, a system overview for a high-performance locomotive is presented. The main circuit elements are given in Figure 1 based on the energy flow from the electrical input (overhead line) to the mechanical output (drive train) of the locomotive.

Firstly, the pantograph, mounted on top of the locomotive, transfers the electrical energy from the AC overhead line to the main transformer. The AC transmission can be 25 kV/50 Hz or 15 kV/16.7 Hz based on the country, however, cross-border locomotives are equipped with generalized transformers that meet each country’s standards. The main transformer consists of a primary high-voltage winding with multiple secondary windings supplying both the traction converters and the auxiliary inverters for on-board purposes, like heating/cooling, lighting, etc.

Then, the traction converter transforms the single-phase input, connected to the main transformer winding, into the three-phase modulated output connected to the traction motor. The traction converter includes the following elements:

• the four-quadrant chopper (4QC),
• the DC-link,
• the switched inverter.

The 4QC is used to provide and regulate the DC voltage of the DC-link. Meanwhile, the DC-link capacitor is used to smooth the effects of power unbalances between 4QC and the inverter. A series resonant circuit (2F) is included to filter the second harmonic content of the line frequency generated by the 4QC due to the single-phase AC input. In addition, a chopper module is added to the DC-link to prevent the capacitor from overvoltages.

After that, the PWM inverter inverts the regulated DC-link voltage to a three-phase voltage with variable amplitude and frequency to feed the traction motor. This function is achieved by the electrical drive control unit which regulates the traction force according to the locomotives’ driver commands. Induction machines (IMs) are commonly used in traction systems for railways due to their robustness with less maintenance requirements, their independency on rare-earth materials (e.g., magnets), and the possibility of feeding more than one motor from a single inverter [19].

Finally, the electromagnetic torque developed by the traction motor (IM) is transferred to the wheels through the mechanical drive train. This transmitted torque provides tangential (traction) force which depends on the wheel–rail condition.

2.1. Electric Drive

High performance locomotives operate with individual axle control i.e., each wheelset is fed from an independent PWM inverter (see Figure 1). Thanks to this, high utilization of wheel–rail adhesion can be achieved. The electric drive control is responsible for achieving the traction force $F_t^{*}$ demanded by the locomotive driver which consists of two cascaded control loops:

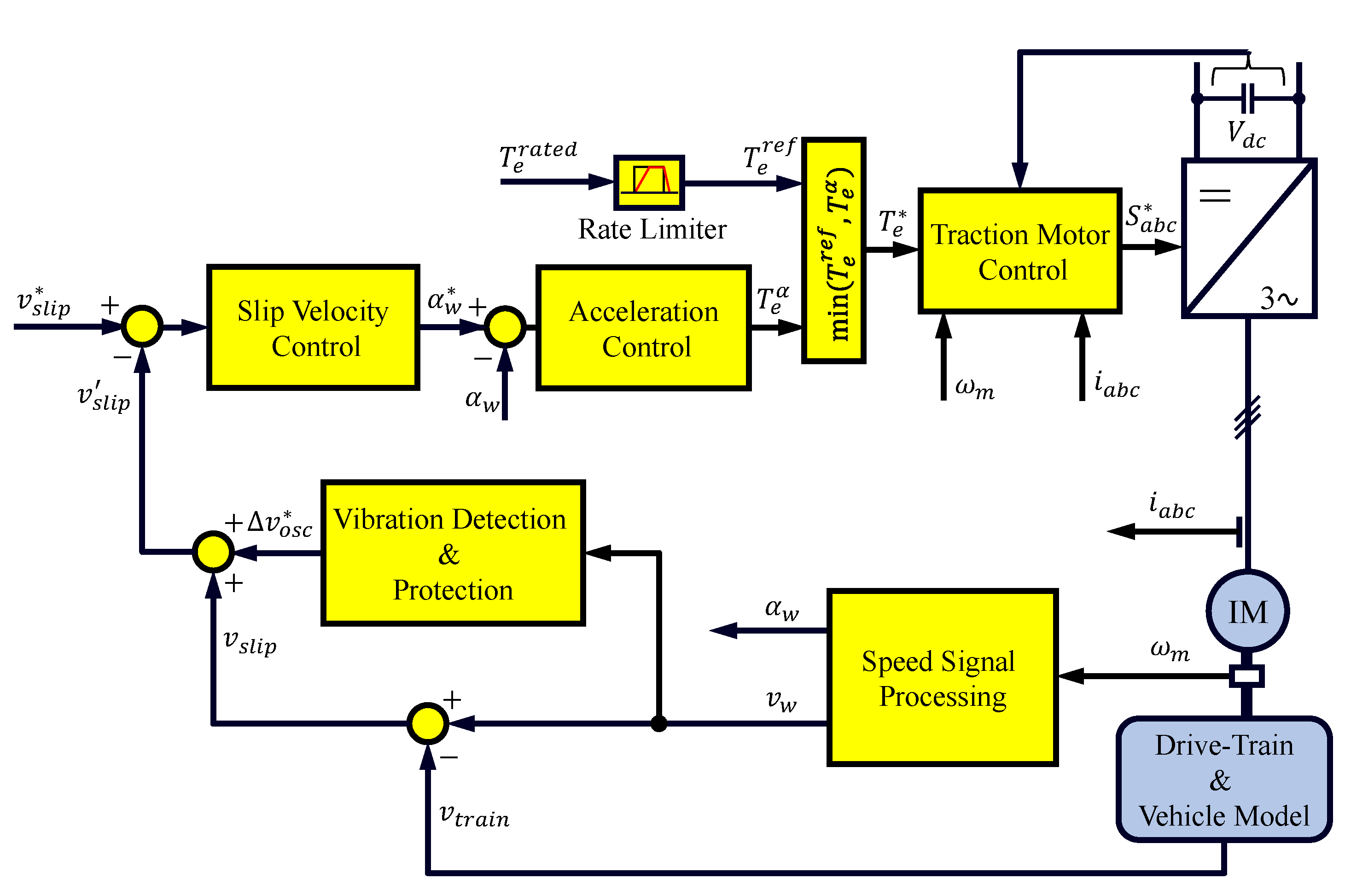
• Adhesion control. This control loop aims to adapt the wheel–rail adhesion level (i.e., the tractive/breaking force) besides preventing the wheel from slipping during acceleration/deceleration of the locomotive or due to changing of the wheel–rail contact conditions caused by slippery rails. More details will be discussed in Section 3.1.
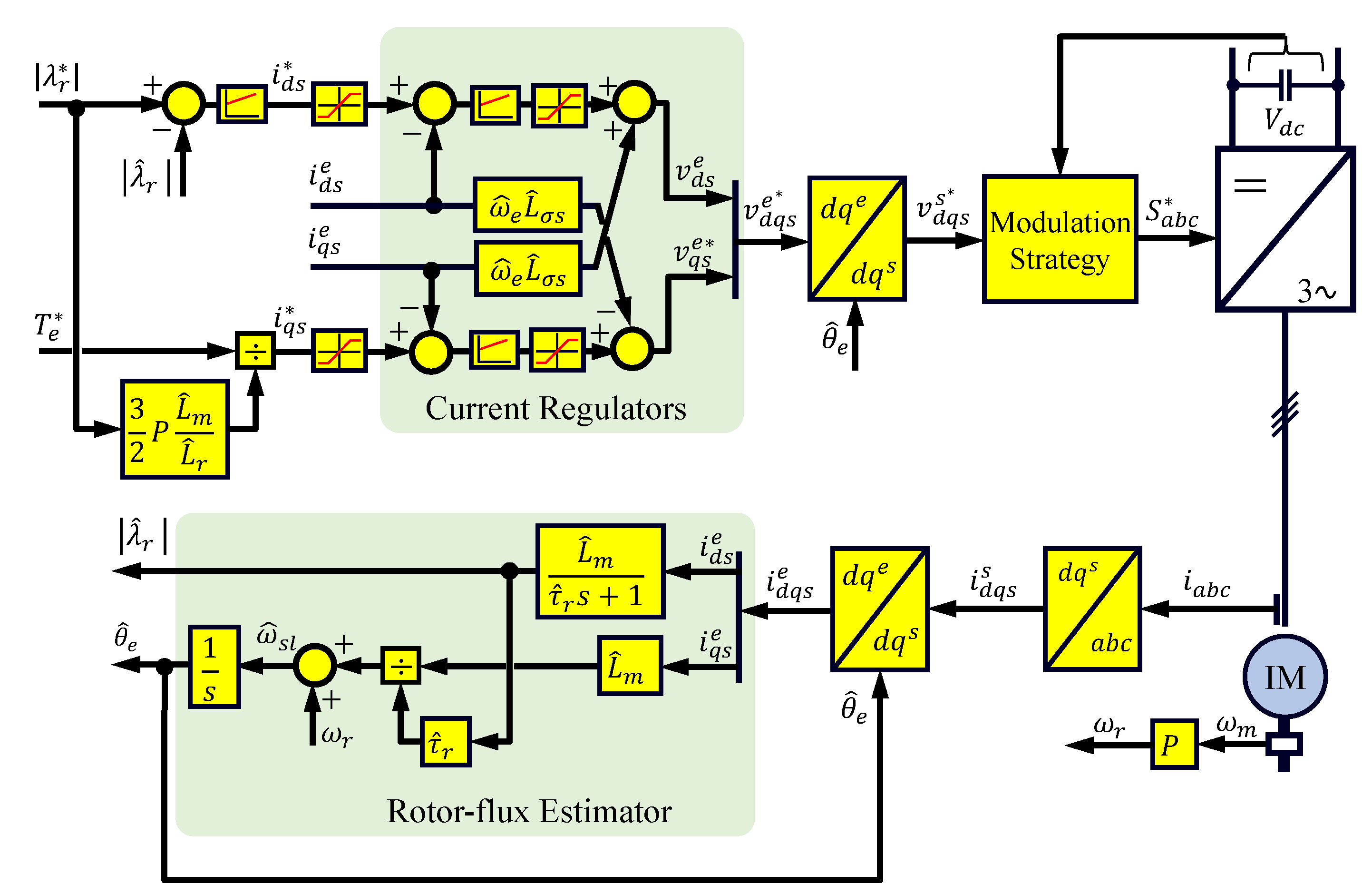
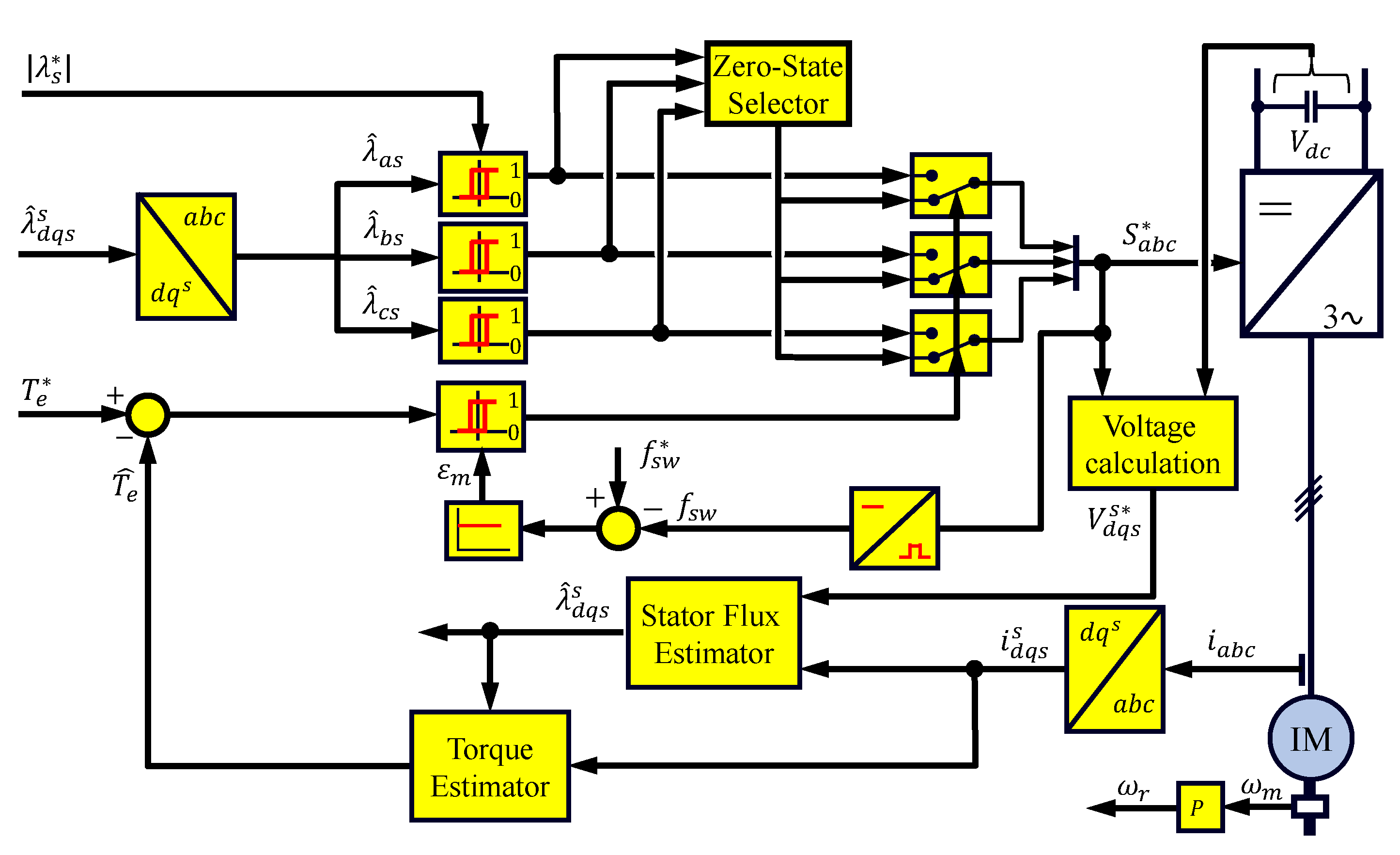
• Torque control. A precise, high dynamic torque control is needed to assure that the machines’ actual torque follows the demanded torque $T_e^{*}$ by the outer adhesion controller. Modern traction drives are equipped with different control strategies, which can change dynamically based on the operating speed [18]. Mainly, vector control schemes are used to decouple the torque and flux components of the machine’s current, which allows to fully exploit machine torque capability without surpassing machine or power converter current limits. Typically rotor flux field-oriented control (RFOC) tuned with a high bandwidth is used (see Figure 2). In this scheme, the d-axis of the rotating reference frame is aligned with the rotor flux, i.e., ${\widehat{\lambda }}_{dqr}^e={\widehat{\lambda }}_{dr}^e={\widehat{\lambda }}_r$, the stator voltage and the stator flux equations become (1) and (2), where ${\omega }_e$ is the angular speed in electrical units of the synchronous reference.

  $$\begin{array}{cc}\hfill v_{dqs}^e& =\widehat{R_s^{\prime }}{i}_{dqs}^e+p{\widehat{\lambda }}_{dqs}^e+j{\omega }_e{\widehat{\lambda }}_{dqs}^e\hfill \end{array}$$

  (1)

  $$\begin{array}{cc}\hfill {\widehat{\lambda }}_{dqs}^e& =\frac{{\widehat{L}}_m}{{\widehat{L}}_r}{\widehat{\lambda }}_{dqr}^e+{\widehat{L}}_{\sigma s}{i}_{dqs}^e\hfill \end{array}$$

  (2)

  $${\omega }_e={\omega }_r+{\widehat{\omega }}_{sl};\mathrm{where}{\widehat{\omega }}_{sl}=\frac{{\widehat{L}}_m}{{\widehat{\tau }}_r\left|{\widehat{\lambda }}_r\right|}{i}_{qs}^e$$

  (3)
  Thus, the electromagnetic torque $T_e$ can be represented by (4) in terms of q-axis of stator current and the estimated rotor flux.

  $$T_e=\frac{3}{2}P\frac{{\widehat{L}}_m}{{\widehat{L}}_r}\left|{\widehat{\lambda }}_r\right|i_{qs}^e$$

  (4)
  The main concerns regarding RFOC methods are their sensitivity to rotor resistance, and the degradation of current regulator performance when the inverter operates near its voltage limit. Alternatively, the stator-flux orientation can be used to overcome these limitations, especially at high speeds. Direct Self-Control (DSC) was proposed for high power drives operating with low switching to fundamental frequency ratio (see Figure 3) [21]. Three hysteresis controllers determine the voltage applied to the machine by comparing the command flux magnitude and the estimated one for each phase. A two-level hysteresis torque controller determines the amount of zero voltage vector to be used. Moreover, the switching frequency is controlled by adapting the torque controller hysteresis band using either proportional or proportional-integral (P/PI) controller. DSC produces a symmetrical hexagonal stator flux trajectory to the origin increasing the robustness against input voltage disturbances. From ≈$30\%$ to ≈$85\%$ of base speed, DSC offers a high dynamic response and reduced switching losses, but at the price of a high current ripple. At high speeds ($>\approx$$85\%$ of base speed), zero voltage vectors are not selected anymore, DSC providing, therefore, a natural transition into overmodulation and eventually into six-step [22]. Below ≈$30\%$ of the base speed there is a degradation of the control performance, a detailed description and potential remedial actions can be found in [23,24].

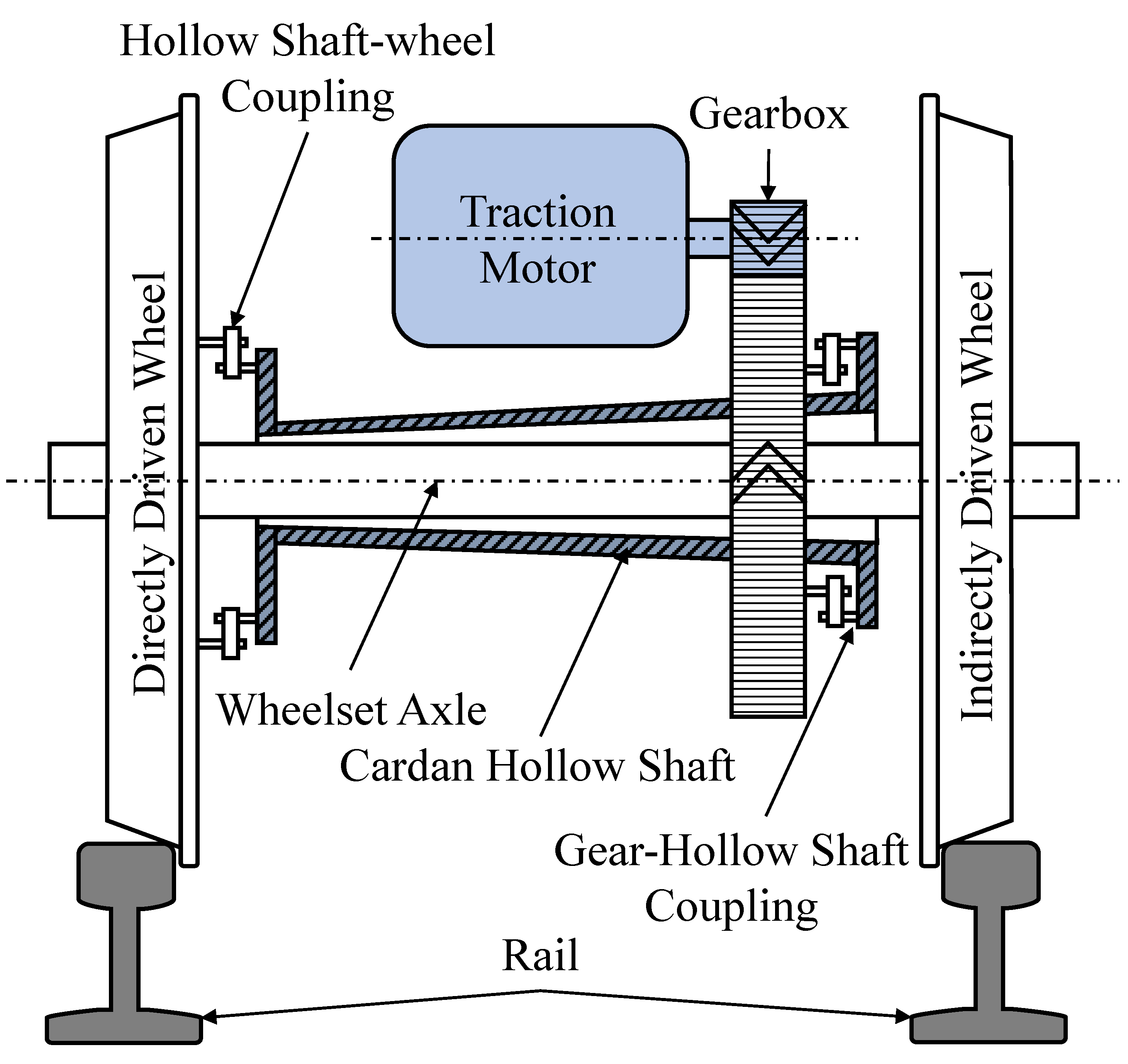
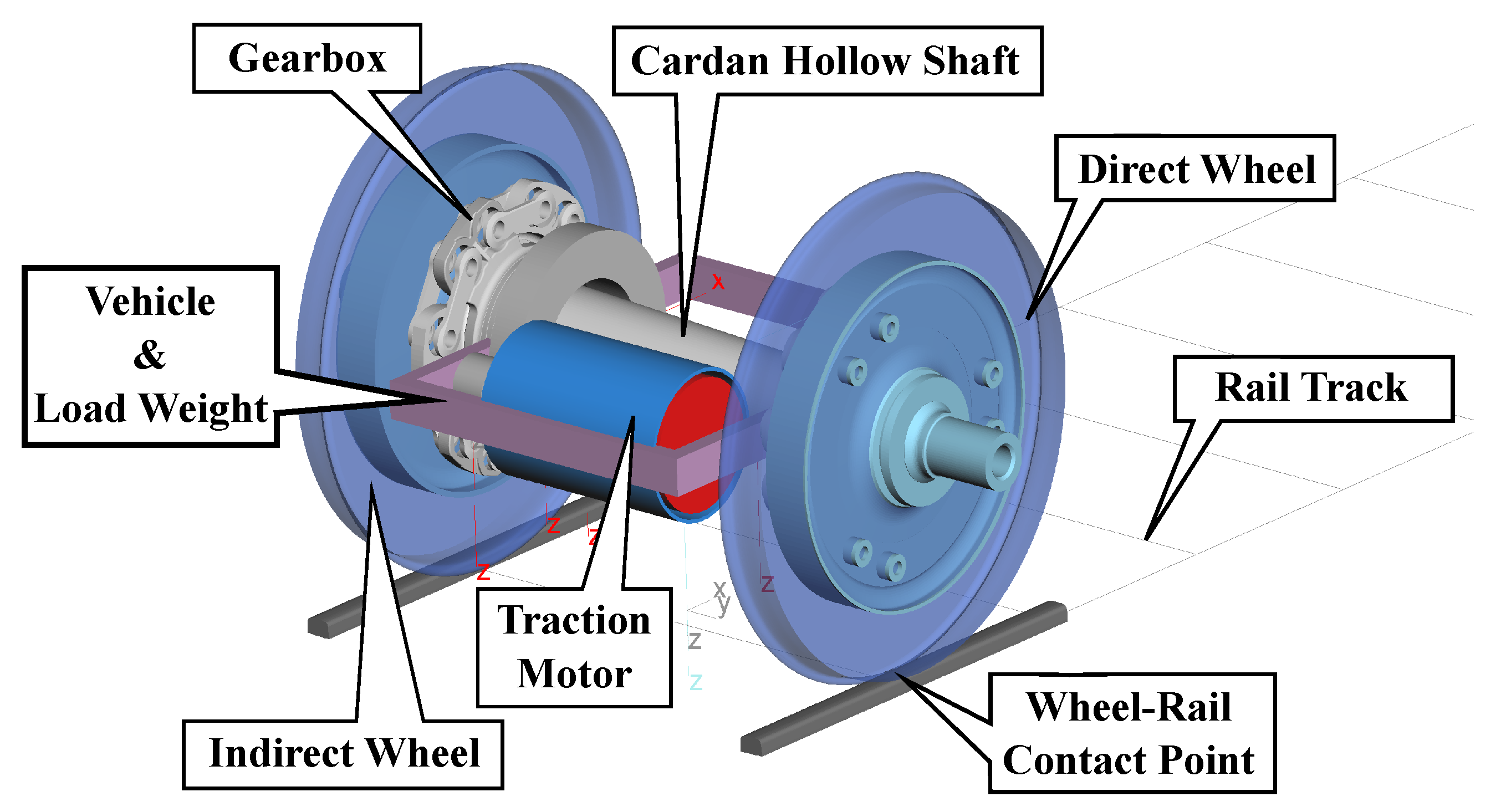
2.2. Mechanical Model of the Drive Train

The mechanical components of the drive train are implemented in a multibody simulation (MBS) model. Figure 4 shows the quarter model of a traction locomotive which is used for the investigations [17]. The mechanical model contains the masses and inertias of a hollow shaft drive train consisting of a rotor, the gear wheels, the coupling, the hollow shaft, the axle and both wheels. The torsional stiffness and damping of the gear, the coupling, the hollow shaft and the axle are considered. Also the single-stage gear is included in the model. Figure 4 gives an overview of the described system. The traction motor drives the gear wheel which is attached onto the cardan hollow shaft. The hollow shaft transmits the torque by its coupling onto the directly driven wheel. Via the wheelset axle the directly driven wheel drives the indirectly driven wheel. Numerical values for the torsional stiffness and torsional damping as well as the moments of inertia used for the MBS model are obtained from [14].

2.2.1. Simulation Model

The simulation model was built up in the MBS software Simpack as depicted in Figure 5. The MBS model is linked to the drive control via co-simulation. The model contains the torque transmitting components of the mechanical drive train, the wheel–rail contact, as well as the friction forces and inertia forces resulting from the train set. The whole model of the drive train can follow the track in longitudinal direction and can move freely in vertical direction. The individual bodies have rotational degrees of freedom around their lateral axis.

For the calculation of the tangential forces in the wheel–rail contact, the analytical approach of Polach is used [26]. This approach was developed to achieve an improved fit of the adhesion characteristics in the simulation with measured data. The tangential force F calculated in Polach’s formalism depends on the wheel load Q, the wheel–rail adhesion coefficient $\mu$ and the weighting factors $k_A$ and $k_S$.

$$F=\frac{2Q\mu }{\pi }\left(\frac{k_Aϵ}{1+{\left(k_Aϵ\right)}^2}+arctan\left(k_Aϵ\right)\right),k_S\le k_A\le 1$$

(5)

The gradient of tangential stress in the adhesion area $ϵ$ is depending on the relative (slip) velocity $v_s$ between wheel and rail and the contact ellipse in the wheel–rail contact.

$$ϵ=\frac{2}{3}\frac{C\pi a^{2}b}{Q\mu }{v}_s$$

(6)

The decrease of the wheel–rail adhesion coefficient for higher relative velocities is realized by a relative velocity $v_s$ dependent friction value. This is highly relevant for the simulation of torsional vibrations. The slope of the adhesion coefficient above its maximum can be determined by the parameters A and B. Figure 6 shows the adhesion characteristics as a function of the driving speed.

$$\mu ={\mu }_0·\left((1-A)·{exp}^{-B·|v_s|}+A\right)$$

(7)

The traction forces are opposed by the friction and inertia forces of the train set. These opposing forces are represented in the MBS model by the following equations taken from the literature [17].

Rolling Resistance:

$$F_{roll}=M_{train}·g·k_{roll},k_{roll}=1.5·{10}^{(-3)}$$

(8)

Air Resistance:

$$F_{air}=M_{train}·g·k_{air},k_{air}=0.25·{10}^{(-3)}$$

(9)

2.2.2. Linear Analysis

A linear eigenvalue analysis was carried out to investigate the dynamics of the drive train. The wheel–rail contact forces are not taken into account in the analysis. The eigenmodes and the eigenfrequencies of the six-mass model were calculated (see Figure 7).

Especially, two eigenmodes are important with regard to the assessment of the drive train dynamics. For mode 2, a chatter oscillation occurs where the whole wheelset is oscillating in counter phase to rotor and gear. As the resulting oscillation amplitudes of the wheelset have a similar magnitude as the oscillation amplitudes of the rotor, chatter oscillations are detectable by the traction motor sensors. As a result, they can actively be damped by an appropriate design of the traction control [14,25].

This is different in mode 3, which is the relevant mode of torsional vibration. Here, both wheels of a wheelset oscillate in counter phase and at the same time, oscillation amplitude of the rotor are close to zero (see Figure 7). As oscillation amplitudes can hardly be detected at the rotor, torsional vibration of the wheelset cannot be actively influenced by the drive control. If wheelset torsional vibrations occur, further measures must be taken. For example, the drive torque of the motor must be reduced or the wheels must be braked.

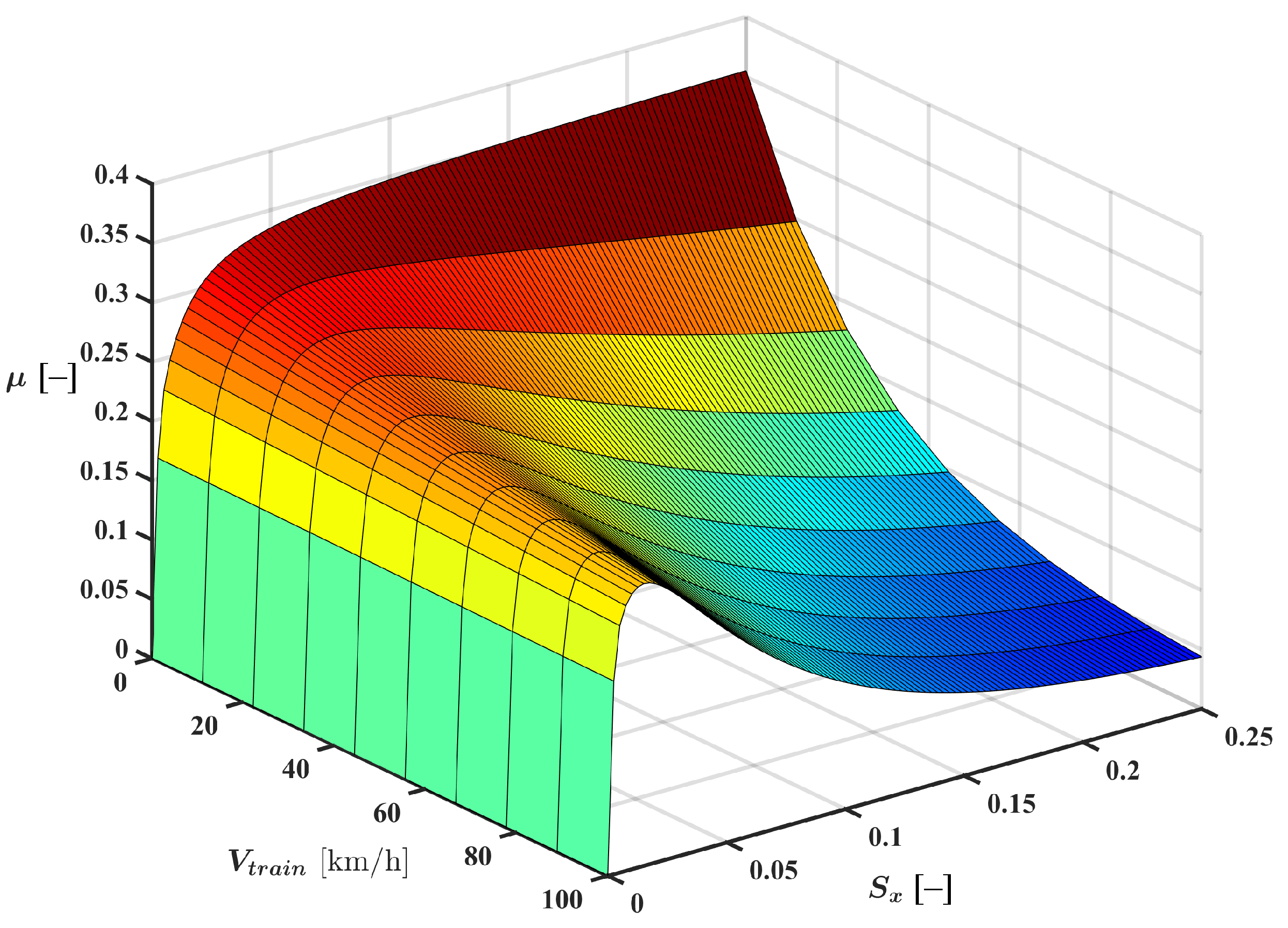
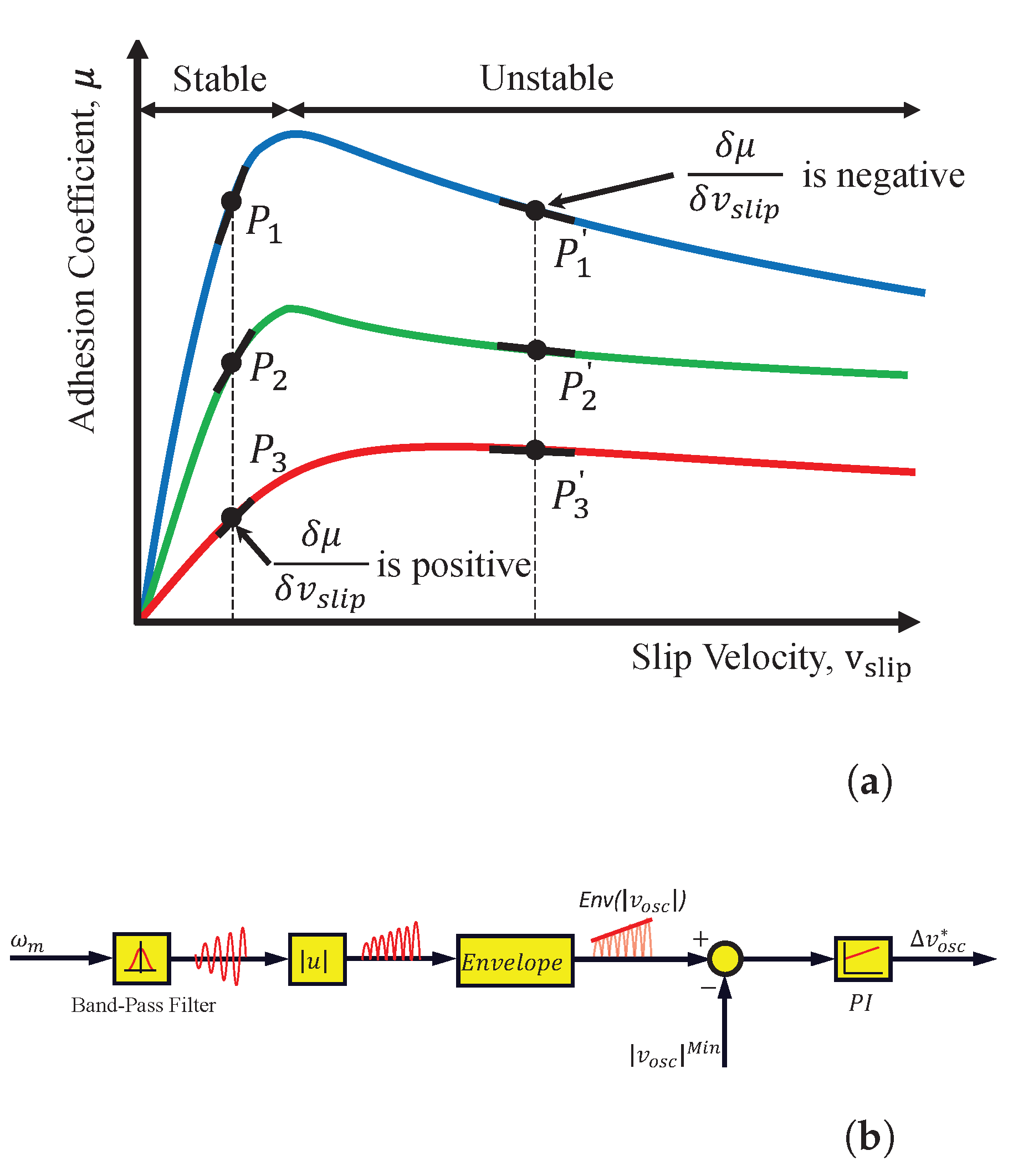
3. Slip Control and Torsional Vibration Protection

3.1. Overview of Slip Control

Anti-slip control is needed in railway traction drives to reduce the wear of the wheel–rail contact surface, increase traction/breaking capability, and increase passenger comfort and safety. Commonly, the torque commanded by the train driver $T_e^{ref}$ is sent to the traction motor control unit (TCU) meanwhile the slip control is running in parallel without any action during normal operation. Once slippage is detected, the slip control becomes active and the output torque correction signal $T_e^{\alpha }$ is sent to the TCU (see Figure 8). Generally, slip controller can be classified into:

• Traditional slip controllers, also known as re-adhesion controllers. They are one of the simplest and stablest solutions to limit the wheel–rail slippage to a predefined value [27,28,29]. The slip velocity reference can be kept at a constant value or varied with the train speed based on previous field-tests and train’ driver experience [30].
• Advanced slip controllers aimed to operate at maximum possible adhesion level [15,31,32,33,34,35,36]. Due to the unpredictability of the adhesion-slip phenomena, finding the optimal slip velocity increases the complexity of the control and its real time implementation becomes more challenging.

In this article, slip velocity control is used. From the measured motor speed signal ${\omega }_m$, the wheel velocity $v_w$ and acceleration signals ${\alpha }_w$ can be obtained (see speed signal processing block in Figure 8). Slip velocity $v_{slip}$ is obtained by subtracting wheel linear velocity $v_w$ from train velocity $v_{train}$. Slip speed is compared to a preset value $v_{slip}^{*}$, the error signal feeding a conventional PI regulator. The correction signal coming out from the slip velocity controller could be the commanded torque directly. However, to ensure passengers comfort, an additional acceleration control is employed to control the acceleration/jerk of the wheel (see Figure 8). Additionally, adaptation of slip velocity $\Delta v_{slip}^{*}$ is added to damp vibrations excited in the drive train wheelset through vibration detection and protection block seen in Figure 8. Vibration suppression will be discussed in the following subsection.

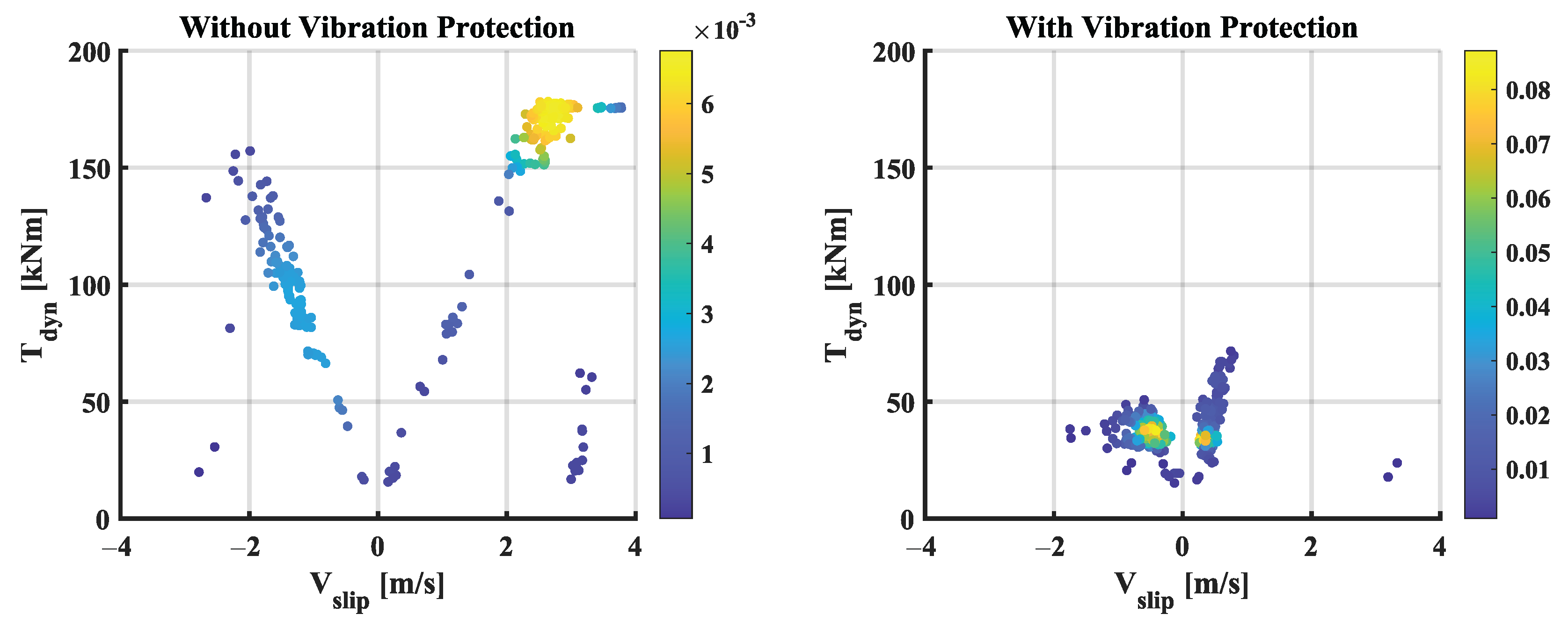
3.2. Torsional Vibration Control

Torsional vibrations occur in the drive trains axle due to changing of the adhesion conditions (from high to low values $P_1\to P_3$ or vice versa), track irregularities, and/or operating at high slip velocities (i.e., unstable region in Figure 9a). The envelope magnitude of the torque vibration component, which is referred to dynamic torque $|T_{dynamic}|$, is proportional to the slope of the adhesion characteristic curve $\frac{\delta \mu }{\delta V_{slip}}$ in the unstable region (i.e., $\frac{\delta {\mu }_{P_1}}{\delta V_{sli{p}_{P_1}}}>\frac{\delta {\mu }_{P_2}}{\delta V_{sli{p}_{P_2}}}>\frac{\delta {\mu }_{P_3}}{\delta V_{sli{p}_{P_3}}}$ in Figure 9a) [5].

To mitigate torsional vibrations in traction drive trains, passive readhesion controller is usually used (see vibration detection and protection block in Figure 8). The readhesion controller reduces the slip velocity to protect the wheelset axle from excessive vibration events. This can be achieved by extracting the vibration component from the speed sensor signal of the IM ${\omega }_m$ using a band-pass filter. Then the envelope of the extracted vibration $Env\left(\right|v_{osc}\left|\right)$ is controlled to avoid surpassing a predefined limit $|v_{osc}|$ using a conventional PI regulator (see Figure 9b). The output signal $\Delta v_{osc}^{*}$ reduces the slip velocity command once the vibration envelope exceeds the defined limit bringing the operating point back into the stable region (e.g., $P_1^{{}^{\prime }}\to P_1$ in Figure 9a). Consequently, the reference torque $T_e^{*}$ is reduced during the vibration mitigation process, $T_e^{*}$ being returned to its original value after vibration events clearance. In this paper, passive readhesion control is used to limit the slip velocity, being aware of its adverse impact on traction. Alternatively, advanced control techniques can be employed to actively damp the torsional vibrations in the traction drive, but at the cost of higher complexity and parameter dependency [20,25].

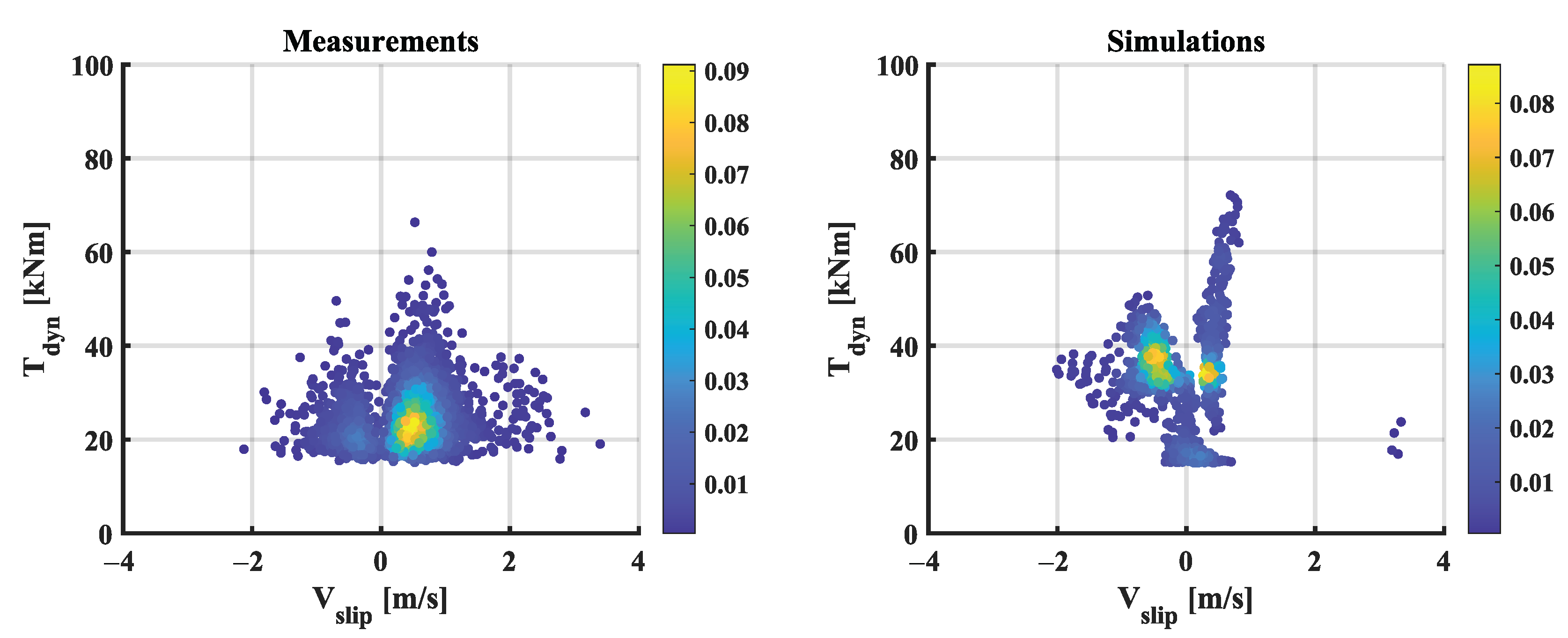
4. Simulation Results and Experimental Verification

In this section, the entire traction drive system and control are modeled and simulated using the MATLAB-SIMPACK co-simulation tool. Furthermore, changes in the wheel–rail conditions with activated and deactivated torsional vibration protection will be analyzed. Finally, simulation results will be compared with measured data already published in [16].

Based on the dependencies between maximum dynamic torque and wheel–rail conditions documented in [16,17], the wheel–rail adhesion coefficient was modified during the simulation at hand during an acceleration process. The introduced co-simulation tool (see Figure 10) was used.

The simulation batch starts by defining the number of simulations to be carried out. This depends on the ranges of train speeds and wheel–rail conditions to be tested. Variables to be set for each simulation include train velocity, adhesion coefficient and the travelling distance where the adhesion change is applied for both wheels. The slip and vibration protection control algorithms are executed via MATLAB/SIMULINK toolbox where the torque command is sent to the drive train and vehicle model implemented in the SIMPACK environment. The train velocity and motor speed measurements are fed back to SIMULINK model where the co-simulation communication is done via internet protocol (IP-Server 2000). Finally, the output data (dynamic torque, slip velocity, etc.) are stored in a vector table then the same process is repeated for the rest of simulation steps.

Three different wheel–rail condition scenarios for both wheels were conducted to investigate effectiveness of torsional vibration protection of electric driven wheelsets (see Figure 11). $x_{1\cdots 4}$ indicates the distance at which the change of the adhesion value $\mu$ is applied (starting from 10 to 400 m with separation of 10 m each step). Additionally, the simulations carried out are repeated (traction and electrical braking) for different train velocities (from 0 to 200 km/h).

Figure 12 shows dynamic torque plotted against slip velocity where all simulation results for different adhesion scenarios (mentioned in Figure 11) are combined and plotted in the same graph (i.e., Figure 12). It is observed that without vibration protection (see left subplot in Figure 12), the vibration magnitude is increasing linearly with slip velocity up to the maximum value ($T_{dyn}\approx 180$kNm at $v_{slip}\approx 2.5$m/s) for traction mode. It is noted that though the maximum dynamic torque is found to be less ($T_{dyn}\approx 160$kNm at $v_{slip}\approx 2$m/s) in braking mode, still the trend is the same as for traction mode.

Enabling vibration protection control limits the dynamic torque magnitude (see right subplot in Figure 12). The maximum dynamic torque achieved is $T_{dyn}\approx 72$kNm at $v_{slip}\approx 0.7$m/s for traction mode and $T_{dyn}\approx 51$kNm at $v_{slip}\approx 0.6$m/s for braking mode.

Given that the adhesion characteristic is highly stochastic, it is striking that data points resulting from simulations show good conformity with data points resulting from measurements. Measurements have been conducted with a similar drive train and traction control as the one implemented in the simulation model at hand. Measurement conductions, as well as measurement data analysis have been published in [16]. Furthermore, for both, simulations and measurements, maximum dynamic torque increases linearly by increasing slip velocity. Although in Figure 13 this linearity appears more accurate for simulations than for measurements, conformity can be considered good as deviations in the accuracy of the linearity can be traced back to the limitations of the real test execution. After exceeding a certain slip velocity $v_{slip,crit}\approx 0.5$m/s) data points are not increasing linearly but rather decreasing. This decreasing process of data points conforms with observations documented in other publications [2,37]. Most likely, for further increasing slip velocities above $v_{slip,crit}$, dynamic processes vanish and the wheelset transitions into global slipping.

5. Conclusions and Outlook

In this article, the implementation of a complete traction drive system including electrical components, control strategies and mechanical drive train is presented. The implementation is realized by a co-simulation tool and this tool is used to simulate torsional vibration. In simulations, torsional vibration is provoked by changes of the wheel–rail conditions. Furthermore, the effectiveness of a torsional vibration detection is investigated. For this, a torsional vibration protection is implemented as part of the traction control. Simulations are conducted with activated and deactivated vibration protection.

As a first step, the functionality of the simulation model implementation has successfully been verified on measurement results. This includes coincidence of maximum dynamic torque of simulations and measurements as well as the linear dependency of dynamic torque and slip (find further investigations on this dependency in [37]).

As a second step, simulations were performed to investigate the effectiveness of a torsional vibration protection. The received results show that the implemented vibration protection helps to suppress torsional vibration and therefore, to prevent the wheelset from high dynamic torque. As torsional vibration is suppressed indirectly by dynamic torque reductions, the vibration detection requires reliable wheelset rotation speed data. Here, linear analysis shows that rotation speed sensors of the traction motors may not provide wheel rotation speed data of sufficient quality.

Consequently, the presented investigations and results verify that suppressing torsional vibration indirectly by dynamically reducing the traction torque is an effective way to prevent a railway wheelset from high dynamic torque. Therefore, the implementation of an effective vibration protection is capable of reducing the maximum torsional loads applied to wheelset axle and press fit by a significant amount. With this, a vibration protection contributes to the safety and reliability of rail traffic.

Moreover, with the introduced model, torsional vibration has been successfully simulated in accordance with track measurements. Basing on this achievement, the simulation model shall be applied to other vehicles in order to validate prediction of maximum dynamic torque values. The capability of predicting maximum dynamic torque values is needed by railway vehicle manufacturers, to enable a more efficient development of new wheelsets. In the same way, such simulations can help manufacturers to study evidence of the effectiveness of their torsional oscillation protection implementations.