Linear Control of a Nonlinear Equipment Mounting Link
Abstract
1. Introduction
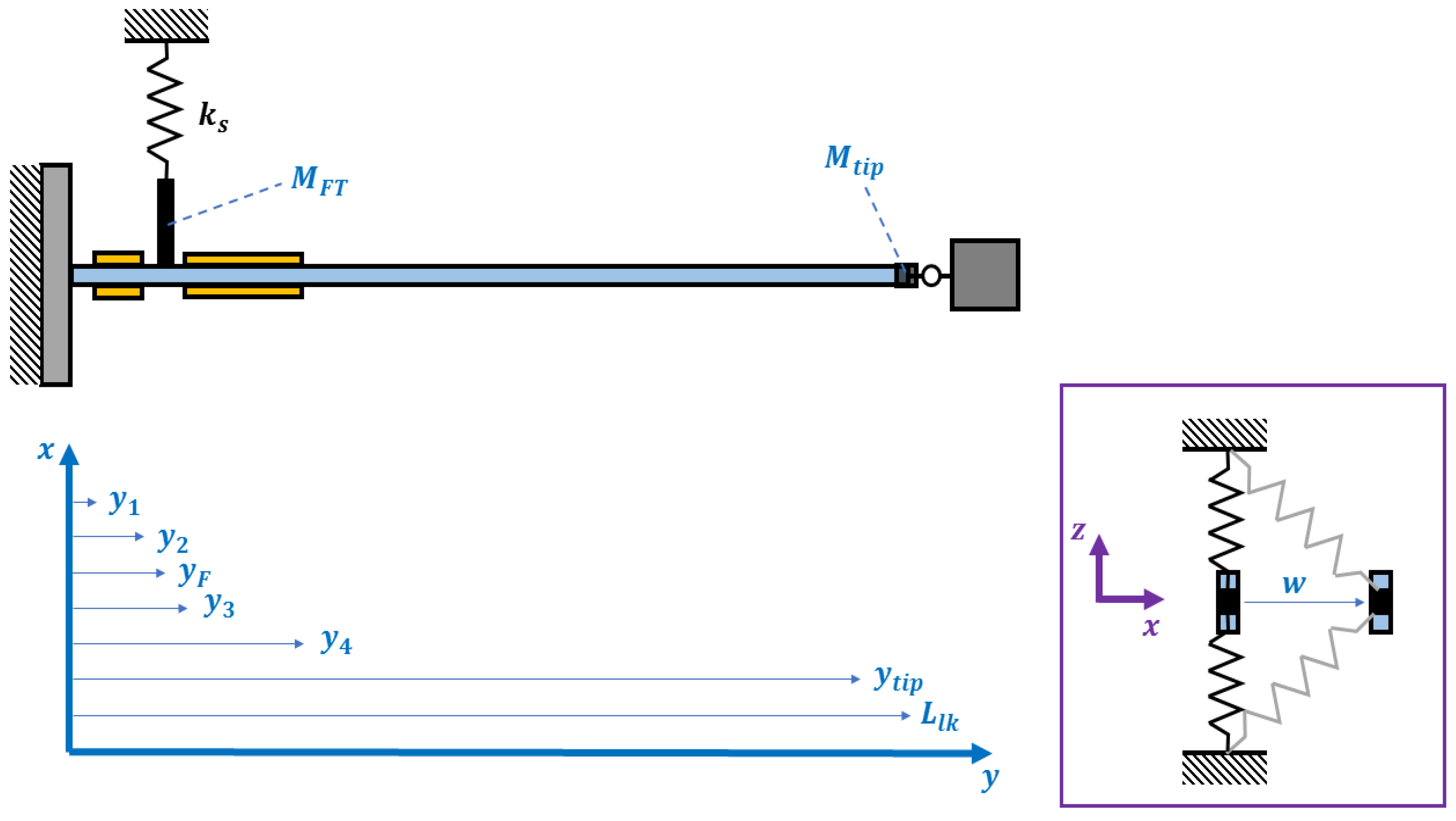
2. Experimental Set-Up
- 1.
- Shaker (Dataphysics V4);
- 2.
- Force sensor (ICP 208 B02);
- 3.
- Clamp and hinge structure connecting beam to force sensor;
- 4.
- PZT elements;
- 5.
- Springs;
- 6.
- Spring bracket;
- 7.
- Laser displacement sensors (LDSs).
- 1.
- “If the equation of state contains a singularity”.
- 2.
- “If the series diverges for strong disturbances”.
- 3.
- “If the linear term is absent, and higher nonlinearity dominates”.
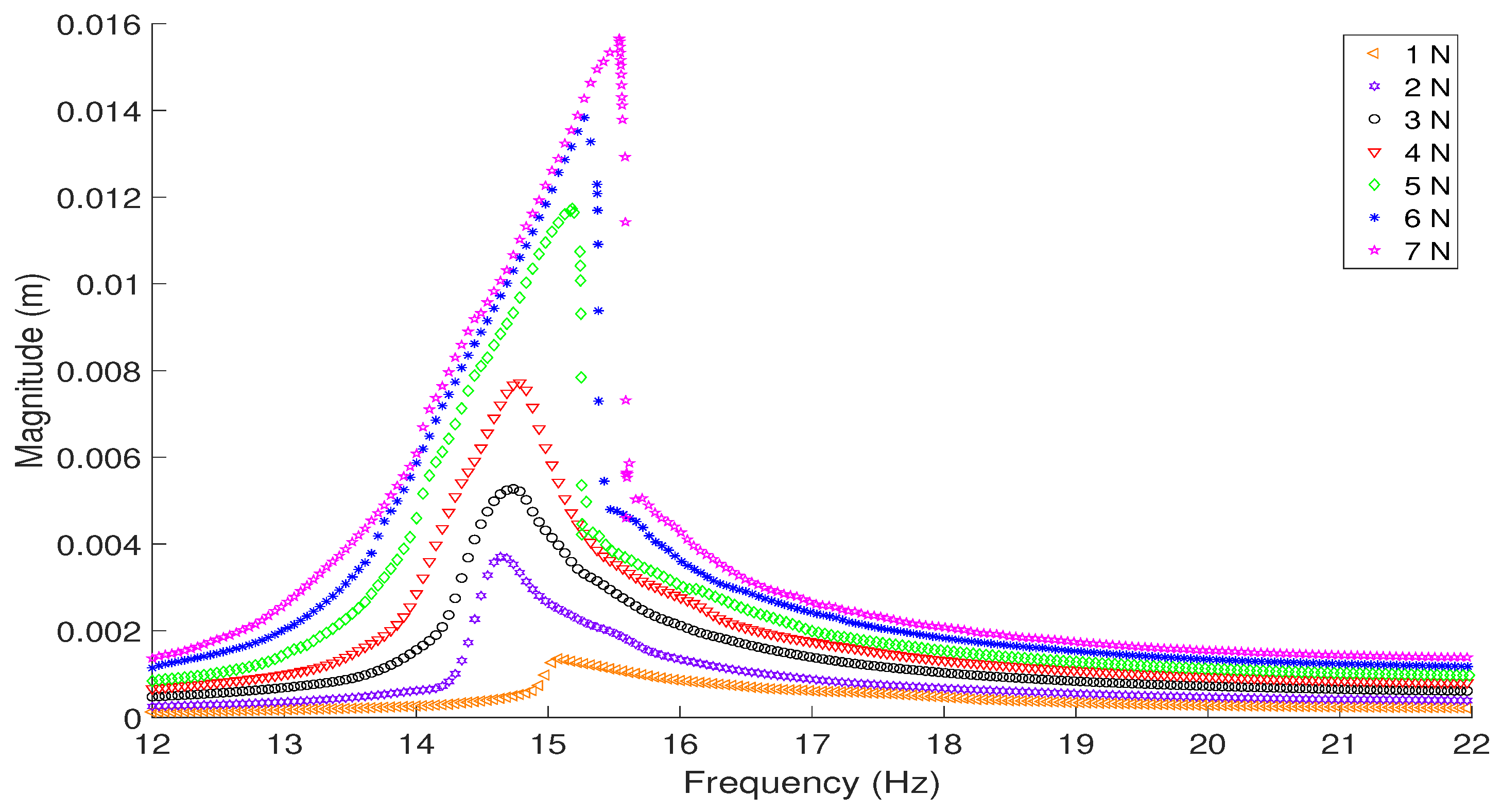
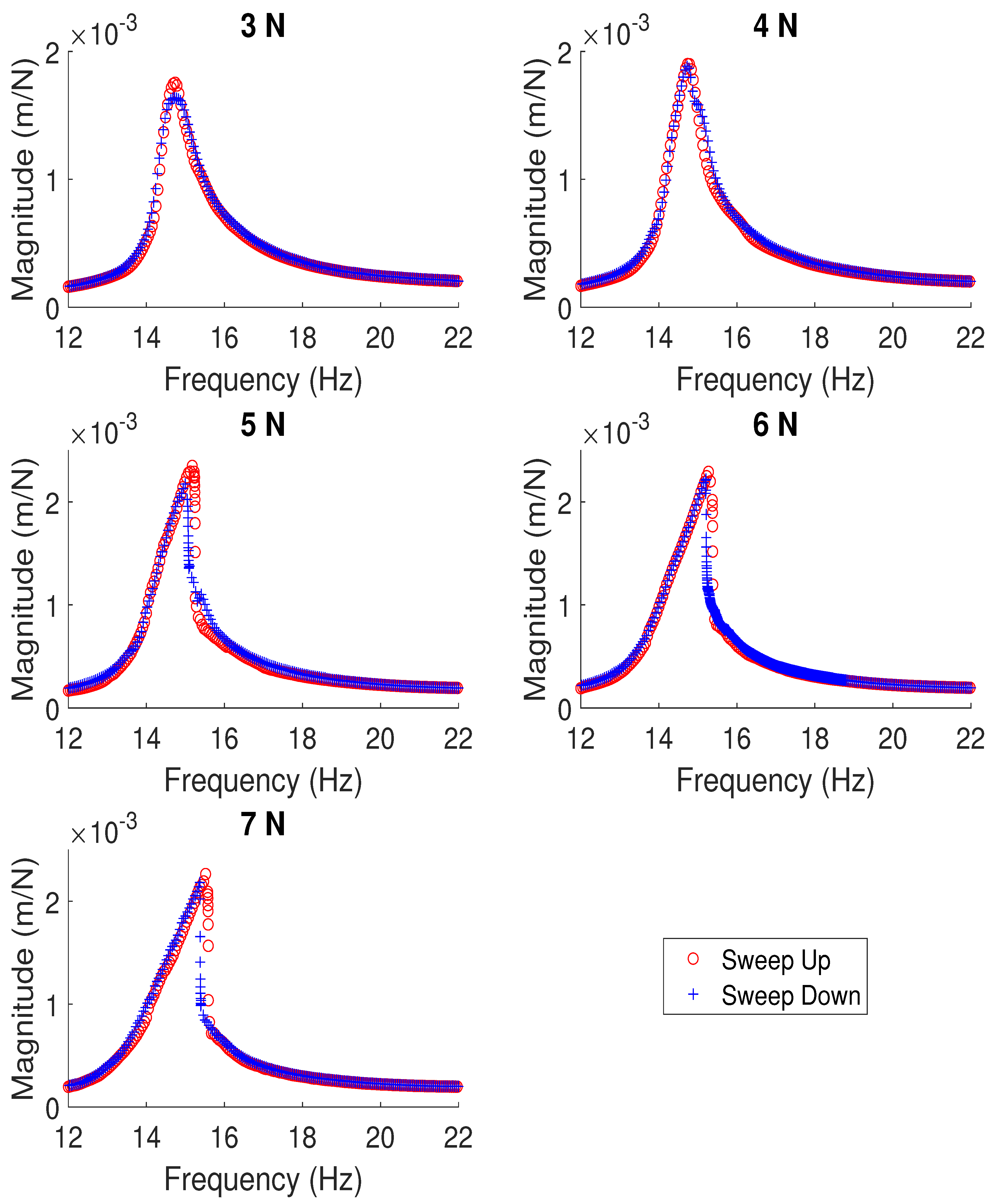
3. Experimental Results
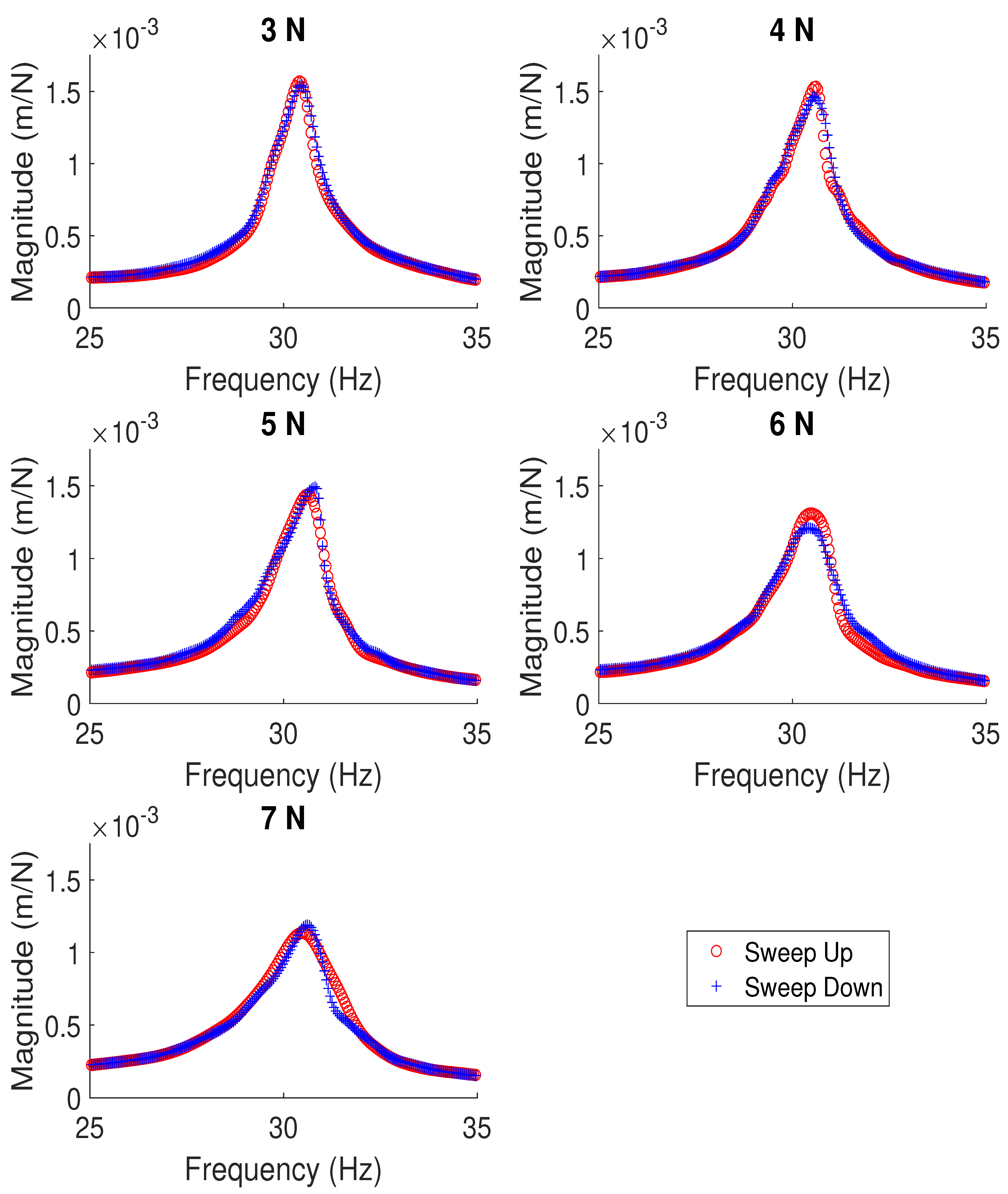
3.1. Verification of a Nonlinear Response
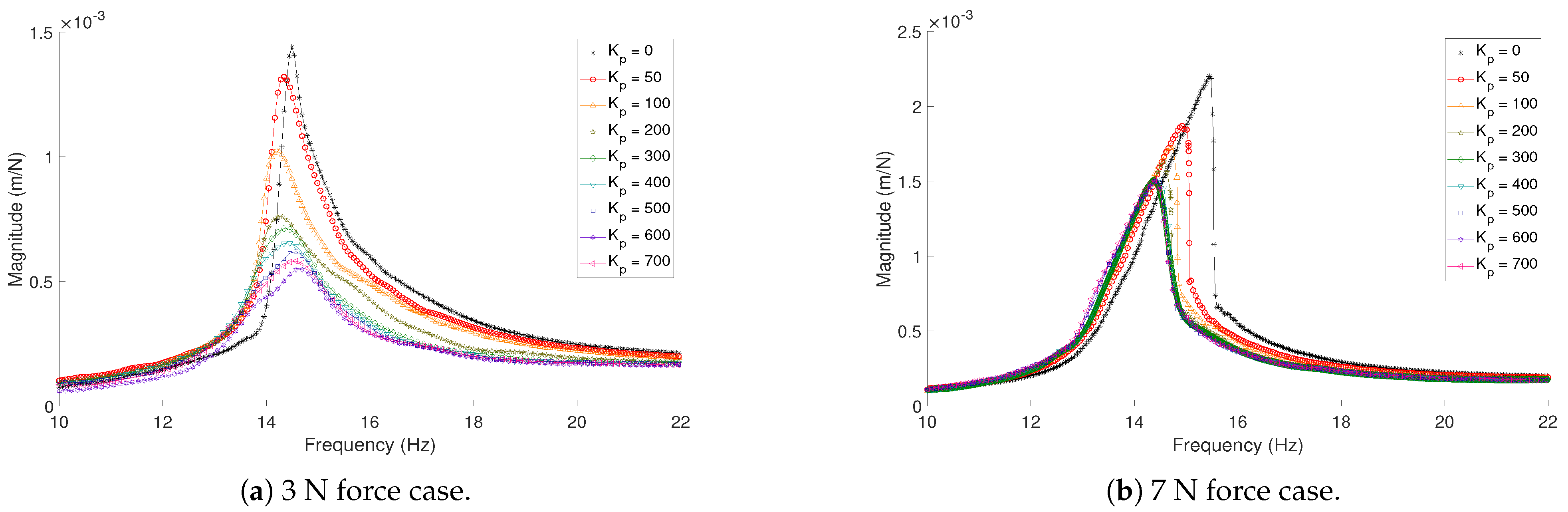
3.2. The Application of Control
4. Analytical Model
4.1. The Controlled System
4.2. The Optimisation Method
- 1.
- For the case of nonlinear systems with multi-solution responses, care should be taken to select the proper set of measured data to reduce the effect of noise. Indeed, using the upper stable branch of the solution may lead to minimising the effect of noise in the results of optimisation. For instance, in the case of hardening nonlinearity, the upper branch, which in the experiment is obtained via the forward sweep test, is used for the optimisation. Therefore, it is important to take this criterion into consideration not only in the stage of data selection but also before carrying out the vibration tests. The simulated response is selected according to the selected experimental data.
- 2.
- The frequency range of the simulated response used in the optimisation process is selected according to the frequency range of the measured data. In addition, weights are given to the selected data based on the gap between the experimental and numerical response.
- 3.
- As the unstable branches of the response of the system are not measured in the experiment, the unstable branches of the simulated response are neglected in the optimisation process.
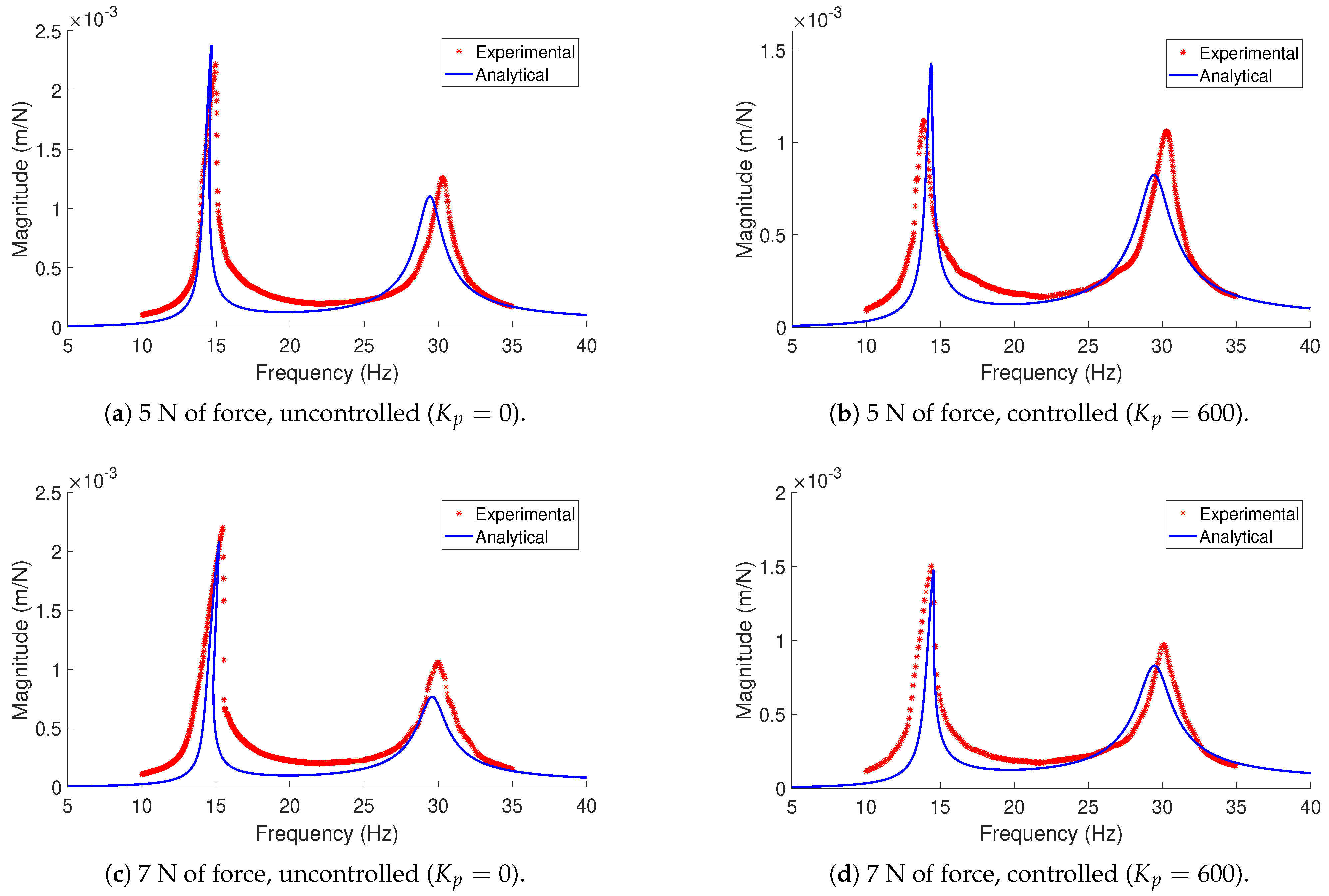
4.3. Model Verification
- Higher modes were not included in the analytical model, and so their influence on the response was excluded.
- A certain degree of compensation of the damping of each mode is necessary when optimising the damping of a system which considers two or more modes.
5. Discussion
5.1. Suitability for Suggested Application
5.2. Validity of Analytical Model
5.3. Additional Future Work
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix A.1
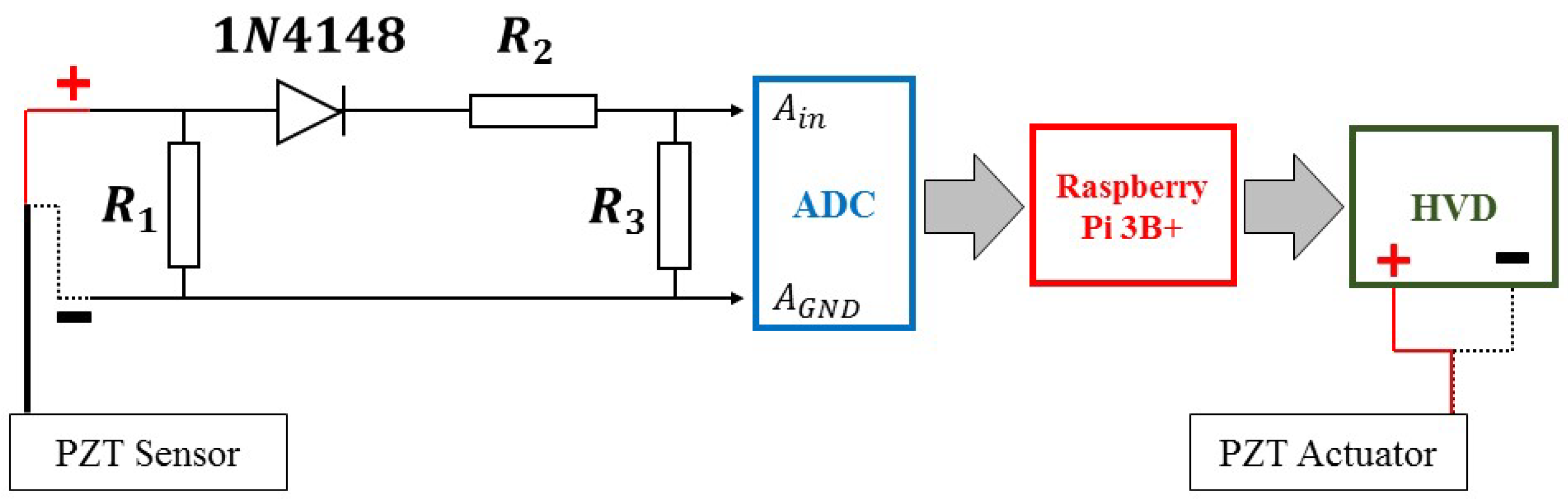
Appendix A.2

References
- Williams, D.; Khodaparast, H.H.; Jiffri, S. Active vibration control of an equipment mounting link for an exploration robot. Appl. Math. Model. 2021, 95, 524–540. [Google Scholar] [CrossRef]
- Qing, X.; Li, W.; Wang, Y.; Sun, H. Piezoelectric transducer-based structural health monitoring for aircraft applications. Sensors 2019, 19, 545. [Google Scholar] [CrossRef]
- Mahmud, M.A.; Bates, K.; Wood, T.; Abdelgawad, A.; Yelamarthi, K. A complete internet of things (IoT) platform for structural health monitoring (shm). In Proceedings of the 2018 IEEE 4th World Forum on Internet of Things (WF-IoT), Singapore, 5–8 February 2018; pp. 275–279. [Google Scholar]
- Wang, Q.; Wang, C.M. Optimal placement and size of piezoelectric patches on beams from the controllability perspective. Smart Mater. Struct. 2000, 9, 558. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, C.; Gao, R.X.; Yan, R.; Chen, X.; Wang, S. A novel hybrid error criterion-based active control method for on-line milling vibration suppression with piezoelectric actuators and sensors. Sensors 2016, 16, 68. [Google Scholar] [CrossRef]
- Dosch, J.J.; Inman, D.J.; Garcia, E. A self-sensing piezoelectric actuator for collocated control. J. Intell. Mater. Syst. Struct. 1992, 3, 166–185. [Google Scholar] [CrossRef]
- Fu, Y.; Li, S.; Liu, J.; Zhao, B. Design and Experimentation of a Self-Sensing Actuator for Active Vibration Isolation System with Adjustable Anti-Resonance Frequency Controller. Sensors 2021, 21, 1941. [Google Scholar] [CrossRef]
- Giorgio, I.; Del Vescovo, D. Energy-based trajectory tracking and vibration control for multilink highly flexible manipulators. Math. Mech. Complex Syst. 2019, 7, 159–174. [Google Scholar] [CrossRef]
- Crawley, E.F.; de Luis, J.; Hagood, N.; Anderson, E. Development of piezoelectric technology for applications in control of intelligent structures. In Proceedings of the 1988 American Control Conference, Atlanta, GA, USA, 15–17 June 1988; pp. 1890–1896. [Google Scholar]
- Hagood, N.W.; von Flotow, A. Damping of structural vibrations with piezoelectric materials and passive electrical networks. J. Sound Vib. 1991, 146, 243–268. [Google Scholar] [CrossRef]
- Alessandroni, S.; Andreaus, U.; Dell’Isola, F.; Porfiri, M. A passive electric controller for multimodal vibrations of thin plates. Comput. Struct. 2005, 83, 1236–1250. [Google Scholar] [CrossRef][Green Version]
- Lefeuvre, E.; Badel, A.; Petit, L.; Richard, C.; Guyomar, D. Semi-passive piezoelectric structural damping by synchronized switching on voltage sources. J. Intell. Mater. Syst. Struct. 2006, 17, 653–660. [Google Scholar] [CrossRef]
- Richard, C.; Guyomar, D.; Audigier, D.; Ching, G. Semi-passive damping using continuous switching of a piezoelectric device. In Smart Structures and Materials 1999: Passive Damping and Isolation. International Society for Optics and Photonics; International Society for Optics and Photonics: Bellingham, WA, USA, 1999; Volume 3672, pp. 104–111. [Google Scholar]
- Kumar, S.; Srivastava, R.; Srivastava, R. Active vibration control of smart piezo cantilever beam using pid controller. Int. J. Res. Eng. Technol. 2014, 3, 392–399. [Google Scholar]
- Bailey, T.; Hubbard, J.E., Jr. Distributed piezoelectric-polymer active vibration control of a cantilever beam. J. Guid. Control. Dyn. 1985, 8, 605–611. [Google Scholar] [CrossRef]
- Vindigni, C.R.; Orlando, C.; Milazzo, A. Computational Analysis of the Active Control of Incompressible Airfoil Flutter Vibration Using a Piezoelectric V-Stack Actuator. Vibration 2021, 4, 369–396. [Google Scholar] [CrossRef]
- Iwaniec, M.; Holovatyy, A.; Teslyuk, V.; Lobur, M.; Kolesnyk, K.; Mashevska, M. Development of vibration spectrum analyzer using the Raspberry Pi microcomputer and 3-axis digital MEMS accelerometer ADXL345. In Proceedings of the 2017 XIIIth International Conference on Perspective Technologies and Methods in MEMS Design (MEMSTECH), Lviv, Ukraine, 20–23 April 2017; pp. 25–29. [Google Scholar]
- Platanitis, G.; Strganac, T.W. Control of a nonlinear wing section using leading-and trailing-edge surfaces. J. Guid. Control. Dyn. 2004, 27, 52–58. [Google Scholar] [CrossRef]
- Khorrami, F.; Jain, S.; Tzes, A. Experimental results on adaptive nonlinear control and input preshaping for multi-link flexible manipulators. Automatica 1995, 31, 83–97. [Google Scholar] [CrossRef]
- Schweickhardt, T.; Allgöwer, F. Linear control of nonlinear systems based on nonlinearity measures. J. Process Control 2007, 17, 273–284. [Google Scholar] [CrossRef]
- Desoer, C.; Wang, Y.T. Foundations of feedback theory for nonlinear dynamical systems. IEEE Trans. Circuits Syst. 1980, 27, 104–123. [Google Scholar] [CrossRef]
- Taghipour, J.; Khodaparast, H.H.; Friswell, M.I.; Jalali, H.; Madinei, H.; Jamia, N. On the sensitivity of the equivalent dynamic stiffness mapping technique to measurement noise and modelling error. Appl. Math. Model. 2021, 89, 225–248. [Google Scholar] [CrossRef]
- Taghipour, J.; Haddad Khodaparast, H.; Friswell, M.I.; Jalali, H. An Optimization-Based Framework for Nonlinear Model Selection and Identification. Vibration 2019, 2, 311–331. [Google Scholar] [CrossRef]
- Shaw, A.D.; Hill, T.; Neild, S.; Friswell, M. Periodic responses of a structure with 3: 1 internal resonance. Mech. Syst. Signal Process. 2016, 81, 19–34. [Google Scholar] [CrossRef]
- Rudenko, O.; Hedberg, C. Strong and weak nonlinear dynamics: Models, classification, examples. Acoust. Phys. 2013, 59, 644–650. [Google Scholar] [CrossRef]
- Rao, S.S. Vibration of Continuous Systems; John Wiley & Sons: Hoboken, NJ, USA, 2019. [Google Scholar]
- Detroux, T.; Renson, L.; Masset, L.; Kerschen, G. The harmonic balance method for bifurcation analysis of large-scale nonlinear mechanical systems. Comput. Methods Appl. Mech. Eng. 2015, 296, 18–38. [Google Scholar] [CrossRef]
- Khodaparast, H.H.; Madinei, H.; Friswell, M.I.; Adhikari, S.; Coggon, S.; Cooper, J.E. An extended harmonic balance method based on incremental nonlinear control parameters. Mech. Syst. Signal Process. 2017, 85, 716–729. [Google Scholar] [CrossRef]
- Vakakis, A.F.; Gendelman, O.V.; Bergman, L.A.; McFarland, D.M.; Kerschen, G.; Lee, Y.S. Nonlinear Targeted Energy Transfer in Mechanical and Structural Systems; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2008; Volume 156. [Google Scholar]
- Taghipour, J.; Dardel, M. Steady state dynamics and robustness of a harmonically excited essentially nonlinear oscillator coupled with a two-DOF nonlinear energy sink. Mech. Syst. Signal Process. 2015, 62, 164–182. [Google Scholar] [CrossRef]
- Taghipour, J.; Dardel, M.; Pashaei, M.H. Vibration mitigation of a nonlinear rotor system with linear and nonlinear vibration absorbers. Mech. Mach. Theory 2018, 128, 586–615. [Google Scholar] [CrossRef]
- Williams, D.; Haddad Khodaparast, H.; Jiffri, S.; Yang, C. Active vibration control using piezoelectric actuators employing practical components. J. Vib. Control 2019, 25, 2784–2798. [Google Scholar] [CrossRef]



| Parameters | Link (Steel) | Piezoelectric Sensor (PZT-5A) | Piezoelectric Actuator (PZT-5A) |
|---|---|---|---|
| Overall length (m) | 0.272 | 0.016 | 0.066 |
| Overall width (m) | 0.0397 | 0.016 | 0.031 |
| Thickness (m) | 0.0004 | 0.0003 | 0.0003 |
| Active length (m) | - | 0.007 | 0.056 |
| Active width (m) | - | 0.014 | 0.028 |
| Density (kg/m) | 7844 | 5440 | 5440 |
| Young’s modulus (GPa) | 204 | 60.48 | 60.48 |
| Piezoelectric coefficient, | - | −11.6 | −11.6 |
| Electromechanical coupling term, k | - | 0.34 | 0.34 |
| Capacitance (nF) | - | 7.89 | 113.06 |
| Parameter | Value |
|---|---|
| 0.0975 N·s/m | |
| N·s·m | |
| N/m | |
| 0.016 kg | |
| 0.00425 kg | |
| 55 N/m | |
| N/m | |
| 600 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Williams, D.; Tagihpour, J.; Haddad Khodaparast, H.; Jiffri, S. Linear Control of a Nonlinear Equipment Mounting Link. Vibration 2021, 4, 679-699. https://doi.org/10.3390/vibration4030038
Williams D, Tagihpour J, Haddad Khodaparast H, Jiffri S. Linear Control of a Nonlinear Equipment Mounting Link. Vibration. 2021; 4(3):679-699. https://doi.org/10.3390/vibration4030038
Chicago/Turabian StyleWilliams, Darren, Javad Tagihpour, Hamed Haddad Khodaparast, and Shakir Jiffri. 2021. "Linear Control of a Nonlinear Equipment Mounting Link" Vibration 4, no. 3: 679-699. https://doi.org/10.3390/vibration4030038
APA StyleWilliams, D., Tagihpour, J., Haddad Khodaparast, H., & Jiffri, S. (2021). Linear Control of a Nonlinear Equipment Mounting Link. Vibration, 4(3), 679-699. https://doi.org/10.3390/vibration4030038







