Detection and Severity Evaluation of Combined Rail Defects Using Deep Learning
Abstract
1. Introduction
2. Literature Review
3. Methodology
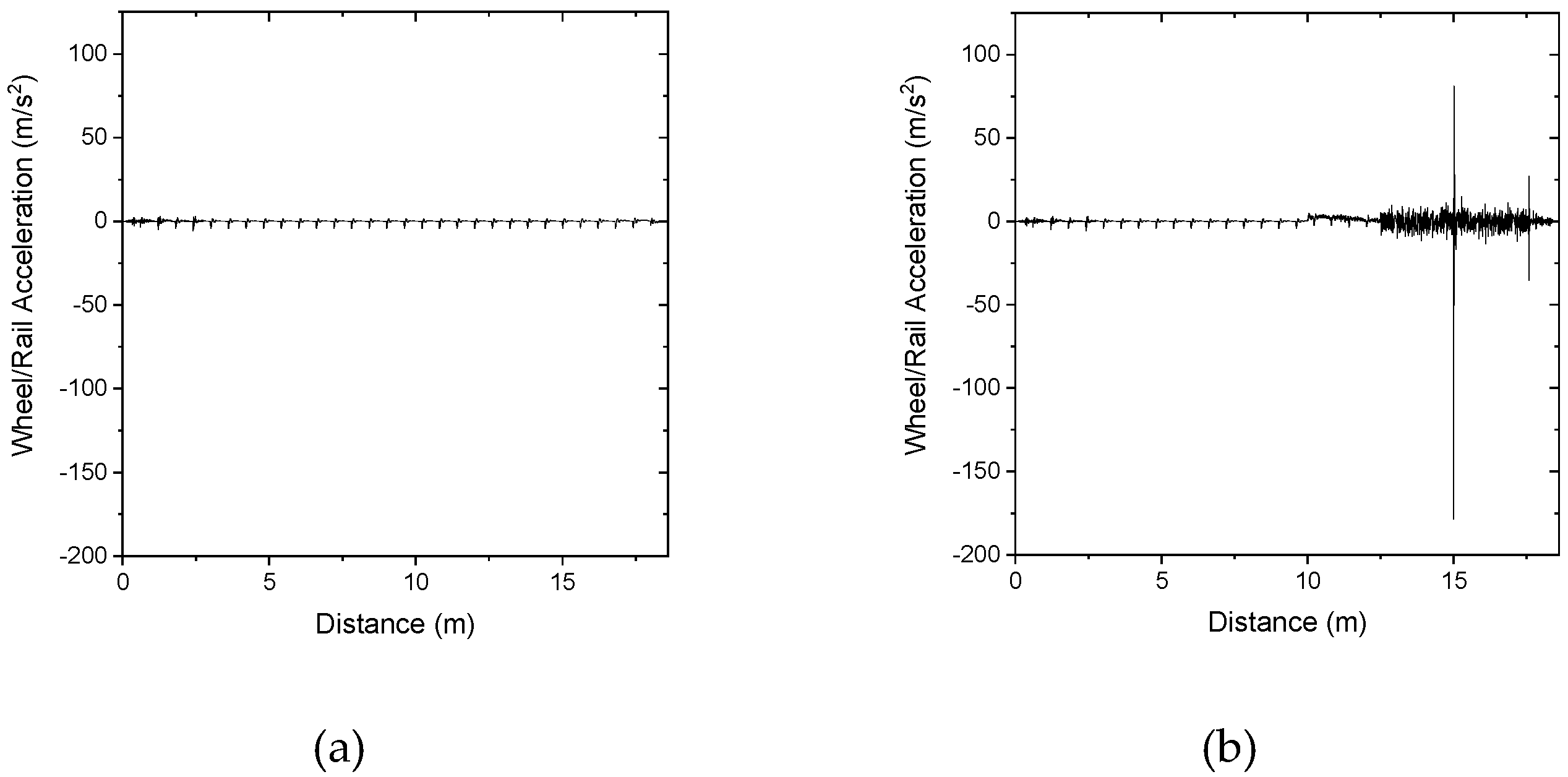
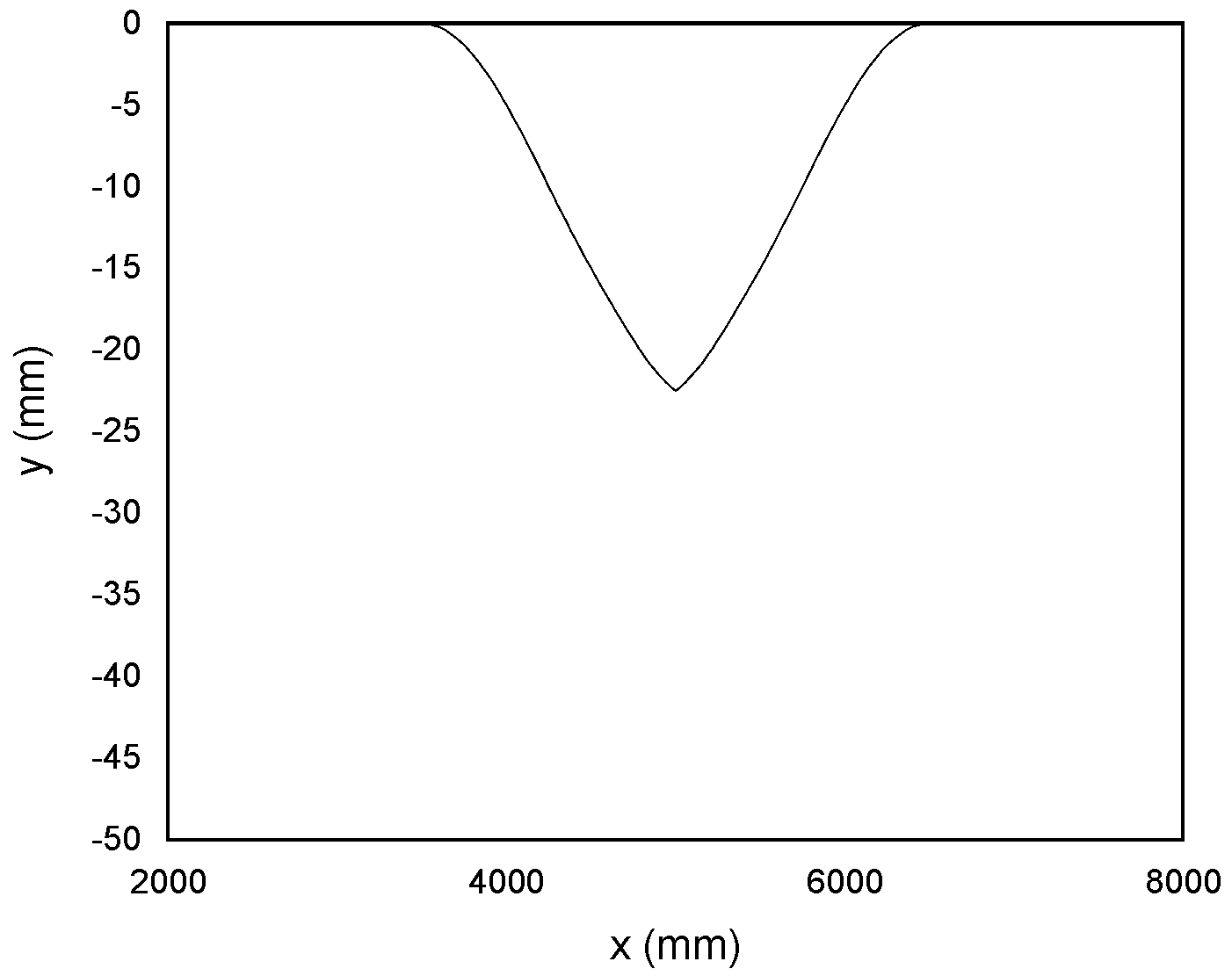
3.1. Numerical Data Simulation and Characteristics
3.2. AI Model Development
3.3. Hyperparameter Tuning
4. Results and Discussion
4.1. Combined Defect Detection
4.1.1. One Model for Detecting Both Dipped Joint and Settlement
4.1.2. Two Models for Detecting Dipped Joint and Settlement Separately
4.2. Combined Defect Severity Evaluation
4.2.1. Severity Classification
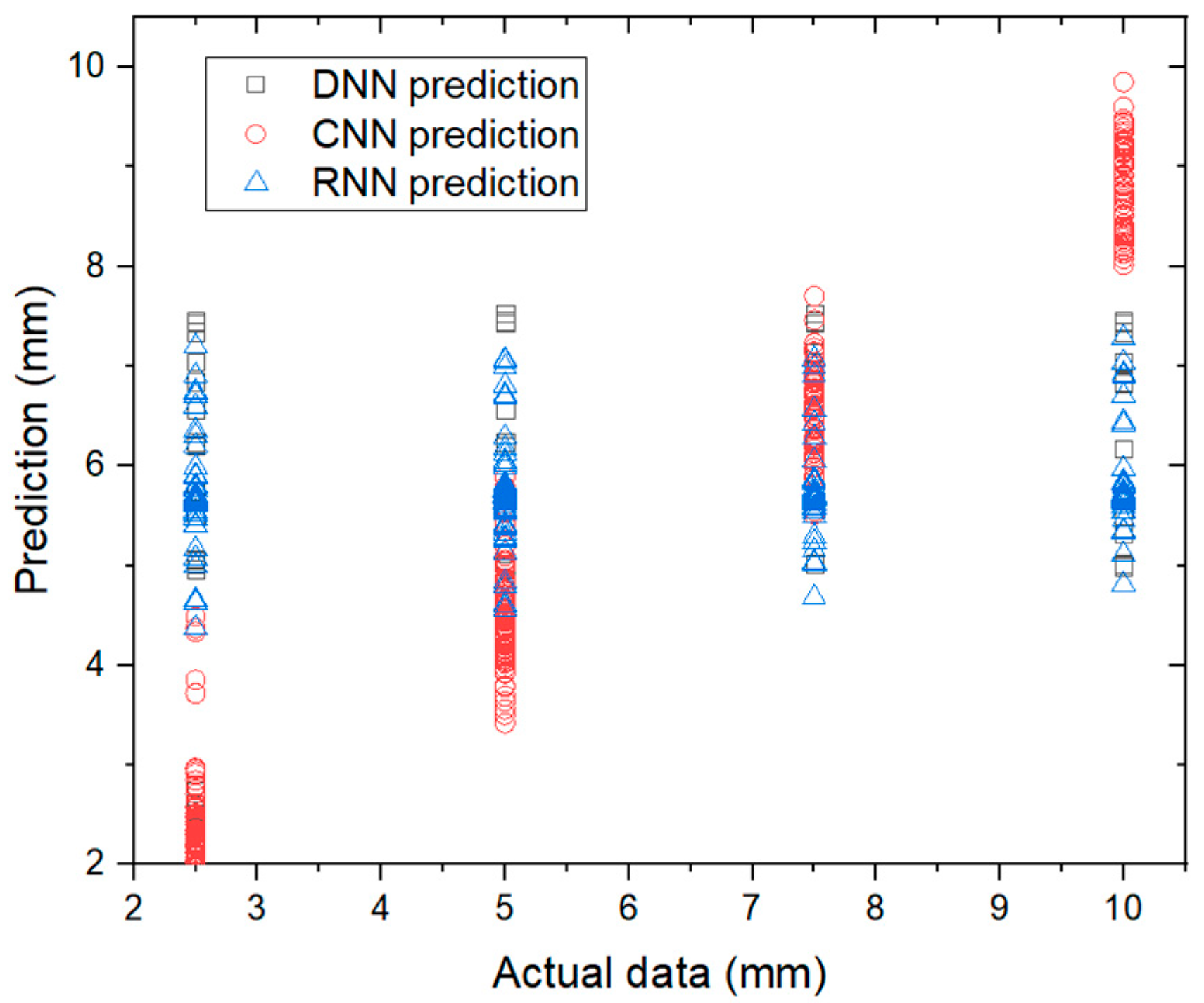
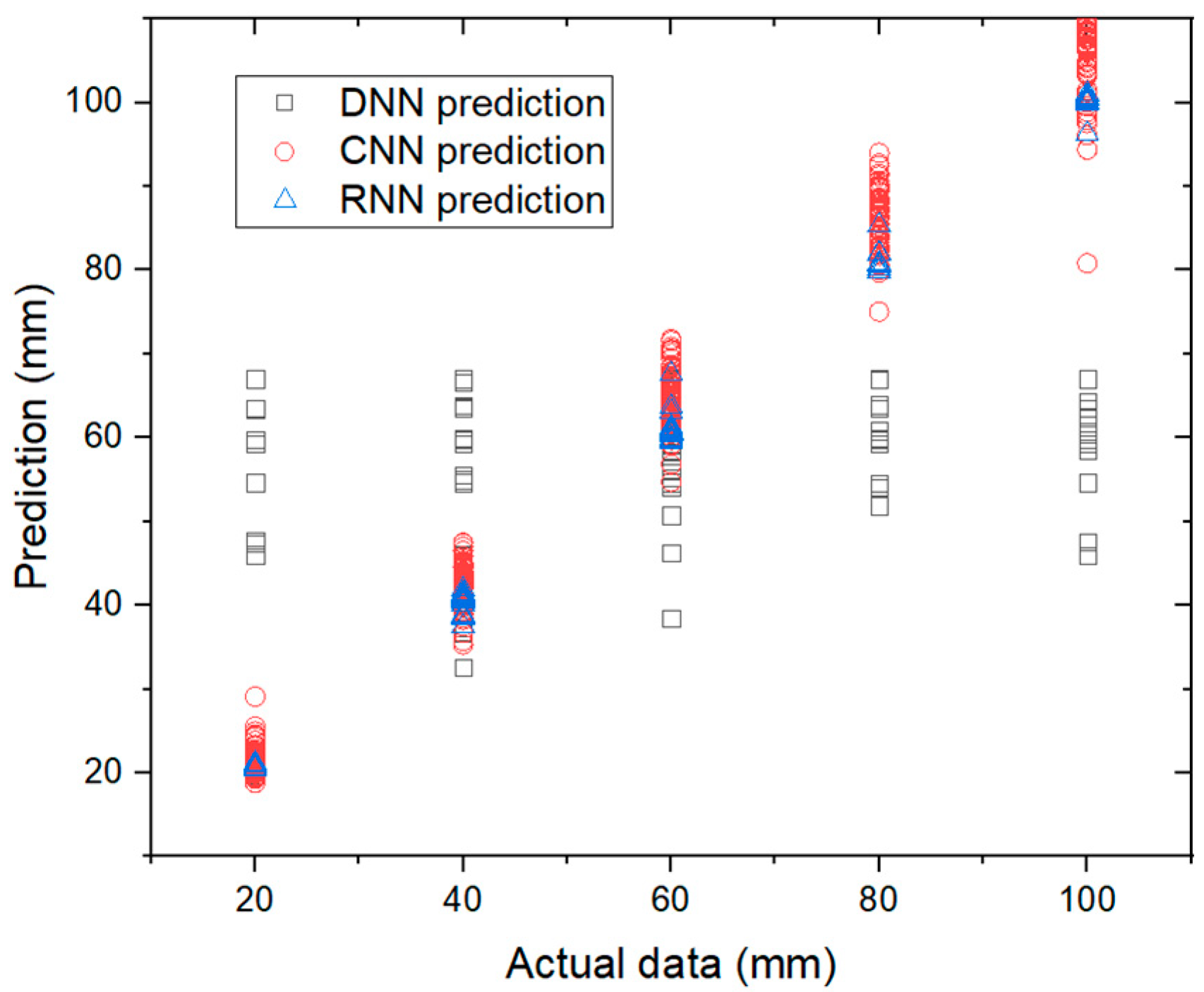
4.2.2. Severity Regression
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Network Rail. Visual Track Inspection; Network Rail: London, UK, 2019. [Google Scholar]
- Network Rail. Ultrasonic Rail Inspection; Network Rail: London, UK, 2019. [Google Scholar]
- Bray, D.E. Historical review of technology development in NDE. In Proceedings of the 15th World Conference on NDT, Roma, Italy, 15–21 October 2000. [Google Scholar]
- Zhang, J.; Ma, H.; Yan, W.; Li, Z. Defect detection and location in switch rails by acoustic emission and Lamb wave analysis: A feasibility study. Appl. Acoust. 2016, 105, 67–74. [Google Scholar] [CrossRef]
- Zhang, X.; Feng, N.; Wang, Y.; Shen, Y. Acoustic emission detection of rail defect based on wavelet transform and Shannon entropy. J. Sound Vib. 2015, 339, 419–432. [Google Scholar] [CrossRef]
- Bruzelius, K.; Mba, D. An initial investigation on the potential applicability of Acoustic Emission to rail track fault detection. NDT E Int. 2004, 37, 507–516. [Google Scholar] [CrossRef]
- Rockstroh, B.; Kappes, W.; Walte, F.; Kröning, M.; Bessert, S.; Schäfer, W. Ultrasonic and eddy-current inspection of rail wheels and wheel set axles. In Proceedings of the 17th World Conference on Nondestructive Testing, Shanghai, China, 25–28 October 2008. [Google Scholar]
- Amerapex. Benefits of Non-Destructive Testing. 2020. Available online: https://amerapex.com/2014/12/benefits-non-destructive-testing/#:~:text=NDT%20is%20particularly%20effective%20because,those%20intended%20for%20future%20use (accessed on 20 January 2021).
- Wei, X.; Yang, Z.; Liu, Y.; Wei, D.; Jia, L.; Li, Y. Railway track fastener defect detection based on image processing and deep learning techniques: A comparative study. Eng. Appl. Artif. Intell. 2019, 80, 66–81. [Google Scholar] [CrossRef]
- ScienceDaily. Artificial Intelligence. 2020. Available online: https://www.sciencedaily.com/terms/artificial_intelligence.htm (accessed on 20 January 2021).
- Kumar, S. Advantages and Disadvantages of Artificial Intelligence. 2019. Available online: https://towardsdatascience.com/advantages-and-disadvantages-of-artificial-intelligence-182a5ef6588c (accessed on 20 January 2021).
- Huang, K.; Wu, J.; Yang, X.; Gao, Z.; Liu, F.; Zhu, Y. Discrete train speed profile optimization for urban rail transit: A data-driven model and integrated algorithms based on machine learning. J. Adv. Transp. 2019, 2019. [Google Scholar] [CrossRef]
- Alawad, H.; Kaewunruen, S.; An, M.J.I.A. Learning from accidents: Machine learning for safety at railway stations. IEEE Access 2019, 8, 633–648. [Google Scholar] [CrossRef]
- Sysyn, M.; Gerber, U.; Nabochenko, O.; Gruen, D.; Kluge, F. Prediction of rail contact fatigue on crossings using image processing and machine learning methods. Urban Rail Transit 2019, 5, 123–132. [Google Scholar] [CrossRef]
- Núñez, A.; Hendriks, J.; Li, Z.; De Schutter, B.; Dollevoet, R. Facilitating maintenance decisions on the Dutch railways using big data: The ABA case study. In Proceedings of the 2014 IEEE International Conference on Big Data (Big Data), Washington, DC, USA, 27–30 October 2014. [Google Scholar]
- Li, Z.; Molodova, M.; Núñez, A.; Dollevoet, R. Improvements in Axle Box Acceleration Measurements for the Detection of Light Squats in Railway Infrastructure. IEEE Trans. Ind. Electron. 2015, 62, 4385–4397. [Google Scholar] [CrossRef]
- Molodova, M. Detection of early squats by axle box acceleration. Engineering 2013. [Google Scholar] [CrossRef]
- Molodova, M.; Li, Z.; Núñez, A.; Dollevoet, R. Validation of a finite element model for axle box acceleration at squats in the high frequency range. Comput. Struct. 2014, 141, 84–93. [Google Scholar] [CrossRef]
- Song, Y.; Liang, L.; Du, Y.; Sun, B. Railway Polygonized Wheel Detection Based on Numerical Time-Frequency Analysis of Axle-Box Acceleration. Appl. Sci. 2020, 10, 1613. [Google Scholar] [CrossRef]
- Wei, Z.; Núñez, A.; Li, Z.; Dollevoet, R. Evaluating Degradation at Railway Crossings Using Axle Box Acceleration Measurements. Sensors 2017, 17, 2236. [Google Scholar]
- Molodova, M.; Oregui, M.; Núñez, A.; Li, Z.; Dollevoet, R. Health condition monitoring of insulated joints based on axle box acceleration measurements. Eng. Struct. 2016, 123, 225–235. [Google Scholar] [CrossRef]
- Oregui, M.; Li, S.; Núñez, A.; Li, Z.; Carroll, R.; Dollevoet, R. Monitoring bolt tightness of rail joints using axle box acceleration measurements. Struct. Contr. Health Monit. 2017, 24, e1848. [Google Scholar] [CrossRef]
- Real Herráiz, J.I.; Montalbán Domingo, M.L.; Real, T.; Puig, V. Development of a system to obtain vertical track geometry measuring axle-box accelerations from in-service trains. J. Vibroengineering 2012, 14, 813–826. [Google Scholar]
- Deutschl, E.; Gasser, C.; Niel, A.; Werschonig, J. Defect detection on rail surfaces by a vision based system. In Proceedings of the IEEE Intelligent Vehicles Symposium, Parma, Italy, 14–17 June 2004. [Google Scholar]
- Mandriota, C.; Nitti, M.; Ancona, N.; Stella, E.; Distante, A. Filter-based feature selection for rail defect detection. Mach. Vis. Appl. 2004, 15, 179–185. [Google Scholar] [CrossRef]
- Jie, L.; Siwei, L.; Qingyong, L.; Hanqing, Z.; Shengwei, R. Real-time rail head surface defect detection: A geometrical approach. In Proceedings of the 2009 IEEE International Symposium on Industrial Electronics, Seoul, Korea, 5–8 July 2009. [Google Scholar]
- Feng, H.; Jiang, Z.; Xie, F.; Yang, P.; Shi, J.; Chen, L. Automatic fastener classification and defect detection in vision-based railway inspection systems. IEEE Trans. Instrum. Meas. 2013, 63, 877–888. [Google Scholar] [CrossRef]
- Tastimur, C.; Yetis, H.; Karaköse, M.; Akin, E. Rail defect detection and classification with real time image processing technique. Int. J. Comput. Sci. Softw. Eng. 2016, 5, 283. [Google Scholar]
- Xiong, Z.; Li, Q.; Mao, Q.; Zou, Q. A 3D laser profiling system for rail surface defect detection. Sensors 2017, 17, 1791. [Google Scholar] [CrossRef]
- Kang, G.; Gao, S.; Yu, L.; Zhang, D. Deep architecture for high-speed railway insulator surface defect detection: Denoising autoencoder with multitask learning. IEEE Trans. Instrum. Meas. 2018, 68, 2679–2690. [Google Scholar] [CrossRef]
- Krummenacher, G.; Ong, C.S.; Koller, S.; Kobayashi, S.; Buhmann, J.M. Wheel Defect Detection With Machine Learning. IEEE Trans. Intell. Transp. Syst. 2018, 19, 1176–1187. [Google Scholar] [CrossRef]
- Yu, H.; Li, Q.; Tan, Y.; Gan, J.; Wang, J.; Geng, Y.A.; Jia, L. A coarse-to-fine model for rail surface defect detection. IEEE Trans. Instrum. Meas. 2018, 68, 656–666. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhou, K.; Liu, X. Broken Rail Prediction With Machine Learning-Based Approach. In ASME/IEEE Joint Rail Conference 2020; American Society of Mechanical Engineers: New York, NY, USA, 2020. [Google Scholar]
- Cai, Z. Modelling of Rail Track Dynamics and Wheel/Rail Interaction; Queen’s University: Kingston, ON, Canada, 1994. [Google Scholar]
- Steffens, D.M. Identification and Development of a Model of Railway Track Dynamic Behaviour. Master’s Thesis, Queensland University of Technology, Brisbane City, Australia, 2005. [Google Scholar]
- Leong, J. Development of a Limit State Design Methodology for Railway Track. Master’s Thesis, Queensland University of Technology, Brisbane City, Australia, 2007. [Google Scholar]
- Kaewunruen, S.; Osman, M.H.B.; Rungskunroch, P. The Total Track Inspection. Front. Built Environ. 2019, 4, 84. [Google Scholar] [CrossRef]
- Kaewunruen, S. Monitoring of rail corrugation growth on sharp curves for track maintenance prioritization. Int. J. Acoustic. Vib. 2018, 23, 35–43. [Google Scholar] [CrossRef]
- Kaewunruen, S.; Chiengson, C. Railway track inspection and maintenance priorities due to dynamic coupling effects of dipped rails and differential track settlements. Eng. Fail. Anal. 2018, 193, 157–171. [Google Scholar] [CrossRef]
- Bin Osman, M.H.; Kaewunruen, S.; Jack, A. Optimisation of schedules for the inspection of railway tracks. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2018, 232, 1577–1587. [Google Scholar] [CrossRef]
- Remennikov, A.M.; Kaewunruen, S. A review of loading conditions for railway track structures due to train and track vertical interaction. Struct. Cont. Health Mon. 2008, 15, 207–234. [Google Scholar] [CrossRef]
- Alawad, H.; Kaewunruen, S. 5G Intelligence Underpinning Railway Safety in the COVID-19 Era. Front. Built Environ. 2021, 7, 639753. [Google Scholar] [CrossRef]
- Kaewunruen, S.; Sresakoolchai, J.; Ma, W.; Phil-Ebosie, O. Digital Twin Aided Vulnerability Assessment and Risk-Based Maintenance Planning of Bridge Infrastructures Exposed to Extreme Conditions. Sustainability 2021, 13, 2051. [Google Scholar] [CrossRef]
- Kaewunruen, S.; Sussman, J.M.; Matsumoto, A. Grand Challenges in Transportation and Transit Systems. Front. Built Environ. 2016, 2, 4. [Google Scholar] [CrossRef]

| Year | Authors | Defects | Techniques | Input | Prediction |
|---|---|---|---|---|---|
| 2004 | Deutschl et al. [24] | Surface defect | Vision-based system | Image | Defect-free, defect, and suspicious |
| 2004 | Mandriota et al. [25] | Corrugation | Filter-based feature selection | Image | Defect and no-defect |
| 2009 | Jie et al. [26] | Rail head surface defect | Vision-based system | Image | Defect and no-defect |
| 2013 | Feng et al. [27] | Fastener defect | Vision-based system | Image | Worn and missing fasteners |
| 2016 | Tastimur et al. [28] | Rail surface defect | AdaBoost | Image | Headcheck, undulation, scour, and fracture defects |
| 2017 | Xiong et al. [29] | Rail surface defect | 3D laser profiling system | Surface profile | Abrasion, corrugation, scratch, corrosion, and peeling |
| 2018 | Kang et al. [30] | Insulator surface defect | CNN | Image | Defect and no-defect |
| 2018 | Krummenacher et al. [31] | Flat spot, shelling, and non-roundness | Support vector machine and DNN | Force and image | Defect and no-defect |
| 2018 | Yu et al. [32] | Rail surface defect | Coarse-to-fine model | Image | Defect and no-defect |
| 2019 | Wei et al. [9] | Fastener defect | Image processing | Image | Complete, broken, and missing fasteners |
| 2020 | Zhang et al. [33] | Broken rail | Extreme gradient boosting | Track characteristics, traffic-related information, maintenance records, and historical defect records | Defect and no-defect |
| Parameters | Value |
|---|---|
| Sizes of dipped joint | 0–10 mm (the length of the dipped joint is 1000 mm.) |
| Sizes of settlement | 0–100 mm (the lengths of the settlement are 3000 and 10,000 mm for short and long settlement, respectively) |
| Speeds of vehicle | 20–200 km/h |
| Weights of vehicle | 40–80 tons |
| Rail type | AS60 |
| Gauge | Standard gauge |
| Pad type | HDPE |
| Sleeper type | Prestressed |
| Sleeper spacing | 600–750 mm |
| Track bed stiffness | 50.1 MN/m |
| Track bed damping | 159 kNs/m |
| Primary suspension stiffness | 1.22 MN/n |
| Primary suspension damping | 4 kNs/m |
| Wheel radius | 460 mm |
| Hertzian contact coefficient | 7.25 × 1010 N/M3/2 |
| Purpose | Type of Label | Label | Meaning |
|---|---|---|---|
| Dipped joint severity classification | Integer | 0 1 2 | 2.5 mm or smaller 2.5–5.0 mm Bigger than 5.0 mm |
| Settlement severity classification | Integer | 0 1 2 | 20 mm or smaller 20–60 mm Bigger than 60 mm |
| Model | Tuned Hyperparameter | |
|---|---|---|
| DNN |
|
|
| CNN |
|
|
| RNN |
|
|
| Model | Accuracy |
|---|---|
| DNN | 0.86 |
| CNN | 0.99 |
| RNN | 0.79 |
| Model | Tuned Hyperparameter | Value |
|---|---|---|
| CNN | The number of convolutional layers | 2 |
| Filter | 80 (conv1) and 64 (conv2) | |
| Kernel | 5 | |
| The number of max pooling layers | 2 | |
| Pool size | 3 | |
| The number of hidden layers | 2 | |
| The number of hidden nodes | 100 | |
| Activation function | ReLu (except dense3 which uses Softmax) | |
| Batch size | 64 | |
| Learning rate | 0.001 | |
| Momentum | 0.9 | |
| Optimizer | Adam | |
| Dropout | N/A |
| Model | Accuracy |
|---|---|
| Dipped joint detection | |
| DNN | 0.94 |
| CNN | 1.00 |
| RNN | 0.86 |
| Settlement detection | |
| DNN | 0.92 |
| CNN | 0.99 |
| RNN | 0.94 |
| Total accuracy | 0.99 |
| Model | Tuned Hyperparameter | Value |
|---|---|---|
| CNN for detecting dipped joint | The number of convolutional layers | 2 |
| Filter | 64 (conv1) and 32 (conv2) | |
| Kernel | 7 | |
| The number of max pooling layers | 2 | |
| Pool size | 2 | |
| The number of hidden layers | 2 | |
| The number of hidden nodes | 100 | |
| Activation function | ReLu (except dense3, which uses Softmax) | |
| Batch size | 64 | |
| Learning rate | 0.001 | |
| Momentum | 0.9 | |
| Optimizer | Adam | |
| Dropout | 0.25 (before maxpooling2) | |
| CNN for detecting settlement | The number of convolutional layers | 2 |
| Filter | 80 (conv1) and 64 (conv2) | |
| Kernel | 6 | |
| The number of max pooling layers | 2 | |
| Pool size | 4 | |
| The number of hidden layers | 2 | |
| The number of hidden nodes | 100 | |
| Activation function | ReLu (except dense3 which uses Softmax) | |
| Batch size | 64 | |
| Learning rate | 0.001 | |
| Momentum | 0.9 | |
| Optimizer | Adam | |
| Dropout | N/A |
| Model | Accuracy |
|---|---|
| Dipped joint severity classification | |
| DNN | 0.61 |
| CNN | 0.84 |
| RNN | 0.51 |
| Settlement severity classification | |
| DNN | 0.51 |
| CNN | 0.95 |
| RNN | 0.99 |
| Total Accuracy | 0.83 |
| Predicted Class 0 | Predicted Class 1 | Predicted Class 2 | |
|---|---|---|---|
| Actual Class 0 | 75 | 8 | 16 |
| Actual Class 1 | 5 | 69 | 24 |
| Actual Class 2 | 1 | 9 | 189 |
| Predicted Class 0 | Predicted Class 1 | Predicted Class 2 | |
|---|---|---|---|
| Actual Class 0 | 94 | 1 | 0 |
| Actual Class 1 | 1 | 171 | 0 |
| Actual Class 2 | 0 | 1 | 182 |
| Model | Tuned Hyperparameter | Value |
| CNN for classifying dipped joint severity | The number of convolutional layers | 2 |
| Filter | 32 | |
| Kernel | 9 | |
| The number of max pooling layers | 2 | |
| Pool size | 3 (maxpoo1ing1) and 6 (maxpooling2) | |
| The number of hidden layers | 2 | |
| The number of hidden nodes | 80 | |
| Activation function | ReLu (except dense3, which uses Softmax) | |
| Batch size | 8 | |
| Learning rate | 0.001 | |
| Momentum | 0.9 | |
| Optimizer | Adam | |
| Dropout | N/A | |
| RNN for classifying settlement severity | The number of LSTM cells | 200 |
| The number of hidden layer | 2 | |
| The number of hidden node | 100 | |
| Activation function | ReLu (except dense3, which uses Softmax) | |
| Batch size | 64 | |
| Learning rate | 0.001 | |
| Momentum | 0.9 | |
| Optimizer | Adam | |
| Dropout | N/A |
| Model | MAE (mm) |
|---|---|
| Dipped joint severity regression | |
| DNN | 2.01 |
| CNN | 1.25 |
| RNN | 2.54 |
| Settlement severity regression | |
| DNN | 21.14 |
| CNN | 3.13 |
| RNN | 1.58 |
| Model | Tuned Hyperparameter | Value |
|---|---|---|
| CNN for estimating dipped joint severity | The number of convolutional layers | 2 |
| Filter | 32 (conv1) and 64 (conv2) | |
| Kernel | 5 (conv1) and 4 (conv2) | |
| The number of max pooling layers | 2 | |
| Pool size | 3 (maxpoo1ing1) and 2 (maxpooling2) | |
| The number of hidden layers | 2 | |
| The number of hidden nodes | 100 (dense1) and 50 (dense2) | |
| Activation function | ReLu (except dense3, which uses Linear) | |
| Batch size | 16 | |
| Learning rate | 0.001 | |
| Momentum | 0.9 | |
| Optimizer | Adam | |
| Dropout | N/A | |
| RNN for estimating settlement severity | The number of LSTM cells | 200 |
| The number of hidden layer | 2 | |
| The number of hidden node | 200 | |
| Activation function | ReLu (except dense3, which uses Linear) | |
| Batch size | 8 | |
| Learning rate | 0.001 | |
| Momentum | 0.9 | |
| Optimizer | Adam | |
| Dropout | N/A |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sresakoolchai, J.; Kaewunruen, S. Detection and Severity Evaluation of Combined Rail Defects Using Deep Learning. Vibration 2021, 4, 341-356. https://doi.org/10.3390/vibration4020022
Sresakoolchai J, Kaewunruen S. Detection and Severity Evaluation of Combined Rail Defects Using Deep Learning. Vibration. 2021; 4(2):341-356. https://doi.org/10.3390/vibration4020022
Chicago/Turabian StyleSresakoolchai, Jessada, and Sakdirat Kaewunruen. 2021. "Detection and Severity Evaluation of Combined Rail Defects Using Deep Learning" Vibration 4, no. 2: 341-356. https://doi.org/10.3390/vibration4020022
APA StyleSresakoolchai, J., & Kaewunruen, S. (2021). Detection and Severity Evaluation of Combined Rail Defects Using Deep Learning. Vibration, 4(2), 341-356. https://doi.org/10.3390/vibration4020022







