Free Vibration Characteristics of Rectangular Membranes Assuming Rounded-Edges Boundary

Abstract

This study examines the vibratory characteristics of rectangular membranes having an outer rounded-edges periphery. This class of membranes with rounded outer corners has a great advantage over membranes with a rectangular platform wave propagation at the boundary being greatly diffused. As a result, such membranes have a great potential for use in practical engineering applications, especially in waveguides-based structures. Based on an effective 2D Differential-Quadrature numerical method, the frequencies and respective modeshapes of a rectangular membrane with rounded-edges are computed. This method is shown to yield better versatility, efficiency and less computational execution than other discretization methods. The simulated results, showing complex mode exchanges occurring for the higher order modes, demonstrate advantageous use for such membrane patterns in the design of tunable waveguides.

1. Introduction

The vibrational properties of the membrane are essential in the design of drums, speakers, receivers, and more significantly acoustic and electromagnetic transverse mode (TM) waveguides. Such devices are basic structures confining and conveying microwaves. Such characteristics of membranes with classical boundary shapes edges, such as circle, ellipse, and rectangle, have been previously investigated using separation of variables methods [1,2]. For all other irregular boundary shapes, numerical or semi-numerical means are necessary. To this end, the present paper considers a rectangular membrane with rounded-edges type of boundaries. For both membranes and waveguides, such arrangement of the boundaries is easier to manufacture than rectangular shaped edges, and because of the rounding, energy losses are expected to be minimal [3].

Previous reports [4,5,6,7,8,9] on the Helmholtz equation governing the free vibrations of rectangular membranes assuming rounded-edges boundaries were somehow incomplete. Using finite elements, Lagasse and Van Bladel [4] considered three fundamental transverse magnetic modes with not a single reported numerical frequency. An improved finite element method was carried out by Ooi and Zhao [5]; however, only one fundamental frequency was reported. A dual-coordinate finite difference method was suggested by Fanti and Mazzarella [6] without reported numerical results. Eigenfunction expansion and boundary integral were suggested by Ruiz-Cruz and Rebollar [7] with one reported fundamental transverse magnetic frequency. A method for a two-region point match was used by Shen and Lu [8], also for one examined frequency. Notice that the rounded-edges boundary arrangement is somehow unsuitable for the boundary-fitting Ritz method, which was formerly applied successfully to rectangular and skew type of membranes in [9,10].

The aim of the present work is to propose the use of an accurate modal expansion methodology along with a point match technique to acquire the first lowest frequencies and modeshapes for a rectangular membrane assuming rounded-edges boundary. The results could be relevant as well for the analysis of the TM modes in membrane like waveguides.

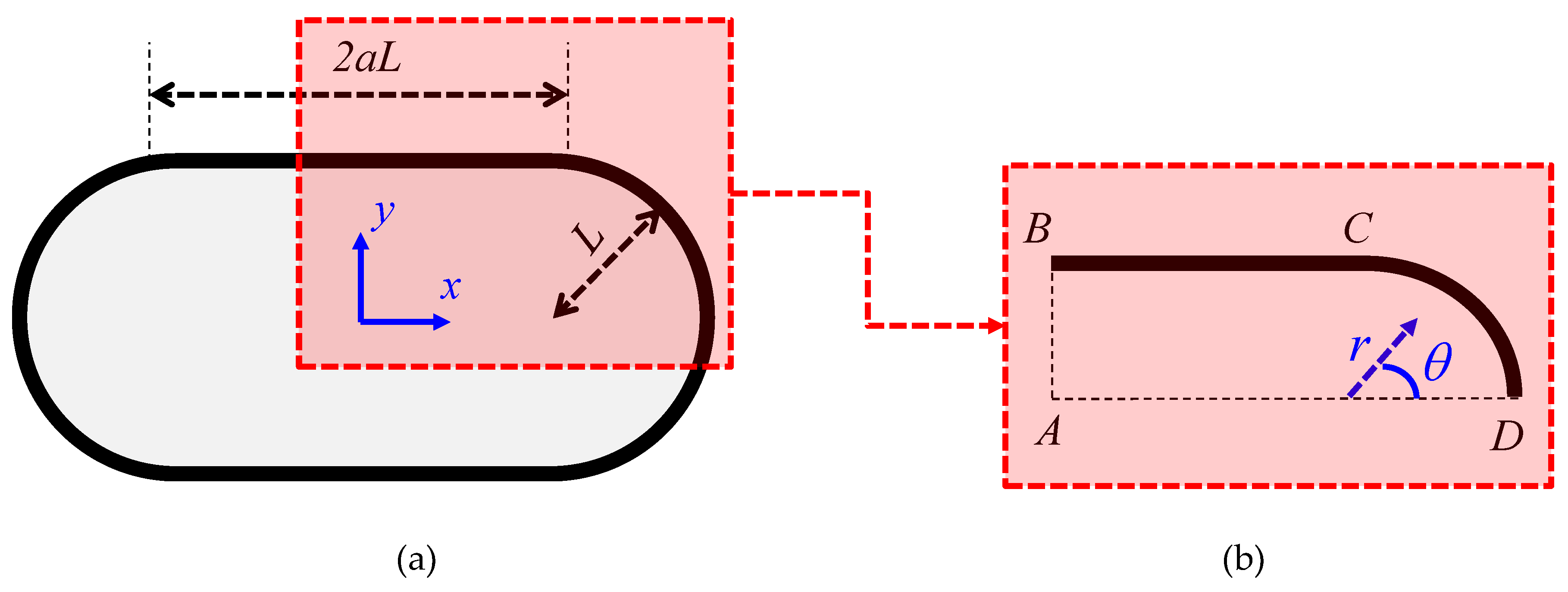
2. Problem Formulation and Numerical Methodology

Figure 1a shows a membrane with rounded-edges boundaries. The membrane is composed of a rectangle of 2L by 2aL (a > 0) with semi-circular ends of radius L. The aspect ratio is thus equal to:

$$AR=\frac{2aL+2L}{2L}=a+1.$$

(1)

Normalizing all the lengths by the membrane half width L and the frequency by $L\sqrt{\rho /T}$ where $\rho$ is the mass per area and $T$ is the tension, the membrane transverse vibration amplitude $w$ is governed by the following Helmholtz equation [2]:

$${\nabla }^{2}w+{\omega }^{2}w=0,$$

(2)

where $\omega$ is the normalized frequency. The boundary conditions are initialized such that w is zero on the boundaries.

Next, let the Cartesian coordinates (x, y) be situated at the membrane centroid. Since the membrane shape has vertical and horizontal symmetries, there can only be four kinds of vibration modes as follows:

• The SS modes: symmetrical in both x and y directions,
• The SA modes: symmetrical in the x direction and anti-symmetrical in the y direction,
• The AS modes: anti-symmetrical in the x direction but symmetrical in the y direction, and
• The AA modes: anti-symmetrical in both x and y directions.

Considering the first quadrant shown in Figure 1b, assuming the displayed polar coordinates (r, θ) at the center of the semi-circle, the solution to Equation (1) can be written as a sum of the membrane eigenfunctions as follows:

$$\{\begin{array}{c}w\left(r,\theta \right)={\displaystyle \sum _{i=0}^{n-1}{A}_i\cos \left(i\theta \right)J_i\left(\omega r\right)}\\ or\\ w\left(r,\theta \right)={\displaystyle \sum _{i=1}^n{A}_i\sin \left(i\theta \right)J_i\left(\omega r\right)}\end{array}.$$

(3)

In the above expressions, $A_i$ are unknown coefficients, $J_i$ are the Bessel function of the first kind, and the infinite sum is truncated to n-terms.

The boundary conditions are fulfilled through an n equally-distributed points on the membrane frontier, consisting of the straight segments: AB, BC and the circular segment: CD. For the points on the segments BC and CD, w is set to zero for all examined modes.

• For the SS mode, the cosine form in Equation (2) is selected, and, for the points on the segment AB, the normal derivative of w is set to zero, i.e.:

  $$\frac{\partial w}{\partial x}=\cos \left(\theta \right)\frac{\partial w}{\partial r}-\frac{\sin \left(\theta \right)}{r}\frac{\partial w}{\partial \theta }=0.$$

  (4)
• For the SA mode, the sine form in Equation (2) is chosen, and Equation (3) on AB holds.
• For the AS mode, the cosine is selected and w is set to zero on AB.
• For the AA mode, the sine is chosen and w is set zero on AB.

The free vibration differential equation (the Helmholtz equation), Equation (2), can be solved for its respective natural frequencies and modeshapes using some numerical descretization techniques such as: the Finite-Difference Method (FDM), the Galerkin Modal Expansion Technique resulting into a Reduced-Order Model (ROM)), the Differential-Quadrature method (DQM), the Rayleigh–Ritz Expansion, etc… In this work, the DQM will be used. The central motivation behind assuming DQM as a discretization technique is that the different order partial derivatives of a function at a given point can be approximated by a weighted sum of function values at all discrete points in the variable domain [11,12]. Therefore, the k^th order derivative of a function at a given point in the space can be approximated within an acceptable error range with weighted linear sum of functional values at all discrete points in the assumed space [12]. It has been observed that DQM has few advantages over the other descretization techniques such as [13]:

• there is no restriction required on the distribution and number of discrete grid points, and
• the weighting coefficient can be determined using a simple recurrence relation instead of solving a set of linear algebraic equations.

The conditions on the discrete N points results into N linear algebraic equations. For non-trivial coefficients $A_i$, the determinant of the coefficients is set to zero, yielding the frequency $\omega$.

Let M be the number of points on segment AB. The total number of points is

$$N=Integer\left(M(1+a+\pi /2)\right).$$

(5)

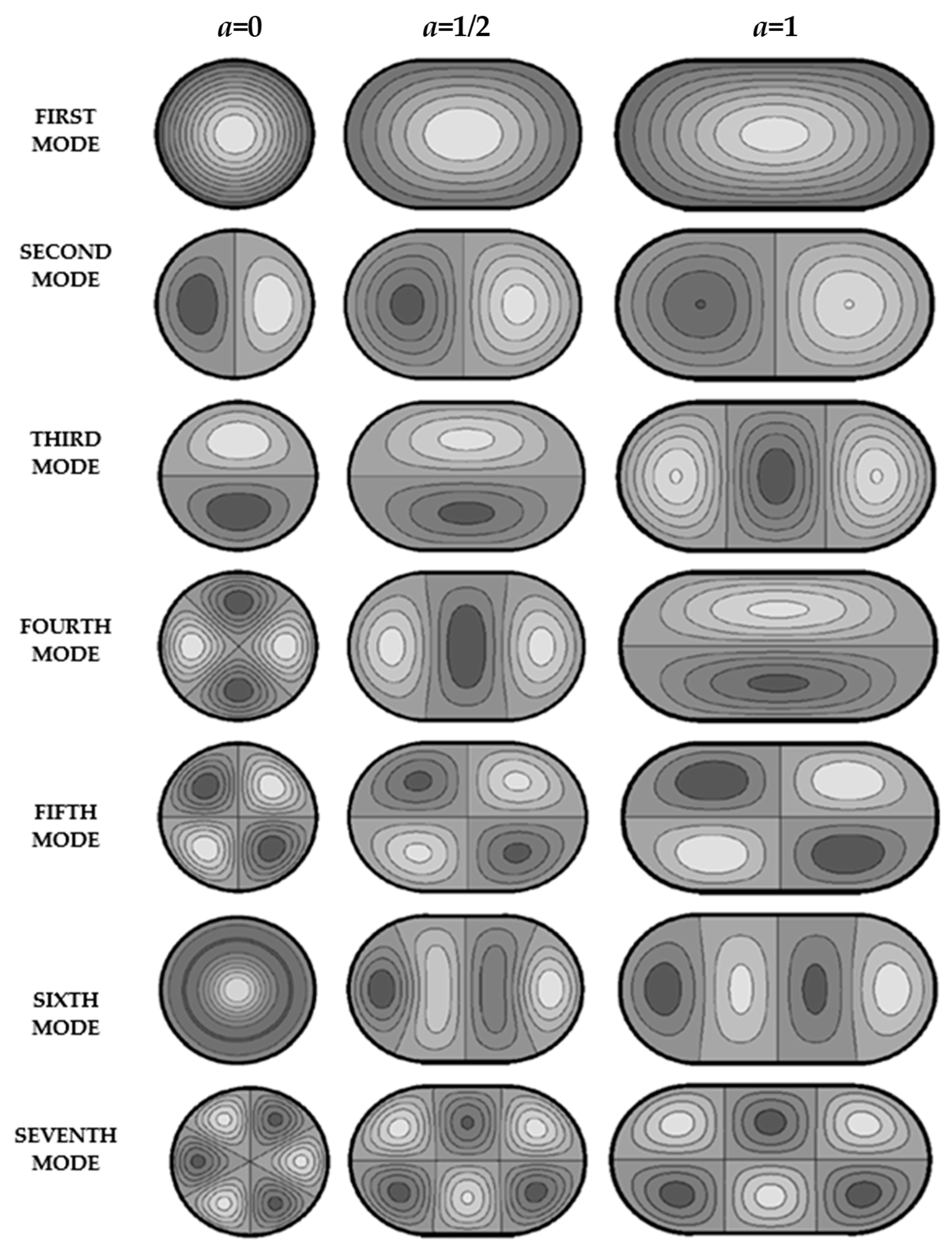
3. Results and Discussion

In this section, the results are presented and discussed.

Table 1. Convergence rate of frequency k for some typical cases.

M	a = 1 1st Mode-SS	a = 1/2 4th Mode-SS	a = 3/2 6th Mode-AA	a = 3/4 7th Mode-SA	a = 2 9th Mode-AS
2	1.7862	3.7204	3.4515	4.3762	3.6150
3	1.7860	3.7203	3.4508	4.4542	3.6153
4	1.7859	3.7209	3.4506	4.4546	3.6154
5	1.7859	3.75209	3.4506	4.4546	3.6154

shows the convergence rate as the considered points in the DQM method are increased. It is worth mentioning that the convergence is fairly fast. We used M = 5 with at least four-digit accuracy (error around 10⁻⁴).

Next,

Table 2. Comparison of the first (fundamental) frequency for the case of a = 1 (AR = 2) and assuming the SS case.

Reference	Numerical Method	Frequency
[4]	Finite elements	1.809
[6]	Boundary integrals	1.7858
[7]	Two regions point match	1.786
Current Work	DQM	1.7858

shows a comparison with the few published results. It is worth noting that, although boundary collocation methods have been used a lot in several mechanics related problems [14], its convergence is not guaranteed. The effectiveness of the present method mainly relies on the centrally located polar coordinates and the evenly-spaced collocation points on the boundaries.

Having examined the accuracy of the numerical approach, we proceed next to study the vibrational properties of the rectangular membrane with rounded-edges.

Table 3. The lowest frequencies of the rectangular membrane with rounded edges assuming different aspect ratio cases. SS, AS, SA and AA denote the respective modeshape.

a = 0	a = 1/4	a = 1/2	a = 3/4	a = 1	a = 3/2	a = 2
2.405 SS	2.118 SS	1.953 SS	1.852 SS	1.785 SS	1.707 SS	1.664 SS
3.832 AS	3.189 AS	2.778 AS	2.501 AS	2.306 AS	2.061 AS	1.918 AS
3.832 SA	3.546 SA	3.4036 SA	3.282 SS	2.962 SS	2.537 SS	2.277 SS
5.135 SS	4.335 SS	3.720 SS	3.324 SA	3.275 SA	3.073 AS	2.69 AS
5.135 AA	4.460 AA	4.056 AA	3.804 AA	3.640 AA	3.222 SA	3.146 SS
5.52 SS	5.071 SS	4.678 AS	4.102 AS	3.668 AS	3.45 AA	3.195 SA
6.38 AS	5.444 AS	4.879 SA	4.454 SA	4.159 SA	3.636 SS	3.35 AA
6.38 SA	5.5 SA	4.921 SS	4.832 SS	4.387 SS	3.794 SA	3.592 SA
7.015 AS	5.967 AS	5.493 AS	4.951 SS	4.761 AA	4.212 AS	3.615 AS
7.015 SA	6.521 SS	5.635 SS	5.177 AA	4.816 SS	4.218 AA	3.900 AA
7.588 SS	6.526 AA	5.745 AA	5.238 AS	5.044 AS	4.692 SA	4.0944 SS
7.588 AA	6.601 SA	6.270 SS	5.812 SS	5.4 SA	4.758 SS	4.257 SA

lists the first lowest frequencies for various assumed aspect ratios and Figure 2 outlines the first vibrational modeshapes assuming three different aspect ratios. Note that, for the case of a = 0, the membrane is simply a circle, for which the exact solution can be written as:

$$w\left(r,\theta \right)=\cos \left(i\theta \right)J_i\left(\omega r\right)\mathrm{or}w\left(r,\theta \right)=\sin \left(i\theta \right)J_i\left(\omega r\right)$$

(6)

and the frequency $\omega$ is the root of $J_i\left(\omega r\right)=0$. In addition, and due to polar symmetry, some circular SS modes and AA modes have the same frequency, and the eigenfunctions are the same when rotated a certain angle. Similarly, some AS modes are the same as the SA modes. We included both forms to illustrate the continuity of the modes.

Considering both Table 3 and Figure 2, one can realize that the normalized frequencies decrease with increasing the membrane aspect ratio. Furthermore, the fundamental (lowest) frequency is always the first SS mode, which has no interior nodal curves. The second lowest frequency denotes the AS mode, with a single nodal line through the centroid and perpendicular to the major axis. For a larger value of the aspect ratios, the modeshapes intersperse sequentially between SS and AS, almost perpendicular to the major axis. The SA mode is the 3^rd mode for a low aspect ratio; nevertheless, it converts to the 4^th mode for the cases of a = 1/2 and a = 3/4. It is then converting to the 5^th mode for a = 3/2 and the 6^th mode for a = 2. In general, SA mode and AA modes decrease in the order hierarchy with increased aspect ratio. Numerous mode changes occurred for several assumed cases, especially for higher modes, offering the possibility for such membranes to be used as waveguides of distinguishing frequency tunability characteristics.

4. Conclusions

In this work, a Differential-Quadrature Method was examined to obtain the frequencies and their respective modeshapes of a rectangular shaped membrane assuming rounded-edges boundaries. The examined method was shown to be numerically effective and accurate in comparison to other methods. The discussed results showed complex mode exchanges occurring for the higher order modes, demonstrating an opportunity of such rounded-edges membrane design to be used in frequency tunable based waveguides-based applications.