Asymmetric Oscillations of AFG Microscale Nonuniform Deformable Timoshenko Beams
Abstract
:1. Introduction
2. Model Development
3. Discretized Equations of Motion and Solution Procedure
4. Asymmetric Size-Dependent Vibrations
5. Concluding Remarks
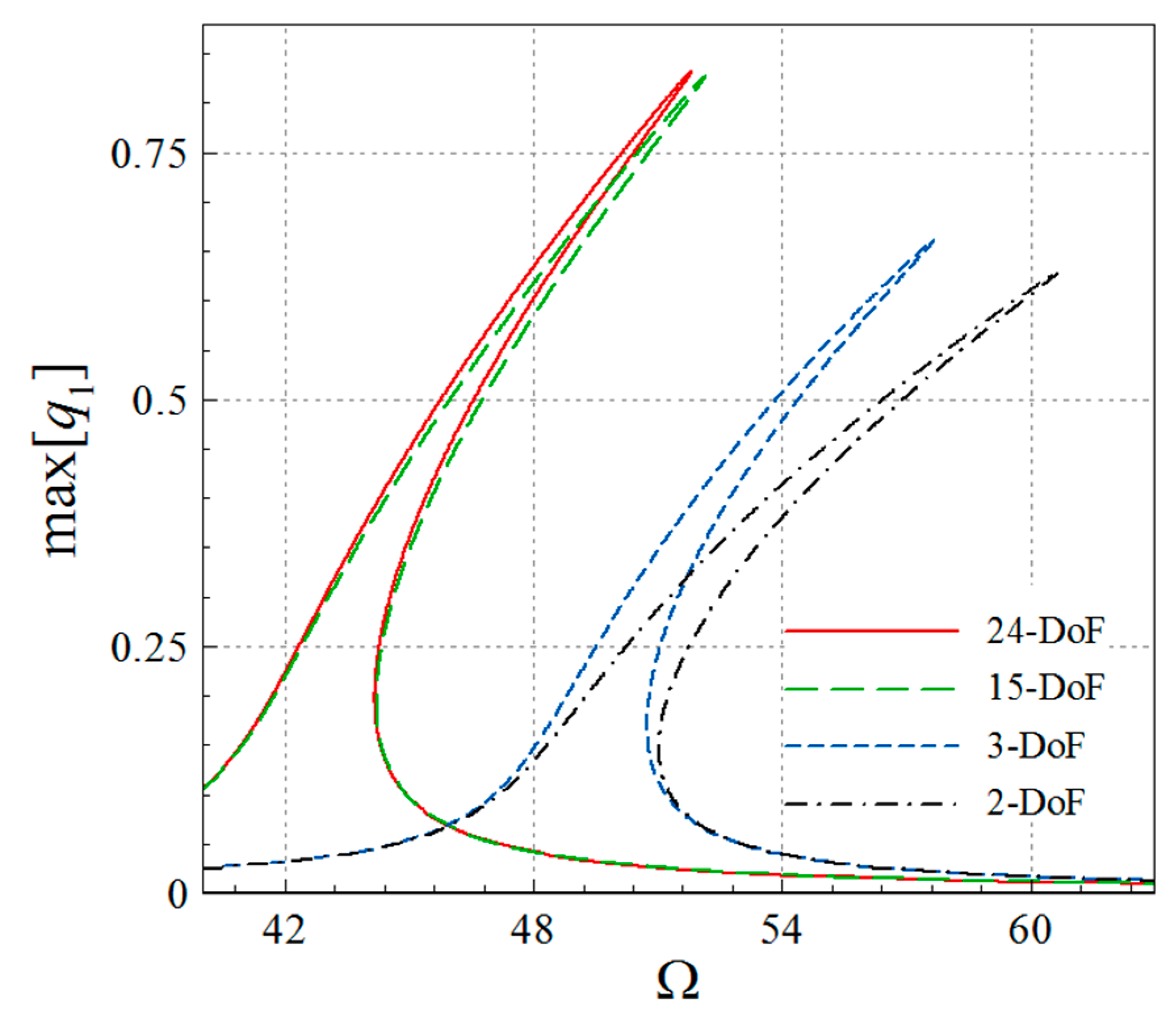
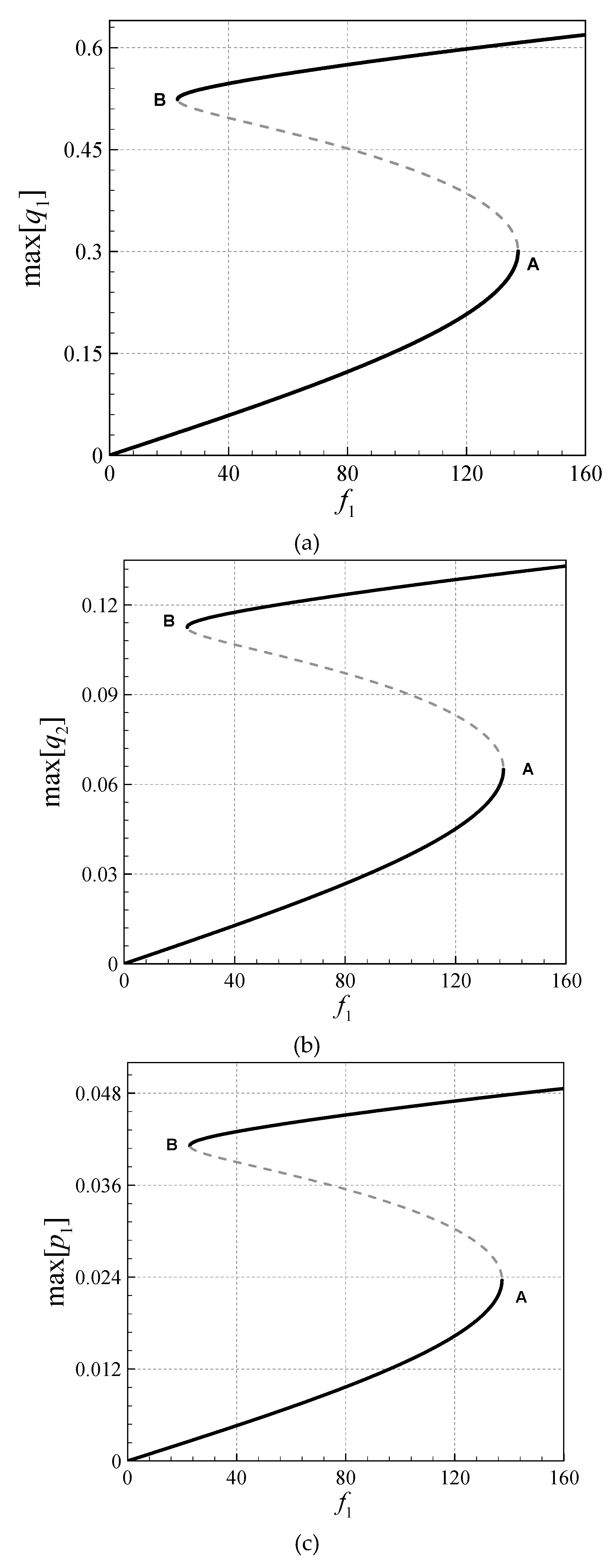
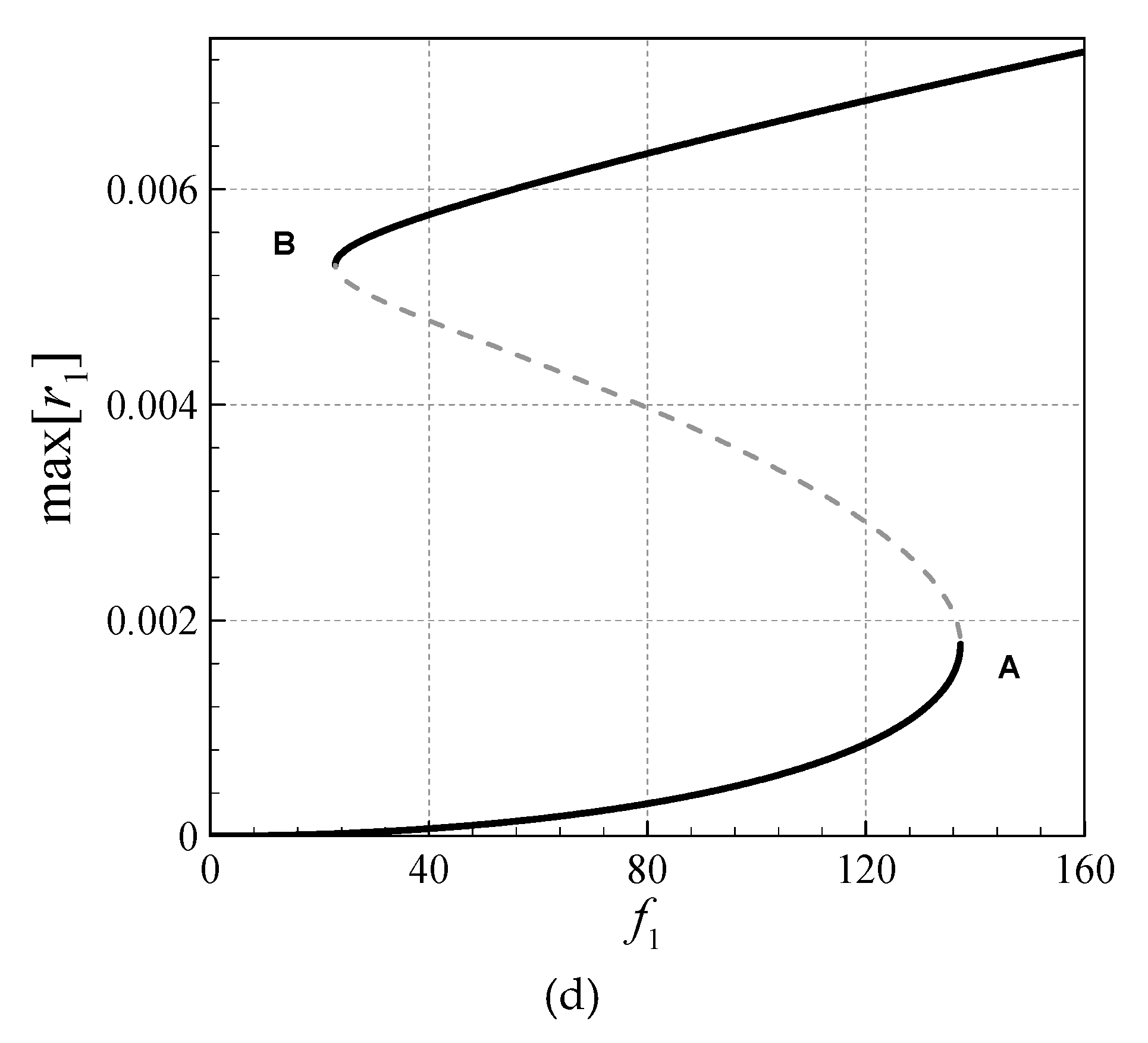
- Asymmetry and stretching-type nonlinearity in the AFG microsystem cause necessity for a high DOF analysis.
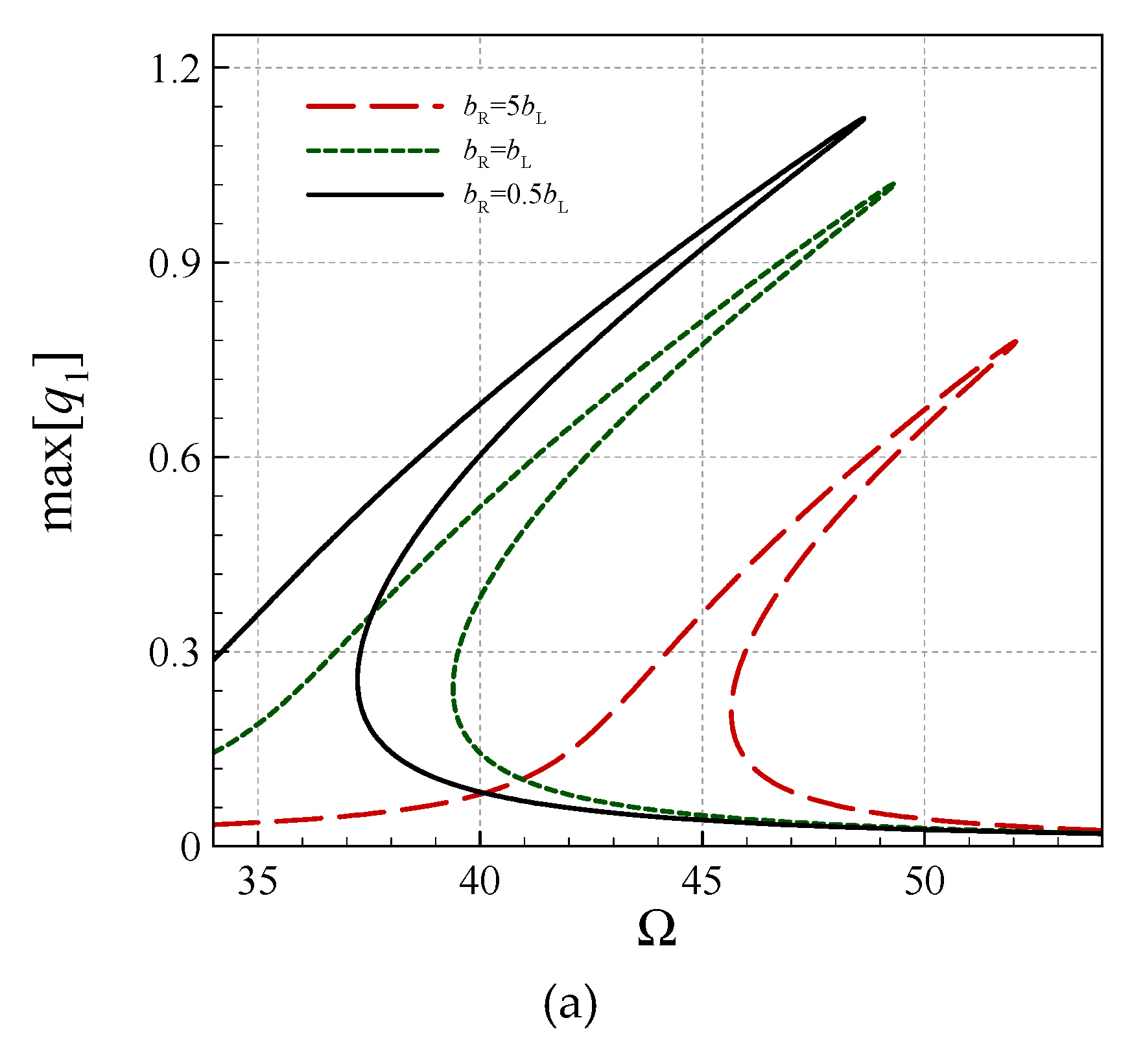
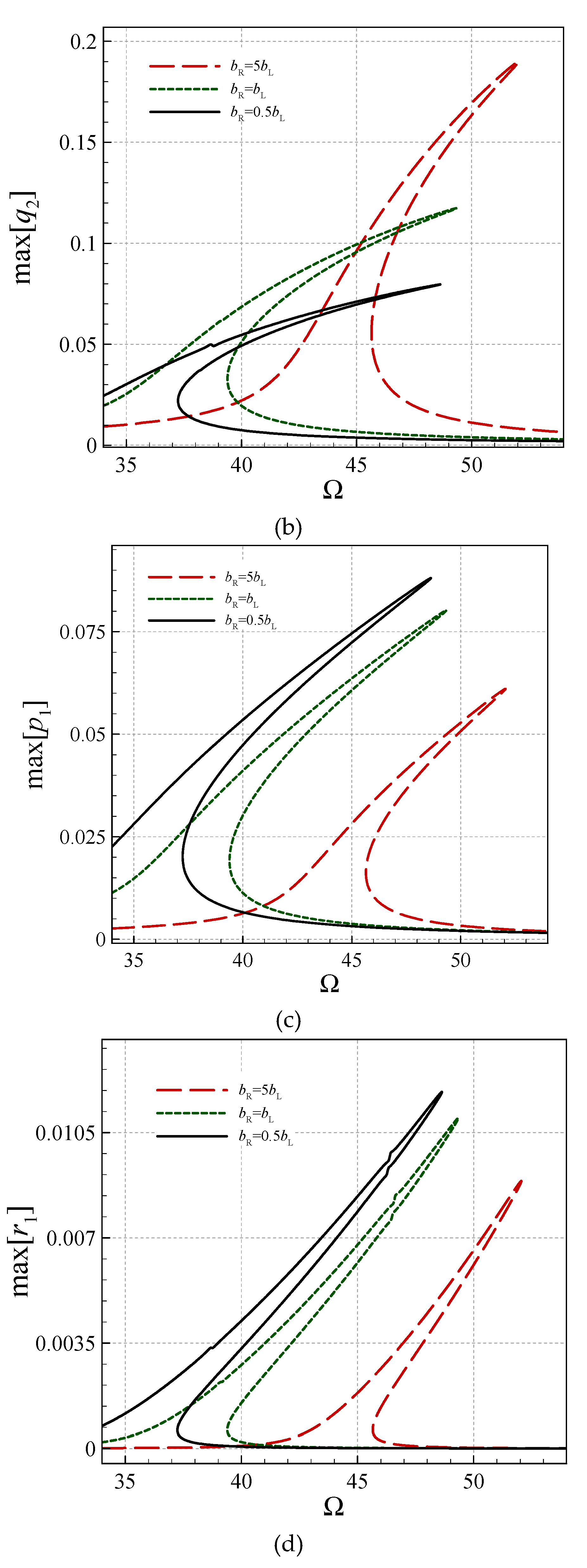
- The size effect is more significant for larger gradient indices.
- For larger gradient indices, the symmetric transverse and rotational-mode peak-amplitudes are larger.
- All the asymmetric and symmetric modes in the coupled transverse/axial/rotational motion display hardening motions.
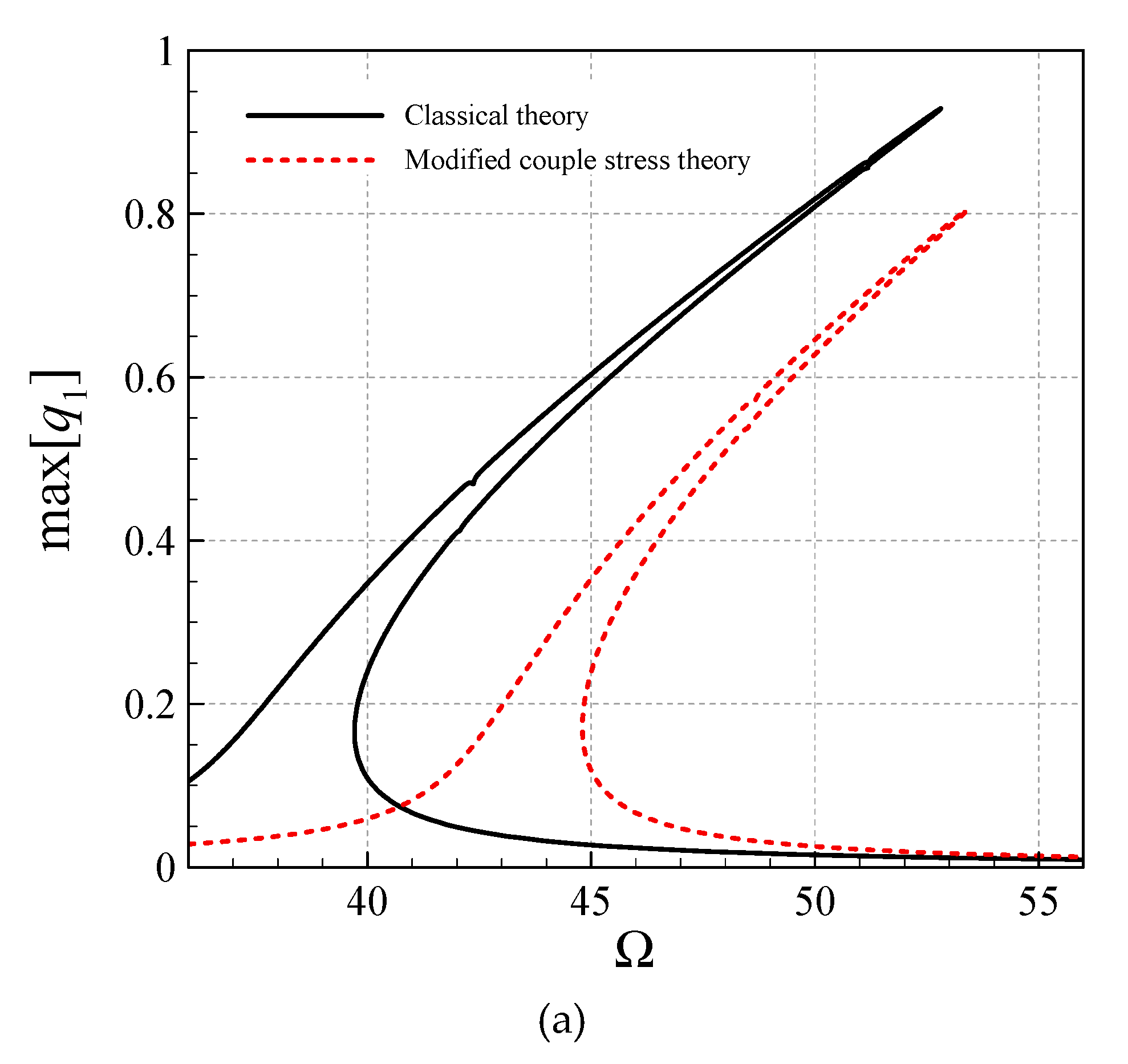
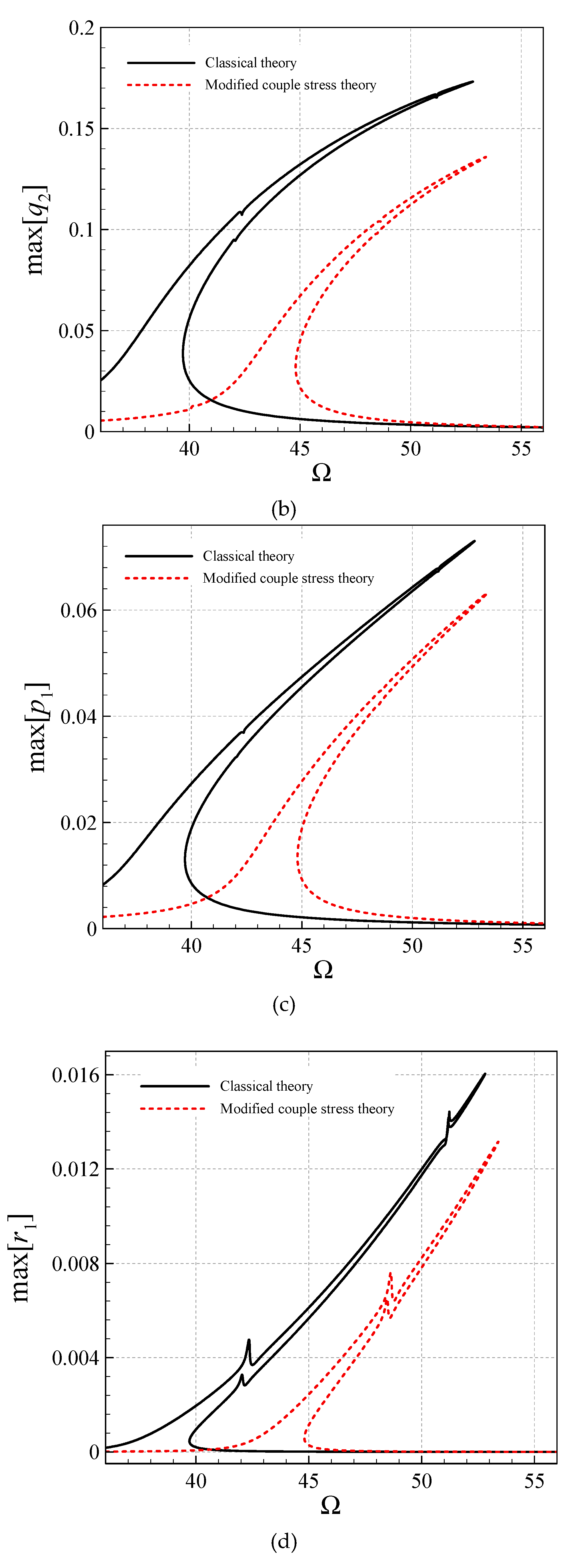
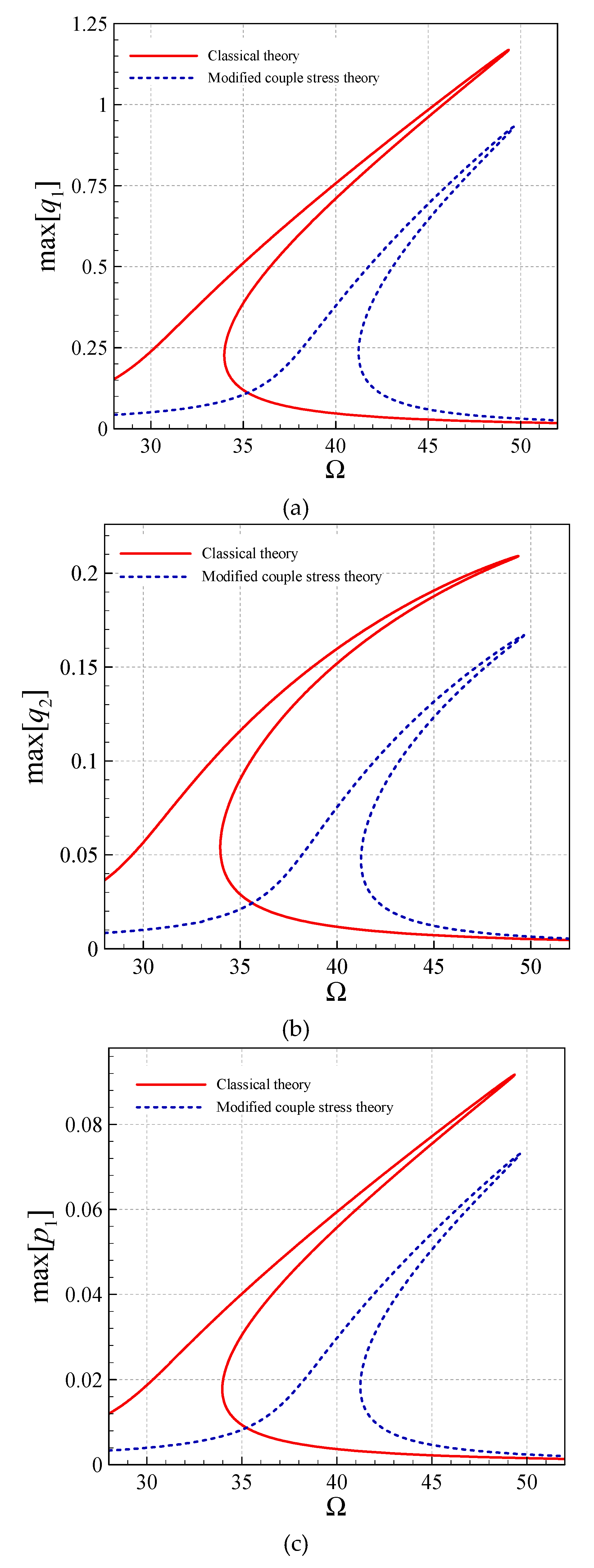
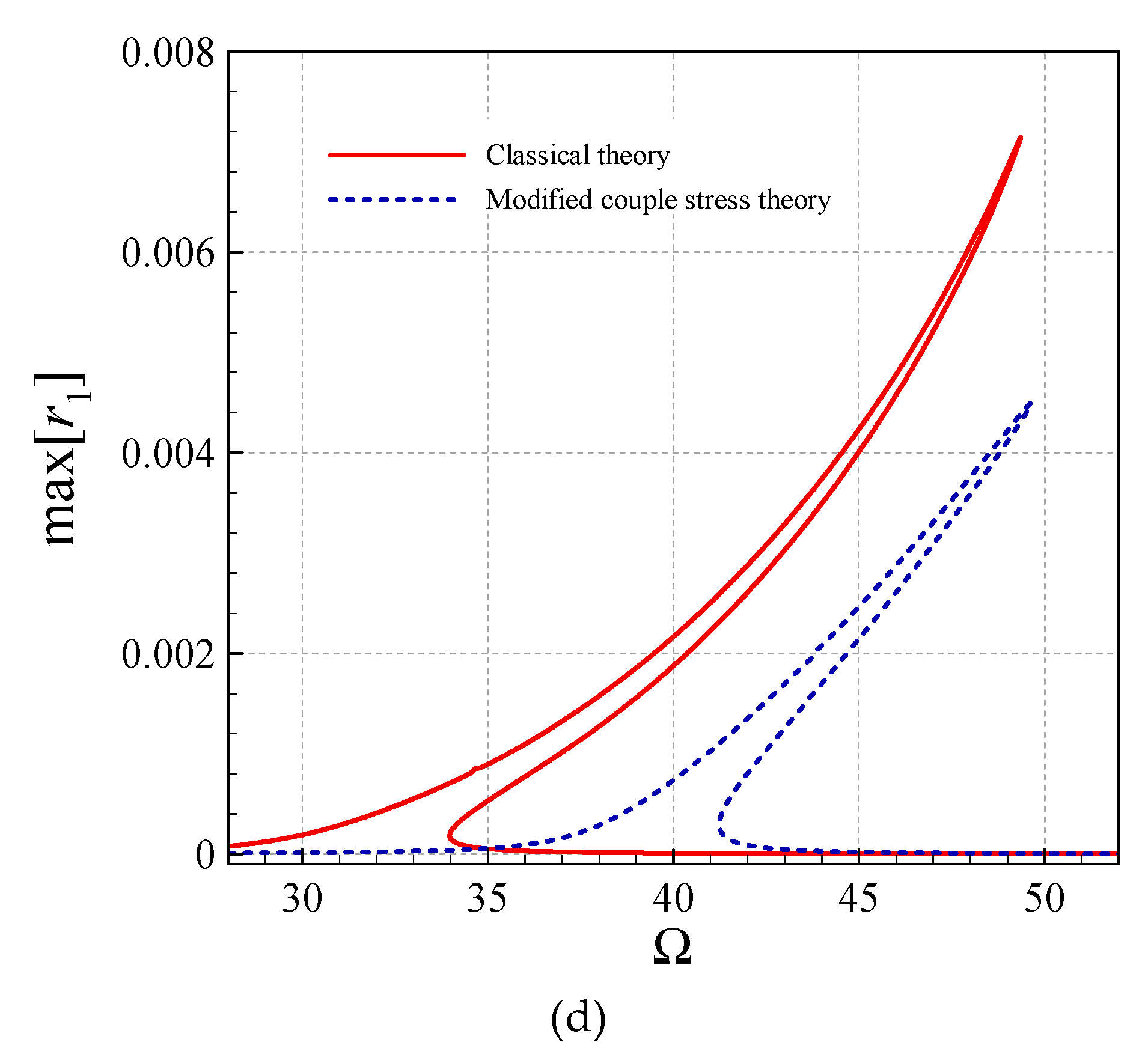
- The modified CST, in all the asymmetric and symmetric modes, reduces the peak-amplitude and shifts the frequency diagrams to the right.
Author Contributions
Funding
Conflicts of Interest
References
- Tophøj, L.; Grathwol, N.; Hansen, S.O. Effective mass of tuned mass dampers. Vibration 2018, 1, 192–206. [Google Scholar] [CrossRef]
- Zaghari, B.; Rustighi, E.; Ghandchi-Tehrani, M. Improved modelling of a nonlinear parametrically excited system with electromagnetic excitation. Vibration 2018, 1, 157–171. [Google Scholar] [CrossRef]
- Martínez-Ayuso, G.; Haddad Khodaparast, H.; Zhang, Y.; Bowen, C.R.; Friswell, M.I.; Shaw, A.D.; Madinei, H. Model validation of a porous piezoelectric energy harvester using vibration test data. Vibration 2018, 1, 123–137. [Google Scholar] [CrossRef]
- Naranjo-Pérez, J.; Jiménez-Manfredi, J.; Jiménez-Alonso, J.F.; Sáez, A. Motion-based design of passive damping devices to mitigate wind-induced vibrations in stay cables. Vibration 2018, 1, 269–289. [Google Scholar] [CrossRef]
- Farokhi, H.; Ghayesh, M.H. Nonlinear mechanics of electrically actuated microplates. Int. J. Eng. Sci. 2018, 123, 197–213. [Google Scholar] [CrossRef]
- Ghayesh, M.H.; Farokhi, H.; Alici, G. Size-dependent electro-elasto-mechanics of MEMS with initially curved deformable electrodes. Int. J. Mech. Sci. 2015, 103, 247–264. [Google Scholar] [CrossRef]
- Ghayesh, M.H.; Farokhi, H.; Amabili, M. Nonlinear behaviour of electrically actuated MEMS resonators. Int. J. Eng. Sci. 2013, 71, 137–155. [Google Scholar] [CrossRef]
- Bognash, M.; Asokanthan, S.F. Stochastic stability of a class of mems-based vibratory gyroscopes under input rate fluctuations. Vibration 2018, 1, 69–80. [Google Scholar] [CrossRef]
- Ghayesh, M.H.; Farokhi, H. Bistable nonlinear response of MEMS resonators. Nonlinear Dyn. 2017, 90, 1627–1645. [Google Scholar] [CrossRef]
- Farokhi, H.; Ghayesh, M.H.; Hussain, S. Pull-in characteristics of electrically actuated MEMS arches. Mech. Mach. Theory 2016, 98, 133–150. [Google Scholar] [CrossRef]
- Ghayesh, M.H.; Farokhi, H.; Alici, G. Size-dependent performance of microgyroscopes. Int. J. Eng. Sci. 2016, 100, 99–111. [Google Scholar] [CrossRef]
- Shen, H.S.; Wang, Z.X. Nonlinear analysis of shear deformable fgm beams resting on elastic foundations in thermal environments. Int. J. Mech. Sci. 2014, 81, 195–206. [Google Scholar] [CrossRef]
- Li, Y.; Meguid, S.A.; Fu, Y.; Xu, D. Nonlinear analysis of thermally and electrically actuated functionally graded material microbeam. Proc. R. Soc. Lond. A Math. Phys. Eng. Sci. 2013, 470, 20130473. [Google Scholar] [CrossRef] [PubMed]
- Oskouie, M.F.; Ansari, R.; Rouhi, H. Bending analysis of functionally graded nanobeams based on the fractional nonlocal continuum theory by the variational legendre spectral collocation method. Meccanica 2018, 53, 1115–1130. [Google Scholar] [CrossRef]
- Huynh, T.A.; Luu, A.T.; Lee, J. Bending, buckling and free vibration analyses of functionally graded curved beams with variable curvatures using isogeometric approach. Meccanica 2017, 52, 2527–2546. [Google Scholar] [CrossRef]
- Yang, B.; Yang, J.; Kitipornchai, S. Thermoelastic analysis of functionally graded graphene reinforced rectangular plates based on 3D elasticity. Meccanica 2017, 52, 2275–2292. [Google Scholar] [CrossRef]
- Tang, Y.; Lv, X.; Yang, T. Bi-directional functionally graded beams: Asymmetric modes and nonlinear free vibration. Compos. Part B Eng. 2019, 156, 319–331. [Google Scholar] [CrossRef]
- Ghayesh, M.H.; Farajpour, A. A review on the mechanics of functionally graded nanoscale and microscale structures. Int. J. Eng. Sci. 2019, 137, 8–36. [Google Scholar] [CrossRef]
- Attia, M.A.; Abdel Rahman, A.A. On vibrations of functionally graded viscoelastic nanobeams with surface effects. Int. J. Eng. Sci. 2018, 127, 1–32. [Google Scholar] [CrossRef]
- Zenkour, A.M.; Radwan, A.F. Compressive study of functionally graded plates resting on winkler–pasternak foundations under various boundary conditions using hyperbolic shear deformation theory. Arch. Civ. Mech. Eng. 2018, 18, 645–658. [Google Scholar] [CrossRef]
- Ghayesh, M.H. Viscoelastically coupled dynamics of FG timoshenko microbeams. Microsyst. Technol. 2019, 25, 651–663. [Google Scholar] [CrossRef]
- Ghayesh, M.H. Mechanics of tapered AFG shear-deformable microbeams. Microsyst. Technol. 2018, 24, 1743–1754. [Google Scholar] [CrossRef]
- Ghayesh, M.H. Stability and bifurcation characteristics of viscoelastic microcantilevers. Microsyst. Technol. 2018, 24, 4739–4746. [Google Scholar] [CrossRef]
- Ghayesh, M.H.; Farajpour, A. Vibrations of shear deformable FG viscoelastic microbeams. Microsyst. Technol. 2018. [Google Scholar] [CrossRef]
- Ghayesh, M.H.; Farokhi, H. Parametric vibrations of imperfect timoshenko microbeams. Microsyst. Technol. 2017, 23, 4917–4929. [Google Scholar] [CrossRef]
- Ghayesh, M.H.; Farokhi, H. Parametric instability of microbeams in supercritical regime. Nonlinear Dyn. 2016, 83, 1171–1183. [Google Scholar] [CrossRef]
- Ghayesh, M.H.; Farokhi, H. Nonlinear dynamics of doubly curved shallow microshells. Nonlinear Dyn. 2018, 92, 803–814. [Google Scholar] [CrossRef]
- Farokhi, H.; Ghayesh, M.H. Size-dependent parametric dynamics of imperfect microbeams. Int. J. Eng. Sci. 2016, 99, 39–55. [Google Scholar] [CrossRef]
- Farokhi, H.; Ghayesh, M.H. On the dynamics of imperfect shear deformable microplates. Int. J. Eng. Sci. 2018, 133, 264–283. [Google Scholar] [CrossRef]
- Farokhi, H.; Ghayesh, M.H. Nonlinear mechanical behaviour of microshells. Int. J. Eng. Sci. 2018, 127, 127–144. [Google Scholar] [CrossRef]
- Farokhi, H.; Ghayesh, M.H.; Amabili, M. Nonlinear dynamics of a geometrically imperfect microbeam based on the modified couple stress theory. Int. J. Eng. Sci. 2013, 68, 11–23. [Google Scholar] [CrossRef]
- Ghayesh, M.H.; Farajpour, A. Nonlinear mechanics of nanoscale tubes via nonlocal strain gradient theory. Int. J. Eng. Sci. 2018, 129, 84–95. [Google Scholar] [CrossRef]
- Rashvand, K.; Rezazadeh, G.; Mobki, H.; Ghayesh, M.H. On the size-dependent behavior of a capacitive circular micro-plate considering the variable length-scale parameter. Int. J. Mech. Sci. 2013, 77, 333–342. [Google Scholar] [CrossRef]
- Farajpour, A.; Ghayesh, M.H.; Farokhi, H. A review on the mechanics of nanostructures. Int. J. Eng. Sci. 2018, 133, 231–263. [Google Scholar] [CrossRef]
- Farokhi, H.; Ghayesh, M.H. Nonlinear resonant response of imperfect extensible timoshenko microbeams. Int. J. Mech. Mater. Des. 2017, 13, 43–55. [Google Scholar] [CrossRef]
- Farajpour, A.; Farokhi, H.; Ghayesh, M.H.; Hussain, S. Nonlinear mechanics of nanotubes conveying fluid. Int. J. Eng. Sci. 2018, 133, 132–143. [Google Scholar] [CrossRef]
- Farokhi, H.; Ghayesh, M.H.; Gholipour, A. Dynamics of functionally graded micro-cantilevers. Int. J. Eng. Sci. 2017, 115, 117–130. [Google Scholar] [CrossRef]
- Farokhi, H.; Ghayesh, M.H.; Gholipour, A.; Hussain, S. Motion characteristics of bilayered extensible timoshenko microbeams. Int. J. Eng. Sci. 2017, 112, 1–17. [Google Scholar] [CrossRef]
- Farajpour, M.; Shahidi, A.; Farajpour, A. A nonlocal continuum model for the biaxial buckling analysis of composite nanoplates with shape memory alloy nanowires. Mater. Res. Express 2018, 5, 035026. [Google Scholar] [CrossRef]
- Farajpour, M.R.; Shahidi, A.; Farajpour, A. Resonant frequency tuning of nanobeams by piezoelectric nanowires under thermo-electro-magnetic field: A theoretical study. Micro Nano Lett. 2018, 13, 1627–1632. [Google Scholar] [CrossRef]
- Farokhi, H.; Ghayesh, M.H.; Kosasih, B.; Akaber, P. On the nonlinear resonant dynamics of timoshenko microbeams: Effects of axial load and geometric imperfection. Meccanica 2016, 51, 155–169. [Google Scholar] [CrossRef]
- Ghayesh, M.H.; Farokhi, H. On the viscoelastic dynamics of fluid-conveying microtubes. Int. J. Eng. Sci. 2018, 127, 186–200. [Google Scholar] [CrossRef]
- Ghayesh, M.H. Nonlinear size-dependent behaviour of single-walled carbon nanotubes. Appl. Phys. A 2014, 117, 1393–1399. [Google Scholar] [CrossRef]
- Farajpour, A.; Rastgoo, A.; Farajpour, M. Nonlinear buckling analysis of magneto-electro-elastic cnt-mt hybrid nanoshells based on the nonlocal continuum mechanics. Compos. Struct. 2017, 180, 179–191. [Google Scholar] [CrossRef]
- Ghayesh, M.H.; Farokhi, H.; Farajpour, A. Global dynamics of fluid conveying nanotubes. Int. J. Eng. Sci. 2019, 135, 37–57. [Google Scholar] [CrossRef]
- Farajpour, M.; Shahidi, A.; Hadi, A.; Farajpour, A. Influence of initial edge displacement on the nonlinear vibration, electrical and magnetic instabilities of magneto-electro-elastic nanofilms. Mech. Adv. Mater. Struct. 2018. [Google Scholar] [CrossRef]
- Dehrouyeh-Semnani, A.M.; Bahrami, A. On size-dependent timoshenko beam element based on modified couple stress theory. Int. J. Eng. Sci. 2016, 107, 134–148. [Google Scholar] [CrossRef]
- Kahrobaiyan, M.; Asghari, M.; Ahmadian, M. A timoshenko beam element based on the modified couple stress theory. Int. J. Mech. Sci. 2014, 79, 75–83. [Google Scholar] [CrossRef]
- Dehrouyeh-Semnani, A.M.; Nikkhah-Bahrami, M.; Yazdi, M.R.H. On nonlinear stability of fluid-conveying imperfect micropipes. Int. J. Eng. Sci. 2017, 120, 254–271. [Google Scholar] [CrossRef]
- Dehrouyeh-Semnani, A.M.; Nikkhah-Bahrami, M.; Yazdi, M.R.H. On nonlinear vibrations of micropipes conveying fluid. Int. J. Eng. Sci. 2017, 117, 20–33. [Google Scholar] [CrossRef]
- Dehrouyeh-Semnani, A.M.; Mostafaei, H.; Dehrouyeh, M.; Nikkhah-Bahrami, M. Thermal pre-and post-snap-through buckling of a geometrically imperfect doubly-clamped microbeam made of temperature-dependent functionally graded materials. Compos. Struct. 2017, 170, 122–134. [Google Scholar] [CrossRef]
- Kahrobaiyan, M.H.; Asghari, M.; Hoore, M.; Ahmadian, M.T. Nonlinear size-dependent forced vibrational behavior of microbeams based on a non-classical continuum theory. J. Vib. Control 2012, 18, 696–711. [Google Scholar] [CrossRef]
- Kahrobaiyan, M.; Asghari, M.; Ahmadian, M. Longitudinal behavior of strain gradient bars. Int. J. Eng. Sci. 2013, 66, 44–59. [Google Scholar] [CrossRef]
- Kahrobaiyan, M.; Asghari, M.; Ahmadian, M. A strain gradient timoshenko beam element: Application to MEMS. Acta Mech. 2015, 226, 505–525. [Google Scholar] [CrossRef]
- Farajpour, M.; Shahidi, A.; Tabataba’i-Nasab, F.; Farajpour, A. Vibration of initially stressed carbon nanotubes under magneto-thermal environment for nanoparticle delivery via higher-order nonlocal strain gradient theory. Eur. Phys. J. Plus 2018, 133, 219. [Google Scholar] [CrossRef]
- Zhu, X.; Li, L. Closed form solution for a nonlocal strain gradient rod in tension. Int. J. Eng. Sci. 2017, 119, 16–28. [Google Scholar] [CrossRef]
- Li, L.; Hu, Y.; Ling, L. Wave propagation in viscoelastic single-walled carbon nanotubes with surface effect under magnetic field based on nonlocal strain gradient theory. Phys. E Low-dimens. Syst. Nanostruct. 2016, 75, 118–124. [Google Scholar] [CrossRef]
- Li, L.; Li, X.; Hu, Y. Free vibration analysis of nonlocal strain gradient beams made of functionally graded material. Int. J. Eng. Sci. 2016, 102, 77–92. [Google Scholar] [CrossRef]
- Li, L.; Hu, Y. Nonlinear bending and free vibration analyses of nonlocal strain gradient beams made of functionally graded material. Int. J. Eng. Sci. 2016, 107, 77–97. [Google Scholar] [CrossRef]
- Akgöz, B.; Civalek, Ö. Free vibration analysis of axially functionally graded tapered bernoulli–euler microbeams based on the modified couple stress theory. Compos. Struct. 2013, 98, 314–322. [Google Scholar] [CrossRef]
- Şimşek, M. Size dependent nonlinear free vibration of an axially functionally graded (AFG) microbeam using he’s variational method. Compos. Struct. 2015, 131, 207–214. [Google Scholar] [CrossRef]
- Shafiei, N.; Kazemi, M.; Ghadiri, M. Nonlinear vibration of axially functionally graded tapered microbeams. Int. J. Eng. Sci. 2016, 102, 12–26. [Google Scholar] [CrossRef]
- Ghayesh, M.H. Viscoelastic dynamics of axially fg microbeams. Int. J. Eng. Sci. 2019, 135, 75–85. [Google Scholar] [CrossRef]
- Ghayesh, M.H.; Farokhi, H.; Farajpour, A. Chaotic oscillations of viscoelastic microtubes conveying pulsatile fluid. Microfluid. Nanofluid. 2018, 22, 72. [Google Scholar] [CrossRef]
- Farajpour, A.; Ghayesh, M.H.; Farokhi, H. Application of nanotubes in conveying nanofluid: A bifurcation analysis with consideration of internal energy loss and geometrical imperfection. Microsyst. Technol. 2019. [Google Scholar] [CrossRef]
- Gholipour, A.; Farokhi, H.; Ghayesh, M.H. In-plane and out-of-plane nonlinear size-dependent dynamics of microplates. Nonlinear Dyn. 2015, 79, 1771–1785. [Google Scholar] [CrossRef]
- Farokhi, H.; Ghayesh, M.H. Nonlinear dynamical behaviour of geometrically imperfect microplates based on modified couple stress theory. Int. J. Mech. Sci. 2015, 90, 133–144. [Google Scholar] [CrossRef]
- Ma, H.; Gao, X.-L.; Reddy, J. A microstructure-dependent timoshenko beam model based on a modified couple stress theory. J. Mech. Phys. Solids 2008, 56, 3379–3391. [Google Scholar] [CrossRef]
- Reddy, J. Microstructure-dependent couple stress theories of functionally graded beams. J. Mech. Phys. Solids 2011, 59, 2382–2399. [Google Scholar] [CrossRef]
- Gholipour, A.; Ghayesh, M.H.; Zander, A.; Mahajan, R. Three-dimensional biomechanics of coronary arteries. Int. J. Eng. Sci. 2018, 130, 93–114. [Google Scholar] [CrossRef]
- Gholipour, A.; Ghayesh, M.H.; Zander, A. Nonlinear biomechanics of bifurcated atherosclerotic coronary arteries. Int. J. Eng. Sci. 2018, 133, 60–83. [Google Scholar] [CrossRef]
- Ghayesh, M.H.; Farokhi, H. Mechanics of tapered axially functionally graded shallow arches. Compos. Struct. 2018, 188, 233–241. [Google Scholar] [CrossRef]
- Ghayesh, M.H. Nonlinear vibration analysis of axially functionally graded shear-deformable tapered beams. Appl. Math. Model. 2018, 59, 583–596. [Google Scholar] [CrossRef]
- Farajpour, A.; Ghayesh, M.H.; Farokhi, H. A coupled nonlinear continuum model for bifurcation behaviour of fluid-conveying nanotubes incorporating internal energy loss. Microfluid. Nanofluid. 2019, 23, 34. [Google Scholar] [CrossRef]
- Farajpour, A.; Ghayesh, M.H.; Farokhi, H. Large-amplitude coupled scale-dependent behaviour of geometrically imperfect nsgt nanotubes. Int. J. Mech. Sci. 2019, 150, 510–525. [Google Scholar] [CrossRef]
- Kazemirad, S.; Ghayesh, M.H.; Amabili, M. Thermo-mechanical nonlinear dynamics of a buckled axially moving beam. Arch. Appl. Mech. 2013, 83, 25–42. [Google Scholar] [CrossRef]
- Ghayesh, M.H.; Kazemirad, S.; Reid, T. Nonlinear vibrations and stability of parametrically exited systems with cubic nonlinearities and internal boundary conditions: A general solution procedure. Appl. Math. Model. 2012, 36, 3299–3311. [Google Scholar] [CrossRef]
- Ghayesh, M.H.; Moradian, N. Nonlinear dynamic response of axially moving, stretched viscoelastic strings. Arch. Appl. Mech. 2011, 81, 781–799. [Google Scholar] [CrossRef]
- Ghayesh, M.H. Functionally graded microbeams: Simultaneous presence of imperfection and viscoelasticity. Int. J. Mech. Sci. 2018, 140, 339–350. [Google Scholar] [CrossRef]
- Ghayesh, M.H.; Farokhi, H. Chaotic motion of a parametrically excited microbeam. Int. J. Eng. Sci. 2015, 96, 34–45. [Google Scholar] [CrossRef]
- Ghayesh, M.H.; Amabili, M.; Farokhi, H. Three-dimensional nonlinear size-dependent behaviour of timoshenko microbeams. Int. J. Eng. Sci. 2013, 71, 1–14. [Google Scholar] [CrossRef]
- Ghayesh, M.H.; Farokhi, H.; Amabili, M. Nonlinear dynamics of a microscale beam based on the modified couple stress theory. Compos. Part B Eng. 2013, 50, 318–324. [Google Scholar] [CrossRef]
- Ghayesh, M.H.; Farokhi, H.; Amabili, M. In-plane and out-of-plane motion characteristics of microbeams with modal interactions. Compos. Part B Eng. 2014, 60, 423–439. [Google Scholar] [CrossRef]
- Ghayesh, M.H.; Farokhi, H.; Gholipour, A.; Tavallaeinejad, M. Nonlinear bending and forced vibrations of axially functionally graded tapered microbeams. Int. J. Eng. Sci. 2017, 120, 51–62. [Google Scholar] [CrossRef]
- Farokhi, H.; Ghayesh, M.H. Size-dependent behaviour of electrically actuated microcantilever-based mems. Int. J. Mech. Mater. Des. 2016, 12, 301–315. [Google Scholar] [CrossRef]
- Ghayesh, M.H.; Farokhi, H.; Gholipour, A.; Hussain, S. On the nonlinear mechanics of layered microcantilevers. Int. J. Eng. Sci. 2017, 120, 1–14. [Google Scholar] [CrossRef]
- Farokhi, H.; Ghayesh, M.H.; Gholipour, A.; Tavallaeinejad, M. Nonlinear oscillations of viscoelastic microplates. Int. J. Eng. Sci. 2017, 118, 56–69. [Google Scholar] [CrossRef]
- Ghayesh, M.H. Dynamics of functionally graded viscoelastic microbeams. Int. J. Eng. Sci. 2018, 124, 115–131. [Google Scholar] [CrossRef]
- Farokhi, H.; Ghayesh, M.H. Supercritical nonlinear parametric dynamics of timoshenko microbeams. Commun. Nonlinear Sci. Numer. Simul. 2018, 59, 592–605. [Google Scholar] [CrossRef]
- Farokhi, H.; Ghayesh, M.H.; Amabili, M. Nonlinear resonant behavior of microbeams over the buckled state. Appl. Phys. A 2013, 113, 297–307. [Google Scholar] [CrossRef]
- Farajpour, A.; Farokhi, H.; Ghayesh, M.H. Chaotic motion analysis of fluid-conveying viscoelastic nanotubes. Eur. J. Mech. A/Solids 2019, 74, 281–296. [Google Scholar] [CrossRef]
- Ghayesh, M.H.; Farokhi, H. Nonlinear dynamics of microplates. Int. J. Eng. Sci. 2015, 86, 60–73. [Google Scholar] [CrossRef]
- Farokhi, H.; Ghayesh, M.H. Thermo-mechanical dynamics of perfect and imperfect timoshenko microbeams. Int. J. Eng. Sci. 2015, 91, 12–33. [Google Scholar] [CrossRef]
- Farajpour, M.R.; Rastgoo, A.; Farajpour, A.; Mohammadi, M. Vibration of piezoelectric nanofilm-based electromechanical sensors via higher-order non-local strain gradient theory. Micro Nano Lett. 2016, 11, 302–307. [Google Scholar] [CrossRef]
- Nejad, M.Z.; Hadi, A.; Farajpour, A. Consistent couple-stress theory for free vibration analysis of euler-bernoulli nano-beams made of arbitrary bi-directional functionally graded materials. Struct. Eng. Mech. 2017, 63, 161–169. [Google Scholar]
- Asemi, S.R.; Farajpour, A. Vibration characteristics of double-piezoelectric-nanoplate-systems. IET Micro Nano Lett. 2014, 9, 280–285. [Google Scholar] [CrossRef]
- Ghayesh, M.H.; Farajpour, A. Nonlinear coupled mechanics of nanotubes incorporating both nonlocal and strain gradient effects. Mech. Adv. Mater. Struct. 2018. [Google Scholar] [CrossRef]
- Ghayesh, M.H.; Farokhi, H.; Gholipour, A.; Tavallaeinejad, M. Nonlinear oscillations of functionally graded microplates. Int. J. Eng. Sci. 2018, 122, 56–72. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ghayesh, M.H.; Farajpour, A.; Farokhi, H. Asymmetric Oscillations of AFG Microscale Nonuniform Deformable Timoshenko Beams. Vibration 2019, 2, 201-221. https://doi.org/10.3390/vibration2020013
Ghayesh MH, Farajpour A, Farokhi H. Asymmetric Oscillations of AFG Microscale Nonuniform Deformable Timoshenko Beams. Vibration. 2019; 2(2):201-221. https://doi.org/10.3390/vibration2020013
Chicago/Turabian StyleGhayesh, Mergen H., Ali Farajpour, and Hamed Farokhi. 2019. "Asymmetric Oscillations of AFG Microscale Nonuniform Deformable Timoshenko Beams" Vibration 2, no. 2: 201-221. https://doi.org/10.3390/vibration2020013
APA StyleGhayesh, M. H., Farajpour, A., & Farokhi, H. (2019). Asymmetric Oscillations of AFG Microscale Nonuniform Deformable Timoshenko Beams. Vibration, 2(2), 201-221. https://doi.org/10.3390/vibration2020013





