1. Introduction
In recent years, robots aimed for social environments have become of great interest to the research and industrial communities alike. In such scenarios, the safety of the robot, its environment and humans or animals therein is a major concern [
1]. For example, if the robot in question exerts an excessive force or collision (impact) in a cooperative task with a human being, the result may be catastrophic and the robot may pose a significant risk to the interacting agent whether it is a human or another robot. Force control and its variants such as compliance or impedance control can help to address some of the safety issues by limiting the interaction forces [
2,
3,
4,
5,
6]. Another safety issue is the development of faults during operation, which cannot be ruled out in robots and other actuated machinery. Faulty actuators may make the system unstable or drastically degrade the tracking performance of the robot. Hence, actuator fault-tolerance is normally considered a very important aspect of the cooperative control of two robot arms. The ideal desired response when a failure is observed is to take immediate action that will ensure the robot arms continue operation as normal as possible during the cooperative task.
Dealing effectively with actuator failures is a challenging task. Over the last couple of decades, numerous studies have explored the subject. The literature related to actuator failures takes several distinct directions. Some studies have focused on complete actuator failures whereby the actuator movement is decoupled from the input signal while others have dealt with those failures that degrade the tracking performance of the actuators due to partial failures [
7]. The most common of these failures are locked joint faults, free swinging or actuator saturation and ramp actuator faults [
8,
9]. The design of fault-tolerant control schemes remains a hot topic. Recently, an intelligent way to deal with actuator faults was presented in [
10]. Also, a fault tolerant control scheme was proposed in [
11] for a differential drive mobile robot using multiple models. Another interesting control scheme is that of [
12], which features a neural network based adaptive actuator fault detection algorithm for robot manipulators.
Robot–Robot cooperation or interaction is inevitable as many daily life tasks cannot be performed solely by a single robot. Cooperative schemes are mostly bio-inspired as humans and other beings are constantly cooperating to accomplish tasks that would otherwise be impossible. Cooperation is not limited to the mirrored action of two arms belonging to a single entity but in many cases also extends to multiple robots working together. The control of a cooperative robotic manipulator is currently a hot research area with interest from specialists in both the academic and industrial sectors. Many different approaches have been studied and applied as reported in the literature. For instance, [
13] proposed a neural network based distributed control scheme for multiple redundant manipulators. In addition, communication networks have been employed to synchronize the positions of all manipulators, see also [
14,
15,
16].
As it will be shown in this paper, once a joint becomes faulty, the robot end effector moves in a chaotic manner [
17]. In general, the term chaos refers to a dynamical system following a trajectory that is neither asymptotically stable nor periodically stable but remains asymptotically bounded to a specific region of phase space. This type of dynamical systems is well known for its extreme dependence on very small variations in the initial conditions. In fact, two trajectories that start from infinitesimally close points in phase space diverge away from one another at an exponential rate, which may be quantified by means of the positive Lyapunov exponents of the system [
18]. The literature related to chaos can be split into two main categories, chaos synthesis and chaos control. The first category deals with the implementation and application of chaotic systems that posses special properties in order to make use of the high level of entropy they entail [
19]. For instance, in the field data and image encryption, the seemingly unpredictable nature of a chaotic system’s states drives the generation of a sequence of secret encryption keys [
20,
21]. Chaos control, on the other hand, deals with the stabilization and synchronization of chaotic phenomena appearing in nature or in engineered systems. This paper is concerned with the latter.
In this paper, we aim to use a well established energy reduction stabilization controller first proposed in [
22] to overcome the chaotic behavior observed as a result of a joint failure. The main contribution of the paper is to use computer simulations of a redundant four-joint robot arm in order to show the effectiveness of the chaos based controller [
22] when an actuator failure is exhibited in the middle of a synchronized two robot arm cooperative scenario. The robot arm cooperation scenario under consideration in this work is similar to that of [
1]. To the best of our knowledge, chaos based control has not been considered before to deal with actuator faults. More specifically, all of the fault identification and accommodation methods we have seen in the literature are rather complicated and do not take into consideration the chaotic nature of the system under fault. The study at hand shows how a very simple energy reduction chaos controller not only suppresses chaos in the motion of the faulty robot arm but also forces it to correctly track the desired trajectory. This paper is organized as follows.
Section 2 describes the cooperative scenario where a master/slave pair is synchronized to carry out a joint task.
Section 3 shows the sliding mode controller (SMC) used to drive the master arm to follow a given trajectory. The slave arm is controlled by means of a simple adaptive synchronization law as discussed in
Section 4. In
Section 5, we discuss the effect of a complete joint failure on the movement of the slave end-effector. In order to overcome the haphazard movement due to the failure, a chaos controller is presented in
Section 6. Finally, the simulation results are discussed in
Section 7 and conclusions are drawn based on the discussion in
Section 8.
3. Sliding Mode Control of the Master Arm
For the control of Masters arm simple sliding mode control is employed. In this section, the controller of the master arm is described which is aimed at to follow a desired trajectory determined by the Cartesian coordinates
, where
is the Cartesian demand in the
X direction and
is the Cartesian demand in the
Z direction. An simple and robust scheme that can be found in the literature is the sliding mode controller (SMC), which has the advantage of counteracting system uncertainties [
23,
24,
25,
26,
27]. SMC is particularly important for mechanical systems with stiction, friction, and small negligible flexibilities. It should also be noted that SMC employed in is dynamic model free and it allows for system uncertainties. This makes it superior to other model based approaches such as feedback linearization and dynamic inversion methods.
In this paper, we employ four-joint robot arm structures whose dynamics can be modeled as
where
is the positive-definite and symmetric inertia matrix as a function of the four joint angles
q,
is the coriolis/centripetal vector, which also represents viscous and nonlinear damping, and
denotes the gravity vector. Note that any practical robot is subject to friction and damping which makes it an open loop stable system. Vector
in Equation (
1) represents the input torque.
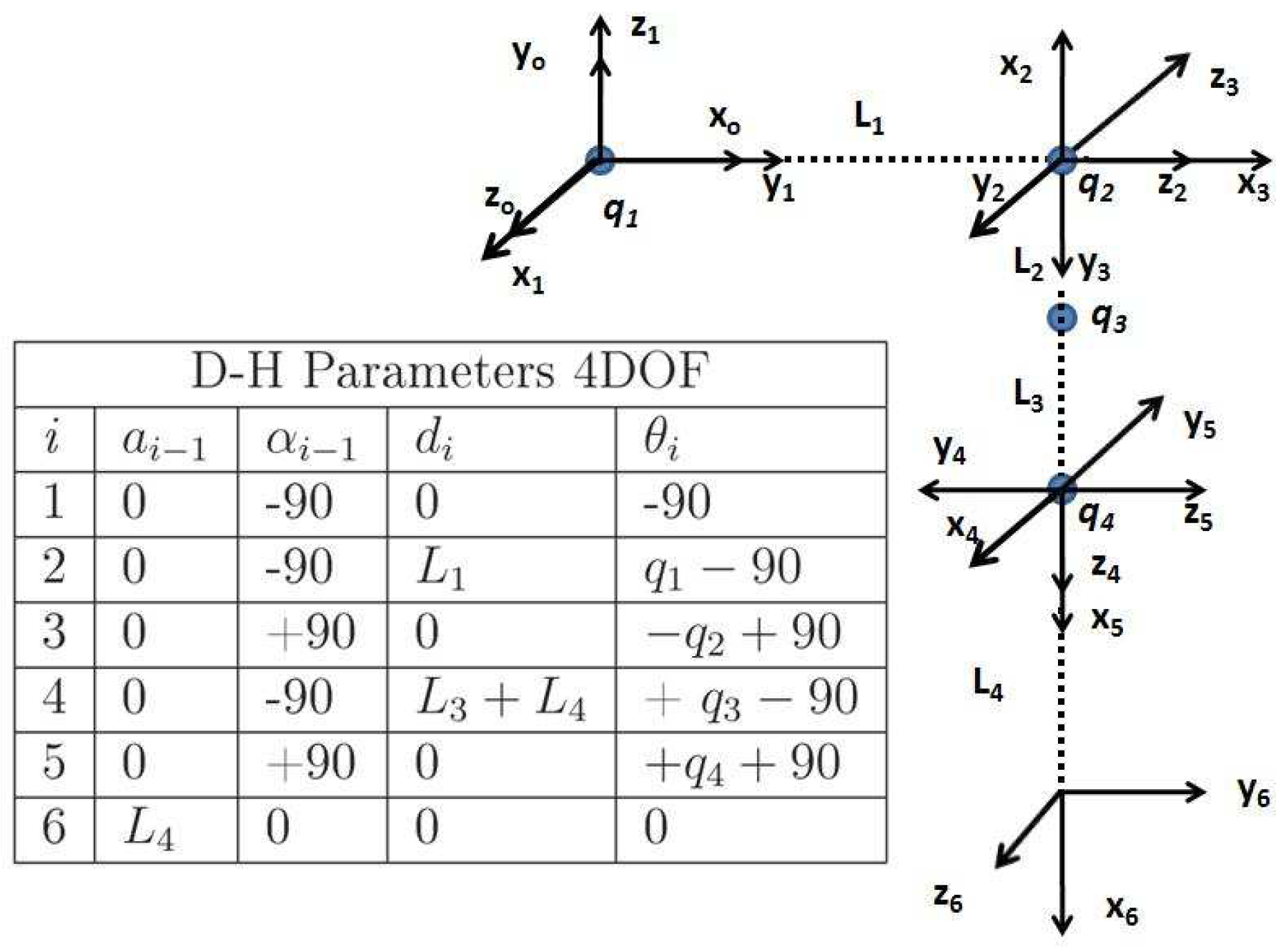
A complete list of the physical parameters of the robot is provided in
Table 1. These parameters are identical for both the master and slave robot arms. The structure of the BERT2 humanoid robot is depicted in
Figure 2. This robot arm has seven degrees of freedom. However, for simplicity, only four are considered in this study.
Figure 3 shows the
parameters for the 4 DOFs in consideration.
In case of manipulation of the robot arm, it is usually more convenient to express the model in Cartesian coordinates by considering the forces acting on the end effector at a point
in two-dimensional Cartesian space. Where
is the global
position and global
position with the respect to origin which is located in shoulder flexion joint,
(see the kinematics given in
Figure 3). As shown in [
28], the required transformation of Equation (
1) that relies on the Jacobian matrix of the kinematics
where
h is the transformation. It is easy to see that
By defining a weighted pseudo Jacobian matrix
as
we can express the transformed model by
where
It follows that
and
are the initial Cartesian position and velocity errors, respectively. According to [
29], the integral sliding mode variable can be defined as
where
is a full rank
real matrix with positive entries chosen appropriately.
In order to improve the performance of the controller, we use a combined SMC and proportional derivative (PD) control law described by
where
and
are
real matrices representing the proportional and derivative gains, respectively,
is a sufficiently large scalar aimed at minimizing the effect of uncertainty and improving the robustness of the SMC controller [
29], and
is an appropriately selected scalar that minimizes the effect of chattering. The controller described in Equation (
8) is well studied in the literature and given a multistep demand
results in the response depicted in
Figure 4.
4. Adaptive Synchronization Control of the Slave
In order to synchronize the motion of the slave arm to follow the same trajectory set out by the master, we use a synchronization adaptive PD controller. We define the instantaneous position synchronization error in discrete time as
Differentiating the position error Equation (
9) yields the velocity error
We define the synchronization control variable as
where
and
are
real matrices chosen appropriately. Using this adaptive variable, we define the adaptive law
for some experimentally selected real constants
. The control signal
is obtained simply by integrating
. Where
n represents time step. The adaptive torque term is then, obtained as
Since we are operating in the Cartesian space, the corresponding force demand can be calculated as
Given the same multi-step demand adopted earlier in
Figure 4,
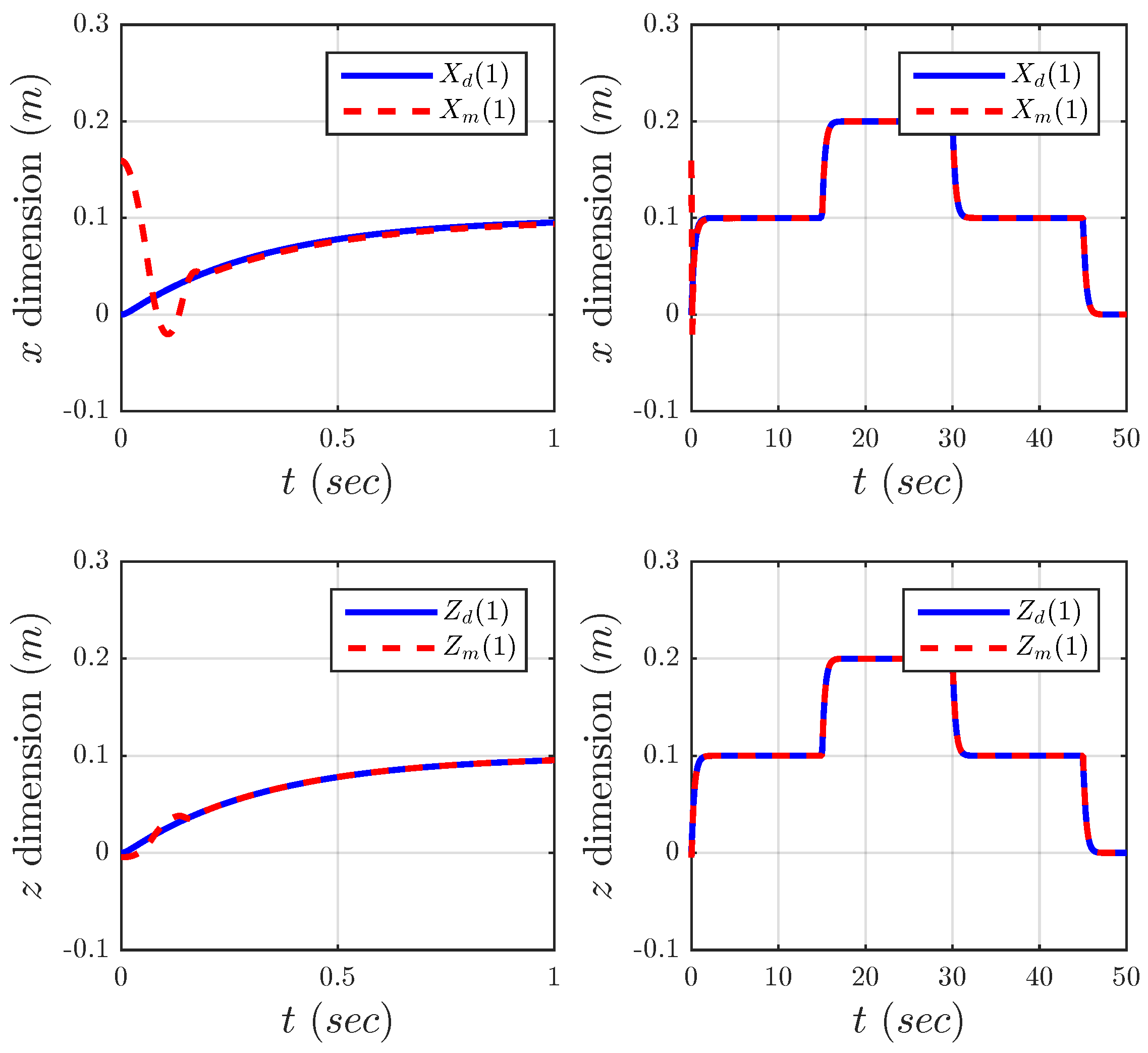
Figure 5 depicts the master and slave positions over a window of 50 s. It is easy to see that the two arms are in fact fully synchronized.
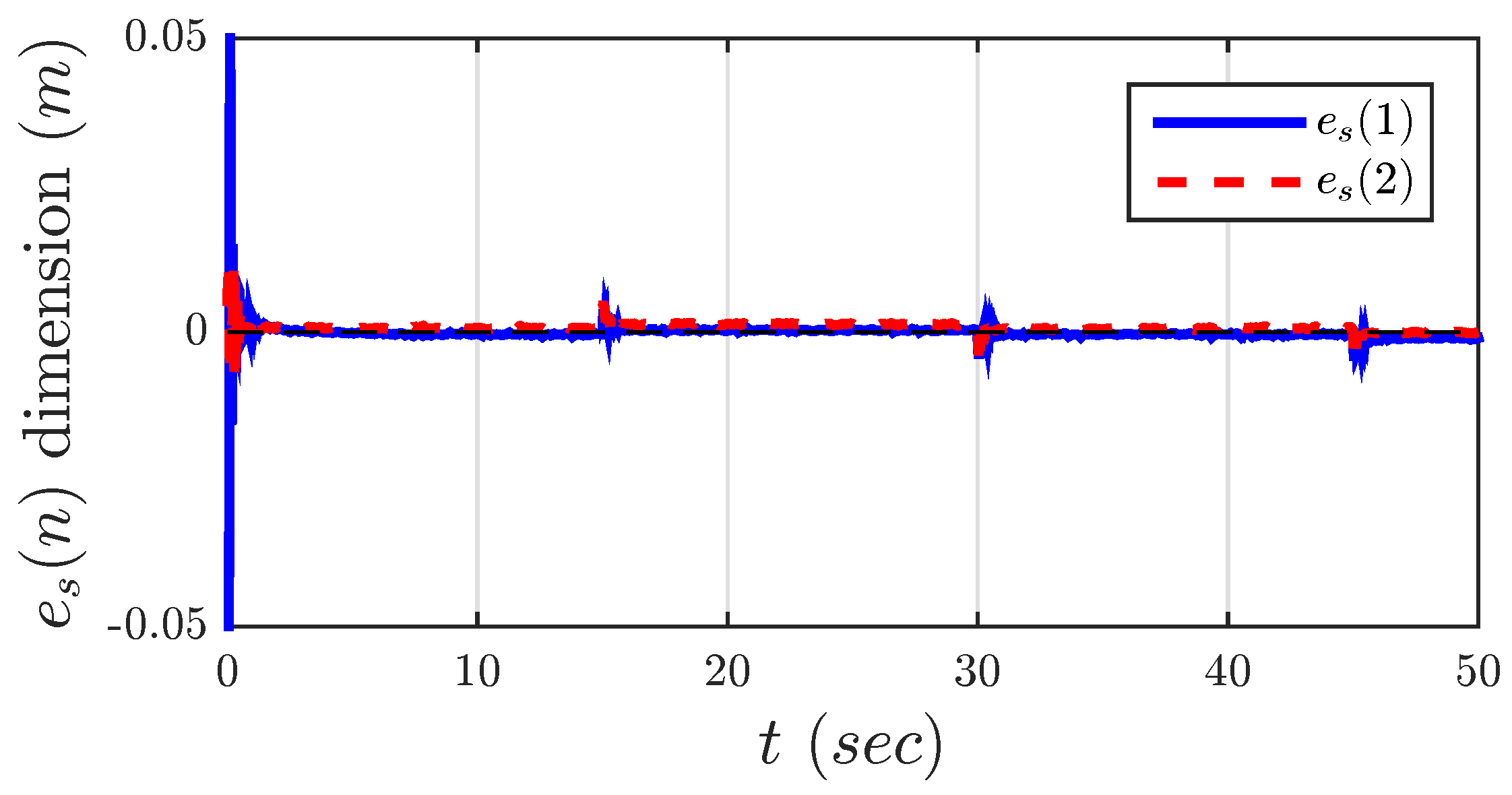
Figure 6 shows the synchronization error, which converges towards a reasonably small value.
5. Joint Malfunction and Chaos
Let us consider a fault taking place at one of the slave joints. According to [
30], when a fault is observed in one of the actuators, then the control input
is disturbed and the modified input is of the form
where
is a diagonal matrix function representing the loss of effectiveness in each actuator and vector
reflects actuator bias faults. Different values for
and
lead to different types of faults. For instance, setting
and
signifies the absence of faults (all healthy actuators). Lowering the diagonal elements of
below 1 corresponds to a loss in the effectiveness of the joints whereas a nonzero vector
signifies a biased actuator. More details on the types of faults and their identification in robot manipulators can be found in [
9]. In what follows we will assume that
This is simply synonymous with one of the joints failing completely meaning that either the joint is non-responsive or that a connection problem exists in the configuration.
As described before, a simple SMC scheme is employed for the master arm control and an adaptive synchronization controller for the slave robot arm. Next, we examine the nature of the response and the trajectory followed by the slave arm when a malfunction happens in one of the joints and the control of that joint fails completely, i.e., the control signal no longer reaches the actuator (or the actuator is free swinging). As expected, the arm starts to move in a haphazard and seemingly random way.
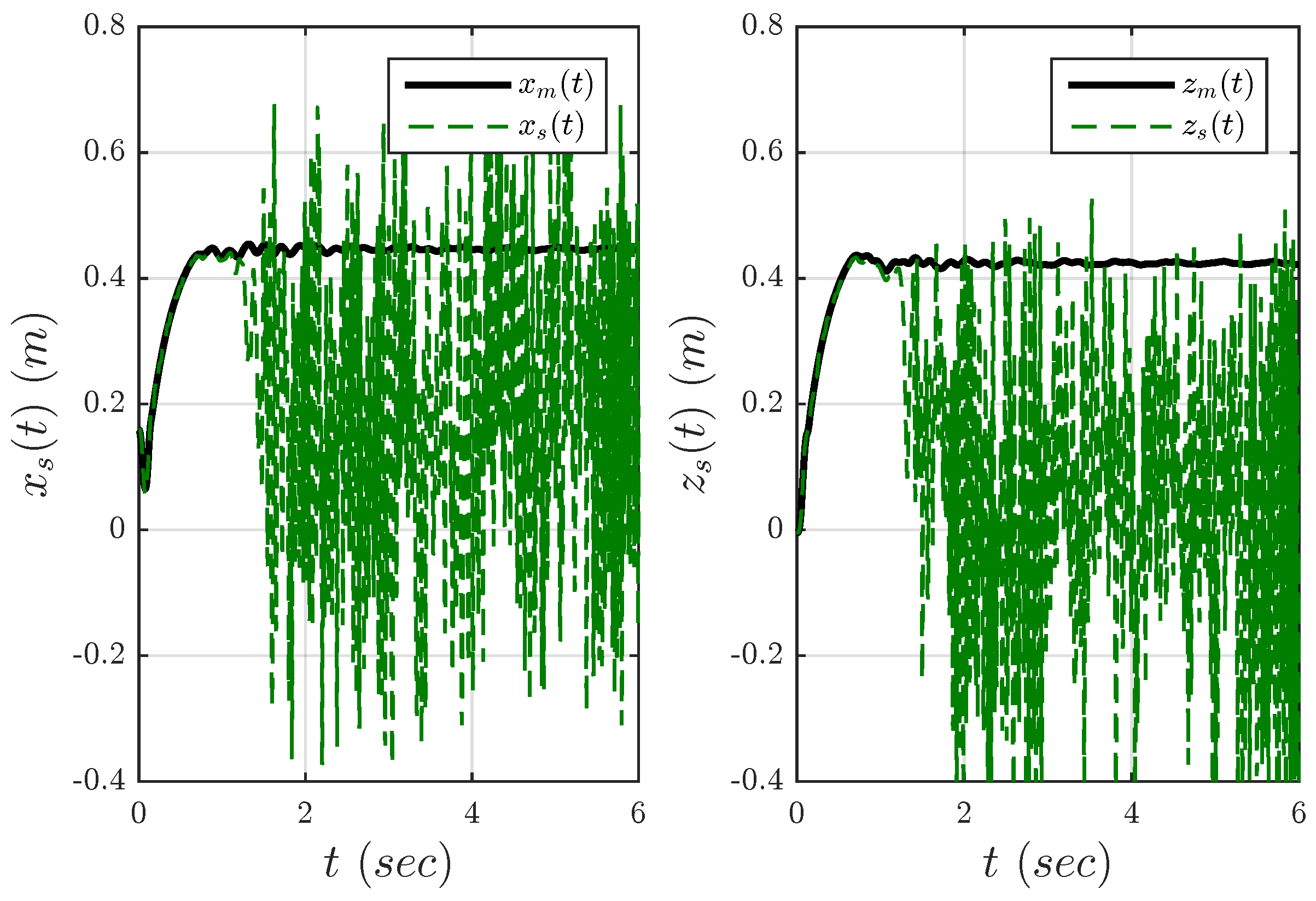
Figure 7 depicts the controlled
x and
z coordinates of the end-effector. The Euclidean space demand
is simply assumed to be a step with a magnitude of
. The malfunction is introduced after
of normal operation. It is easy to see that the
x-
z coordinates start to oscillate in a random fashion.
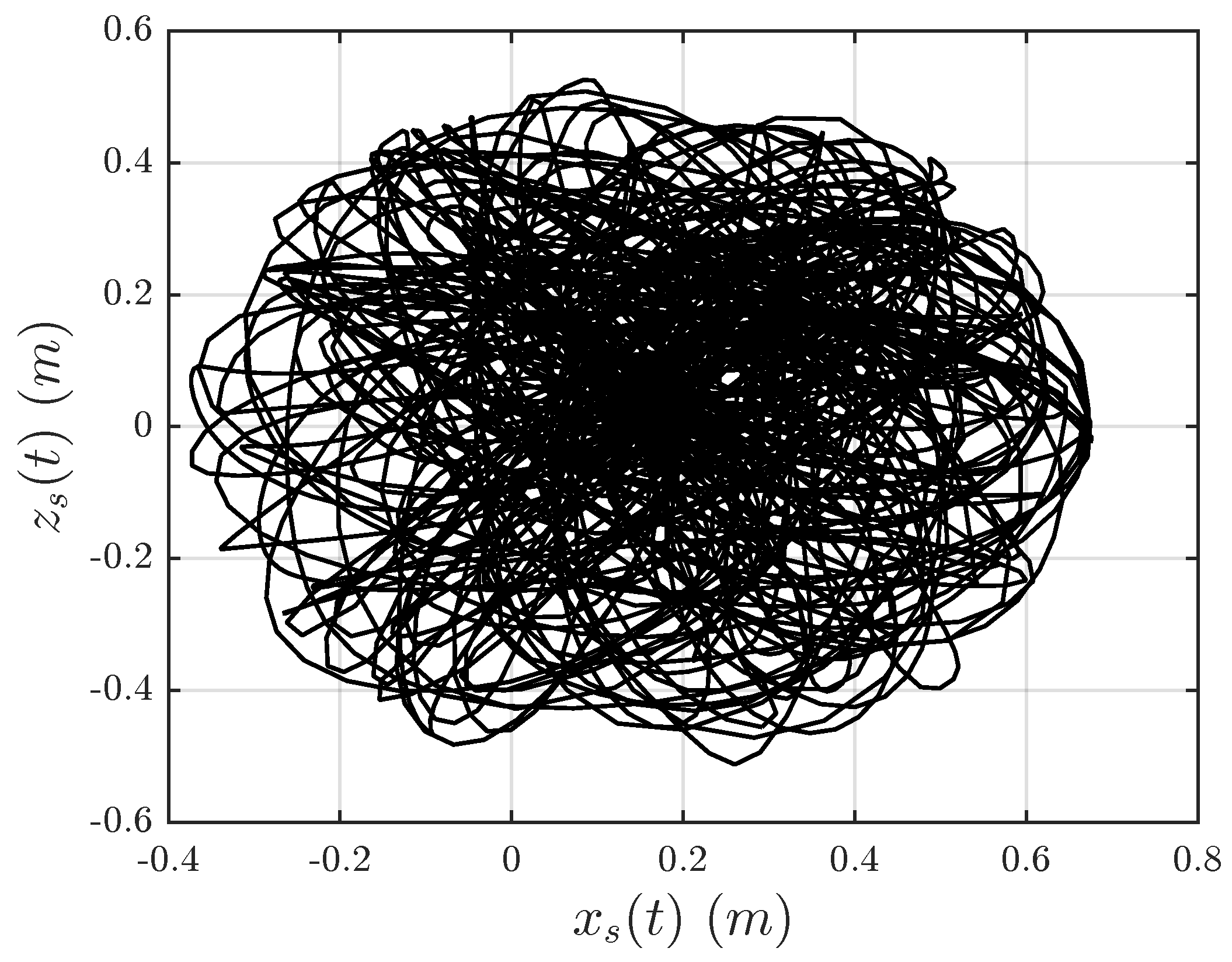
Figure 8 shows the same results in the
x-
z plane.
Although the phase space plot in
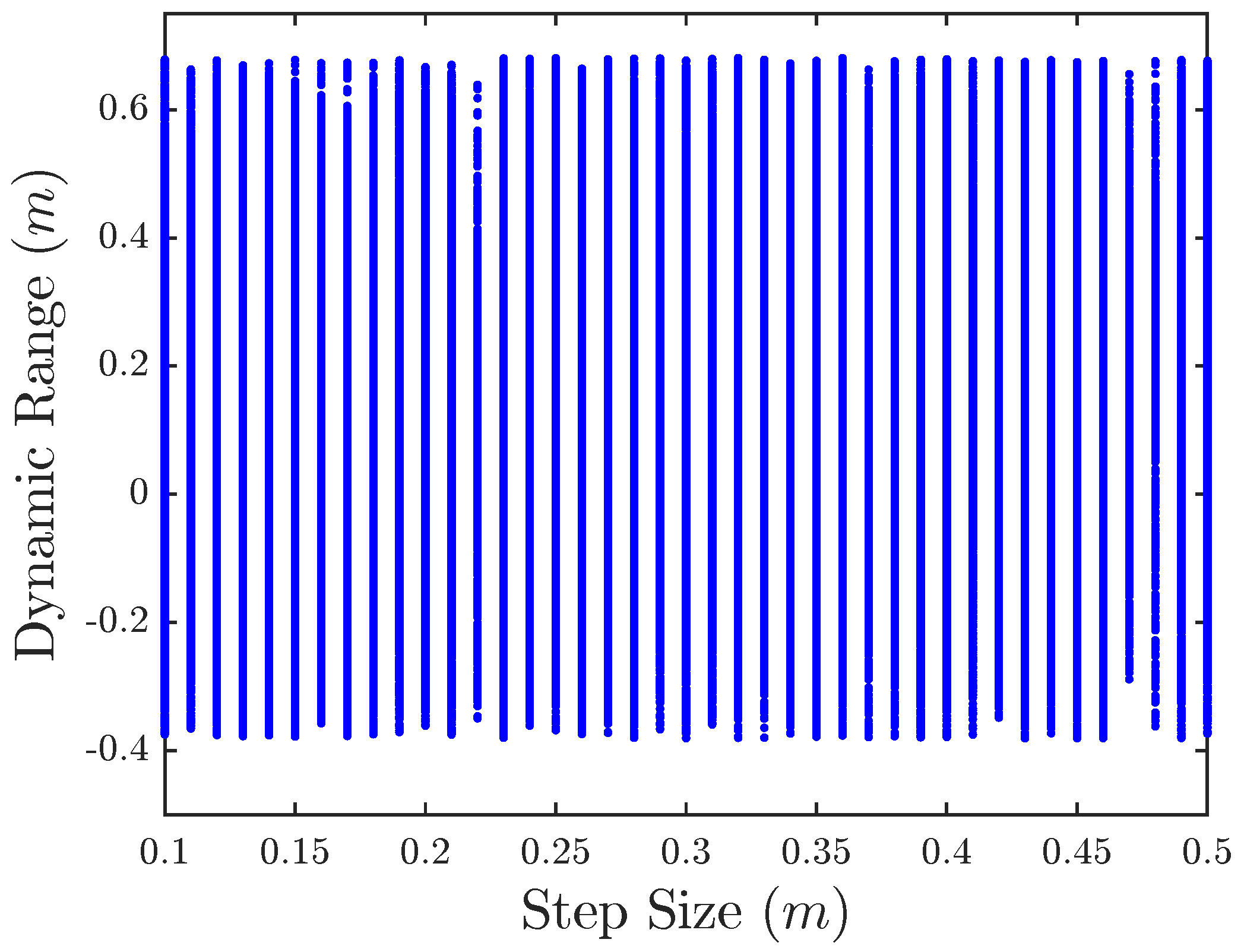
Figure 8 shows the boundedness of the position, it does not clearly indicate the dynamic range of the end-effector position and at the same time does not suggest the change in the dynamic range as the input level changes. In order to assess these characteristics, experiment was repeated for step inputs ranging from
to
in steps of
.
Figure 9 shows the dynamic range of the slave end-effector as a function of the input level. It is easy to see that the dynamic range remains mostly constant throughout the plot.
6. Chaos Stabilization via Feedback Control
The aim of this section is to introduce a new controller that will operate once a joint fails completely and works to counteract the chaotic tendency of the end-effector. This type of controller is generally referred to as a stabilization scheme. The amount of literature related to the stabilization of chaotic dynamical systems is vast but one set of methods that stands out is based on altering the energy of the system. These methods generally utilize information obtained experimentally from the time series of the system’s observable variables to guide the controller. For instance, the Ott-Grebogi-Yorke (OGY) method [
31] stabilizes an otherwise unstable periodic orbit (UPO) by means of a small perturbation in the control parameter. However, this can only work if the chaotic trajectory is sufficient close to the desired UPO, which unfortunately is not always the case. The OGY method has been studies extensively in the literature and many variations have proposed including the quasi-continuous OGY [
32]. A good comparative study between OGY based methods, multi-parameter methods, and time-delayed feedback methods is given in [
33].
Perhaps one of the most interesting perturbation-based control methods for chaotic systems is the tangent scheme proposed in [
22]. This controller aims to alter the time averaged compound kinetic and potential oscillatory energy of the system to that of a desired behavior. This type of chaos based control has recently gained popularity in the field of robotics especially for the suppression of unnecessary vibration and the stabilization of an otherwise unstable system. A recent study employs chaos based control to stabilize an electromechanical pendulum [
34]. Considering a system of the form
where
represents the control force, the author showed that in general the control must satisfy the law
for all
. The function
g can be reduced to a function of the velocity
only and can in general be of the form
, where
k is a scalar and
is an odd function. One particularly interesting controller is the hyperbolic tangent based one, which is given by
with
. Although this controller was first proposed in [
22] for chaotic oscillators such as the Van der pol and Duffing nonlinear oscillators, it has since been shown that the hyperbolic tangent term can stabilize faulty chaotic systems in general [
30]. In this paper, we will show that by adding the feedback term
with
to control law Equation (
13), the chaotic behavior observed when a joint fails can be suppressed.
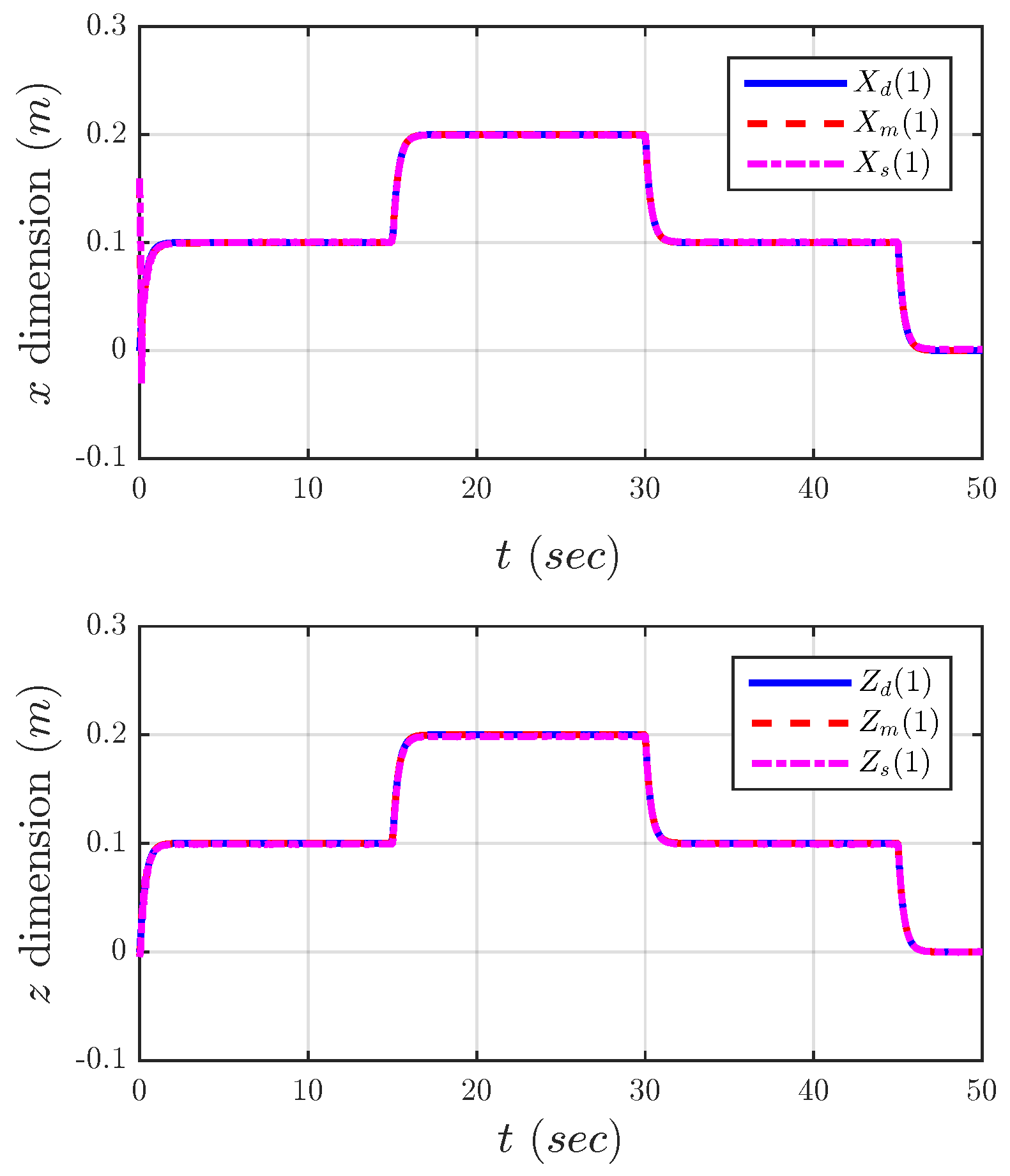
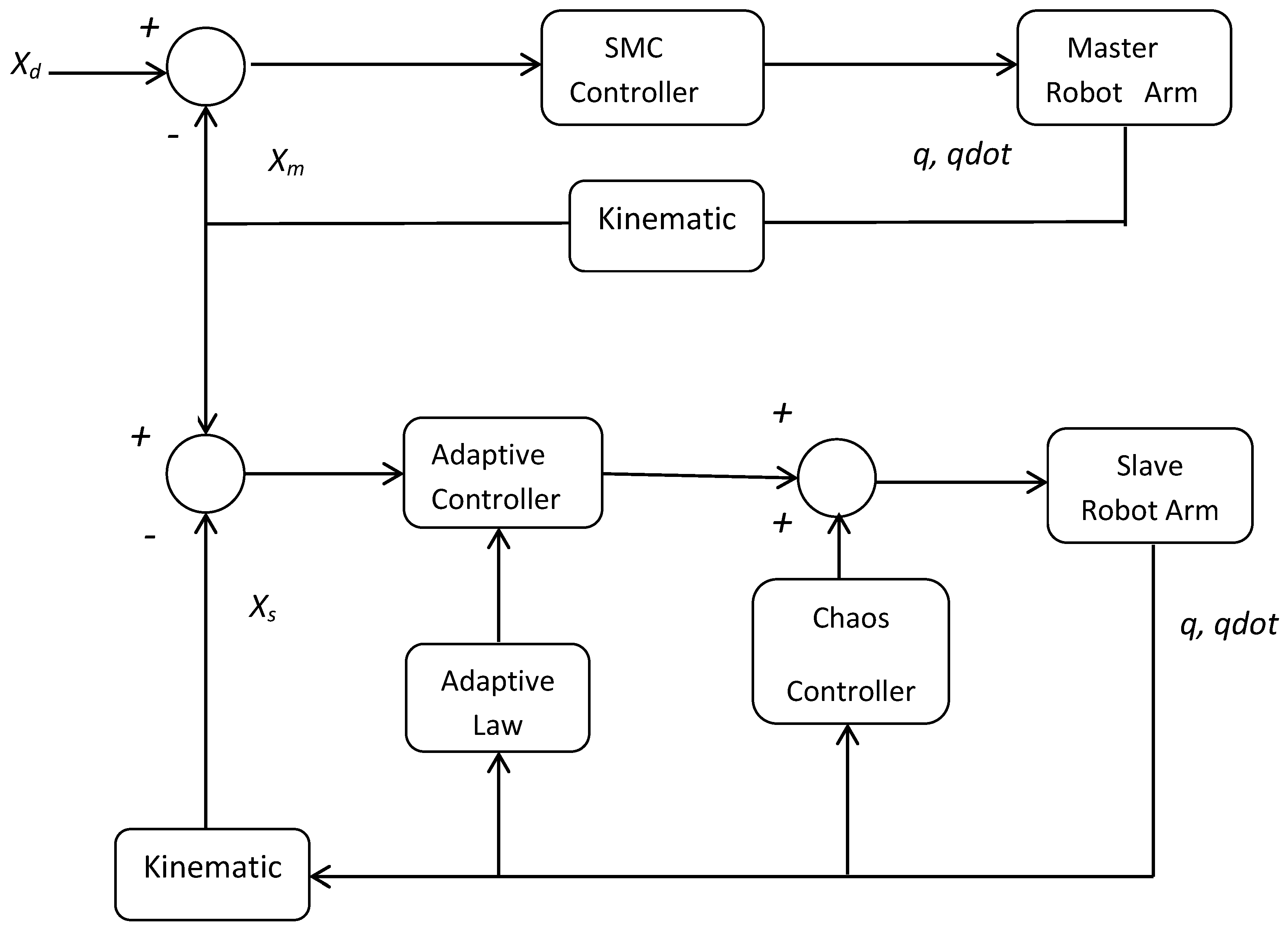
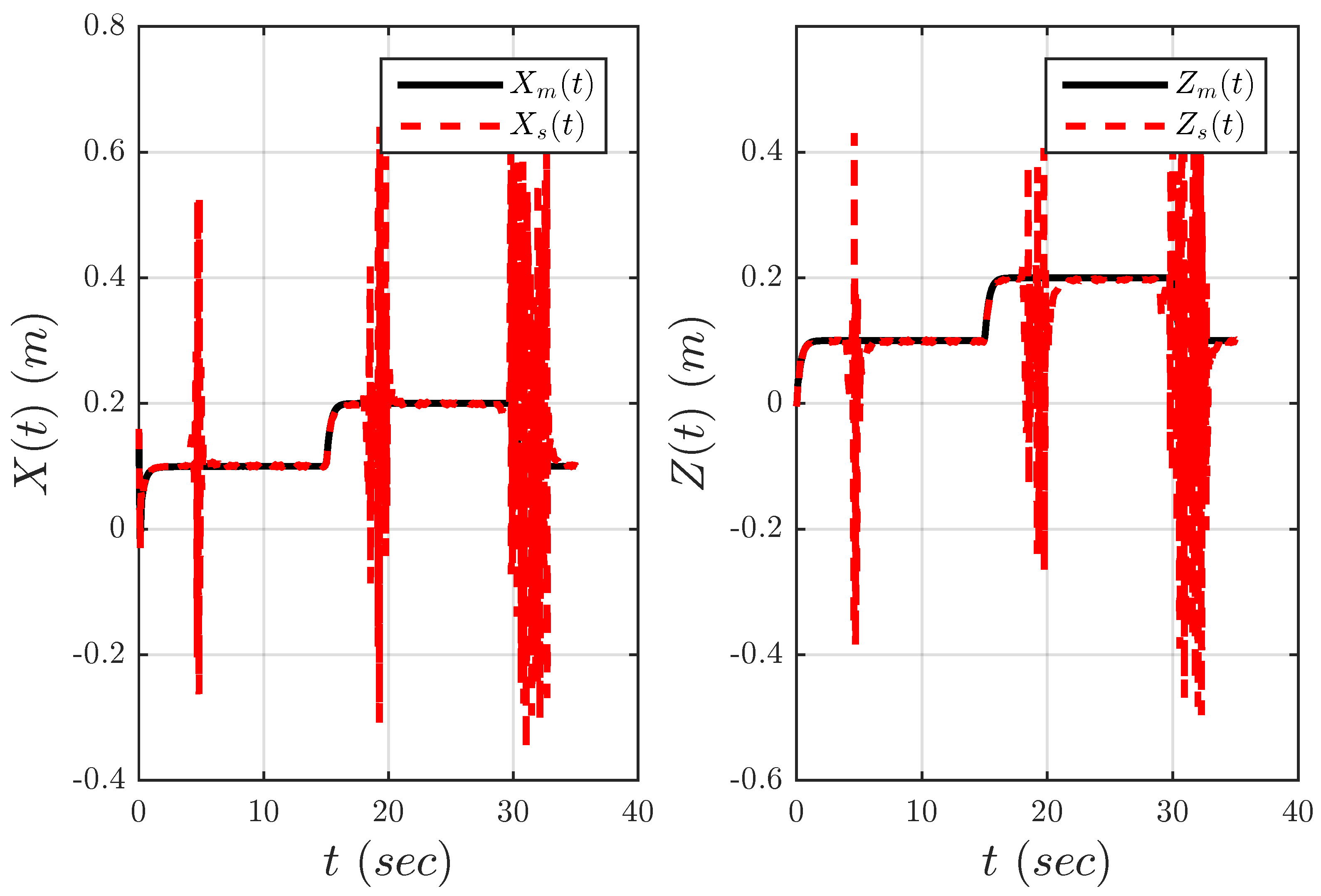
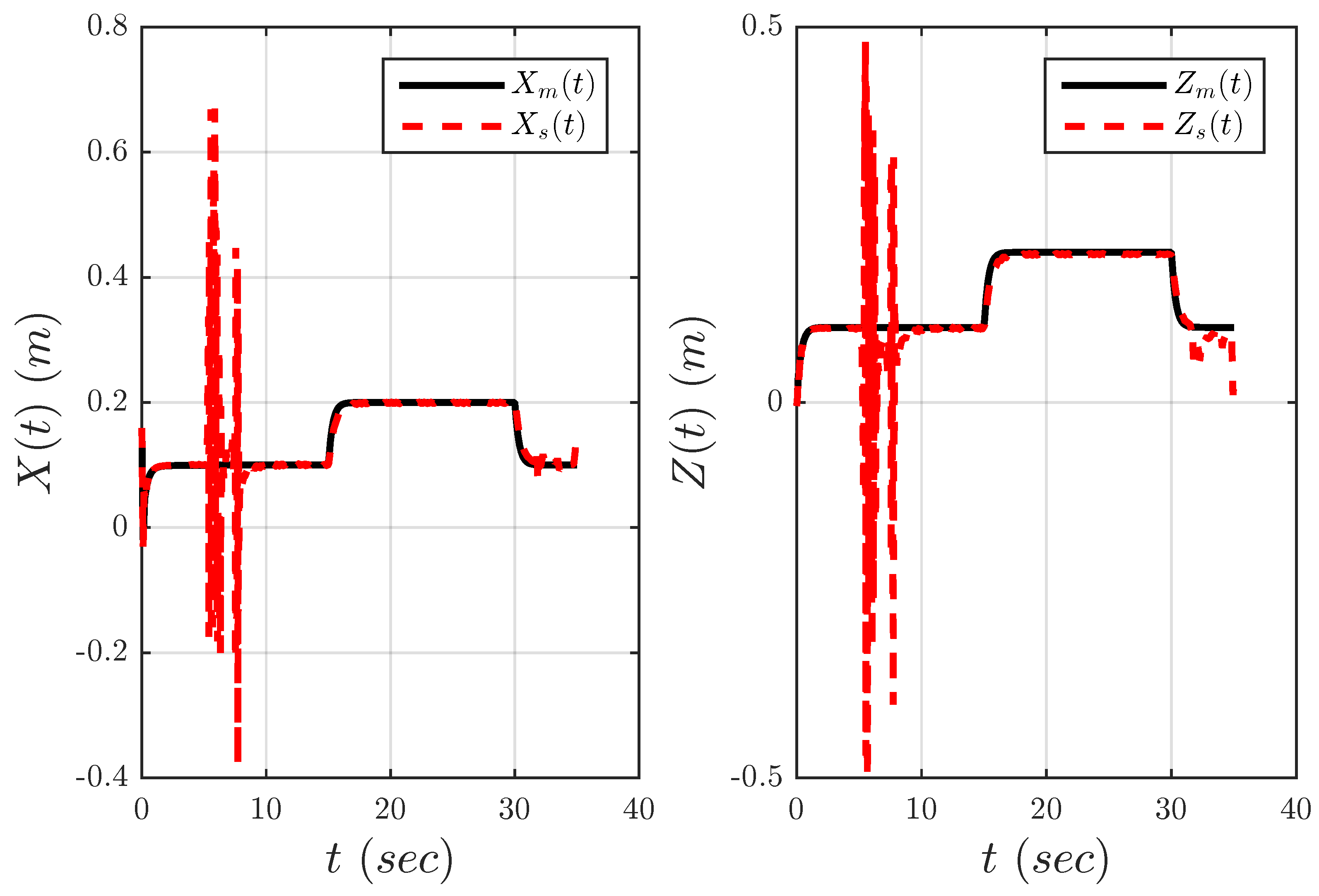
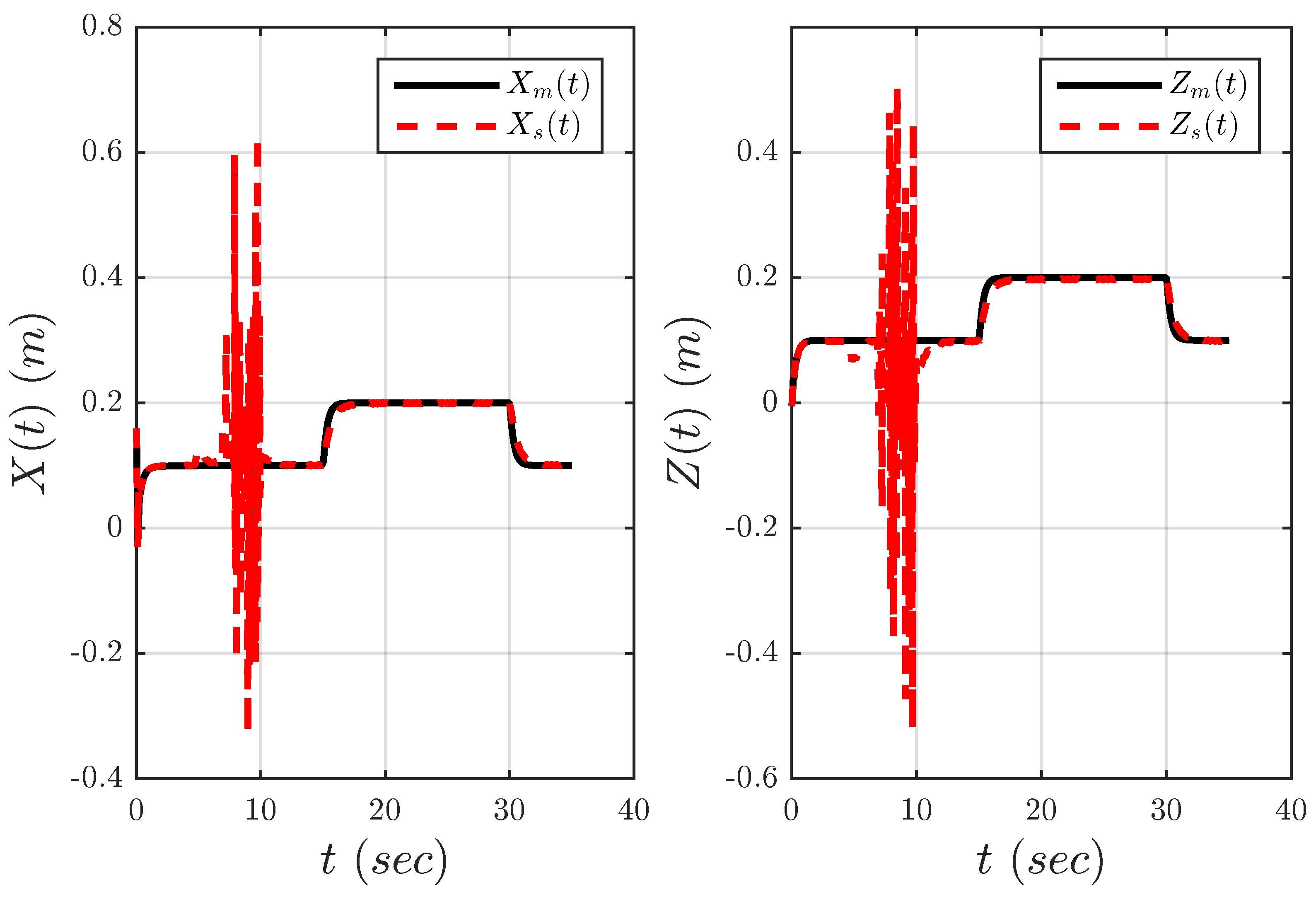
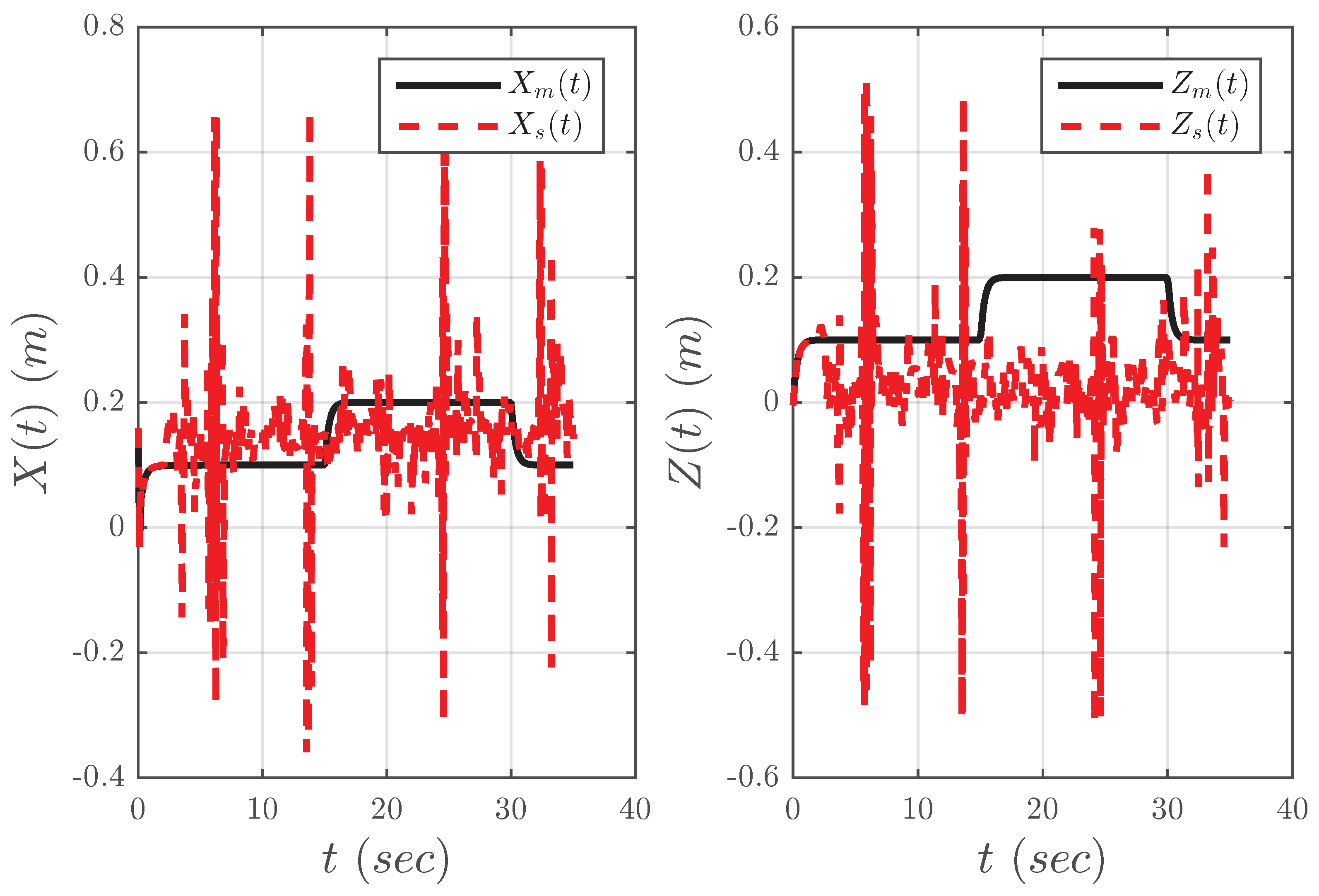
The overall control scheme is depicted in
Figure 10. The complete system has been implemented by means of the Matlab/Simulink environment. The master and slave arms were modeled using the SimMechanics toolbox with a sampling time of 1 ms. As expected, the performance of the stabilization controller Equation (
21) depends heavily on the constant parameters
and
. The stabilized Cartesian position of the slave end-effector is depicted in
Figure 11,
Figure 12,
Figure 13 and
Figure 14 for different values of
and
. Note that in all experiments, the fault is introduced after the first 3 s of normal operation.
8. Conclusions
Actuator faults during robot cooperative tasks would lead into a risky scenario. There need arises to minimize the impact of fault on tracking performance and complete the cooperative task successfully. In this paper a Master-Salve robot arms cooperative scenario is considered. During operation, when an actuator of the slave robot fails, it leads to the chaotic motion of the end effector. In this paper a possible remedy is presented in terms of a chaos controller. Which helps recover the tracking performance and help to complete the ongoing cooperative task.
The control scheme have some limitations. For instance, it will work well for a redundant system, i.e., if more DOF are available than required to complete the task (For Instance, in our case, we are controlling Cartesian X and Z position while we are employing four joints of the robots arms). In addition, the controller parameter and need to be tuned to get better results. This is a trail error process and involve some efforts. It will be good if these parameters are made adaptive or self-tuned. However, this is beyond the scope of the current work and it is potential future work.