Abstract
This paper investigates the coupled mechanics of a fluid-conveying microtube embedded inside an elastic medium and subject to a pretension. The fluid-structure interaction model of the microsystem is developed based on Lagrange’s equations for the open system of a clamped-clamped microtube. A continuation model is used to examine the nonlinear mechanics of this microsystem prior to and beyond losing stability; the growth and the response in the supercritical regime is analysed. It is shown that the microtube stays stable prior to losing stability at the so-called critical flow velocity; beyond that point, the amplitude of the buckled microsystem grows with the velocity of the flowing fluid. The effects of different system parameters such as the linear and nonlinear stiffness coefficients of the elastic medium as well as the length-scale parameter and the slenderness ratio of the microtube on the critical speeds and the post-buckling behaviour are analysed.
1. Introduction
Many microelectromechanical systems (MEMS) using microscale structures such as microshells, microplates and microtubes have been designed and analysed in recent years [1,2]. Fluid-conveying microtubes, as an advanced class of fluid-structure systems, are widely used in different MEMS and microfluidic devices. Fluid-conveying microtubes are available in applications such as actuators, drug-delivery devices, fluid filtration, micromachines, sensors, and as fluid transport microdevices [3]. For a better design of both macroscale and microscale systems, developing advanced knowledge of the stability and vibration responses [4,5,6,7] would be helpful.
Even though the mechanics of macroscale fluid-conveying structures has been studied extensively in the literature, studies on the mechanical behaviour of microscale tubes are limited. The early studies mostly focused on determining the natural frequencies and mode shapes. To obtain the natural frequency and mode shape, size-dependent theories have been used since size effects are important at small-scale levels [8,9,10,11,12]. For instance, Ahangar et al. [13] obtained the natural frequencies of a microtube conveying fluid as a function of the fluid velocity while the microsystem is modelled based on the modified couple stress (MCS) theory [14,15,16,17,18,19]; it was shown that depending on the type of the boundary conditions, the microsystem may possess real, imaginary, or a combination of real and imaginary natural frequencies. Kural and Özkaya [20] employed the method of multiple scales to obtain the natural frequencies in the oscillation behaviour of fluid-conveying microtubes resting on an elastic bed. Xia and Wang [21], based on the Timoshenko beam theory, analysed the motion of fluid-conveying microtubes via use of the MCS theory and the differential quadrature method to determine the critical flow velocities of the microsystem. Hosseini and Bahaadini [22] analysed the vibration behaviour of a cantilevered microtube in order to obtain the natural frequencies and mode functions for the transverse motion. Abbasnejad et al. [23] analysed the fluid-structure interaction vibrations of a piezoelectrically actuated microtube with the aim of determining critical flow velocities and extracting natural frequency diagrams. Wang [24] examined the vibration behaviour of a fluid-conveying microtube to determine the natural frequencies of the system as a function of different system parameters such as the flow speed. Dai et al. [25] analysed the pull-in characteristics of a fluid-conveying microtube based on a non-local theory in order to determine the instability regions. Li et al. [26] contributed to the field by obtaining the critical flow velocities of a fluid-conveying microtube employing both the Euler-Bernoulli and Timoshenko beam theories, based on the Eringen theory [27]. Deng et al. [28] employed a linear theory in order to analyse the size-dependent oscillations of microtubes conveying fluid so as to determine the natural frequencies as a function of the fluid velocity.
In addition to the above-mentioned studies, Dehrouyeh-Semnani et al. [29] extended these studies by including geometric imperfections and nonlinearities; they constructed bifurcation diagrams for the transverse bending of the microsystem. Mashrouteh et al. [30] employed the variational iteration method in order to analyse the nonlinear vibrations of fluid-conveying microtubes; the main aim was to obtain the relation between the amplitude of the transverse motion and the nonlinear natural frequency of the microsystem. Yang et al. [31] employed a reduction approach in order to discretise the model of the system, and then analysed the forced vibrations with the help of the modified couple stress theory; the bifurcation diagram was developed by means of a single-mode approximation. Setoodeh and Afrahim [32] determined the natural frequencies of a functionally graded microtube conveying fluid using a size-dependent continuum mechanics; a stretching type geometric nonlinearity was considered in the model of the microsystem.
There are two important factors in the model development of the microtube of this study. The first one is that since there are no work at the boundaries and the system is in the absence of any energy dissipation, this system is categorised in the class of conservative systems; this system is prone to divergence via losing stability by means of a pitchfork bifurcation. The second important factor to be considered is that since the size of the microsystem is small [33], the classical continuum mechanics cannot capture the response accurately anymore; hence, an advanced continuum mechanics such as the MCS theory or strain gradient scheme should be employed in order to incorporate the small-size effects.
This paper, for the first time, analyses the buckling and post-buckling behaviour of a fluid-conveying microtube embedded in an elastic medium by means of the MCS theory. To this end, Lagrange’s equations along with as assumed-mode method are utilised to derive the equations of motion of the microsystem. A continuation method is then used to obtain the critical flow velocities for divergence as well as the flow-induced post-divergence behaviour of the microsystem. Effects of different microsystem parameters, such as the flow velocity and the length scale parameter on the critical flow velocities and post-buckling behaviour are highlighted.
2. Fluid-Structure Interaction Model of the Microtube
In the following section, an attempt is made to present a scale-dependent model for the buckling instability of a microtube conveying flowing flow while undergoing large deflections. Consider a microscale tube of length L and outer diameter D as shown in Figure 1. It is assumed that the microtube contains flowing fluid of a constant speed (U) while embedded in a nonlinear elastic foundation. Furthermore, the fluid-conveying microscale tube is subject to an axial preload (Ta). As seen in the figure, a Cartesian coordinate frame with axes x and z is employed to describe the geometrical properties of the microsystem.
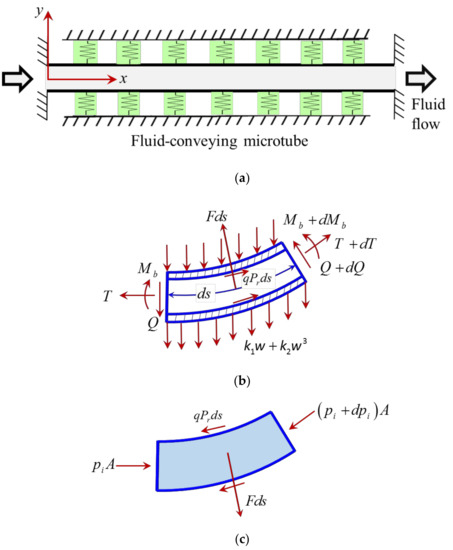
Figure 1.
(a) A fluid-conveying microtube resting on a nonlinear elastic foundation; (b) the free-body diagram of an ultrasmall element of the microtube; (c) the free-body diagram of an element of the fluid.
In the present work, the effects of geometric nonlinearity [34,35,36,37,38,39,40,41] are considered. Accounting for the geometric nonlinearities caused by large deformations, the axial strain of the microtube () can be written as:
where u and w are, respectively, the axial and transverse. The symmetric curvature components () are obtained as follows:
The symmetric curvature and the deviatoric part of symmetric couple stress ( and ) are related through [18]:
in which and stand for the length scale parameter and the shear modulus of the microtube, respectively. To obtain the vibration characteristics of microstructures, a size-dependent theory is used since size effects are important at small-scale levels [42,43,44,45,46]. Next, an assumed-mode technique for divergence analysis is utilised to approximate the longitudinal and transverse displacements as:
where and stand for the mth generalised coordinate for the w and u motions, respectively. and are respectively the base functions for the axial and transverse displacements of a clamped-clamped beam [27]. The potential strain energy of the fluid/elastic microsystem can be constructed as:
The kinetic energy for divergence is [27]:
where M is fluid mass per unit length. Substituting Equations (5) and (6) into Lagrange’s equations for open systems proposed by Irschik and Holl [47] and introducing the following dimensionless parameters:
yields the following coupled Equations:
In this study, 20 generalised coordinates are retained in the discretised model by setting Nu = Nw = 10 (see Appendix A for the convergence analysis). To the best of our knowledge, the above Equations (i.e., Equations (8) and (9)) with this high degree of freedom have not been presented for the post-buckling of fluid-conveying microtubes. It is worth noticing that in Equations (8) and (9), the first term of each Equation incorporates the effects of the fluid flow on the coupled buckling and post-buckling of microtubes. A continuation method is employed to solve this high-dimensional discretised model; the Floquet theory for the stability analysis is used. The continuation method is a numerical technique for periodic vibration problems as well as nonlinear buckling analyses. Near the divergence state, there are multiple solutions for the nonlinear differential equations. The continuation method is employed since it is capable of obtaining both stable and unstable solutions. In this method, there are two main loops: (1) internal loop, and (2) external loop. It is worth mentioning that in the external loop, a predictor is applied to the system of Equations. For more information about this numerical technique, the reader is referred to chapter 4 (pages 169–197) of the book written by Seydel [48] about bifurcation analysis.
3. Results and Discussion
In this section, the effects of the speed of flowing fluid, the length scale parameter and the slenderness ratio on the buckling behaviour of the microtube are examined and discussed. In addition, the numerical results are presented for different values of the linear and nonlinear spring coefficients. Finally, the influence of the axial pretension on the nonlinear response of the fluid-conveying microsystem is investigated. In the numerical simulations, Young’s modulus, Poisson’s ratio, and the mass density of the microtube as well as the fluid mass density are set to: E = 1.44 GPa, ν = 0.38, ρp = 1220 kg/m3, and ρf = 1000 kg/m3, respectively. Moreover, in this paper, the length scale parameter, the inner diameter, the outer diameter and the length-to-diameter ratio of the microtube are assumed as l = 17.6 µm, Di = 25 µm, D = 50 µm, L/D = 100, respectively. It should be noted that the small-scale parameter is a material constant obtained from the results of experimental measurements. In Appendix B, the experiment setup for obtaining the small-scale parameter is explained. For instance, for epoxy microtubes, it is 17.6 μm while a value of 53.7 μm is obtained for polypropylene microtubes [24,49].
Figure 2a,b show the variation of the dimensionless transverse displacement of the microscale tube at and that of the dimensionless axial displacement at with the speed of the flowing fluid. The effects of the longitudinal pretension and the elastic foundation are not taken into consideration for this case (i.e., ). The non-dimensional parameters of the microsystem are obtained as = 0.5746 and = 1.28 × 105. It is seen in Figure 2 that both transverse and axial displacements are zero until a certain dimensionless velocity of the flowing fluid (uf = 7.8845). At this critical point, a buckling instability occurs through a branch point bifurcation, causing lateral and longitudinal displacements to increase suddenly. After this point, there are two possible stable solutions (solid line) and one unstable solution (dashed line) for the transverse displacement. For the case of the axial displacement, there is only one stable solution, as well as one unstable solution after the occurrence of buckling.
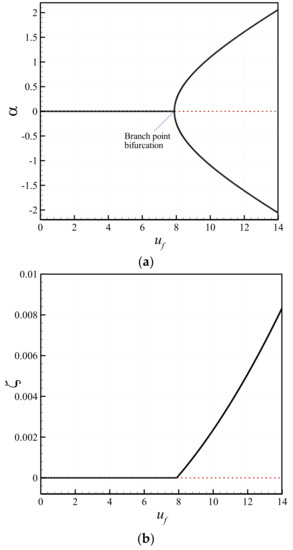
Figure 2.
Bifurcation diagrams of the microtube conveying fluid; (a) the transverse displacement at xd = 0.5; (b) the longitudinal displacement at xd = 0.125.
In order to compare the results of the classical elasticity theory with those of the MCS theory, the variation of the axial and lateral deflections of the microtube with the velocity of the flowing fluid is plotted in Figure 3 for both theories. It has been proven that size effects cannot be ignored at small-scale levels [43,50,51,52,53,54,55,56]. While the length scale parameter is equal to zero for the classical theory, this parameter is assumed to be = 0.5746 for the MCS theory. It is observed that the critical buckling fluid velocity obtained by the classical theory is smaller than that of the MCS theory for both longitudinal and transverse deflections. In other words, the classical nonlinear beam theory underestimates the branch point bifurcation of the fluid-conveying microscale system.
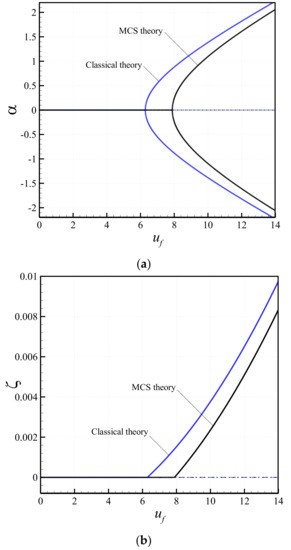
Figure 3.
Comparison of the bifurcation diagrams of the microtube obtained via the classical ( = 0.0) and MCS ( = 0.5746) theories: (a) the transverse displacement at xd = 0.5; (b) the longitudinal displacement at xd = 0.125.
The effect of the linear spring coefficient on the bifurcation diagrams of the microtube containing flowing fluid is shown in Figure 4. The non-dimensional length-scale parameter and the slenderness ratio of the tube are = 0.5746 and S = 100, respectively. To put more emphasis on the influence of the linear spring coefficient, the axial pretension and the nonlinear coefficient of the elastic foundation are set to zero. From the figure, it is found that as the linear spring coefficient increases from 0 to 400, the critical fluid velocity, at which the microscale tube buckles, increases. In fact, a linear elastic foundation with greater stiffness increases the buckling capacity of the system. Furthermore, at a velocity in the post-buckling region, the lateral deflection of the microtube decreases with increasing non-dimensional spring coefficient. The change of the transverse displacement of the microsystem with the fluid velocity for different nonlinear spring coefficients is plotted in Figure 5. The dimensionless linear spring coefficient and the axial pretension are set to zero. It is that the critical buckling fluid velocity of the system is independent of the nonlinear spring coefficient. However, after the occurrence of the bifurcation point, increasing the nonlinear spring coefficient reduces the transverse deflection of the microscale tube.
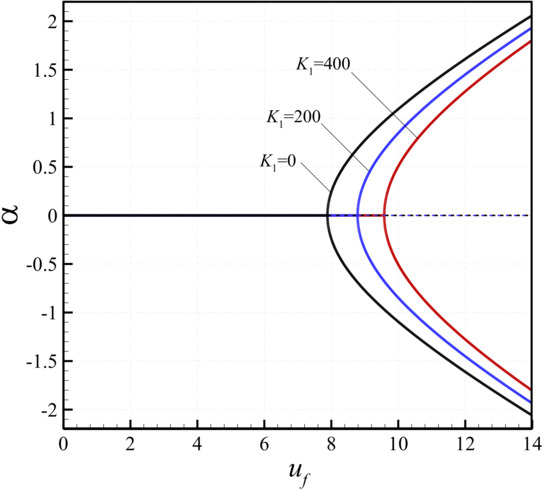
Figure 4.
Bifurcation diagrams of the microtube showing the effect of the linear spring coefficient on the transverse displacement at the centre.
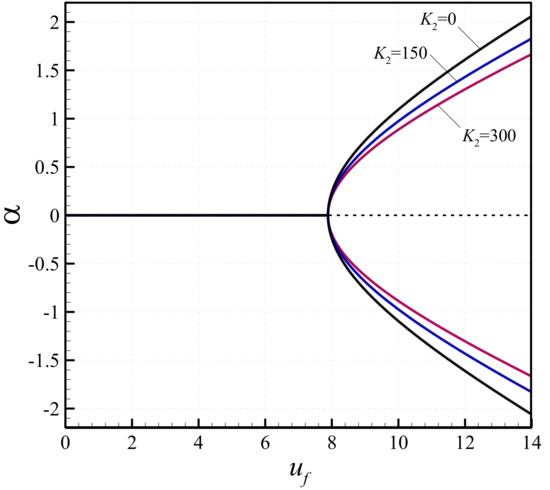
Figure 5.
Bifurcation diagrams of the microtube showing the effect of the nonlinear spring coefficient on the transverse displacement at the centre.
To illustrate the effect of the slenderness ratio on the bifurcation diagrams of the microtube, the change of the lateral deflection with the dimensional flow velocity (m/s) is shown in Figure 6 for various values of the slenderness ratio; for this case, . Higher values of the slenderness ratio lead to a significant reduction in the critical fluid velocity associated with the instability of the microscale system. It implies that as the length-to-diameter ratio increases, the microtube buckles at a lower fluid velocity. Another interesting observation is that in the post-buckling region (after the bifurcation point), the lateral displacement of the microscale tube increases with increasing the slenderness ratio. To better show the relation between the slenderness ratio and the critical flow velocity, Figure 7 is constructed. As seen in this figure, the critical flow velocity decreases in general with increasing slenderness ratio. It is interesting to note that as the length of the pipe increases, the critical flow velocity becomes less sensitive to changes in the length.
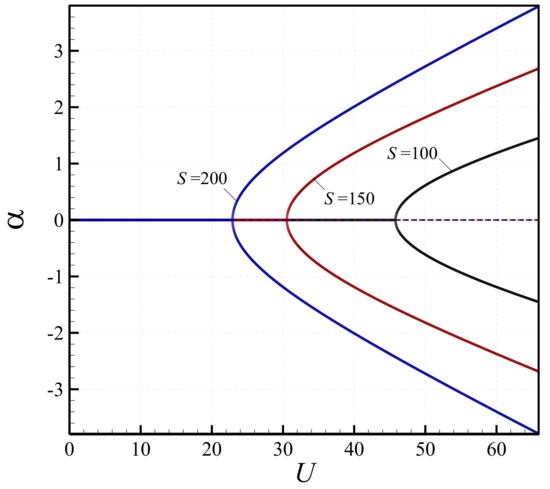
Figure 6.
Bifurcation diagrams of the microtube showing the effect of the slenderness ratio on the transverse displacement at centre; U is the dimensional flow velocity.
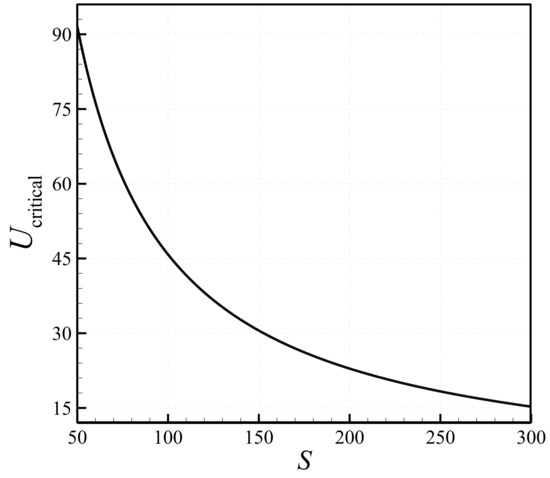
Figure 7.
Variation of the dimensional critical flow velocity with slenderness ratio.
In order to investigate the influence of the axial pretension on the buckling behaviour of the fluid-conveying microtube, the variation of the non-dimensional transverse displacement at centre with the dimensionless velocity of the fluid is plotted in Figure 8 for different values of the longitudinal pretention. The material and geometric parameters of the microsystem are set to = 0.5746, = 1.28 × 105 and S = 100. It is assumed that the microscale tube containing flowing fluid is not embedded in an elastic foundation, i.e. both the linear and nonlinear spring coefficients are set to zero . As seen, the critical fluid velocity related to the buckling of the microsystem increases with increasing the axial pretension. In other words, the presence of a pretension strengthens the microtube conveying fluid against buckling. Moreover, it is found that the lateral deflection of the system decreases when larger axial pretensions are applied. Finally, to show the accuracy and reliability of the present results, the bifurcation diagrams of a clamped-clamped pipe conveying fluid obtained by the present model are compared with those obtained in [57] (see Figure 9). An excellent agreement is found between the present results and those previously published in the literature.
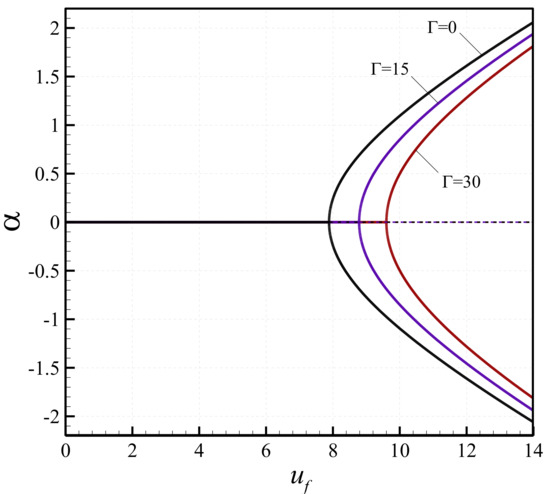
Figure 8.
Bifurcation diagrams of the microtube showing the effect of the axial pretension on the transverse displacement at centre.
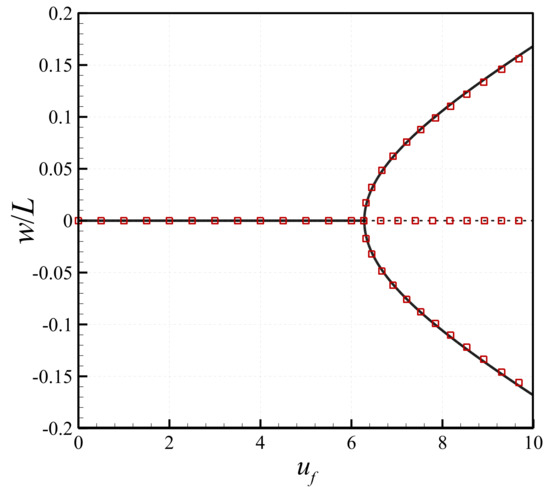
Figure 9.
Bifurcation diagrams of a clamped-clamped pipe conveying fluid, showing the centre transverse displacement; solid and dashed lines show the result of the present study while symbols show the results obtained in [57].
4. Conclusions
A nonlinear scale-dependent model was developed to study the large amplitude buckling instability of fluid-conveying microscale tubes under axial pretension and embedded in a nonlinear elastic foundation. The length scale effect was taken into consideration within the framework of the MCS theory. In addition, both longitudinal and lateral deflections, as well as the nonlinearity induced by nonlinear stretching and curvature were taken into account in the theoretical formulation and the numerical simulations. The coupled nonlinear discretised equations of motion of the microsystem were derived based on Lagrange’s equations to open medium together with an assumed-mode technique. To numerically solve the equations, a solution procedure on the basis of a continuation technique was used. It was found that the critical buckling fluid velocity of the microtube predicted using the MCS theory is larger than that obtained by the classical theory. It was shown that while the linear spring coefficient has an increasing effect on the buckling fluid velocity, the nonlinear spring coefficient does not affect the critical fluid velocity. Furthermore, the transverse displacement of the microtube decreases with the increase of each coefficient of the elastic foundation. It was also observed that microtubes of higher slenderness ratio tend to buckle at a lower fluid velocity with greater lateral deflections. Additionally, it was shown that buckling capacity of the microscale system carrying flowing fluid increases with increasing longitudinal pretension.
Author Contributions
Each author contributes equally in this paper. Conceptualization, A.F., H.F. and M.H.G.; Methodology, A.F., H.F. and M.H.G.; Software, A.F., H. F. and M.H.G.; Writing–Original Draft Preparation, A.F.; Writing–Review & Editing, M.H.G.; Supervision, M.H.G. and H.F.
Funding
This research received no funding.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Convergence Analysis
A convergence analysis is conducted in this section to verify the accuracy of the discretised model employed in this study. To this end, the bifurcation diagram of the system of Figure 2 is reconstructed using three discretized models: a 4-degree-of-freedom (4-DOF) model, an 8-DOF model, and the 20-DOF model employed in this study. The comparison between these discretized models is shown in Figure A1. It should be noted that for all cases, the number of degrees of freedom for the transverse and longitudinal motions is the same. As seen in Figure A1, the 4-DOF model does not yield accurate results. There is slight difference between the predictions of the 20-DOF and 8-DOF models, indicating that the 20-DOF model yields converged results.
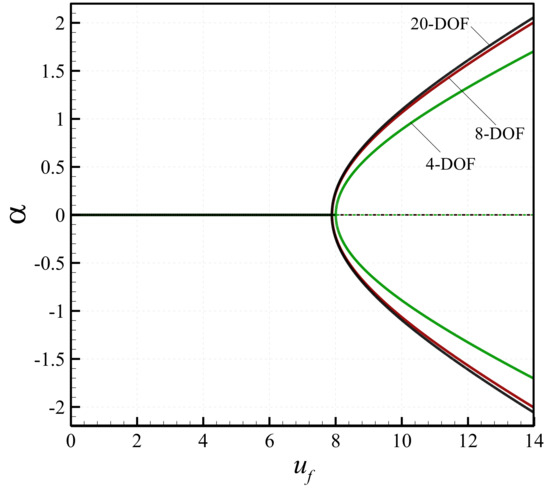
Figure A1.
Comparison of different discretised models of the system.
Appendix B. Experiment Setup for Obtaining the Small-Scale Parameter
Figure A2 illustrates an experiment setup for determining the small-scale parameter of a microscale beam with clamped-free boundary conditions [58]. A louder speaker, laser probe, signal generator, computer and laser Doppler vibrometer (LDV) are required as shown in the figure. By comparing the results obtained by this setup and those predicted using the modified elasticity theory, the small-scale parameter of the microbeam can be determined.
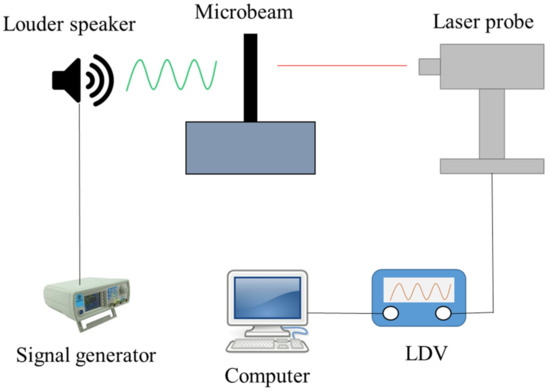
Figure A2.
Experiment setup for obtaining the small-scale parameter.
References
- Shi, Q.; Wang, T.; Lee, C. MEMS based broadband piezoelectric ultrasonic energy harvester (pueh) for enabling self-powered implantable biomedical devices. Sci. Rep. 2016, 6, 24946. [Google Scholar] [CrossRef] [PubMed]
- Bognash, M.; Asokanthan, S. Stochastic stability of a class of mems-based vibratory gyroscopes under input rate fluctuations. Vibration 2018, 1, 69–80. [Google Scholar] [CrossRef]
- Ho, C.-M.; Tai, Y.-C. Micro-electro-mechanical-systems (MEMS) and fluid flows. Annu. Rev. Fluid Mech. 1998, 30, 579–612. [Google Scholar] [CrossRef]
- Martínez-Ayuso, G.; Haddad Khodaparast, H.; Zhang, Y.; Bowen, C.R.; Friswell, M.I.; Shaw, A.D.; Madinei, H. Model validation of a porous piezoelectric energy harvester using vibration test data. Vibration 2018, 1, 123–137. [Google Scholar] [CrossRef]
- Naranjo-Pérez, J.; Jiménez-Manfredi, J.; Jiménez-Alonso, J.F.; Sáez, A. Motion-based design of passive damping devices to mitigate wind-induced vibrations in stay cables. Vibration 2018, 1, 269–289. [Google Scholar] [CrossRef]
- Tophøj, L.; Grathwol, N.; Hansen, S.O. Effective mass of tuned mass dampers. Vibration 2018, 1, 192–206. [Google Scholar] [CrossRef]
- Zaghari, B.; Rustighi, E.; Ghandchi Tehrani, M. Improved modelling of a nonlinear parametrically excited system with electromagnetic excitation. Vibration 2018, 1, 157–171. [Google Scholar] [CrossRef]
- Farajpour, A.; Farokhi, H.; Ghayesh, M.H. Chaotic motion analysis of fluid-conveying viscoelastic nanotubes. Eur. J. Mech. A/Solids 2019, 74, 281–296. [Google Scholar] [CrossRef]
- Farokhi, H.; Ghayesh, M.H. Nonlinear mechanical behaviour of microshells. Int. J. Eng. Sci. 2018, 127, 127–144. [Google Scholar] [CrossRef]
- Ghayesh, M.H.; Farajpour, A. Nonlinear coupled mechanics of nanotubes incorporating both nonlocal and strain gradient effects. Mech. Adv. Mater. Struct. 2018. [Google Scholar] [CrossRef]
- Ghayesh, M.H.; Farokhi, H.; Gholipour, A.; Hussain, S. On the nonlinear mechanics of layered microcantilevers. Int. J. Eng. Sci. 2017, 120, 1–14. [Google Scholar] [CrossRef]
- Farajpour, A.; Ghayesh, M.H.; Farokhi, H. A coupled nonlinear continuum model for bifurcation behaviour of fluid-conveying nanotubes incorporating internal energy loss. Microfluid. Nanofluid. 2019, 23, 34. [Google Scholar] [CrossRef]
- Ahangar, S.; Rezazadeh, G.; Shabani, R.; Ahmadi, G.; Toloei, A. On the stability of a microbeam conveying fluid considering modified couple stress theory. Int. J. Mech. Mater. Des. 2011, 7, 327. [Google Scholar] [CrossRef]
- Ghayesh, M.H.; Amabili, M.; Farokhi, H. Three-dimensional nonlinear size-dependent behaviour of timoshenko microbeams. Int. J. Eng. Sci. 2013, 71, 1–14. [Google Scholar] [CrossRef]
- Ghayesh, M.H.; Farokhi, H.; Amabili, M. Nonlinear dynamics of a microscale beam based on the modified couple stress theory. Compos. Part B Eng. 2013, 50, 318–324. [Google Scholar] [CrossRef]
- Ghayesh, M.H.; Farokhi, H.; Amabili, M. In-plane and out-of-plane motion characteristics of microbeams with modal interactions. Compos. Part B Eng. 2014, 60, 423–439. [Google Scholar] [CrossRef]
- Ghayesh, M.H. Nonlinear dynamics of multilayered microplates. J. Comput. Nonlinear Dyn. 2017, 13, 021006. [Google Scholar] [CrossRef]
- Gholipour, A.; Farokhi, H.; Ghayesh, M.H. In-plane and out-of-plane nonlinear size-dependent dynamics of microplates. Nonlinear Dyn. 2015, 79, 1771–1785. [Google Scholar] [CrossRef]
- Farokhi, H.; Ghayesh, M.H.; Amabili, M. Nonlinear dynamics of a geometrically imperfect microbeam based on the modified couple stress theory. Int. J. Eng. Sci. 2013, 68, 11–23. [Google Scholar] [CrossRef]
- Kural, S.; Özkaya, E. Size-dependent vibrations of a micro beam conveying fluid and resting on an elastic foundation. J. Vib. Control 2017, 23, 1106–1114. [Google Scholar] [CrossRef]
- Xia, W.; Wang, L. Microfluid-induced vibration and stability of structures modeled as microscale pipes conveying fluid based on non-classical Timoshenko beam theory. Microfluid. Nanofluid. 2010, 9, 955–962. [Google Scholar] [CrossRef]
- Hosseini, M.; Bahaadini, R. Size dependent stability analysis of cantilever micro-pipes conveying fluid based on modified strain gradient theory. Int. J. Eng. Sci. 2016, 101, 1–13. [Google Scholar] [CrossRef]
- Abbasnejad, B.; Shabani, R.; Rezazadeh, G. Stability analysis of a piezoelectrically actuated micro-pipe conveying fluid. Microfluid. Nanofluid. 2015, 19, 577–584. [Google Scholar] [CrossRef]
- Wang, L. Size-dependent vibration characteristics of fluid-conveying microtubes. J. Fluid. Struct. 2010, 26, 675–684. [Google Scholar] [CrossRef]
- Dai, H.; Wang, L.; Ni, Q. Dynamics and pull-in instability of electrostatically actuated microbeams conveying fluid. Microfluid. Nanofluid. 2015, 18, 49–55. [Google Scholar] [CrossRef]
- Li, L.; Hu, Y.; Li, X.; Ling, L. Size-dependent effects on critical flow velocity of fluid-conveying microtubes via nonlocal strain gradient theory. Microfluid. Nanofluid. 2016, 20, 76. [Google Scholar] [CrossRef]
- Ghayesh, M.H.; Farokhi, H.; Farajpour, A. Chaotic oscillations of viscoelastic microtubes conveying pulsatile fluid. Microfluid. Nanofluid. 2018, 22, 72. [Google Scholar] [CrossRef]
- Deng, J.; Liu, Y.; Liu, W. Size-dependent vibration analysis of multi-span functionally graded material micropipes conveying fluid using a hybrid method. Microfluid. Nanofluid. 2017, 21, 133. [Google Scholar] [CrossRef]
- Dehrouyeh-Semnani, A.M.; Nikkhah-Bahrami, M.; Yazdi, M.R.H. On nonlinear stability of fluid-conveying imperfect micropipes. Int. J. Eng. Sci. 2017, 120, 254–271. [Google Scholar] [CrossRef]
- Mashrouteh, S.; Sadri, M.; Younesian, D.; Esmailzadeh, E. Nonlinear vibration analysis of fluid-conveying microtubes. Nonlinear Dyn. 2016, 85, 1007–1021. [Google Scholar] [CrossRef]
- Yang, T.-Z.; Ji, S.; Yang, X.-D.; Fang, B. Microfluid-induced nonlinear free vibration of microtubes. Int. J. Eng. Sci. 2014, 76, 47–55. [Google Scholar] [CrossRef]
- Setoodeh, A.; Afrahim, S. Nonlinear dynamic analysis of fg micro-pipes conveying fluid based on strain gradient theory. Compos. Struct. 2014, 116, 128–135. [Google Scholar] [CrossRef]
- Rajabi, F.; Ramezani, S. A nonlinear microbeam model based on strain gradient elasticity theory with surface energy. Arch. Appl. Mech. 2012, 82, 363–376. [Google Scholar] [CrossRef]
- Ghayesh, M.H.; Moradian, N. Nonlinear dynamic response of axially moving, stretched viscoelastic strings. Arch. Appl. Mech. 2011, 81, 781–799. [Google Scholar] [CrossRef]
- Ghayesh, M.H.; Farokhi, H.; Farajpour, A. Global dynamics of fluid conveying nanotubes. Int. J. Eng. Sci. 2019, 135, 37–57. [Google Scholar] [CrossRef]
- Farokhi, H.; Ghayesh, M.H. Nonlinear mechanics of electrically actuated microplates. Int. J. Eng. Sci. 2018, 123, 197–213. [Google Scholar] [CrossRef]
- Kazemirad, S.; Ghayesh, M.H.; Amabili, M. Thermo-mechanical nonlinear dynamics of a buckled axially moving beam. Arch. Appl. Mech. 2013, 83, 25–42. [Google Scholar] [CrossRef]
- Farajpour, A.; Rastgoo, A.; Farajpour, M. Nonlinear buckling analysis of magneto-electro-elastic CNT-MT hybrid nanoshells based on the nonlocal continuum mechanics. Compos. Struct. 2017, 180, 179–191. [Google Scholar] [CrossRef]
- Farajpour, A.; Ghayesh, M.H.; Farokhi, H. Large-amplitude coupled scale-dependent behaviour of geometrically imperfect nsgt nanotubes. Int. J. Mech. Sci. 2019, 150, 510–525. [Google Scholar] [CrossRef]
- Farajpour, A.; Farokhi, H.; Ghayesh, M.H.; Hussain, S. Nonlinear mechanics of nanotubes conveying fluid. Int. J. Eng. Sci. 2018, 133, 132–143. [Google Scholar] [CrossRef]
- Ghayesh, M.H. Subharmonic dynamics of an axially accelerating beam. Arch. Appl. Mech. 2012, 82, 1169–1181. [Google Scholar] [CrossRef]
- Farokhi, H.; Ghayesh, M.H. On the dynamics of imperfect shear deformable microplates. Int. J. Eng. Sci. 2018, 133, 264–283. [Google Scholar] [CrossRef]
- Farokhi, H.; Ghayesh, M.H. Supercritical nonlinear parametric dynamics of Timoshenko microbeams. Commun. Nonlinear Sci. Numer. Simul. 2018, 59, 592–605. [Google Scholar] [CrossRef]
- Ghayesh, M.H. Viscoelastic dynamics of axially FG microbeams. Int. J. Eng. Sci. 2019, 135, 75–85. [Google Scholar] [CrossRef]
- Ghayesh, M.H.; Farokhi, H. On the viscoelastic dynamics of fluid-conveying microtubes. Int. J. Eng. Sci. 2018, 127, 186–200. [Google Scholar] [CrossRef]
- Ghayesh, M.H.; Farokhi, H.; Gholipour, A.; Hussain, S. Complex motion characteristics of three-layered Timoshenko microarches. Microsyst. Technol. 2017, 23, 3731–3744. [Google Scholar] [CrossRef]
- Irschik, H.; Holl, H.J. The equations of Lagrange written for a non-material volume. Acta Mech. 2002, 153, 231–248. [Google Scholar] [CrossRef]
- Seydel, R. Practical Bifurcation and Stability Analysis; Springer Science & Business Media: Berlin, Germany, 2009; Volume 5. [Google Scholar]
- Lam, D.C.; Yang, F.; Chong, A.; Wang, J.; Tong, P. Experiments and theory in strain gradient elasticity. J. Mech. Phys. Solids 2003, 51, 1477–1508. [Google Scholar] [CrossRef]
- Farajpour, A.; Ghayesh, M.H.; Farokhi, H. A review on the mechanics of nanostructures. Int. J. Eng. Sci. 2018, 133, 231–263. [Google Scholar] [CrossRef]
- Farokhi, H.; Ghayesh, M.H.; Gholipour, A.; Hussain, S. Motion characteristics of bilayered extensible Timoshenko microbeams. Int. J. Eng. Sci. 2017, 112, 1–17. [Google Scholar] [CrossRef]
- Ghayesh, M.H.; Farajpour, A. Vibrations of shear deformable FG viscoelastic microbeams. Microsyst. Technol. 2018. [Google Scholar] [CrossRef]
- Farajpour, M.R.; Shahidi, A.; Farajpour, A. Resonant frequency tuning of nanobeams by piezoelectric nanowires under thermo-electro-magnetic field: A theoretical study. Micro Nano Lett. 2018, 13, 1627–1632. [Google Scholar] [CrossRef]
- Ghayesh, M.H.; Farokhi, H.; Gholipour, A. Oscillations of functionally graded microbeams. Int. J. Eng. Sci. 2017, 110, 35–53. [Google Scholar] [CrossRef]
- Ghayesh, M.H.; Farajpour, A. A review on the mechanics of functionally graded nanoscale and microscale structures. Int. J. Eng. Sci. 2019, 137, 8–36. [Google Scholar] [CrossRef]
- Ghayesh, M.H.; Farajpour, A. Nonlinear mechanics of nanoscale tubes via nonlocal strain gradient theory. Int. J. Eng. Sci. 2018, 129, 84–95. [Google Scholar] [CrossRef]
- Paidoussis, M.P. Fluid-Structure Interactions: Slender Structures and Axial Flow; Academic Press: Cambridge, MA, USA, 1998; Volume 1. [Google Scholar]
- Li, Z.; He, Y.; Lei, J.; Han, S.; Guo, S.; Liu, D. Experimental investigation on size-dependent higher-mode vibration of cantilever microbeams. Microsyst. Technol. 2018. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).