Recent Advances in Seismocardiography
Abstract
1. Introduction
1.1. Definition of SCG Signals
1.2. Physiological Sources of SCG Signals
1.3. Measurement Methods
- Airborne ultrasound surface motion camera (AUSMC) [53].
1.4. Parameters Affecting SCG Waveform
2. Signal Processing
2.1. Noise Reduction
2.2. Segmentation
2.3. Feature Extraction
2.3.1. Time-Domain Features
2.3.2. Frequency-Domain Features
2.4. Machine Learning
3. Recent Human Studies Suggesting Clinical Utilities
3.1. Portable Detection of SCG
3.2. Heart Rate Monitoring
3.3. Pulse Transit Time
3.4. Cardiac Time Intervals
3.5. SCG in Patients with Cardiac Conditions
4. Conclusions, Limitations, and Future Directions
- SCG variability: SCG morphology is affected by different factors such as respiration, sensor location, subject posture, the amount of chest surface soft tissue, and different heart diseases. Although studies investigated some of these factors, further research is needed to adequately account for SCG variations. The results of such investigations might improve utility for cardiac disease diagnosis and monitoring.
- Lack of accepted standard for the cardio-mechanical SCG fiducial points: A small number of recent studies focused on robust documentation of the relationship between fiducial points and their physiological sources. In addition, SCG morphology changes with different factors (e.g., sensor location, patient posture, etc.). It would be useful to investigate the effect of these factors on the SCG signal fiducial points.
- SCG genesis: Although several studies aimed to elucidate the physiological source(s) of the SCG signals, much work remains to be done. SCG signals are likely affected by extra-cardiac factors including respiration and intrathoracic pressure. Therefore, considering these parameters may further help elucidate SCG sources.
- Computational models: Realistic computational simulations utilizing finite element and other modeling methodologies with realistic geometries and material properties might be helpful in predicting the effects of varied cardiac conditions on SCG features.
- Library of SCG signals: A common comprehensive database would provide a basis for researchers interested in analyzing SCG and other biomedical signals. The MIT-BIH arrhythmia database is a good example of a biomedical signals database. This database plays an important role in stimulating both basic research and medical device development. A similar SCG database would attract more researchers to investigate and compare the performance of different algorithms and approaches.
- Correlation between SCG and other electro-mechanical signals: Combining information from ECG, PCG, and BCG with that of SCG may lead to a hybrid modality with increased diagnostic utility of cardiac disease. This may result in more complex features that require increase use of machine learning approaches.
Author Contributions
Funding
Conflicts of Interest
References
- Mozaffarian, D.; Benjamin, E.J.; Go, A.S.; Arnett, D.K.; Blaha, M.J.; Cushman, M.; de Ferranti, S.; Despres, J.-P.; Fullerton, H.J.; Howard, V.J.; et al. Heart Disease and Stroke Statistics—2015 Update: A Report From the American Heart Association. Circulation 2015, 131, e29–e322. [Google Scholar] [CrossRef] [PubMed]
- Lee, L.; Markwick, A.; Horsfall, M.; Sinhal, A.; Chew, D. Prognostic implications of moderate and severe mitral regurgitation in contemporary clinical care. EuroIntervention 2012, 8, Q111. [Google Scholar]
- Otto, C.M. Timing of aortic valve surgery. Heart 2000, 84, 211–218. [Google Scholar] [CrossRef] [PubMed]
- Khalili, F.; Mansy, H.A. Blood Flow through a Dysfunctional Mechanical Heart Valve. In Proceedings of the 38th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Orlando, FL, USA, 17–20 August 2016. [Google Scholar]
- Khalili, F.; Gamage, P.P.T.; Mansy, H.A. Hemodynamics of a Bileaflet Mechanical Heart Valve with Different Levels of Dysfunction. J. Appl. Biotechnol. Bioeng. 2017, 2, 00044. [Google Scholar] [CrossRef]
- Zanetti, J.; Tavakolian, K. Seismocardiography: Past, present and future. In Proceedings of the 35th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Osaka, Japan, 3–7 July 2013; pp. 7004–7007. [Google Scholar]
- Inan, O.T.; Migeotte, P.F.; Park, K.S.; Etemadi, M.; Tavakolian, K.; Casanella, R.; Zanetti, J.; Tank, J.; Funtova, I.; Prisk, G.K.; et al. Ballistocardiography and Seismocardiography: A Review of Recent Advances. IEEE J. Biomed. Health Inform. 2015, 19, 1414–1427. [Google Scholar] [CrossRef] [PubMed]
- Starr, I.; Rawson, J.; Schroeder, H.; Joseph, N. Studies on the estimation of cardiac ouptut in man, and of abnormalities in cardiac function, from the heart’s recoil and the blood’s impacts; the Ballistocardiogram. Am. J. Physiol. 1939, 127, 1–28. [Google Scholar] [CrossRef]
- Salerno, D.M.; Zanetti, J.M.; Green, L.A.; Mooney, M.R.; Madison, J.D.; Van Tassel, R.A. Seismocardiographic changes associated with obstruction of coronary blood flow during balloon angioplasty. Am. J. Cardiol. 1991, 68, 201–207. [Google Scholar] [CrossRef]
- Salerno, D.M.; Zanetti, J. Seismocardiography for monitoring changes in left ventricular function during ischemia. Chest 1991, 100, 991–993. [Google Scholar] [CrossRef]
- Pandia, K.; Inan, O.T.; Kovacs, G.T.; Giovangrandi, L. Extracting respiratory information from seismocardiogram signals acquired on the chest using a miniature accelerometer. Physiol. Meas. 2012, 33, 1643–1660. [Google Scholar] [CrossRef]
- Bifulco, P.; Gargiulo, G.D.; D’Angelo, G.; Liccardo, A.; Romano, M.; Clemente, F.; Cesarelli, M.; Angelo, G.; Liccardo, A.; Romano, M.; et al. Monitoring of respiration, seismocardiogram and heart sounds by a PVDF piezo film sensor. Measurement 2014, 11, 786–789. [Google Scholar]
- Zanetti, J.; Salerno, D. Seismocardiography: A new technique for recording cardiac vibrations. Concept, method, and initial observations. J. Cardiovasc. Technol. 1990, 9, 111–118. [Google Scholar]
- Crow, R.S.; Hannan, P.; Jacobs, D.; Hedquist, L.; Salerno, D.M. Relationship between Seismocardiogram and Echocardiogram for Events in the Cardiac Cycle. Am. J. Noninvasive Cardiol. 1994, 8, 39–46. [Google Scholar] [CrossRef]
- Taebi, A.; Mansy, H.A. Time-frequency Analysis of Vibrocardiographic Signals. In Proceedings of the 2015 BMES Annual Meeting, Tampa, FL, USA, 7–10 October 2015. [Google Scholar]
- Eddleman, E. Kinetocardiographic Changes in Ischemic Heart Disease. Circulation 1965, 32, 650–655. [Google Scholar] [CrossRef] [PubMed]
- Starr, I.; Wood, E. Twenty-year studies with the ballistocardiograph, the relation between the amplitude of the first record of ‘health’ adults and eventual mortality and morbidity form heart disease. Circulation 1961, 23, 714–732. [Google Scholar] [CrossRef]
- Starr, I.; Noordegroaf, A. Ballistocardiography in Cardiovascular Research; Lippincott: Philadelphia, PA, USA, 1967. [Google Scholar]
- Phibbs, B.; Lowe, C.; Holmes, R. The ultra lowfrequency force ballistocardiograph in acute cardiomyopathy. Circulation 1967, 36, 92–100. [Google Scholar] [CrossRef]
- Scherhag, A.W.; Pfleger, S.; Ceconi, C.; Voelker, W.; Gehring, J.; Staedt, U.; Heene, D.L. Evaluation of signal-averaged cardiokymography for the detection of ischaemic left ventricular dysfunction. Int. J. Cardiol. 1997, 59, 305–312. [Google Scholar] [CrossRef]
- Matsui, T.; Hagisawa, K.; Ishizuka, T.; Takase, B.; Ishihara, M.; Kikuchi, M. A Novel Method to Prevent Secondary Exposure of Medical and Rescue Personnel to Toxic Materials Under Biochemical Hazard Conditions Using Microwave Radar and Infrared Themography. IEEE Trans. Biomed. Eng. 2004, 51, 2184–2188. [Google Scholar] [CrossRef]
- Morbiducci, U.; Scalise, L.; De Melis, M.; Grigioni, M. Optical vibrocardiography: A novel tool for the optical monitoring of cardiac activity. Ann. Biomed. Eng. 2007, 35, 45–58. [Google Scholar] [CrossRef]
- Tavakolian, K.; Vaseghi, A.; Kaminska, B. Improvement of ballistocardiogram processing by inclusion of respiration information. Physiol. Meas. 2008, 29, 771–781. [Google Scholar] [CrossRef]
- Mack, D.C.; Patrie, J.T.; Suratt, P.M.; Felder, R.A.; Alwan, M. Development and preliminary validation of heart rate and breathing rate detection using a passive, ballistocardiography-based sleep monitoring system. IEEE Trans. Inf. Technol. Biomed. 2009, 13, 111–120. [Google Scholar] [CrossRef]
- Jafari Tadi, M.; Lehtonen, E.; Hurnanen, T.; Koskinen, J.; Eriksson, J.; Pänkäälä, M.; Teräs, M.; Koivisto, T. A real-time approach for heart rate monitoring using a Hilbert transform in seismocardiograms. Physiol. Meas. 2016, 37, 1885–1909. [Google Scholar] [CrossRef] [PubMed]
- Cosoli, G.; Casacanditella, L.; Tomasini, E.; Scalise, L. Heart Rate assessment by means of a novel approach applied to signals of different nature. J. Phys. Conf. Ser. 2017, 778, 012001. [Google Scholar] [CrossRef]
- Gurev, V.; Tavakolian, K.; Constantino, J.; Kaminska, B.; Blaber, A.P.; Trayanova, N.A. Mechanisms underlying isovolumic contraction and ejection peaks in seismocardiogram morphology. J. Med. Biol. Eng. 2012, 32, 103–110. [Google Scholar] [CrossRef] [PubMed]
- Tadi, M.; Koivisto, T.; Pankaala, M.; Paasio, A.; Knuutila, T.; Teras, M.; Hanninen, P. A new algorithm for segmentation of cardiac quiescent phases and cardiac time intervals using seismocardiography. In Proceedings of the Sixth International Conference on Graphic and Image Processing (ICGIP 2014), Beijing, China, 24–26 October 2015; p. 94432K. [Google Scholar]
- Tavakolian, K.; Khosrow-Khavar, F.; Kajbafzadeh, B.; Marzencki, M.; Rohani, S.; Kaminska, B.; Menon, C. Seismocardiographic adjustment of diastolic timed vibrations. In Proceedings of the Annual International Conference of the IEEE Engineering in Medicine and Biology Society, EMBS, San Diego, CA, USA, 28 August–1 September 2012; pp. 3797–3800. [Google Scholar]
- Zanetti, J.M.; Poliac, M.O.; Crow, R.S. Seismocardiography: Waveform identification and noise analysis. In Proceedings of the Computers in Cardiology 1991, Venice, Italy, 23–26 September 1991; pp. 49–52. [Google Scholar]
- Tadi, M.J.; Lehtonen, E.; Saraste, A.; Tuominen, J.; Koskinen, J.; Teräs, M.; Airaksinen, J.; Pänkäälä, M.; Koivisto, T. Gyrocardiography: A new non-invasive monitoring method for the assessment of cardiac mechanics and the estimation of hemodynamic variables. Sci. Rep. 2017, 7, 6823. [Google Scholar] [CrossRef] [PubMed]
- Tavakolian, K. Charachterization and Analysis of Seismocardiogram for Estimation of Hemodynamic Parameters. Ph.D. Thesis, Simon Fraser University, Burnaby, BC, Canada, 2010. [Google Scholar]
- Choudhary, T.; Sharma, L.N.; Bhuyan, M.K. Automatic Detection of Aortic Valve Opening using Seismocardiography in Healthy Individuals. IEEE J. Biomed. Health Inform. 2018. [Google Scholar] [CrossRef] [PubMed]
- Lin, W.; Chou, W.; Chang, P.; Chou, C.; Wen, M.; Ho, M.; Lee, M. Identification of Location Specific Feature Points in a Cardiac Cycle Using a Novel Seismocardiogram Spectrum System. IEEE J. Biomed. Health Inform. 2018, 22, 442–449. [Google Scholar] [CrossRef] [PubMed]
- Sengupta, P.P.; Krishnamoorthy, V.K.; Korinek, J.; Narula, J.; Vannan, M.A.; Lester, S.J.; Tajik, J.A.; Seward, J.B.; Khandheria, B.K.; Belohlavek, M. Left Ventricular Form and Function Revisited: Applied Translational Science to Cardiovascular Ultrasound Imaging. J. Am. Soc. Echocardiogr. 2007, 20, 539–551. [Google Scholar] [CrossRef]
- Yang, C.; Tang, S.; Tavassolian, N. Utilizing Gyroscopes Towards the Automatic Annotation of Seismocardiograms. IEEE Sens. J. 2017, 17, 2129–2136. [Google Scholar] [CrossRef]
- Migeotte, P.-F.; Mucci, V.; Delière, Q.; Lejeune, L.; van de Borne, P. Multi-dimensional kineticardiography a new approach for wearable cardiac monitoring through body acceleration recordings. In XIV Mediterranean Conference on Medical and Biological Engineering and Computing 2016; Springer: Cham, Switzerland, 2016; pp. 1125–1130. [Google Scholar]
- Yang, C.; Tavassolian, N. Combined Seismo-and Gyro-cardiography: A More Comprehensive Evaluation of Heart-Induced Chest Vibrations. IEEE J. Biomed. Health Inform. 2017. [Google Scholar] [CrossRef]
- Taebi, A.; Bomar, A.J.; Sandler, R.H.; Mansy, H.A. Heart Rate Monitoring During Different Lung Volume Phases Using Seismocardiography. In Proceedings of the IEEE SoutheastCon 2018, Saint Petersburg, FL, USA, 19–22 April 2018; pp. 1–5. [Google Scholar]
- Solar, B.E.; Taebi, A.; Mansy, H.A. Classification of Seismocardiographic Cycles into Lung Volume Phases. In 2017 IEEE Signal Processing in Medicine and Biology Symposium (SPMB); IEEE: Philadelphia, PA, USA, 2017; pp. 1–2. [Google Scholar]
- Ashouri, H.; Inan, O.T. Automatic Detection of Seismocardiogram Sensor Misplacement for Robust Pre-Ejection Period Estimation in Unsupervised Settings. IEEE Sens. J. 2017, 17, 3805–3813. [Google Scholar] [CrossRef]
- Koegelenberg, S. Application of Laser Doppler Vibrocardiography for Human Heart Auscultation. Ph.D. Thesis, Stellenbosch University, Stellenbosch, South Africa, 2014. [Google Scholar]
- Jain, P.K.; Tiwari, A.K. A novel method for suppression of motion artifacts from the seismocardiogram signal. In Proceedings of the 2016 IEEE International Conference on Digital Signal Processing (DSP), Beijing, China, 16–18 October 2016; pp. 6–10. [Google Scholar]
- Jain, P.K.; Tiwari, A.K.; Chourasia, V.S. Performance analysis of seismocardiography for heart sound signal recording in noisy scenarios. J. Med. Eng. Technol. 2016, 40, 106–118. [Google Scholar] [CrossRef]
- Yang, C.; Tang, S.; Tavassolian, N. Annotation of seismocardiogram using gyroscopic recordings. In Proceedings of the 2016 IEEE Biomedical Circuits and Systems Conference (BioCAS), Shanghai, China, 17–19 October 2016; pp. 204–207. [Google Scholar]
- Landreani, F.; Martin-Yebra, A.; Casellato, C.; Frigo, C.; Pavan, E.; Migeotte, P.-F.; Caiani, E.G. Beat-to-beat heart rate detection by smartphone’s accelerometers: Validation with ECG. In Proceedings of the 2016 IEEE 38th Annual International Conference of the Engineering in Medicine and Biology Society (EMBC), Orlando, FL, USA, 16–20 August 2016; pp. 525–528. [Google Scholar]
- Lahdenoja, O.; Hurnanen, T.; Iftikhar, Z.; Nieminen, S.; Knuutila, T.; Saraste, A.; Kiviniemi, T.; Vasankari, T.; Airaksinen, J.; Pankaala, M.; et al. Atrial Fibrillation Detection via Accelerometer and Gyroscope of a Smartphone. IEEE J. Biomed. Health Inform. 2018, 22, 108–118. [Google Scholar] [CrossRef] [PubMed]
- Iftikhar, Z.; Lahdenoja, O.; Tadi, M.J.; Hurnanen, T.; Vasankari, T.; Kiviniemi, T.; Airaksinen, J.; Koivisto, T.; Pänkäälä, M. Multiclass Classifier based Cardiovascular Condition Detection Using Smartphone Mechanocardiography. Sci. Rep. 2018, 8, 9344. [Google Scholar] [CrossRef] [PubMed]
- Metzler, J.; Kroschel, K.; Willersinn, D. Automatic detection of measurement points for non-contact vibrometer-based diagnosis of cardiac arrhythmias. In SPIE Medical Imaging. International Society for Optics and Photonics; Webster, R.J., Fei, B., Eds.; SPIE: Bellingham, WA, USA, 2017; p. 101351S. [Google Scholar]
- Xia, Z.; Shandhi, M.D.M.H.; Inan, O.T.; Zhang, Y. Interference and Removal of Respiration Harmonics on Noncontact Seismo-cardiogram Signals. In Structural Health Monitoring 2017; DEStech Publications: Lancaster, PA, USA, 2017. [Google Scholar]
- Shandhi, M.D.M.H.; Xia, Z.; Inan, O.T.; Zhang, Y. Clutter Effect on the Noncontact Seismocardiogram Signals Measured using Microwave Radars. In Structural Health Monitoring 2017; DEStech Publications: Lancaster, PA, USA, 2017. [Google Scholar]
- Xia, Z.; Shandhi, M.M.H.; Inan, O.T.; Zhang, Y. Non-Contact Sensing of Seismocardiogram Signals Using Microwave Doppler Radar. IEEE Sens. J. 2018, 18, 5956–5964. [Google Scholar] [CrossRef]
- Shirkovskiy, P.; Laurin, A.; Jeger-Madiot, N.; Chapelle, D.; Fink, M.; Ing, R.K. Airborne ultrasound surface motion camera: Application to seismocardiography. Appl. Phys. Lett. 2018, 112, 213702. [Google Scholar] [CrossRef]
- Alamdari, N.T. A Morphological Approach To Identify Respiratory Phases Of Seismocardiogram. Master’s Thesis, The University of North Dakota, Grand Forks, ND, USA, 2016. [Google Scholar]
- Paukkunen, M.; Parkkila, P.; Hurnanen, T.; Pankaala, M.; Koivisto, T.; Nieminen, T.; Kettunen, R.; Sepponen, R. Beat-by-Beat Quantification of Cardiac Cycle Events Detected From Three-Dimensional Precordial Acceleration Signals. IEEE J. Biomed. Health Inform. 2016, 20, 435–439. [Google Scholar] [CrossRef] [PubMed]
- Zakeri, V.; Akhbardeh, A.; Alamdari, N.; Fazel-Rezai, R.; Paukkunen, M.; Tavakolian, K. Analyzing Seismocardiogram Cycles to Identify the Respiratory Phases. IEEE Trans. Biomed. Eng. 2017, 64, 1786–1792. [Google Scholar] [CrossRef]
- Jain, P.K.; Tiwari, A.K.; Bhagat, O.L. Seismocardiography: An alternate method to estimate electro-mechanical window. In Proceedings of the 2016 International Conference on Systems in Medicine and Biology (ICSMB), Kharagpur, India, 4–7 January 2016; pp. 136–139. [Google Scholar]
- Dinh, A.; Bui, F.M.; Nguyen, T. An accelerometer based system to measure myocardial performance index during stress testing. In Proceedings of the 2016 IEEE 38th Annual International Conference of the Engineering in Medicine and Biology Society (EMBC), Orlando, FL, USA, 16–20 August 2016; pp. 4877–4880. [Google Scholar]
- Zhang, G.; Cottrell, A.C.; Henry, I.C.; McCombie, D.B. Assessment of pre-ejection period in ambulatory subjects using seismocardiogram in a wearable blood pressure monitor. In Proceedings of the 2016 IEEE 38th Annual International Conference of the Engineering in Medicine and Biology Society (EMBC), Orlando, FL, USA, 16–20 August 2016; pp. 3386–3389. [Google Scholar]
- Khosrow-Khavar, F. Automatic and Non-Invasive Delineation of the Seismocardiogram Signal for the Estimation of Cardiac Time Intervals with Applications in Diastolic Timed Vibration and Early Stage Hemorrhage Detection. Ph.D. Thesis, Simon Fraser University, Burnaby, BC, Canada, 2016. [Google Scholar]
- Khosrow-Khavar, F.; Tavakolian, K.; Blaber, A.; Menon, C. Automatic and Robust Delineation of the Fiducial Points of the Seismocardiogram Signal for Noninvasive Estimation of Cardiac Time Intervals. IEEE Trans. Biomed. Eng. 2017, 64, 1701–1710. [Google Scholar] [CrossRef]
- Shafiq, G.; Tatinati, S.; Veluvolu, K.C. Automatic annotation of peaks in seismocardiogram for systolic time intervals. In Proceedings of the 2016 IEEE 38th Annual International Conference of the Engineering in Medicine and Biology Society (EMBC), Orlando, FL, USA, 16–20 August 2016; pp. 2672–2675. [Google Scholar]
- Shafiq, G.; Tatinati, S.; Ang, W.T.; Veluvolu, K.C. Automatic Identification of Systolic Time Intervals in Seismocardiogram. Sci. Rep. 2016, 6, 37524. [Google Scholar] [CrossRef]
- Jain, P.K.; Tiwari, A.K. An algorithm for automatic segmentation of heart sound signal acquired using seismocardiography. In Proceedings of the 2016 International Conference on Systems in Medicine and Biology (ICSMB), Kharagpur, India, 4–7 January, 2016; pp. 157–161. [Google Scholar]
- Taebi, A.; Solar, B.E.; Mansy, H.A. An Adaptive Feature Extraction Algorithm for Classification of Seismocardiographic Signals. In Proceedings of the IEEE SoutheastCon 2018, Saint Petersburg, FL, USA, 19–22 April 2018; pp. 1–5. [Google Scholar]
- Taebi, A.; Mansy, H.A. Grouping Similar Seismocardiographic Signals Using Respiratory Information. In 2017 IEEE Signal Processing in Medicine and Biology Symposium (SPMB); IEEE: Philadelphia, PA, USA, 2017; pp. 1–6. [Google Scholar]
- Taebi, A.; Mansy, H.A. Time-Frequency Distribution of Seismocardiographic Signals: A Comparative Study. Bioengineering 2017, 4, 32. [Google Scholar] [CrossRef]
- Pänkäälä, M.; Koivisto, T.; Lahdenoja, O.; Kiviniemi, T.; Saraste, A.; Vasankari, T.; Airaksinen, J. Detection of atrial fibrillation with seismocardiography. In Proceedings of the 2016 IEEE 38th Annual International Conference of the Engineering in Medicine and Biology Society (EMBC), Orlando, FL, USA, 16–20 August 2016; pp. 4369–4374. [Google Scholar]
- Tadi, M.J.; Lehtonen, E.; Lahdenoja, O.; Pankaala, M.; Koivisto, T. An adaptive approach for heartbeat detection based on S-transform in seismocardiograms. In Proceedings of the 2016 IEEE 38th Annual International Conference of the Engineering in Medicine and Biology Society (EMBC), Orlando, FL, USA, 16–20 August 2016; pp. 2370–2373. [Google Scholar]
- Hurnanen, T.; Lehtonen, E.; Tadi, M.J.; Kuusela, T.; Kiviniemi, T.; Saraste, A.; Vasankari, T.; Airaksinen, J.; Koivisto, T.; Pankaala, M. Automated Detection of Atrial Fibrillation Based on Time–Frequency Analysis of Seismocardiograms. IEEE J. Biomed. Health Inform. 2017, 21, 1233–1241. [Google Scholar] [CrossRef] [PubMed]
- Sahoo, P.K.; Thakkar, H.K.; Lin, W.-Y.; Chang, P.-C.; Lee, M.-Y. On the Design of an Efficient Cardiac Health Monitoring System Through Combined Analysis of ECG and SCG Signals. Sensors 2018, 18, 379. [Google Scholar] [CrossRef] [PubMed]
- Yang, C.; Tavassolian, N. Motion Artifact Cancellation of Seismocardiographic Recording From Moving Subjects. IEEE Sens. J. 2016, 16, 5702–5708. [Google Scholar] [CrossRef]
- Di Rienzo, M.; Lombardi, P.; Scurati, D.; Vaini, E. A new technological platform for the multisite assessment of 3D seismocardiogram and pulse transit time in cardiac patients. In Proceedings of the 2016 Computing in Cardiology Conference (CinC), Vancouver, BC, Canada, 11–14 September 2016; pp. 781–784. [Google Scholar]
- Canino, N.K.; Wang, R.R.; Robinson, C.J. Using multiple placements of accelerometers to measure cardiovascular pulse transit times. In Proceedings of the 2016 IEEE 38th Annual International Conference of the Engineering in Medicine and Biology Society (EMBC), Orlando, FL, USA, 16–20 August 2016; pp. 4248–4251. [Google Scholar]
- Javaid, A.Q.; Dowling, S.; Etemadi, M.; Heller, J.A.; Roy, S.; Klein, L.; Inan, O.T. Quantification of posture induced changes in wearable seismocardiogram signals for heart failure patients. In Proceedings of the 2016 Computing in Cardiology Conference (CinC), Vancouver, BC, Canada, 11–14 September 2016; pp. 777–780. [Google Scholar]
- Javaid, A.Q.; Ashouri, H.; Dorier, A.; Etemadi, M.; Heller, J.A.; Roy, S.; Inan, O.T. Quantifying and Reducing Motion Artifacts in Wearable Seismocardiogram Measurements During Walking to Assess Left Ventricular Health. IEEE Trans. Biomed. Eng. 2017, 64, 1277–1286. [Google Scholar] [CrossRef] [PubMed]
- Chuo, Y.; Tavakolian, K.; Kaminska, B. Evaluation of a novel integrated sensor system for synchronous measurement of cardiac vibrations and cardiac potentials. J. Med. Syst. 2011, 35, 445–455. [Google Scholar] [CrossRef]
- Inan, O.T.; Baran Pouyan, M.; Javaid, A.Q.; Dowling, S.; Etemadi, M.; Dorier, A.; Heller, J.A.; Bicen, A.O.; Roy, S.; De Marco, T.; et al. Novel Wearable Seismocardiography and Machine Learning Algorithms Can Assess Clinical Status of Heart Failure Patients. Circ. Heart Fail. 2018, 11, e004313. [Google Scholar] [CrossRef] [PubMed]
- Yang, C.; Tavassolian, N. Pulse Transit Time Measurement Using Seismocardiogram, Photoplethysmogram, and Acoustic Recordings: Evaluation and Comparison. IEEE J. Biomed. Health Inform. 2017. [Google Scholar] [CrossRef] [PubMed]
- Yao, J.; Tridandapani, S.; Wick, C.A.; Bhatti, P.T. Seismocardiography-Based Cardiac Computed Tomography Gating Using Patient-Specific Template Identification and Detection. IEEE J. Transl. Eng. Health Med. 2017, 5, 1–14. [Google Scholar] [CrossRef]
- Di Rienzo, M.; Vaini, E.; Lombardi, P. An algorithm for the beat-to-beat assessment of cardiac mechanics during sleep on Earth and in microgravity from the seismocardiogram. Sci. Rep. 2017, 7. [Google Scholar] [CrossRef]
- Ashouri, H.; Hersek, S.; Inan, O.T. Universal Pre-Ejection Period Estimation using Seismocardiography: Quantifying the Effects of Sensor Placement and Regression Algorithms. IEEE Sens. J. 2018, 18, 1665–1674. [Google Scholar] [CrossRef]
- Lee, H.; Lee, H.; Whang, M. An Enhanced Method to Estimate Heart Rate from Seismocardiography via Ensemble Averaging of Body Movements at Six Degrees of Freedom. Sensors 2018, 18, 238. [Google Scholar] [CrossRef] [PubMed]
- Antognoli, L.; Marchionni, P.; Nobile, S.; Carnielli, V.P.; Scalise, L. Assessment of cardio-respiratory rates by non-invasive measurement methods in hospitalized preterm neonates. In Proceedings of the 2018 IEEE International Symposium on Medical Measurements and Applications (MeMeA), Rome, Italy, 11–13 June 2018; pp. 1–5. [Google Scholar]
- Kon, S.; Oldham, K.; Horowitz, R. Piezoresistive and piezoelectric MEMS strain sensors for vibration detection. In Sensors and Smart Structures Technologies for Civil, Mechanical, and Aerospace Systems 2007; SPIE: Bellingham, WA, USA, 2007; Volume 6529, p. 65292V. [Google Scholar]
- Libonati, J.R.; Colby, A.M.; Caldwell, T.M.; Kasparian, R.; Glassberg, H.L. Systolic and diastolic cardiac function time intervals and exercise capacity in women. Med. Sci. Sports Exerc. 1999, 31, 258–263. [Google Scholar] [CrossRef] [PubMed]
- Korzeniowska-kubacka, I.; Kuśmierczyk-droszcz, B.; Bilińska, M.; Barbara, D.-W.; Mazurek, K.; Ryszard, P. Seismocardiography—A noninvasive method of assessing systolic and diastolic left ventricular function in ischaemic heart disease. Folia Cardiol. 2006, 13, 319–325. [Google Scholar]
- Di Rienzo, M.; Vaini, E.; Castiglioni, P.; Merati, G.; Meriggi, P.; Parati, G.; Faini, A.; Rizzo, F. Wearable seismocardiography: Towards a beat-by-beat assessment of cardiac mechanics in ambulant subjects. Auton. Neurosci. Basic Clin. 2013, 178, 50–59. [Google Scholar] [CrossRef] [PubMed]
- Castiglioni, P.; Faini, A.; Parati, G.; Di Rienzo, M. Wearable seismocardiography. In Proceedings of the 2007 29th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Lyon, France, 22–26 August 2007; pp. 3954–3957. [Google Scholar]
- Inan, O.T.; Etemadi, M.; Paloma, A.; Giovangrandi, L.; Kovacs, G.T.A. Non-invasive cardiac output trending during exercise recovery on a bathroom-scale-based ballistocardiograph. Physiol. Meas. 2009, 30, 261–274. [Google Scholar] [CrossRef] [PubMed]
- Di Rienzo, M.; Vaini, E.; Castiglioni, P.; Meriggi, P.; Rizzo, F. Beat-to-beat estimation of LVET and QS2 indices of cardiac mechanics from wearable seismocardiography in ambulant subjects. In Proceedings of the 2013 35th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Osaka, Japan, 3–7 July 2013; pp. 7017–7020. [Google Scholar]
- Taebi, A.; Mansy, H.A. Effect of Noise on Time-frequency Analysis of Vibrocardiographic Signals. J. Bioeng. Biomed. Sci. 2016, 6, 202. [Google Scholar] [CrossRef]
- Abbasi-Kesbi, R.; Valipour, A.; Imani, K. Cardiorespiratory System Monitoring Using a Developed Acoustic Sensor. Healthc. Technol. Lett. 2017. [Google Scholar] [CrossRef]
- Taebi, A.; Mansy, H.A. Noise Cancellation from Vibrocardiographic Signals Based on the Ensemble Empirical Mode Decomposition. J. Appl. Biotechnol. Bioeng. 2017, 2, 00024. [Google Scholar] [CrossRef]
- Sundar, A.; Pahwa, V. Evaluating the Performance of State of the Art Algorithms for Enhancement of Seismocardiogram Signals. In Proceedings of the First International Conference on Intelligent Computing and Communication; Springer: Singapore, 2017; pp. 37–45. [Google Scholar]
- Choudhary, T.; Sharma, L.N.; Bhuyan, M.K. Heart Sound Extraction from Sternal Seismocardiographic Signal. IEEE Signal Process. Lett. 2018, 25, 482–486. [Google Scholar] [CrossRef]
- Wu, Z.; Huang, N.E. Ensemble Empirical Mode Decomposition: A Noise-Assisted Data Analysis Method. Adv. Adapt. Data Anal. 2009, 1, 1–41. [Google Scholar] [CrossRef]
- Malcangi, M.; Quan, H.; Vaini, E.; Lombardi, P.; Di Rienzo, M. Applying the EFuNN Evolving Paradigm to the Recognition of Artefactual Beats in Continuous Seismocardiogram Recordings. In Proceedings of the 2017 International Conference on Engineering Applications of Neural Networks, Athens, Greece, 25–27 August 2017; pp. 256–264. [Google Scholar]
- Yang, C.; Tavassolian, N. Motion noise cancellation in seismocardiogram of ambulant subjects with dual sensors. In Proceedings of the 2016 IEEE 38th Annual International Conference of the Engineering in Medicine and Biology Society (EMBC), Orlando, FL, USA, 16–20 August 2016; pp. 5881–5884. [Google Scholar]
- Pouyan, M.B.; Dowling, S.; De Marco, T.; Klein, L.; Inan, O.T. Quantifying the Accuracy of Heart Failure Decompensation Classification Using Wearable Seismocardiography and Graph Mining Algorithms. J. Card. Fail. 2017, 23, S125–S126. [Google Scholar] [CrossRef]
- Yang, C.; Tavassolian, N. Motion noise cancellation in seismocardiographic monitoring of moving subjects. In Proceedings of the 2015 IEEE Biomedical Circuits and Systems Conference: Engineering for Healthy Minds and Able Bodies (BioCAS), Atlanta, GA, USA, 22–24 October 2015. [Google Scholar]
- Yang, C.; Tavassolian, N. An Independent Component Analysis Approach to Motion Noise Cancellation of Cardio-Mechanical Signals. IEEE Trans. Biomed. Eng. 2018. [Google Scholar] [CrossRef]
- Pandia, K.; Ravindran, S.; Cole, R.; Kovacs, G.; Giovangrandi, L. Motion artifact cancellation to obtain heart sounds from a single chest-worn accelerometer. In Proceedings of the 2010 ICASSP, IEEE International Conference on Acoustics, Speech and Signal Processing, Dallas, TX, USA, 14–19 March 2010; pp. 590–593. [Google Scholar]
- Taebi, A.; Mansy, H.A. Time-frequency Description of Vibrocardiographic Signals. In Proceedings of the 38th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Orlando, FL, USA, 16–20 August 2016. [Google Scholar]
- Taebi, A.; Mansy, H.A. Analysis of Seismocardiographic Signals Using Polynomial Chirplet Transform and Smoothed Pseudo Wigner-Ville Distribution. In 2017 IEEE Signal Processing in Medicine and Biology Symposium (SPMB); IEEE: Philadelphia, PA, USA, 2017; pp. 1–6. [Google Scholar]
- Zakeri, V.; Tavakolian, K. Identification of respiratory phases using seismocardiogram: A machine learning approach. In Proceedings of the 2015 Computing in Cardiology Conference, Nice, France, 6–9 September 2015; Volume 42, pp. 305–308. [Google Scholar]
- Poliac, M.O.; Zanetty, J.M.; Salerno, D.; Wilcox, G.L. Seismocardiogram (SCG) interpretation using neural networks. In Proceedings of the Fourth Annual IEEE Symposium on Computer-Based Medical Systems, Baltimore, MD, USA, 12–14 May 1991; pp. 288–295. [Google Scholar]
- Wahlstrom, J.; Skog, I.; Handel, P.; Khosrow-khavar, F.; Tavakolian, K.; Stein, P.K.; Nehorai, A. A Hidden Markov Model for Seismocardiography. IEEE Trans. Biomed. Eng. 2017. [Google Scholar] [CrossRef]
- Taebi, A. Characterization, Classification, and Genesis of Seismocardiographic Signals. Ph.D. Thesis, University of Central Florida, Orlando, FL, USA, 2018. [Google Scholar]
- Malcangi, M.; Quan, H.; Vaini, E.; Lombardi, P.; Di Rienzo, M. Evolving fuzzy-neural paradigm applied to the recognition and removal of artefactual beats in continuous seismocardiogram recordings. Evol. Syst. 2018, 1–10. [Google Scholar] [CrossRef]
- Neary, J.P.; MacQuarrie, D.S.; Jamnik, V.; Gledhill, N.; Gledhill, S.; Busse, E.F.G. Assessment of mechanical cardiac function in elite athletes. Open Sport. Med. J. 2011, 5, 26–37. [Google Scholar] [CrossRef]
- Giorgis, L.; Hernandez, A.I.; Amblard, A.; Senhadji, L.; Cazeau, S.; Jauvert, G.; Donal, E. Analysis of cardiac micro-acceleration signals for the estimation of systolic and diastolic time intervals in cardiac resynchronization therapy. In Proceedings of the 2008 Computers in Cardiology, Bologna, Italy, 14–17 September 2008; Volume 35, pp. 393–396. [Google Scholar]
- Etemadi, M.; Inan, O.T. Wearable Ballistocardiogram and Seismocardiogram Systems for Health and Performance. J. Appl. Physiol. 2017. [Google Scholar] [CrossRef] [PubMed]
- Sieciński, S.; Kostka, P. Determining Heart Rate Beat-to-Beat from Smartphone Seismocardiograms: Preliminary Studies. In Proceedings of the Conference on Innovations in Biomedical Engineering, Zabrze, Poland, 19–20 October 2017; pp. 133–140. [Google Scholar]
- Sahoo, P.K.; Thakkar, H.K.; Lee, M.Y. A cardiac early warning system with multi channel SCG and ECG monitoring for mobile health. Sensors 2017, 17, 711. [Google Scholar] [CrossRef]
- Mafi, M. Signal Processing Methods for Heart Rate Detection Using the Seismocardiogram. Ph.D. Thesis, University of Saskatchewan, Saskatoon, SK, Canada, 2016. [Google Scholar]
- Casacanditella, L.; Cosoli, G.; Casaccia, S.; Tomasini, E.P.; Scalise, L. Indirect measurement of the carotid arterial pressure from vibrocardiographic signal: Calibration of the waveform and comparison with photoplethysmographic signal. In Proceedings of the 2016 IEEE 38th Annual International Conference of the Engineering in Medicine and Biology Society (EMBC), Orlando, FL, USA, 16–20 August 2016; pp. 3568–3571. [Google Scholar]
- Casacanditella, L.; Cosoli, G.; Casaccia, S.; Rohrbaugh, J.W.; Scalise, L.; Tomasini, E.P. Characterization and calibration of the central arterial pressure waveform obtained from vibrocardiographic signal. In AIP Conference Proceedings; AIP Publishing: Melville, NY, USA, 2016; p. 050006. [Google Scholar]
- Verma, A.K.; Zanetti, J.; Fazel-Rezai, R.; Tavakolian, K. Pulse Transit Time Derivation using Xiphoidal and Carotid Seismocardiograms. In Proceedings of the 2017 Design of Medical Devices Conference, Minneapolis, MN, USA, 10–13 April 2017; p. V001T01A010. [Google Scholar]
- Peter, L.; Noury, N.; Cerny, M. A review of methods for non-invasive and continuous blood pressure monitoring: Pulse transit time method is promising? IRBM 2014, 35, 271–282. [Google Scholar] [CrossRef]
- Yang, C.; Tavassolian, N. Pulse transit time measurement using seismocardiogram and in-ear acoustic sensor. In Proceedings of the 2016 IEEE Biomedical Circuits and Systems Conference (BioCAS), Shanghai, China, 17–19 October 2016; pp. 188–191. [Google Scholar]
- Carek, A.M.; Conant, J.; Joshi, A.; Kang, H.; Inan, O.T. SeismoWatch: Wearable Cuffless Blood Pressure Monitoring Using Pulse Transit Time. Proc. ACM Interact. Mob. Wearable Ubiquitous Technol. 2017, 1, 40. [Google Scholar] [CrossRef]
- Lombard, W.P.; Cope, O.M. The duration of the systole of the left ventricle of man. Am. J. Physiol.-Legacy Content 1926, 77, 263–295. [Google Scholar] [CrossRef]
- Weissler, A.M.; Harris, W.S.; Schoenfeld, C.D. Systolic Time Intervals in Heart Failure in Man. Circulation 1968, 37, 149–159. [Google Scholar] [CrossRef] [PubMed]
- Pouymiro, I.R.; Cordova, E.V.; Perez, F.E.V. Robust Detection of AO and IM Points in the Seismocardiogram Using CWT. IEEE Lat. Am. Trans. 2016, 14, 4468–4473. [Google Scholar] [CrossRef]
- Tavakolian, K.; Khosrow-Khavar, F.; Kajbafzadeh, B.; Marzencki, M.; Blaber, A.P.; Kaminska, B.; Menon, C. Precordial acceleration signals improve the performance of diastolic timed vibrations. Med. Eng. Phys. 2013, 35, 1133–1140. [Google Scholar] [CrossRef] [PubMed]
- Benjamin, E.J.; Blaha, M.J.; Chiuve, S.E.; Cushman, M.; Das, S.R.; Deo, R.; de Ferranti, S.D.; Floyd, J.; Fornage, M.; Gillespie, G.; et al. Heart disease and stroke statistics—2017 update: A report from the American Heart Association. Circulation 2017, 135, e146. [Google Scholar] [CrossRef] [PubMed]
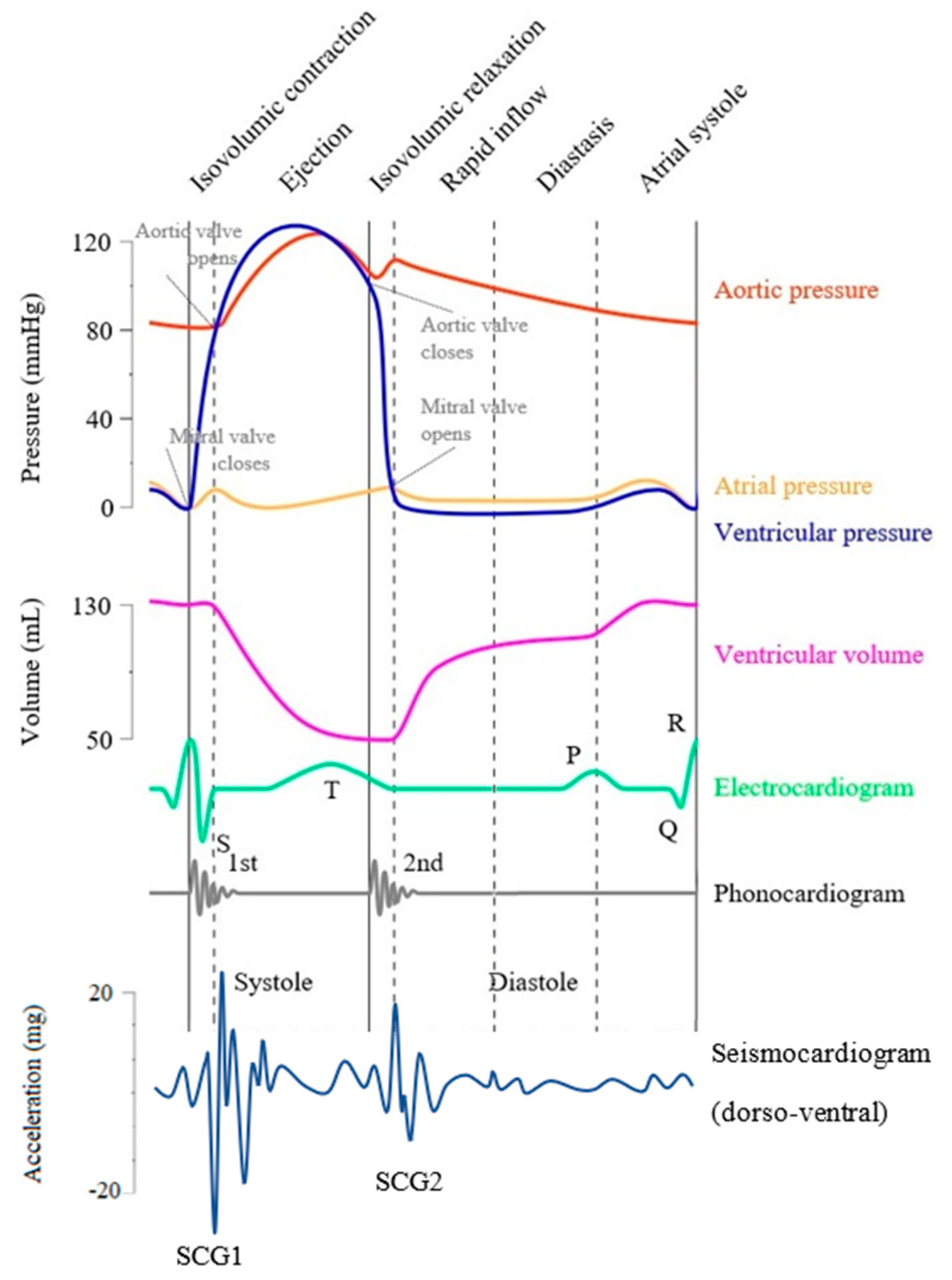
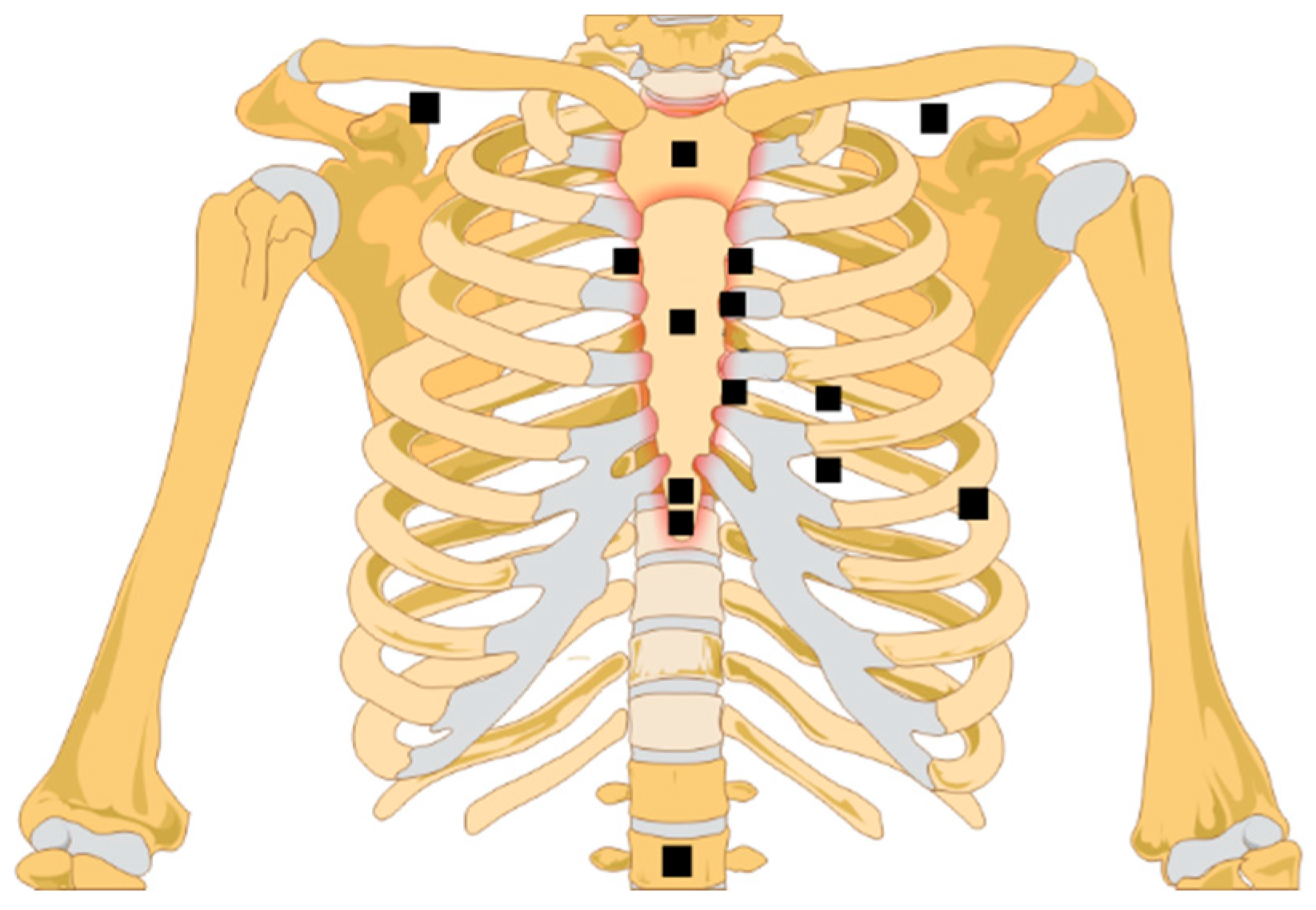

| Feature Point | Reference |
|---|---|
| Peak of atrial systole (AS) | [10,14,30] |
| Mitral valve closure (MC) | [10,14,28,30,31] |
| Peak of rapid systolic ejection (RE) | [10,14,30,32] |
| Peak of rapid diastolic filling (RF) | [10,14,30] |
| Isovolumic contraction (IC) | [10] |
| Mitral valve opening (MO) | [14,28,30,31] |
| Aortic valve closure (AC) | [14,28,30,31,32] |
| Aortic valve opening (AO) | [14,28,30,31,32,33] |
| Isovolumic movement (IM) | [14] |
| Rapid diastolic filling time | [14] |
| Isotonic contraction (IC) | [14] |
| Isovolumic relaxation time (IVRT) | [14,28,31] |
| Left ventricular ejection time (LVET) | [14,28,31,32] |
| Maximum acceleration in aorta (MA) | [28,32] |
| Pre-ejection period (PEP) | [28,31,32] |
| Total electromechanical systole period (QS2) | [28,31,32] |
| Maximum blood injection (MI) | [28] |
| Isovolumic contraction time (IVCT) | [28,31] |
| Left ventricular lateral wall contraction peak velocity (LCV) | [34] |
| Septal wall contraction peak velocity (SCV) | [34] |
| Trans-aortic peak flow (AF) | [34] |
| Trans-pulmonary peak flow (PF) | [34] |
| Trans-mitral ventricular relaxation flow (MFE) | [34] |
| Atrial contraction flow (MFA) | [34] |
| Reference | Sensor Type | Sensor Model | Sensor Location |
|---|---|---|---|
| [54,55,56] | 3-Acc | SCA610-C21H1A, Murata Electronic | 1 cm above xiphoid |
| [43,44] | 3-MEMS-Acc | MMA 7361, Freescale Semiconductor | Heart apex |
| [57] | 3-MEMS-Acc | MMA 7361, Freescale Semiconductor | Above xiphoid |
| [58] | 3-MEMS-Acc | Analog Devices | 2 cm above xiphoid |
| [36,38,45] | 3-MEMS-Acc 3-MEMS-Gyr | KXRB5-2042, Kionix MPU9150, Invensense | Left sternal border along the 3rd rib |
| [59] | 3-Acc | ViSi Mobile, Sotera Wireless | Chest wall |
| [60,61] | 1-Acc 1-Acc | 4381, Brüel & Kjær 393C, PCB Piezotronics | Above xiphoid |
| [62,63] | 1-Acc | DS1104, DSPACE | Xiphoid process |
| [64] | 3-Acc | ADXL 335, Analog Devices | Chest wall |
| [46] | 3-SP-Acc | iPhone6, Apple | Midclavicular line and 4th intercostal space Belly above navel |
| [65,66] | 3-Acc | 356A32, PCB Piezotronics | Left sternal border along the 4th intercostal space |
| [67] | 3-Acc | X6-2mini, GCDC | Left sternal border along the 4th intercostal space |
| [68] | 1-MEMS-Acc | SCA620, Murata Electronic | Sternum—anterior chest |
| [25,69,70] | 3-MEMS-Acc | MMA8451Q, Freescale Semiconductor | Sternum |
| [34,71] | 1-Acc | LIS331DLH, STMicroelectronics | Mitral valve, tricuspid valve, aortic valve, pulmonary valve |
| [72] | 3-MEMS-Acc | MMA 7361, Freescale Semiconductor | Left sternal border along the 3rd rib |
| [73] | 3-MEMS-Acc | MMA8451Q, Freescale Semiconductor | Sternum, aortic valve, heart apex |
| [74] | 3-Acc 1-Acc | CXL01LF3, Crossbow Technology 7290-A, Endevco Microtron | Manubrium Xiphoid |
| [75,76,77,78] | 3-Acc | BMA280, Bosch Sensortec GmbH | Mid-sternum |
| [79] | 3-MEMS-Acc | TSD109C, Biopac Systems | Left sternal border along the 3rd rib |
| [41] | 3-Acc | 356A32, PCB Piezotronics | Sternum, upper and lower sternum |
| [80] | 1-Acc | N/A | Sternum |
| [81] | 3-MEMS-Acc 3-Gyr | MMA8451Q, Freescale Semiconductor L3GD20, STMicroelectronics | N/A |
| [82] | 3-Acc | ADXL 335, Analog Devices | Mid-sternum, upper sternum, lower sternum Point of max impulse, below left clavicle, below right clavicle |
| [83] | 3-MEMS-Acc 3-MEMS-Gyr | SparkFun, Intel Edison | Sensor clipped on subjects clothes |
| [50,51] | Microwave Doppler radar | ||
| [47,48] | 3-SP-Acc | Xperia Z-series, Sony | Chest |
| [49] | Laser Doppler vibrometer | PDV-100, Polytec | |
| [37] | 3-MEMS-Acc 2-MEMS-Gyr | LIS344ALH, STMicroelectronics LPY403AL, STMicroelectronics | Heart apex Lower back of subject between 2nd and 3rd lumbar vertebrae |
| [31] | 3-MEMS-Acc 3-MEMS-ARS | MMA8451Q, Freescale Semiconductor MAX21000, Maxim Integrated | Sternum |
| [53] | AUSMC | Composed of the following sensors: - MA40S4S, Murata Electronics - FG-23629 Knowles microphone | ~30 × 40 cm2 thoracic and abdominal surface |
| Method | Application | Reference |
|---|---|---|
| low-, band-, high-pass, notch filtering | Baseline wandering, breathing and body movement artefact removal | [26,36,38,41,45,46,55,58,59,60,61,62,63,67,71,75,76,78,79,80,82,93] |
| Adaptive filtering | Motion artefact removal | [88,95] |
| Averaging theory | Motion artefact removal | [101] |
| Comb filtering | Removing respiration noise from radar signal | [50] |
| Empirical mode decomposition | Baseline wandering, breathing and body movement artefact removal | [76,94,95] |
| Independent component analysis | Motion artefact removal | [102] |
| Median filtering | [96] | |
| Morphological filtering | [95] | |
| Polynomial smoothing | Motion artefact removal | [103] |
| Savitzky–Golay filtering | Motion artefact removal | [83,103] |
| Wavelet denoising | Segmentation of HSs and SCG | [64,95,96] |
| Wiener filtering | [94] |
| SCG Features | Reference |
|---|---|
| Simple time domain | [47,61,81,82,107] |
| Statistical time domain | [41,56,65,106] |
| Simple frequency domain | [41,56] |
| Statistical frequency domain | [40,41,47,78] |
| Reference | ||
|---|---|---|
| Classification | NN | [107,109] |
| EFuNN | [98,110] | |
| SVM | [40,47,56,65,106,109] | |
| Random forest | [47,109] | |
| Logistic regression | [61] | |
| J48 decision tree | [41] | |
| Clustering | k-means | [109] |
| Regression | Xgboost | [82] |
| Graph-Similarity | k-NN graph | [78] |
| HMM | Viterbi sequence | [108] |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Taebi, A.; Solar, B.E.; Bomar, A.J.; Sandler, R.H.; Mansy, H.A. Recent Advances in Seismocardiography. Vibration 2019, 2, 64-86. https://doi.org/10.3390/vibration2010005
Taebi A, Solar BE, Bomar AJ, Sandler RH, Mansy HA. Recent Advances in Seismocardiography. Vibration. 2019; 2(1):64-86. https://doi.org/10.3390/vibration2010005
Chicago/Turabian StyleTaebi, Amirtahà, Brian E. Solar, Andrew J. Bomar, Richard H. Sandler, and Hansen A. Mansy. 2019. "Recent Advances in Seismocardiography" Vibration 2, no. 1: 64-86. https://doi.org/10.3390/vibration2010005
APA StyleTaebi, A., Solar, B. E., Bomar, A. J., Sandler, R. H., & Mansy, H. A. (2019). Recent Advances in Seismocardiography. Vibration, 2(1), 64-86. https://doi.org/10.3390/vibration2010005







