Abstract
A novel characterization method for discrete saw filters’ vibrational sensitivity is presented. The proposed approach allows the characterization of filters under vibrations and the extraction of a behavioural model. Filters are assumed to be transducers so that external induced vibrational energy is partially transformed in an undesired simultaneous amplitude and phase modulation of the input RF signal. When the filter is mechanically excited with vibrations, it introduces spurious amplitude and phase modulation to the input signal that can potentially affect the link quality.
1. Introduction
Filtering stages are fundamental blocks in all communication systems, from mobile terminals to complex aerospace and defence ones. When volumes and weights are limited and good electrical performance must be guaranteed, a plethora of new technologies seems available to the system designer. Surface Acoustic Wave (SAW) or Dielectric Resonator (DR) filters, for example, appear to be ideal candidates. A big concern arises when severe or very hard enviromental conditions have to be taken into account; such environments are well known in the aerospace and defence fields [1]. Besides high temperature variations there is a big concern about the presence of mechanical vibrations even at acoustic frequencies with very high pressure levels. Undesired phenomena generated by vibrations are well known also in crystal oscillators [2] where some fundamental figure of merit are currently available. Vibrational energy can affect the electrical performance of filtering stages, introducing spurious signal modulations that can degrade the RF link quality. In this paper, we proposed a novel characterisation method that can be used to model the vibration sensitivity of saw filters when subjected to vibrational energy.
2. General Theory and Characterization Technique
Induced phase noise characterisation methods as well vibration sensitivity figure of merit for filters [3,4] are available, but from these it is not easy to directly infer behavioural models of discrete microwave filters. Usually, manufacturers perform vibration and shock tests according to international standards [5,6,7] in order to certify that the devices meet electrical performance after the trials [8], but sometimes evidence of correct operation of the device is required during the application of the solicitation. A filter subjected to vibrations can be reasonably treated as a transducer so that external induced vibrational energy is partially transformed in simultaneous amplitude and phase modulation of the input RF or IF signal. The signal bandwidth is supposed to be much wider than the vibration induced modulation bandwidth. The theory of operation can be understood by referring to the test-bed reported in Figure 1. Using a compact complex envelope notation [9], the RF source generates an in-band CW (Continuous Wave) signal:
at node A of the circuit, where it is splitted in two paths: upper and lower. The signal in the upper path flows through the filter where emerges modulated both in amplitude and phase due to the vibrational energy as:
with . The signal in the lower path flows in a through-line and recombines with the signal coming form the upper path in an isolated RF combiner. The signals flow is regulated by two couples of SPDTs (Single Pole Double Throw) in order to provide high isolations level: the first couple controls the upper path; the second couple controls the lower path. Each couple of SPDT is driven by a dedicated driver. The signal from the output RF combiner is injected in a zero bias schottky detector whose output signal, being eventually conveniently amplified by a low noise stage, is acquired. A dedicated fixture is designed and fixed to the shaker to allow vibration tests to be performed. The filter, generally available in a SMT package (Surface Mount Technology), is soldered over a microstrip circuit with dedicated input and output connectors. A microstrip through line is located near the filter with its own input and output connectors. So, two input ports and two output ports are available on the test jig, each circuit is independent from the other but both shares the same vibrational energy. Following the scheme, it is possible to note that the jig, fixed to the shaker, is connected to the isolated RF power divider and combiner using phase invariant coaxial cables so that when the SPDTs are driven as in Figure 2, it is possible to identify an upper and lower path, where the input signal is first splitted and then recombined. Using the superposition principle, the input signal to the power detector due to the upper path is:
where:
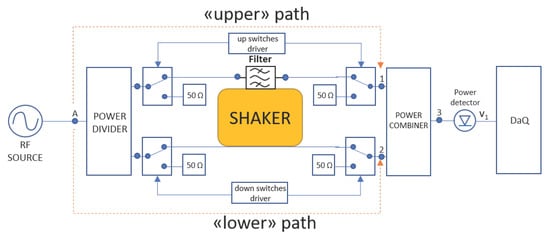
Figure 1.
Characterisation set-up.
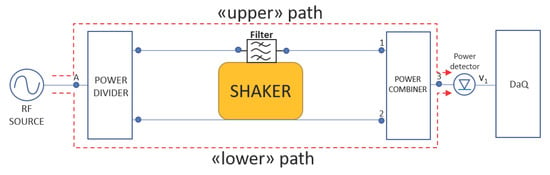
Figure 2.
General characterisation set-up.
- is the transmittance from port A to port 3 through the upper path when there is no vibration
- is the instantaneous transmittance of the filter under vibrations and is a real valued function.
While the input signal to the power detector due to the lower path is:
where:
- is the transmittance from port A to port 3 through the lower path when there is no vibration
- is the instantaneous transmittance of the microstrip line under vibration, being a real valued function.
So, the recombined output signal arising from the RF combiner can be put in the form:
this signal is injected in a zero bias schottky detector, whose output signal is of the form:
where is the detector’s sensitivity and the instantaneous power of the RF input signal. When the system is under vibration, the instantaneous output signal is:
while, when no vibrational energy is injected to the system:
so, , is time independent. If the filter’s microphonicity is negligible, the output signal is constant. If the microstrip circuit, that’s part of the lower path, can be assumed to be quite insensible to vibrations, it is possible to simplify the output signal as:
now, when the SPDT couple of the down path is driven in order to open the signal’s flow, the test-bed is equivalent to Figure 3.
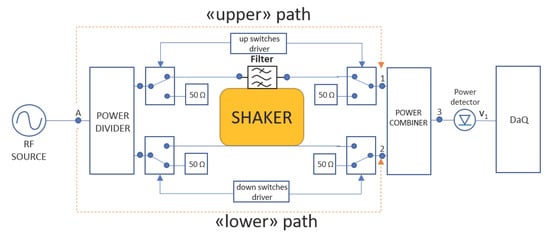
Figure 3.
Characterisation set-up with lower path opened.
The output signal, under vibration, is:
while, in static conditions:
when the SPDT couple of the upper path is driven in order to open the signal’s flow, the test-bed is equivalent to that reported in Figure 4.
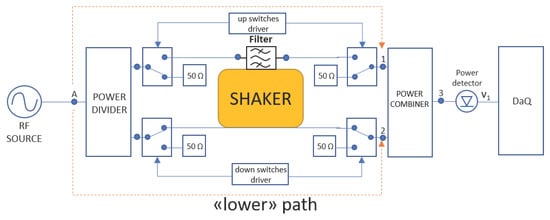
Figure 4.
Characterisation set-up with upper path opened.
The output signal, under vibration and in static condition, is:
so the filter amplitude modulation, if present, constitutes the signal:
If the DC component is prevalent, then the amplitude modulation is negligible and . Under these conditions the signals: , , are DC voltages and the phase induced modulation function is recoverable from the output signal:
apart from a constant phase term . The vibration induced phase modulation is transformed in a amplitude modulation of the low frequency signal , so a wise choice of the phase term allows to maximize the signal’s dynamic range. If the low signal phase difference between upper and lower paths with , than the slope of the cosine function in Equation (14) is maximized. Changing the vibrational sine frequency, it is possible to extract the relative induced phase modulation and the characterization process can be fully automated.
2.1. System Simulation and Validation
The theoretical approach has been validated through RF system simulations using NI AWR VSS Visual System Simulator™ [10] and MATLAB® [11]. The NI AWR VSS schematic is reported in Figure 5 and includes, in a more detailed form, the characterisation set-up depicted in Figure 3 and Figure 4.
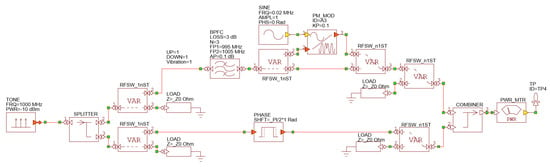
Figure 5.
Characterisation set-up VSS system model.
A signal generator injects a −10 dBm CW tone at 1 GHz into a power divider where it is divided in two branches. The upper path contains an RF filter, in this case a 3 poles, 10 MHz bandwidth Bandpass Chebyshev type 1 filter with an insertion loss of 3 dB, followed by a phase modulator that represents the induced phase modulation due the vibrational energy. The vibration induced phase modulating signal is a 20 KHz unit amplitude sine wave injected in a phase modulator with a phase sensitivity coefficient . The presence or absence of vibrations and the path selection is performed by dedicated SPDTs whose insertion loss take into account the additional losses introduced by the cables also. The lower path contains the dedicated branch selection SPDTs, cable and a RF phase shifter. The signals arising from the upper and lower paths are injected in a RF combiner whose output port is terminated in a power detector. The low frequency signal from the power detector, described by Equation (14) is reported in Figure 6, the same signal exctracted using the Matlab model is reported in Figure 7 with an excellent agreement between both models. The induced phase modulating signal and the recovered signal are depicted in Figure 8.
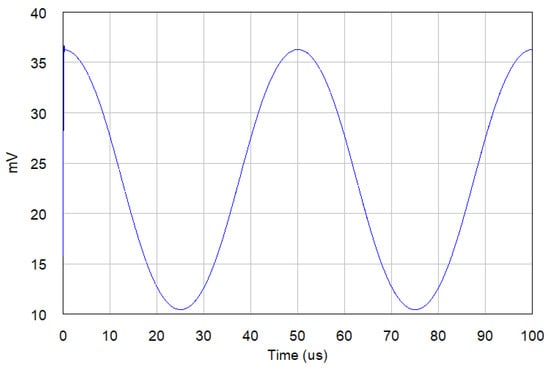
Figure 6.
Low frequency signal from power detector (VSS model) with .
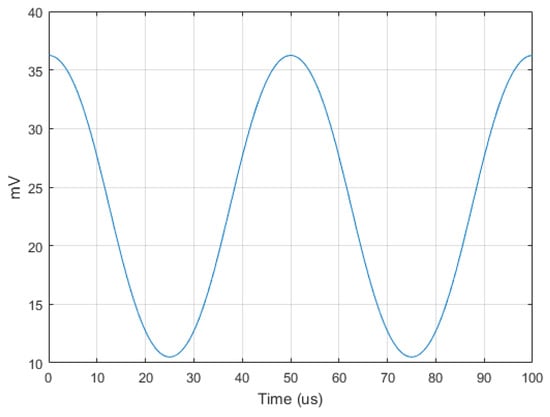
Figure 7.
Low frequency signal from power detector (Matlab) with .
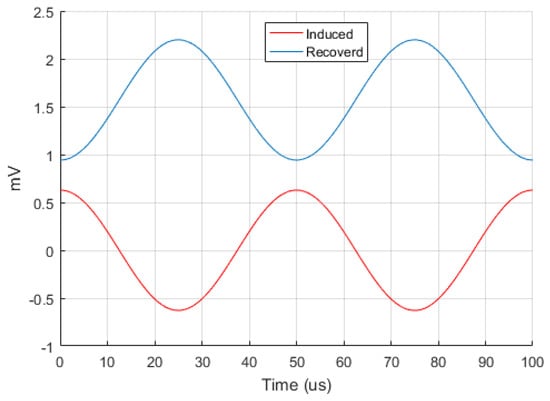
Figure 8.
Induced phase noise modulating signal and recovered with .
2.2. Extension to Weak Time-Dependent Amplitude Modulation Case
If the induced amplitude modulation is time-dependent, a signal processing approach can be adopted in order to extract the induced phase modulation. If a more precise technique can be exploited, deleting the DC terms in (9) in post-processing. In fact, looking at Figure 9, if a generic low pass signal: is injected in a hard limiter, the corresponding output signal can be put in the form:
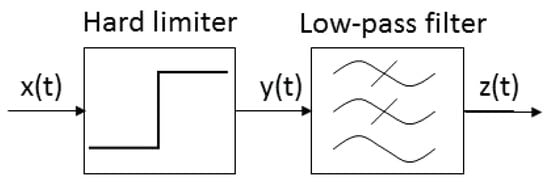
Figure 9.
Signal Processing Approach for Induced Phase Modulation Extraction.
The function y(t) is periodic in , so the corresponding Fourier series expansion can be written as:
with coefficients:
a low-pass filter eliminates the high order harmonics so that
this allows to easily extract the phase induced modulation function.
3. High Induced Amplitude Modulation Case
When the induced amplitude modulation function is not negligible, it is necessary to modify the test-bed in order to be able to extract the phase and the amplitude modulating functions. To this purpose, the output RF combiner is replaced by a 180° hybrid where two different power detectors are connected to the and ports. The output signals arising from the power detectors, eventually conveniently amplified by low noise stage amplifiers, are injected in a simultaneous sampling DaQ (Data Acquisition device). Looking at Figure 10, if the RF source generates a signal of the form (1), the signals arising from the power detectors are:
where are the modules of the trasmittances of the 180° hybrid and are the modules of the trasmittances of the upper path from node A to node 1 and lower path from node A to node 2 respectively. In general, the detectors sensitivity coefficients k and k, the parameters S, S, S, S are different, even slightly, from each other. Opening the upper path in static conditions (no vibrations), the output voltages from the detectors are constants, respectively equal to:
closing the upper path, while opening the lower, the output voltages from the detectors are constants and respectively equal to:
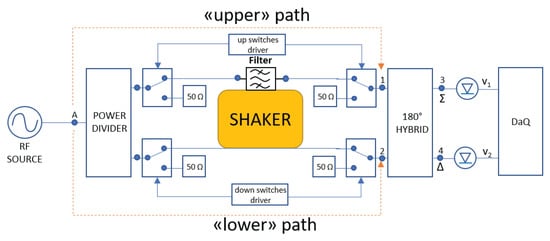
Figure 10.
Extended characterisation set-up.
Variables A,B,C,D have been introduced only to simplify the expressions in static conditions and allow compact notations. When vibrations are present, and both upper and lower paths are closed, the signals from the detectors are time dependent and respectively equal to:
after some algebraic manipulations, it is possible to write:
while the phase induced modulation is:
where are constant and vibration independent phase terms.
System Simulation and Validation
This characterisation method, as the simpler described before, has been validated through RF system simulations. The NI AWR VSS schematic is reported in Figure 11 and includes, in a more detailed form, the characterisation set-up depicted in Figure 10.
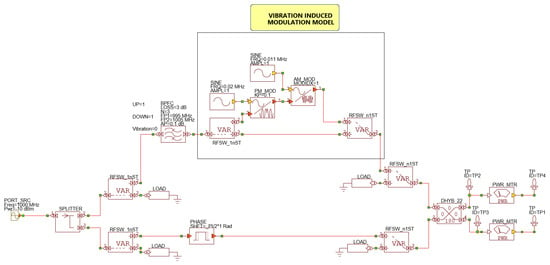
Figure 11.
Extended characterisation set-up.
The first part of the scheme is similar to that reported in Figure 5 with two main differences: after the RF filter there are two separated amplitude and phase modulators, each of these modulates the RF signal indipendently from the other with different modulation frequencies and modulation indices. The signal travelling the upper path and that travelling the lower path recombines into a 180° hybrid coupler. The and output signals are then injected in two RF power detectors whose output voltages have been stored and processed. The vibration induced phase modulating signal is a 20 KHz unit amplitude sine wave injected in a phase modulator with a phase sensitivity coefficient . The vibration induced amplitude modulating signal is a 11 KHz unit amplitude sine wave injected in a amplitude modulator with a normalized sensitivity coefficient . The amplitude and phase modulating frequencies are not harmonically related and have been choosen different in order to verify the correct recover of both. The output voltages from the power detectors and under vibrations are reported in Figure 12 while the induced amplitude modulating signal and the one recovered are reported in Figure 13.
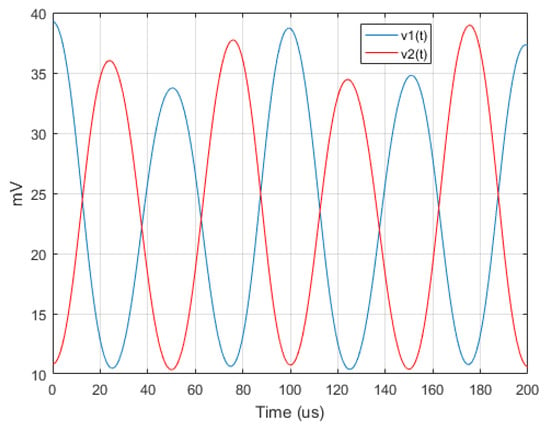
Figure 12.
Low frequency signals from power detectors with .
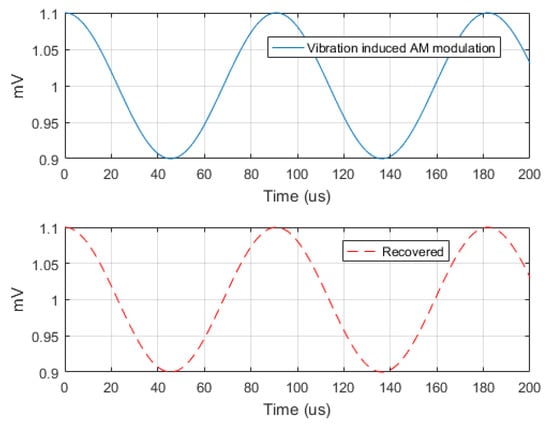
Figure 13.
Vibration induced amplitude modulating signals with .
The induced phase modulating signal and the one recovered are reported in Figure 14.
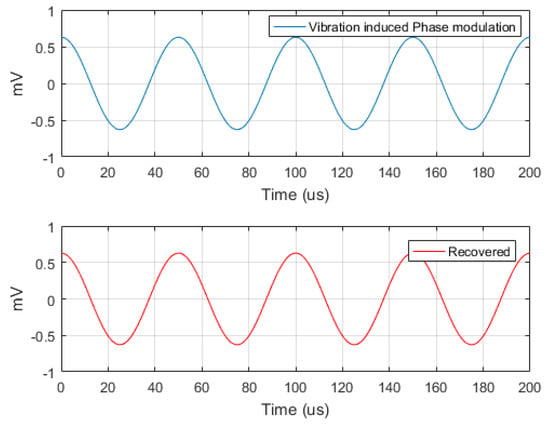
Figure 14.
Vibration induced phase modulating signals with .
For a fixed vibrational frequency, a change of the vibrational energy is modeled as a corresponding change of phase and amplitude modulation indices. If the amplitude and phase modulation indices are raised to and respectively, the output voltages from the power detectors and are reported in Figure 15.
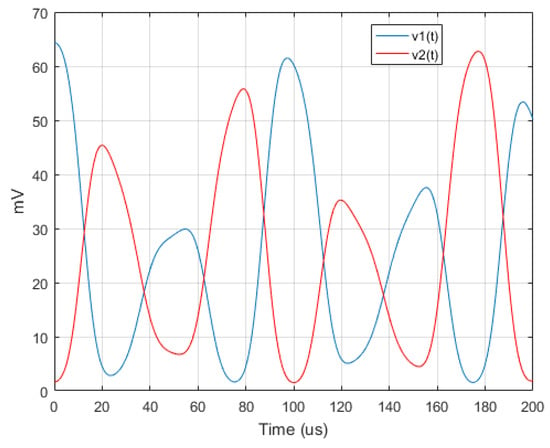
Figure 15.
Low frequency signals from power detectors with and .
The induced amplitude and phase waveforms and the recovered signals are reported in Figure 16 and Figure 17.
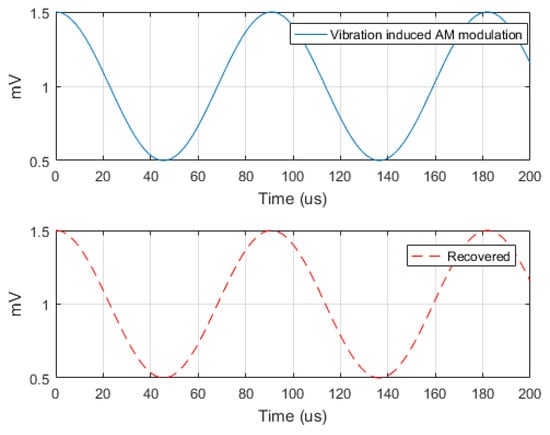
Figure 16.
Vibration induced amplitude modulating signals and .
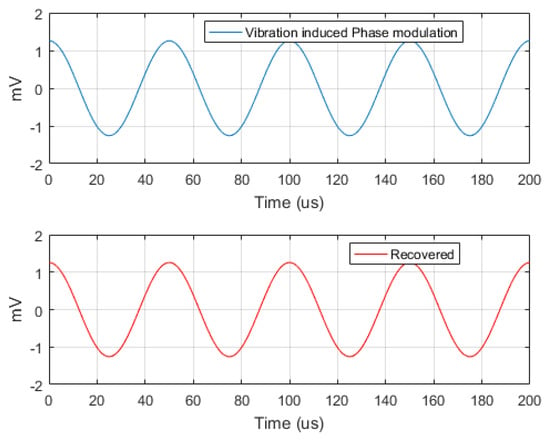
Figure 17.
Vibration induced phase modulating signals and .
It is noteworthy that the quantities: can be frequency dependent, but all of them can be characterized in the frequency domain, if necessary. The quantities are also allowed to be temperature-dependent as these are directly related to the transmittance of the filter under test. Moreover, the proposed method does not require a sinusoidal vibrational spectrum in order to extract the amplitude and phase induced modulations, but it can be theoretically arbitrary.
4. System Sensitivity Considerations
All the schemes discussed in previous sections works at high Signal to Noise Ratios by design, insertion losses of the devices are quite small even that of SAW filters (usually dB). The input signal is provided by a RF source with a very high SNR (Signal to Noise Ratio) while power detectors operate with signal levels dB higher their typical tangential sensitivity [12]. Limiting the analysis to the induced phase modulation recovering, it is possible to focus the attention to Equation (14) reported below for convenience, in order to derive some considerations.
If the term , than it is possible to write
the induced phase modulation can be assumed to be , being the vibration frequency. As vibrational induced phase modulation comes from low frequency mechanical excitation (sometimes up to acoustic frequencies), it is reasonable to suppose [13] that the bandwidth of the signal (29) is limited to KHz. The estimated SNR at the output port of the RF combiner (or the output ports of the 180° hybrid) is reported in Figure 18. It can be assumed that the low frequency signal, acquired by the DaQ, is mainly contaminated by thermal noise coming from the RF section and by the intrinsic thermal noise of the device. The noise power from RF stages is −124 dBm corresponding to a RMS noise voltage μV. The RMS noise voltage of a DaQ is tipically much higher. For example, the National Instruments 6356 [14] in the smallest input voltage range, is characterized by a RMS noise voltage μV, so it is prevalent over the contribution due the RF section.
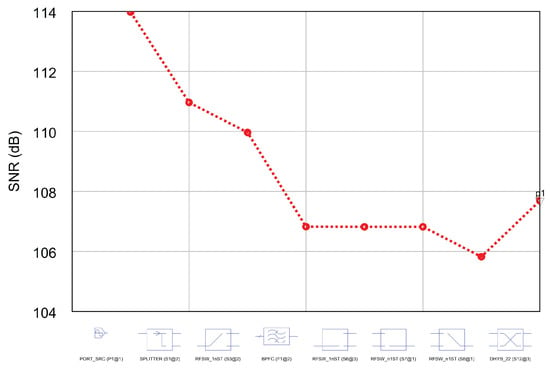
Figure 18.
SNR at the output ports of the 180° hybrid.
Small values of push the system to the limit of sensibility as tends to a DC value, but at the same time, makes the filter able to operate in a severe environment. If is small, it is possible to approximate the sine function in Equation (30)
the signals measured experimentally can be written as:
where ,, are indipendent zero-mean gaussian noise components having the same standard deviation . As we searching for the minimum detectable phase modulation index , the problem is reduced to the estimation of the amplitude of the induced modulating tone at the vibrational frequency . In fact, it is possible to write
being n a gaussian noise contribution with power . In this case, a powerful tool is represented by the FFT (Fast Fourier Transform). If the DaQ operates at a sample frequency of Hz and N samples are acquired for each signal, the FFT of the signal reported in Equation (35) generates points in the frequency domain where every frequency "bin" is Hz wide. A Matlab simulation has been used to estimate the parameter with a relative error in order to define the minimum detectable phase sensitivity coefficient . The vibrational frequency has been set KHz with a DaQ sample frequency MHz. The effective system where is the signal power and the processing gain of the FFT. The magnitude of the spectrum at the frequency “bin” corresponding to the vibrational frequency has been calculated while sweeping the parameter , thus changing the SNR of the system and determining the relative error; the procedure has been iterated in order to obtain a distribution of the error. Some amplitude spectra are reported in Figure 19 for different values of while in Figure 20 is reported the estimated probability density function (pdf) of the relative error (nearly gaussian) corresponding to the identified minimum detectable .
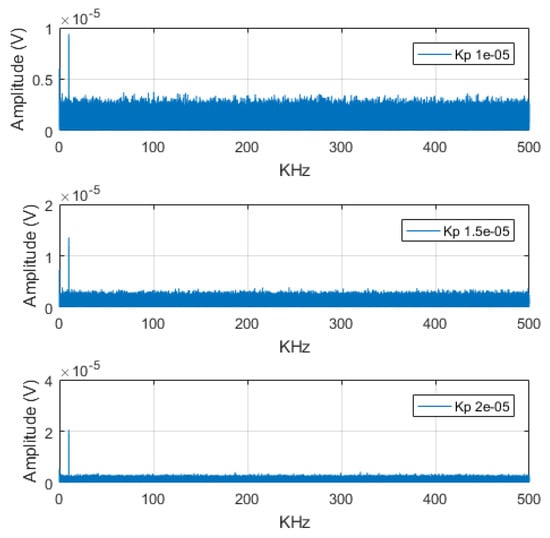
Figure 19.
Amplitude spectra of signal (35) for different values of .
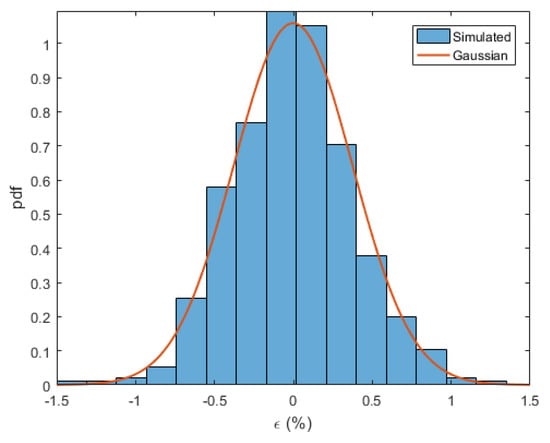
Figure 20.
Probability density function estimation and gaussian fit of the relative error distribution.
From simulations it has been found a minimum detectable phase sensitivity coefficient rad/V with relative errors within .
5. Conclusions
In this paper, we derived low-cost characterisation techniques for discrete filters under vibrations. The method allows the extraction of both the vibration induced amplitude and phase modulation using scalar measurements only. The first technique requires few components, but is suitable for filters that exhibit negligible amplitude induced modulation. The second, more powerful and general technique requires two independent power detectors that do not have to be matched. It is noteworthy that the proposed characterization methodology is theoretically inherently robust against the RF generator phase noise. The signals extracted by the RF power detectors depends on the difference between the phases of the upper and the lower paths thus erasing spurious contribution coming before the first power divider. The proposed approaches allow us to characterize a microwave filter under vibrations, but also to derive behavioural models that can be used to simulate a RF chain where vibrational induced phenomena are taken into account.
Acknowledgments
Theoretical analysis has been developed within Seekers Division.
Conflicts of Interest
The author declares no conflict of interest.
References
- MIL-STD-810G: Environmental Engineering Considerations and Laboratory Tests. Department Of Defence Test Method Standard. 2014. Available online: https://snebulos.mit.edu/projects/reference/MIL-STD/MIL-STD-810G.pdf (accessed on 27 February 2018).
- Filler, R.L. The acceleration sensitivity of quartz crystal oscillators: A review. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 1988, 35, 297–305. [Google Scholar] [CrossRef] [PubMed]
- Hati, A.; Nelson, C.W.; Howe, D.A. Vibration-Induced PM and AM Noise in Microwave Components. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2009, 56, 2050–2059. [Google Scholar] [CrossRef] [PubMed]
- Hati, A.; Nelson, C.W.; Howe, D.A.; Ashby, N.; Taylor, J.; Hudek, K.M.; Hay, C.; Seidel, D.; Eliyahu, D. Vibration Sensitivity of Microwave Components. In Proceedings of the 2007 IEEE International Frequency Control Symposium Joint with the 21st European Frequency and Time Forum, Geneva, Switzerland, 29 May–1 June 2007; pp. 541–546. [Google Scholar]
- Locke, S.; Sinha, B.K. Acceleration and Vibration Sensitivity of SAW Devices. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 1987, 34, 29–38. [Google Scholar]
- International Electrotechnical Commission. IEC 60068-2-6:2007: Environmental Testing—Part 2-6: Tests—Test Fc: Vibration (sinusoidal), 7th ed.; International Electrotechnical Commission: Geneva, Switzerland, 2007. [Google Scholar]
- International Electrotechnical Commission. IEC-60068-2-27:2008: Environmental Testing—Part 2-27: Tests—Test Ea and Guidance: Shock, 4th ed.; International Electrotechnical Commission: Geneva, Switzerland, 2008. [Google Scholar]
- MIL-STD 801G: Test Method Standard, Environmental Engineering Considerations and Laboratory Tests. 2008. Available online: http://everyspec.com/MIL-STD/MIL-STD-0800-0899/download.php?spec=MIL-STD-810G.00002212.PDF (accessed on 27 February 2018).
- Miller, S.L.; Childers, D.G. Probability and Random Processes: With Applications to Signal Processing and Communications; Academic Press: Cambridge, MA, USA, 2012. [Google Scholar]
- National Instruments AWR VSS. Available online: http://www.awrcorp.com/products/ni-awr-design-environment/visual-system-simulator (accessed on 27 February 2018).
- Matlab. Available online: https://www.mathworks.com/products/matlab.html (accessed on 27 February 2018).
- Rao, R.S. Microwave Engineering; PHI Learning Pvt. Ltd.: Delhi, India, 2015. [Google Scholar]
- Rao, R.S. Communication Systems; Tata McGraw-Hill Education: New York City, NY, USA, 2013. [Google Scholar]
- National Instruments 6356 DaQ. Available online: http://www.ni.com/nisearch/app/main/p/ap/tech/lang/en/pg/1/sn/ssnav:spc/aq/pmdmid:124938/ (accessed on 27 February 2018).
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).