Canopy Fuel Characteristics and Potential Fire Behavior in Dwarf Pine (Pinus pumila) Forests
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Field Sampling
2.3. Calculation of Canopy Fuel Load and Canopy Bulk Density
2.4. Calorific Value Determination of Fuels
2.5. Construction of the Allometric Equation for Canopy Fuel in Dwarf Pine
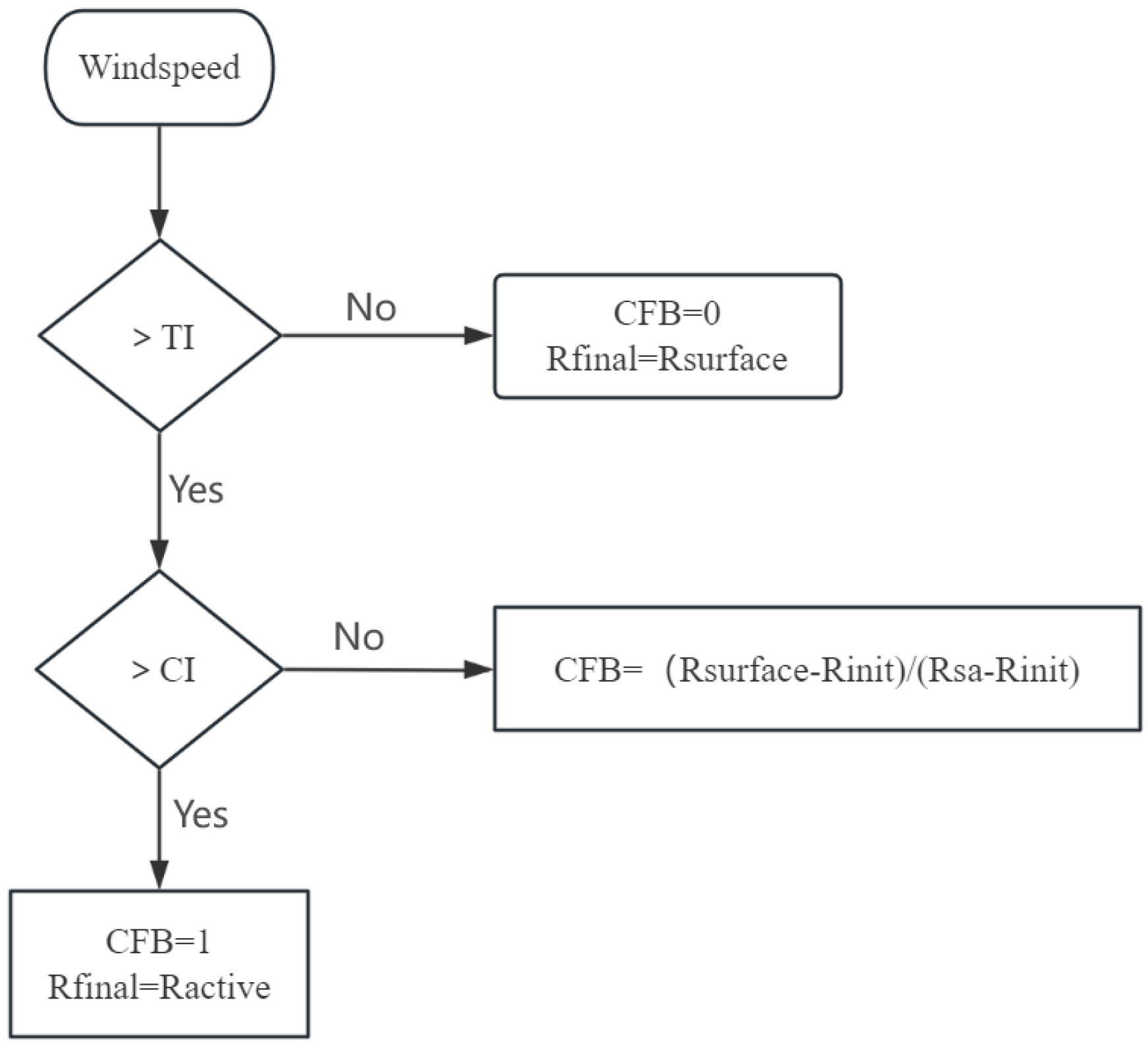
2.6. Calculation of Potential Fire Behavior Parameters
3. Results
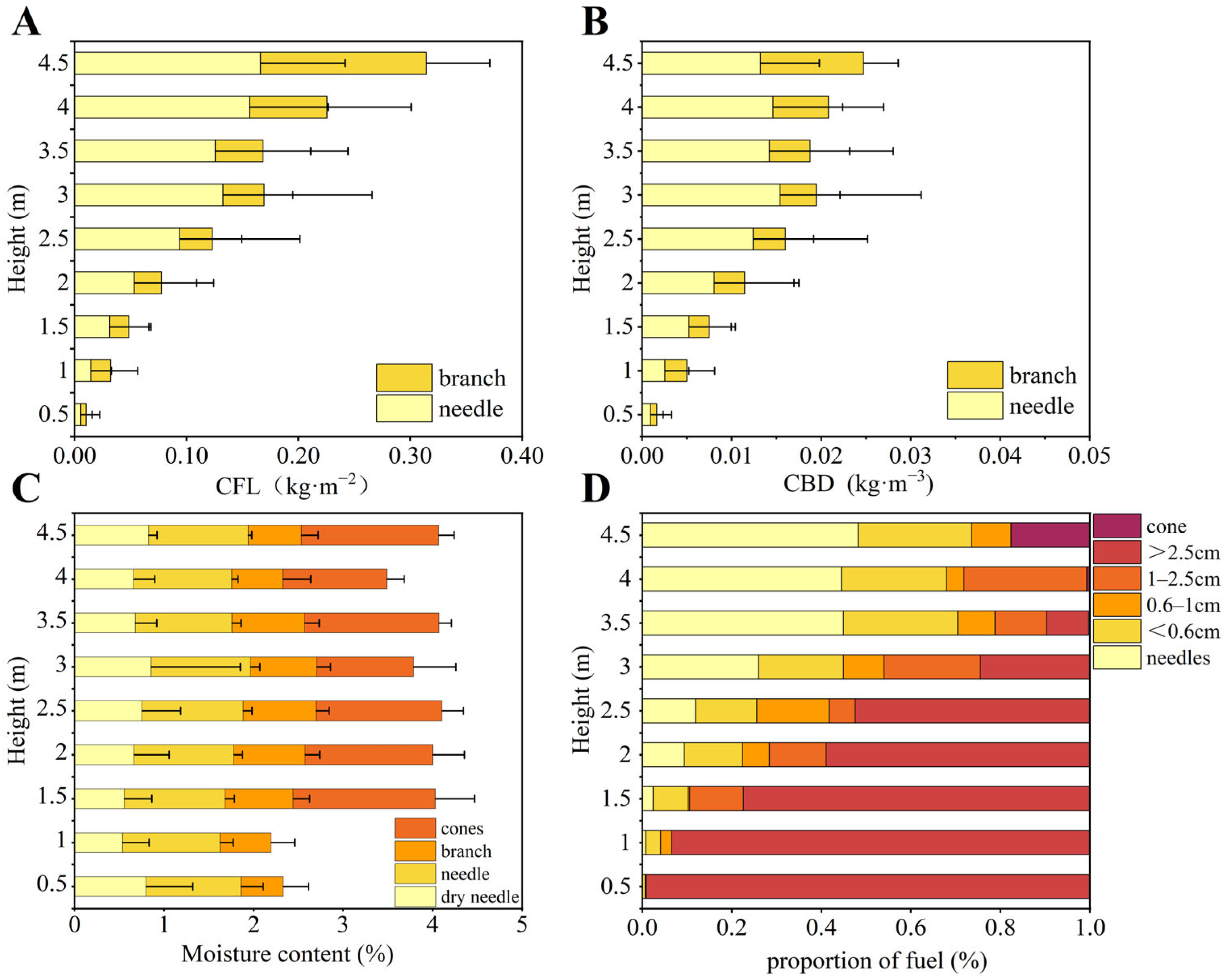
3.1. Analysis of the Vertical Distribution of Dwarf Pine Canopy Fuel
3.2. Construction of the Canopy Fuel Model for Dwarf Pines
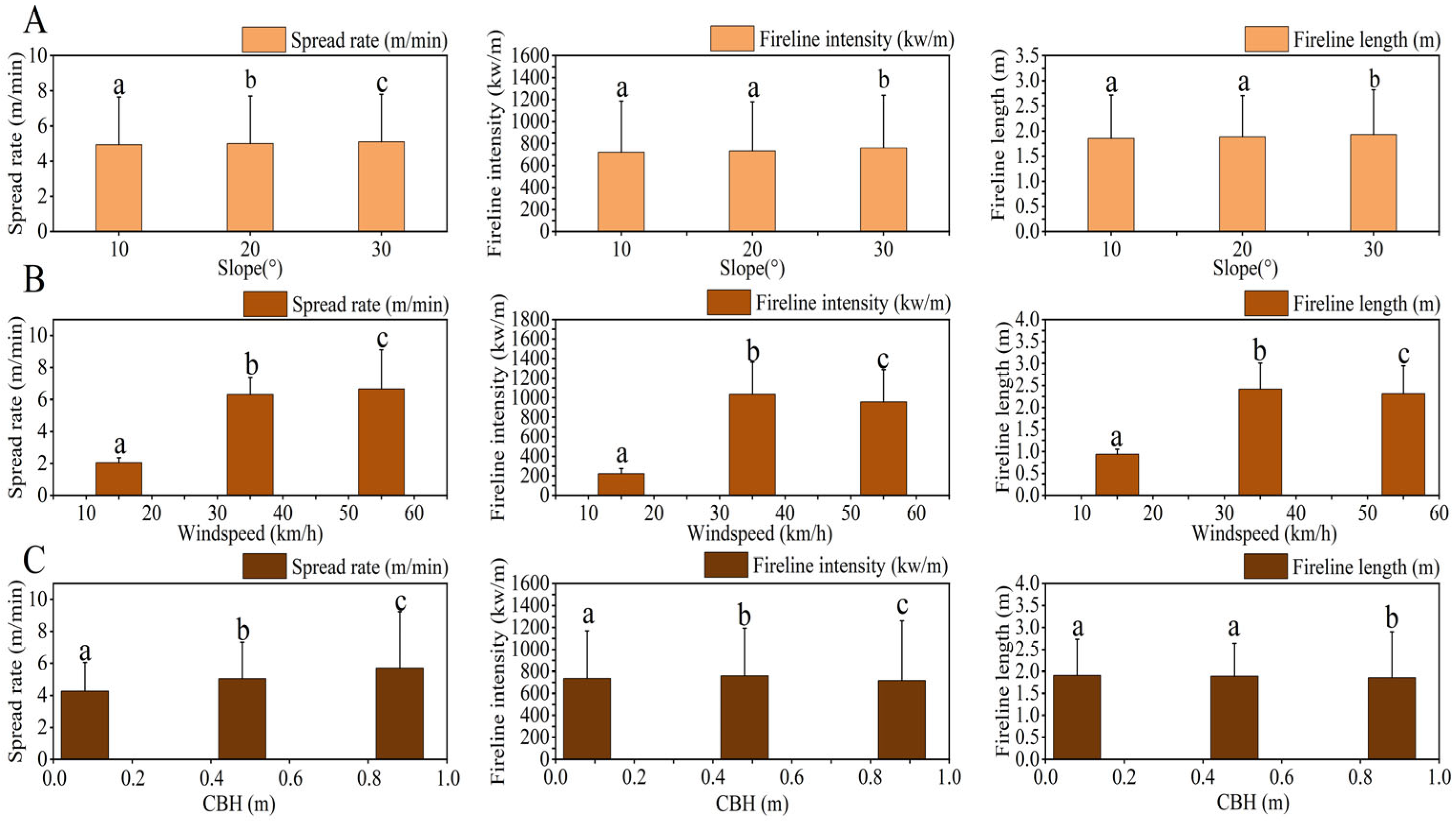
3.3. Potential Fire Behavior of Dwarf Pines
4. Discussion
4.1. Characteristics of Available Canopy Fuel Distribution
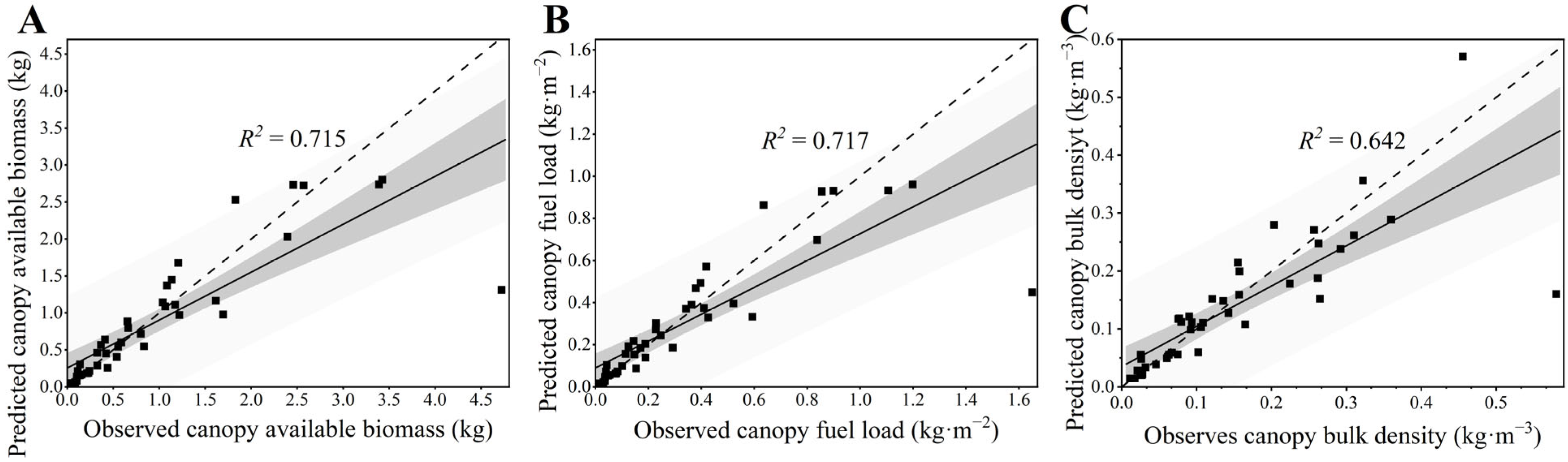
4.2. Assessment of Available Canopy Biomass, CFL, and CBD Equations
4.3. Analysis of the Potential Fire Behavior of Dwarf Pine
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lv, Q.C.; Chen, Z.Y.; Wu, C.Y.; Peuelas, J.; Fan, L.; Su, Y.X.; Yang, Z.Y.; Li, M.C.; Gao, B.B.; Hu, J.Q.; et al. Increasing severity of large-scale fires prolongs the recovery time of forests globally since 2001. Nat. Ecol. Evol. 2025, 9, 980–992. [Google Scholar] [CrossRef] [PubMed]
- Chebykina, E.; Polyakov, V.; Abakumov, E.; Petrov, A. Wildfire Effects on Cryosols in Central Yakutia Region, Russia. Atmosphere 2022, 13, 1889. [Google Scholar] [CrossRef]
- Han, Y.L.; Li, X.Y.; Cai, H.Y.; Liu, J.; Chen, K. The impact of wildfire on soil carbon and nitrogen storage in permafrost regions of the Greater Khingan. J. Glaciol. Geocryol. 2024, 46, 1341–1355. [Google Scholar] [CrossRef]
- Wang, J.; Du, Y.L.; Gao, Z.; Lv, H.Y.; Shi, L. Exploring the spatio-temporal variations and forest restoration of burned zones in the Great Xing’an Range based on MODIS time series data. Remote Sens. Nat. Resour. 2024, 36, 142–150. [Google Scholar] [CrossRef]
- Liu, J.X.; Li, R.; Wang, H. Analysis of the spatiotemporal dynamics of forest fires in major forest regions of China. J. Hubei Univ. (Nat. Sci. Ed.). 2024, 46, 809–819. [Google Scholar] [CrossRef]
- Shu, L.F.; Wang, M.Y.; Li, Z.Q.; Xiao, Y.J.; Tian, X.R. Study on the fire environment of dwarf pine forests in the Greater Khingan Mountains. Mt. Res. 2004, 22, 36–39. [Google Scholar] [CrossRef]
- Zhao, F.J.; Shu, L.F.; Wang, M.Y.; Tiao, X.R. Emissions of volatile organic compounds from heated needles and twigs of Pinus pumila. J. For. Res. 2011, 22, 243–248. [Google Scholar] [CrossRef]
- Jiang, M.X. Preliminary studies on the distribution and growth of dwarf pine in the Greater Khingan Region. Sci. Silvae Sin. 1982, 18, 203–205. [Google Scholar]
- Zhuang, H.X.; Liu, Q.J.; Meng, S.W.; Jia, Q.Q.; Deng, L.B. Biomass model for individual dwarf pine trees in the Mangui Area. J. Northeast. For. Univ. 2015, 43, 97–101. [Google Scholar] [CrossRef]
- Cruz, M.G.; Alexander, M.E.; Wakimoto, R.H. Development and testing of models for predicting crown fire rate of spread in conifer forest stands. Can. J. For. Res. 2005, 35, 1626–1639. [Google Scholar] [CrossRef]
- Keanea, R.E.; Burgana, R.; Wagtendonkb, J.V. Mapping wildland fuels for fire management across multiple scales: Integrating remote sensing, GIS, and biophysical modeling. Int. J. Wildland Fire 2001, 10, 301–319. [Google Scholar] [CrossRef]
- Cameron, H.A.; Díaz, G.M.; Beverly, J.L. Estimating canopy fuel load with hemispherical photographs: A rapid method for opportunistic fuel documentation with smartphones. Methods Ecol. Evol. 2021, 12, 2101–2108. [Google Scholar] [CrossRef]
- Stocks, B.J.; Alexander, M.E.; Wotton, B.M.; Stefner, C.N.; Flannigan, M.D.; Taylor, S.W.; Lavoie, N.; Mason, J.A.; Hartley, G.R.; Dalrymple, G.N.; et al. Crown fire behaviour in a northern jack pine-black spruce forest. Can. J. For. Res. 2004, 34, 1548–1560. [Google Scholar] [CrossRef]
- Keyes, R.C.; O’Hara, L.K. Quantifying Stand Targets for Silvicultural Prevention of Crown Fires. West. J. Appl. For. 2002, 17, 101–109. [Google Scholar] [CrossRef]
- Fo, E. Development and structure of the Canadian Forest Fire Behavior Prediction System; Forestry Canada, Headquarters, Fire Danger Group and Science and Sustainable Development Directorate: Ottawa, ON, Canada, 2002; p. 64.
- Finney, M.A. FARSITE: Fire Area Simulator-Model Development and Evaluation; Research Paper; Department of Agriculture, Forest Service, Rocky Mountain Research Station: Ogden, UT, USA, 1998. Available online: https://www.fs.usda.gov/rm/pubs/rmrs_rp004.pdf (accessed on 27 July 2025).
- Byram, G.M. Combustion of forest fuels. For. Fire Control. Use 1959, 61–89. [Google Scholar]
- Scott, J.H.; Reinhardt, E.D. Assessing Crown Fire Potential by Linking Models of Surface and Crown Fire Behavior; Research Paper; Rocky Mountain Research Station: Fort Collins, CO, USA, 2001. Available online: https://research.fs.usda.gov/treesearch/4623 (accessed on 27 July 2025).
- Ruiz-González, A.D.; Álvarez-González, J.G. Canopy bulk density and canopy base height equations for assessing crown fire hazard in Pinus radiata plantations. Can. J. For. Res. 2011, 41, 839–850. [Google Scholar] [CrossRef]
- Wang, M.J.; Sun, R.; Xiao, Z.Q. Estimation of Forest Canopy Height and Aboveground Biomass from Spaceborne LiDAR and Landsat Imageries in Maryland. Remote Sens. 2018, 10, 344. [Google Scholar] [CrossRef]
- Kucuk, O.; Saglam, B.; Bilgili, E. Canopy fuel characteristics and fuel load in Young Black Pine trees. Biotechnol. Biotechnol. Equip. 2007, 21, 235–240. [Google Scholar] [CrossRef][Green Version]
- Smith, F.W.; Keyser, T.; Shepperd, W. Estimating canopy fuels and their impact on potential fire behavior for ponderosa pine in the Black Hills, South Dakota. Environ. Sci. 2009. [Google Scholar]
- Smith, S.A.; Keyser, F.W.; Rebain, T.L. Estimating Canopy Bulk Density and Canopy Base Height for Interior Western US Conifer Stands. For. Sci. 2016, 62, 690–697. [Google Scholar] [CrossRef]
- Anne, G.; Andreu, J.I.; Blake, S.J.; Stanley, J.Z. Estimating canopy fuel characteristics for predicting crown fire potential in common forest types of the Atlantic Coastal Plain, USA. Int. J. Wildland Fire 2018, 27, 742. [Google Scholar] [CrossRef]
- Chang, Y.; He, S.H.; Hu, Y.M.; Bu, R.C.; Li, X.Z. Historic and current fire regimes in the Great Xing’an Mountains, northeastern China: Implications for long-term forest management. For. Ecol. Manag. 2008, 254, 445–453. [Google Scholar] [CrossRef]
- Keane, R.E.; Reinhardt, E.D.; Scott, J.; Gray, K.; Reardon, J. Estimating forest canopy bulk density using six indirect methods. Can. J. For. Res. 2005, 35, 724–739. [Google Scholar] [CrossRef]
- Zhu, Y.L.; Zhou, G.; Zhang, H.F.; Zhang, J.L.; Dilixiati, B. Study on the Calorific Value and Ash Content of European Mountain Poplar. For. Environ. Sci. 2022, 38, 79–87. [Google Scholar] [CrossRef]
- Willmott, C.J. Comments on the evaluation of model performance. Bull. Am. Meteorol. Soc. 1982, 63, 1309–1313. [Google Scholar] [CrossRef]
- Rothermel, R.C. A Mathematical Model for Predicting Fire Spread in Wildland Fuels; Research Paper; Department of Agriculture, Intermountain Forest and Range Experiment Station: Ogden, UT, USA, 1972.
- Mitsopoulos, I.D.; Dimitrakopoulos, A.P. Canopy fuel characteristics and potential crown fire behavior in Aleppo pine (Pinus halepensis Mill.) forests. Ann. For. Sci. 2007, 64, 287–299. [Google Scholar] [CrossRef]
- Chamberlain, C.P.; Meador, A.J.S.; Thode, A.E. Airborne lidar provides reliable estimates of canopy base height and canopy bulk density in southwestern ponderosa pine forests. For. Ecol. Manag. 2021, 481, 118695. [Google Scholar] [CrossRef]
- Reinhardt, E.; Scott, J.; Gray, K.; Keane, R. Estimating canopy fuel characteristics in five conifer stands in the western United States using tree and stand measurements. Can. J. For. Res. 2006, 36, 2262–2263. [Google Scholar] [CrossRef]
- Zianis, D.; Xanthopoulos, G.; Kalabokidis, K.; Kazakis, G.; Ghosn, D.; Roussou, O. Allometric equations for aboveground biomass estimation by size class for Pinus brutia Ten. Eur. J. For. Res. 2011, 130, 145–160. [Google Scholar] [CrossRef]
- Scott, J.H. Comparison of Crown Fire Modeling Systems Used in Three Fire Management Applications; U.S. Forest Service, Rocky Mountain Research Station: Fort Collins, CO, USA, 2006; pp. 1–25. [CrossRef]
- Li, J.; Mahalingam, S.; Weise, D.R. Experimental investigation of fire propagation in single live shrubs. Int. J. Wildland Fire 2016, 26, 58–70. [Google Scholar] [CrossRef]
- Cruz, M.G.; Alexander, M.E.; Wakimoto, R.H. Assessing canopy fuel stratum characteristics in crown fire prone fuel types of western North America. Int. J. Wildland Fire 2003, 12, 39–50. [Google Scholar] [CrossRef]
- Perry, D.A.; Jing, H.; Oetter, Y.D.R. Forest Structure and Fire Susceptibility in Volcanic Landscapes of the Eastern High Cascades, Oregon. Conserv. Biol. 2004, 18, 913–926. [Google Scholar] [CrossRef]
- Williams, C.J.; Lepage, B.A.; Vann, D.R.; Tange, T.; Ikeda, H.; Ando, M.; Kusakabe, T.; Tsuzuki, H.; Sweda, T. Structure, allometry, and biomass of plantation Metasequoia glyptostroboides in Japan. For. Ecol. Manag. 2003, 180, 287–301. [Google Scholar] [CrossRef]
- He, L.; Zhang, X.; Wang, X.; Ullah, H.; Liu, Y.; Duan, J. Tree Crown Affects Biomass Allocation and Its Response to Site Conditions and the Density of Platycladus orientalis Linnaeus Plantation. Forests 2023, 14, 20. [Google Scholar] [CrossRef]
- Li, Q.C.; Liu, Z.L.; Jin, G.Z. Impacts of stand density on tree crown structure and biomass: A global meta-analysis. Agric. For. Meteorol. 2022, 326, 109181. [Google Scholar] [CrossRef]
- Kholdaenko, Y.A.; Babushkina, E.A.; Belokopytova, L.V.; Zhirnova, D.F.; Koshurnikova, N.N.; Yang, B.; Vaganov, E.A. The More the Merrier or the Fewer the Better Fare? Effects of Stand Density on Tree Growth and Climatic Response in a Scots Pine Plantation. Forests 2023, 14, 915. [Google Scholar] [CrossRef]
- Cruz, M.G.; Alexabder, M.E. Evaluating regression model estimates of canopy fuel stratum characteristics in four crown fire-prone fuel types in western North America. Int. J. Wildland Fire 2011, 21, 168–179. [Google Scholar] [CrossRef]
- Hodson, T.O. Root-mean-square error (RMSE) or mean absolute error (MAE): When to use them or not. Geosci. Model. Dev. 2022, 15, 5481–5487. [Google Scholar] [CrossRef]
- Mitchell, R.J.; Liu, Y.Q.; O’Brien, J.J.; Elliott, K.J.; Starr, G.; Miniat, C.F.; Hiers, J.K. Future climate and fire interactions in the south-eastern region of the United States. For. Ecol. Manag. 2014, 327, 316–326. [Google Scholar] [CrossRef]
- Agee, J.K.; Skinner, C.N. Basic principles of forest fuel reduction treatments. For. Ecol. Manag. 2005, 211, 83–96. [Google Scholar] [CrossRef]
- Schoennagel, T.; Veblen, T.T.; Romme, W.H. The interaction of fire, fuels, and climate across rocky mountain forests. Bioscience 2004, 54, 661–676. [Google Scholar] [CrossRef]
- Wang, E.; Wan, H.X.; Simeoni, A.; Mou, C.J.; Zhang, Y.C. Experimental Study on Effects of Moisture Content and Tree Height on Crown Fire Behaviors of Live Cypress Trees. Combust. Sci. Technol. 2024, 197, 2727–2742. [Google Scholar] [CrossRef]
- Cai, L.Y.; He, H.S.; Wu, Z.W.; Lewis, B.L.; Liang, Y. Development of Standard Fuel Models in Boreal Forests of Northeast China through Calibration and Validation. PLoS ONE 2014, 9, e94043. [Google Scholar] [CrossRef]


| Three Burning Scenarios | CBH (m) | Stand Density (Trees·ha−1) | Wind Speed (km·h−1) | Sloop (°) |
|---|---|---|---|---|
| Low-burning scenario | 0.88 | 667 | 15 | 10 |
| Medium burning scenario | 0.48 | 1167 | 35 | 20 |
| High burning scenario | 0.08 | 1667 | 55 | 30 |
| Model Factor | Available Biomass | CFL | CBD |
|---|---|---|---|
| H | 0.804 ** | 0.804 ** | 0.804 ** |
| D | 0.759 ** | 0.759 ** | 0.762 ** |
| Wc | 0.704 ** | 0.704 ** | 0.641 ** |
| CBH | 0.491 ** | 0.491 ** | 0.489 ** |
| Lc | 0.788 ** | 0.788 ** | 0.789 ** |
| Dependent Variable | Estimation Model | R2 | Adjusted R2 | p | RMSE |
|---|---|---|---|---|---|
| Available biomass | lnY1 = −2.916 + 0.58lnX1 + 1.611lnX2 + 0.866lnX3 | 0.917 | 0.911 | <0.001 | 0.354 |
| CFL | lnY2 = −3.978 + 0.57ln X1 + 1.624 lnX2 + 0.864lnX3 | 0.914 | 0.908 | <0.001 | 0.36 |
| CBD | lnY1 = −3.965 + 0.58lnX1 + 0.611lnX2 + 0.866lnX3 | 0.865 | 0.855 | <0.001 | 0.354 |
| Independent Variable | Dependent Variable | df | F-Value | p-Value |
|---|---|---|---|---|
| Slope | ROS | 2 | 40.455 | <0.001 |
| FLI | 2 | 14.417 | 0.002 | |
| FL | 2 | 15.116 | 0.002 | |
| Wind speed | ROS | 2 | 38,494.181 | <0.001 |
| FLI | 2 | 8581.862 | <0.001 | |
| FL | 2 | 7263.969 | <0.001 | |
| CBH | ROS | 2 | 3054.675 | <0.001 |
| FLI | 2 | 21.514 | <0.001 | |
| FL | 2 | 7.480 | 0.015 | |
| Slope × CBH | ROS | 4 | 0.414 | 0.794 |
| FLI | 4 | 0.073 | 0.989 | |
| FL | 4 | 0.057 | 0.993 | |
| Wind speed × CBH | ROS | 4 | 8000.130 | <0.001 |
| FLI | 4 | 2071.252 | <0.001 | |
| FL | 4 | 1817.699 | <0.001 | |
| Slope × wind speed | ROS | 4 | 3.827 | 0.050 |
| FLI | 4 | 2.189 | 0.161 | |
| FL | 4 | 1.916 | 0.201 |
| Dependent Variable | R2 | RMSE | MAE |
|---|---|---|---|
| Available canopy biomass | 0.841 | 0.472 | −0.232 |
| CFL | 0.824 | 0.500 | −0.242 |
| CBD | 0.726 | 0.472 | −0.233 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, X.; Zheng, X.; Cui, R.; Chi, C.; Wang, Q.; Wang, S.; Zhang, G.; Cai, H.; Shan, Y.; Wang, M.; et al. Canopy Fuel Characteristics and Potential Fire Behavior in Dwarf Pine (Pinus pumila) Forests. Fire 2025, 8, 347. https://doi.org/10.3390/fire8090347
He X, Zheng X, Cui R, Chi C, Wang Q, Wang S, Zhang G, Cai H, Shan Y, Wang M, et al. Canopy Fuel Characteristics and Potential Fire Behavior in Dwarf Pine (Pinus pumila) Forests. Fire. 2025; 8(9):347. https://doi.org/10.3390/fire8090347
Chicago/Turabian StyleHe, Xinxue, Xin Zheng, Rong Cui, Chenglin Chi, Qianxue Wang, Shuo Wang, Guoqiang Zhang, Huiying Cai, Yanlong Shan, Mingyu Wang, and et al. 2025. "Canopy Fuel Characteristics and Potential Fire Behavior in Dwarf Pine (Pinus pumila) Forests" Fire 8, no. 9: 347. https://doi.org/10.3390/fire8090347
APA StyleHe, X., Zheng, X., Cui, R., Chi, C., Wang, Q., Wang, S., Zhang, G., Cai, H., Shan, Y., Wang, M., & Zhang, J. (2025). Canopy Fuel Characteristics and Potential Fire Behavior in Dwarf Pine (Pinus pumila) Forests. Fire, 8(9), 347. https://doi.org/10.3390/fire8090347






