Abstract
This paper presents an integrated computational framework for predicting temperature fields in glulam beam–column connections under fire conditions, combining finite element modeling, automated parametric analysis, and deep learning techniques. A high-fidelity heat transfer finite element model was developed, incorporating the anisotropic thermal properties of wood and temperature-dependent material behavior, validated against experimental data with strong agreement. To enable large-scale parametric studies, an automated Abaqus model modification and data processing system was implemented, improving computational efficiency through the batch processing of geometric and material parameters. The extracted temperature field data was used to train a DeepONet neural network, which achieved accurate temperature predictions (with a L2 relative error of 1.5689% and an R2 score of 0.9991) while operating faster than conventional finite element analysis. This research establishes a complete workflow from fundamental heat transfer analysis to efficient data generation and machine learning prediction, providing structural engineers with practical tools for the performance-based fire safety design of timber connections. The framework’s computational efficiency enables comprehensive parametric studies and design optimizations that were previously impractical, offering significant advancements for structural fire engineering applications.
1. Introduction
In recent years, with the growing emphasis on environmental sustainability, the use of engineered wood products—such as glulam, cross-laminated timber (CLT), and laminated veneer lumber (LVL)—has increased significantly [1,2,3]. Timber construction has gained popularity due to its numerous advantages, including prefabrication, a low carbon footprint, ease of transportation and assembly, and esthetically pleasing appearance. Fire safety, however, remains one of the most critical challenges in the design of timber structures. In particular, the fire resistance of connections plays a pivotal role, not only influencing the overall fire performance of timber structures, but also determining their mechanical behavior under both ambient and elevated temperatures.
Over the past three decades, extensive full-scale fire tests have been conducted on timber connections to investigate their mechanical performance under fire conditions. Many researchers worldwide have carried out fire resistance tests on dowel-type connections, including nails, dowels, and bolts. Based on a wide range of experimental studies [4,5,6], it has been established that the fire performance of dowel-type connections is primarily influenced by factors such as timber thickness, load ratio, loading configuration (e.g., tension parallel to the grain, tension perpendicular to the grain, inclined tension, shear, and bending), and fastener properties [7,8,9].
Nevertheless, large-scale fire testing of timber connections is both costly and complex. To address this challenge, researchers have developed numerical models [10,11,12,13,14]. Thermal models, based on the temperature-dependent thermophysical properties of materials, have been used to simulate the evolution of internal temperature fields in connections during fire exposure. Coupled thermo-mechanical models employ finite element methods to simulate the mechanical response of connections under fire conditions by incorporating the temperature-dependent degradation of material properties. Furthermore, analytical models have been developed to predict the fire resistance of connections, often relying on prior temperature field simulations. For instance, Palma [15], Erchinger [16], and Racher [17] proposed fire resistance calculation models for timber connections based on the temperature-dependent Johansen yield theory, particularly for connections subjected to tension parallel to the grain and perpendicular to the grain. However, the existing methods are often limited by high computational, money, and labor costs, indicating a strong demand for efficient data-driven or machine learning-based approaches, which remain at an early stage of exploration in this field.
Machine learning (ML) and deep learning (DL) techniques have shown great potential in structural fire performance prediction, offering efficient alternatives to traditional numerical methods [18,19,20]. Esteghamati et al. [21] developed explainable ML models to predict the fire resistance of timber columns based on geometry and material properties, with random forest models outperforming traditional prescriptive methods in both accuracy and interpretability. Naser [22] applied artificial intelligence to derive temperature-dependent material models for wood and proposed simplified expressions for thermo-structural response prediction, demonstrating the advantages of AI in enhancing the efficiency of fire resistance evaluation. Chaudhary et al. [23] introduced a surrogate modeling framework for probabilistic fire analysis, significantly reducing the computational burden while maintaining high accuracy. Panev et al. [24] established an expert system based on support vector machines to predict the insulation performance of shallow floor systems with good accuracy, eliminating the need for extensive finite element simulations. Fu [25] developed a machine learning framework for assessing the progressive collapse potential of steel-framed buildings under fire, providing an effective and rapid tool for fire safety evaluation. Lazarevska et al. [26] applied fuzzy neural networks to predict the fire resistance of eccentrically loaded reinforced concrete columns, highlighting the potential of hybrid intelligent models for rapid fire performance prediction. These studies collectively demonstrate that machine learning techniques offer promising pathways for faster and more accurate fire performance prediction across a variety of structural systems.
As a prominent method within the family of physics-informed machine learning approaches [27,28,29], the Deep Operator Network (DeepONet) [30] has emerged as a powerful framework for tackling complex scientific and engineering problems. Unlike traditional neural networks that map input data to output data, DeepONet learns mappings between function spaces, making it particularly suitable for high-dimensional, nonlinear problems where the input and output are both continuous functions. The network architecture typically consists of a branch network to encode the input function and a trunk network to represent the spatial or parametric domain, enabling the efficient and accurate prediction of functional outputs. Due to its strong generalization ability and fast inference speed, DeepONet has found increasing applications in engineering, including structural response prediction, time-dependent reliability analysis, shape optimization, and material behavior modeling.
Several recent studies have demonstrated the effectiveness of DeepONet in various engineering applications. He et al. [31] proposed a ResUNet-based DeepONet architecture for predicting elastoplastic stress fields under complex geometries and variable loading conditions, achieving high prediction accuracy with a significantly reduced computational cost. Garg et al. [32] applied DeepONet to time-dependent reliability analysis of dynamical systems under stochastic loading, highlighting its potential in uncertainty quantification and zero-shot learning. Ahmed et al. [33] proposed a physics-informed DeepONet enhanced with stiffness-based loss functions, enabling the accurate real-time prediction of structural displacements and rotations under static loading scenarios. Furthermore, Koric et al. [34] extended DeepONet to small-strain plasticity problems with variable loads and material properties, achieving rapid and precise stress field predictions across a wide range of conditions. These studies collectively demonstrate that DeepONet offers a flexible and efficient alternative to traditional numerical simulations in civil and structural engineering. Furthermore, Xu et al. [35] proposed a multi-fidelity DeepONet framework to perform real-time reconstruction of the settlement field induced by tunnel boring machine construction, which enables an efficient fusion of simulation-based data and real-world measurement data.
Despite significant progress, the application of DeepONet in the domain of timber structures, particularly under fire hazard conditions, remains largely unexplored. The accurate prediction of the temperature field evolution in timber connections under fire is crucial for structural fire safety design. However, conventional finite element simulations are often computationally intensive and not well-suited for rapid assessment in engineering practice. To address these challenges, this study aims to develop a DeepONet-based model for predicting the temperature field in glulam timber connections exposed to fire. By leveraging the strong predictive capabilities of DeepONet, the proposed approach seeks to provide an efficient and reliable tool for enhancing the fire safety design of timber structures.
In this study, a validated finite element model is established, considering the anisotropic and temperature-dependent thermal properties of wood. Then, an automated system is implemented for large-scale parametric model generation and temperature data extraction. Finally, a DeepONet model is trained on the generated dataset to achieve efficient and accurate temperature field prediction. This framework provides a practical tool for the rapid evaluation and optimization of timber connections in fire safety design. The novelty of this work lies in the integration of automated parametric simulation and operator learning-based prediction, enabling the efficient, accurate, and scalable thermal analysis of glulam timber connections under fire exposure, an approach not yet widely adopted in existing studies.
2. Heat Transfer Analysis
2.1. Model Detail
In glulam beam-to-column connections exposed to fire, the beam end is particularly vulnerable due to its direct exposure to high temperatures, leading to rapid charring and potential structural failure. This critical region has been the focus of numerous experimental studies, where the column is often insulated to isolate the thermal effects on the beam end. To better understand the heat transfer mechanisms in this zone, a finite element model was developed to simulate temperature distribution and thermal behavior under fire conditions.
The thermal properties of steel components, including plates and bolts, were modeled based on Eurocode 3 (EN 1993-1-2 [36]), incorporating temperature-dependent thermal conductivity, specific heat, and density. High-temperature effects such as thermal expansion and reduced material strength were also accounted for to ensure accurate heat transfer representation. For the glulam timber, the thermal properties (Figure 1) were defined as functions of temperature, with conductivity values derived from Janssens et al. [37], density from EN 1995-1-2 [38], and specific heat from Fredlund et al. [37,39]. Considering the anisotropic nature of wood, the longitudinal thermal conductivity was set to four times the transverse value, following the theoretical framework established by Cachim and Franssen [40]. This distinction is crucial, as heat propagates much faster along the grain than across it, significantly influencing the temperature distribution in the beam end.
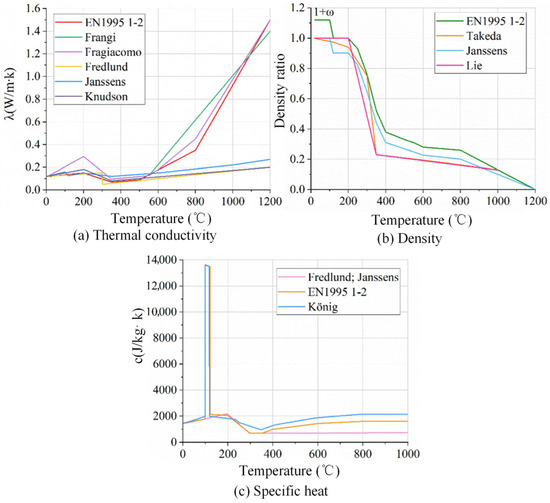
Figure 1.
The thermal properties of wood.
In fire resistance tests, the temperature–time curve of the fire environment follows the standard ISO 834-1:1999 [41], with the temperature expressed as follows:
where θg represents the furnace temperature and t denotes the exposure time.
The net heat flux consists of two parts, the convective heat flux and radiative heat flux . The heat conduction is calculated using the following:
where ac is the heat transfer coefficient for convection [W∙m−2∙K−1], taken as 25 W∙m−2∙K−1 [15], θg is the furnace temperature, and θm is the surface temperature.
The thermal radiation is calculated as follows:
where ϕ is the configuration factor (taken as 1.0 [15]). εm is the surface emissivity of the member (taken as 0.7 [36] for steel and 0.8 for wood [16]). θr is the effective radiation temperature of the fire environment [°C] and θm is the surface temperature of the member [°C]. Here, “member” refers to the structural components of the model, including both steel and timber elements (e.g., bolts, plates, beams), each assigned appropriate thermal emissivity values based on their material properties. The parameter εf represents the fire emissivity and is taken as 1.0. σ is the Stefan–Boltzmann constant [W∙m−2∙K−4], taken as 5.67 × 10−8 W∙m−2∙K−4 [15].
In the present numerical model, the glulam beam is exposed to fire on all four sides, necessitating the careful consideration of heat transfer parameters for both the timber members and steel components (bolts and steel splice plates). The thermal modeling approach accounts for the complex interactions between these materials under elevated temperatures, as illustrated in Figure 2.
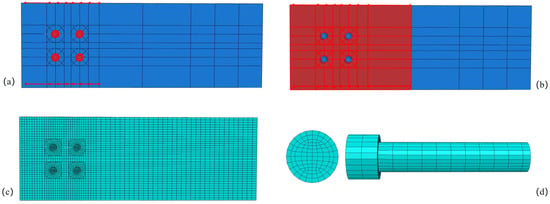
Figure 2.
Temperature field modeling and meshing of the connection model: (a) Heat convection and heat radiation zone for steel, (b) heat convection and heat radiation zone for wood, (c) meshed model of the connection, and (d) mesh of bolt.
The thermal analysis utilizes DC3D8 elements (eight-node linear heat transfer brick elements) for their demonstrated accuracy in simulating three-dimensional heat conduction problems. A critical aspect of the modeling strategy involves the implementation of Tie constraints at all material interfaces, which maintains mesh continuity and enables proper heat transfer across different components. This approach effectively simulates the thermal bridging effects that occur at steel–timber junctions while preventing artificial thermal resistance at connection points.
Special attention was given to several key modeling aspects that significantly influence the thermal behavior. The mesh density was carefully optimized, particularly around critical regions such as bolt holes and steel–timber interfaces, where steep temperature gradients are expected, and this meshing strategy has been validated by our previous studies [4,42] and also widely adopted in related fire performance simulations by other researchers [5,11,43,44]. In these regions, bolt-bearing zones were discretized using a near-quadrilateral meshing strategy. The bolts were partitioned into three parts to address varying geometries and ensure compatibility at contact interfaces. A radial slicing method centered on the bolt axis was adopted to improve mesh quality in cylindrical areas.
2.2. Validation
The heat transfer analysis model developed in this study was rigorously validated against experimental data from a previous study. According to [42], the test specimen consisted of a glulam beam–column connection with the following specifications: Douglas fir glulam beams measuring 350 mm (height) × 200 mm (width) × 1000 mm (length), connected using Grade 8.8 M20 high-strength bolts and 10 mm thick Q355 steel splice plates. The connection configuration featured four bolts at the beam end and six bolts at the column end, representing a typical heavy timber construction (Figure 3).
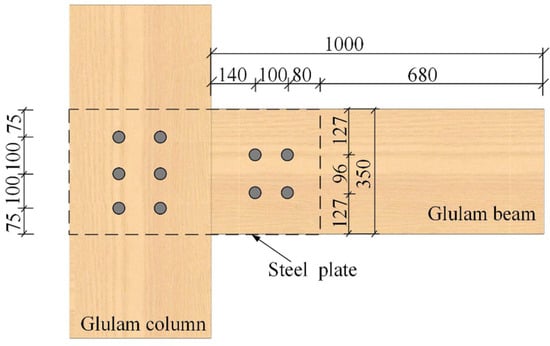
Figure 3.
Connection details.
The validation process focused on comparing the model’s temperature predictions with experimental measurements at multiple critical locations within the connection assembly. As shown in Figure 4, Figure 5 and Figure 6, the numerical results demonstrate excellent agreement with the experimental data throughout the entire heating period. These validation results confirm that the current modeling approach, incorporating temperature-dependent material properties, proper interface treatments, and appropriate boundary conditions, can reliably predict the complex thermal behavior of glulam bolt connections under fire conditions. This successful validation provides a solid foundation for the subsequent parametric studies and DeepONet training presented in this study.
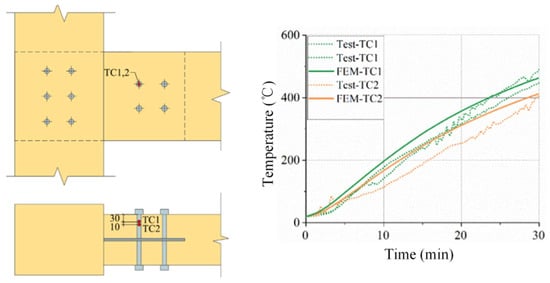
Figure 4.
Comparison of bolt temperature between test and model.
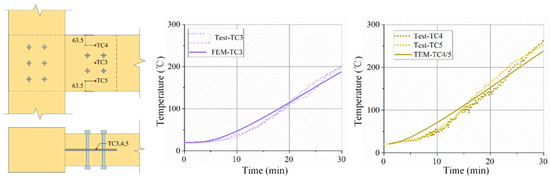
Figure 5.
Comparison of steel plate temperature between test and model.
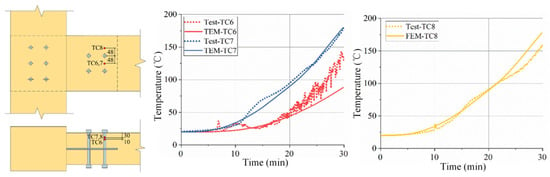
Figure 6.
Comparison of wood temperature between test and model.
3. Automated Abaqus Model Modification and Temperature Field Data Processing System
To efficiently explore the thermal behavior of glulam connections and support the training of the DeepONet model, an automated system for Abaqus model modification and data extraction was developed. Although the framework is capable of batch processing several key parameters, including the bolt diameter (mm), wood density (kg/m3), beam thickness (mm), and edge distance (mm), this study focused on a subset of three representative parameters (timber density, edge distance, and beam thickness) to ensure clarity and the interpretability of results. A total of 275 finite element simulations were conducted by systematically varying these three parameters across practical ranges: timber density from 400 to 600 kg/m3 (5 levels), edge distance from 60 to 140 mm (5 levels), and beam thickness from 100 to 300 mm (11 levels). This structured dataset not only supports DeepONet training, but also serves as a basis for assessing the connections’ behavior under fire scenarios.
The system was built on the Abaqus finite element analysis platform and integrates four functional modules to streamline the workflow: (1) parametric modeling, (2) automated parameter iteration, (3) simulation result extraction, and (4) data post-processing. The parametric modeling module allows for the rapid generation of finite element models with varying geometric and material properties. The automated iteration module systematically adjusts the input parameters and executes simulations without manual intervention. The result extraction module collects temperature field data along predefined paths (line sets), ensuring consistent data sampling across different models. Finally, the post-processing module performs data cleaning, normalization, and structured output to Excel files, facilitating seamless integration with the DeepONet training procedure.
A key advantage of this system is its ability to significantly enhance computational efficiency while maintaining data consistency. By automating repetitive tasks such as model generation, simulation execution, and data extraction, the system minimizes human error and accelerates large-scale parametric studies. The modular architecture, illustrated in Figure 7, ensures flexibility for future expansions, such as incorporating additional material properties or fire scenarios. This systematic approach not only supports DeepONet training, but also provides a scalable framework for other data-driven structural fire engineering applications.
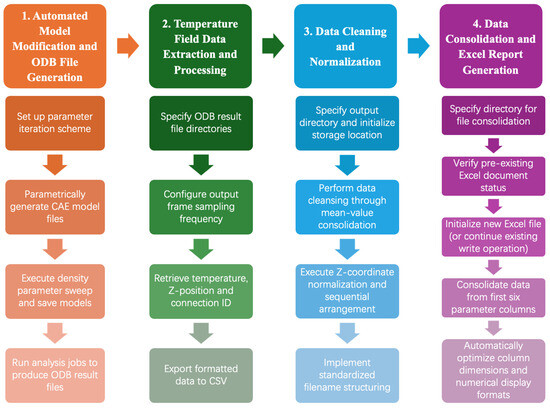
Figure 7.
Automated Abaqus model modification and temperature field data processing system.
3.1. Automated Model Modification and ODB File Generation
The parametric modeling workflow initiates by loading a baseline ABAQUS CAE model containing predefined components with standardized nomenclature. Through Python (Python 3.12.8) scripting integrated with the ABAQUS API, the system programmatically modifies key parameters, including edge distance increments, thickness variations, and material density, etc. Each parameter combination triggers a complete model update sequence: the geometric regeneration of relevant parts using Boolean operations, material property reassignment through the material repository, and adaptive remeshing with predefined seed controls. The system implements a job queuing mechanism that sequentially submits modified models to the ABAQUS solver while monitoring memory usage and processor allocation. Particular attention is given to path management, where absolute references are dynamically converted to relative paths using Python’s os module, ensuring portability across different computing environments. The automation script incorporates error handling for common failure modes, including geometric incompatibility and mesh generation errors. To ensure computational robustness, the script also includes feature regeneration, element type reassignment, and sequential job execution, with each step logged using timestamped diagnostics for subsequent analysis.
3.2. Temperature Field Data Extraction and Processing
The developed Python-based post-processing system systematically interrogates all ODB result files within a user-specified directory through ABAQUS/CAE’s ODB API. For each simulation case, the algorithm extracts time–temperature histories from predefined node sets (e.g., “Beam_Web_Nodes”, “Bolt_Contact_Nodes”) at multiple analysis frames, capturing the complete thermal transient response. The extraction protocol features adaptive time stepping that maintains temporal resolution during rapid temperature changes while reducing sampling frequency during stable phases. Spatial data organization follows a hierarchical structure where each node’s temperature profile is tagged with its original coordinates (X,Y,Z) and part affiliation, enabling subsequent thickness-based normalization. The raw output is initially stored in a memory-efficient HDF5 format before final conversion to CSV, with automatic checks for data integrity including frame completeness verification and NaN value handling.
3.3. Data Cleaning and Normalization
The preprocessing pipeline addresses several challenges inherent to timber connection thermal analysis through a multi-step refinement process. First, spatial redundancy is eliminated by merging columns with identical thickness coordinates via arithmetic averaging, significantly reducing dataset dimensionality while preserving thermal gradient accuracy. To enhance system efficiency, a data-cleaning step was implemented to eliminate nearly 1650 redundant nodes arising from overlapping mesh points, significantly reducing the computational overhead. For irregular temperature distributions caused by parametric thickness variations, a normalization scheme transforms physical coordinates to the dimensionless interval [0, 1] using the relationship ξ = (z − zmin)/(zmax − zmin), where z represents the through-thickness coordinate. This normalization enables consistent cross-comparison between different geometric configurations. The cleaning process also handles missing data through context-aware interpolation, applying either linear fills for single-frame gaps or polynomial fitting for larger discontinuities, with all modifications logged in a companion metadata file for traceability.
3.4. Data Consolidation and Excel Report Generation
The data integration phase employs a systematic approach to combine multiple CSV files into well-structured Excel workbooks. The system first verifies the existence of target Excel files through a checksum-based validation protocol. When processing new data, it intelligently determines whether to create fresh workbooks or append to existing ones while maintaining strict version control through timestamped backups.
For optimal data organization, the algorithm implements several key formatting features. Parameter groupings are visually emphasized through merged cells in the first six columns, which contain critical metadata including simulation identifiers and geometric parameters. Temperature data is systematically organized into chronologically sequenced worksheets, with each sheet representing a specific time interval in the thermal analysis. These worksheets employ color-coded tabs that correspond to different temperature ranges, enabling the rapid visual assessment of thermal progression.
Quality assurance measures are embedded throughout the export process. Each workbook contains a dedicated “Processing Log” worksheet that documents all data transformations, including normalization parameters and cleaning operations. Checksum verification ensures data integrity during both the consolidation and formatting stages.
4. Temperature Field Prediction Using DeepONet
4.1. Model Architecture
The developed DeepONet architecture provides an efficient framework for predicting temperature distributions in glulam beam–column connections under fire exposure. As illustrated in Figure 8, the model architecture follows the design proposed in [30,35], consisting of two neural networks: a branch network (NNB) and a trunk network (NNT). These networks work synergistically to map input parameters to complete temperature fields.
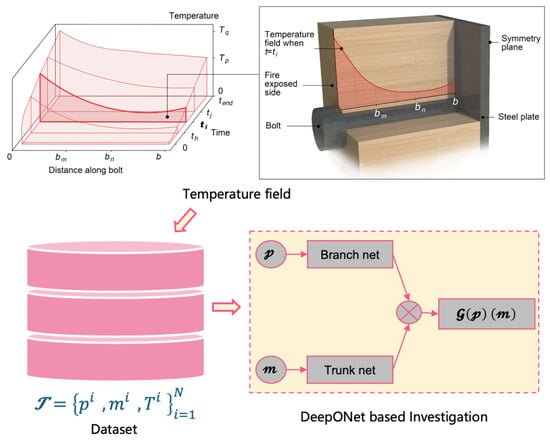
Figure 8.
DeepONet-based surrogate model for temperature field prediction of connections.
The branch network processes five key geometric and material parameters through a multilayer perceptron (MLP) with three hidden layers, each containing 50 neurons, transforming them into a high-dimensional feature representation. Simultaneously, the trunk network, which is also a three-layer MLP with 50 neurons per layer, encodes the spatial and temporal coordinates into another feature representation. The final temperature prediction is obtained via an inner product between the outputs of the two networks, effectively capturing the complex relationships between input parameters and thermal responses.
More specifically, for a given data sample i during a single forward pass, the branch network receives the five geometric and material parameters pi associated with the corresponding simulation and outputs NNB(pi). Meanwhile, the trunk network takes a space–time coordinate mi = (t,b)—where t denotes time and b represents the distance along the bolt—and outputs NNT(mi). The final DeepONet prediction, i(pi)(mi) = NNB(pi)·NNT(mi), represents the temperature at the spatial–temporal coordinate mi under the physical conditions specified by pi.
4.2. Data Preparation and Model Training
The training dataset was carefully constructed from 275 finite element simulations covering the full range of parameter variations. Each simulation provides temperature field data sampled at regular spatial and temporal intervals, resulting in approximately 1.5 million data points for network training. All data were rescaled using min–max normalization. The dataset was randomly split into training, validation, and test sets with a ratio of 80%, 10%, and 10%, respectively. The network was trained by minimizing the mean squared error (MSE) loss function, defined as follows:
where i(pi)(mi) denotes the model prediction and Ti is the corresponding ground truth temperature value.
All the machine learning processes were implemented in JAX and trained in Google Colab on a NVIDIA T4 GPU (NVIDIA, Santa Clara, CA, USA). We use the Glorot normal scheme to initialize the weights of all the DeepONet networks and adopt the hyperbolic tangent activation function (Tanh). The parameters were optimized using the Adam optimizer. The learning rate was set to 0.001, with a weight decay parameter of 0.0001. The whole model was trained with a total of 5000 training epochs to ensure convergence.
4.3. Performance Evaluation and Validation
The evolution of the training and validation loss during model training is shown in Figure 9. Both losses decrease consistently over iterations and follow a similar trend, indicating effective optimization and good generalization performance.
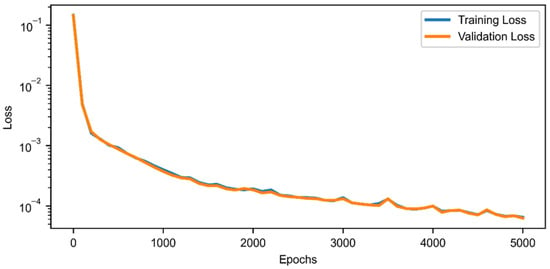
Figure 9.
Training and validation loss during model training.
On the test dataset, the trained DeepONet model achieved an L2 relative error of 1.5689% and an R2 score of 0.9991, indicating excellent predictive accuracy. The low L2 error confirms that the predicted temperature values closely match the reference finite element results, while the R2 value near unity demonstrates the model’s strong ability to capture the underlying thermal distribution patterns across different geometric and material configurations. These results validate the DeepONet architecture as a reliable and efficient surrogate model for temperature prediction in glulam connections under fire exposure, which are critical for assessing fire-induced degradation in timber connections.
The high predictive accuracy of the DeepONet model is mainly attributed to the extensive and representative training dataset, the inner product-based architecture tailored for function-to-function mapping, and effective training strategies including adaptive learning rate optimization. These factors jointly contribute to its excellent generalization capability and strong consistency, with numerical and experimental references.
Figure 10 and Figure 11 provide a detailed visualization of the DeepONet model’s predictive performance under varying thermal exposure conditions. In Figure 10, the label “working condition” refers to four temperature–depth distributions corresponding to different fire durations, while maintaining identical timber density, edge distance, beam thickness, bolt number, and bolt diameter. Figure 11, in contrast, illustrates temperature–time evolutions at different depths under the same set of geometric and material parameters. The X-axis of Figure 10 represents the non-dimensional depth ratio (distance from the surface divided by the total beam thickness), and the Y-axis denotes temperature in °C. In Figure 11, the X-axis indicates the fire exposure time in minutes, and the Y-axis represents the temperature at each depth.
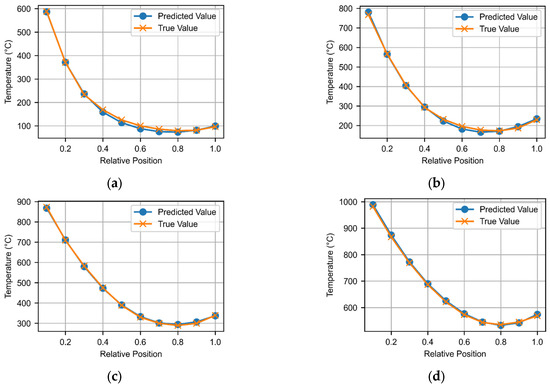
Figure 10.
Temperature spatial distribution at different times under working condition #270 (timber density = 600 kg/m3, edge distance = 140 mm, and beam thickness = 200 mm): (a) Time = 5 min; (b) Time= 10 min; (c) Time= 15 min; and (d) Time= 20 min.
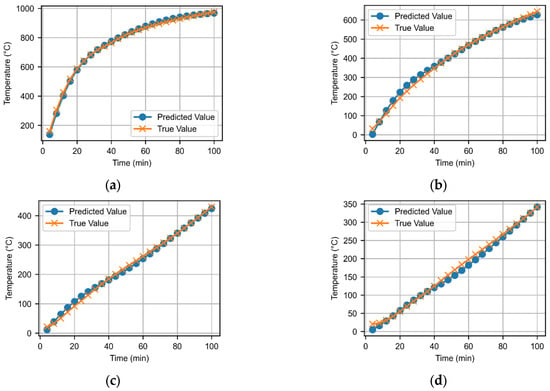
Figure 11.
Temperature development over time at different locations under working condition #274 (timber density = 600 kg/m3, edge distance = 140 mm, and beam thickness = 280 mm): (a) Relative location 0.1; (b) Relative location 0.3; (c) Relative location 0.5; and (d) Relative location 0.7.
Figure 10 shows that the temperature generally decreases with depth, but then increases slightly near the steel interface due to thermal bridging. Notably, a deviation between the predicted and measured values occurs when the depth ratio reaches 0.4, but consistency is restored by 0.8. Subfigures (a) and (b) capture early fire exposure scenarios, where the internal timber temperature remains at around 100 °C—corresponding to the evaporation of free moisture. At a depth ratio of 0.4, temperatures surpass 220 °C, indicating the onset of charring. In subfigures (c) and (d), after prolonged exposure, the section becomes fully charred, and the predicted values align closely with measured data.
Figure 11 demonstrates that as the fire exposure time increases, the temperature rises accordingly at all measurement points. Surface-adjacent locations exhibit strong agreement between predicted and measured temperatures, while deeper points show increased deviations. This discrepancy is likely attributed to delayed thermal penetration and moisture migration within the timber core. The observed differences between conditions provide a qualitative validation of the DeepONet model’s accuracy across spatial and temporal domains.
5. Conclusions
This study has developed an integrated computational framework for analyzing and predicting temperature fields in glulam beam–column connections under fire conditions, consisting of three key components:
- (1)
- The heat transfer analysis component successfully developed a robust finite element model that accurately simulates thermal behavior in timber–steel connections. By incorporating the anisotropic thermal properties of wood and temperature-dependent material characteristics, validation against experimental data confirmed the model’s ability to predict temperature progression with high fidelity. This analysis provides fundamental insights into the heat transfer mechanisms that govern connection performance during fire exposure;
- (2)
- The automated Abaqus model modification and data processing system represents a significant advancement in parametric thermal analysis methodology. By implementing automated model generation and result extraction algorithms, the system achieves a reduction in processing time compared to conventional manual approaches while maintaining rigorous quality control standards. The system’s efficiency enables the generation of comprehensive datasets that would be impractical to obtain through traditional methods, thereby facilitating a more thorough investigation of parameter influences on thermal performance;
- (3)
- The DeepONet architecture demonstrates remarkable capabilities in temperature field prediction, achieving prediction accuracy with L2 relative error of 1.5689% and an R2 score of 0.9991 while operating faster than conventional finite element analysis. The network’s specialized architecture successfully captures complex thermal phenomena, including through-thickness temperature gradients and localized heating effects. This computational efficiency makes the framework particularly valuable for design optimization and probabilistic analysis applications where numerous evaluations are required. The model’s performance represents a significant advancement in surrogate modeling techniques for structural fire engineering applications. This study bridges the gap between high-fidelity simulations and rapid-fire performance evaluation, providing a scalable surrogate modeling framework for advancing the fire safety design of timber structures. Future work will extend the framework to include different fire scenarios and composite timber systems to further generalize the model.
Author Contributions
Conceptualization, J.L., G.T., C.X., S.Z., and Z.L.; methodology, J.L., C.X., and Z.L.; software, J.L., G.T., and C.X.; validation, J.L.; formal analysis, G.T.; investigation, J.L., G.T., S.Z., and Z.L.; resources, J.L.; data curation, J.L., G.T., and C.X.; writing—original draft preparation, J.L. and C.X.; writing—review and editing, J.L., C.X., S.Z., and Z.L.; visualization, J.L.; supervision, J.L.; project administration, J.L.; funding acquisition, J.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (Jing Luo, grant number 52308268) and the Shanghai Sailing Program (Jing Luo, grant number 23YF1430900).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data is contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Teweldebrhan, B.T.; Tesfamariam, S. Performance-based design of tall-coupled cross-laminated timber wall building. Earthq. Eng. Struct. Dyn. 2022, 51, 1677–1696. [Google Scholar] [CrossRef]
- Luo, J.; Guo, Y.; Liu, Z.; Tian, G.; Zheng, X. Experimental investigations on influence of initial damage and accumulated cyclic damage on mechanical performance of glulam bolted connections. Structures 2025, 77, 109147. [Google Scholar] [CrossRef]
- Zheng, X.; He, M.; Li, Z.; Luo, Q. Long-term performance of post-tensioned cross-laminated timber (CLT) shear walls: Hygro-mechanical model validation and parametric analysis. Arch. Civ. Mech. Eng. 2022, 22, 68. [Google Scholar] [CrossRef]
- Luo, J.; Li, Z.; He, M.; Gan, Z.; Wang, X. Analytical investigation and parametric study on the fire behavior of glulam bolted beam-to-column connections based on the quasi-non-linear fracture mechanics model. Fire Saf. J. 2022, 133, 103662. [Google Scholar] [CrossRef]
- Audebert, M.; Dhima, D.; Taazount, M.; Bouchaïr, A. Experimental and numerical analysis of timber connections in tension perpendicular to grain in fire. Fire Saf. J. 2014, 63, 125–137. [Google Scholar] [CrossRef]
- Dhima, D.; Audebert, M.; Bouchaïr, A. Analysis of the thermo-mechanical behaviour of steel-to-timber connections in bending. J. Struct. Fire Eng. 2014, 5, 97–112. [Google Scholar] [CrossRef]
- Bartlett, A.I.; Hadden, R.M.; Bisby, L.A. A review of factors affecting the burning behaviour of wood for application to tall timber construction. Fire Technol. 2019, 55, 1–49. [Google Scholar] [CrossRef]
- Fonseca, E.M.; Silva, L.; Leite, P.A. Numerical model to predict the effect of wood density in wood–steel–wood connections with and without passive protection under fire. J. Fire Sci. 2020, 38, 122–135. [Google Scholar] [CrossRef]
- Peng, L.; Hadjisophocleous, G.; Mehaffey, J.; Mohammad, M. On the fire performance of double-shear timber connections. Fire Saf. Sci. 2011, 42, 1207–1218. [Google Scholar] [CrossRef]
- Chen, Z.; Ni, C.; Dagenais, C. Advanced Wood-Based Solutions for Mid-Rise and High-Rise Construction: Modelling of Timber Connections Under Force And Fire; FPInnovations Project (#301012203); FPInnovations: Québec, QC, Canada, 2018. [Google Scholar]
- Audebert, M.; Dhima, D.; Taazount, M.; Bouchaïr, A. Numerical investigations on the thermo-mechanical behavior of steel-to-timber joints exposed to fire. Eng. Struct. 2011, 33, 3257–3268. [Google Scholar] [CrossRef]
- Fonseca, E.M.; Silva, V. Design of steel-wood-steel connections at the ambient and elevated temperature. J. Comput. Appl. Mech. 2021, 52, 85–101. [Google Scholar] [CrossRef]
- Tavakkol-Khah, M.; Klingsch, W. Calculation model for predicting fire resistance time of timber members. Fire Saf. Sci. 1997, 5, 1201–1211. [Google Scholar] [CrossRef][Green Version]
- Laplanche, K.; Dhima, D.; Racher, P. Thermo-mechanical analysis of the timber connection under fire using 3D finite element model. In Proceedings of the 9th World Conference on Timber Engineering (WCTE), Portland, OR, USA, 6–10 August 2006; pp. 279–286. [Google Scholar]
- Palma, P.; Frangi, A. Modelling the fire resistance of steel-to-timber dowelled connections loaded perpendicularly to the grain. Fire Saf. J. 2019, 107, 54–74. [Google Scholar] [CrossRef]
- Erchinger, C.; Frangi, A.; Fontana, M. Fire design of steel-to-timber dowelled connections. Eng. Struct. 2010, 32, 580–589. [Google Scholar] [CrossRef]
- Racher, P.; Laplanche, K.; Dhima, D.; Bouchaïr, A. Thermo-mechanical analysis of the fire performance of dowelled timber connection. Eng. Struct. 2010, 32, 1148–1157. [Google Scholar] [CrossRef]
- Luo, J.; Guo, Y.; Liu, Z.; Hu, Q.; Hoque, M.A.; Ahmed, A. Enhancing Deep Line Segment Detection and Performance Evaluation for Wood: A Deep Learning Approach with Experiment-Based, Domain-Specific Implementations. Forests 2024, 15, 1393. [Google Scholar] [CrossRef]
- Ji, W.; Li, G.-Q.; Zhu, S.; Li, J.; Qi, H.; Wang, Y. Machine learning-driven real-time identification of large-space building fires and forecast of temperature development. Expert Syst. Appl. 2024, 255, 124758. [Google Scholar] [CrossRef]
- Qi, H.-H.; Li, G.-Q.; Zhu, S. Real-time prediction of axial force in concrete-filled steel tubular columns under fire conditions using modular artificial intelligence techniques. Eng. Appl. Artif. Intell. 2025, 150, 110617. [Google Scholar] [CrossRef]
- Esteghamati, M.Z.; Gernay, T.; Banerji, S. Evaluating fire resistance of timber columns using explainable machine learning models. Eng. Struct. 2023, 296, 116910. [Google Scholar] [CrossRef]
- Naser, M. Fire resistance evaluation through artificial intelligence—A case for timber structures. Fire Saf. J. 2019, 105, 1–18. [Google Scholar] [CrossRef]
- Chaudhary, R.K.; Van Coile, R.; Gernay, T. Potential of surrogate modelling for probabilistic fire analysis of structures. Fire Technol. 2021, 57, 3151–3177. [Google Scholar] [CrossRef]
- Panev, Y.; Kotsovinos, P.; Deeny, S.; Flint, G. The use of machine learning for the prediction of fire resistance of composite shallow floor systems. Fire Technol. 2021, 57, 3079–3100. [Google Scholar] [CrossRef]
- Fu, F. Fire induced progressive collapse potential assessment of steel framed buildings using machine learning. J. Constr. Steel Res. 2020, 166, 105918. [Google Scholar] [CrossRef]
- Lazarevska, M.; Gavriloska, A.T.; Laban, M.; Knezevic, M.; Cvetkovska, M. Determination of fire resistance of eccentrically loaded reinforced concrete columns using fuzzy neural networks. Complexity 2018, 2018, 8204568. [Google Scholar] [CrossRef]
- Karniadakis, G.E.; Kevrekidis, I.G.; Lu, L.; Perdikaris, P.; Wang, S.; Yang, L. Physics-informed machine learning. Nat. Rev. Phys. 2021, 3, 422–440. [Google Scholar] [CrossRef]
- Raissi, M.; Perdikaris, P.; Karniadakis, G.E. Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J. Comput. Phys. 2019, 378, 686–707. [Google Scholar] [CrossRef]
- Xu, C.; Cao, B.T.; Yuan, Y.; Meschke, G. Transfer learning based physics-informed neural networks for solving inverse problems in engineering structures under different loading scenarios. Comput. Methods Appl. Mech. Eng. 2023, 405, 115852. [Google Scholar] [CrossRef]
- Lu, L.; Jin, P.; Pang, G.; Zhang, Z.; Karniadakis, G.E. Learning nonlinear operators via DeepONet based on the universal approximation theorem of operators. Nat. Mach. Intell. 2021, 3, 218–229. [Google Scholar] [CrossRef]
- He, J.; Koric, S.; Kushwaha, S.; Park, J.; Abueidda, D.; Jasiuk, I. Novel DeepONet architecture to predict stresses in elastoplastic structures with variable complex geometries and loads. Comput. Methods Appl. Mech. Eng. 2023, 415, 116277. [Google Scholar] [CrossRef]
- Garg, S.; Gupta, H.; Chakraborty, S. Assessment of DeepONet for time dependent reliability analysis of dynamical systems subjected to stochastic loading. Eng. Struct. 2022, 270, 114811. [Google Scholar] [CrossRef]
- Ahmed, B.; Qiu, Y.; Abueidda, D.W.; El-Sekelly, W.; de Soto, B.G.; Abdoun, T.; Mobasher, M.E. Physics-informed deep operator networks with stiffness-based loss functions for structural response prediction. Eng. Appl. Artif. Intell. 2025, 144, 110097. [Google Scholar] [CrossRef]
- Koric, S.; Viswantah, A.; Abueidda, D.W.; Sobh, N.A.; Khan, K. Deep learning operator network for plastic deformation with variable loads and material properties. Eng. Comput. 2024, 40, 917–929. [Google Scholar] [CrossRef]
- Xu, C.; Cao, B.T.; Yuan, Y.; Meschke, G. A multi-fidelity deep operator network (DeepONet) for fusing simulation and monitoring data: Application to real-time settlement prediction during tunnel construction. Eng. Appl. Artif. Intell. 2024, 133, 108156. [Google Scholar] [CrossRef]
- EN 1993-1-2:2005; Eurocode 3: Design of Steel Structures—Part 1-2: General Rules—Structural Fire Design. European Committee for Standardization (CEN): Brussels, Belgium, 2005.
- Janssens, M. Thermo-physical properties for wood pyrolysis models. In Proceedings of the Pacific Timber Engineering Conference, Gold Coast, QLD, Australia, 11–15 July 1994; pp. 607–618. [Google Scholar]
- EN 1995-1-2:2004; Eurocode 5: Design of Timber Structures—Part 1-1: General—Structural Fire Design. European Committee for Standardization (CEN): Brussels, Belgium, 2004.
- Fredlund, B. Modelling of heat and mass transfer in timber structures during fire Fire Saf. Fire Saf. J. 1993, 20, 39–69. [Google Scholar] [CrossRef]
- Cachim, P.B.; Franssen, J.M. Comparison between the charring rate model and the conductive model of Eurocode 5. Fire Mater. Int. J. 2009, 33, 129–143. [Google Scholar] [CrossRef]
- ISO 834-1:1999; Fire Resistance Tests-Elements of Building Construction. International Organization for Standardization: Geneva, Switzerland, 1999.
- Luo, J.; He, M.; Li, Z.; Gan, Z.; Wang, X.; Liang, F. Experimental and numerical investigation into the fire performance of glulam bolted beam-to-column connections under coupled moment and shear force. J. Build. Eng. 2022, 46, 103804. [Google Scholar] [CrossRef]
- Moss, P.; Buchanan, A.; Fragiacomo, M.; Austruy, C. Experimental testing and analytical prediction of the behaviour of timber bolted connections subjected to fire. Fire Technol. 2010, 46, 129–148. [Google Scholar] [CrossRef]
- Zhang, J.; He, M.-J.; Li, Z. Numerical analysis on tensile performance of bolted glulam joints with initial local cracks. J. Wood Sci. 2018, 64, 364–376. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).