Double vs. Single Shear in Dowelled Timber Connections Under Fire Conditions, Thermal Analysis
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials and Fire Curve
2.2. Theoretical Methods
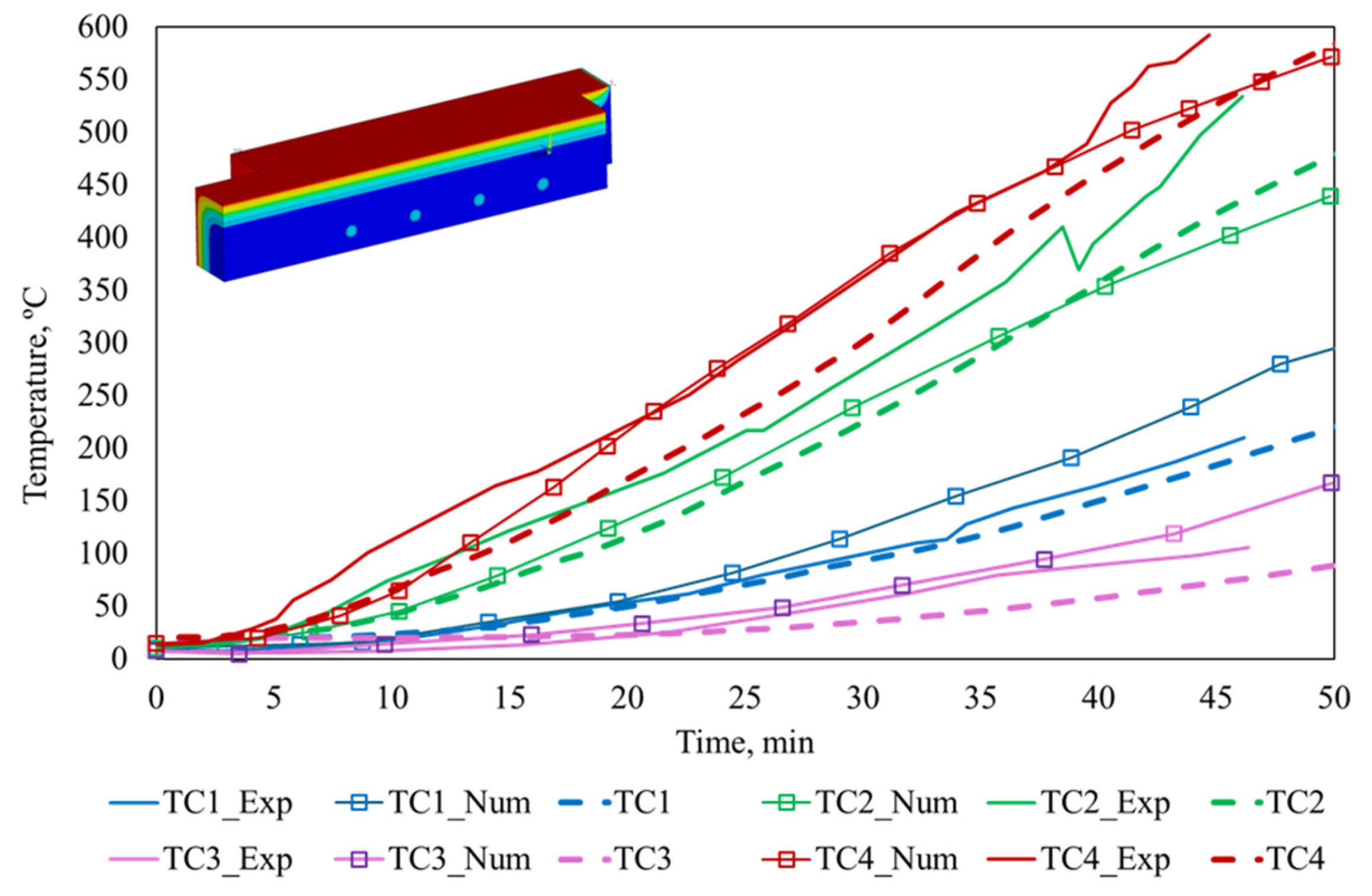
2.3. Computational Method
2.4. Computational Models for Double and Single Shear Connections
3. Results and Discussion
4. Conclusions
- -
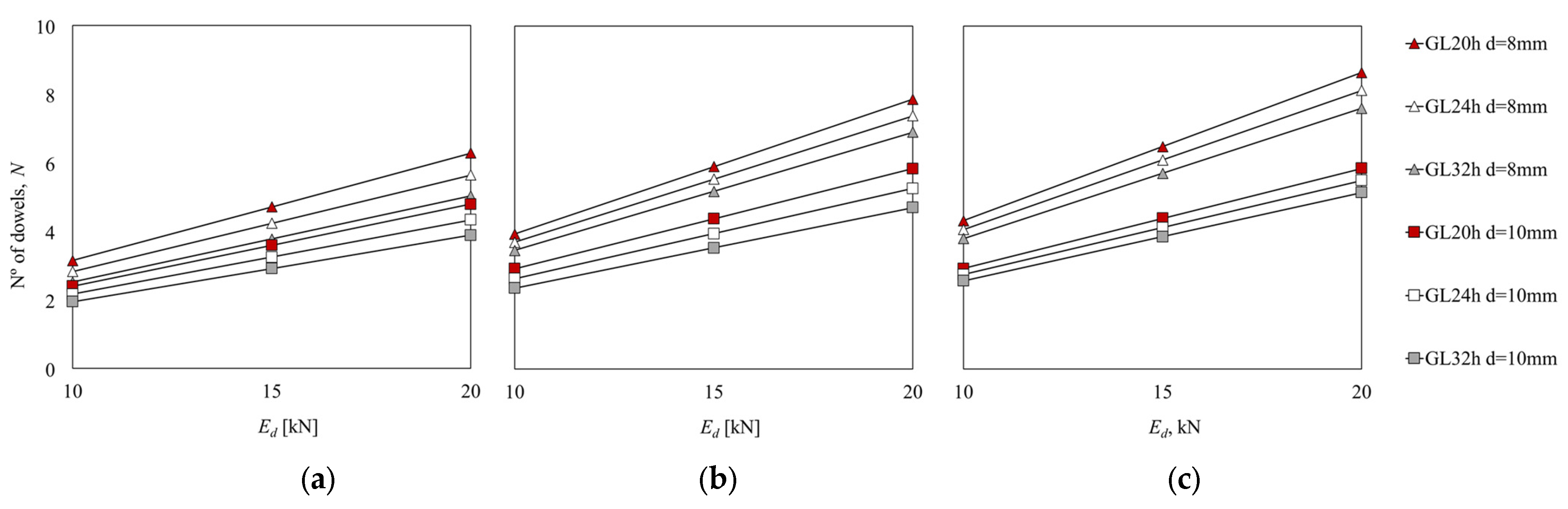
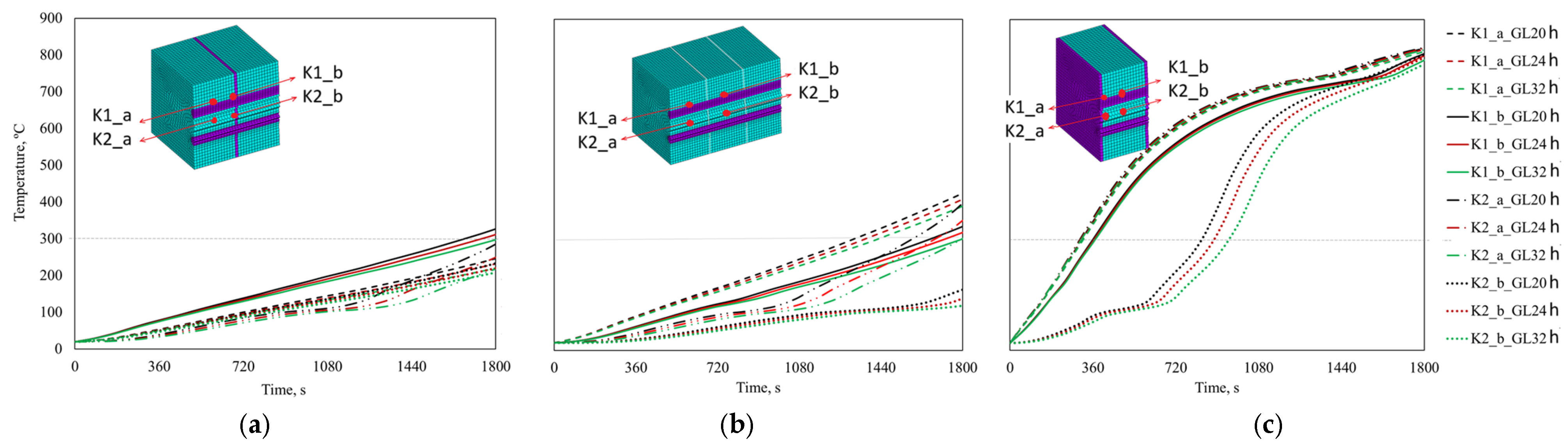
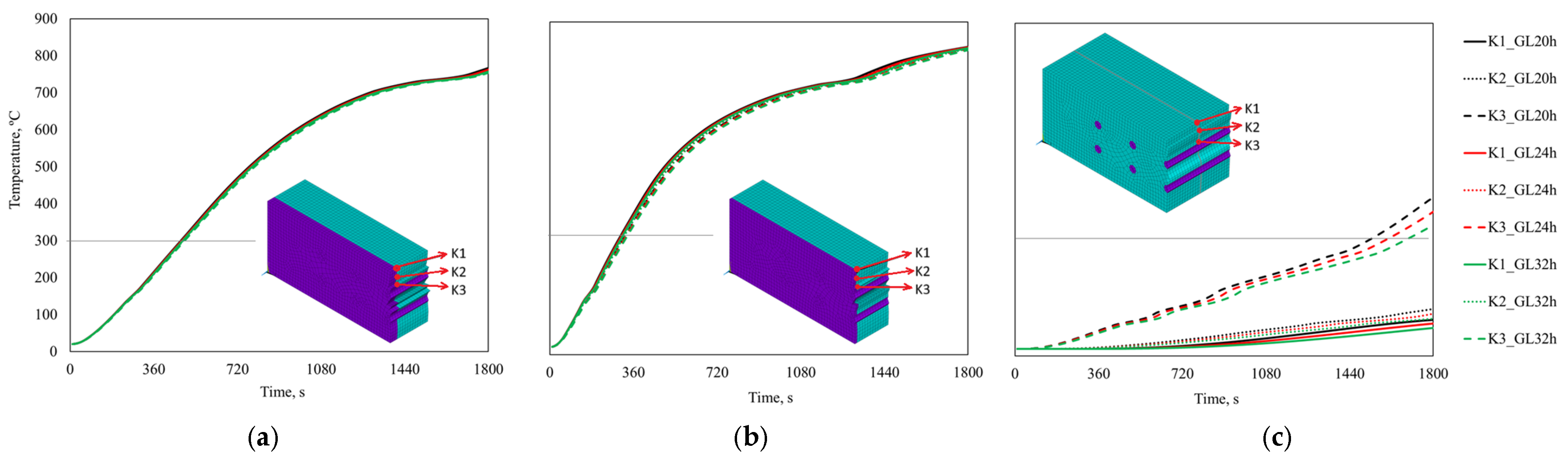
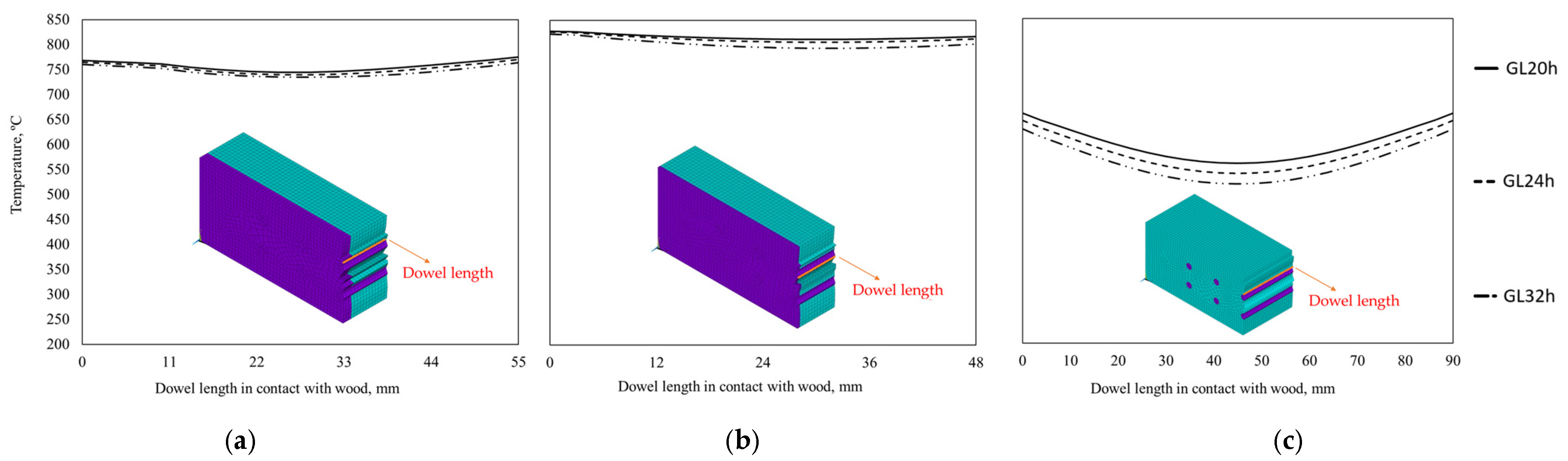
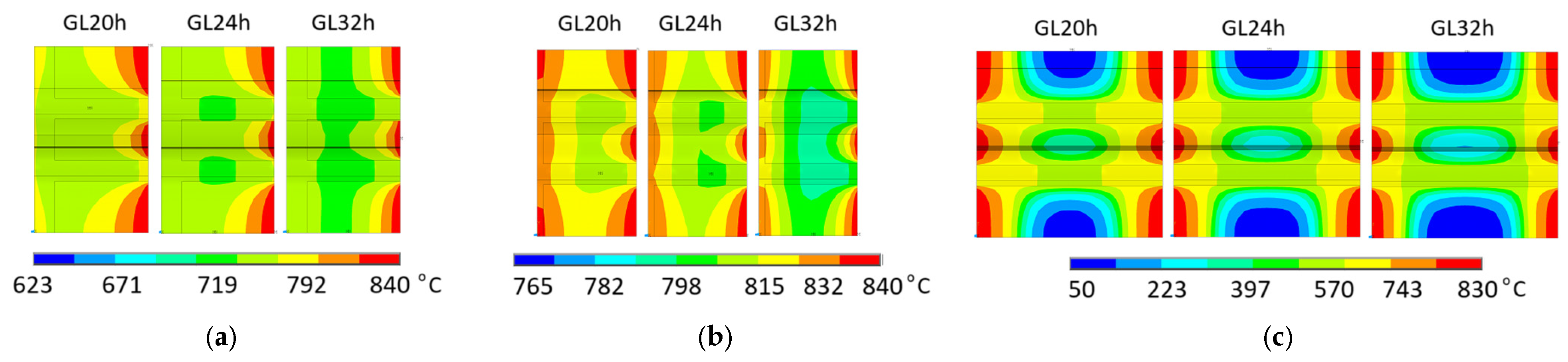
- For double shear connections, the temperature varies between 20 and 830 °C for steel-to-timber with a steel plate of any thickness as the central member and timber-to-timber; while for steel-to-timber with thin steel plates as the external members, it varies between 750 and 830 °C.
- -
- For single shear connections, the temperature varies between 623 and 840 °C for steel-to-timber with a thick steel plate, 765 and 840 °C for steel-to-timber with a thin plate, and 50 and 830 °C for timber-to-timber.
- -
- For double shear connections, the temperature varies between 450 and 250 °C for steel-to-timber with a steel plate of any thickness as the central member and between 550 and 350 °C for timber-to-timber; while for steel-to-timber with thin plates as the external members, it is almost constant at 800 °C.
- -
- For single shear connections for steel-to-timber with a thick plate and for steel-to-timber with a thin plate, both in steel, it is almost constant at 750–800 °C; it is between 550 and 650 °C for timber-to-timber.
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Nguyen, M.; Ouldboukhitine, S.; Durif, S.; Saulnier, V.; Bouchair, A. Passive fire protection of steel profiles using wood. Eng. Struct. 2023, 275 Pt A, 115274. [Google Scholar] [CrossRef]
- Richardson, L.; Batista, M. Fire resistance of timber decking for heavy timber construction. Fire Mater. 2001, 25, 21–29. [Google Scholar] [CrossRef]
- Kia, L.; Valipour, H.R. Composite timber-steel encased columns subjected to concentric loading. Eng Struct. 2021, 232, 111825. [Google Scholar] [CrossRef]
- Maraveas, C.; Miamis, K.; Matthaiou, C.E. Performance of Timber Connections Exposed to Fire: A Review. Fire Technol. 2013, 51, 1401–1432. [Google Scholar] [CrossRef]
- Li, X.; Yue, K.; Zhu, L.; Lv, C.; Wu, J.; Wu, P.; Li, Q.; Xu, C.; Sun, K. Relationships between wood properties and fire performance of glulam columns made from six wood species commonly used in China. Case Stud. Therm. Eng. 2024, 54, 104029. [Google Scholar] [CrossRef]
- Bartlett, A.; Hadden, R.; Bisby, L.A. A Review of Factors Affecting the Burning Behaviour of Wood for Application to Tall Timber Construction. Fire Technol. 2018, 55, 1–49. [Google Scholar] [CrossRef]
- Fonseca, E.M.M.; Leite, P.A.; Silva, L. Wood Connections Under Fire Conditions Protected with Gypsum Plasterboard Types A and F. In Advances in Fire Safety Engineering; Springer Nature: Cham, Switzerland, 2020; Chapter 7; Volume 1, pp. 93–106. [Google Scholar] [CrossRef]
- EN1995-1-2:2004; Eurocode 5. Design of timber structures. Part 1-2: General Structural Fire Design. European Union: Brussels, Belgium, 2004.
- Fonseca, E.M.M. Steel-to-Timber and Timber-to-Timber Simple Shear Connections. WSEAS Trans. Appl. Theor. Mech. 2024, 19, 156–160. [Google Scholar] [CrossRef]
- Just, A.; Schmid, J.; König, J. Gypsum Plasterboards Used as Fire Protection—Analysis of a Database; SP Report; SP Technical Research Institute of Sweden: Sweden, Stockholm, 2010. [Google Scholar]
- Fonseca, E.M.M. Brief overview of the thermal and mechanical properties of wood, steel, and gypsum board for structural connections. GeoStruct Innov. 2024, 2, 77–89. [Google Scholar] [CrossRef]
- EN 1993-1-2:2005; Eurocode 3. Design of Steel Structures. Part 1-2: General Rules—Structural Fire Design. European Union: Brussels, Belgium, 2005.
- Audebert, M.; Dhima, D.; Taazount, M.; Bouchaïr, A. Behavior of dowelled and bolted steel-to-timber connections exposed to fire. Eng. Struct. 2022, 39, 116–125. [Google Scholar] [CrossRef]
- Schenk, M.; Ohm, J.; Winter, S. Eurocode 5: From Mandate to Second Generation—Review, Insight and Outlook. In Proceedings of the World Conference on Timber Engineering, Brisbane, Australia, 22–26 June 2025; pp. 36–45. [Google Scholar] [CrossRef]
- Palma, P.; Munch-Andersen, J.; Dietsch, P. Updating Eurocode 5—Design Guidance for Increasing the Robustness of Timber Structures. In Proceedings of the World Conference on Timber Engineering, Oslo, Norway, 19–22 June 2023; pp. 3054–3061. [Google Scholar] [CrossRef]
- Miguel, O.; Fonseca, E.M.M.; Pereira, D. Fire Resistance in Screwed and Hollow Core Wooden Elements Filled with Insulating Material. Fire 2014, 8, 288. [Google Scholar] [CrossRef]
- Fonseca, E.M.M.; Gomes, C. FEM Analysis of 3D Timber Connections Subjected to Fire: The Effect of Using Different Densities of Wood Combined with Steel. Fire 2023, 6, 193. [Google Scholar] [CrossRef]
- EN 1995-1-1:2004; Eurocode 5. Design of Timber Structures. Part 1-1: General—Common Rules and Rules for Buildings. European Union: Brussels, Belgium, 2004.
- EN 1993-1-1:2005; Eurocode 3: Design of Steel Structures. Part 1-1: General Rules and Rules for Buildings. European Union: Brussels, Belgium, 2005.
- Filippo, F.; Jan, S.; Roald, R. Load-Carrying Capacity and Stiffness of Softwood Wooden Dowel Connections. Int. J. Archit. Herit. 2018, 14, 376–397. [Google Scholar] [CrossRef]
- Ramage, M.H.; Burridge, H.; Busse-Wicher, M.; Fereday, G.; Reynolds, T.; Shah, D.U.; Wu, G.; Yu, L.; Fleming, P.; Densley-Tingley, D.; et al. The wood from the trees: The use of timber in construction. Renew. Sustain. Energy Rev. 2017, 68 Pt 1, 333–359. [Google Scholar] [CrossRef]
- EN1991-1-2:2003; Eurocode 1. Actions on Structures. Part 1-2: General Actions—Actions on Structures Exposed to Fire. European Union: Brussels, Belgium, 2003.
- Rossi, S.; Crocetti, R.; Honfi, D.; Hansson, E. Load-bearing capacity of ductile multiple shear steel-to-timber connections. In Proceedings of the WCTE 2016 World Conference on Timber Engineering, Vienna, Austria, 22–25 August 2016. [Google Scholar]
- Fonseca, E.M.M.; Barreira, L. Experimental and Numerical Method for Determining Wood Char-Layer at High Temperatures due an Anaerobic Heating. Int. J. Saf. Secur. Eng. 2011, 1, 65–76. [Google Scholar] [CrossRef]
- Audebert, M.; Dhima, D.; Taazount, M.; Bouchaır, A. Thermo-mechanical behaviour of timber-to-timber connections exposed to fire. Fire Saf. J. 2013, 56, 52–64. [Google Scholar] [CrossRef]


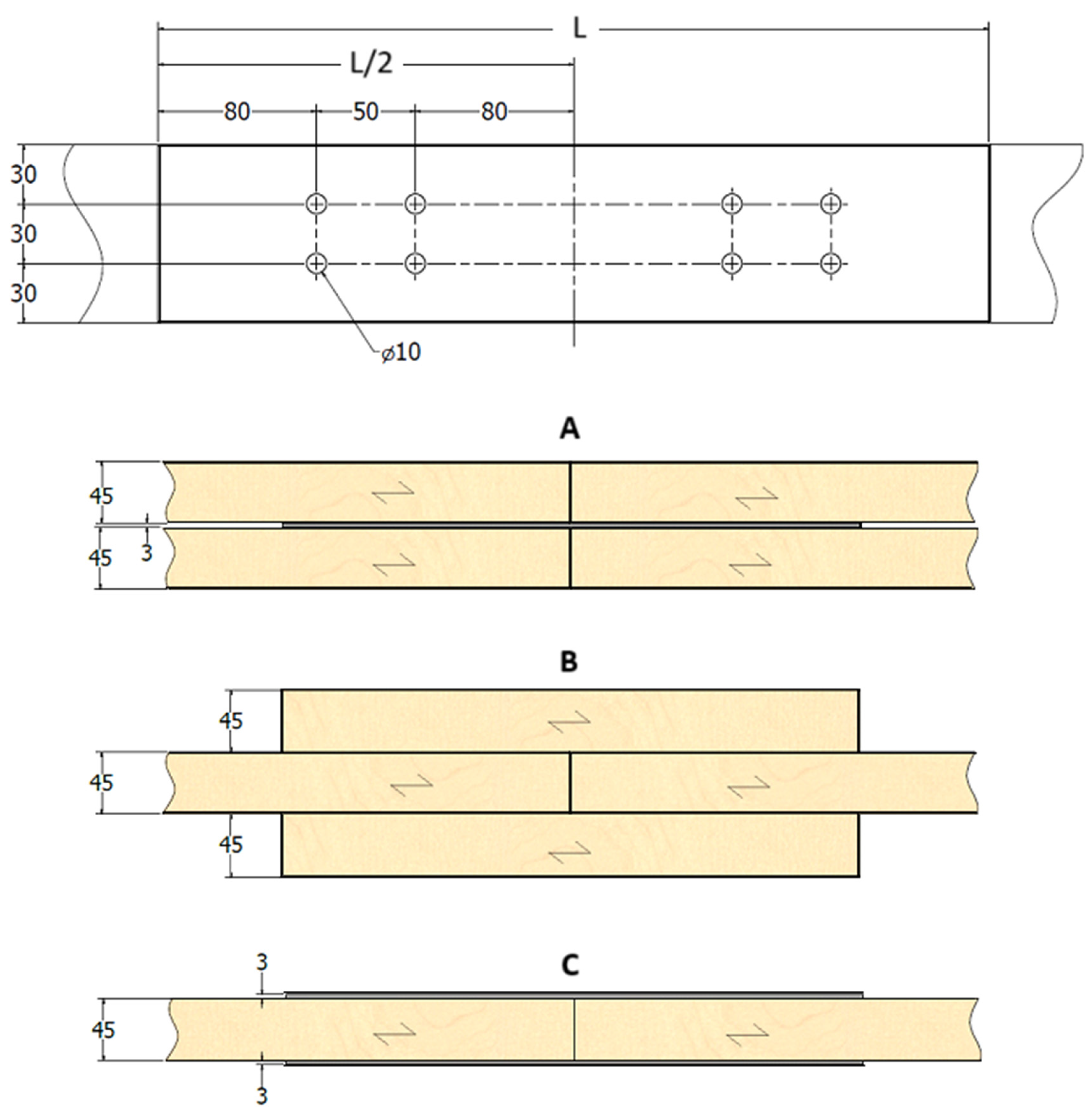
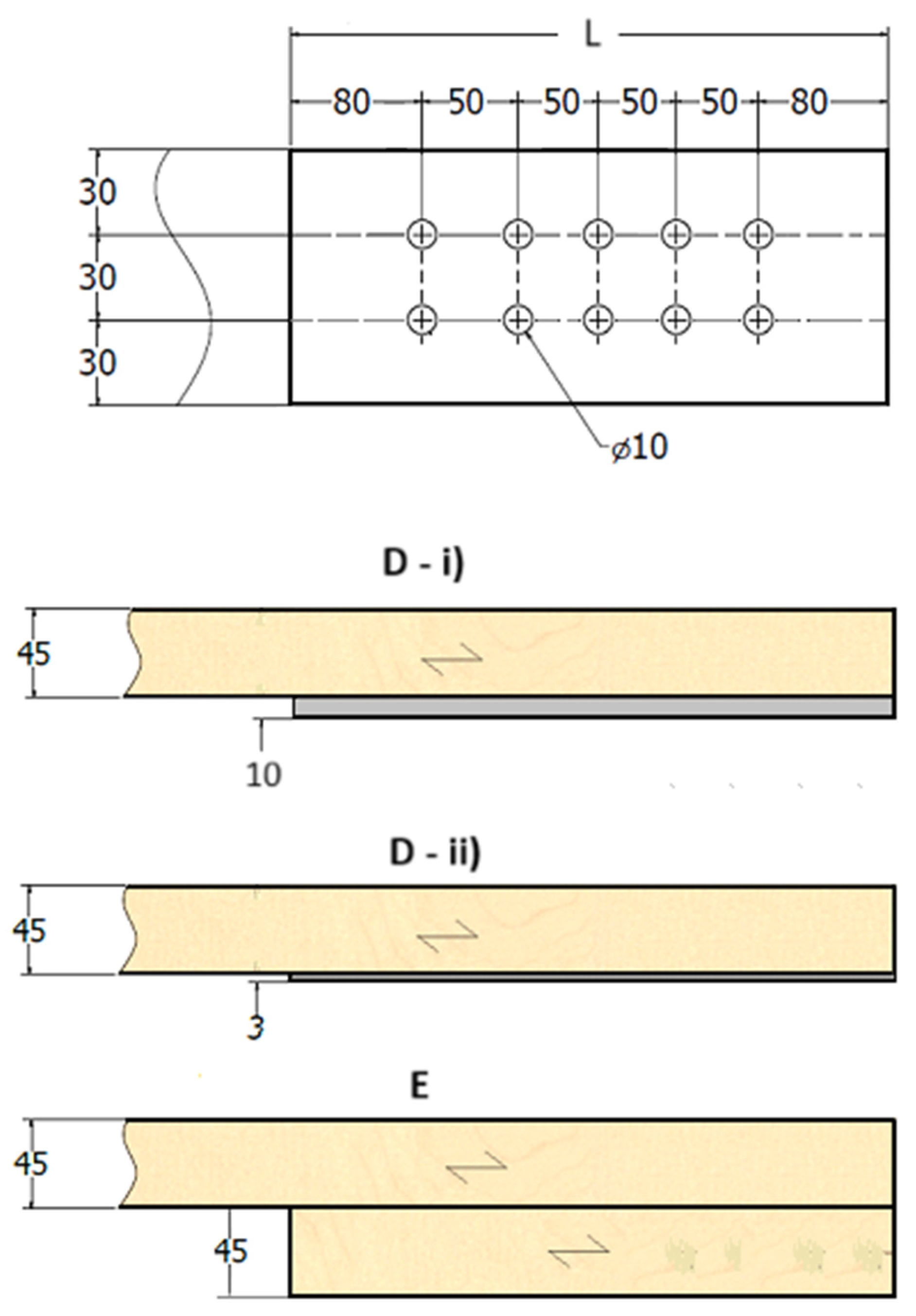
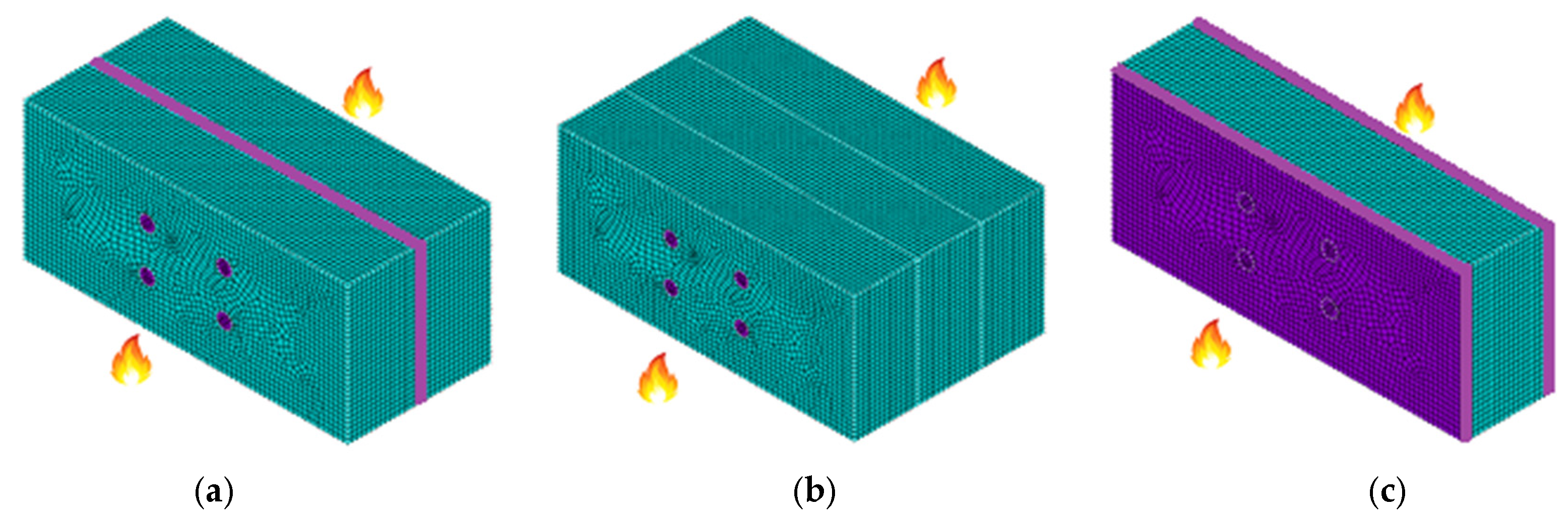
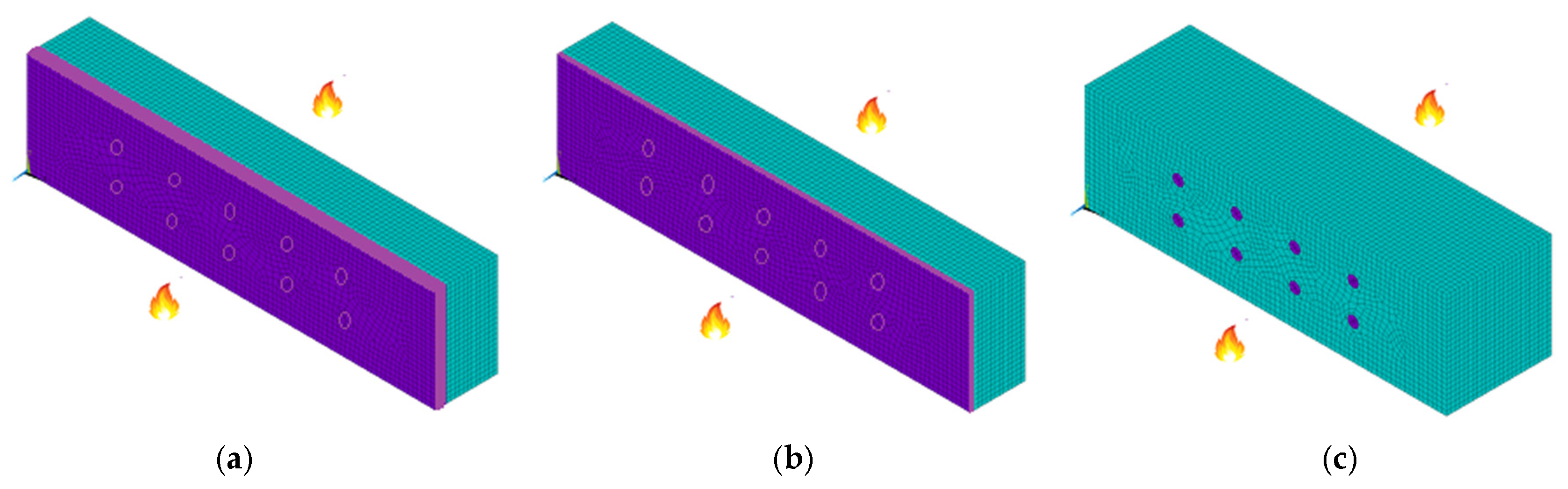


 | With a steel plate of any thickness as the central member |
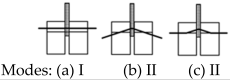 | |
 | |
 |
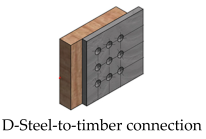 | i) With a thick steel plate in single shear |
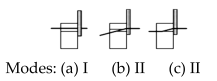 | |
| ii) With a thin steel plate in single shear | |
 | |
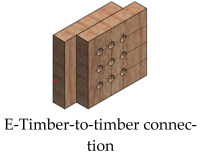 | |
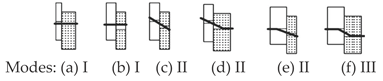 |
| Spacing and Edge/End Distances | Minimum Spacing or Edge/End Distance |
|---|---|
| a1 (parallel to grain) | (3 + 2 + |cos α|) d |
| a2 (perpendicular to grain) | 3 d |
| a3,t (loaded end) | Max (7 d; 80 mm) |
| a4,c (unloaded edge) | 3 d |
| Connection Type | GL20h | GL24h | GL32h | |||
|---|---|---|---|---|---|---|
| d = 8 mm | d = 10 mm | d = 8 mm | d = 10 mm | d = 8 mm | d = 10 mm | |
| A | 3.187 | 4.180 | 3.548 | 4.624 | 3.982 | 5.157 |
| B | 2.544 | 3.424 | 2.710 | 3.801 | 2.897 | 4.251 |
| C | 2.313 | 3.419 | 2.461 | 3.638 | 2.631 | 3.889 |
| D-i) | 2.179 | 3.256 | 2.387 | 3.566 | 2.756 | 4.118 |
| D-ii) | 2.544 | 3.146 | 2.710 | 3.571 | 2.897 | 4.081 |
| E | 2.544 | 3.759 | 2.710 | 4.005 | 2.897 | 4.282 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fonseca, E.M.M. Double vs. Single Shear in Dowelled Timber Connections Under Fire Conditions, Thermal Analysis. Fire 2025, 8, 310. https://doi.org/10.3390/fire8080310
Fonseca EMM. Double vs. Single Shear in Dowelled Timber Connections Under Fire Conditions, Thermal Analysis. Fire. 2025; 8(8):310. https://doi.org/10.3390/fire8080310
Chicago/Turabian StyleFonseca, Elza M. M. 2025. "Double vs. Single Shear in Dowelled Timber Connections Under Fire Conditions, Thermal Analysis" Fire 8, no. 8: 310. https://doi.org/10.3390/fire8080310
APA StyleFonseca, E. M. M. (2025). Double vs. Single Shear in Dowelled Timber Connections Under Fire Conditions, Thermal Analysis. Fire, 8(8), 310. https://doi.org/10.3390/fire8080310








