A Proposal for a Deflection-Based Evaluation Method for Barrel Support Brackets in the Extended Application of Fire Shutters in Logistics Facilities
Abstract
1. Introduction
2. Importance of Fire Compartmentation According to the Characteristics of Logistics Facilities and Problems with Existing Extended Application Methods
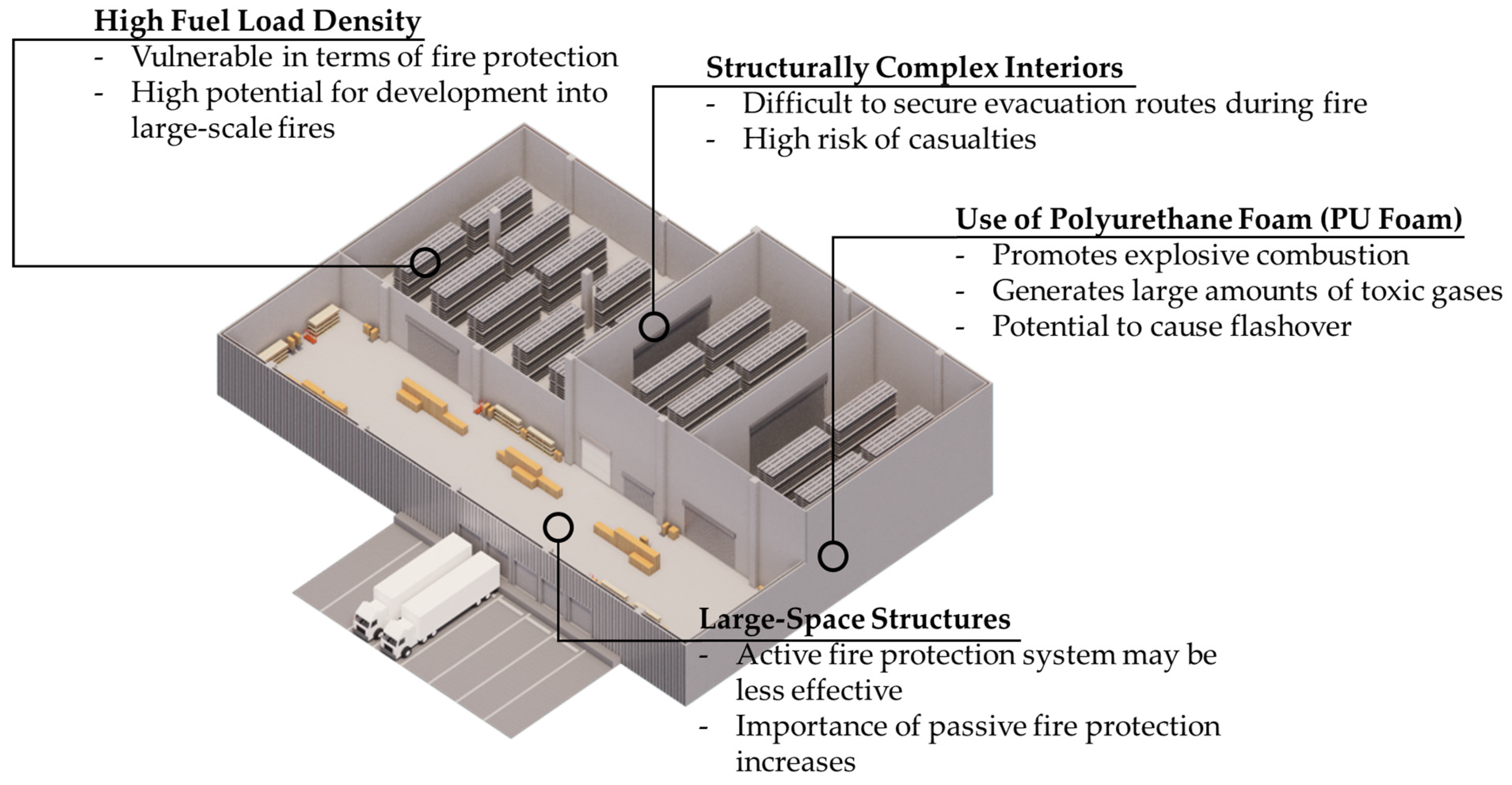
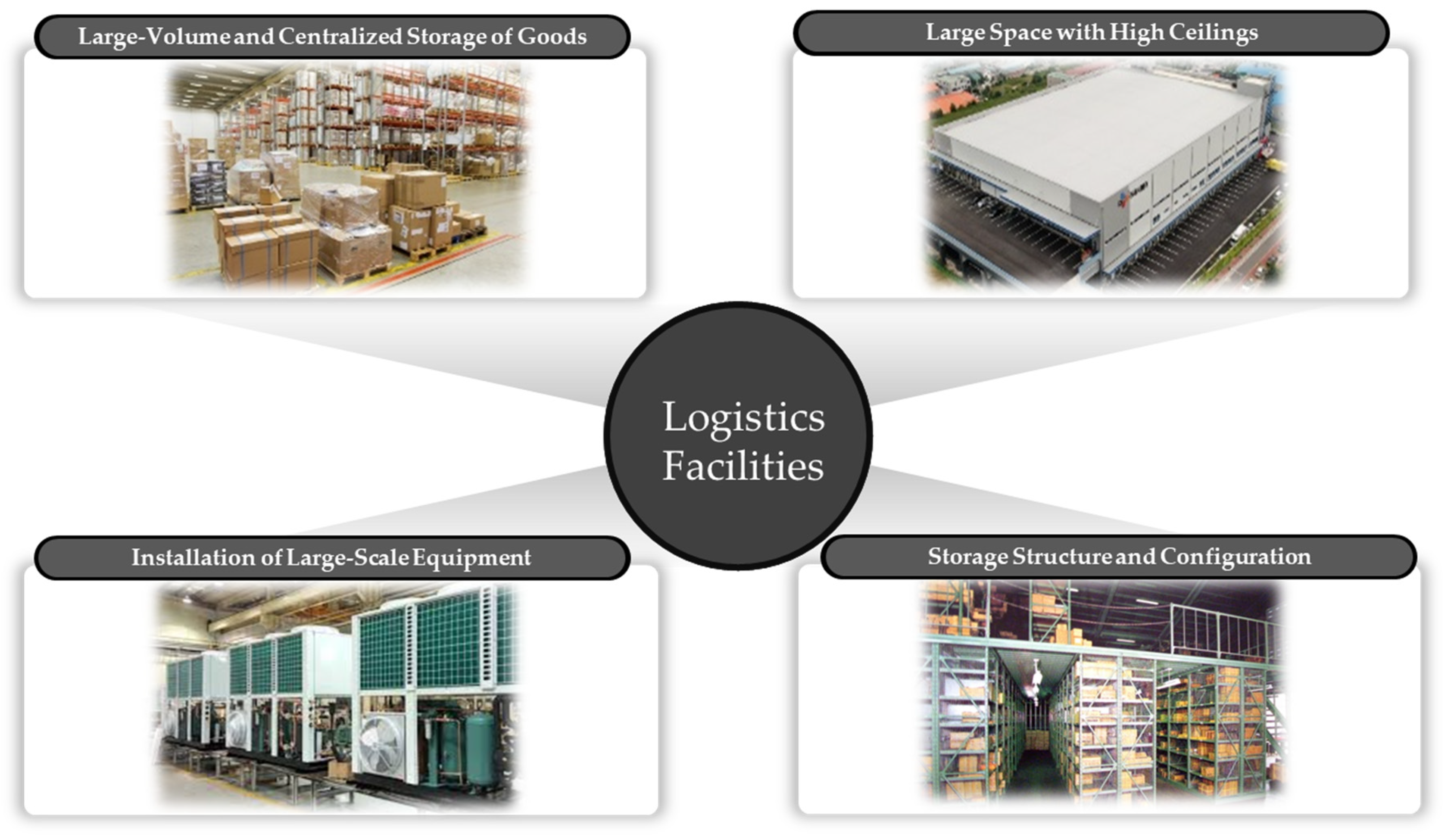
2.1. Fire Characteristics of Logistics Facilities and Performance of Fire Shutters
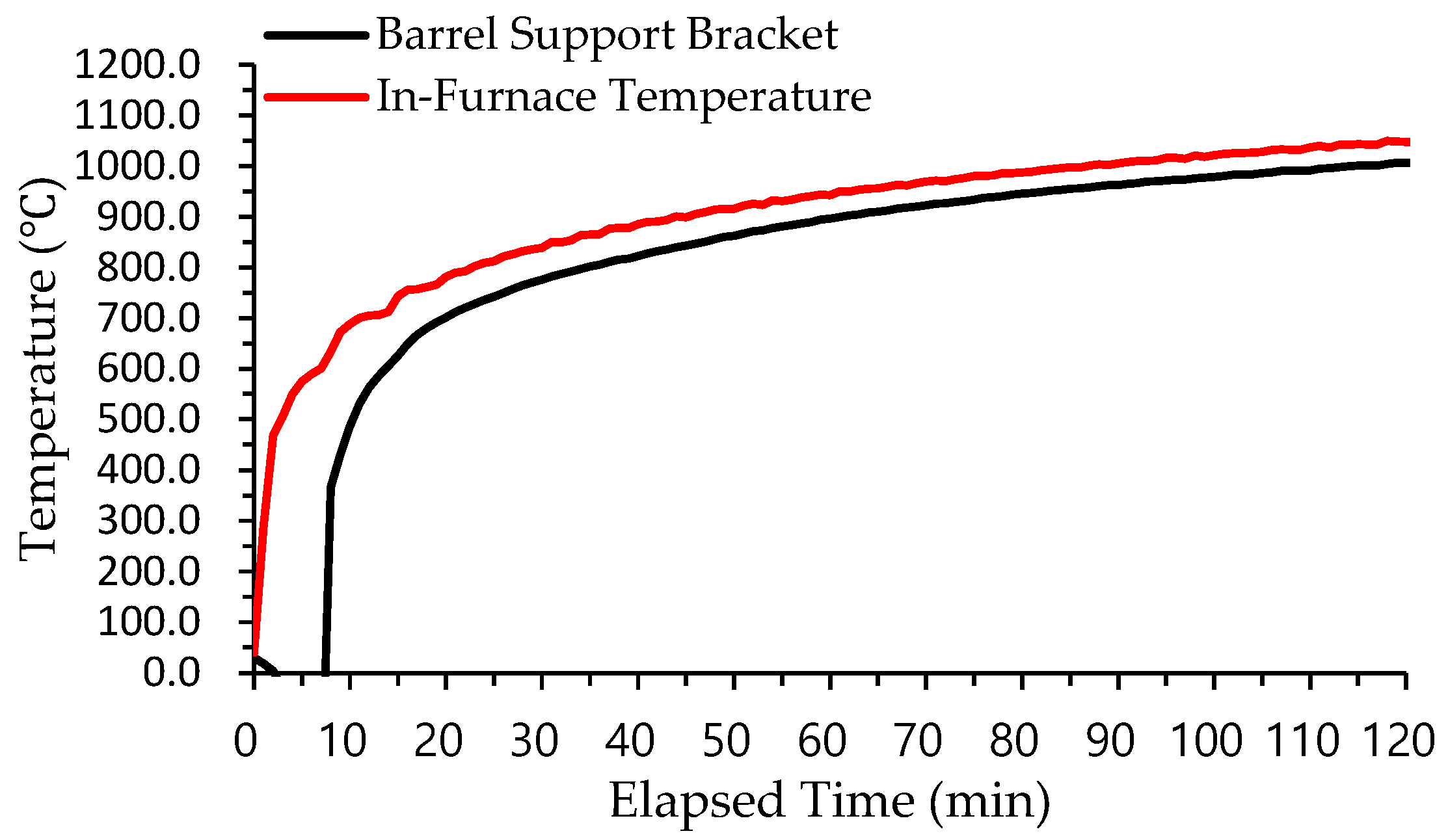
2.2. Issues in Performance Evaluation of Existing Large Fire Shutters and Proposal for Incorporating Deflection Criteria
2.3. Stress Analysis Incorporating Deflection Compared to the Conventional Calculation Method
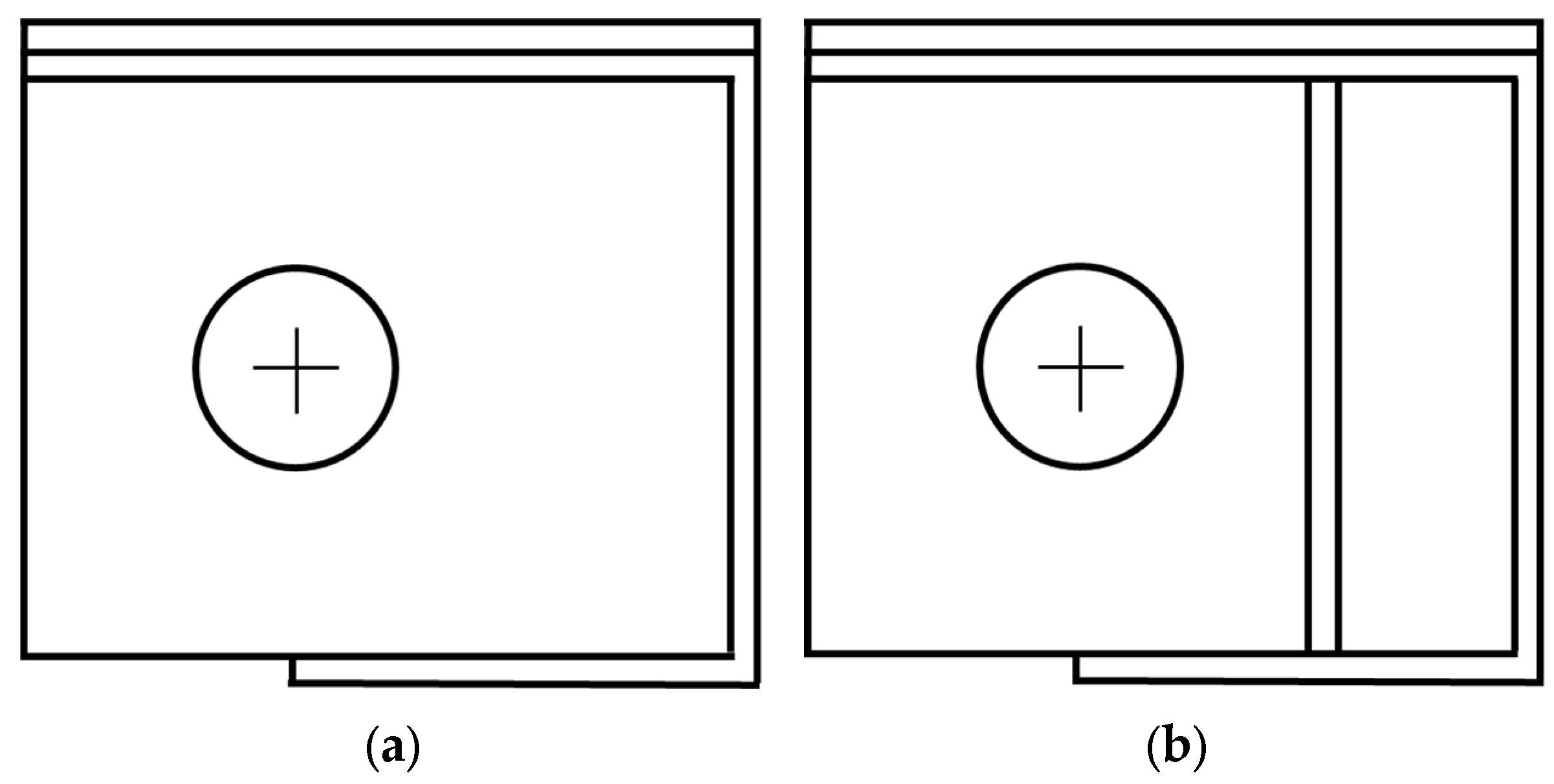
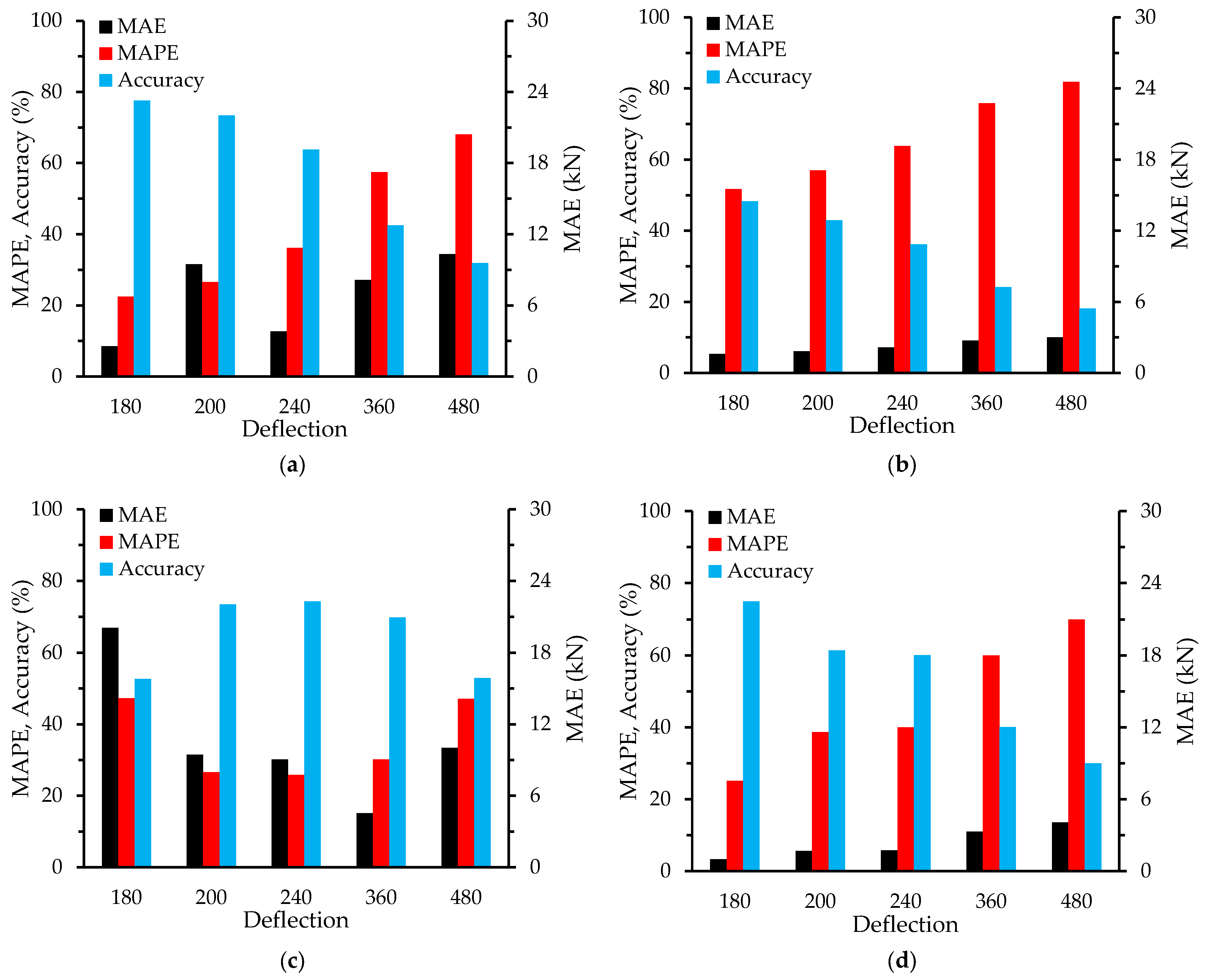
3. Comparison of Deflection by Bracket Type and Optimal Deflection Design Through Regression Analysis
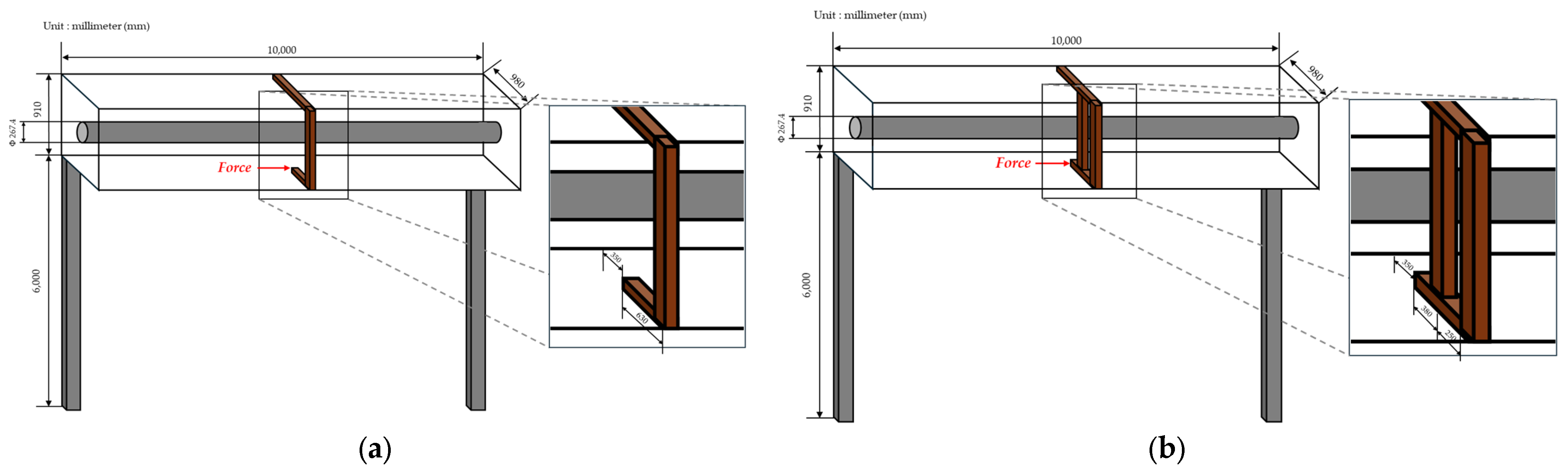
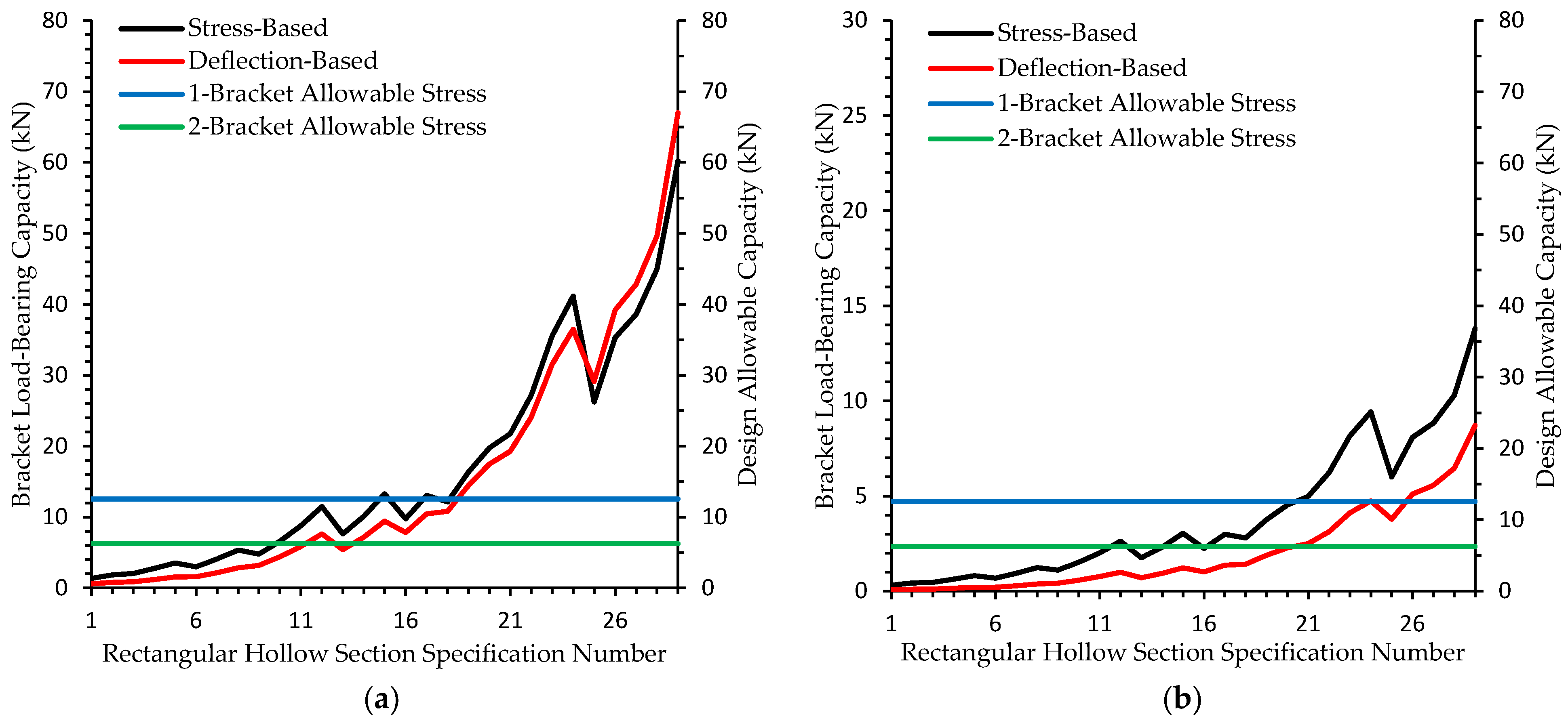
3.1. Comparison of Stress and Deflection at Ambient Temperature and 700 °C in Type-1 Brackets
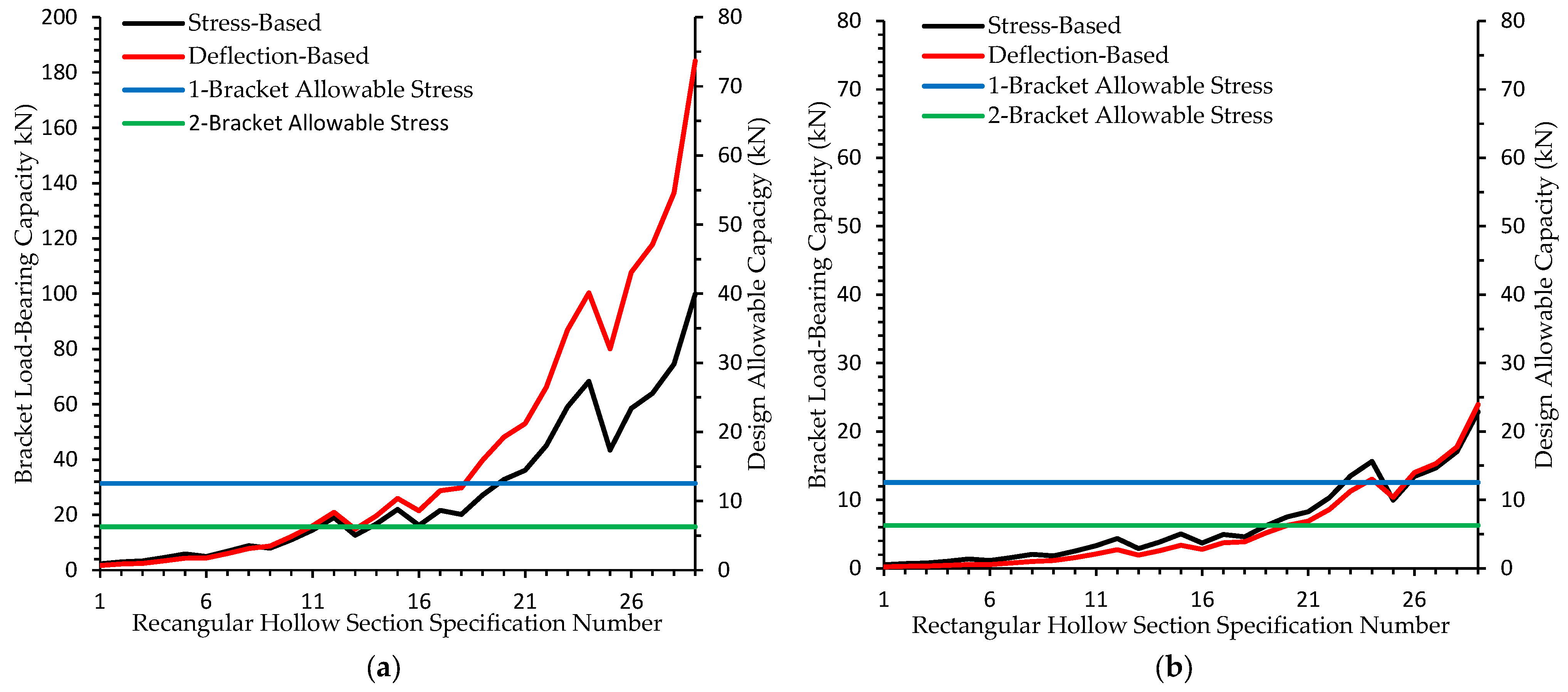
3.2. Comparison of Stress and Deflection at Ambient Temperature and 700 °C in Type-2 Brackets
3.3. Application of Optimal Deflection Limits Through Regression Analysis
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Han, S.W. Characteristics & Fire Hazard Analysis of Logistics Warehouse and a Study on the Optimal Fire Detection Method—Focusing on the Air Sampling Detector. Master’s Thesis, Gachon University Graduate School of Industrial Environment, Seongnam, Republic of Korea, 2023. [Google Scholar]
- You, H.J. A Study on the Fire Risk Analysis and Fire Fighting System of Large Logistis Warehouse. Master’s Thesis, Gachon University Graduate School of Industrial Environment, Seongnam, Republic of Korea, 2020. [Google Scholar]
- Kim, B.H. A Study on the Application of the Fire Shutter Detector According to the Height of the Ceiling in Warehouse. Master’s Thesis, Seoul National University of Science and Technology, Seoul, Republic of Korea, 2018. [Google Scholar]
- National Fire Agency. Standard Guidelines for Performance-Based Design Assessment of Fire Protection Facilities: Causes and Safety Measures of Fire Accidents at Construction Sites; National Fire Agency: Seoul, Republic of Korea, 2023. [Google Scholar]
- Lee, S.B.; Seo, H.W.; Kim, D.H.; Lee, G.Y. Study on Fire Load and Duration of Fire in Logistics Facilities. J. Korea Soc. Hazard Mitig. 2023, 23, 177–185. [Google Scholar] [CrossRef]
- Jung, T.H.; Park, S.H.; Kim, H.K. A study on enhancing institutionalization on the fire analysis of the warehouse at Icheon City. In Proceedings of the 2008 Spring Annual Conference of the Korean Institute of Fire Science and Engineering, Daejeon, Republic of Korea, 24 April 2008; pp. 80–84. [Google Scholar]
- Kim, M.S. A Study on the Fire Simulation of Refrigerated Warehouse for the Analysis of the Relationship Between Oxygen Concentration and Fire Risk. Master’s Thesis, Gachon University, Seongnam, Republic of Korea, 2023. [Google Scholar]
- Lee, Y.W. A Study on Performance Criteria for Fire Compartment and Fire Door. Master’s Thesis, University of Korea, Seoul, Republic of Korea, 2017. [Google Scholar]
- Lee, J.G.; Min, S.H. A Study on the Operational Characteristics and Adaptability of Sprinkler Systems in Frozen Warehouses. J. Soc. Disaster Inf. 2025, 21, 300–309. [Google Scholar]
- An, B.K.; Kim, W.H.; Yang, S.J.; Ham, E.G. A study on the improvement of field activity for firemen in sandwich panel warehouse. J. Soc. Disaster Inf. 2020, 16, 421–429. [Google Scholar]
- Han, H.S. Methodology for Predicting Fire Growth Curves Using Combustibles Based on Fire Risk Classification of Commodities in Rack Storage Warehouse. Ph.D. Thesis, Daejeon University, Daejeon, Republic of Korea, 2025. [Google Scholar]
- Campbell, R. Warehouse Structure Fires; National Fire Protection Association NFPA, Research, Data and Analytics Division: Quincy, MA, USA, 2022. [Google Scholar]
- Nadile, L. The Problem with Big; National Fire Protection Association NFPA-192-Journal: Quincy, MA, USA, 2009. [Google Scholar]
- Harrington, J.L. Lessons Learned From Understanding Warehouse Fires. Fire Prot. Eng. 2006, 29, 22–28. [Google Scholar]
- Seo, H.W. A Study on the Standard Improvement of the Firestop System Installed in the Penetration Within the Fire Separating Element. Ph.D. Thesis, University of Seoul, Seoul, Republic of Korea, 2020. [Google Scholar]
- Lee, E.C. Case Analysis of Warehouse Fire by Fire Dynamic Simulation. Master’s Thesis, Chungbuk National University Graduate School of Industry, Cheongju, Republic of Korea, 2012. [Google Scholar]
- Ministry of Land, Infrastructure and Transport (MOLIT). Standards for Automatic Fire Shutters and Fire Doors, Article 2(2); MOLIT Notification No. 2019-592; Ministry of Land, Infrastructure and Transport: Sejong, Republic of Korea, 2019. [Google Scholar]
- BS 476-22:1987; Fire Tests on Building Materials and Structures—Part 22: Methods for Determination of the Fire Resistance of Non-Loadbearing Elements of Construction. BSI: London, UK, 1987.
- AS 1530.4:1994; Methods for Fire Tests on Building Materials, Components and Structures—Fire Resistance Tests of Elements of Building Construction. Standards Australia: Sydney, Australia, 1994.
- ISO 3008-1:2007; Fire Resistance Tests—Door and Shutter Assemblies—Part 1: General Requirements. ISO: Geneva, Switzerland, 2007.
- ISO 834-1:2017; Fire Resistance Tests—Elements of Building Construction—Part 1: General Requirements. ISO: Geneva, Switzerland, 2017.
- NFPA 252:2017; Standard Methods of Fire Tests of Door Assemblies. NFPA: Quincy, MA, USA, 2017.
- ASTM E119-19; Standard Test Methods for Fire Tests of Building Construction and Materials. ASTM: West Conshohocken, PA, USA, 2019.
- Woo, Y.J. A Suggested Method for Performance Evaluation of Large Scale Fireproof Shutters. J. Korea Soc. Hazard Mitig. 2020, 20, 111–116. [Google Scholar] [CrossRef]
- BS EN 15269-10; Extended Application of Test Results for Fire Resistance and/or Smoke Control for Door, Shutter and Openable Window Assemblies—Part 10: Fire Resistance for Steel Hinged and Pivoted Doorsets. BSI: London, UK, 2011.
- BS EN 15269-11; Extended Application of Test Results for Fire Resistance and/or Smoke Control for Door, Shutter and Openable Window Assemblies—Part 11: Fire Resistance for Rolling Shutters. BSI: London, UK, 2018.
- EN 1993-1-2; Eurocode 3: Design of Steel Structures—Part 1-2: General Rules—Structural Fire Design. CEN: Brussels, Belgium, 2005.
- Kim, S.Y.; Chu, D.S.; Lee, H.D.; Shin, K.J. Mechanical Properties of Structural Steel at Elevated Temperature. J. Korean Soc. Steel Constr. 2018, 30, 257–264. [Google Scholar] [CrossRef]
- Daw, T.A.; Daw, A.M. Stress and Deflection Analysis of Cantilever Mean by Numerically. Int. J. Inov. Sci. Res. Technol. 2020, 5, 718–721. [Google Scholar]
- Ministry of Land, Infrastructure and Transport (MOLIT). Standards of Structural Design for Buildings; MOLIT Notification No. 2016-317; Ministry of Land, Infrastructure and Transport: Sejong, Republic of Korea, 2016. [Google Scholar]
- International Code Council. International Building Code 2015; International Code Council: Country Club Hills, IL, USA, 2014. [Google Scholar]
- KS D 3568; Hot-Rolled Structural Rectangular Hollow Sections of Non-Alloy and Fine Grain Steels. Korean Agency for Technology and Standards: Eumseong, Republic of Korea, 2023.
- Lee, H.J.; Shon, J.G. Non-Integral AC Capacitor Voltage Calculation Method for Shunt Hybrid Active Power Filter. IEEE Access 2023, 11, 67968–67978. [Google Scholar] [CrossRef]
- Lee, J.W.; Park, K.J.; Cho, J.T.; Kim, J.Y.; Son, S.Y. Novel monitoring system for low-voltage DC distribution network using deep-learning-based disaggregation. IEEE Access 2020, 8, 185266–185275. [Google Scholar] [CrossRef]
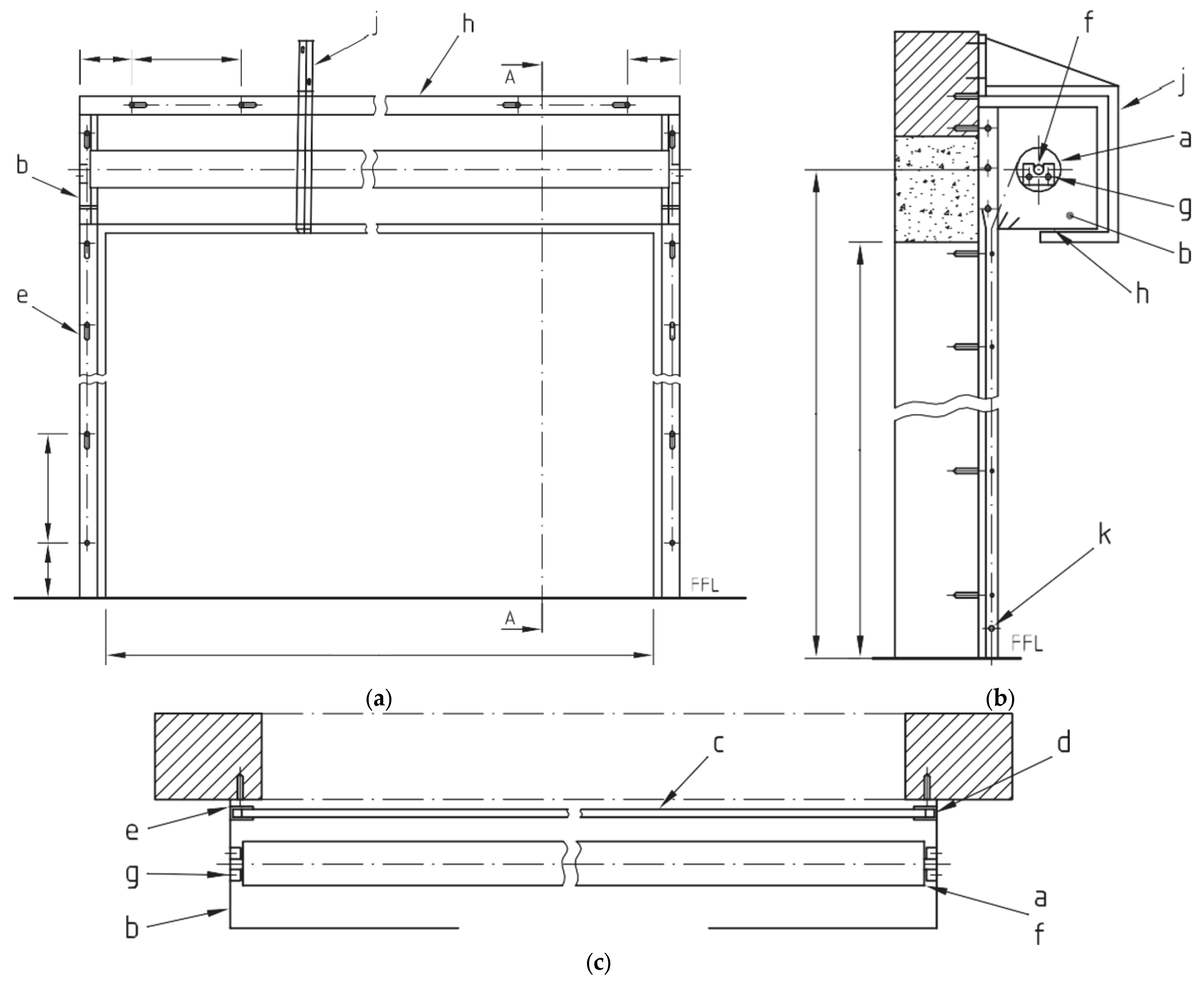

| Component Names | ||
|---|---|---|
| a: Barrel | b: End Plate/Bracket | c: Curtain |
| d: Guide g: Shaft Cup/Support k: Bottom rail | e: Guide Fixing Angle h: Coil Casing/Hood | f: Shaft j: Barrel Support Bracket |
| Reduction Factors | ||
|---|---|---|
| Steel Temperature θa | Linear Elastic Range kE, θ = Ea, θ/Ea | Effective Yield Strength K y, θ = f y, θ/fy (f u, θ/f y, θ) * |
| 20 °C | 1.000 | 1.000 (1.25) |
| 100 °C | 1.000 | 1.000 (1.25) |
| 200 °C | 0.900 | 1.000 (1.25) |
| 300 °C | 0.800 | 1.000 (1.25) |
| 400 °C | 0.700 | 1.000 (1.00) |
| 500 °C | 0.600 | 0.780 (1.00) |
| 600 °C | 0.310 | 0.470 (1.00) |
| 700 °C | 0.130 | 0.230 (1.00) |
| 800 °C | 0.090 | 0.110 (1.00) |
| 900 °C | 0.0675 | 0.060 (1.00) |
| 1000 °C | 0.0450 | 0.040 (1.00) |
| 1100 °C | 0.0225 | 0.020 (1.00) |
| 1200 °C | 0.0000 | 0.000 (1.00) |
| Construction | Live Load | Snow or Wind Load | Dead + Live Load |
|---|---|---|---|
| Roof Members Supporting Plaster or Stucco Ceiling Supporting Non-Plaster Ceiling Not Supporting Ceiling Floor Members | |||
| //360 //240 //180 | //360 //240 //180 | //240 //180 //120 | |
| //360 | - | //240 | |
| Exterior Walls With Plaster or Stucco Finishes With Other Brittle Finishes With Flexible Finishes | |||
| - - - | //360 //240 //120 | - - - | |
| Interior Partition With Plaster or Stucco Finishes With Other Brittle Finishes With Flexible Finishes Farm Buildings Greenhouses | |||
| //360 //240 //120 - - | - - - - - | - - - //180 //120 |
| Rectangular Hollow Section Specification Number | Side Length A × B, mm | Thickness mm | Area Moment of Inertia Ix, Iy, cm4 | Section Modulus Zx, Zy, cm3 |
|---|---|---|---|---|
| 1 | 50 × 30 | 1.6 | 7.96, 6.3 | 3.18, 2.4 |
| 2 | 50 × 30 | 2.3 | 10.6, 4.7 | 4.25, 3.17 |
| 3 | 50 × 50 | 1.6 | 11.7 | 4.68 |
| 4 | 50 × 50 | 2.3 | 15.9 | 6.34 |
| 5 | 50 × 50 | 3.2 | 20.4 | 8.16 |
| 6 | 60 × 60 | 1.6 | 20.7 | 6.89 |
| 7 | 60 × 60 | 2.3 | 28.3 | 9.44 |
| 8 | 60 × 60 | 3.2 | 36.9 | 12.3 |
| 9 | 75 × 75 | 1.6 | 41.3 | 11 |
| 10 | 75 × 75 | 2.3 | 57.1 | 15.2 |
| 11 | 75 × 75 | 3.2 | 75.5 | 20.1 |
| 12 | 75 × 75 | 4.5 | 98.6 | 26.3 |
| 13 | 80 × 80 | 2.3 | 69.9 | 17.5 |
| 14 | 80 × 80 | 3.2 | 92.7 | 23.2 |
| 15 | 80 × 80 | 4.5 | 122 | 30.4 |
| 16 | 90 × 90 | 2.3 | 101 | 22.4 |
| 17 | 90 × 90 | 3.2 | 135 | 29.9 |
| 18 | 100 × 100 | 2.3 | 140 | 27.9 |
| 19 | 100 × 100 | 3.2 | 187 | 37.5 |
| 20 | 100 × 100 | 4 | 226 | 45.3 |
| 21 | 100 × 100 | 4.5 | 249 | 49.9 |
| 22 | 100 × 100 | 6 | 311 | 62.3 |
| 23 | 100 × 100 | 9 | 408 | 81.6 |
| 24 | 100 × 100 | 12 | 471 | 94.3 |
| 25 | 125 × 125 | 3.2 | 376 | 60.1 |
| 26 | 125 × 125 | 4.5 | 506 | 80.9 |
| 27 | 125 × 125 | 5 | 553 | 88.4 |
| 28 | 125 × 125 | 6 | 641 | 103 |
| 29 | 125 × 125 | 9 | 865 | 138 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shon, J.W.; Seo, H.; Kim, D.; Lee, S.; Hong, S.; Jung, S. A Proposal for a Deflection-Based Evaluation Method for Barrel Support Brackets in the Extended Application of Fire Shutters in Logistics Facilities. Fire 2025, 8, 253. https://doi.org/10.3390/fire8070253
Shon JW, Seo H, Kim D, Lee S, Hong S, Jung S. A Proposal for a Deflection-Based Evaluation Method for Barrel Support Brackets in the Extended Application of Fire Shutters in Logistics Facilities. Fire. 2025; 8(7):253. https://doi.org/10.3390/fire8070253
Chicago/Turabian StyleShon, Jong Won, Heewon Seo, Daehoi Kim, Seungjea Lee, Sungho Hong, and Subin Jung. 2025. "A Proposal for a Deflection-Based Evaluation Method for Barrel Support Brackets in the Extended Application of Fire Shutters in Logistics Facilities" Fire 8, no. 7: 253. https://doi.org/10.3390/fire8070253
APA StyleShon, J. W., Seo, H., Kim, D., Lee, S., Hong, S., & Jung, S. (2025). A Proposal for a Deflection-Based Evaluation Method for Barrel Support Brackets in the Extended Application of Fire Shutters in Logistics Facilities. Fire, 8(7), 253. https://doi.org/10.3390/fire8070253






