Regression Analysis of Heat Release Rate for Box-Type Power Bank Based on Experimental and Machine Learning Methods

Abstract

In recent years, new fire loads dominated by power banks have caused multiple fire incidents in transportation hubs, posing severe challenges to fire safety. This study uses experimental testing and machine learning regression analysis to explore the heat release rate (HRR) characteristics and influencing factors of box-type power banks under fire conditions. A 1 MW calorimeter was used to conduct four sets of experiments involving a total of 15 box-type power banks, measuring the HRR and analyzing its correlation with oxygen consumption, carbon dioxide generation, smoke temperature, and the fire growth rate. Based on the experimental data, HRR prediction models were constructed using decision tree regression (DT), K-nearest neighbor regression (KNN), and linear regression (LR). The results indicate that the DT model performs best in HRR prediction (MAE = 0.4889, MSE = 0.7414, RMSE = 0.8571, R² = 0.9991), effectively capturing the nonlinear variation patterns in the HRR. The correlation analysis and regression analysis conducted in this study provide crucial data support for fire combustion characteristics research, fire risk assessment, and fire safety optimization. Furthermore, the findings provide crucial data support for research on fire combustion characteristics and data-driven fire risk assessment, which may serve as a foundation for future AI-based real-time fire detection applications.

1. Introduction

With the rapid development of transportation hubs [1], the variety of electronic devices carried by passengers has increased significantly. Among them, various types of power banks are widely used in railway stations, airports, and subways due to their convenience, as shown in Figure 1. However, the high passenger density in public transportation areas has raised concerns regarding emergency evacuation in fire incidents. Studies have shown that in high-density metro stations, fire incidents could result in mass casualties due to limited evacuation time [2,3]. Recent fire incidents caused by the thermal runaway of power banks indicate that they have become a critical fire load, posing a significant threat to fire safety in transportation hubs. According to the U.S. Federal Aviation Administration (FAA), the number of thermal runaway incidents involving portable electronic devices in aircraft cabins—such as power banks—has been increasing rapidly, with lithium battery-related accidents frequently occurring [4]. Similarly, in China, a fire incident caused by a power bank’s thermal runaway occurred at the boarding bridge of Shanghai Hongqiao Airport, significantly impacting transportation operations and passenger safety [5]. In enclosed or high-density environments, power bank thermal runaway can lead to severe fire propagation risks, highlighting the urgent need for in-depth research on its fire characteristics and safety implications.

Currently, research on power banks mainly focuses on the safety of their internal lithium-ion batteries. Many studies have extensively explored the thermal runaway phenomenon and its triggers. For example, the University of Science and Technology of China conducted thermal runaway experiments on 243 Ah lithium-ion batteries, analyzing temperature, voltage, mass loss, heat release characteristics, and gas emissions. The results indicate that fire risk increases with a higher state of charge (SOC), accelerating thermal runaway propagation [6]. Similarly, researchers at the University of Bologna conducted multiple battery fire tests to investigate the impact of thermal runaway on fire propagation and spread [7]. These studies reveal that thermal runaway is influenced not only by material properties and electrochemical behavior but also by environmental factors and the presence of combustible materials. However, existing research primarily focuses on individual battery cells, with limited studies on the overall fire behavior of power banks, particularly their heat release characteristics as a fire load. The heat release rate (HRR) is a key parameter for evaluating fire hazard, as it directly determines the fire growth rate and intensity. Accurate HRR measurement and analysis are thus crucial. Currently, HRR studies primarily rely on experimental testing, with common methods including oxygen consumption calorimetry (OCC) [8] and mass loss calorimetry (MLC) [9]. OCC quantifies the relationship between oxygen consumption and heat release during combustion, offering high measurement accuracy and making it suitable for full-scale and medium-scale fire tests. MLC measures sample mass loss during combustion and estimates the HRR based on the material’s thermal properties, making it more suitable for small-scale studies. While traditional experimental methods effectively measure the HRR, they incur high costs, require long testing cycles, and have limitations in simulating complex fire conditions. Consequently, researchers have explored numerical simulations and machine learning techniques to develop HRR prediction models for improving assessment efficiency and accuracy. However, numerical simulation methods require precise material parameters, such as the smoke production rate, thermal conductivity, and specific heat capacity, which limits their broader application.

In contrast, machine learning offers significant advantages in HRR research. Firstly, it enables fast HRR prediction under different conditions based on experimental data, reducing dependence on expensive physical tests, and thereby lowering research costs. Secondly, the HRR is influenced by various complex factors (e.g., material properties, environmental conditions, and battery status), making it challenging for traditional methods to accurately model its nonlinear relationships. Machine learning can automatically learn underlying patterns in a data-driven manner, improving predictive accuracy. Additionally, machine learning models can be integrated with numerical simulations and real-time monitoring to predict the HRR across different conditions and enhance early fire warning systems.

Although prior research has extensively explored the thermal runaway behavior of individual lithium-ion cells and battery modules [10,11], relatively few studies have examined the fire development and HRR characteristics of complete power bank units in real-use scenarios. Existing HRR studies often focus on small-scale combustion testing or idealized simulation environments, which do not fully capture the nonlinear and complex behavior of emerging fire loads such as box-type power banks. Moreover, traditional modeling methods rely on predefined equations and assumptions, limiting their ability to adapt to diverse materials and configurations. To address these limitations, this study investigates the heat release behavior of box-type power banks under realistic fire conditions and develops data-driven HRR prediction models using machine learning. By focusing on complete power bank units and quantifying their combustion characteristics experimentally, this research provides novel insights into the fire risk posed by such devices in public buildings and transportation terminals. Thus, this study investigates box-type power banks in railway stations, conducting four sets of experiments with 15 samples to measure HRR and apply machine learning analysis. This aims to provide a scientific basis for fire safety in transportation hubs. In the data analysis phase, multiple machine learning regression models were tested for HRR prediction. The decision tree algorithm was found to effectively capture nonlinear relationships, demonstrating the best predictive performance. To improve model generalization and stability, five-fold cross-validation was used for training and evaluation. Additionally, by quantifying the heat release characteristics of box-type power banks, this study provides valuable data for optimizing fire safety strategies in transportation hubs.

In this paper, Section 1 introduces the background of transportation hubs, the emerging fire risk posed by power banks, and the current state of research and methodologies. In the second section, the experimental methods, test equipment, correlation analysis model, and HRR regression models used in the study are described. The third section presents and discusses the results, comparing the prediction performance of different models. Section 4 concludes the study, summarizing key findings and future research directions.

2. Methods

2.1. Experimental Method for HRR

A 1 MW calorimetry system (made by Fire Institute, China Academy of Building Research, Beijing, China) was employed to conduct HRR tests on box-type power banks. As illustrated in Figure 2, the experimental setup consisted of an electronic scale, a smoke collection hood, a data acquisition station, and a smoke measurement system. The 1 MW calorimeter used in this study was equipped with an integrated gas analysis system to continuously monitor combustion gas concentrations. Oxygen (O₂) concentration was measured using a paramagnetic oxygen analyzer, while carbon dioxide (CO₂) and carbon monoxide (CO) concentrations were detected using non-dispersive infrared (NDIR) sensors. The gas sampling was conducted from the exhaust duct, with automatic compensation for humidity and temperature effects. These gas measurements were synchronized with the HRR calculation based on the oxygen consumption method, ensuring accurate and reliable data acquisition.

The samples were sourced from a railway station in China, including both the charging box and power banks. The charging box was made of PC and ABS V0-grade fire-resistant materials, with dimensions of 21 cm × 21 cm × 21 cm, containing six slots for power banks. Each power bank had a rated capacity of 5000 mAh. Before testing, samples were stored in a controlled environment for 24 h (relative humidity: 56.5%; temperature: 24.6 °C) to minimize external influences. During the experiment, 20 mL of gasoline was used to ignite the box-type power bank, allowing for an assessment of heat release characteristics and combustion behavior under fire conditions. The 1 MW calorimeter measured the HRR using the oxygen consumption calorimetry (OCC) method, based on the assumption that 1 g of oxygen consumption releases approximately 13.1 MJ of energy [12]. The HRR was calculated using the following formulas:

$$\dot{q}=E\left({\dot{m}}_{o_2}^0-{\dot{m}}_{o_2}\right)$$

(1)

$$E={\displaystyle \frac{{∆H}_c}{{\gamma }^0}}$$

(2)

$\dot{q}$ represents the heat release rate; $E$ is the heat of combustion per unit mass of oxygen consumed (MJ·kg⁻¹); ${\dot{m}}_{o_2}^0{, \dot{m}}_{o_2}$ denote the mass flow rate of oxygen in the initial air and during combustion, respectively (kg·s⁻¹); ${∆H}_c$ represents the heat of combustion of the fuel (MJ·kg⁻¹); and ${\gamma }^0$ is the stoichiometric ratio of oxygen to fuel in a complete combustion reaction.

A total of 4 test scenarios were conducted for the box-type power banks, as shown in

Table 1. Summary of experimental test for box-type power banks.

Test	Number of Boxes	Number of Power Banks
I	1	6
II	2	12
III	4	24
IV	8	48

.

It is important to note that the state of charge (SOC) of the individual power banks was not measured or standardized prior to testing. The samples were directly obtained from a railway station’s charging box to replicate realistic fire scenarios. Although this may introduce uncontrolled variation, it reflects real-world fire loads more accurately. Future studies are encouraged to examine the influence of SOC levels on HRR characteristics to enhance model robustness and fire risk interpretation.

2.2. Selection of Combustion Process-Related Features

To comprehensively analyze the relationship between the HRR and combustion process-related features, this study selects ten key features for analysis. These features encompass critical variables in the combustion process and provide a comprehensive reflection of combustion dynamics [13,14]. The selected features and their descriptions are presented in

Table 2. Feature abbreviations and descriptions.

Abbreviations	Full Name	Descriptions	Unit
O2	Oxygen	Oxygen concentration, commonly used for combustion and fire testing analysis.	% (volume)
CO2	Carbon Dioxide	A combustion byproduct, commonly used for fire testing and environmental monitoring.	% (volume)
CO	Carbon Monoxide	A toxic byproduct of incomplete combustion, commonly used for fire and air quality analysis.	% (volume)
ST	Smoke Temperature	Smoke temperature, commonly used for fire characteristic analysis.	Kelvin (K)
THR	Total Heat Release	The total amount of heat released during material combustion.	MJ
FIGRA	Fire Growth Rate	A key parameter used to measure the development speed of a fire	kW/s
SPR	Smoke Production Rate	Describes the rate at which smoke is generated during a fire	m2/s
ARHE	Average Rate of Heat Emission	Represents the average heat release rate per unit time during combustion	kW
SMOGRA	Smoke Growth Rate	Measures the rate of smoke growth during a fire	m2/s2
TP	Total Propagation	Represents the overall spread potential, which may be related to fire spread indicators	(dimensionless)
PBN	Power Box Number	The number of box-type power banks	count (integer)

.

The fire growth rate (FIGRA) is defined as the ratio between the measured heat release rate (HRR) and the time taken to reach that value from the onset of ignition. It is used to characterize how rapidly a fire develops, with higher FIGRA values indicating faster fire growth and greater hazard potential. In this study, the FIGRA was automatically computed by the calorimeter’s internal software based on the real-time HRR data acquired during each test.

2.3. Correlation Analysis

To further investigate the relationship between O₂, CO₂, CO, ST, THR, FIGRA, SPR, ARHE, SMOGRA, TP, and the number of box-type power banks (PBN) with the HRR, this study conducts a correlation analysis [14] to reveal the influence of various combustion characteristic variables on HRR variations. Additionally, to explore the interrelationships among the combustion feature variables, we also calculate the pairwise correlations between them. Prior to analysis, all features were standardized (z-score normalization) to eliminate scale effects. The correlation was computed over the full dataset, including all experimental test scenarios. The Pearson coefficient, ranging from −1 to 1, was used to measure the strength and direction of linear relationships. A positive r-value indicates a direct correlation, while a negative r-value indicates an inverse correlation. The results were visualized using a heatmap and a bar chart, calculated in MATLAB 2024b and created in Origin 2025, to highlight the most influential variables related to the HRR. When the correlation value is close to 0, it implies a weak or negligible relationship between the two variables, indicating that their variations are largely independent of each other. The Pearson correlation coefficient is calculated as follows:

$$r_{XY}={\displaystyle \frac{{\sum }_{i=1}^n\left(x_i-\overline{x}\right)\left(y_i-\overline{y}\right)}{\sqrt{{\sum }_{i=1}^n{\left(x_i-\overline{x}\right)}^2}\cdot \sqrt{{\sum }_{i=1}^n{\left(y_i-\overline{y}\right)}^2}}}$$

(3)

where $x_i$, $y_i$ are the individual sample points; $\overline{x}$, $\overline{y}$ are the means of $X$ and $Y$, respectively; the numerator represents the covariance between $X$ and $Y$; and the denominator is the product of their standard deviations.

Furthermore, to provide an intuitive representation of variable correlations, a heatmap visualization is employed, displaying correlation coefficients using a color gradient, which facilitates the identification of variables with significant impacts on the HRR. Additionally, a bar chart is plotted to visually examine the correlations between the HRR and selected features.

2.4. Regression Analysis

To predict HRR variations based on combustion characteristics, ten combustion-related features—O₂, CO₂, CO, ST, THR, FIGRA, SPR, ARHE, SMOGRA, and TP—were selected for regression analysis. In this study, three representative regression models—DT, LR, and KNN [15]—were selected to explore different modeling paradigms for HRR prediction. The selection was based on the need to balance interpretability, flexibility, and suitability for modeling nonlinear relationships. DT models can effectively capture nonlinear dependencies and feature interactions. LR provides a simple, interpretable baseline for evaluating the presence of linear trends in the data. KNN, as a non-parametric and instance-based learner, offers a flexible approach that does not impose assumptions about the data distribution. This combination allows for a comprehensive comparative evaluation to identify the most suitable approach for fire-related regression tasks. During the regression analysis, the selected features are first standardized or normalized to eliminate differences in scale. Additionally, missing values and outliers are processed to ensure data consistency. The dataset is then randomly split into a training set (70%) and a testing set (30%), where the training set is used for model training and five-fold cross-validation, while the testing set is employed for final model evaluation. In the five-fold cross-validation, the training dataset is further divided into five subsets. In each iteration, four subsets are used for training, while the remaining one is used for validation. This process is repeated five times, ensuring that each subset is used as a validation set once. This approach evaluates the model’s stability across different data subsets and helps mitigate overfitting. After completing the training and validation phases, the final evaluation is performed using the remaining 30% of the test data, comparing the models’ performance metrics to select the optimal model for practical prediction.

DT is a non-parametric regression method based on a tree structure [15]. In this study, the combustion characteristic variables are used as input variables (X, feature matrix), while the heat release rate (HRR) serves as the target variable (Y, regression target) for predictive modeling. To prevent overfitting, hyperparameters such as maximum depth (max_depth) and minimum samples per leaf node (min_samples_leaf) are tuned. The model is then trained using the training dataset. After training, the test dataset is used to assess the model’s generalization ability. The trained model predicts HRR values from the test data, and the correlation coefficient is calculated to evaluate prediction accuracy. Finally, to visually analyze the model’s fitting performance, a scatter plot is generated to compare the actual HRR values with the predicted HRR values.

In constructing the LR model [16], it is assumed that there is a linear relationship between the HRR and the ten selected combustion features:

$$y={\beta }_0+{\beta }_1{x}_1+{\beta }_2{x}_2+\cdots +{\beta }_{10}{x}_{10}+ϵ$$

(4)

In this study, the HRR is defined as the target variable ($y$), while x₁ to x₁₀ represent the ten selected combustion feature variables. The regression coefficients β₁ to β₁₀ indicate the contribution of each feature to the HRR, while β₀ is the intercept term, representing the baseline HRR value when all feature values are zero. The error term (ϵ) accounts for random variations not explained by the model. The Ordinary Least Squares (OLS) method is used to estimate the regression coefficients by minimizing the sum of squared residuals, ensuring the predicted values closely approximate the actual values. After training the model, the magnitude and direction of the regression coefficients are analyzed to determine which combustion features have the most significant impact on the HRR.

The KNN regression is an instance-based non-parametric method that does not require a predefined functional relationship between the HRR and combustion features. Instead, it predicts the HRR by identifying historical samples most similar to the target sample [17]. To predict the HRR, the model first calculates the distance between the target sample and all training samples and then selects the k-nearest neighbors whose combustion features are most similar to the target sample. The final HRR prediction is determined based on the HRR values of these k-nearest neighbors. Since KNN regression can adapt to complex nonlinear relationships, it is suitable for HRR prediction, and its accuracy can be improved through optimal parameter selection. All regression models were implemented in MATLAB R2024a. The DT regression model was built with a minimum leaf size set to 1, allowing for high-resolution tree growth suitable for small datasets. The KNN model was constructed with the number of neighbors set to 5, and standardization ensured that features were on a comparable scale. The LR model was implemented with default settings based on the Ordinary Least Squares method. Five-fold cross-validation was applied uniformly across all models to ensure fair and robust evaluation.

Based on the error calculations in regression analysis, this study employs four key metrics to evaluate the performance of the regression models: Mean Absolute Error (MAE), Mean Squared Error (MSE), Root Mean Squared Error (RMSE), and the Coefficient of Determination (R²). The mathematical formulations of these metrics are as follows:

(1) MAE: Measures the average absolute difference between the predicted and actual values, providing an intuitive interpretation of prediction accuracy.

$$\mathrm{M}\mathrm{A}\mathrm{E}={\displaystyle \frac{1}{n}}\sum _{i=1}^n \left|y_i-{\widehat{y}}_i\right|$$

(5)

(2) MSE: Calculates the average squared difference between the predicted and actual values, emphasizing larger errors more significantly.

$$\mathrm{M}\mathrm{S}\mathrm{E}={\displaystyle \frac{1}{n}}\sum _{i=1}^n {\left(y_i-{\widehat{y}}_i\right)}^2$$

(6)

(3) RMSE: Represents the square root of MSE, maintaining the same unit as the target variable, which facilitates easier interpretation.

$$\mathrm{R}\mathrm{M}\mathrm{S}\mathrm{E}=\sqrt{\mathrm{M}\mathrm{S}\mathrm{E}}$$

(7)

(4) R²: Evaluates the proportion of variance in HRR explained by the model, where a value closer to 1 indicates higher predictive accuracy.

$$R^2=1-{\displaystyle \frac{\sum _{i=1}^n {\left(y_i-{\widehat{y}}_i\right)}^2}{\sum _{i=1}^n {\left(y_i-\overline{y}\right)}^2}}$$

(8)

$y_i$ represents the actual value of HRR, ${\widehat{y}}_i$ denotes the predicted value of HRR, $\overline{y}$ is the mean of the actual values, and n refers to the total number of samples.

3. Results and Discussion

3.1. Box-Type Power Bank Combustion Test Results and Discussion

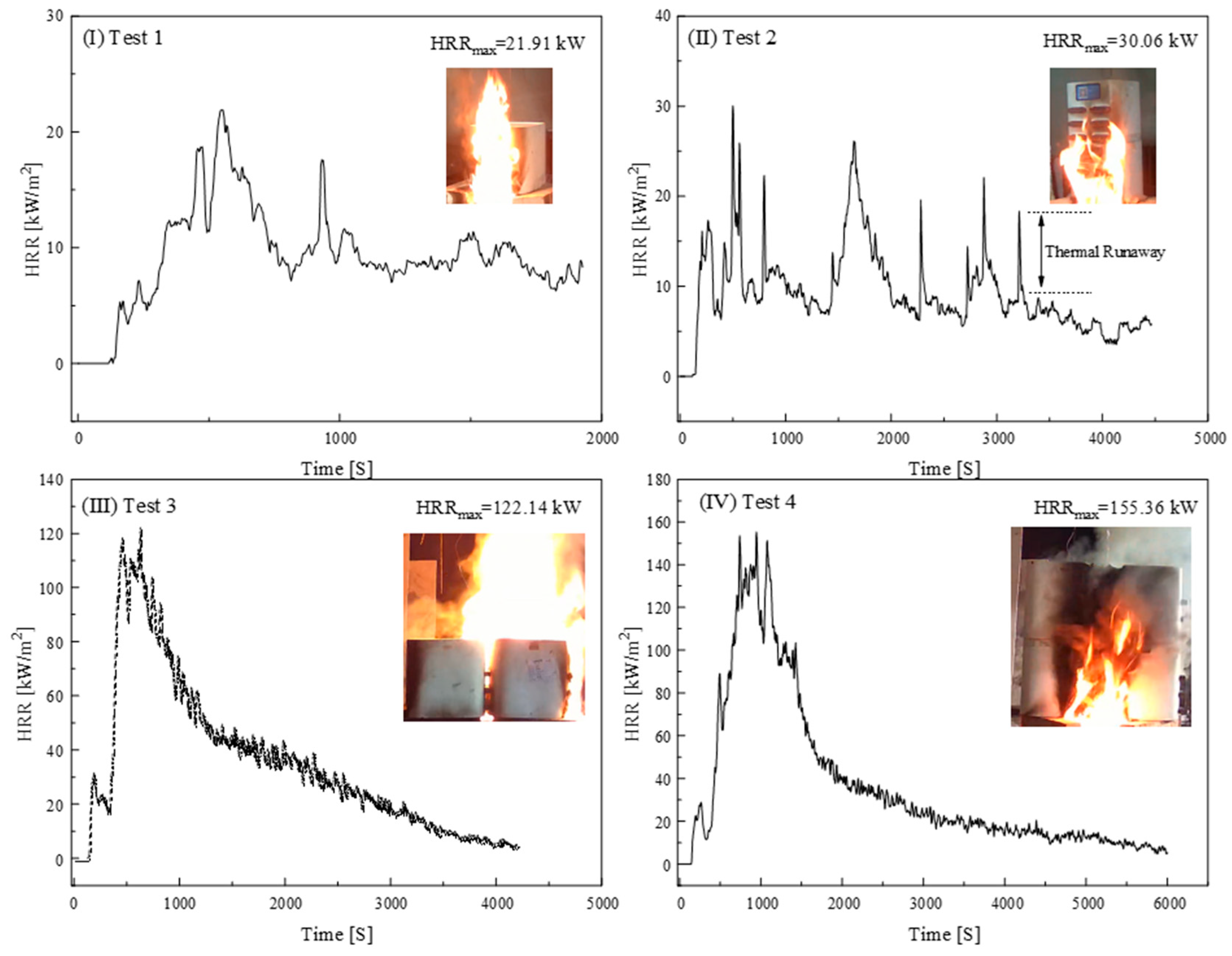
The variation in heat release rate over time under different conditions is shown in Figure 3 (derived from calorimeter raw measurements; full datasets are not disclosed due to institutional confidentiality policy). To initiate combustion, a cotton pad soaked with 20 mL of ethanol was inserted into the gap between the bottom-layer power bank and the slot inside the box. This ensured direct contact with the battery casing while preventing fuel dispersion. In all tests, the ignition was simultaneously applied to the power banks located at the lowest layer. The spatial layout was based on observations from actual high-speed railway station areas. In the two-box configuration, the boxes were arranged vertically. In the four-box configuration, they were placed in a single layer (2 × 2). The eight-box setup consisted of a two-layer stack of four boxes per layer. This layout was designed to simulate realistic storage density and ignition locations in public infrastructure environments, and it can be seen in Figure 3 (the upper right corner of each subgraph).

The experimental results revealed distinct differences in HRR behavior across the four test scenarios. In Test I, the HRR peaked at 21.91 kW at 553 s. In Test II, the samples’ HRR reached the peak value of 30.36 kW. In the third one, the HRR surged to 122.14 kW at 628 s. Finally, the HRR reached a peak of 155.36 kW at 946 s in the fourth test. Throughout these tests, thermal runaway was observed when the power bank was subjected to heat. Thermal runaway refers to a phenomenon where the internal battery or electrical components of a power bank, due to excessive temperature, trigger a self-accelerating reaction that causes rapid heat accumulation. This process leads to intense combustion, generating a large amount of heat and gas in a short period, which significantly increases the heat release rate. For example, in Test II, after a single power bank experienced a thermal runaway, the heat release rate increased by 9.97 kW within 15 s, accompanied by large flames and a significant noise.

The sharp rise in HRR from Test I to Test III can be attributed to several compounding factors. First, the number of power banks increased from 6 to 24, significantly raising the total combustible load. Second, the close spatial arrangement of multiple units likely facilitated a cascading thermal runaway effect, where the ignition of one unit triggered rapid sequential failures in adjacent units. This chain reaction amplified the combustion intensity and accelerated the fire growth rate. Additionally, the confined geometry of the calorimeter hood may have restricted ventilation and heat dissipation, leading to localized flame accumulation and elevated HRR peaks. Moreover, the HRR–time curves frequently exhibited multiple peaks, particularly in tests with larger numbers of power banks. These multiple peaks are indicative of staged combustion behavior. Due to uneven heating and varying battery conditions, thermal runaway did not occur simultaneously across all units. Instead, individual devices ignited at different times, resulting in distinct HRR surges corresponding to successive ignition events. Furthermore, the polymer casing materials and internal lithium battery components likely underwent multi-stage degradation, where the initial combustion of external casings was followed by delayed ignition of the battery cores. This sequential degradation and combustion process contributed to the multi-peak profiles observed in the HRR data.

3.2. Correlation Analysis Results and Discussion

The bar chart illustrating the correlation between selected features and the HRR, as well as the heatmap displaying the correlation between all features, are presented in Figure 4 and Figure 5, respectively.

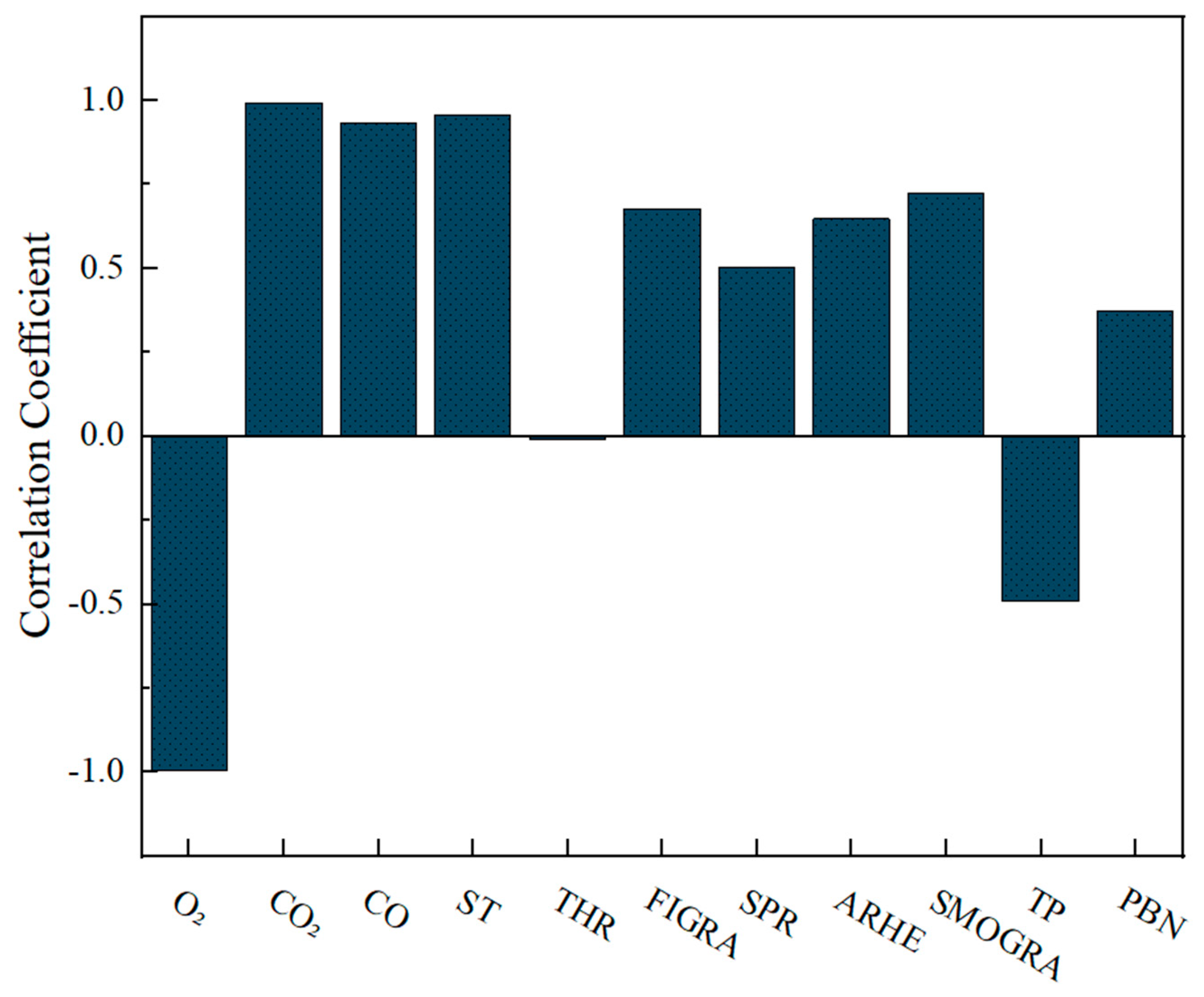
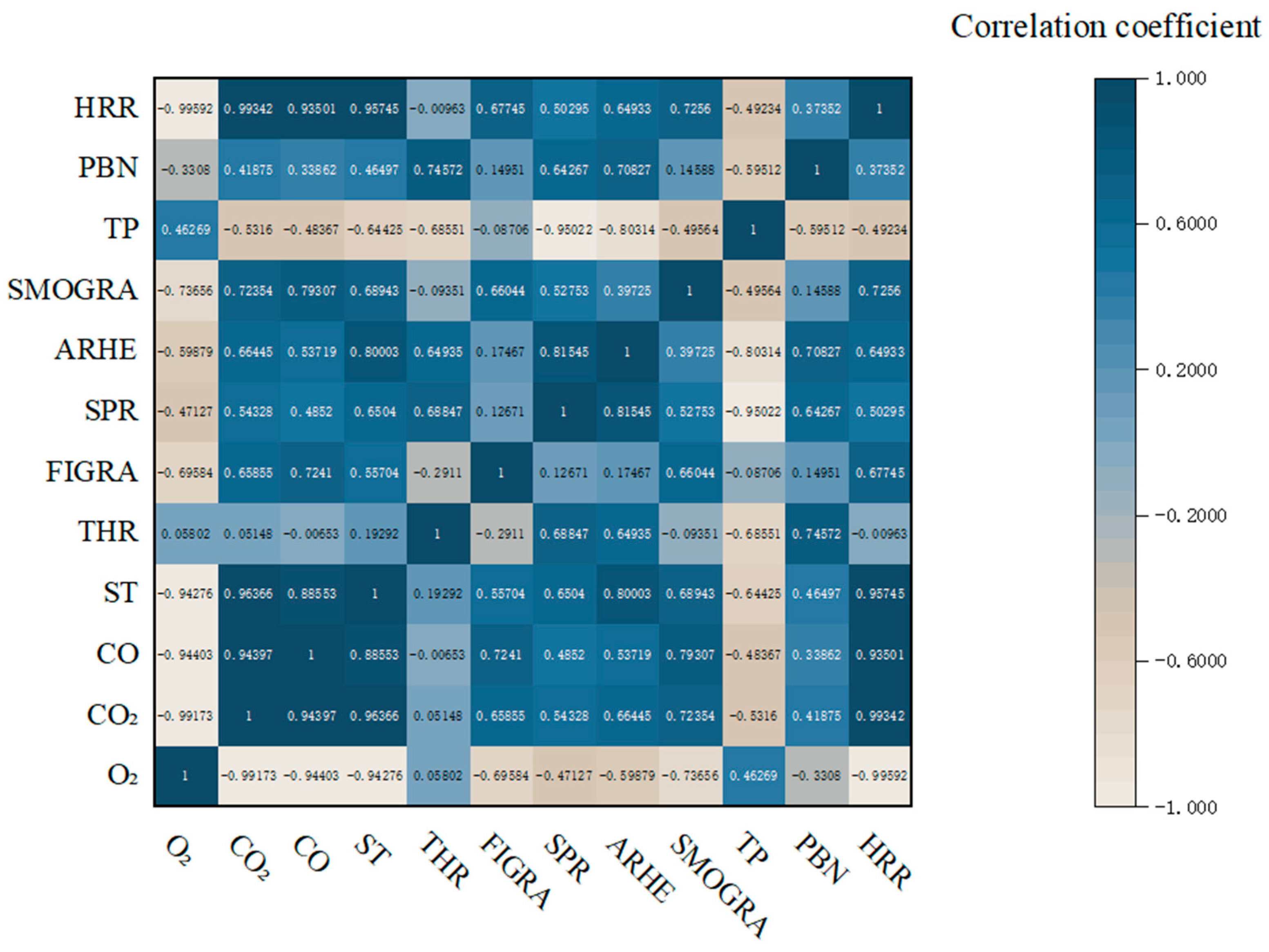
The results indicate significant differences in the correlation between various combustion feature variables and the HRR. Specifically, CO₂ (r = 0.99173), CO (r = 0.99301), and ST (r = 0.99745) exhibit a strong positive correlation with the HRR, suggesting that the increase in CO₂ and CO production and the rising smoke temperature are closely associated with the growth in the HRR. Similarly, the PBN (Power Bank Number, r = 0.37352) also shows a positive correlation with the HRR, indicating that the number of power banks contributes to heat release. Conversely, O₂ (r = −0.99952) demonstrates a highly negative correlation with the HRR, which aligns with the physical characteristics of combustion, where the decrease in oxygen volume fraction corresponds to a progressive increase in the HRR. Additionally, the SPR (r = 0.50295), FIGRA (r = 0.67745), and ARHE (r = 0.64933) exhibit a moderate positive correlation with the HRR, though to a lesser degree than CO₂, CO, and ST. TP (r = −0.4923) also shows a moderate negative correlation with the HRR, indicating that denser smoke (lower transmittance) is typically associated with more severe fire behavior. Interestingly, THR has a very weak correlation (r = −0.0096), suggesting that the instantaneous HRR does not directly align with cumulative heat release at each time point.

Regarding the correlation between combustion feature variables, CO₂, CO, and ST display strong intercorrelations, particularly between CO₂ and CO (r = 0.94937) and ST and CO (r = 0.88553), indicating a synergistic variation trend during combustion. Similarly, the SPR and FIGRA (r = 0.81454) demonstrate a strong correlation, reflecting the close relationship between smoke release rate and fire growth rate. However, the PBN (r = −0.3308) shows relatively low correlation with most variables, suggesting that the number of power banks has limited direct influence on other combustion characteristics. Overall, O₂, CO₂, CO, and ST emerge as the key variables influencing HRR variations, highlighting their significance in understanding combustion behavior. These findings provide important insights for fire combustion characteristic analysis and fire dynamics model optimization, offering a valuable reference for fire risk assessment and prevention strategies.

3.3. Regression Analysis Results and Discussion

The results of the five-fold cross-validation regression analysis are presented in

Table 3. Regression model analysis results.

Model	Dataset	MAE	MSE	RMSE	R2
DT	Train	0.3355 ± 0.0029	0.2434 ± 0.0083	0.4933 ± 0.0083	0.9997
	Validation	0.4970 ± 0.0219	0.7552 ± 0.1623	0.8654 ± 0.0888	0.9991
	Test	0.4889 ± 0.0121	0.7414 ± 0.1620	0.8570 ± 0.0924	0.9991
LR	Train	0.8435 ± 0.0230	3.3488 ± 0.0925	1.8298 ± 0.0252	0.9960
	Validation	0.8435 ± 0.0921	3.3489 ± 0.3702	1.8277 ± 0.1016	0.9960
	Test	0.9824 ± 0.0	4.7136 ± 0.0	2.1710 ± 0.0	0.9947
KNN	Train	0.7965 ± 0.0079	3.1647 ± 0.0613	1.7789 ± 0.0172	0.9962
	Validation	0.9725 ± 0.0304	4.2185 ± 0.8545	2.0460 ± 0.2010	0.9949
	Test	0.9839 ± 0.0114	4.6703 ± 0.2600	2.1604 ± 0.0599	0.9947

, where the MAE, MSE, and RMSE are expressed as mean ± Std. Among the three models, DT demonstrated the best performance, achieving an MAE of 0.4889, MSE of 0.7414, RMSE of 0.8571, and R² of 0.9991 on the test set. These results indicate that the DT model accurately captures the variations in the HRR, exhibiting high predictive accuracy and strong generalization capability. In comparison, both LR and KNN yielded slightly higher MAE, MSE, and RMSE values on the test set, indicating relatively larger prediction errors. However, the R² values for both models reached 0.9947, demonstrating that they still possess strong explanatory power. This suggests that the ten selected combustion features play a crucial role in HRR prediction, effectively reflecting the dynamic variations in the combustion process.

The regression equation obtained from the linear regression model is expressed as follows:

$$\begin{gathered} \begin{array}{c}HRR=2914.5262+\left(-137.0369\times O_2\right)+\left(95.2149\times C{O}_2\right)+\left(-2.0350\times C\right)+\left(-0.1457\times ST\right)+\left(-0.0233\times TH\right)\end{array} \\ \begin{array}{c}+\left(0.0068\times FIGR\right)+\left(-0.5605\times SP\right)+\left(0.1789\times ARH\right)+\left(-0.0148\times SMOGR\right)+\left(0.0088\times TP\right)\end{array} \end{gathered}$$

(9)

The coefficients in the linear regression equation provide valuable insights into how each combustion feature affects the heat release rate (HRR). Oxygen concentration (O₂) exhibits the strongest negative coefficient (−137.0369), indicating that the HRR increases significantly as oxygen is consumed—a behavior that aligns with combustion theory. Conversely, CO₂ (95.2149) shows the strongest positive influence, suggesting that higher CO₂ levels are strongly associated with more intense combustion. Other features contribute in more moderate ways. CO has a modest negative coefficient (−2.0350), which may reflect incomplete combustion processes that emit CO during less efficient burning. Smoke temperature (ST) also shows a small negative coefficient (−0.1457), which appears counterintuitive compared to the positive correlation observed earlier; this may be due to collinearity with other features such as CO and CO₂ in the regression model. THR has a near-zero negative coefficient (−0.0233), suggesting limited incremental value in predicting the instantaneous HRR when other features are considered. The FIGRA, with a small positive coefficient (0.0068), contributes marginally to HRR growth, in line with its definition as a fire growth metric. Similarly, the ARHE (0.1789) has a moderate positive effect, representing sustained heat output during combustion. On the other hand, the SPR (−0.5605) and SMOGRA (−0.0148) show small negative coefficients, which may reflect complex interactions or overlaps with other predictors related to the combustion rate and smoke production dynamics. TP (Total Propagation) has a minimal positive effect. This regression model effectively captures the complex relationships between combustion features and the HRR, providing theoretical support for fire prediction and combustion process control.

The DT model demonstrated optimal performance on the test set, achieving the lowest MAE, MSE, and RMSE, with an R² value of 0.9991. This indicates that the model effectively explains HRR variations, achieving high predictive accuracy and strong generalization ability. The superior performance of the DT model in HRR prediction is primarily due to its ability to handle complex nonlinear relationships and to automatically identify hierarchical interactions among combustion features. The fire development process involves multiple interacting variables—such as gas concentrations, temperature, and smoke production—which influence the HRR in a highly nonlinear manner. By recursively partitioning the input space, the DT model can adaptively fit such nonlinear dependencies, making it particularly well suited for fire dynamics data. Additionally, decision trees impose minimal assumptions on feature distributions and are robust to outliers and noise, both of which are common in combustion experiments. Although the LR model achieved a relatively high R² value, it relies on the assumption of linearity between features and the target variable. This limitation reduces its ability to capture nonlinear effects and complex feature interactions. For example, while the negative coefficient for oxygen concentration and the positive coefficient for carbon dioxide concentration align with combustion chemistry principles, the model fails to fully represent the nonlinear growth patterns observed in HRR evolution. The KNN model, while non-parametric and theoretically capable of capturing nonlinearities, lacks an internal mechanism for modeling feature importance or dependencies. Its reliance on local distance metrics also makes it sensitive to feature scaling, noise, and sparsity in high-dimensional spaces. Furthermore, KNN does not generalize well when data samples are limited, as in this study. Overall, among the three models tested, DT’s structural flexibility, interpretability, and noise tolerance make it the most suitable choice for modeling the HRR based on combustion features in this context.

3.4. Application Discussion

This study has developed a fire risk assessment framework, as illustrated in Figure 6, which integrates experimental combustion data, correlation analysis, and machine learning-based HRR prediction models. The framework begins with data collection from power bank fire tests, where combustion feature variables such as O₂, CO₂, CO, and smoke temperature are recorded. These data are preprocessed and used to train regression models capable of estimating the HRR in real-time or in scenario simulations. Following feature analysis, interpretable models such as LR are used to identify key risk-driving variables, while more flexible models like DT regression capture complex nonlinear fire growth behavior. Together, these models contribute to quantifying fire development potential and provide theoretical support for risk estimation in enclosed environments. While the current study does not directly implement a real-time fire early warning system, the trained regression models offer valuable tools for real-time HRR monitoring and hazard classification. With further integration of sensor networks and system-level validation, this modeling approach could support intelligent fire safety systems, including scenario-based simulation, risk zoning, and response planning. The framework shows potential for practical applications in transportation terminals, warehouse safety management, and fire-prone public areas.

4. Conclusions

In the environment of transportation hubs, the thermal runaway of power banks can lead to fires that pose severe threats to passenger safety. Conducting a comprehensive analysis based on real fire scenarios involving box-type power banks is crucial for achieving effective fire early warning. This study adopted a combination of experimental measurement and machine learning modeling to investigate the fire load characteristics of box-type power banks in transportation hubs. Four sets of experiments involving 15 box-type power banks were conducted to systematically analyze the HRR and its key influencing factors. This is the first time that a predictive model was developed based on a real experimental dataset of box-type power banks. The main conclusions are as follows:

(1) Based on experimental data, the peak HRR for a single box-type power bank during combustion is 21.91 kW; for box-type power banks, it is 30.06 kW; for box-type power banks, it is 122.14 kW; and for eight box-type power banks, it is 155.36 kW.

(2) The correlation analysis results indicate that among the eleven analyzed features, O₂, CO₂, ST, and CO are the four most critical variables affecting HRR variation, with correlation coefficients of −0.99, 0.99, 0.96, and 0.93, respectively. These variables can serve as core predictive factors in fire dynamics models.

(3) The DT model effectively predicted the HRR based on combustion characteristics. The DT model achieved an RMSE of 0.8570, reducing the MSE by 1.3 compared to KNN and LR. The R² is 0.9991, improving by 0.0044 over KNN and LR. With its excellent predictive performance, this model provides an efficient, data-driven approach for fire risk assessment in transportation hubs, enhancing the accuracy of fire risk identification and prediction. It also offers scientific support for fire prevention and control strategies for box-type power banks.

Despite the significant progress made in fire risk assessment for box-type power banks, this study has certain limitations. Firstly, it does not fully account for environmental factors in transportation hubs, such as ventilation conditions, humidity variations, and surrounding combustible materials, which may significantly influence the combustion process. Future research could incorporate numerical simulations or real-world measurement data to more comprehensively evaluate the impact of environmental variables on HRR variations. Secondly, the experimental dataset is relatively limited, with a small sample size, which may affect the generalization ability of the machine learning model. Thirdly, it should be noted that the ignition location and spatial arrangement of the power banks may influence combustion development and the HRR due to thermal feedback and flame propagation effects. While the experimental setup was designed to reflect realistic layouts observed in railway station charging areas, variations in stacking patterns or ignition positions may introduce uncertainty in fire behavior. Future studies should integrate larger-scale real-world data to enhance the model’s robustness and applicability across different fire scenarios. Additionally, this study primarily focuses on HRR variation patterns and predictive modeling but does not extensively explore the impact of fire suppression measures on the HRR. Fire suppression systems, such as automatic sprinkler systems, fire-retardant coatings, and ventilation control strategies, could play a crucial role in fire prevention and control within transportation hubs. Therefore, future research should incorporate fire suppression control variables to assess the effectiveness of different fire suppression strategies on the combustion process of box-type power banks. This would provide a more comprehensive scientific basis for fire safety management in transportation hubs, contributing to the development of a precise fire prevention and control system.