Evaluation of Topographic Effect Parameterizations in Weather Research and Forecasting Model over Complex Mountainous Terrain in Wildfire-Prone Regions
Abstract
1. Introduction
2. Materials and Methods
2.1. Parameterizations for Terrain Effect
2.2. Model Description and Experimental Design
2.3. Observation Data and Analysis Method
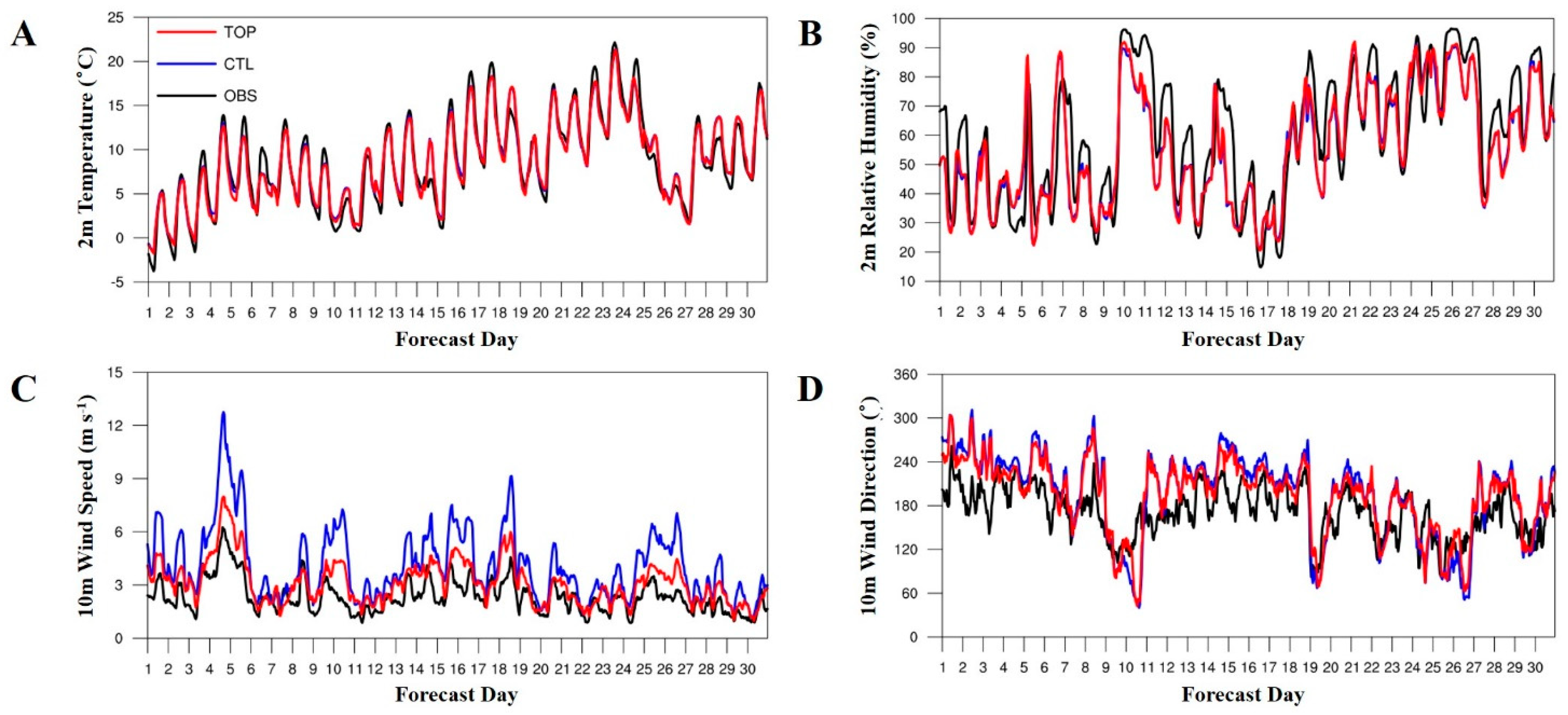
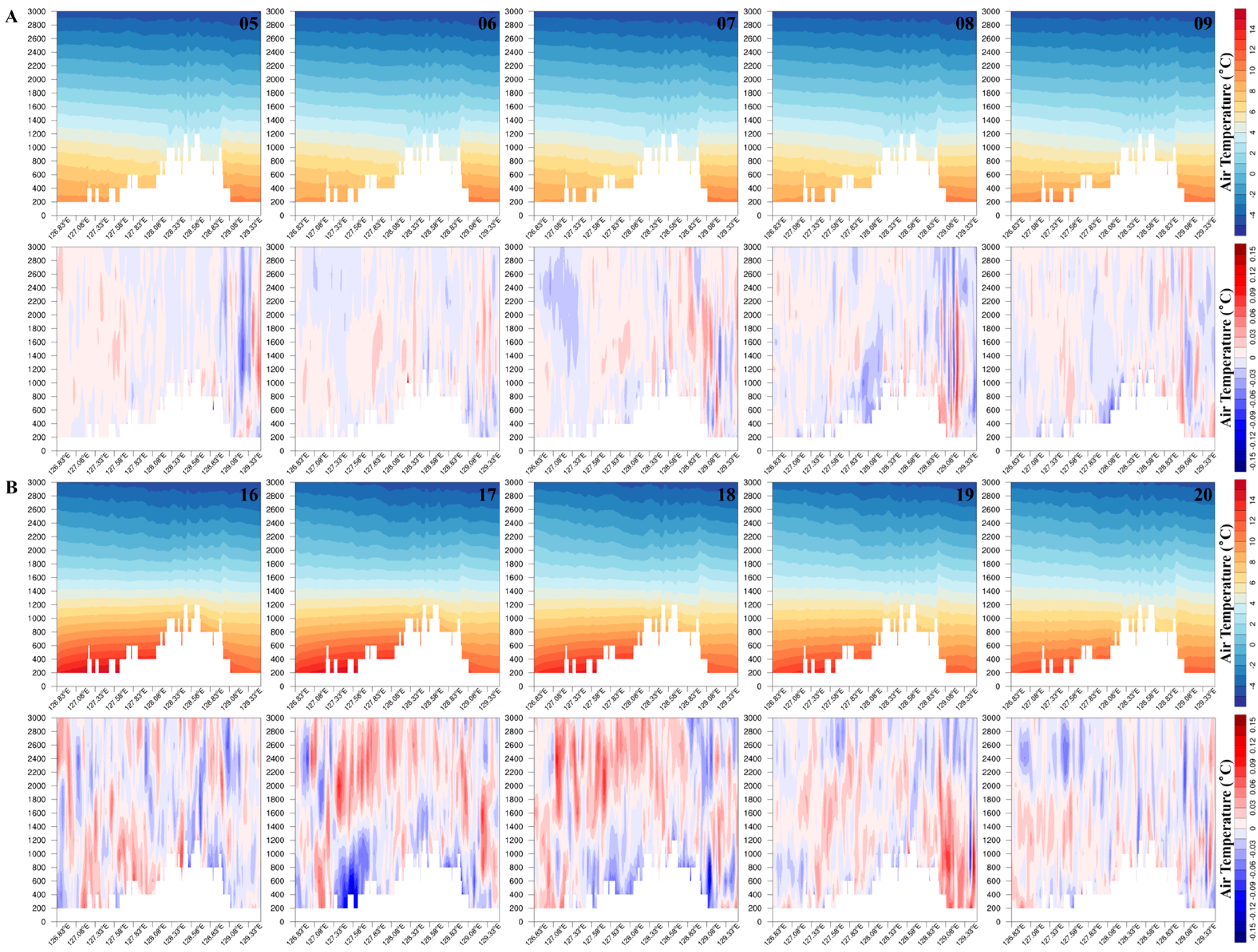
3. Results
3.1. Subgrid-Scale Topographic Parameterization
3.2. Topographic Shading and Slope Parameterization
4. Concluding Remarks and Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| WRF | Weather Research and Forecasting |
| RMSE | Root Mean Square Error |
| NWP | Numerical Weather Prediction |
References
- KFS (Korea Forest Service). 2020 Forest Basic Statistics; Korea Forest Service: Daejeon, Republic of Korea, 2021; pp. 21–24. [Google Scholar]
- Kim, J.W.; Lee, J.G. A Qualitative Analysis of WRF Simulation Results of Typhoon ‘Rusa’ Case. Atmosphere 2007, 17, 393–405, (In Korean with English Abstract). [Google Scholar]
- Han, S.H.; Lee, J.G. A numerical simulation study on the sensitivity of WRF model in the wind field to the steepness of mountain slopes. Atmosphere 2007, 17, 349–364, (In Korean with English Abstract). [Google Scholar]
- Yun, H.S.; Um, M.J.; Cho, W.C.; Heo, J.H. Orographic precipitation analysis with regional frequency analysis and multiple linear regression. J. Korea Water Resour. Assoc. 2009, 42, 465–480. [Google Scholar] [CrossRef]
- Lee, J.H.; Jun, H.D. A methodology for rain gauge network evaluation considering the altitude of rain gauge. J. Wet. Res. 2014, 16, 113–124, (In Korean with English Abstract). [Google Scholar] [CrossRef][Green Version]
- Yoon, S.; Jang, K.; Won, M. The spatial distribution characteristics of Automatic Weather Stations in the mountainous area over South Korea. Korean J. Agric. For. Meteorol. 2018, 20, 117–126. [Google Scholar][Green Version]
- Vogt, J.V.; Viau, A.A.; Paquet, F. Mapping regional air temperature fields using satellite-derived surface skin temperatures. Int. J. Climatol. 1997, 17, 1559–1579. [Google Scholar] [CrossRef]
- Jang, K.; Kang, S.; Kimball, J.S.; Hong, S.Y. Retrieval of all-weather daily air temperature using MODIS and AMSRE data. Remote Sens. 2014, 6, 8387–8404. [Google Scholar] [CrossRef]
- Jang, K.; Won, M.; Yoon, S. Evaluation of the satellite-based air temperature for all sky conditions using the automated mountain meteorology station (AMOS) records: Gangwon Province case study. Korean J. Agric. For. Meteorol. 2017, 19, 19–26. [Google Scholar] [CrossRef]
- IPCC. Climate Change 2007: Synthesis Report; Core Writing Team, Pachauri, R.K., Reisinger, A., Eds.; Contribution of Working Groups 1, 2, and 3 to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change; IPCC: Geneva, Switzerland, 2007. [Google Scholar]
- IPCC. Climate Change 2014: Synthesis Report; Core Writing Team, Pachauri, R.K., Meyer, L.A., Eds.; Contribution of Working Groups I, II, and III to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; IPCC: Geneva, Switzerland, 2014. [Google Scholar]
- IPCC. Climate Change 2021: The Physical Science Basis; Masson-Delmotte, V., Zhai, P., Pirani, A., Connors, S.L., Péan, C., Berger, S., Caud, N., Chen, Y., Goldfarb, L., Gomis, M.I., et al., Eds.; Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; IPCC, Cambridge University Press: Cambridge, UK; New York, NY, USA, 2021. [Google Scholar]
- Piñol, J.; Terradas, J.; Lloret, F. Climate warming, wildfire hazard, and wildfire occurrence in coastal eastern Spain. Clim. Change 1998, 11, 95–106. [Google Scholar]
- Flannigan, M.D.; Stocks, B.J.; Wotton, B.M. Climate change and forest fires. Sci. Total Environ. 2000, 262, 221–229. [Google Scholar] [CrossRef]
- Hély, C.; Flannigan, M.; Bergeron, Y.; McRae, D. Role of vegetation and weather on fire behavior in the Canadian mixedwood boreal forest using two fire behavior prediction systems. Can. J. For. Res. 2001, 31, 430–441. [Google Scholar] [CrossRef]
- Balshi, M.S.; McGUIRE, A.D.; Duffy, P.; Flannigan, M.; Walsh, J.; Melillo, J. Assessing the response of area burned to changing climate in western boreal North America using a Multivariate Adaptive Regression Splines (MARS) approach. Glob. Change Biol. 2009, 15, 578–600. [Google Scholar] [CrossRef]
- Lima, C.H.; AghaKouchak, A.; Randerson, J.T. Unraveling the role of temperature and rainfall on active fires in the Brazilian Amazon using a nonlinear Poisson model. J. Geophys. Res. Biogeosci. 2018, 123, 117–128. [Google Scholar] [CrossRef]
- Lu, W.; Zhong, S.; Charney, J.J.; Bian, X.; Liu, S. WRF simulation over complex terrain during a southern California wildfire event. J. Geophys. Res. Atmos. 2012, 117, D05125. [Google Scholar] [CrossRef]
- Goss, M.; Swain, D.L.; Abatzoglou, J.T.; Sarhadi, A.; Kolden, C.A.; Williams, A.P.; Diffenbaugh, N.S. Climate change is increasing the likelihood of extreme autumn wildfire conditions across California. Environ. Res. Lett. 2020, 15, 094016. [Google Scholar] [CrossRef]
- Dong, L.; Leung, L.R.; Qian, Y.; Zou, Y.; Song, F.; Chen, X. Meteorological environments associated with California wildfires and their potential roles in wildfire changes during 1984–2017. J. Geophys. Res. Atmos. 2021, 126, e2020JD033180. [Google Scholar] [CrossRef]
- Povak, N.A.; Hessburg, P.F.; Salter, R.B. Evidence for scale-dependent topographic controls on wildfire spread. Ecosphere 2018, 9, e02443. [Google Scholar] [CrossRef]
- Evers, C.; Holz, A.; Busby, S.; Nielsen-Pincus, M. Extreme Winds Alter Influence of Fuels and Topography on Megafire Burn Severity in Seasonal Temperate Rainforests under Record Fuel Aridity. Fire 2022, 5, 41. [Google Scholar] [CrossRef]
- Estes, B.L.; Knapp, E.E.; Skinner, C.N.; Miller, J.D.; Preisler, H.K. Factors influencing fire severity under moderate burning conditions in the Klamath Mountains, northern California, USA. Ecosphere 2017, 8, e01794. [Google Scholar] [CrossRef]
- Skamarock, W.C.; Klemp, J.B.; Dudhia, J.; Gill, D.O.; Barker, D.M.; Duda, M.G.; Huang, X.Y.; Wang, W.; Powers, J.G. NCAR TECHNICAL NOTE (NCAR/TN–475+ STR): A Description of the Advanced Research WRF Version 3; National Center for Atmospheric Research: Boulder, CO, USA, 2008. [Google Scholar]
- Mass, C.; Ovens, D. Fixing WRF’s high-speed wind bias: A new subgrid scale drag parameterization and the role of detailed verification. In Proceedings of the 24th Conference on Weather and Forecasting and 20th Conference on Numerical Weather Prediction, Preprints, 91st American Meteorological Society Annual Meeting, Seattle, WA, USA, 26 January 2011; Volume 23727, pp. 23–27. [Google Scholar]
- Jiménez, P.A.; Dudhia, J. Improving the representation of resolved and unresolved topographic effects on surface wind in the WRF model. J. Appl. Meteorol. Climatol. 2012, 51, 300–316. [Google Scholar] [CrossRef]
- Lee, J.; Shin, H.H.; Hong, S.Y.; Jimenez, P.A.; Dudhia, J.; Hong, J. Impacts of subgrid-scale orography parameterization on simulated surface layer wind and monsoonal precipitation in the high-resolution WRF model. J. Geophys. Res. Atmos. 2015, 120, 644–653. [Google Scholar] [CrossRef]
- Arthur, R.S.; Lundquist, K.A.; Mirocha, J.D.; Chow, F.K. Topographic Effects on Radiation in the WRF Model with the Immersed Boundary Method: Implementation, validation, and application to complex terrain. Mon. Weather Rev. 2018, 146, 3277–3292. [Google Scholar] [CrossRef]
- Lim, K.S.S.; Lim, J.M.; Shin, H.H.; Hong, J.; Ji, Y.Y.; Lee, W. Impacts of subgrid-scale orography parameterization on simulated atmospheric fields over Korea using a high-resolution atmospheric forecast model. Meteorol. Atmos. Phys. 2019, 131, 975–985. [Google Scholar] [CrossRef]
- Cheng, W.Y.Y.; Steenburgh, W.J. Evaluation of surface sensible weather forecasts by the WRF and the Eta models over the western United States. Weather Forecast. 2005, 20, 812–821. [Google Scholar] [CrossRef]
- Bernardet, L.; Nance, L.; Demirtas, M.; Koch, S.; Szoke, E.; Fowler, T.; Loughe, A.; Mahoney, J.L.; Chuang, H.; Pyle, M.; et al. The developmental testbed center and its winter forecast experiment. Bull. Amer. Meteor. Soc. 2008, 89, 611–627. [Google Scholar] [CrossRef]
- Seo, B.K.; Byon, J.Y.; Lim, Y.J.; Choi, B.C. Evaluation of surface wind forecast over the Gangwon province using the mesoscale WRF model. J. Korean Earth Sci. Soc. 2015, 36, 158–170. [Google Scholar] [CrossRef]
- Tsai, C.C.; Hong, J.S.; Chang, P.L.; Chen, Y.R.; Su, Y.J.; Li, C.H. Application of bias correction to improve WRF ensemble wind speed forecast. Atmosphere 2021, 12, 1688. [Google Scholar] [CrossRef]
- Mass, C.; Ovens, D. WRF model physics: Problems, solutions and a new paradigm for progress. In Proceedings of the 2010 WRF Users’ Workshop, Boulder, CO, USA, 15–21 June 2010. [Google Scholar]
- Papadopoulos, K.H.; Helmis, C.G. Evening and morning transition of katabatic flows. Bound.-Layer Meteorol. 1999, 92, 195–227. [Google Scholar] [CrossRef]
- Katurji, M.; Zawar-Reza, P.; Zhong, S. Surface layer response to topographic solar shading in Antarctica’s dry valleys. J. Geophys. Res. Atmos. 2013, 118, 12332–12344. [Google Scholar] [CrossRef]
- Lehner, M.; Whiteman, C.D.; Hoch, S.W.; Jensen, D.; Pardyjak, E.R.; Leo, L.S.; Di Sabatino, S.; Fernando, H.J.S.; Lehner, M.; Whiteman, C.D.; et al. A case study of the nocturnal boundary layer evolution on a slope at the foot of a desert mountain. J. Appl. Meteorol. Climatol. 2015, 54, 732–751. [Google Scholar] [CrossRef]
- Colette, A.; Chow, F.K.; Street, R.L. A numerical study of inversion-layer breakup and the effects of topographic shading in idealized valleys. J. Appl. Meteorol. 2003, 42, 1255–1272. [Google Scholar] [CrossRef]
- Garnier, B.J.; Ohmura, A.A. method for calculating direct shortwave radiation income of slopes. J. Appl. Meteorol. 1968, 7, 796–800. [Google Scholar] [CrossRef]
- Zängl, G. Formation of extreme cold-air pools in elevated sinkholes: An idealized numerical process study. Mon. Wea. Rev. 2005, 133, 925–941. [Google Scholar] [CrossRef][Green Version]
- Hong, S.Y.; Lim, J.O.J. The WRF single-moment 6-class microphysics scheme (WSM6). J. Korean Meteorol. Soc. 2006, 42, 129–151. [Google Scholar][Green Version]
- Iacono, M.J.; Delamere, J.S.; Mlawer, E.J.; Shephard, M.W.; Clough, S.A.; Collins, W.D. Radiative forcing by long-lived greenhouse gases: Calculations with the AER radiative transfer models. J. Geophys. Res. 2008, 113, D13103. [Google Scholar] [CrossRef]
- Hong, S.Y.; Noh, Y.; Dudhia, J. A new vertical diffusion package with an explicit treatment of entrainment processes. Mon. Weather Rev. 2006, 134, 2318–2341. [Google Scholar] [CrossRef]
- Jiménez, P.A.; Dudhia, J.; González-Rouco, J.F.; Navarro, J.; Montávez, J.P.; García-Bustamante, E. A revised scheme for the WRF surface layer formulation. Mon. Weather Rev. 2012, 140, 898–918. [Google Scholar] [CrossRef]
- Chen, F.; Dudhia, J. Coupling an advanced land surface-hydrology model with the Penn State–NCAR MM5 modeling system. Part I: Model implementation and sensitivity. Mon. Weather Rev. 2001, 129, 569–585. [Google Scholar] [CrossRef]
- Kain, J.S. The Kain–Fritsch convective parameterization: An update. J. Appl. Meteorol. 2004, 43, 170–181. [Google Scholar] [CrossRef]
- Mansoor, S.; Farooq, I.; Kachroo, M.M.; Mahmoud, A.E.D.; Fawzy, M.; Popescu, S.M.; Alyemeni, M.N.; Sonne, C.; Rinklebe, J.; Ahmad, P. Elevation in wildfire frequencies with respect to the climate change. J. Environ. Manag. 2022, 301, 113769. [Google Scholar] [CrossRef]
- Lim, C.H.; Kim, Y.S.; Won, M.; Kim, S.J.; Lee, W.K. Can satellite-based data substitute for surveyed data to predict the spatial probability of forest fire? A geostatistical approach to forest fire in the Republic of Korea. Geomat. Nat. Hazards Risk 2019, 10, 719–739. [Google Scholar] [CrossRef]
- Zhang, G.; Wang, M.; Liu, K. Forest fire susceptibility modeling using a convolutional neural network for Yunnan province of China. Int. J. Disaster Risk Sci. 2019, 10, 386–403. [Google Scholar] [CrossRef]
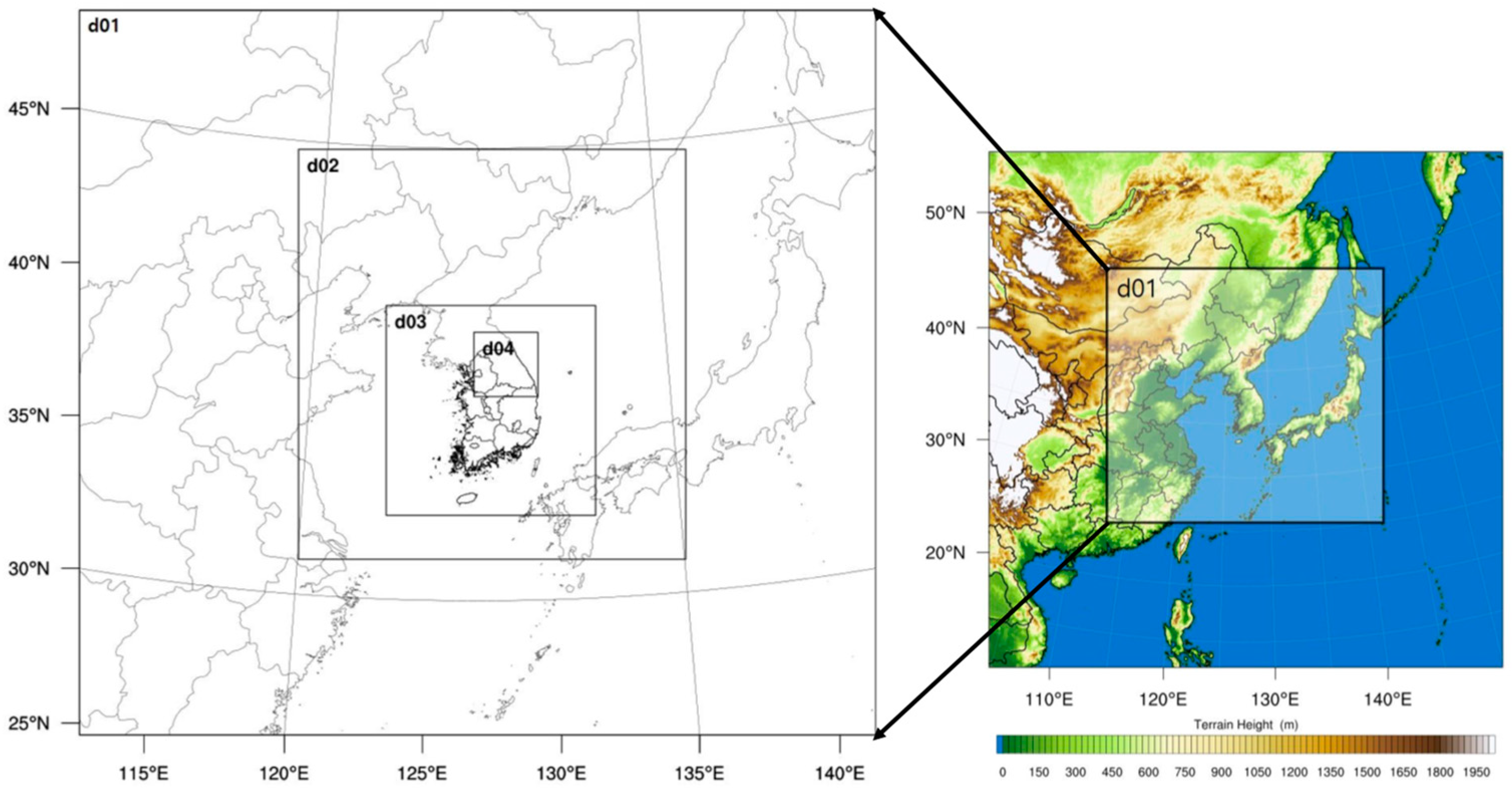
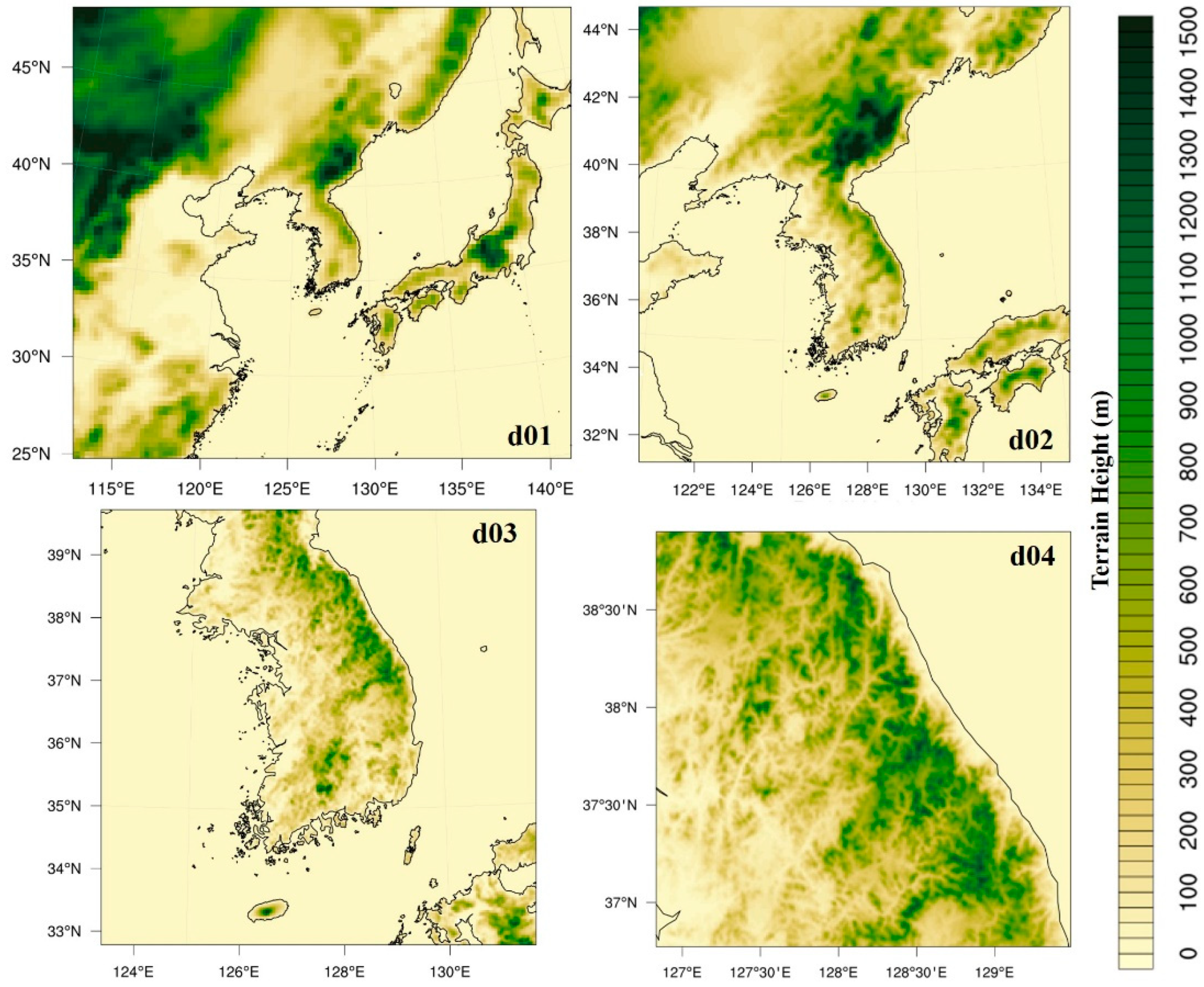
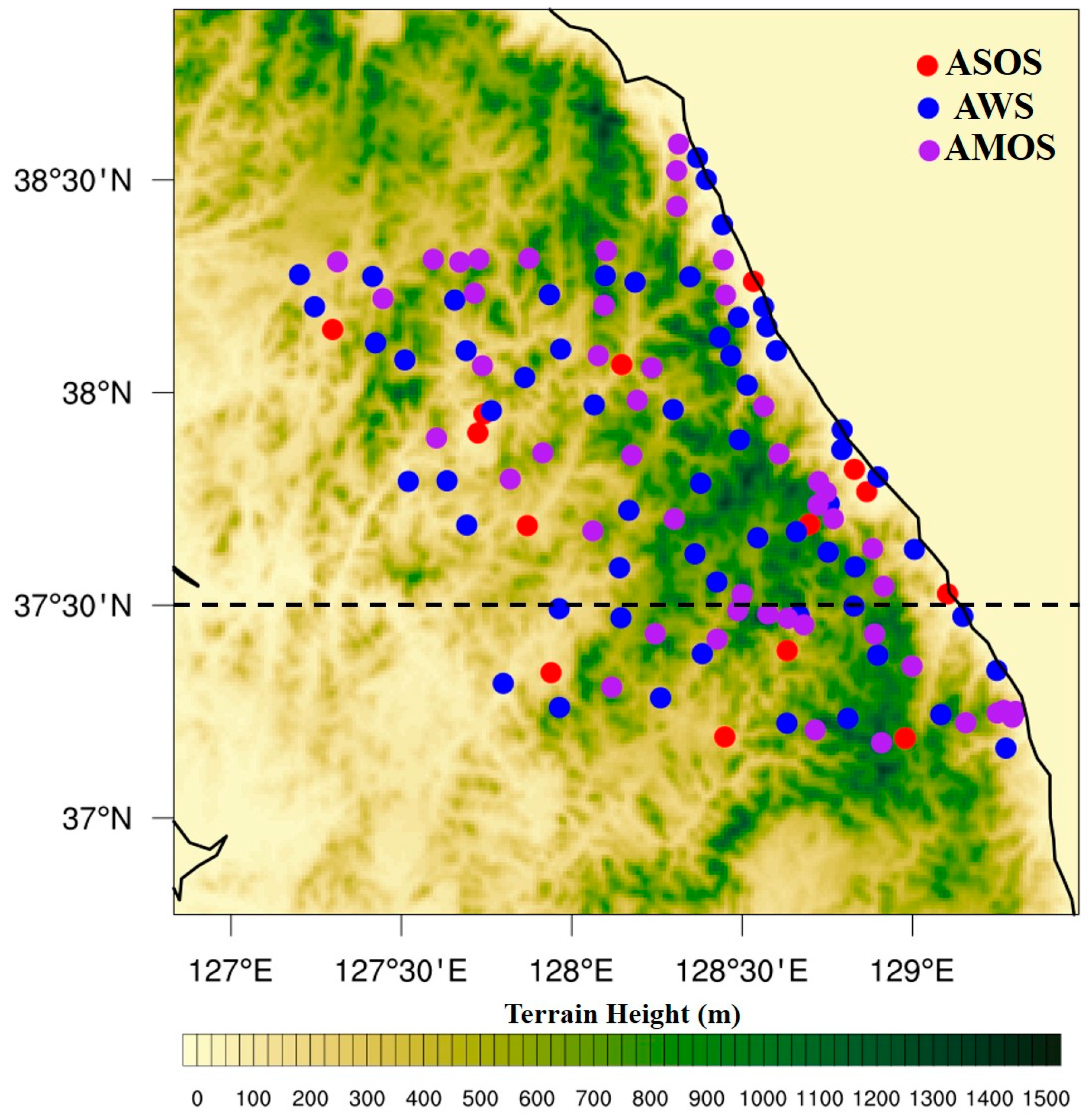


| Version | v 3.7.1 | ||
| Grib datasets | 6-h NCEP GDAS FNL | ||
| Simulation period | 31 March–1 May 2019 | ||
| Domain (126.9782° E, 37.5666° N) | d01 | 27 km | 110 × 100 |
| d02 | 9 km | 160 × 169 | |
| d03 | 3 km | 259 × 259 | |
| d04 | 1 km | 238 × 238 | |
| Vertical levels | 33 | ||
| Model top pressure | 50 hPa | ||
| Nesting approach | One way | ||
| Model physics | |||
| Microphysics | WRF Single-Moment 6-class | ||
| LW radiation | Rapid Radiative Transfer Model for GCMs | ||
| SW radiation | Rapid Radiative Transfer Model for GCMs | ||
| Surface layer | Revised MM5 Monin–Obukhov | ||
| Land surface | Unified Noah land surface model | ||
| PBL | Yonsei University | ||
| Cumulus | Kain–Fritsch (new Eta) (only d01, d02) | ||
| Experiment | |
|---|---|
| CTL | Control run (default) |
| TOP | Applying the subgrid-scale topographic parameterization (topographic correction for surface winds) |
| SSE | Applying the slope and shading parameterization (neighboring-grid shadow effects and slope-dependent radiation) |
| OBS | CTL | TOP | |||||
|---|---|---|---|---|---|---|---|
| Avg | Avg | RMSE | Bias | Avg | RMSE | Bias | |
| 2 m T | 8.61 | 8.74 | 1.34 | 0.13 | 8.67 | 1.32 | 0.06 |
| 2 m RH | 60.43 | 55.56 | 11.86 | −4.87 | 55.73 | 11.60 | −4.70 |
| 10 m WS | 2.34 | 4.14 | 2.18 | 1.79 | 3.12 | 1.02 | 0.77 |
| PRE | 62.20 | 77.22 | 28.65 | 15.02 | 76.49 | 26.63 | 14.29 |
| OBS | CTL | SSE | |||||
|---|---|---|---|---|---|---|---|
| Avg | Avg | RMSE | Bias | Avg | RMSE | Bias | |
| 2 m T | 8.61 | 8.74 | 1.34 | 0.13 | 8.73 | 1.34 | 0.12 |
| 2 m RH | 60.43 | 55.56 | 11.86 | −4.87 | 55.59 | 11.89 | −4.84 |
| 10 m W | 2.34 | 4.14 | 2.18 | 1.79 | 4.13 | 2.18 | 1.79 |
| PRE | 62.20 | 77.22 | 28.65 | 15.02 | 76.92 | 28.44 | 14.72 |
| OBS | CTL | SSE | ||||||
|---|---|---|---|---|---|---|---|---|
| Avg | Avg | RMSE | Bias | Avg | RMSE | Bias | ||
| East | 2 m T | 9.19 | 9.33 | 0.59 | 0.14 | 9.32 | 0.61 | 0.13 |
| 2 m RH | 59.88 | 54.26 | 7.01 | −5.61 | 54.30 | 7.04 | −5.58 | |
| 10 m W | 2.23 | 4.02 | 1.80 | 1.79 | 4.02 | 1.79 | 1.78 | |
| West | 2 m T | 8.22 | 8.22 | 0.81 | 0.00 | 8.22 | 0.79 | −0.01 |
| 2 m RH | 62.03 | 56.62 | 7.72 | −5.41 | 56.64 | 7.69 | 5.39 | |
| 10 m W | 2.16 | 4.07 | 1.92 | 1.91 | 4.06 | 1.92 | 1.90 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jo, Y.H.; Kim, S.H.; Lee, Y.G.; Kim, C.K.; Hong, J.; Lee, J.; Jang, K. Evaluation of Topographic Effect Parameterizations in Weather Research and Forecasting Model over Complex Mountainous Terrain in Wildfire-Prone Regions. Fire 2025, 8, 196. https://doi.org/10.3390/fire8050196
Jo YH, Kim SH, Lee YG, Kim CK, Hong J, Lee J, Jang K. Evaluation of Topographic Effect Parameterizations in Weather Research and Forecasting Model over Complex Mountainous Terrain in Wildfire-Prone Regions. Fire. 2025; 8(5):196. https://doi.org/10.3390/fire8050196
Chicago/Turabian StyleJo, Yong Han, Seung Hee Kim, Yun Gon Lee, Chang Ki Kim, Jinkyu Hong, Junhong Lee, and Keunchang Jang. 2025. "Evaluation of Topographic Effect Parameterizations in Weather Research and Forecasting Model over Complex Mountainous Terrain in Wildfire-Prone Regions" Fire 8, no. 5: 196. https://doi.org/10.3390/fire8050196
APA StyleJo, Y. H., Kim, S. H., Lee, Y. G., Kim, C. K., Hong, J., Lee, J., & Jang, K. (2025). Evaluation of Topographic Effect Parameterizations in Weather Research and Forecasting Model over Complex Mountainous Terrain in Wildfire-Prone Regions. Fire, 8(5), 196. https://doi.org/10.3390/fire8050196











