Influence of Recirculation Zones on Flaming Ignition of Porous Wood Fuel Beds

Abstract

Understanding environmental factors that control the ignition of fuel beds exposed to firebrands is necessary to help reduce the risk of losses of structures. Ignition by firebrands has been reported to be sensitive to wind, but identification and quantification of the physical cause(s) of such sensitivities are still limited. The objective of this study was to quantify the influence of wind speed and direction on the ignition of a fuel bed exposed to firebrands and to understand the causes of this sensitivity. Fuel beds of Douglas fir shavings were exposed to a firebrand surrogate (i.e., a resistive heater) to determine flaming ignition probability and time to ignition for three different wind speeds and three wind directions. Increases in wind speed above quiescent reduced the temperature required for flaming ignition. However, a wind speed threshold above which ignition probability decreased was observed for some wind directions. The temperatures required for flaming ignition to occur and the time to ignition were sensitive to the wind direction. High-speed images and corresponding CFD calculations indicated that ignition occurred in the regions with the most prominent recirculation zones. Thus, sensitivities to wind speed and direction are attributable to differences in the pyrolysate residence time as controlled by recirculation zones. The results indicate that the local flow characteristics can significantly influence ignition, and characterization of the freestream velocity alone may not be sufficient.

1. Introduction

There is an increasing need to better protect homes from wildfires as the number of homes in the wildland–urban interface (WUI) increases [1,2,3,4]. A common way that homes are destroyed during wildfires is by the ignition of fuel beds (e.g., needles, leaves, or landscaping materials) by firebrands. Flames may then spread to and subsequently engulf the structure [5,6]. More comprehensive characterization of how fuel beds ignite around homes is necessary in order to better protect homes from this phenomenon; while the overall mechanisms by which ignition by firebrands occur are generally understood, predicting when ignition will occur remains elusive [7].

Many studies have been conducted to characterize ignition across a wide variety of firebrands and fuel bed configurations. For examples of these studies, the reader is referred to review papers by Fernandez-Pello [7] and, more recently, by Manzello et al. [4,5]. These review articles highlight, among other things, the use of several approaches to evaluate the propensity of fuel bed materials to be ignited by firebrands or other hot objects [8]. The most common method to characterize ignition is dropping flaming or smoldering firebrands on fuel beds and evaluating ignition propensity. Hot metal particles have also been commonly evaluated as ignition sources for fuel beds [7,9,10]. From these studies, significant progress in the understanding of ignition by firebrands/hot objects and the identification of key parameters has been made in recent years. For example, the temperature and energy content of the firebrand/ignition source, the fuel bed material, the fuel bed moisture content, and the environmental conditions near the firebrand(s) have been consistently identified as primary parameters that control ignition. Of the characteristics that influence ignition by firebrands, the effects of wind dynamics near the ignition point are less understood than many of the other primary ignition parameters (e.g., fuel bed moisture content).

Wind can influence the spread of fire by firebrands through several processes. First, increases in wind speed increase the size, and thus the energy content, of firebrands produced [11]. Second, firebrand-laden winds flowing around structures can lead to the accumulation of firebrands in particular regions [12,13,14]. In turn, the local heat flux can remain elevated for a longer duration as firebrands accumulate [15]. Third, the amount of heat imparted to a fuel bed by firebrands can increase as wind speeds increase [15,16,17]. In many studies, the presence of wind increases the probability of ignition by firebrands [8,18,19,20,21,22,23]. Wind has also been observed to facilitate ignitions that do not occur in quiescent conditions [24]. For example, increases in wind speed and changes in wind direction have been shown to increase the ignition probability of natural fuel beds exposed to natural firebrands [25]. Similar sensitivities of ignition probability attributed to wind speed increases have been observed in fuel beds with hot metal particles as ignition sources [26]. Increases in ignition propensity have been postulated to be caused by greater oxygen availability and/or increased mixing as a result of wind speed.

In the aforementioned studies, the heat transfer rates from the firebrands to the fuel beds likely changed (i.e., increased due to faster reaction rates) due to the presence of wind. Changes in the heat transfer rate from the firebrands and changes in the flow field near the fuel bed make it challenging to fully identify the cause(s) of wind-altered ignition behavior. As a result, it is not clear to what extent changes in ignition behavior are caused by the interaction of the fuel bed with wind (e.g., formation of local recirculation zones) or changes in heat transfer from the firebrands. Moreover, sensitivities of ignition to changes in the direction of wind have been observed but not specifically addressed [25]. It is important to decouple the aforementioned factors to better understand how each factor impacts ignition.

With this background and motivation, the objective of this study is to quantify how changing wind speed and direction influence the ignition of a fuel bed in contact with a surrogate firebrand of a fixed temperature. It is expected that the results of this work will help further the understanding of the influence of wind on the ignition of fuel beds and may allow better protection of structures in the WUI.

2. Methodology

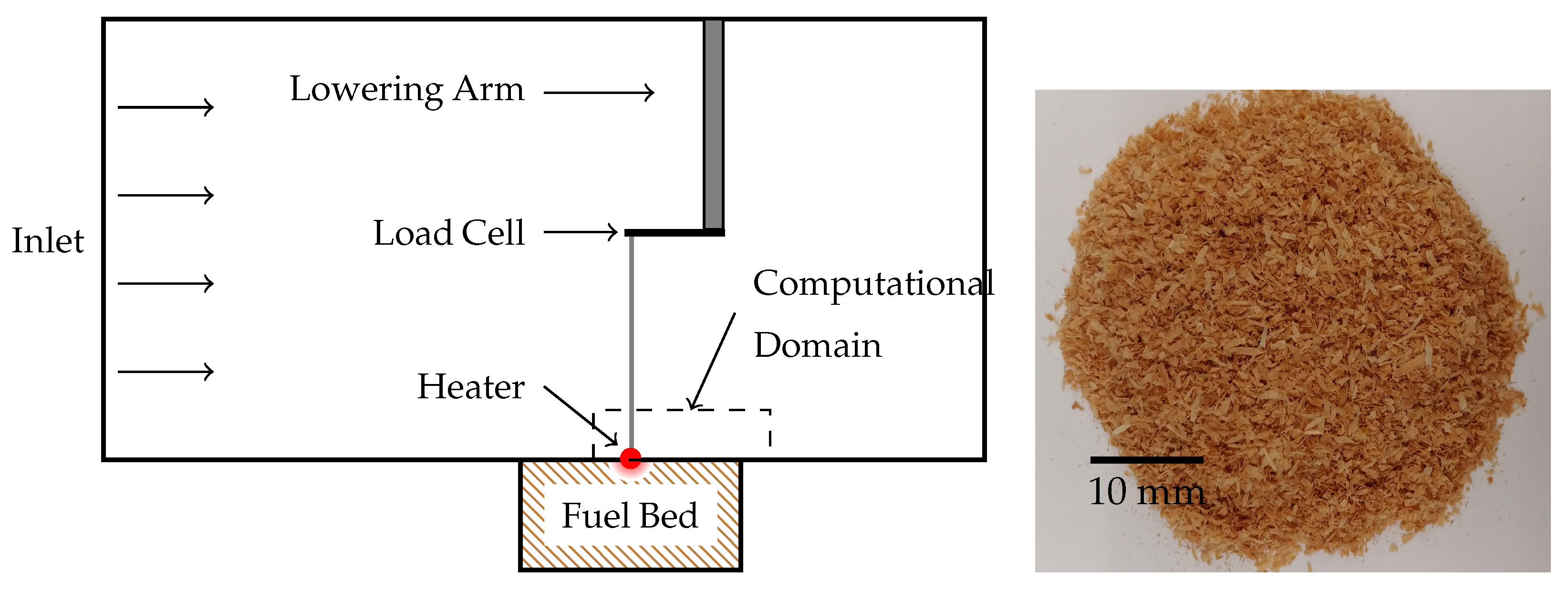
2.1. Experimental

The ignition experiments in this study were conducted by lowering a cartridge heater with a controlled surface temperature onto a prepared fuel bed and observing whether ignition did or did not occur. The cartridge heater had a diameter of 6.4 $\mathrm{m}\mathrm{m}$ and was 51 $\mathrm{m}\mathrm{m}$ long. The size of the heater aligns with the sizes of firebrands that have previously been shown to ignite fuel beds [27]. The temperature of the heater was controlled and closely monitored using a PID controller in LabVIEW. Heater temperatures ranging from 250 °C to 750 °C were evaluated. The temperatures were measured using a type K thermocouple. The thermocouple was affixed to the longitudinal center of the heater and the circumferential opposite side of the fuel bed. The heater was lowered onto the fuel bed, and the pressure between the heater and the fuel bed was controlled with an automated lowering device equipped with a load cell. The pressure of the heater on the fuel bed was set to be equivalent to that of a 10 $\mathrm{g}$ firebrand. The heater was affixed to 4–40 threaded rods that extend 100 $\mathrm{m}\mathrm{m}$ below the load cell and lowering apparatus. This arrangement was used to minimize flow disruptions caused by fixtures.

Although heaters have been used previously as surrogates for firebrands [28,29,30,31], physical limitations exist in the use of heaters to represent firebrands. Some of these limitations have been noted previously [4] and are now described, as are the advantages. Specifically, the release of pyrolysates from the firebrand and the participation of pyrolysates released by the firebrand are absent from heaters. For this reason, heaters may be more representative of pieces of hot metal [4]. In addition, the temperature evolution and values will differ between firebrands and cartridge heaters. However, the estimated heat flux values from a cartridge heater to the fuel can be representative of measured firebrand heat fluxes [15,16,17,32]. An advantage of using a heater as a surrogate firebrand is that the temperature of the heater can be controlled and varied independently of wind conditions. This makes it possible to gain unique insights into the influence of wind. Moreover, the measurements associated with the heater allow more accurate boundary conditions for the modeling efforts. In light of the aforementioned limitations and advantages, the results presented are considered representative and should be compared to each other.

The fuel beds were created in a multi-step process. Kiln-dried Douglas fir lumber was planed, granulated, and finally screened such that the particles fit through a 2.3 $\mathrm{m}\mathrm{m}$ screen but not a 1.3 $\mathrm{m}\mathrm{m}$ screen. Douglas fir particles were evaluated because they are representative of fine organic material prone to flaming or smoldering ignition. The fuel was placed in a 140 $\mathrm{m}\mathrm{m}$ diameter glass container with a depth of 70 $\mathrm{m}\mathrm{m}$ before insertion into the wind tunnel. The average bulk density of the fuel beds was 74.2 $\mathrm{k}\mathrm{g}{\mathrm{m}}^{-3}$. Figure 1 shows an image of the fuel bed particles. Other porous fuels of varying fuels and sizes have been evaluated using a similar methodology, as reported previously by this group [33].

A minimum of 20 ignition tests were conducted for each experimental condition with a total of 241 tests. The temperature setpoints of the heater for the various experiments were identified using the three-phase optimal design procedure [34,35]. Three-phase optimal design is a sequential procedure used to ascertain the probability of a binary outcome (i.e., ignition or non-ignition) with a limited number of tests. The logistic regressions and 95% confidence intervals of the ignition probability were calculated using the scikit-learn Python package [36]. A fuel bed was considered to ignite if a flame was observed and persisted after the heater was removed. If flaming ignition was not observed after 3000 $\mathrm{s}$ of heater contact the heater was removed, and the test was considered to have a non-ignition outcome.

The energy imparted to the fuel bed was estimated by applying an energy balance to the heater. Typical heat fluxes to the fuel bed ranged from 5 $\mathrm{k}\mathrm{W}{\mathrm{m}}^{-2}$ to 50 $\mathrm{k}\mathrm{W}{\mathrm{m}}^{-2}$. Similar values have been reported for studies of heat fluxes from firebrands of burning wood [15,16,32]. The power delivered to the heater was measured using a CR9580-10 current sensor and a ZMPT101B voltage sensor. Temperature distributions, created from infrared images of the heater taken with a FLIR SC6700 camera, were used to estimate radiant and convective heat losses to the surroundings. A blackbody calibration was performed to correlate photon counts from the camera with temperature and produce the longitudinal temperature distribution of the heater. The circumferential temperature of the heater was considered uniform.

High-speed images of the ignition process were captured using a Phantom VEO 710 camera for select conditions. The images were used to provide insights into the differences between ignition processes. Images were collected at 5 $\mathrm{k}\mathrm{Hz}$.

2.2. Computational

A simplified zero-dimensional chemical and three-dimensional flow computational model was implemented to provide further insights into the processes leading up to ignition for the different configurations. Specifically, the local pyrolysate concentrations and sizes of flow structures near the ignition sites were characterized. The methodology builds on the approach used previously by this group [31]. Physically, the fluid flow around the heater, the heat transfer from the heater to the fluid and the fuel bed, and the release of pyrolysis gases into the fluid domain were captured in the simulations. Simulations were performed for a 5.8 ${\mathrm{m}\mathrm{s}}^{-1}$ wind speed and three heater orientations to better understand the sensitivities to wind direction. In addition, calculations were performed with the heater orthogonal to the wind direction for the three experimentally evaluated wind speeds to better understand sensitivities to wind speed.

Simulations were conducted in two parts. First, the average mass flux, average temperature, and average thermal properties of the pyrolysates were calculated. These results were used to determine the mass flow and composition of the pyrolysates entering the fluid domain. The next step of the computational effort simulated the distribution of pyrolysis gas near the heater using the 3D LES solver FireFOAM implemented in OpenFOAM [37]. The combination of these modeling efforts enabled visualization of the conditions near the ignition source for which experimental data suggested that ignitions were likely to occur.

Estimates of the fuel bed combustion process were calculated using a model of non-reacting heat transfer from the heater to the fuel bed; these estimates, in turn, were used to estimate the mass of the fuel bed above a temperature of 220 °C.This temperature was assumed to be the threshold for pyrolysis to occur. The thermal properties of the fuel bed were estimated using correlations for porous media [38] and the average measured bulk density of the fuel beds. The heat transferred to the fuel bed was determined from the measured energy supplied to the fuel bed from the heater. More specifically, an energy balance was applied to the measured total energy and surface temperature profile to obtain the heat flux boundary condition for the fuel bed. With this boundary condition, we solved the heat diffusion equation to observe the spatial and temporal evolution of the fuel bed temperatures. The heat diffusion equation is as follows:

$${\displaystyle \frac{\partial \left(\rho h\right)}{\partial t}}={\displaystyle \frac{\partial }{\partial x_j}}\left(\alpha {\displaystyle \frac{\partial h}{\partial x_j}}\right).$$

(1)

Calculations were conducted for 1 $\mathrm{s}$. A simulation time of 1 $\mathrm{s}$ provided sufficient insight into trends observed in the experiments but was shorter than the physical system’s time to ignition. The assumptions associated with modeling the temperature of the fuel bed were as follows:

• Fuel beds were considered to have constant thermal properties; although pyrolysis did occur during the experiments, changing the properties of the fuel bed, the mass loss from the start of heat transfer to a typical ignition event is small compared to the total mass that undergoes heating.
• The temperature evolution of the fuel bed was assumed to be symmetric around the centerline of the heater.
• Heat losses from the fuel bed to the surroundings were assumed to be significantly less than the heat transfer from the heater to the fuel bed. Thus, the interface between the fuel bed and the air was considered insulated.
• The fuel bed was modeled as a solid with thermal and physical properties representative of a porous material; its properties were either measured or derived from measurements. Density and particle size were directly measured. Thermal conductivity and chemical composition were derived.

The mass of pyrolysis gases released was estimated using 0D calculations in Cantera based on the calculated temperature distribution and the estimated chemical composition. The chemical composition of the fuel bed was estimated using Douglas fir data from the Bioengineering Feedstock Library database [39]. Once the temperature distribution and composition of the fuel bed were determined, the pyrolysis species were determined from chemical equilibrium calculations using the BioPox mechanism [40]. The BioPox mechanism is a detailed solid- and gas-phase pyrolysis mechanism well suited for porous fuel beds. Species were considered to be released into the flow domain if they existed in the gas-phase biomass mechanism Bio1412 [41]. More detail about the species selection process is available in previous work [31]. The Cantera calculations treated the fuel bed material as an insulated fixed-mass reactor. The mass, species, and energy equations were solved to obtain the temperature and species concentrations of the pyrolysis products exiting the fuel bed and entering the air around the heater:

$${\displaystyle \frac{\partial m}{\partial t}}=0,$$

(2)

$$m{\displaystyle \frac{\partial \left(m{Y}_k\right)}{\partial t}}={\dot{m}}_{k,gen}=V{\dot{\omega }}_{k}M{W}_k,$$

(3)

$$m{c}_v{\displaystyle \frac{\partial T}{\partial t}}=\dot{Q}-\sum _k{\dot{m}}_{k,gen}{u}_k.$$

(4)

Here, $Y_k$, ${\dot{m}}_k$, and ${\dot{\omega }}_k$ are the mass fraction, mass generation rate, and generation rate (respectively) of each species k included in the mechanism. V is the volume of the fuel bed material in the reactor.

The equations used to calculate the reaction rates for the elementary reaction are as follows:

$$\begin{array}{cc}\hfill k_f& =A{T}^b{e}^{-E_a/RT},\hfill \end{array}$$

(5)

and

$$\begin{array}{cc}\hfill R_f& =\left[A\right]\left[B\right]k_f,\hfill \end{array}$$

(6)

where $R_f$ is the forward reaction rate, $k_f$ is the reaction rate constant, $E_a$ is the activation energy, b is the temperature exponent, and R is the gas constant. Note that A is the pre-exponential factor for the Arrhenius reaction and [A] is the concentration of species A. Similarly, the reaction rates for three-body reactions were calculated as follows:

$$\begin{array}{cc}\hfill R_f& =\left[A\right]\left[B\right]\left[M\right]k_f,\hfill \end{array}$$

(7)

and

$$\begin{array}{cc}\hfill \left[M\right]& =\sum _k{ϵ}_k{C}_k,\hfill \end{array}$$

(8)

where ${ϵ}_k$ and $C_k$ are the collision efficiency and concentration of each species, respectively. Falloff reaction rates were calculated using the reduced pressure P, defined as follows:

$$P={\displaystyle \frac{k_0\left[M\right]}{k_{\infty }}}.$$

(9)

The reaction rate for the falloff reactions is then calculated as follows:

$$k_f(T,P)=k_{\infty }\left({\displaystyle \frac{P}{1+P}}\right)F(T,P).$$

(10)

Pressure-dependent P-Log reaction rates were calculated for intermediate pressure values using a logarithmic interpolation between two reaction rates $k_1$ and $k_2$ at pressures $P_1$ and $P_2$ as follows:

$$log{k}_f(T,P)=log{k}_1\left(T\right)+(log{k}_2\left(T\right)-log{k}_1\left(T\right)){\displaystyle \frac{logP-log{P}_1}{log{P}_2-log{P}_1}}.$$

(11)

The overall generation rate of each species (${\dot{\omega }}_k$) is defined as the sum of the individual reaction rates $R_f$ for all of the reactions where the species (k) is present, where ${\nu }_i$ corresponds to the number of each species (k) produced for each reaction (i). Equation (12) results in the source term for Equation (3), the solution of which determines the mass fractions of the species that are released into the fluid domain above the fuel bed:

$${\dot{\omega }}_k=\sum _i^N{\nu }_i{R}_{f,i}.$$

(12)

Simulations of the fluid-domain pyrolysis gas distribution were carried out using the 3D LES solver FireFOAM implemented in OpenFOAM [37]. The mass, momentum, species, and energy equations solved in the FireFOAM calculations are shown below:

$${\displaystyle \frac{\partial p}{\partial t}}+{\displaystyle \frac{\partial \rho u_j}{\partial x_j}}=0,$$

(13)

$${\displaystyle \frac{\partial \left(\rho Y_k\right)}{\partial t}}+{\displaystyle \frac{\partial \left(\rho u_j{Y}_k\right)}{\partial x_j}}={\displaystyle \frac{\partial {\mu }_{eff}}{\partial x_j}}{\displaystyle \frac{\partial Y_k}{\partial x_j}},$$

(14)

$${\displaystyle \frac{\partial \left(\rho u_i\right)}{\partial t}}+{\displaystyle \frac{\partial \left(\rho u_{rj}{u}_i\right)}{\partial x_j}}+\rho {ϵ}_{ijk}{\omega }_i{u}_j=-{\displaystyle \frac{\partial p_{rgh}}{\partial x_i}}-{\displaystyle \frac{\partial \left(\rho g_i{x}_j\right)}{\partial x_i}}+{\displaystyle \frac{\partial }{\partial x_j}}\left({\tau }_{ij}+{\tau }_{t_{ij}}\right),$$

(15)

$$\begin{array}{ccc}{\displaystyle \frac{\partial \left(\rho h\right)}{\partial t}}+{\displaystyle \frac{\partial \left(\rho u_{j}h\right)}{\partial x_j}}+{\displaystyle \frac{\partial \left(\rho k\right)}{\partial t}}+{\displaystyle \frac{\partial \left(\rho u_{j}k\right)}{\partial x_j}}\hfill & =& \\ & -& {\displaystyle \frac{\partial \left(q_i+q_{ti}\right)}{\partial x_i}}+\rho r+q_{rad}+{\displaystyle \frac{\partial p}{\partial t}}-\rho g_j{u}_j+{\displaystyle \frac{\partial \left({\tau }_{ij}{u}_i\right)}{\partial x_j}}.\hfill \end{array}$$

(16)

The computational domain used is outlined in Figure 1 with a dashed rectangle. More specifically, a subset of the wind tunnel test section surrounding the heater(s) was considered for the simulation of the flow over the heater(s). A constant cross-section normal to the flow direction was used for all three heater angles. The dimensions of the plane normal to the flow were 110 $\mathrm{m}\mathrm{m}$ wide and 48 $\mathrm{m}\mathrm{m}$ high. The lengths of the domains were varied to maintain a domain size of 5D upstream and 14D downstream of the heater. The domain lengths were 170 $\mathrm{m}\mathrm{m}$ for the 45° and parallel configurations and 120 $\mathrm{m}\mathrm{m}$ for the configuration with the heater perpendicular to the flow. The numbers of cells in each domain were 420,728, 424,308, and 307,252 for the parallel, 45°, and perpendicular cases. Cell sizes ranged from 0.1 $\mathrm{m}\mathrm{m}$ near the heater to 4 $\mathrm{m}\mathrm{m}$ in the bulk flow region in the center of the domain. For validation, the separation angle of the flow was compared to a correlation from the literature [42] and was found to predict the angle within 1% of the recommended correlation. Reducing the cell size by a factor of two did not appreciably reduce the error.

The inlet wind speed and turbulence intensity boundary conditions were determined from hot-wire anemometer measurements. The measured turbulence intensities were 1.6%, 0.23%, and 0.14% for the 0.5 ${\mathrm{m}\mathrm{s}}^{-1}$, 3.5 ${\mathrm{m}\mathrm{s}}^{-1}$, and 5.8 ${\mathrm{m}\mathrm{s}}^{-1}$ wind speeds, respectively. The solid surfaces (i.e., cartridge heater, holding rods, fuel bed, and wind tunnel floor) were considered to have a no-slip boundary condition, and their temperatures were assumed to be fixed. All temperatures except those of the heater surfaces and pyrolysate injection were 300 $\mathrm{K}$. The heater was maintained at the measured temperature corresponding to 50% ignition probability from experimental tests. The inlet temperature and mass flux of the pyrolysis gases were determined from the fuel bed thermal model and Cantera calculations. The outlet and sides of the domain used a zero-gradient boundary condition. The local equivalence ratio was calculated after one second of pyrolysis release; although one second is shorter than the average time to ignition, insights were still gained into the distribution of pyrolysates with respect to the observed ignition locations for the various heater orientations.

3. Results

The ignition or non-ignition outcomes for the various conditions are reported in Figure 2. Individual markers in the plots represent the outcome of each test. Tests that resulted in self-sustained flames are denoted as one; tests with no self sustained flames are denoted as zero. The curves are logistic regressions for each of the tests with the same wind speed and heater angle. Shaded regions associated with the curves indicate the 95% confidence interval of the regressions. The topmost plot shows the results when the heater is parallel to the direction of the flow, the middle plot when the heater is at 45° with respect to the direction of the flow, and the bottom plot when the heater is perpendicular to the flow.

In each panel, the three different wind speeds are represented as unique datasets and logistic regression curves. For clarity, Figure 3 shows the heater temperatures estimated to produce a 50% ignition probability for the results shown in Figure 2. The error bars correspond to the 95% confidence interval. Three observations are noted from the results in Figure 2 and Figure 3. First, the ignition probability increased as the temperature increased. Ignition probabilities for the 0.5 ${\mathrm{m}\mathrm{s}}^{-1}$ wind speed were similar to previously published results for a similar fuel bed and apparatus with a measured wind speed of 0.1 ${\mathrm{m}\mathrm{s}}^{-1}$ [31]. Second, increasing the wind speed beyond 0.5 ${\mathrm{m}\mathrm{s}}^{-1}$ increased the ignition probability. This observation is consistent with previously reported work [21,25] showing that the presence of wind can increase the likelihood of ignition. What has not been quantified previously is the magnitude of changes in ignition probability due to changes in wind speed. For example, when heaters were oriented parallel to the flow with a heater temperature of 550 °C, ignition occurred in 99% of instances when the wind speed was 3.5 ${\mathrm{m}\mathrm{s}}^{-1}$ and 5.8 ${\mathrm{m}\mathrm{s}}^{-1}$ but 25% of instances at 0.5 ${\mathrm{m}\mathrm{s}}^{-1}$. The sensitivity to wind speed was even more pronounced for the 45° and perpendicular orientations, in which heater temperatures of 500 °C resulted in ignition in under 1% of tests at 0.5 ${\mathrm{m}\mathrm{s}}^{-1}$ but over 99% of tests at 5.8 ${\mathrm{m}\mathrm{s}}^{-1}$. This observation illustrates that an increase in wind speed that is relatively modest (compared to winds often accompanying wildfires) can shift fuel bed ignition probability from less than 5% to very likely with no other changes in conditions.

The third observation from Figure 2 and Figure 3 is that an increase in wind speed from 0.5 ${\mathrm{m}\mathrm{s}}^{-1}$ to 3.5 ${\mathrm{m}\mathrm{s}}^{-1}$ resulted in an increase in ignition probability for all heater angles. However, an increase from 3.5 ${\mathrm{m}\mathrm{s}}^{-1}$ to 5.8 ${\mathrm{m}\mathrm{s}}^{-1}$ did not result in an increase in ignition probability for any of the heater orientations. Similarly, the heater temperature needed to produce a 50% ignition probability decreased as the wind speed was increased from 0.5 ${\mathrm{m}\mathrm{s}}^{-1}$ to 3.5 ${\mathrm{m}\mathrm{s}}^{-1}$. This occurs, in general, because of changes in the recirculation zones near the heaters, as will be explained shortly. In contrast, no statistical difference in ignition temperature was observed with an increase in wind speed from 3.5 ${\mathrm{m}\mathrm{s}}^{-1}$ to 5.8 ${\mathrm{m}\mathrm{s}}^{-1}$ in either the perpendicular or the parallel heater orientation. However, the corresponding temperature required for 50% ignition probability in the 45° orientation increased as the wind speed was increased from 3.5 ${\mathrm{m}\mathrm{s}}^{-1}$ to 5.8 ${\mathrm{m}\mathrm{s}}^{-1}$. These trends in ignition propensity and ignition threshold temperature show that there is a threshold for ignition enhancement that depends on both wind speed and orientation. An "optimum" wind speed for inducing ignition has been postulated [22], but this study confirms its existence and shows that the threshold also depends on the orientation of the wind. What is unclear, thus far, are the specific physical processes that promote or retard ignition as the wind speed is increased or the heater angle is changed.

The time to flaming ignition is more sensitive to the heater orientation than the wind speed. Figure 4 shows histograms of the time required for ignition. Information from tests where the fuel did not ignite is not included. The wind speed increases from the top to the bottom plot, and the colors represent the different heater angles. Note that the time-to-ignition axis is on a log scale. Three observations are noted about the time to flaming ignition. First, the times to ignition for the 3.5 ${\mathrm{m}\mathrm{s}}^{-1}$ and 5.8 ${\mathrm{m}\mathrm{s}}^{-1}$ wind speeds are often sufficiently long (i.e., >100 $\mathrm{s}$) to suggest that the fuel beds ignite in a smoldering manner and then transition to flaming. Visible observations showed that ignition occurred at the edge of smoldering fronts at extended times (i.e., >100 $\mathrm{s}$). Second, for the 0.5 ${\mathrm{m}\mathrm{s}}^{-1}$ tests, the difference in time to ignition for the different heater angles was much smaller than for the other two wind speeds. This observation shows a greater sensitivity of ignition times to the direction of the wind at higher wind speeds, suggesting a change in local physical conditions leading to ignition. Third, for the 3.5 ${\mathrm{m}\mathrm{s}}^{-1}$ and 5.8 ${\mathrm{m}\mathrm{s}}^{-1}$ cases, ignition times were typically longest when the heater was oriented parallel to the flow. The shortest times to ignition typically occurred when the heater was perpendicular to the flow. The sensitivity of ignition latency to different heater angles shows that the ignition process changes as the heater angle changes.

High-speed images were recorded for a subset of test configurations to provide insights into changes in ignition location resulting from variations in the heater angle. Figure 5 shows images of the initial flames observed during tests of the three different heater angles. While only a single representative image is provided, the general location of the ignition was confirmed by comparing three different ignition events for each heater orientation. A heater temperature of 450 °C and a wind speed of 5.8 ${\mathrm{m}\mathrm{s}}^{-1}$ were used for all tests. For tests where the heater was oriented either at 45° or perpendicular to the flow (i.e., Figure 5b,c), ignition was observed to occur on the upwind side of the heater near the fuel bed. For the parallel heater orientation (i.e., Figure 5a), ignition was observed underneath the heater in the downstream side in a cavity in the fuel bed. The cavity was formed by the pyrolysis of the fuel bed during the heating process.

The differences in ignition location and the subsequent changes in ignition times are attributable to changes in the local velocity field around the heater as the orientation relative to the wind changes. As the heater is rotated from parallel to perpendicular to the flow, pyrolysates are more likely to remain near the highest-temperature region of the heater (approximately the center) due to the recirculation zones that form on the upwind side of the heater. When the heater is parallel to the flow, pyrolysates tend to advect away from the heater. Thus, for the condition where the heater perpendicular to the flow, the recirculation zone is expected to have the longest residence time of the pyrolysates. The pyrolysates are also anticipated to remain near the highest-temperature part of the heater. This explanation is consistent with the observation that tests where the heater is oriented perpendicular to the flow typically ignited at lower temperatures and in shorter times than the other orientations, as shown in Figure 3 and Figure 4.

The observation that the temperature needed for ignition lowers with an increase in wind speeds when the heater is parallel to the wind warrants further investigation in light of the influence of recirculation zones on ignition. Specifically, it would be expected that when the heater is parallel to the wind direction, the pyrolysates would tend to advect away, ultimately requiring higher temperatures to achieve ignition (i.e., counter to measurements). However, as previously noted, when the wind flows parallel to the heater, ignition occurs inside a cavity in the fuel bed underneath the heater. The flow that develops within this cavity will have a longer local residence times for pyrolysates. In short, the reduction in ignition temperatures as wind speeds increase when heaters are parallel further illustrates the important role that recirculation zones can play in affecting ignition behavior.

Computational results for the three heater orientations at a wind speed of 5.8 ${\mathrm{m}\mathrm{s}}^{-1}$ are now considered to gain further insight into the effects of recirculation zones on ignition behavior. Figure 6 shows streamlines passing through the pyrolysis release zones along with the temperature distributions in regions where pyrolysates are present (i.e., $\varphi >$0.05) for the three heater orientations. The results shown in Figure 6 correspond to 1 $\mathrm{s}$ after the start of pyrolysate release; although typical ignition times are significantly longer than 1 $\mathrm{s}$, the time evaluated is sufficient to provide insights into the fluid motion. The streamlines shown in Figure 6 confirm that a recirculation zone was present near the center of the heater when the orientation was perpendicular or 45° with respect to the wind direction. The center of the heater also coincides with the peak surface temperature (i.e., the reported temperature) of the heater.

The presence of recirculation zones previously attributed to ignition enhancement in experimental observations is shown in Figure 6a,c (i.e., as evidenced by the streamlines of the flow upstream). Figure 7 show velocity streamlines for the three wind speed cases with the heater oriented perpendicular to the flow. Figure 7 shows velocity streamlines for the three wind speed cases with the heater oriented perpendicular to the flow to illustrate the affects of changes in wind speed, while the relative sizes of the recirculation zones in Figure 7 for each wind speed illustrate the further correlation between recirculation zone size and the ignition temperature.

Specifically, the largest change in both the recirculation zone size and the temperature required for ignition occurred when the wind speed increased from 0.5 ${\mathrm{m}\mathrm{s}}^{-1}$ to 3.5 ${\mathrm{m}\mathrm{s}}^{-1}$ (≈50–100 °C). A smaller change in recirculation zone occurred between the 3.5 ${\mathrm{m}\mathrm{s}}^{-1}$ and 5.8 ${\mathrm{m}\mathrm{s}}^{-1}$ wind speeds (<10 °C), which is consistent with experimental ignition sensitivities.

Perhaps unexpected in the results shown in Figure 6 are the characteristics of the volume of pyrolysates with the potential to be ignited, arbitrarily selected as $\Phi >0.85$. For both the parallel and 45° heater orientations, the total volume of ignitable pyrolysates was larger than in the perpendicular heater orientation. The calculated volumes of ignitable pyrolysates were 61 ${\mathrm{m}\mathrm{m}}^3$, 34 ${\mathrm{m}\mathrm{m}}^3$, and 24 ${\mathrm{m}\mathrm{m}}^3$ for the parallel, 45°, and perpendicular orientations, respectively. The average temperatures of the pyrolysates were highest in the parallel and 45° heater orientations, with calculated values of 600 °C, 590 °C, and 580 °C for the parallel, 45°, and perpendicular orientations, respectively. Larger volumes of flammable pyrolysates at higher temperatures suggest that ignition is favored when the heater is parallel or at 45° to the flow. Order-of-magnitude estimates of residence time were computed to provide further insights into the ignition behavior. The ratio of the average velocity magnitude of the pyrolysis gases with $\Phi >0.85$ and the mass release rate of the pyrolysates from the fuel bed were considered for the residence time estimations. The average velocity of the pyrolysates serves as a proxy for the removal of combustible gases from the high-temperature zone near the heater. The estimated residence time of the pyrolysates in the perpendicular heater orientation is more than 25 times longer when than that of the parallel heater orientation and 15 times longer than that of the 45° heater orientation. The differences in residence times for the three heater orientations align with trends in ignition probability, consistent with the assertion that combinations of wind and geometry that extend pyrolysate residence times enable the fuel to ignite more readily. The correlations between time to ignition, ignition temperatures, ignition locations, and estimated residence times show that ignition events are sensitive to the residence time of pyrolysates in a high-temperature zone. In other words, a firebrand is much more likely to ignite a fuel bed if the wind speed and geometry of the firebrand or firebrands promote extended residence times of pyrolysates in a recirculation zone near the firebrand(s). A pilot ignition source (i.e., a burning firebrand) may alter this sensitivity and may warrant additional investigation.

4. Summary and Conclusions

Flaming ignition tests were conducted in fuel beds made of Douglas fir particles. Ignition was induced by a cartridge heater, which served as a surrogate for a firebrand. The heater was maintained at a fixed temperature throughout each test, thus allowing the sensitivities of ignition to wind speed and orientation to be further understood. The ignition probability, time to ignition, high-speed imagery, and CFD results were used to quantify the sensitivities of ignition to wind speed and angle. The specific conclusions of this work are as follows:

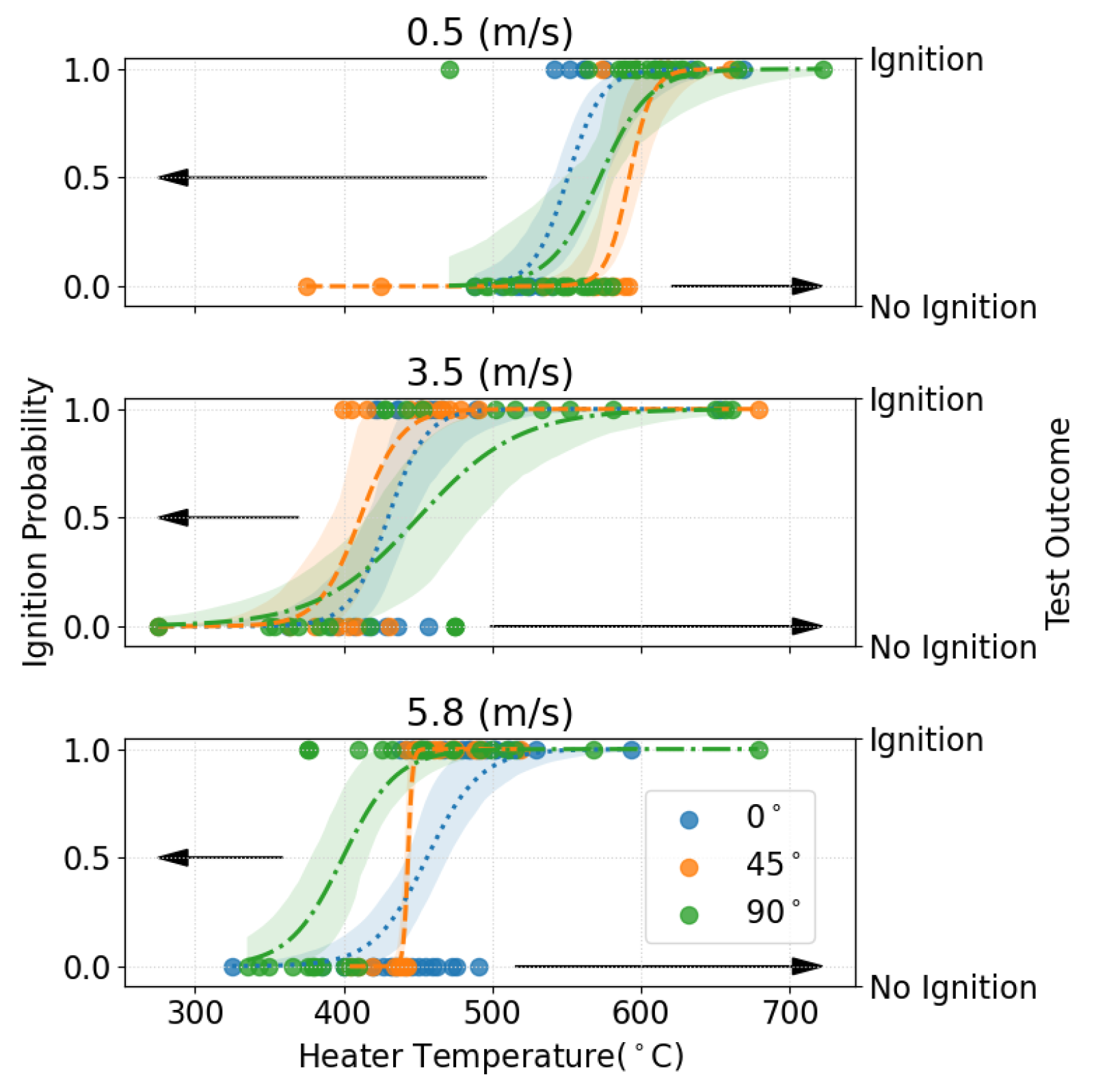
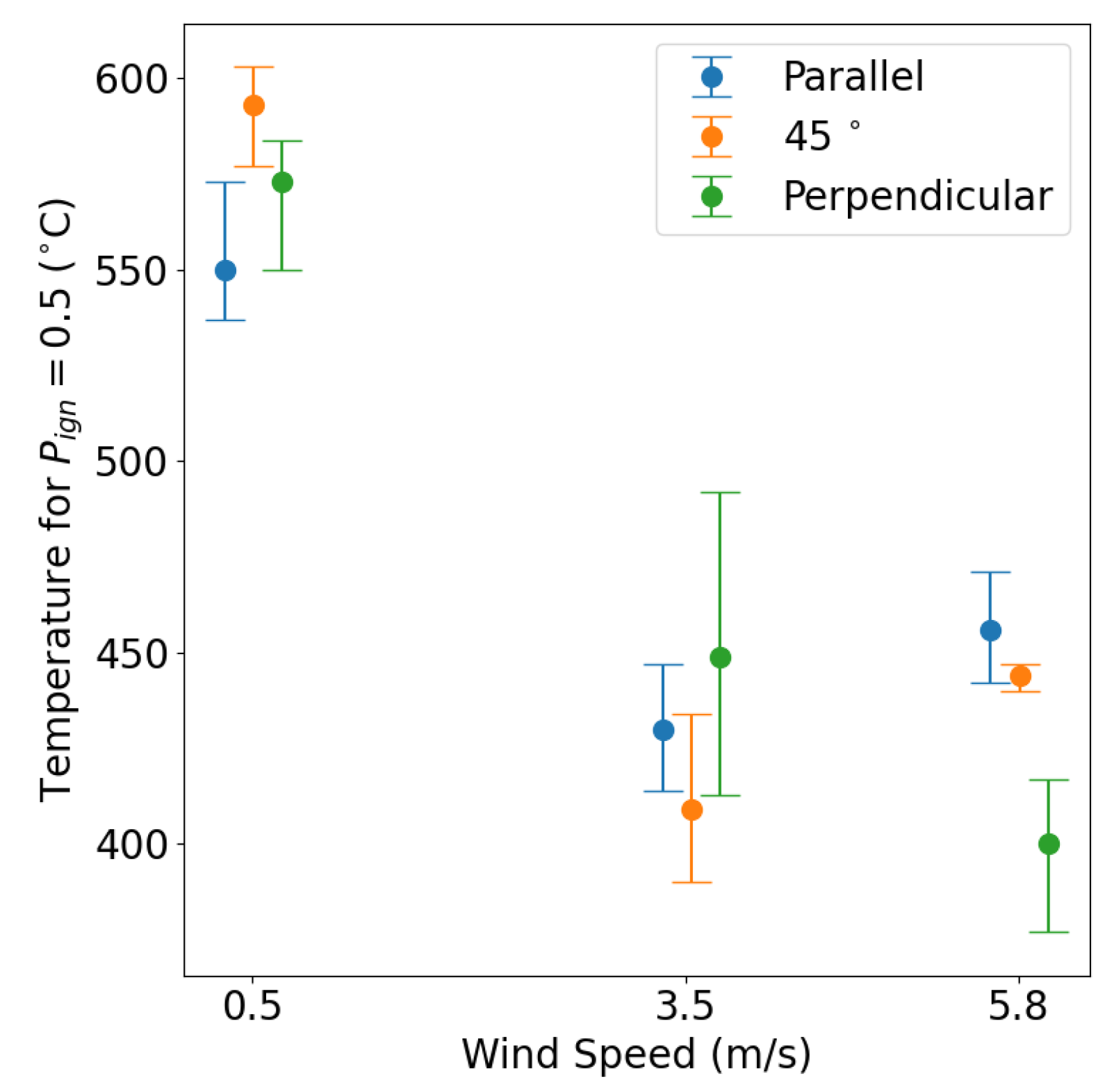
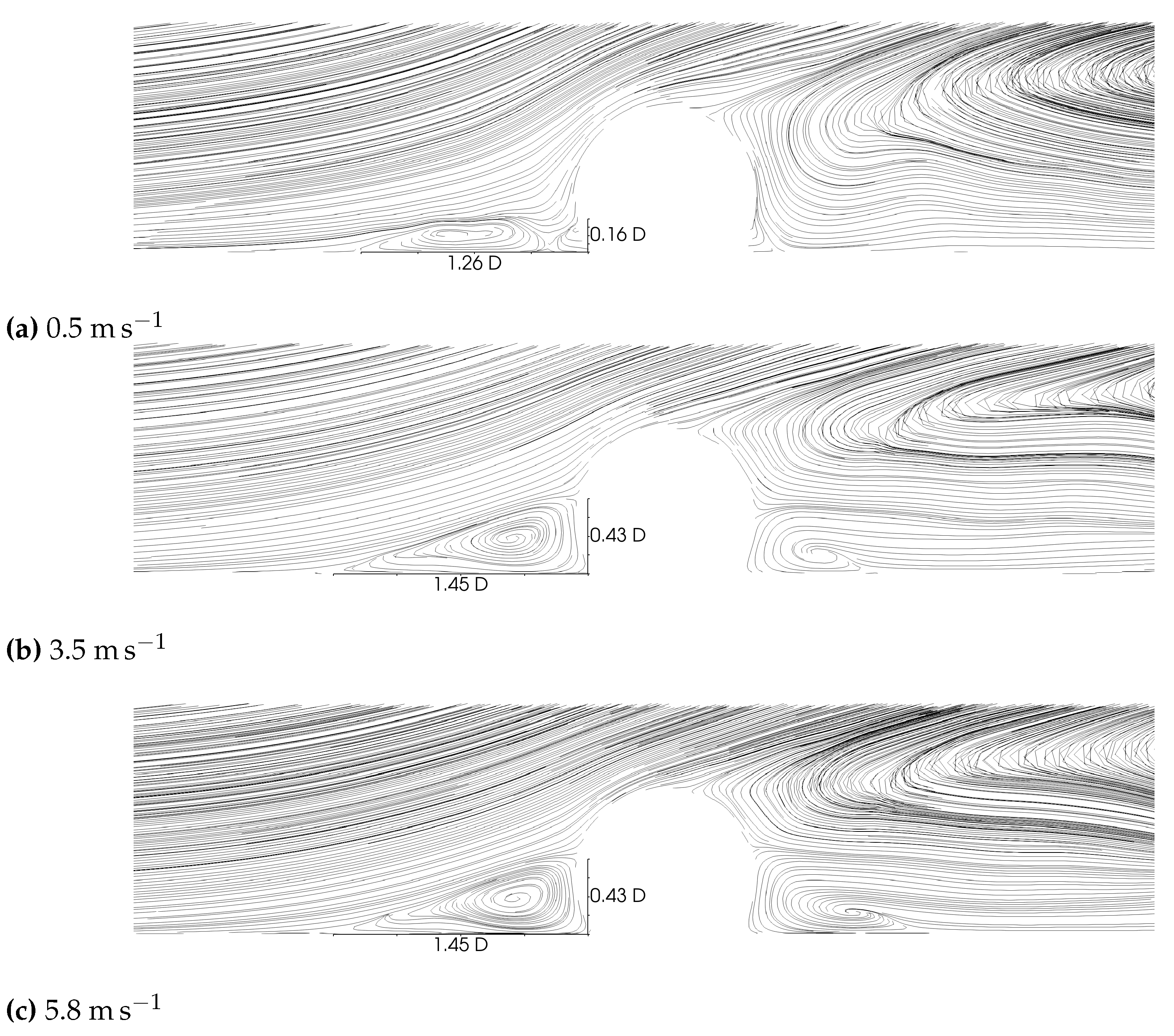
• Increasing the wind speed reduces the temperatures required for the flaming ignition of a fuel bed, at least for the conditions evaluated in this study. However, increases in wind speed do not result in a linear increase in ignition probability. In contrast, increasing the wind speed from quiescent to 5.8 ${\mathrm{m}\mathrm{s}}^{-1}$ reduces the temperature required for ignition by only 25%, suggesting a threshold above which increasing wind speed does not enhance ignition. It is noted that, at sufficient wind speeds, ignition is expected to be suppressed due to heat losses, although this limit was not found in the present study.
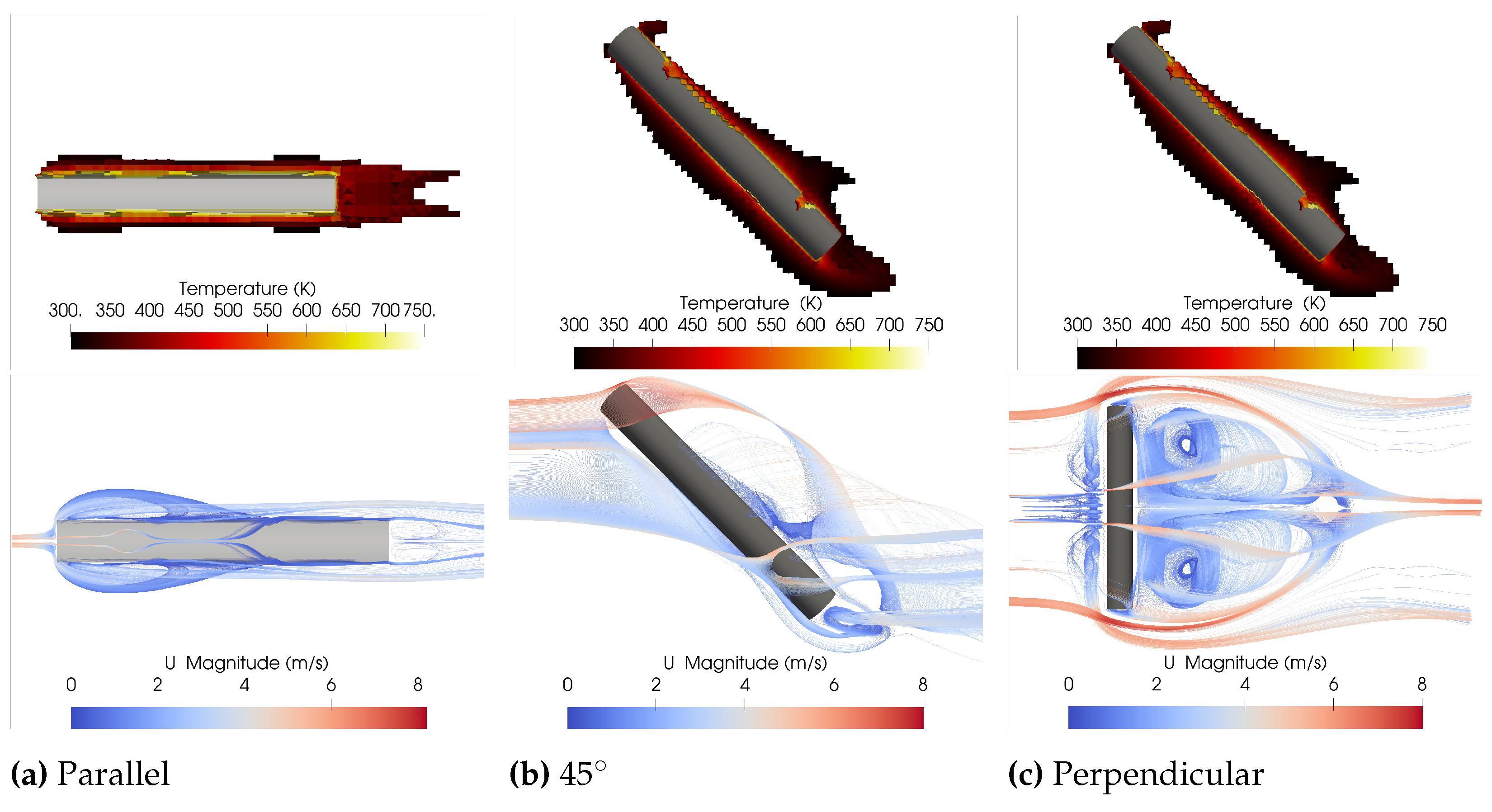
• The temperature at which ignition occurs in porous fuel beds such as Douglas fir is sensitive to the orientation of an object of constant temperature relative to the wind direction. Higher temperatures are typically required for ignition when the heater is parallel to the flow than when it is 45° or perpendicular to the flow. This sensitivity is attributable to differences in recirculation zones and residence times of air and pyrolysates near the hottest region of the heater.
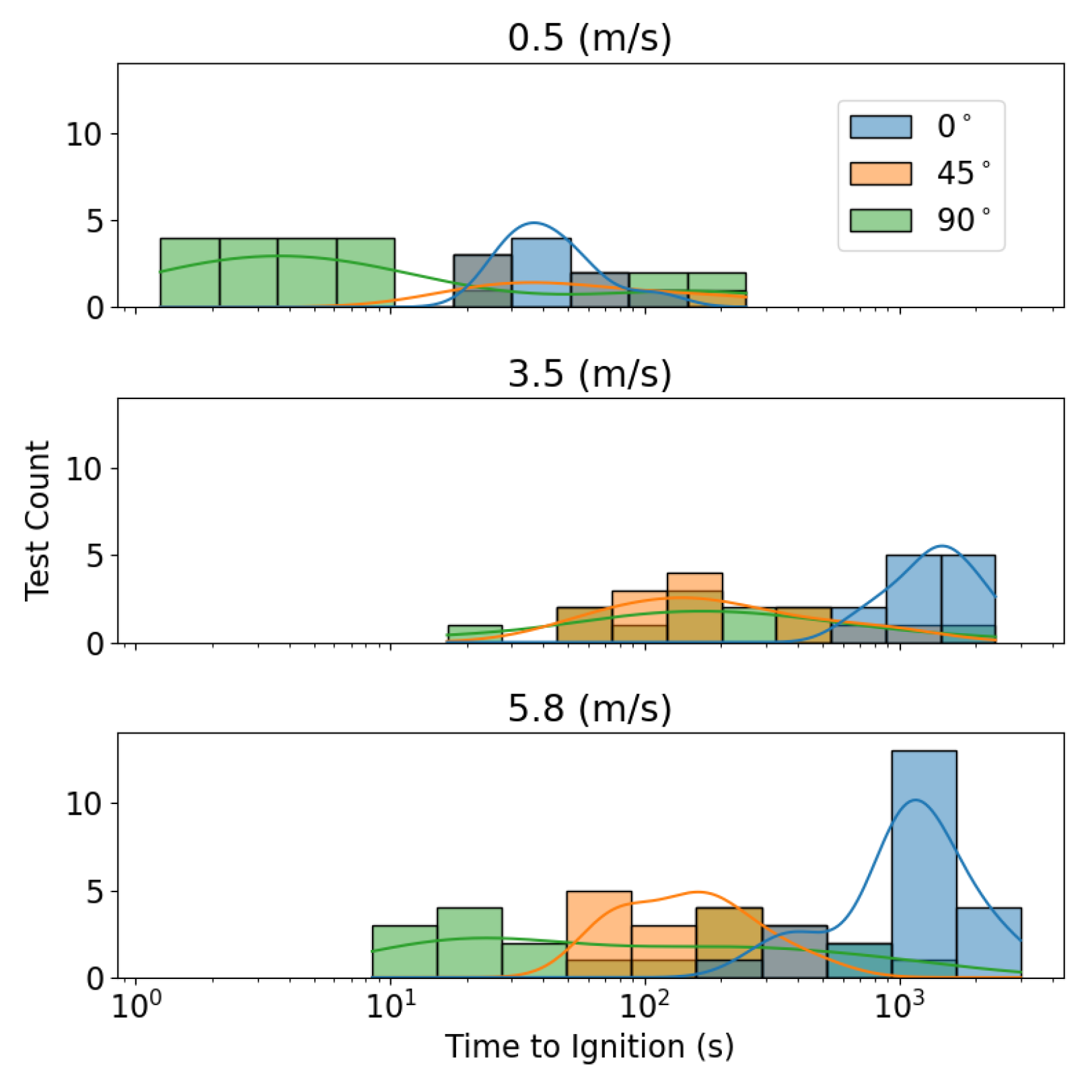
• Times required for flaming ignition of porous fuel beds are sensitive to the angle of a constant-temperature ignition source. A heater in a parallel orientation takes the longest time to ignite the fuel, followed by the 45° case, with the perpendicular case igniting the fuel in the shortest amount of time. High-speed images indicate that ignition typically occurs in regions where recirculation zones occur, as indicated by CFD calculations. The heightened propensity toward ignition is attributable to increased residence times of pyrolysates in the recirculation zones, as supported by calculations.

The conclusions of this work indicate that ignition is favored when firebrands land on a fuel bed under wind speeds and orientations that promote greater residence times of pyrolysates near high-temperature regions of the firebrands. As such, characterizing the freestream velocity may not be sufficient to capture ignition sensitivities. Additional work is needed to verify that the results from this study, using a heater as a surrogate firebrand, are consistent with ignition by actual firebrands. In addition, what is not considered in this work is ignition of char if ignition does not occur in the gas phase first. Thus, the influence of changes in wind speed on ignition of char may warrant further investigation.