Study on the Influence of Smoke Vent Arrangement on the Natural Smoke Exhaust Effect in Urban Traffic Link Tunnels
Abstract
1. Introduction
2. Experimental Design
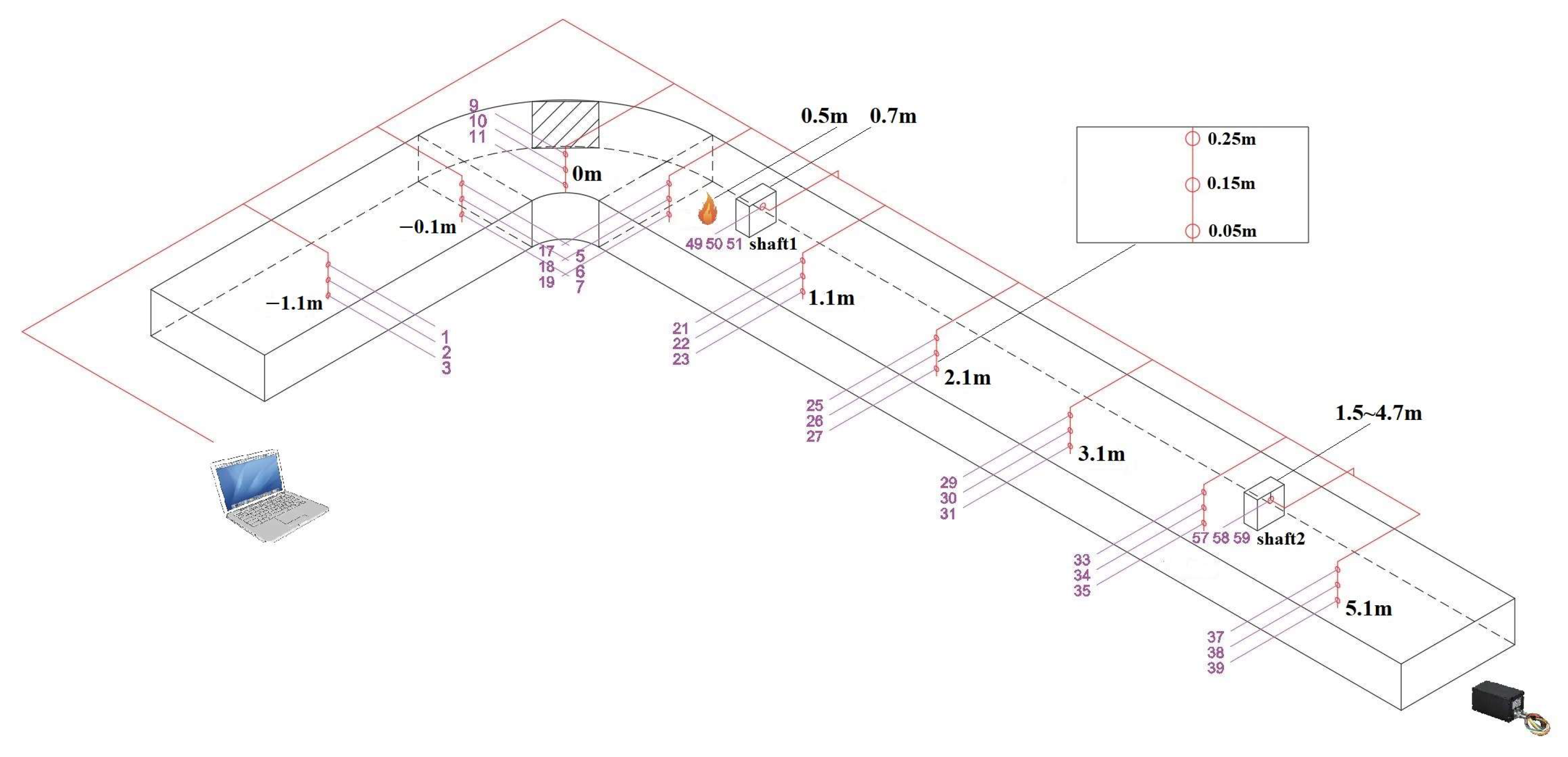
2.1. Design of UTLT Smoke Control Experimental Platform
2.2. Fire Source
3. Analysis of the Influence of Smoke Vent Arrangement on Smoke Exhaust Effect
3.1. Analysis of Smoke Flow Rate in Shafts
3.2. Analysis of Mass Flow Rate
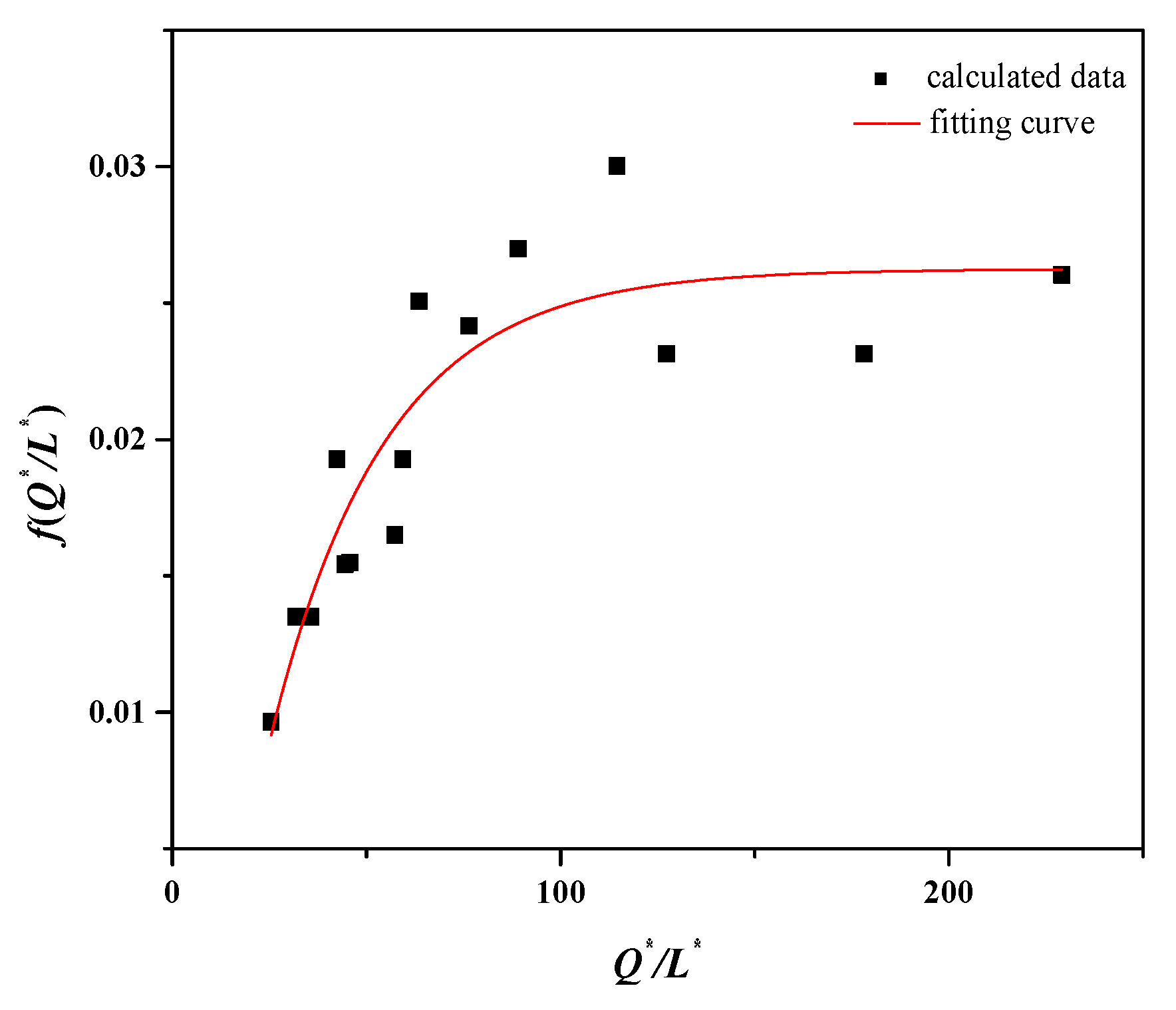
4. Calculating the Model for the Mass Flow Rate of Smoke
5. Conclusions
- (1)
- As the distance between the smoke vents increases, the driving force generated by the stack effect is weakened, leading to a decrease in the smoke exhaust efficiency and a decrease in the smoke mass flow rate.
- (2)
- Under the experimental condition that the fire source is located near the curved section and the fire size is from 5 to 9 kW, the smoke vent distance of 1.6 m (corresponding to the fire size of 2.5~4.5 MW and the distance of 20 m between the smoke vents in the actual tunnel) has the highest smoke exhaust efficiency.
- (3)
- A calculation model of the mass flow rate of the smoke vent was obtained through the dimensionless analysis of the mass flow rate in the shaft. The mass flow rate is mainly related to the height of the tunnel, the dimensionless heat release rate of the fire source, and the dimensionless distance between the smoke vents. The model is applicable to natural smoke extraction for small car fires near UTLT bends by double top vents that are located downstream of the fire source.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Shi, Y.; Qian, S.; Zhao, P.; Guo, P.; Gao, Z. Influence of Smoke Exhaust Volume and Smoke Vent Layout on the Ceiling Centralized Smoke Exhaust Effect in Tunnel Fires. Fire 2024, 7, 78. [Google Scholar] [CrossRef]
- Alpert, R. Calculation of response time of ceiling-mounted fire detectors. Fire Technol. 1972, 8, 181–195. [Google Scholar] [CrossRef]
- Strang, E.J.; Fernando, H.J.S. Entrainment and mixing in stratified shear flows. J. Fluid Mech. 2001, 428, 349–386. [Google Scholar] [CrossRef]
- Kurioka, H.; Oka, Y.; Satoh, H.; Sugawa, O. Fire properties in near field of square fire source with longitudinal ventilation in tunnels. Fire Saf. J. 2003, 38, 319–340. [Google Scholar] [CrossRef]
- Viot, J.; Vauquelin, O.; Rhodes, N. Characterisation of the plug-holing phenomenon for the exhausting of a low density gas layer. In Proceedings of the 14th Australasian Fluid Mechanics Conference, Adelaide, Australia, 10–14 December 2001. [Google Scholar]
- Yoon, C.H.; Kim, M.S.; Kim, J. The evaluation of natural ventilation pressure in Korean long road tunnels with vertical shafts. Tunn. Undergr. Space Technol. 2006, 21, 472. [Google Scholar] [CrossRef]
- Brahim, K.; Zouhaier, M.; Mourad, B.; Belghith, A. Temperature stratification in a road tunnel. Therm. Sci. 2016, 176, 156. [Google Scholar] [CrossRef]
- Jiang, X.; Xu, Z.; Huang, Y.; Chen, C.K. Fire ventilation control scheme for traffic link tunnel in Suzhou Railway Station. Sci. Technol. Rev. 2009, 27, 77–82. [Google Scholar] [CrossRef]
- Fan, C. Studies on Characteristics of Tunnel Fire Development and Natural Ventilation Mode Using Shafts. Ph.D. Thesis, University of Science and Technology of China, Hefei, China, 2015. [Google Scholar]
- Han, J.; Liu, F.; Wang, F.; Liao, S. Full-scale experimental investigation on smoke spreading and thermal characteristic in a transversely ventilated urban traffic link tunnel. Int. J. Therm. Sci. 2021, 170, 107–130. [Google Scholar] [CrossRef]
- Lei, P.; Chen, C.; Zhang, Y.; Xu, T.; Sun, H. Experimental study on temperature profile in a branched tunnel fire under natural ventilation considering different fire locations. Int. J. Therm. Sci. 2021, 159, 31–38. [Google Scholar] [CrossRef]
- Liu, S. Study on the effect of width and slope of large cross-section tunnel on critical velocity of fire. Therm. Sci. 2024, 28, 1635. [Google Scholar] [CrossRef]
- Zhang, S.; Liao, S.; Shi, L.; Lin, B.; Liu, J.; Wang, J. Promotion Effect of Solid Screen on the Smoke Extraction of Vertical Shaft in Urban Road Tunnel Fire. Fire Technol. 2024, 60, 1333–1355. [Google Scholar] [CrossRef]
- Li, J.; Li, Y.; Li, J.; Tian, W. A simplified calculation method on the smoke back-layering length and inlet air velocity in a tilted tunnel fire without shaft. Indoor Built Environ. 2022, 32, 274–285. [Google Scholar] [CrossRef]
- Guo, J.; Gao, W.; Cai, G.; Liu, Y.; Wen, H. Numerical study on fire-induced smoke temperature characteristics in small curvature radius UTLT-like tunnels under emergency state. Tunn. Undergr. Space Technol. 2022, 127, 104599. [Google Scholar] [CrossRef]
- Li, Y.; Lei, B.; Ingason, H. The maximum temperature of buoyancy-driven smoke flow beneath the ceiling in tunnel fires. Fire Saf. J. 2011, 46, 204–210. [Google Scholar] [CrossRef]
- Ingason, H.; Lönnermark, A. Heat release rates from heavy goods vehicle trailer fires in tunnels. Fire Saf. J. 2005, 40, 646–668. [Google Scholar] [CrossRef]
- Fan, C.G.; Li, Y.Z.; Ingason, H.; Lönnermark, A. Effect of tunnel cross section on gas temperatures and heat fluxes in case of large heat release rate. Appl. Therm. Eng. 2016, 93, 405–415. [Google Scholar] [CrossRef]
- Kalsson, B.; Quintiere, J. Enclosure Fire Dynamics, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2022; pp. 41–69. [Google Scholar]



| Distance (m) | 0.8 | 1.6 | 2.4 | 3.2 | 4.0 | |
|---|---|---|---|---|---|---|
| Fire Size (MW) | ||||||
| 2.5 | 0.84 | 0.86 | 0.88 | 0.88 | 0.79 | |
| 3.5 | 1.05 | 1.02 | 1.04 | 1.09 | 0.99 | |
| 4.5 | 1.13 | 1.20 | 1.19 | 1.09 | 1.05 | |
| Distance (m) | 0.8 | 1.6 | 2.4 | 3.2 | 4.0 | |
|---|---|---|---|---|---|---|
| Fire Size (MW) | ||||||
| 2.5 | 0.49 | 0.53 | 0.38 | 0.26 | 0.20 | |
| 3.5 | 0.55 | 0.59 | 0.41 | 0.32 | 0.27 | |
| 4.5 | 0.57 | 0.62 | 0.49 | 0.34 | 0.31 | |
| Distance (m) | 0.8 | 1.6 | 2.4 | 3.2 | 4.0 | |
|---|---|---|---|---|---|---|
| Fire Size (MW) | ||||||
| 2.5 | 12 | 13 | 10 | 7 | 5 | |
| 3.5 | 12 | 14 | 10 | 8 | 7 | |
| 4.5 | 14 | 16 | 13 | 9 | 8 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Yang, Y. Study on the Influence of Smoke Vent Arrangement on the Natural Smoke Exhaust Effect in Urban Traffic Link Tunnels. Fire 2025, 8, 49. https://doi.org/10.3390/fire8020049
Li X, Yang Y. Study on the Influence of Smoke Vent Arrangement on the Natural Smoke Exhaust Effect in Urban Traffic Link Tunnels. Fire. 2025; 8(2):49. https://doi.org/10.3390/fire8020049
Chicago/Turabian StyleLi, Xiaokang, and Yongbin Yang. 2025. "Study on the Influence of Smoke Vent Arrangement on the Natural Smoke Exhaust Effect in Urban Traffic Link Tunnels" Fire 8, no. 2: 49. https://doi.org/10.3390/fire8020049
APA StyleLi, X., & Yang, Y. (2025). Study on the Influence of Smoke Vent Arrangement on the Natural Smoke Exhaust Effect in Urban Traffic Link Tunnels. Fire, 8(2), 49. https://doi.org/10.3390/fire8020049







