Effect of Twin-Fluid Mass Ratio on Near-Field Spray Characteristics and Dynamics of a Novel Two-Phase Injector with an Internal Swirl
Abstract
1. Introduction
2. Materials and Methods
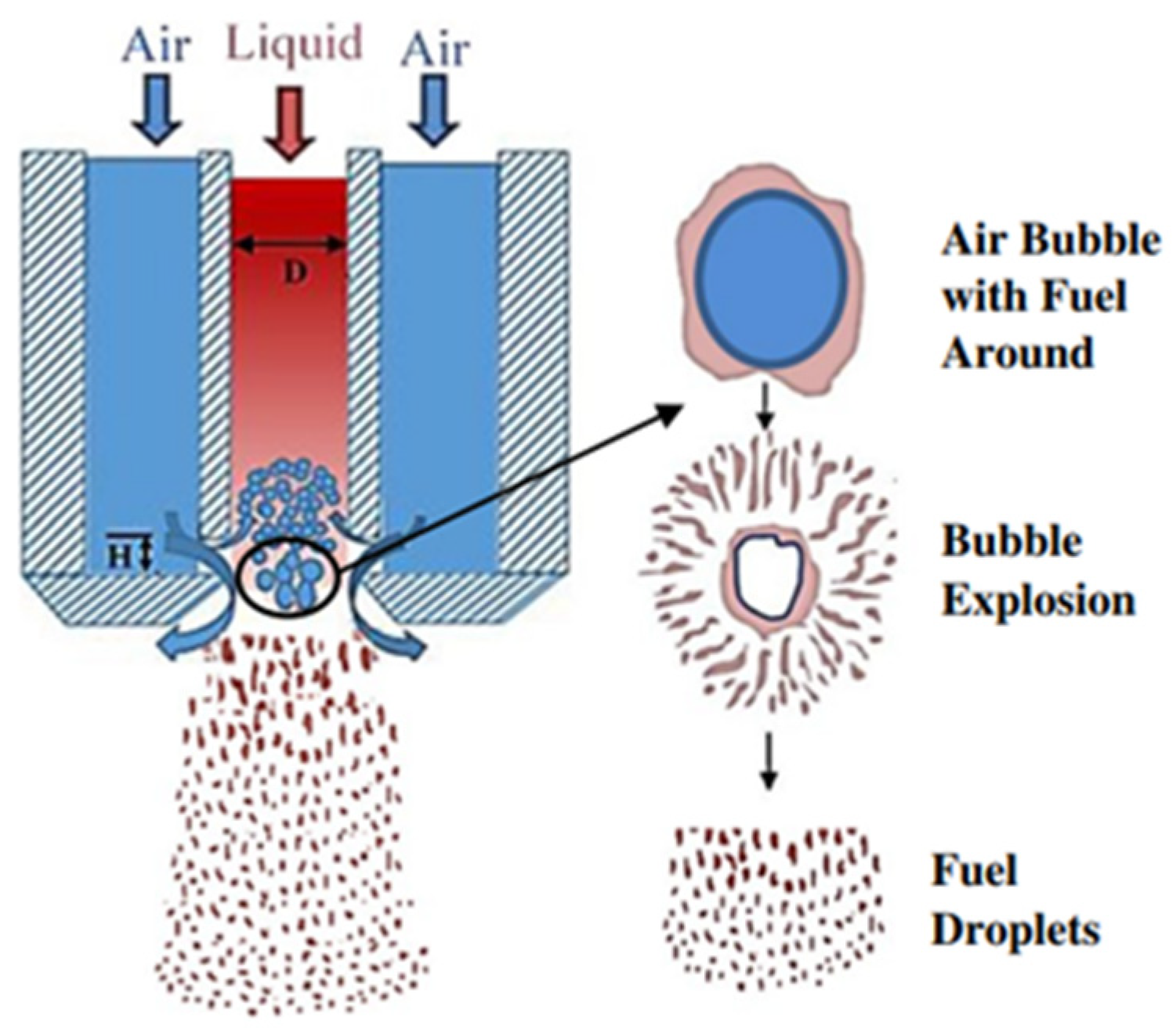
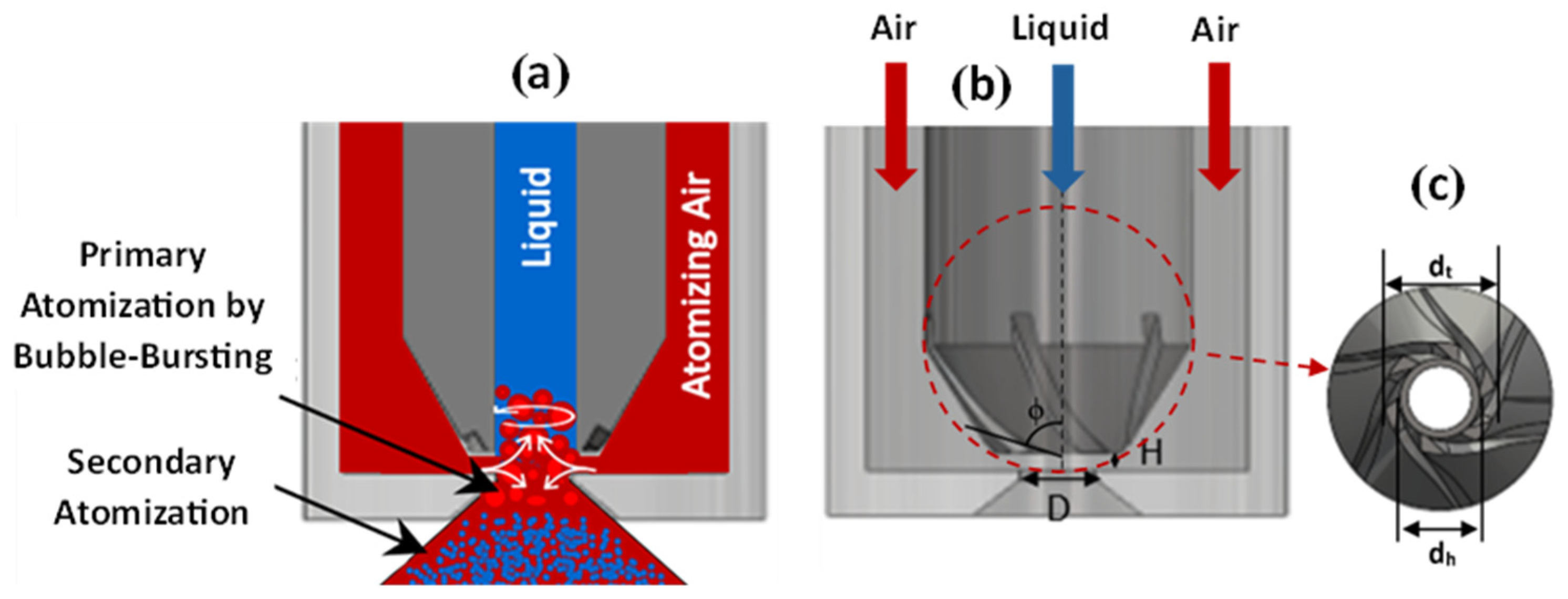
2.1. Design of Swirl Burst Injector with Enhanced Primary Atomization
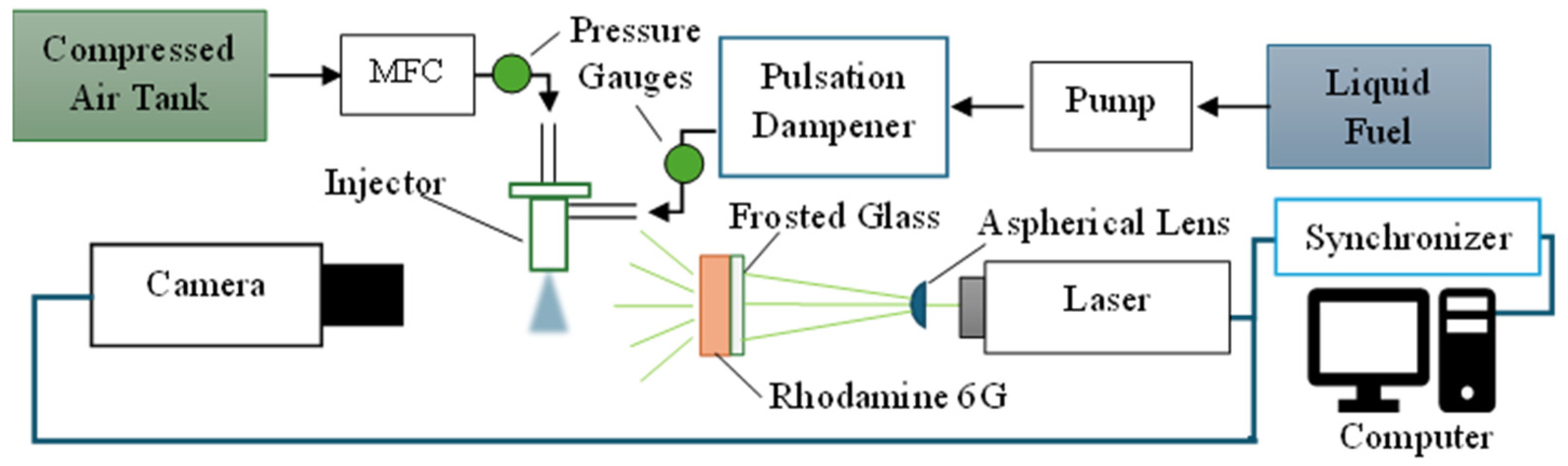
2.2. The Spraying System Setup
2.3. Experimental Setup of the High-Speed Laser-Driven Shadowgraph Imaging
2.4. Image Processing
2.5. Data Analysis
3. Results and Discussion
3.1. Spray Images and Pressure Change Across Injector Exit
3.2. Droplet Size Distribution
3.3. Droplet Mass Distribution Analysis
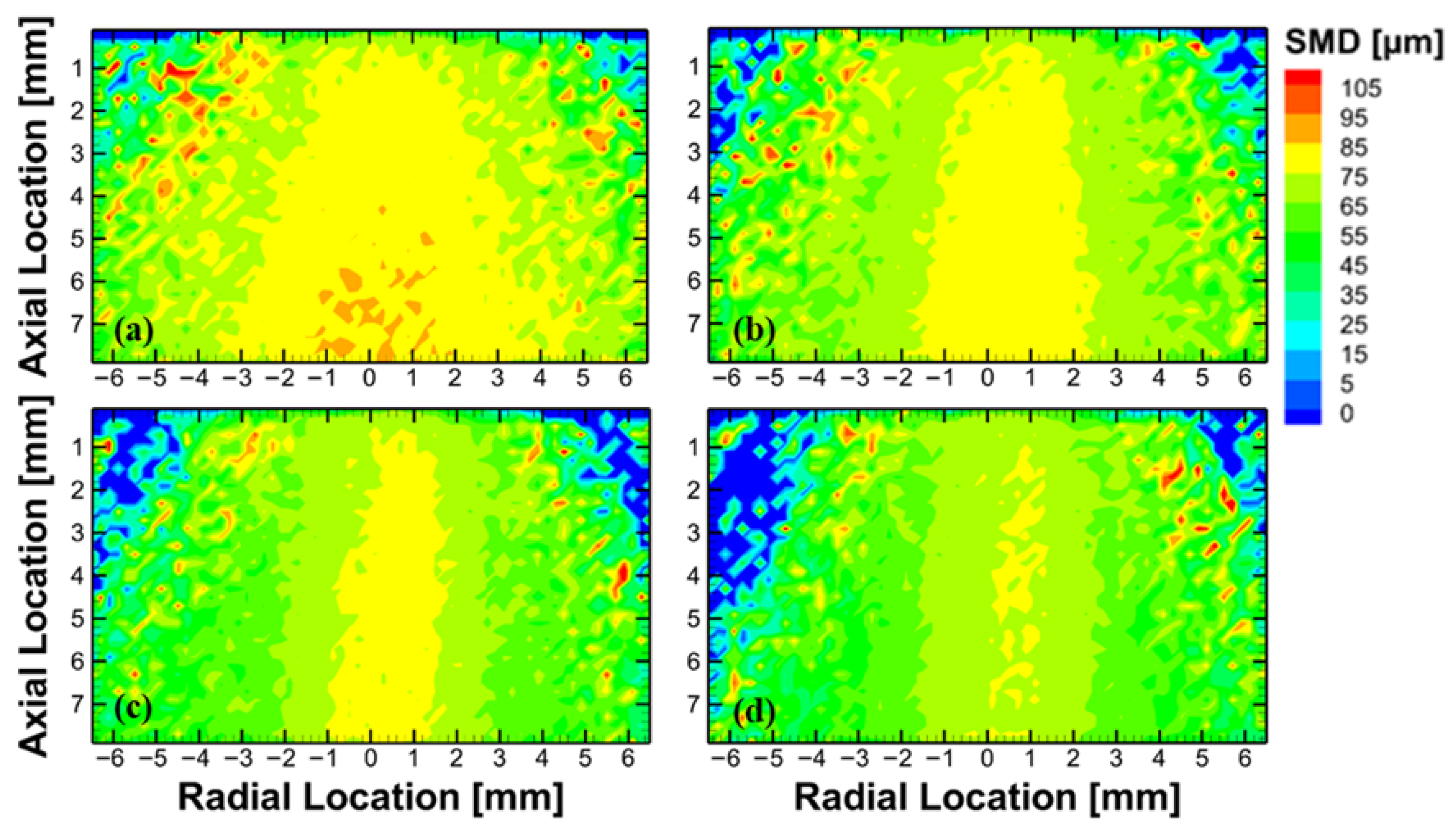
3.4. Sauter Mean Diameter Analyses
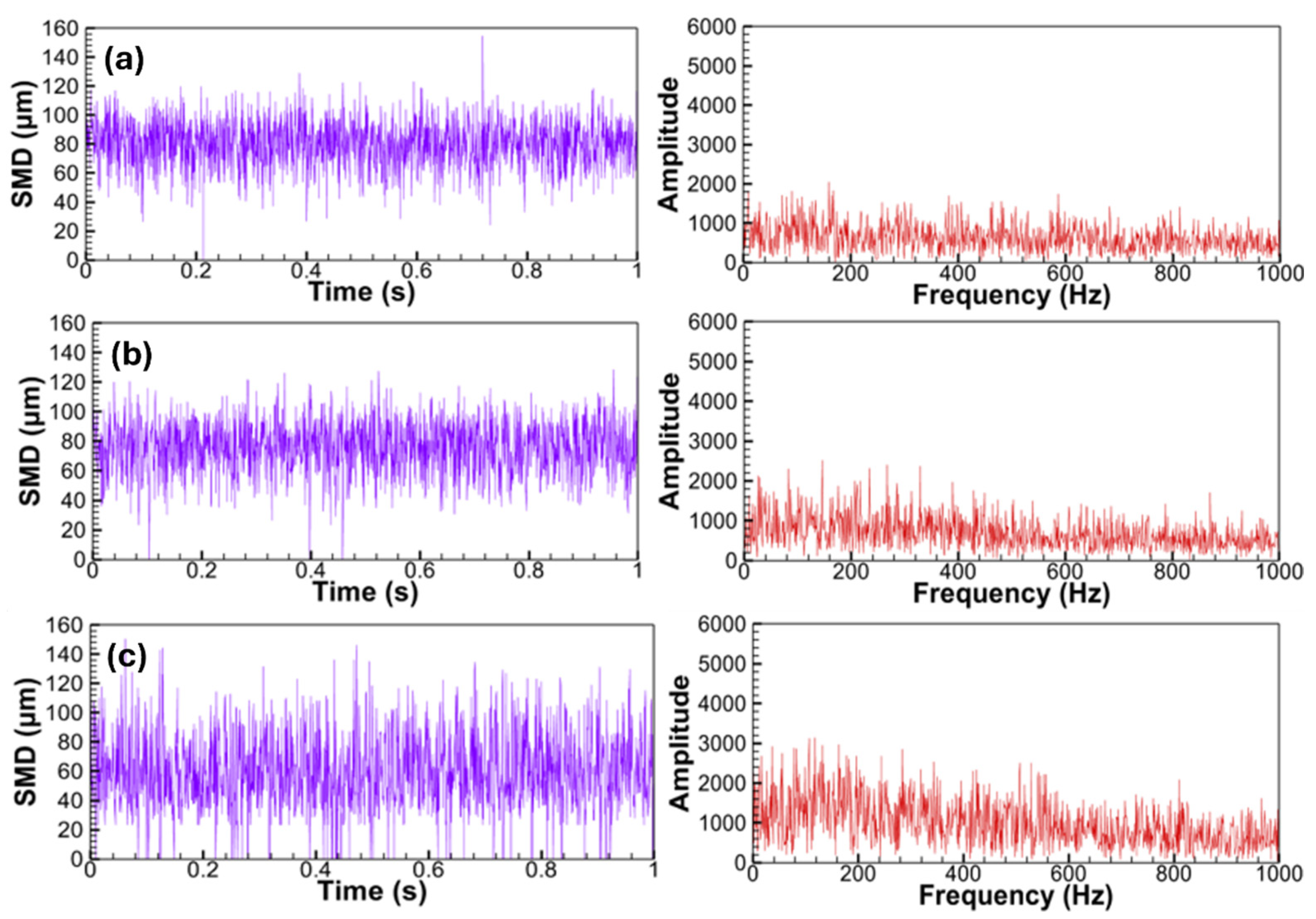
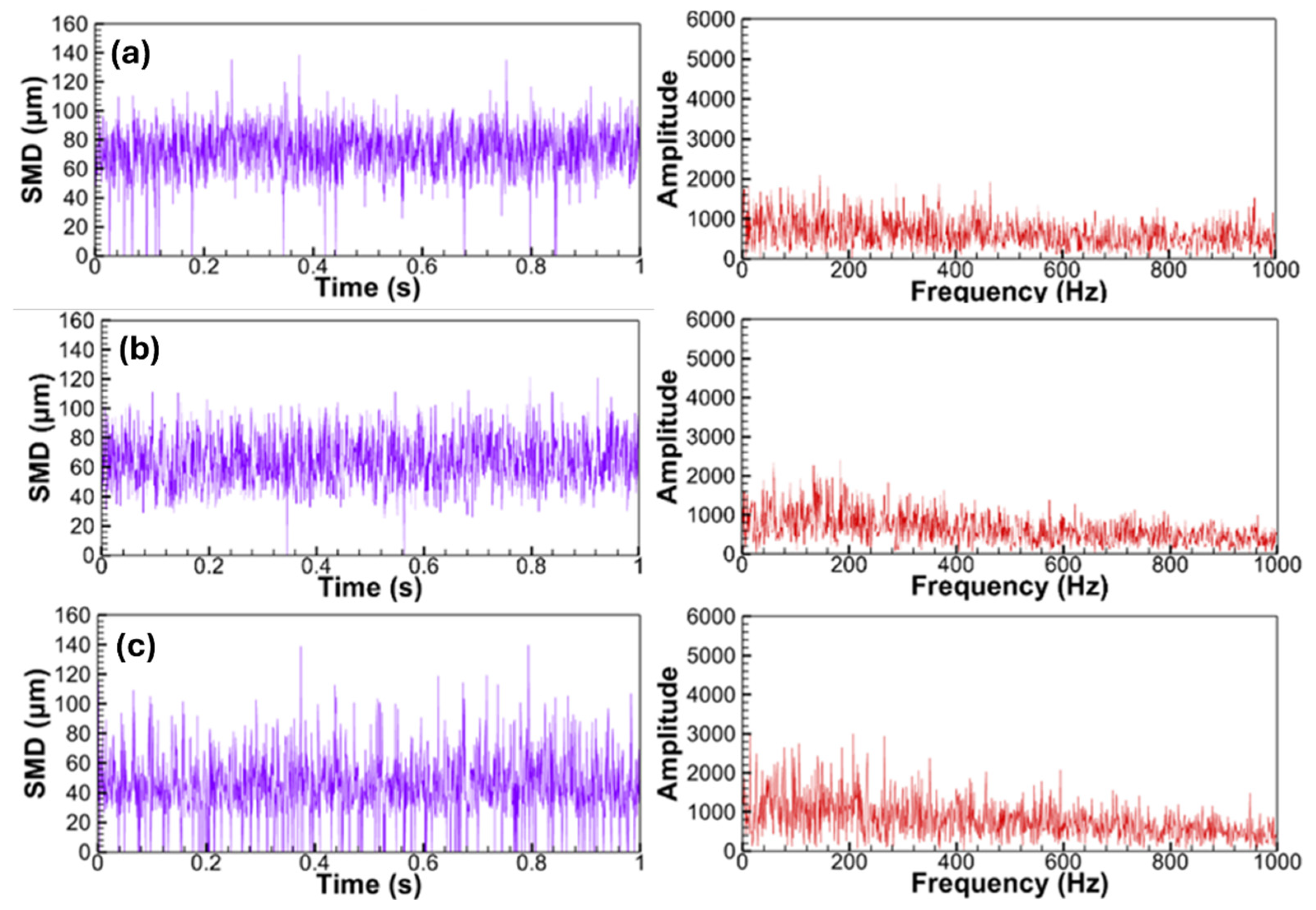
3.5. Time and Frequency Domain Analyses
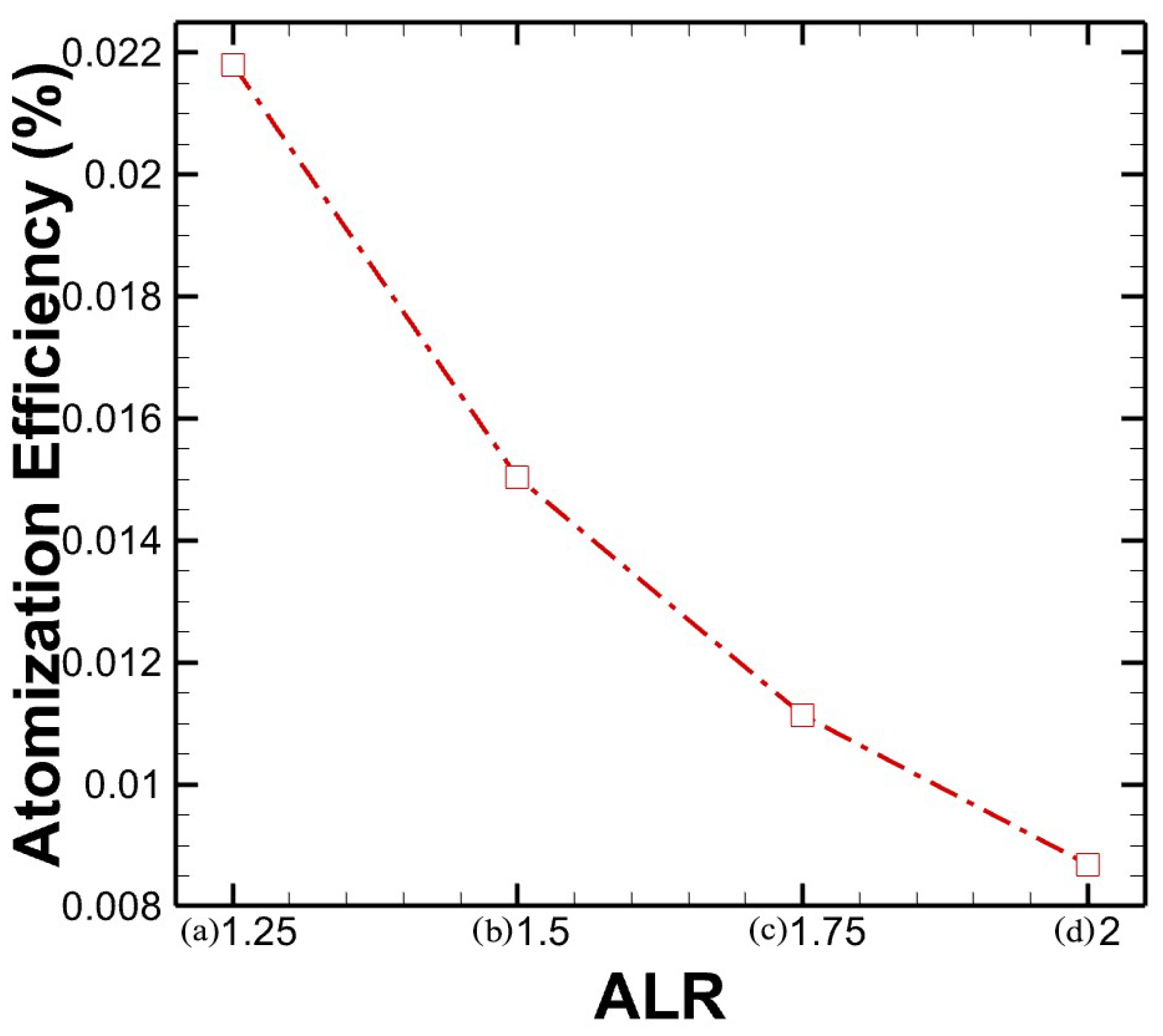
3.6. Atomization Efficiency Estimation
3.7. Energy/Air-Usage Budget Estimation
4. Conclusions
- Each tested ALR generated stable SBP sprays with fine droplets discharged immediately at the injector near-field even for a scaled-up injector with an exit diameter of 4.37 mm [19].
- Each ALR seemed to have similar cumulative volume distributions of droplet sizes; however, there was a trend wherein the droplet size and SMD decreased as the ALR increased [19].
- Mass distribution contour maps revealed the evolution of mass distribution in the SBP injector exit across ALRs, demonstrating a progressive concentration of the spray pattern with increasing ALR. At the ALR of 1.25, the most spread-out mass distribution was seen.
- The SMD contours revealed that among the tested ALRs, an ALR of 2.00 produced the most consistent droplet size distribution, as evidenced by the relatively uniform SMD values throughout the spray region.
- Temporal evolution of SMD and the FFT analysis were employed to investigate the spray dynamics at various ALRs [19]. Lack of peak frequencies in the FFT showed the stability of the SBP injection at all the tested ALRs with the optimum ALR of 1.75 having the most stable sprays with fine droplet evolution [19].
- The experimental analysis revealed a critical inverse relationship between air-to-liquid ratio (ALR) and atomization efficiency, with peak performance observed at the lowest tested ALR of 1.25 in terms of atomization efficiency.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AA | Atomizing Air |
| AB | Air-Blast |
| ALR | Atomizing Air-to-Liquid Mass Ratio |
| FB | Flow-Blurring |
| FOV | Field of View |
| FFT | Fast Fourier Transform |
| MFC | Mass Flow Controller |
| ROI | Region of Interest |
| SBP | Swirl Burst Primary |
| SBS | Swirl Burst Secondary |
| SMD | Sauter Mean Diameter |
References
- Farrell, K.; Hassan, M.K.; Hossain, M.D.; Ahmed, B.; Rahnamayiezekavat, P.; Douglas, G.; Saha, S. Water Mist Fire Suppression Systems for Building and Industrial Applications: Issues and Challenges. Fire 2023, 6, 40. [Google Scholar] [CrossRef]
- Ko, Y.J.; Elsagan, N. Investigation of the Performance of Fire Suppression Systems in Protection of Mass Timber Residential Buildings. Indoor Built Environ. 2023, 32, 230–241. [Google Scholar] [CrossRef]
- Keyes, F.G.; Smith, L.B.; Gerry, H.T. The Specific Volume of Steam in the Saturated and Superheated Condition Together with Derived Values of the Enthalpy, Entropy, Heat Capacity and Joule Thomson Coefficients: Part IV. Steam Research Program. Proc. Am. Acad. Arts Sci. 1936, 70, 319–364. [Google Scholar] [CrossRef]
- Xu, M.; Wei, Y.; Qin, A.; Xu, Y.; Xu, M.; Li, B.; Liu, L. Novel Silica Hydrogel-Based Forest Fire Extinguishing Agent: Construction, Fire Extinguishing Performance and Mechanism Study. J. Clean. Prod. 2025, 486, 144490. [Google Scholar] [CrossRef]
- Mlkvik, M.; Stähle, P.; Schuchmann, H.P.; Gaukel, V.; Jedelsky, J.; Jicha, M. Twin-Fluid Atomization of Viscous Liquids: The Effect of Atomizer Construction on Breakup Process, Spray Stability and Droplet Size. Int. J. Multiph. Flow 2015, 77, 19–31. [Google Scholar] [CrossRef]
- Liu, C.; Peng, S.; Du, X.; Wu, P.; Li, Y.; Feng, Z. Study on the Atomization Characteristics of Gel by Liquid Carbon Dioxide. J. Aerosol Sci. 2025, 184, 106496. [Google Scholar] [CrossRef]
- Zhao, Y.; Liang, J.; Xie, Y.; Wu, J.; Huang, W.; Li, W.; Huang, R.; Huang, Y.; Wu, J.; Li, J.; et al. Hydrogel-Based Fire Extinguishing Technology for Lithium-Ion Battery Fires: Mechanisms, Applications, and Future Perspectives. J. Polym. Res. 2025, 32, 250. [Google Scholar] [CrossRef]
- Ma, L.; Huang, X.; Sheng, Y.; Liu, X.; Wei, G. Experimental Study on Thermosensitive Hydrogel Used to Extinguish Class A Fire. Polymers 2021, 13, 367. [Google Scholar] [CrossRef]
- Li, G.; Wang, Q.; Liu, G.; Yao, M.; Wang, Y.; Li, Y.; Lin, K.; Liu, X. Hydrogel Extinguishants. Nanomaterials 2024, 14, 1128. [Google Scholar] [CrossRef]
- Lefebvre, A.H.; McDonell, V.G. Atomization and Sprays, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2017; ISBN 978-1-315-12091-1. [Google Scholar]
- Hendershott, T.H.; Stouffer, S.; Monfort, J.R.; Diemer, J.; Busby, K.; Corporan, E.; Wrzesinski, P.; Caswell, A.W. Ignition of Conventional and Alternative Fuel at Low Temperatures in a Single-Cup Swirl-Stabilized Combustor. In Proceedings of the 2018 AIAA Aerospace Sciences Meeting, Kissimmee, FL, USA, 8–12 January 2018; AIAA SciTech Forum; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2018. [Google Scholar]
- Breerwood, J.; Jiang, L.; Ahmed, M.S. Near-Field Spray Characteristics and Steadiness of a Novel Twin-Fluid Injector with Enhanced Primary Atomization. J. Aerosol Sci. 2024, 180, 106402. [Google Scholar] [CrossRef]
- Jiang, L.; Agrawal, A.K.; Taylor, R.P. Clean Combustion of Different Liquid Fuels Using a Novel Injector. Exp. Therm. Fluid Sci. 2014, 57, 275–284. [Google Scholar] [CrossRef]
- Huber, M.L.; Perkins, R.A.; Laesecke, A.; Friend, D.G.; Sengers, J.V.; Assael, M.J.; Metaxa, I.N.; Vogel, E.; Mares, R.; Miyagawa, K. New International Formulation for the Viscosity of H2O. J. Phys. Chem. Ref. Data 2009, 38, 101–125. [Google Scholar] [CrossRef]
- Caputo, G.; Adami, R.; Reverchon, E. Analysis of Dissolved-Gas Atomization: Supercritical CO2 Dissolved in Water. Ind. Eng. Chem. Res. 2010, 49, 9454–9461. [Google Scholar] [CrossRef]
- Sher, E.; Bar-Kohany, T.; Rashkovan, A. Flash-Boiling Atomization. Prog. Energy Combust. Sci. 2008, 34, 417–439. [Google Scholar] [CrossRef]
- Hong, M.; Fleck, B.A.; Nobes, D.S. Unsteadiness of the Internal Flow in an Effervescent Atomizer Nozzle. Exp. Fluids 2014, 55, 1855. [Google Scholar] [CrossRef]
- Jiang, L.; Agrawal, A.K. Investigation of Glycerol Atomization in the Near-Field of a Flow-Blurring Injector Using Time-Resolved PIV and High-Speed Visualization. Flow Turbul. Combust. 2015, 94, 323–338. [Google Scholar] [CrossRef]
- Swinney, R.; Jiang, L. Investigation of the Effect of Atomizing Air-to-Liquid Mass Ratio on Spray Dynamics for a Novel Injector Design. In Proceedings of the AIAA SCITECH 2023 Forum, National Harbor, MD, USA, 23–27 January 2023; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2023. [Google Scholar]
- Qavi, I.; Jiang, L.; Akinyemi, O.S. Near-Field Spray Characterization of a High-Viscosity Alternative Jet Fuel Blend C-3 Using a Flow Blurring Injector. Fuel 2021, 293, 120350. [Google Scholar] [CrossRef]
- Gañán-Calvo, A. Enhanced Liquid Atomization: From Flow-Focusing to Flow-Blurring. Appl. Phys. Lett. 2005, 86, 214101. [Google Scholar] [CrossRef]
- Kourmatzis, A.; Jaber, O.J.; Singh, G.; Masri, A.R. Review of Flow Blurring Atomization: Advances and Perspectives. Energy Fuels 2022, 36, 4224–4233. [Google Scholar] [CrossRef]
- Jafari, M.; Jowkar, S.; Morad, M.R. Low Flow Rate Spray Cooling by a Flow Blurring Injector. Int. Commun. Heat Mass Transf. 2021, 122, 105168. [Google Scholar] [CrossRef]
- Rayleigh Investigation of the Character of the Equilibrium of an Incompressible Heavy Fluid of Variable Density. Proc. Lond. Math. Soc. 1882, s1-14, 170–177. [CrossRef]
- Jiang, L.; Agrawal, A.K. Spray Features in the near Field of a Flow-Blurring Injector Investigated by High-Speed Visualization and Time-Resolved PIV. Exp. Fluids 2015, 56, 103. [Google Scholar] [CrossRef]
- Khan, M.A.; Gadgil, H.; Kumar, S. Experimental Investigations into Liquid Breakupmorphology and Spray Characteristics of a Cross-Flow Injector. At. Sprays 2021, 31, 63–86. [Google Scholar] [CrossRef]
- Simmons, B.; Agrawal, A. Spray Characteristics of a Flow-Blurring Atomizer. At. Sprays 2010, 20, 821–835. [Google Scholar] [CrossRef]
- Danh, V.; Jiang, L.; Akinyemi, O.S. Investigation of Water Spray Characteristics in the Near Field of a Novel Swirl Burst Injector. Exp. Therm. Fluid Sci. 2019, 102, 376–386. [Google Scholar] [CrossRef]
- Nasim, M.N.; Qavi, I.; Jiang, L. Effect of Varying Internal Geometry on the Near-Field Spray Characteristics of a Swirl Burst Injector. Flow Turbul. Combust. 2023, 111, 641–674. [Google Scholar] [CrossRef]
- Akinyemi, O.S.; Jiang, L. Development and Combustion Characterization of a Novel Twin-Fluid Fuel Injector in a Swirl-Stabilized Gas Turbine Burner Operating on Straight Vegetable Oil. Exp. Therm. Fluid Sci. 2019, 102, 279–290. [Google Scholar] [CrossRef]
- Akinyemi, O.; Jiang, L.; Bruno, J. Effect of Fuel Properties and Atomizing Air to Liquid Ratio on Combustion Performance of a Novel Twin-Fluid Injector. In Proceedings of the 2018 Spring Technical Meeting Central States Section of the Combustion Institute, Minneapolis, MN, USA, 20–22 May 2018. [Google Scholar]
- Hall, T.; Williams, D.; Islam, S.M.R.; Patel, I.; Chakmakjian, C.; Jiang, L. Clean Co-Combustion of Glycerol and Methanol Blends Using a Novel Fuel-Flexible Injector. Fuel 2024, 371, 132125. [Google Scholar] [CrossRef]
- Islam, S.M.R.; Jiang, L.; Swinney, R.; Horn, D.V.; Chakmakjian, C.; Corporan, E. Global Combustion Characteristics of a Viscous Alternative Jet Fuel and Conventional Jet A-2 Using a Novel Twin-Fluid Injector. Fuel 2025, 386, 134303. [Google Scholar] [CrossRef]
- Akinyemi, O.; Qavi, I.; Taylor, C.E.; Jiang, L. Effect of the Air-to-Liquid Mass Ratio on the Internal Flow and near-Field Spray Characteristics of a Two-Phase Swirl Burst Injector. J. Aerosol Sci. 2023, 167, 106092. [Google Scholar] [CrossRef]
- Lee, S.J.; Kim, J.Y.; Lee, M.H.; Hong, J.G. Experimental Study of Twin-Fluid Flow Differences and Sauter Mean Diameter Prediction According to Y-Jet Nozzle Mixing-Tube Design. Int. J. Multiph. Flow 2025, 183, 105063. [Google Scholar] [CrossRef]
- Lilley, D.G. Swirl Flows in Combustion: A Review. AIAA J. 1977, 15, 1063–1078. [Google Scholar] [CrossRef]
- Castrejón-García, R.; Castrejón-Pita, J.R.; Martin, G.D.; Hutchings, I.M. The Shadowgraph Imaging Technique and Its Modern Application to Fluid Jets and Drops. Rev. Mex. Fís. 2011, 57, 266–275. [Google Scholar]
- Settles, G.S. Schlieren and Shadowgraph Techniques: Visualizing Phenomena in Transparent Media; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2001; ISBN 978-3-540-66155-9. [Google Scholar]
- Settles, G.S.; Hargather, M.J. A Review of Recent Developments in Schlieren and Shadowgraph Techniques. Meas. Sci. Technol. 2017, 28, 042001. [Google Scholar] [CrossRef]
- Braeuer, A. Chapter 4—Shadowgraph and Schlieren Techniques. In Supercritical Fluid Science and Technology; Braeuer, A., Ed.; Spectroscopic Techniques at High Pressure; Elsevier: Amsterdam, The Netherlands, 2015; Volume 7, pp. 283–312. [Google Scholar]
- Jain, S.; Somasundaram, S.; Anand, T. A Fluorescent Laser-Diffuser Arrangement for Uniform Backlighting. Meas. Sci. Technol. 2016, 27, 025406. [Google Scholar] [CrossRef]
- Danh, V.; Akinyemi, O.S.; Taylor, C.E.; Frank, J.T.; Jiang, L. Effect of Injector Swirl Number on Near-Field Spray Characteristics of a Novel Twin-Fluid Injector. Exp. Fluids 2019, 60, 80. [Google Scholar] [CrossRef]
- Li, G.; Li, C. Experimental Study on the Spray Steadiness of an Internal-Mixing Twin-Fluid Atomizer. Energy 2021, 226, 120394. [Google Scholar] [CrossRef]
- TSI Incorporated. Fiber Optic Probes for Ldv/Pdpa Systems; TSI Incorporated: Shoreview, MN, USA, 2019. [Google Scholar]
- Panão, M. On the Interpretation of Atomization Efficiency and Application to Air-Assisted Sprays. MOP 2020. [Google Scholar] [CrossRef]
- Wang, D.; Fan, L.-S. 2—Particle Characterization and Behavior Relevant to Fluidized Bed Combustion and Gasification Systems. In Fluidized Bed Technologies for Near-Zero Emission Combustion and Gasification; Scala, F., Ed.; Woodhead Publishing Series in Energy; Woodhead Publishing: Cambridge, UK, 2013; pp. 42–76. ISBN 978-0-85709-541-1. [Google Scholar]
- Machado, D.A.; Costa, F.S.; Dias, G.S.; Mota, F.A.S. Simultaneous Analysis of Swirl Spray Dynamics Using a Telecentric Shadowgraphy System. Meas. Sci. Technol. 2024, 36, 016047. [Google Scholar] [CrossRef]
- Jedelsky, J.; Jicha, M. Energy Considerations in Spraying Process of a Spill-Return Pressure-Swirl Atomizer. Appl. Energy 2014, 132, 485–495. [Google Scholar] [CrossRef]
- Khan, M.A.; Gadgil, H.; Kumar, S. Influence of Liquid Properties on Atomization Characteristics of Flow-Blurring Injector at Ultra-Low Flow Rates. Energy 2019, 171, 1–13. [Google Scholar] [CrossRef]
- Lefebvre, A.H. Energy Considerations in Twin-Fluid Atomization. J. Eng. Gas Turbines Power 1992, 114, 89–96. [Google Scholar] [CrossRef]


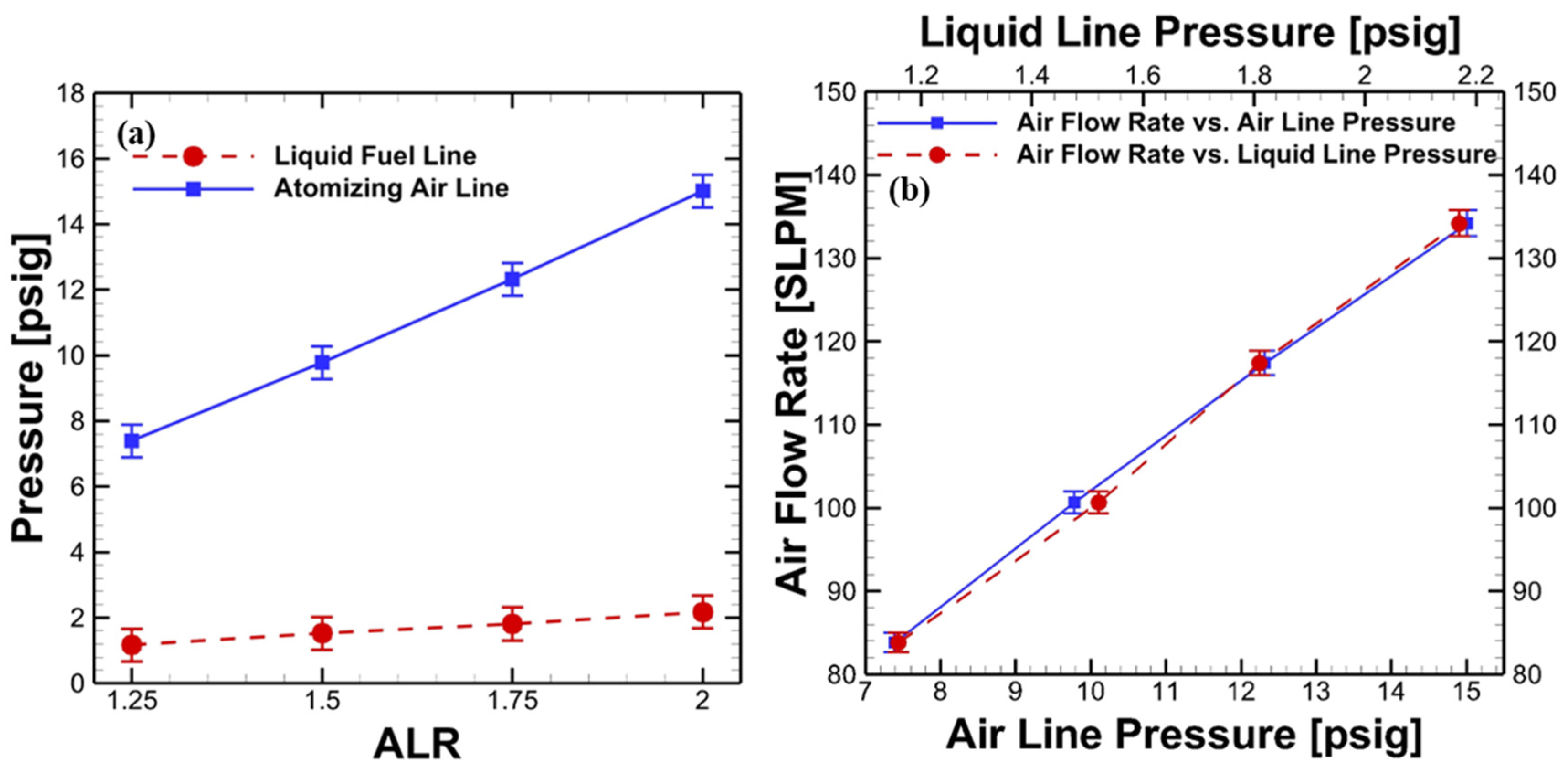




| ALR | 1.25 | 1.50 | 1.75 | 2.00 |
|---|---|---|---|---|
| Air Flow Rate (SLPM) | 83.85 | 100.62 | 117.39 | 134.16 |
| Liquid Flow Rate (mLPM) | 80.00 | |||
| ALR | Liquid Phase Energy Input, El (Fixed) | Gas Phase Energy Input, Ea | Total Energy Etotal = El + Ea | Atomization Efficiency, ηa (%) | Average SMD (μm) |
|---|---|---|---|---|---|
| 1.25 | 1.00 | 1.25 | 2.25 | 0.022 | 45.80 |
| 1.50 | 1.00 | 1.50 | 2.50 | 0.015 | 44.17 |
| 1.75 | 1.00 | 1.75 | 2.75 | 0.011 | 42.88 |
| 2.00 | 1.00 | 2.00 | 3.00 | 0.009 | 41.59 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Swinney, R.; Ahmed, M.S.; Jiang, L. Effect of Twin-Fluid Mass Ratio on Near-Field Spray Characteristics and Dynamics of a Novel Two-Phase Injector with an Internal Swirl. Fire 2025, 8, 425. https://doi.org/10.3390/fire8110425
Swinney R, Ahmed MS, Jiang L. Effect of Twin-Fluid Mass Ratio on Near-Field Spray Characteristics and Dynamics of a Novel Two-Phase Injector with an Internal Swirl. Fire. 2025; 8(11):425. https://doi.org/10.3390/fire8110425
Chicago/Turabian StyleSwinney, Rachel, Md Shakil Ahmed, and Lulin Jiang. 2025. "Effect of Twin-Fluid Mass Ratio on Near-Field Spray Characteristics and Dynamics of a Novel Two-Phase Injector with an Internal Swirl" Fire 8, no. 11: 425. https://doi.org/10.3390/fire8110425
APA StyleSwinney, R., Ahmed, M. S., & Jiang, L. (2025). Effect of Twin-Fluid Mass Ratio on Near-Field Spray Characteristics and Dynamics of a Novel Two-Phase Injector with an Internal Swirl. Fire, 8(11), 425. https://doi.org/10.3390/fire8110425