Abstract
Forest and grassland fire behavior prediction is increasingly critical under climate change, as rising fire frequency and intensity threaten ecosystems and human societies worldwide. This paper reviews the status and future development trends of wildfire behavior modeling and prediction technologies. It provides a comprehensive overview of the evolution of models from empirical to physical and then to data-driven approaches, emphasizing the integration of multidisciplinary techniques such as machine learning and deep learning. While conventional physical models offer mechanistic insights, recent advancements in data-driven models have enabled the analysis of big data to uncover intricate nonlinear relationships. We underscore the necessity of integrating multiple models via complementary, weighted fusion and hybrid methods to bolster robustness across diverse situations. Ultimately, we advocate for the creation of intelligent forecast systems that leverage data from space, air and ground sources to provide multifaceted fire behavior predictions in regions and globally. Such systems would more effectively transform fire management from a reactive approach to a proactive strategy, thereby safeguarding global forest carbon sinks and promoting sustainable development in the years to come. By offering forward-looking insights and highlighting the importance of multidisciplinary approaches, this review serves as a valuable resource for researchers, practitioners, and policymakers, supporting informed decision-making and fostering interdisciplinary collaboration.
1. Introduction
Forest and grassland fires are among the most destructive natural disasters, causing severe impacts on ecosystems, biodiversity, and human lives and property. In recent years, the frequency and scale of these fires have increased significantly due to global warming, extreme weather events, and human-induced disturbances [1]. Notably, forest fires have encroached upon the Arctic Circle, and significant fires have occurred in Australia (2019), California (2020), and Greece and Turkey (2021), inflicting enormous ecological and economic losses [2,3,4]. Accurate prediction of fire behavior is crucial for effective fire management, enabling rational suppression strategies, minimizing losses, and supporting ecological conservation and sustainable development.
Fire behavior is influenced by a variety of complex factors, including meteorological conditions, topography and geomorphology, vegetation types and their distribution in the wildland, as well as human activity (e.g., land-use change, fuel accumulation due to fire exclusion, and increased ignition sources from agriculture or tourism) [5,6]. These factors interact in complex ways, creating a high degree of complexity and uncertainty in fire behavior. This complexity poses significant challenges to the evaluation and prediction of fire behavior, making it difficult to develop effective fire management strategies. Consequently, the need for improved research and applied technologies has driven substantial evolution in the field over time.
The current state of fire behavior modeling encompasses a range of approaches, from empirical and physical models to data-driven models that leverage big data and artificial intelligence [7,8,9,10,11,12,13,14,15]. Each approach has its strengths and limitations. Physical models offer mechanistic insights but struggle with adaptability under complex terrain and vegetation conditions [11,12]. Data-driven models require high-quality data and lack a deep understanding of underlying physical processes [16]. Empirical models, while simpler, remain relevant and can provide necessary insights, especially in contexts where data availability is limited or rapid assessments are required. Given these diverse approaches, the choice of model should be guided by the specific research or management objectives, as well as the availability of data and computational resources. The integration and collaborative application of different models are still in the exploratory stage, and a mature comprehensive prediction system has yet to be established [17,18]. The effective integration of these models can enhance the robustness and accuracy of fire behavior predictions, making it a promising direction for future research. This integration not only leverages the strengths of each model type but also helps to mitigate their individual weaknesses, leading to more reliable and versatile prediction systems.
Understanding the historical context of fire behavior modeling is essential for grasping the current state and future directions of the field. Tracing the evolution from empirical models to modern data-driven approaches can reveal significant advancements and ongoing challenges. This historical perspective provides valuable insights for current research and informs the development of future models by building on past successes and avoiding past pitfalls. Moreover, it highlights the importance of continuous innovation and interdisciplinary collaboration in addressing the increasing complexity of wildfire behavior under changing environmental conditions.
To provide a comprehensive overview of the current research status and future development trends in forest and grassland fire behavior prediction, this study examines key fire behavior parameters, explores the strengths and limitations of various models, and proposes strategies for multi-model integration. By analyzing the diversity and complexity of fire behaviors, this research advances the innovation and development of prediction technologies, providing an up-to-date scientific basis for wildfire prevention and control. It also offers robust support for global forest resource protection and ecological security.
2. Central Parameters Shaping Fire Behavior Prediction
Fire behavior refers to the characteristics and dynamic changes exhibited by wildfires located in specific areas, while a wildfire can be a forest fire or grassland fire [19]. Characterized by burning forest fuels, forest fires can be classified into three types: surface fire, crown fire, and underground fire. Surface fire is the most common one, accounting for over 90% of all forest fires, and its occurrence is largely connected with human activities. Categorized as an extreme event, crown fire requires specific meteorological and vegetation conditions and occurs at low frequency. Underground fire burns in subsurface peat layers, humus, or tree roots and accounts for less than 1% of the total forest fires. Wildfire behavior can be quantitatively described by four major parameters as below.
2.1. Fire Spread Rate: Dynamic Feature of Firelines
Defined as the distance advanced by a fire front per unit time, fire spread rate is a critical indicator for evaluating the development momentum of wildfires. Its value ranges from 0.1 m/min (for fires in wetlands or shady areas) to 50 m/min (for crown fire under strong winds) [20], relying on the meteorological conditions, terrain, and fuel properties. As revealed by Rothermel [9], increases by 2 to 3 times for every 5 m/s increase in wind speed. High temperatures accelerate fire spread, while high humidity slows it down [21]. On mountainous terrain, the steeper the slope, the faster the fire spreads upward [5,22]. Affected by fuel conditions, faster spread often occurs in the areas with abundant herbaceous plants and litter, while slow spread is maintained in the regions covered by the moist fuels (e.g., wetland vegetation) [23]. This parameter is of great significance for fire management, given that firebreaks should be prioritized in directions of rapid fire spread, and evacuation routes should be dynamically adjusted to avoid being cut off by a spreading fire.
2.2. Flame Residence Time: Temporal Dimension of Disaster Impact
Flame residence time is defined as the duration during which a flame or high-temperature body continuously move through a specific spatial point, which plays a role in altering the properties of local vegetation and the environment [24]. Often called fire duration, can be evaluated by dividing the fire front depth by . In general, highly flammable materials, such as herbs, burn rapidly with short durations, while fuels like fallen logs burn more slowly and for longer periods. Additionally, a large quantity of fuels such as high-density coniferous forests typically results in a longer burning period [25]. Climatic conditions also play a crucial role in modifying . Prolonged burning durations favor drought, high temperature and low humidity situations, whereas precipitation can significantly shorten them [26]. The duration of a fire is a crucial metric for evaluating the impact of fire thermal impact on local ecosystems, including the effects on the survival capability of the affected plants, decomposition of soil organic matters, the persistence of smoldering embers and the generation of smoke as well as toxic gases [24].
2.3. Fireline Intensity: Temporal and Spatial Distribution of Energy Release
Fireline intensity is an indicator for measuring the severity of a burning wildfire, typically expressed as the energy release rate per fire front width (kW/m). It is comprehensively influenced by multiple factors such as climate, vegetation and terrain [5,27]. Byram [28] suggested a power–law relationship between and flame length or height for surface fire. Alexander and Cruz [29] further validated and extended this relationship to broad fire scenarios (crown fire), in combination of the field test results with the principles of energy conservation and combustion kinetics. It is often recognized that mild fires with < 500 kW/m and < 1 m only damage surface vegetation, while moderate fires at the level of ∈ (500–2000) kW/m and ∈ (1–3) m result in tree bark scorching [23,30]. High-intensity fires with ∈ (500–2000) kW/m and ∈ (3–6) m can destroy the forest canopy, while extremely high-intensity fires with > 5000 kW/m and > 6 m can trigger crown fire and spotting fire. High-intensity fires can lead to vegetation incineration, decreased soil fertility, damaged biodiversity, and difficult ecosystem restoration [31]. In fire suppression practice, direct attack is typically employed in areas with low-intensity fires, whereas indirect attack strategies are utilized in areas with high-intensity fires. Indirect attack strategies involve firefighting tactics that do not directly engage the fire front but instead aim to control the spread of the fire from a distance. These tactics include constructing firebreaks, utilizing natural barriers, conducting backfiring operations, or applying fire retardants ahead of the fire.
It should be noted that the fire effect thresholds based on fireline intensity and flame height are not absolute and can vary significantly. Factors such as species traits (e.g., bark thickness, age), seasonal conditions, and fuel moisture can all influence these thresholds. Additionally, even low-intensity fires can cause substantial soil impacts under certain conditions, such as prolonged smoldering of organic layers or coarse woody debris, leading to soil nutrient loss, increased hydrophobicity, and impacts on microbial communities. Furthermore, the presence of invasive species or changes in land use can also alter the fire behavior and its subsequent effects, highlighting the need for adaptive management strategies that consider these dynamic factors.
2.4. Burned Area: Spatial Scale of Disaster
Defined as the region affected by wildfires, the burned area serves as a critical indicator for assessing fire scale and impact [27,32]. This metric is driven by some key mechanisms, including meteorological ones. Strong winds and dry conditions accelerate fire spread, even a daily increase of 200–500 ha was observed in a grassland fire once > 15 km/h [27]. Predicting dynamic burning areas not only provides direct guidance for fire response and supports community evacuation strategies, but also facilitates post-fire assessment efforts. According to the burned status in forest areas, China forest and grassland authority divides the forest fires into four levels: general fire for < 1 ha, significant fire for ∈ (1–100) ha, major fire for ∈ (100–1000) ha, and particularly major fire for > 1000 ha.
The four core fire behavior parameters directly describe the ongoing status of fire behavior and serve as the cornerstone for constructing a spatiotemporal assessment system of fire scenes. This system addresses critical questions about when and where the fire occurs, its intensity, duration, and extent of spread. As illustrated in Figure 1, these parameters are integral to the “space-air-ground” data closed loop, acting as a quantitative bridge between scientific understanding and prediction. They enable fireline deduction, risk zoning, and early warning, supporting dynamic and intelligent decision-making that transitions from reactive to proactive strategies. Importantly, fire behavior prediction platforms provide critical insights for both immediate response and proactive management, facilitating efficient resource allocation for prevention and landscape management.
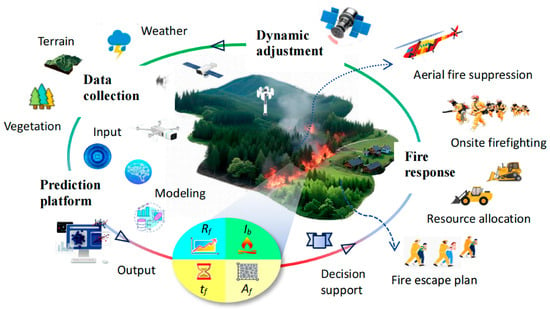
Figure 1.
General technical routines for wildfire behavior prediction and fire response, which can be seamlessly shifted into proactive fire management.
3. Milestones and Applications of Classical Fire Behavior Models
3.1. Milestones of Physical and Empirical Models
Wildfire behavior prediction originated in the first half of the 20th century, primarily focusing on surface fire [7,8,9]. In 1946, Fons developed a mathematical model based on the concept of forest fuels as a bed of independent and discrete fuel particles. Each fuel particle is characterized by specific geometric dimensions, moisture content, thermal properties, and spatial distribution [7]. By applying discretized physical modeling and the principle of energy conservation during fire spread, Fons transformed the fire spread process into a computable mathematical model for the first time. This model delineated the quantitative relationships between fuel bed parameters, environmental factors, and fire behavior parameters, thereby pioneering the field of wildfire prediction. The basic characteristics and application limitations of this model are summarized in Table 1.

Table 1.
Development foundation, characteristics, and applicability of classical models.
To further unravel the driving mechanisms of fire behavior, McArthur [8] constructed an empirical model for predicting fire behavior in Eucalyptus forests through field observations, laboratory tests, and model deductions. As a nation dominated by Eucalyptus forests, Australia has long relied on this model for its simplicity and applicability in bushfire risk assessment and emergency management (see Table 1). Similarly, through field observations in the Greater Hinggan Mountains and analysis of experimental data, Chinese scholar Zhengfei Wang [33] developed an empirical model for surface fire spread, which is expressed as , where denotes the initial fire spread rate, , and represent the adjustment coefficients given by local wind and slope and fuel conditions, respectively. Mao [40] further supplemented this model by expanding the original 5 spread directions to 8 (including left uphill, right downhill and so on), which improved its applicability and simulation accuracy under complex terrain conditions. In recent years, Zhengfei Wang’s empirical model has been used as a framework for cellular automata or maze algorithms, serving fire risk forecasting, burned area estimation, and decision-making management of firefighting force deployment in certain forest areas [41,42].
The year of 1972 witnessed the public unveiling of the classical model crafted by Rothermel [9]. Through extensive laboratory burning experiments and behavioral parameter evaluation, a semi-physical and semi-empirical model was systematically developed. This model is designed to evaluate the rate of fire spread under various fuel, terrain, and weather conditions. The core equation was derived from the heat required by the adjacent unburnt fuels to reach the ignition condition , and has the following form [9]:
where denotes the reaction intensity, i.e., heat production rate per unit area of the fire front, and and represent the adjustment coefficients for including wind and slope effects based on the indoor measurements. The fraction term on the right-hand side of Equation (1) can be labeled as , corresponding to the rate expression by omitting the impact of environmental factors.
This model adopts the elliptical surface assumption to predict the burnt area, while introducing concepts such as equivalent wind speed to incorporate the influences of wind speed and slope into the elliptical burnt area assumption. Despite its empirical nature and simplifications, it remains highly valuable in practical applications so far. As indicated in Table 1, Rothermel’s model is suitable for predicting surface fire spread on flat terrain covered with herbaceous vegetation, dead branches, and leaf litter, and was then developed into a comprehensive prediction software to support wildfire management and fire ecology studies [43].
Given that the major direction of fire spread is oriented by wind direction and the terrain slope, the impact of wind and terrain slope on the maximum fire spread rate should be integrated by a superposition of two vectors, i.e., . As a result, Wang and co-workers [44] derived the rate equation into the following form:
where and denote the adjustment coefficients for wind and slope effects, and indicates the angle between the wind and upslope directions. The parameters and can be derived from the empirical correlations presented in the Rothemel’s research report, as detailed in the paper of Wang et al. [44].
In developing a surface fire behavior forecasting system, Zhu et al. [45] refined the elliptical burnt area assumption. By applying the principles of differentiation, the advance of the fire line is regarded as continuous motion of discretized fire locations along an existing fire front. While sitting on a focus of an ellipse, the fire spread from a localized fire spot still follows the elliptical surface burnt area assumption. Its rate of fire spread can be determined by Equations (2) and (3) in conjunction with some other empirical correlations, with the integration of the dynamic variations in local wind, slope and fuel conditions [45]. The algorithms developed to quantify fire spread rates and burnt areas have shown high consistency with the results from multiple field tests, confirming their capacity to accurately predict the development of local fires under various fuel distribution patterns, including isolated non-fuel zones [45].
3.2. Spotting Models
In the realm of forest fire behavior prediction, spotting fire is particularly challenging due to its “leapfrog” spread and random nature. The model proposed by Albini [10] stands out as a milestone in predicting the travel distance of firebrands (Table 1). Through extensive field experiments, correlations were established to determine the maximum ascent height and travel distance of firebrands, thereby providing a crucial theoretical foundation for predicting spotting fire. By considering firebrands generated from various fuel types, a series of models were developed, allowing for a more comprehensive understanding of firebrand propagation characteristics across different fire scenarios [10,34].
To better understand the distribution patterns of firebrands downwind, Wang [30] investigated the physical processes involved in firebrand generation, transport, and ignition conditions. For the first time, a transport model integrating statistical and physical principles was developed to describe how firebrands distribute within the wind field. The ignition threshold was determined based on the critical mass accumulation of firebrands. Moreover, the minimum fireline intensity needed to trigger spot fires was quantified, which is in excellent agreement with the field observations. This model effectively explained the extensive damage of houses in a residential area during the 2003 Canberra Bushfires. The predicted peak spot fire density within 160 m of the forest edge closely aligned with the actual survey results, thereby confirming its applicability in assessing fire risks at the wildland and urban interface (WUI) [30].
3.3. Crown Fire Models
In 1977, van Wagner [23] proposed a crown fire initiation model that quantifies the critical conditions for the transition from surface fire to crown fire (Table 1). Based on energy balance and the thermodynamic properties of fuels, the model specifies the surface fire heat flux required to initiate crown fires. This was the first time that physical mechanisms such as flame height and heat flux were integrated with stand structural parameters, including crown base height and fuel continuity. Additionally, the dynamic effect of moisture content was incorporated to quantify the inhibitory role of humidity [23,35].
Based on 71 field experiments, Cruz et al. [36] developed a probabilistic model to predict the likelihood of crown fire occurrence in coniferous forests. This model integrates multiple environmental variables and fire behavior parameters, overcoming the limitations of traditional models that rely solely on single indicators. By introducing the concept of fuel strata gaps and employing logistic regression to develop a probability equation, the model assesses how the crown structure can impede flame propagation. Application studies in coniferous forests, such as black spruce–lichen woodland and mature jack pine stands, demonstrate that for 10-m open wind speed ≥ 8 km/h, fuel strata gaps ≤ 3 m, and estimated fine fuel moisture content < 10%, the model achieves an 85% prediction accuracy. This performance is much better than that of conventional empirical models [36,37].
To further quantify the coupling relationship between flame length and fireline intensity in crown fire, as well as to predict crown fire initiation and crown scorch height, Alexander and Cruz [29] established a fire dynamics model based on the principle of energy conservation. The combination of field experiments, wind tunnel simulations with numerical simulations using Fire Dynamics Simulator (FDS) enabled full-scale validation ranging from microscale flame structure to macroscale fire behavior. Parameters such as fireline intensity, flame length, and crown height were then integrated into a unified framework. Existing practice shows that the integration of the Alexander and Cruz model significantly boosts the accuracy of fire simulation, particularly exhibiting superior performance amidst complex fuel conditions and meteorological factors [38]. As a further work on the modeling of crown fire behavior published by Cruz and Alexander [39], the uncertainty in the prediction of nonlinear fire behavior was investigated under the Monte Carlo simulation framework. Their study not only enhanced the accuracy of fire spread prediction but also consolidated the scientific basis for crown fire management.
The core value of classical models lies in establishing the research paradigm of “physical mechanism analysis → mathematical modeling → experimental validation → application and promotion.” This paradigm has transformed wildfire behavior studies from fragmented observations into a systematic science, providing a groundbreaking methodology for addressing the increased frequency of fires in the context of climate change. For example, Rothermel’s model is widely used for surface fire spread prediction, and van Wagner’ model is crucial for understanding crown fire initiation [9,23]. These models remain the logical starting point for understanding fire and ecosystem interactions and can be regarded as the conceptual pillars of wildfire science. They have enabled the shift in fire management from empiricism to scientific quantification, laying the technical foundation for modern wildfire prevention and control with efficacy. Building on these models, researchers can develop more advanced and accurate prediction systems, thereby enhancing our ability to manage and mitigate wildfire risks.
4. Associated Software for Wildfire Behavior Prediction and Control
4.1. Behave and BehavePlus
The Behave software and its subsequent iteration, BehavePlus, are the most representative among the diverse array of fire behavior prediction technologies and systems [43,46]. In 1977, based on Rothermel’s physical model of fire spread, experts from the U.S. Forest Service (USFS) successfully developed the Behave system to evaluate surface fire behavior and predict key parameters such as fire spread rate, fire intensity, and burned area [43]. To enhance the practical applicability of the computational model, 13 standard fuel models were defined and embedded. With the calculation of as the foundational framework, this software enables quantitative predictions of potential fire behavior and fireground dynamics, thereby establishing itself as an auxiliary decision-making tool for fuel management and fire suppression operations [43,46].
As the updated version of Behave, BehavePlus features a modular design that allows users to customize fuel models [47,48]. By integrating van Wagner’s crown fire model, it expands the prediction scenarios from surface fire to crown fire risk assessment. The BehavePlus system quantifies how fuel treatments inhibit fire behavior, supports the USFS Forest Health Program, and has a vast user base across North America [21]. As a typical work using BehavePlus 5.0, Stratton [49] simulated potential fire behavior parameters in mechanically thinned areas and untreated areas in Oregon’s Willamette National Forest. The results showed that fuel treatments not only effectively dropped the potential and but also reduced the wind’s acceleration effect on fire spread.
Through quantitative fire behavior simulation, the Behave system and its upgraded versions have emerged as core tools driving the transformation of forest insurance from an experience-driven paradigm to a data-driven one. Their applications in risk assessment, disaster response, and claims optimization have significantly enhanced the risk management capabilities and service efficiency of insurance institutions. In 2023, American International Group (AIG) partnered with the California Department of Forestry and Fire Protection to integrate the Behave system into the forest carbon sink insurance framework [50]. By offering policyholders the simulation reports generated by Behave or BehavePlus, AIG guides them to implement fuel management practices, such as prescribed burning, to reduce their insurance premiums.
4.2. FARSITE/FlamMap
FARSITE is a parallel application software collaboratively developed by the USFS and Colorado State University [47]. It excels in its integration of three key models: Rothermel’s surface fire spread model, Albini’s fire spotting model, and van Wagner’s crown fire initiation model. By incorporating Huygens’ principle to track the movement of fire fronts, FARSITE can more accurately simulate fire spread under diverse conditions, including varying fuel continuity, topography and wind directions. This integration allows for the simulation of fire behavior across a wide range of fire regimes [47,51,52]. The system utilizes spatial data, such as digital elevation models (DEMs) and vegetation type maps, along with real-time meteorological parameters as inputs. It generates visualized outputs, including fire spread paths, risk zones, and occurrence probabilities, all under three-dimensional terrain conditions [52].
Since 2010, FARSITE has incorporated corrections for fine fuel moisture content (FMC) in its crown fire spread predictions, quantifying the inhibitory effect of live fuel moisture on [38]. Additionally, the parameter “site-adjusted moisture” was introduced to enhance model accuracy. With its spatially explicit characteristics and multi-model synergy, FARSITE excels in complex landscape management and can conduct large-scale fire and atmosphere coupling simulations. It has now been integrated into the FlamMap platform, which specialized in static fire behavior simulation. By leveraging geographic information systems (GIS), FlamMap enables dynamic fire behavior simulation under complex meteorological conditions and diverse landscape distributions.
The MTT (Minimum Travel Time) algorithm, first introduced by Finney [51], is a method for calculating fire spread paths based on the “fastest arrival” concept. It has been incorporated into American forest fire analysis systems such as FlamMap and FARSITE. Utilizing Huygens’ principle, the algorithm identifies paths with the “minimum propagation time” across a 2D raster landscape. It computes fire spread rates at each pixel using the Rothermel model and expands nodes with the smallest “arrival time” through Dijkstra’s algorithm or similar techniques. This process generates a raster or vector “arrival time” layer that includes fire behavior parameters. After conducting numerous simulations, the algorithm produces a burn probability distribution map. Effective in complex terrain, the MTT algorithm supports strategic fuel management and tactical fire suppression, enhancing fire management capabilities.
Ager et al. [52] applied the MTT algorithm to simulate burn probability and wildfire size in Oregon’s Emily Hill landscape under various fuel treatment intensities (ranging from 0% to 66%). Their results indicated that a 20% fuel treatment reduced the average fire size by 31% under Stand Density (SDEN) and by 29% under Residential Density (RDEN) scenarios (Figure 2). The MTT algorithm is instrumental in devising comprehensive fuel treatment plans and is widely used in both strategic and tactical fire management planning across the U.S. It is integrated into the Wildland Fire Decision Support System (WFDSS), enhancing the ability to manage and mitigate wildfire risks effectively [53].
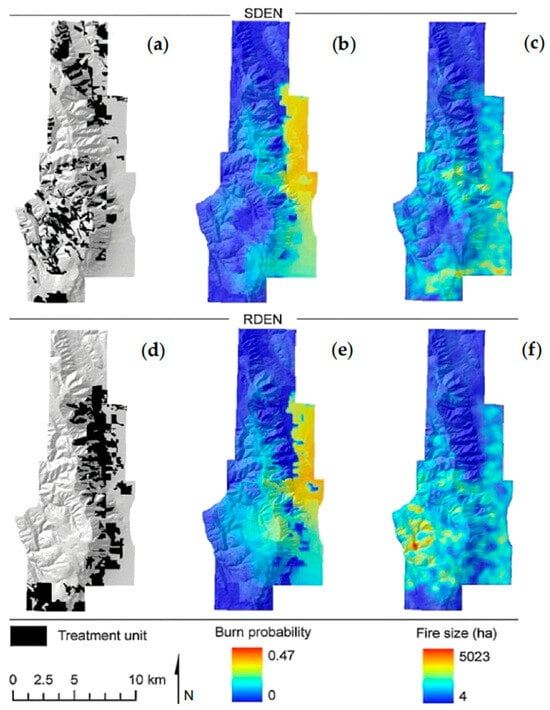
Figure 2.
Three-dimensional visualization of treatment units (a,d), burn probabilities (b,e), and kernel-smoothed fire sizes (c,f) in the 20% treatment areas at the stand density (SDEN) and the residential density (RDEN) treatment priorities [52].
4.3. CFFDRS and Future Systems
The Canadian Forest Fire Danger Rating System (CFFDRS), released in 1987, is renowned for its core technical component—the Fire Behavior Prediction (FBP) subsystem. This subsystem integrates van Wagner’s crown fire model and the Cruz-Alexander modified model, enabling a comprehensive assessment from fire danger levels to crown fire spread rates [54]. The input parameters of the system include meteorological data, topographic slope positions, and fuel types, while its outputs consist of a five-level fire danger classification and the probability of crown fire occurrence [55].
Wotton et al. [19] integrated the CFFDRS with the spatial fire spread model Prometheus to develop FireBC 2.0. This new system supports 3D visualization and real-time data input. A new crown fire prediction module was introduced, incorporating parameters such as canopy density, tree height, and fire whirl index. Applying the software to the 2003 Hinton fire in the boreal forest of Alberta, Canada, it was found that the simulated results of have an error of <10% compared to the measured values, while the error in fire intensity is below 12% [19]. FireBC 2.0 supports integrated calculations with multiple fuel models and can simulate fire behavior under extreme conditions, such as slopes greater than 30° and wind speeds exceeding 20 km/h, achieving a threefold increase in speed compared to earlier versions of CFFDRS. With its modular design and robust spatial analysis capabilities, the modified version has become a handful tool for global boreal forest fire research [19].
The upgrade pathways of the three systems collectively reflect the shared characteristics of model refinement, data comprehensiveness and application scenario expansion. Behave has evolved from integrating static fuel parameters to incorporating dynamic meteorological data. FARSITE has advanced from two-dimensional terrain analysis to coordinating multiple fire points and conducting three-dimensional dynamic simulations. Meanwhile, CFFDRS has made a leap from empirical statistics to physical mechanisms by integrating the Alexander–Cruz model and fuzzy logic algorithms. In terms of core technological breakthroughs, FARSITE’s spatial simulation and CFFDRS’ data-driven calibration (with experimental data exceeding 1000 sets) are particularly prominent, and Behave’s modular design has provided a basic architectural paradigm for subsequent system integration. Through continuous integration, these three systems have gradually evolved from static simulation to dynamic and multi-scale analysis, offering multi-level technical support for wildfire prediction and control.
5. Numerical Simulation: Integration of Fire Physics with Prediction Techniques
5.1. Development of Key Tools under the CFD Framework
Computational Fluid Dynamics (CFD) package employs numerical analysis to solve the governing equations that describe fluid flow and related physical phenomena, thereby simulating and predicting fluid flow and burning behaviors [12,56,57]. The fundamental governing equations encompass the continuity, momentum, energy conservation and species conservation equations, which are mathematically formulated in conjunction with the physical processes involved in fire phenomena [56]. The four basic equations can be expressed in a general form as follows [5,58]:
During model development, complex processes necessitate reasonable simplifications (e.g., assuming a homogeneous fuel bed, steady-state combustion, and neglecting minor physical effects). Additionally, model parameters such as fuel thermophysical properties, reaction kinetic parameters and heat of combustion must be calibrated using experimental data to improve prediction accuracy [57]. In the context of wildfire behavior simulation, CFD packages are primarily employed to track and quantify processes such as air flow, flame propagation, and smoke dispersion. The features of representative software, including Fluent, FDS, WFDS and FIRETEC, are outlined and compared in Table 2.

Table 2.
Overview of software related to wildfire behavior prediction under the CFD framework.
As an intellectual property offered by National Institute of Standards and Technology (NIST), conventional FDS lacks targeted modeling of vegetation fuel properties and terrain effects, which restricts its direct application in forest fire scenarios. The Wildland–Urban Interface Fire Dynamics Simulator (WFDS) was then developed, specifically designed to tackle the complex issues of vegetation combustion and atmosphere–terrain coupling in wildfires [63]. It incorporates parameters such as fuel bed porosity and thermal conductivity and introduces reaction–diffusion equations to describe fuel pyrolysis and flame propagation. Nested grid technology is adopted to tackle the impact of complex terrains (e.g., valleys and ridges) on airflow, thereby simulating the interaction between terrain-induced winds and fire behavior. Large eddy simulation (LES) is utilized to capture turbulent structures near the fire front. Furthermore, radiation models were refined to simulate the shielding effect of vegetation canopies. By integrating with the Weather Research and Forecasting (WRF) model, fire-weather bidirectional feedback can also be achieved through simulation.
5.2. Crucial Tactics in Performing Numerical Simulation
With the ongoing progress in GIS technology and the enhancement of modern computing capabilities, GIS can now be seamlessly integrated into detailed computer simulations of fire behavior. This integration has significantly advanced wildfire simulation and prediction technologies, moving them from simplified hypothetical models to realistic and accurate representations [15,64]. GIS can aggregate various fire-related datasets, including meteorological, topographic, vegetation, and historical fire data. By incorporating dynamically computed fire behavior data into GIS for preprocessing and integration, a robust geospatial database is created. This not only improves prediction accuracy but also enables researchers and fire managers to visualize the three-dimensional dynamics of fires [13].
As shown in Table 2, CFD packages enable precise characterization of flame propagation and smoke dispersion in forest and grassland fire simulations. For example, FIRETEC is built on the conservation equations of mass, momentum, and energy. It is coupled with pyrolysis and combustion modules to simulate the multiphase transport processes of fire spread [65]. Through coupled simulations using HIGRAD-FIRETEC, Pimont et al. [5] observed that narrow valleys and steep slopes in Mediterranean shrublands accelerate the lateral spread of fire. Clearly, this computational platform can resolve the coupled effects of complex terrains (such as valleys and hillsides) on airflow and fire behavior. It then provides technical support for mountain fire suppression operations. These capabilities are irreplaceable by traditional physical models.
At the large-scale fire laboratory of NIST, Mell et al. [66] simulated the burning behavior of Douglas fir trees in a natural forest setting. They also conducted numerical simulations of Douglas fir experiments under the WFDS-LES framework. Validation of these simulations was achieved by comparing the time histories of predicted and measured mass loss rates and radiant heat fluxes. The results indicate that WFDS is capable of accurately simulating the combustion behavior of Douglas fir at the laboratory scale. In a study of fire behavior in North American forests, Hoffman et al. [13] utilized a compiled dataset of crown fire spread rates from Alexander and Cruz [38] to conduct a preliminary assessment of crown fire predictions from prior studies that employed WFDS or FIRETEC. Overall, 86% of all simulated values using WFDS or FIRETEC fell within the 95% prediction interval of the empirical data. This performance far exceeded the target of 75% for dynamic ecological modeling. The outcomes of this study provided valuable insights into the mechanisms that dominate fire behavior in North American forests.
In the realm of CFD simulation, tools like FDS and WFDS often incorporate traditional fire behavior prediction models as sub-modules to forecast wildfire behavior [15]. For instance, core parameters from the Rothermel model, such as fuel load, surface area-to-volume ratio, and fuel bed depth, are directly mapped to the fuel bed settings in WFDS. This integration allows for a more accurate definition of fuel-related parameters [11]. Meanwhile, parallel fire behavior prediction software can enhance each other’s capabilities through data integration. For example, FARSITE software can be used initially to integrate the Rothermel fire spread model for predicting wildfire risks and potentially affected areas. Subsequently, coupled models like WFDS can be invoked to simulate specific fire spread processes. This approach allows for the concurrent prediction of wildfire occurrence probability and dynamic simulation of fire behavior [15]. To date, numerical analysis has become a crucial tool for addressing complex issues in wildfire modeling. Its ability to conduct multi-physics field coupling simulations provides precise and efficient solutions for forest resource management.
6. Implanting Artificial Intelligence in Prediction Techniques
6.1. Existing Data-Driven Models in Prediction Practice
Data-driven models are based on extensive historical datasets and utilize statistical and machine learning techniques to reveal hidden relationships among variables. These models establish mapping relationships between input variables and fire behavior parameters. Their primary methods encompass statistical regression analysis, time series analysis, and analogy approaches that rely on data similarity and pattern recognition [67,68]. As shown in Figure 3, the input variables for predicting fire behavior usually include meteorological data, topographic data, and vegetation data. The output variables are key parameters such as spread rate, fire intensity, and burned area. By learning from large amounts of historical fire data, data-driven models can capture the nonlinear relationships among these variables, enabling the dynamic prediction of wildfire behavior and helping to identify the most effective measures for fire management [67,68]. These models are particularly useful in regions with extensive historical data, where they can leverage past events to improve predictive accuracy and provide valuable insights for proactive fire management strategies.
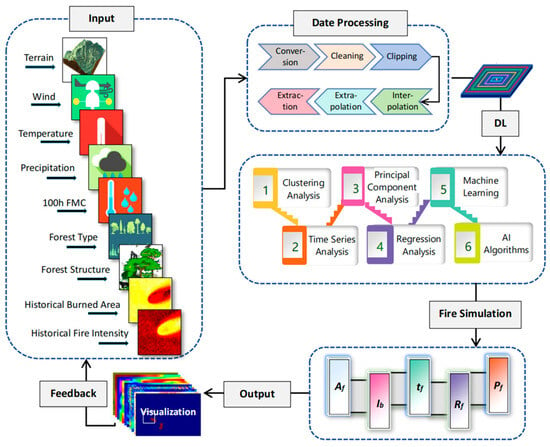
Figure 3.
Representative technical flowchart for predicting wildfire behavior and providing management aids based on data-driven models [68].
Physical models can offer valuable insights for feature engineering in data-driven models. On the other hand, data-driven models, through their analysis of large datasets, can reveal influencing factors and parameter interactions that may not be accounted for in physical models. This capability can, in turn, assist in refining and optimizing the parameters of physical models. Xu et al. [64] developed a coupled model that integrates Least Squares Support Vector Machine (LSSVM) with three-dimensional cellular automaton (CA). Trained by the terrain and vegetation data from Landsat 8 and historical fire data from Xichang, Sichuan Province, China, the model achieved a 97.9% fire spread overlap coefficient, demonstrating its effectiveness in fire probability prediction and spread simulation. Khanmohammadi et al. [14] investigated semi-arid shrublands in Australia and found that the SVM model achieved prediction accuracies of 70% for fire spread and 79% for crown fire types. Additionally, the prediction accuracy for crown fire increased by 4% after optimization using synthetic datasets. These studies highlight the potential of data-driven models to complement traditional physical models, providing a more comprehensive approach to wildfire prediction and management.
6.2. Breakthrough in Deep Learning
Deep learning (DL) has revolutionized the modeling and prediction of wildfire spread by analyzing the complex spatiotemporal characteristics of wildfire behavior. It primarily relies on architectures such as Convolutional Neural Networks (CNN), Artificial Neural Networks (ANN), Recurrent Neural Networks (RNN), Generative Adversarial Networks (GAN) and Long Short-Term Memory Networks (LSTM) [69]. Compared to traditional machine learning methods, DL demonstrates superior capabilities in processing high-dimensional data and extracting spatiotemporal features. It performs well in estimating fire spread rates, predicting burned areas and temporal dynamics [69].
ANN, as a computational model simulating biological neurons, has been widely employed in fire behavior prediction, risk assessment, and fire type classification owing to its nonlinear fitting capabilities [69]. For instance, Multilayer Perceptrons (MLPs) take temperature, humidity, wind speed, fuel moisture content and other parameters as inputs to output predicted values of spread rate; time-series models, like LSTM networks, can forecast the trajectory of fire behavior over the subsequent hours by leveraging sequential data, including historical meteorological information and the locations of fire spots [70]. Wu et al. [71] built up a flame propagation model under the ANN framework, incorporating multidimensional physical and environmental variables to quantify the uncertainty in fire propagation. In comparison to the Zhengfei Wang–CA model, the ANN model achieved an average accuracy of 85.0%, a sensitivity of 95.3%, and an F1-score of 89.9% after training and testing. Notably, in the realm of image analysis, CNNs can identify characteristics of fire-affected areas from satellite surveillance images [72], while GANs can generate simulated fire scenarios for firefighting training by learning from real fire images [73].
The advent of large models, which leverage vast amounts of data and advanced computational techniques, represents a significant advancement in the field. These large models have the potential to capture intricate patterns and relationships in fire behavior data that were previously unattainable. They can process and integrate data from multiple sources, including satellite imagery, weather stations, and ground sensors, to provide more accurate and comprehensive predictions (refer to Figure 1 and Figure 3). The development and application of large models are expected to play a crucial role in enhancing the robustness and reliability of wildfire prediction systems.
6.3. Strategies for Fusing Fire Modeling and Prediction Techniques
The integration of forest fire modeling and prediction technology leverages the strengths of physics-based models, numerical simulations, and machine learning techniques, employing the following three distinct strategies or their combinations:
- (1)
- Complementary integration—Given the differences in applicable scenarios of various models, a serial integration mode characterized by “division of labor and collaboration” is adopted. For instance, during the fire risk assessment phase, physical models are used to calculate the critical ignition conditions of fuels, while machine learning models such as random forests are employed to handle the nonlinear relationship between meteorological data and fire occurrence probability, thereby constructing a dual-layer prediction framework of “physical mechanism screening” with “data-driven classification”. Marjani et al. [18] combined CNN with Bidirectional Long Short-Term Memory (BiLSTM) modules to generate a novel DL model named CNN-BiLSTM, which is used for near-real-time wildfire spread prediction.
- (2)
- Weighted fusion—Among statistical weighting methods for multi-model outputs, Bayesian Model Averaging (BMA) and dynamic weight assignment are commonly adopted. BMA allocates weights by estimating the posterior probabilities of models, which is suitable for long-term prediction of wildfire behavior. For instance, the FireCAST system, developed by the USFS, integrates the Rothermel model, LSTM model, and CFD model, thereby enhancing the rate prediction accuracy in complex terrain [74]. Dynamic weight assignment can be adjusted according to real-time data, highlighting the response mechanism to abrupt changes in fire behavior under strong winds.
- (3)
- Hybrid modeling—A “physics-constrained, data-driven” hybrid model is constructed by embedding physical equations as regularization terms into the machine learning framework. A typical example is the Deep Convolutional Inverse Graphics Network (DCIGN) proposed by Hodges et al. [68]. This model integrates Rothermel’s phenomenological fire spread model into a convolutional inverse graphics network. The energy balance equation from Rothermel’s model ensures that the predicted heat release rates align with actual values while adhering to the constraints of Equation (1). Trained and tested on wildfires in both simple homogeneous landscapes and complex heterogeneous terrains, the DCIGN avoids the physical inconsistencies often found in purely data-driven models. This makes it particularly well-suited for data-sparse high-altitude forest areas [68]. By combining machine learning’s nonlinear fitting capabilities with the physical constraints of burning phenomena, this approach significantly enhances the accuracy and reliability of the model predictions.
Integrating complex physical models with machine learning in weighted and hybrid approaches incurs high computational costs, impeding real-time predictions. In fact, handling heterogeneous data necessitates normalization and multi-scale fusion to ensure effective processing. Combining deterministic and statistical models can introduce inconsistencies, requiring rigorous validation to maintain physical consistency. It is understandable that operational maturity varies with models like FireCAST, which needs refinement for real-time use, and DCIGN, which requires further validation for broader application.
For long-term seasonal predictions, weighted fusion approaches (e.g., BMA) that handle large-scale data and provide probabilistic forecasts are preferred. In real-time scenarios, complementary integration of fast machine learning models with simplified physical models balances accuracy and efficiency. Under complex terrain and diverse fuel conditions, hybrid models incorporating physical constraints offer reliable results, maintaining consistency in heterogeneous environments.
As illustrated in Figure 1 and Figure 3, wildfire behavior parameters are not only core variables in theoretical research but also function as a critical bridge linking scientific early warning with practical prevention and control. Their accuracy and real-time performance directly determine the effectiveness of disaster prevention and mitigation. With the advancement of multi-source data fusion, the development of AI technologies, and the improvement of computing power, parameter-driven precision fire management will become an inevitable trend. By taking fire behavior prediction as a bridge to guide fire prevention and suppression decisions, a complete chain of early risk warning, dynamic simulation and emergency decision-making can be constructed with efficacy. This integrated approach will not only enhance the ability to predict and manage wildfires more accurately but also significantly reduce the potential damage to ecosystems and human societies. Moreover, it will pave the way for sustainable and resilient forest management in the face of increasing wildfire threats due to climate change.
7. Concluding Remarks and Prospect
Wildfire behavior prediction models have evolved significantly over the past decades, transitioning from empirical models to more sophisticated CFD and data-driven approaches. Empirical models, such as those developed by Fons, McArthur, Rothermel, and Albini, have provided foundational tools for rapid assessments of fire behavior. These models are particularly useful for quick predictions in specific biomes but face limitations in transferability across different ecosystems. More recently, CFD models have offered detailed process-level insights into fire behavior, although they come with high computational costs. Data-driven models, including machine learning and deep learning approaches, have shown great promise in capturing complex nonlinear relationships from large datasets, but they require extensive, high-quality data for accurate predictions.
While significant advancements have been made in wildfire behavior prediction models, several challenges remain. Computational costs associated with complex CFD models, data requirements for accurate data-driven predictions, and the transferability of empirical models across different ecosystems are critical issues that need to be addressed. These limitations highlight the importance of continued research to improve model efficiency, data accessibility, and model adaptability.
Future research should focus on exploring these limitations further and developing strategies to overcome them. Multi-model integration, which combines the strengths of different approaches, offers a promising avenue for enhancing prediction accuracy and robustness. By integrating empirical models for rapid assessments, CFD models for detailed process-level insights, and data-driven models for capturing nonlinearities, researchers can develop more comprehensive and reliable prediction systems. This integrated approach not only addresses the individual limitations of each model type but also leverages their complementary strengths to provide a more holistic understanding of wildfire behavior.
In addition to multi-model integration, future research should also focus on interdisciplinary collaboration, combining insights from forestry, meteorology, geography, physics, and mathematics. This collaborative effort will enable a more comprehensive understanding of wildfire dynamics under various conditions. Special emphasis should be placed on the impact of unique meteorological patterns, such as extreme weather events and climate anomalies, which can significantly influence fire behavior and spread. Furthermore, the development of intelligent, comprehensive prediction systems that integrate space–air–ground data collection, model forecasting, and emergency decision-making processes will enhance prediction reliability and efficacy in practical use. These initiatives are intended to provide more scientific and effective technical support for fire prevention and ecological conservation, ultimately contributing to the development of a digital support system for global forest and grassland protection.
Author Contributions
Conceptualization, H.-H.W., K.-X.Z., S.A. and Z.-P.W.; methodology, H.-H.W., K.-X.Z., S.A. and Z.-P.W.; formal analysis, K.-X.Z.; investigation, H.-H.W. and Z.-P.W.; resources, H.-H.W., K.-X.Z., S.A. and Z.-P.W.; data curation, K.-X.Z.; writing—original draft preparation, H.-H.W. and K.-X.Z.; writing—review and editing, H.-H.W. and K.-X.Z., S.A. and Z.-P.W.; visualization, K.-X.Z. and S.A.; supervision, H.-H.W.; project administration, H.-H.W.; funding acquisition, H.-H.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Key Technologies Research and Development Program under the grant number 2022YFC3003000.
Conflicts of Interest
The authors declare no conflicts of interest.
Nomenclature
| burned area | |
| flame height | |
| fireline intensity | |
| reaction intensity | |
| adjustment coefficient induced by fuel conditions | |
| adjustment coefficient induced by terrain slope | |
| adjustment coefficient induced by local wind | |
| flame length | |
| fire probability | |
| heat required for ignition | |
| rate of fire spread | |
| initial fire spread rate/fire spread rate without considering wind and slope effects | |
| unified source term | |
| time | |
| flame residence time | |
| velocity vector | |
| wind speed | |
| gradient operator | |
| general variable specifying density, velocity, temperature or mass fraction of a medium considered | |
| porosity of a fuel bed | |
| angle between the wind and upslope directions | |
| heat absorption coefficient | |
| density of a medium | |
| fuel apparent density | |
| wind adjustment coefficient | |
| slope adjustment coefficient | |
| AI | Artificial Intelligence |
| AIG | American International Group |
| ANN | Artificial Neural Networks |
| BiLSTM | Bidirectional Long Short-Term Memory |
| BMA | Bayesian Model Averaging |
| CA | Cellular Automaton |
| CFD | Computational Fluid Dynamics |
| CFFDRS | Canadian Forest Fire Danger Rating System |
| CNN | Convolutional Neural Networks |
| DCIGN | Deep Convolutional Inverse Graphics Network |
| DEMs | Digital Elevation Models |
| DL | Deep Learning |
| FBP | Fire Behavior Prediction |
| FDS | Fire Dynamics Simulator |
| FMC | Fine Fuel Moisture Content |
| GAN | Generative Adversarial Networks |
| GIS | Geographic Information System |
| LES | Large Eddy Simulation |
| LSSVM | Least Squares Support Vector Machine |
| LSTM | Long Short-Term Memory Networks |
| MTT | Minimum Travel Time |
| MLPs | Multilayer Perceptrons |
| NIST | National Institute of Standards and Technology |
| RDEN | Residential Density |
| RNN | Recurrent Neural Networks |
| SDEN | Stand Density |
| SVM | Support Vector Machine |
| USFS | U.S. Forest Service |
| WFDS | Wildland–Urban Interface Fire Dynamics Simulator |
| WFDSS | Wildland Fire Decision Support System |
| WRF | Weather Research and Forecasting |
| WUI | Wildland and Urban Interface |
References
- Jolly, W.M.; Cochrane, M.A.; Freeborn, P.H.; Holden, Z.A.; Brown, T.J.; Williamson, G.J.; Bowman, D.M. Climate-induced variations in global wildfire danger from 1979 to 2013. Nat. Commun. 2015, 6, 7537. [Google Scholar] [CrossRef] [PubMed]
- Cook, T.M. Personal protective equipment during the coronavirus disease (COVID) 2019 pandemic—A narrative review. Anaesthesia 2020, 75, 920–927. [Google Scholar] [CrossRef] [PubMed]
- Stougiannidou, D.; Zafeiriou, E. Wildfire economic impact assessment: An empirical model-based investigation for Greek agriculture. Model. Earth Syst. Environ. 2022, 8, 3357–3371. [Google Scholar] [CrossRef]
- Li, T.; Cui, L.; Liu, L.; Chen, Y.; Liu, H.; Song, X.; Xu, Z. Advances in the study of global forest wildfires. J. Soils Sediments 2023, 23, 2654–2668. [Google Scholar] [CrossRef]
- Pimont, F.; Dupuy, J.L.; Linn, R.R. Coupled slope and wind effects on fire spread with influences of fire size: A numerical study using FIRETEC. Int. J. Wildland Fire 2012, 21, 828–842. [Google Scholar] [CrossRef]
- Povak, N.A.; Hessburg, P.F.; Brion Salter, R. Evidence for scale-dependent topographic controls on wildfire spread. Ecosphere 2018, 9, e02443. [Google Scholar] [CrossRef]
- Fons, W.R. Analysis of fire spread in light forest fuels. J. Agric. Res. 1946, 72, 93–121. [Google Scholar]
- McArthur, A.G. Fire Behaviour in Eucalypt Forest; Leaflet No.107; Forestry and Timber Bureau, Department of National Development, Commonwealth of Australia: Canberra, Australia, 1967; 35p.
- Rothermel, R.C. A Mathematical Model for Predicting Fire Spread in Wildland Fuels; Res. Pap. INT-115; U.S. Department of Agriculture, Intermountain Forest and Range Experiment Station: Ogden, UT, USA, 1972.
- Albini, F.A. Spot Fire Distance from Burning Trees: A Predictive Model; USDA Forest Service General Technical Report INT-56; U.S. Department of Agriculture Forest Service: Portland, OR, USA, 1979.
- Scott, J.H.; Burgan, R.E. Standard Fire Behavior Fuel Models: A Comprehensive Set for Use with Rothermel’s Surface Fire Spread Model; Gen. Tech. Rep. RMRS-GTR-153; U.S. Department of Agriculture, Forest Service, Rocky Mountain Research Station: Fort Collins, CO, USA, 2005; p. 72. [CrossRef]
- Ganteaume, A.; Guillaume, B.; France, E.; Guerra, F. CFD modelling of WUI fire behaviour in historical fire cases according to different fuel management scenarios. Int. J. Wildland Fire 2023, 32, 513–526. [Google Scholar] [CrossRef]
- Hoffman, C.M.; Canfield, J.; Linn, R.R.; Mell, W.; Sieg, C.; Pimont, F.; Ziegler, J. Evaluating Crown Fire Rate of Spread Predictions from Physics-Based Models. Fire Technol. 2016, 52, 221–237. [Google Scholar] [CrossRef]
- Khanmohammadi, S.; Arashpour, M.; Golafshani, E.M.; Cruz, M.G.; Rajabifard, A. An artificial intelligence framework for predicting fire spread sustainability in semiarid shrublands. Int. J. Wildland Fire 2023, 32, 636–649. [Google Scholar] [CrossRef]
- Goleiji, E.; Aliani, H.; Hosseini, S.M. Integrating FARSITE and GIS for enhanced forest fire spread prediction and simulation. Nat. Hazards 2025, 1–19. [Google Scholar] [CrossRef]
- Coen, J.L.; Schroeder, W.; Rudlosky, S.D. Transforming wildfire detection and prediction using new and underused sensor and data sources integrated with modeling. In Handbook of Dynamic Data Driven Applications Systems; Blasch, E., Ravela, S., Aved, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2018; pp. 1–22. [Google Scholar] [CrossRef]
- Singh, H.; Ang, L.M.; Lewis, T.; Paudyal, D.; Acuna, M.; Srivastava, P.K.; Srivastava, S.K. Trending and emerging prospects of physics-based and ML-based wildfire spread models: A comprehensive review. J. For. Res. 2024, 35, 135. [Google Scholar] [CrossRef]
- Marjani, M.; Mahdianpari, M.; Mohammadimanesh, F. CNN-BiLSTM: A Novel Deep Learning Model for Near-Real-Time Daily Wildfire Spread Prediction. Remote Sens. 2024, 16, 1467. [Google Scholar] [CrossRef]
- Wotton, B.M.; Alexander, M.E.; Taylor, S.W. Updates and Revisions to the 1992 Canadian Forest Fire Behavior Prediction System; Natural Resources Canada Information Report GLC-X-10; Natural Resources Canada: Ottawa, ON, Canada, 2009.
- Beer, T. The interaction of wind and fire. Bound. Layer Meteorol. 1991, 54, 287–308. [Google Scholar] [CrossRef]
- Andrews, P.L.; Rothermel, R.C. The Rothermel fire-spread model: Still running like a champ. Int. J. Wildland Fire 2007, 16, 327–338. [Google Scholar] [CrossRef]
- Forthofer, J.M. Modeling Wind in Complex Terrain for Use in Fire Spread Prediction. Master’s Thesis, Colorado State University, Fort Collins, CO, USA, 2007; p. 123. [Google Scholar]
- van Wagner, C.E. Conditions for the start and spread of crown fire. Can. J. For. Res. 1977, 7, 23–34. [Google Scholar] [CrossRef]
- Wotton, B.M.; Gould, J.S.; Mccaw, W.L.; Mccaw, L.; Cheney, N.P. Flame temperature and residence time of fires in dry eucalypt forest. Int. J. Wildland Fire 2012, 21, 270–281. [Google Scholar] [CrossRef]
- Ferrer Palomino, A.; Sánchez Espino, P.; Borrego Reyes, C.; Jiménez Rojas, J.A.; Rodríguez, Y.; Silva, F. Estimation of moisture in live fuels in the mediterranean: Linear regressions and random forests. J. Environ. Manag. 2022, 322, 116069. [Google Scholar] [CrossRef]
- Abatzoglou, J.T.; Williams, A.P. Impact of anthropogenic climate change on wildfire across western US forests. Proc. Natl. Acad. Sci. USA 2016, 113, 11770–11775. [Google Scholar] [CrossRef]
- Flannigan, M.D.; Stocks, B.J.; Wotton, B.M. Climate change and forest fires. Sci. Total Environ. 2000, 262, 221–229. [Google Scholar] [CrossRef]
- Byram, G.M. Combustion of forest fuels. In Forest Fire—Control and Use; Davis, K.P., Ed.; McGraw-Hill Book Company: New York, NY, USA, 1959; pp. 61–89. [Google Scholar]
- Alexander, M.E.; Cruz, M.G. Interdependencies between flame length and fireline intensity in predicting crown fire initiation and crown scorch height. Int. J. Wildland Fire 2011, 21, 95–113. [Google Scholar] [CrossRef]
- Wang, H.-H. Analysis on downwind distribution of firebrands sourced from a wildland fire. Fire Technol. 2011, 47, 321–340. [Google Scholar] [CrossRef]
- Pausas, J.G.; Keeley, J.E. A burning story: The role of fire in the history of life. Bioscience 2009, 59, 593–601. [Google Scholar] [CrossRef]
- Loehman, R.A.; Reinhardt, E.; Riley, K.L. Wildland fire emissions, carbon, and climate: Seeing the forest and the trees—A cross-scale assessment of wildfire and carbon dynamics in fire-prone, forested ecosystems. For. Ecol. Manag. 2014, 317, 9–19. [Google Scholar] [CrossRef]
- Wang, Z.F. The measurement method of the wildfire initial spread rate. Mt. Res. 1983, 1, 42–51. (In Chinese) [Google Scholar]
- Albini, F.A.; Alexander, M.E.; Cruz, M.G. A mathematical model for predicting the maximum potential spotting distance from a crown fire. Int. J. Wildland Fire 2012, 21, 609–627. [Google Scholar] [CrossRef]
- van Wagner, C.E. Prediction of crown fire behavior in two stands of jack pine. Can. J. For. Res. 1993, 23, 442–449. [Google Scholar] [CrossRef]
- Cruz, M.G.; Alexander, M.E.; Wakimoto, R.H. Modeling the likelihood of crown fire occurrence in conifer forest stands. For. Sci. 2004, 50, 640–658. [Google Scholar] [CrossRef]
- Cruz, M.G.; Alexander, M.E. Assessing crown fire potential in coniferous forests of western North America: A critique of current approaches and recent simulation studies. Int. J. Wildland Fire 2010, 19, 377–398. [Google Scholar] [CrossRef]
- Alexander, M.E.; Cruz, M.G. Assessing the effect of foliar moisture on the spread rate of crown fires. Int. J. Wildland Fire 2013, 22, 415–427. [Google Scholar] [CrossRef]
- Cruz, M.G.; Alexander, M.E. Modelling the rate of fire spread and uncertainty associated with the onset and propagation of crown fires in conifer forest stands. Int. J. Wildland Fire 2017, 26, 413–426. [Google Scholar] [CrossRef]
- Mao, X.M. The influence of wind and relief on the speed of the forest fire spreading. J. Appl. Meteor. Sci. 1993, 4, 100–104. (In Chinese) [Google Scholar]
- Tian, Y.C.; Liu, S.G.; Zhao, G.; Hu, J.; Li, W.B. Multi-model forecasting system of forest fire spreading based on deductive database. J. Beijing For. Univ. 2007, 29, 49–53. (In Chinese) [Google Scholar] [CrossRef]
- Zhang, Y.C.; Ye, Z.Q.; Gao, Y.J.; Xiang, Z.Y.; Wang, C.X.; Peng, Y.; Xiang, D.; Ren, F.; Yue, W.T. Research on forest fire combustion and spread prediction model and forecast platform. J. Wuhan Univ. 2025, 50, 1137–1149. (In Chinese) [Google Scholar] [CrossRef]
- Andrews, P.L. Behave: Fire Behavior Prediction and Fuel Modeling System: Burn Subsystem, Part 1; General Technical Report INT 194; US Department of Agriculture, Forest Service, Intermountain Research Station: Ogden, UT, USA, 1986.
- Wang, H.-H.; Zhu, J.P.; Jiang, W.; Shao, J. A mathematical model for estimating forest surface fire behavior. Fire Saf. Sci. 1994, 3, 33–41. (In Chinese) [Google Scholar]
- Zhu, J.P.; Wang, H.H.; Wang, Q.A.; Zhang, J.H.; Jiang, W.; Ding, M.L. A new method for predicting ground (surface) fire boundaries. Fire Saf. Sci. 1995, 4, 10–16. (In Chinese) [Google Scholar]
- Burgan, R.E.; Rothermel, R.C. BEHAVE: Fire Behavior Prediction and Fuel Modeling System; USDA Forest Service, General Technical Report INT-167; USDA Forest Service: Portland, OR, USA, 1984.
- Andrews, P.L. Current status and future needs of the BehavePlus fire modeling system. Int. J. Wildland Fire 2004, 23, 21–33. [Google Scholar] [CrossRef]
- Andrews, P.L. BehavePlus fire modeling system: Past, present, and future. In Proceedings of the Seventh Symposium on Fire and Forest Meteorology, Bar Harbor, ME, USA, 23–25 October 2007. [Google Scholar]
- Stratton, R.D. Assessing the Effectiveness of Landscape Fuel Treatments on Fire Growth and Behavior. J. For. 2004, 102, 32–40. [Google Scholar] [CrossRef]
- Brunette, M.; Couture, S. Forest insurance for natural events: An overview by economists. Forests 2023, 14, 289. [Google Scholar] [CrossRef]
- Finney, M.A. FARSITE: Fire Area Simulator—Model Development and Evaluation; USDA Forest Service Research Paper RMRS-RP-4; USDA Forest Service: Portland, OR, USA, 1998. [CrossRef]
- Ager, A.A.; Vaillant, N.M.; Finney, M.A. A comparison of landscape fuel treatment strategies to mitigate wildland fire risk in the urban interface and preserve old forest structure. For. Ecol. Manag. 2010, 259, 1556–1570. [Google Scholar] [CrossRef]
- Kalabokidis, K.; Athanasis, N.; Palaiologou, P.; Ager, A.A.; Finney, M.; Vasilakos, C. Minimum travel time algorithm for fire behavior and burn probability in a parallel computing environment. In Proceedings of the 7th International Conference on Forest Fire Research, Coimbra, Portugal, 17–20 November 2014. [Google Scholar] [CrossRef][Green Version]
- Taylor, S.W.; Alexander, M.E. Science, technology, and human factors in fire danger rating: The Canadian experience. Int. J. Wildland Fire 2006, 15, 121–135. [Google Scholar] [CrossRef]
- Stocks, B.J.; Lawson, B.D.; Alexander, M.E.; Van Wagner, C.E.; McAlpine, R.S.; Lynham, T.J.; Dubé, D.E. The Canadian Forest Fire Danger Rating System: An Overview. For. Chron. 1989, 65, 450–457. [Google Scholar] [CrossRef]
- Linn, R.R.; Cunningham, P. Numerical simulations of grass fires using a coupled atmosphere-fire model: Basic fire behavior and dependence on wind speed. J. Geophys. Res. Atmos. 2005, 110, D13107. [Google Scholar] [CrossRef]
- Coen, J.L.; Riggan, P.J. Simulation and thermal imaging of the 2006 Esperanza Wildfire in southern California: Application of a coupled weather-wildland fire model. Int. J. Wildland Fire 2014, 23, 755–770. [Google Scholar] [CrossRef]
- McGrattan, K.; McDermott, R.; Weinschenk, C.; Forney, G.P. Fire Dynamics Simulator, Technical Reference Guide, 6th ed.; NIST SP; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2013. [Google Scholar] [CrossRef]
- Dayanandan, S.; Chong, D. Performance Based Evaluation of Fire Scenarios Using Fluent. Eng. Environ. Sci. 2008. Available online: https://api.semanticscholar.org/CorpusID:56372294 (accessed on 10 August 2025).
- Lapointe, C.; Wimer, N.T.; Glusman, J.F.; Makowiecki, A.S.; Daily, J.W.; Rieker, G.B.; Hamlington, P.E. Efficient simulation of turbulent diffusion flames in OpenFOAM using adaptive mesh refinement. Fire Saf. J. 2020, 111, 102934. [Google Scholar] [CrossRef]
- Pimont, F.; Dupuy, J.L.; Linn, R.R.; Dupont, S. Impacts of tree canopy structure on wind flows and fire propagation simulated with FIRETEC. Ann. For. Sci. 2011, 68, 523–530. [Google Scholar] [CrossRef]
- Weise, D.R.; Mell, W.; Zhou, X.; Mahalingam, S. Use of the wildland-urban interface fire dynamics simulator to model fire spread in chamise chaparral fuel beds. In Proceedings of the 2012 Spring Technical Meeting of the Western States Section of the Combustion Institute, 12S-06, Tempe, AZ, USA, 19–20 March 2012. [Google Scholar]
- Moinuddin, K.A.M.; Sutherland, D.; Mell, W. Simulation study of grass fire using a physics-based model: Striving towards numerical rigour and the effect of grass height on the rate of spread. Int. J. Wildland Fire 2018, 27, 800–814. [Google Scholar] [CrossRef]
- Xu, Y.; Li, D.; Ma, H.; Lin, R.; Zhang, F. Modeling Forest Fire Spread Using Machine Learning-Based Cellular Automata in a GIS Environment. Forests 2022, 13, 1974. [Google Scholar] [CrossRef]
- Bonner, S.R.; Hoffman, C.M.; Linn, R.R.; Tinkham, W.T.; Atchley, A.L.; Sieg, C.H.; Varner, J.M.; O’Brien, J.J.; Hiers, J.K. Forest structural complexity and ignition pattern influence simulated prescribed fire effects. Fire Ecol. 2024, 20, 82. [Google Scholar] [CrossRef]
- Mell, W.; Maranghides, A.; McDermott, R.; Manzello, S.L. Numerical simulation and experiments of burning douglas fir trees. Combust. Flame 2009, 156, 2023–2041. [Google Scholar] [CrossRef]
- Sayad, Y.O.; Mousannif, H.; Al Moatassime, H. Predictive modeling of wildfires: A new dataset and machine learning approach. Fire Saf. J. 2019, 104, 130–146. [Google Scholar] [CrossRef]
- Hodges, J.L.; Lattimer, B.Y. Wildland fire spread modeling using convolutional neural networks. Fire Technol. 2019, 55, 2115–2142. [Google Scholar] [CrossRef]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning representations by back-propagating errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Lazcano, A.; Miguel, A.J.M. Data preprocessing techniques and neural networks for trended time series forecasting. Appl. Soft Comput. 2025, 174, 113063. [Google Scholar] [CrossRef]
- Wu, Z.; Wang, B.; Li, M.; Tian, Y.; Quan, Y.; Liu, J. Simulation of forest fire spread based on artificial intelligence. Ecol. Indic. 2022, 136. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet classification with deep convolutional neural networks. Commun. ACM 2012, 60, 84–90. [Google Scholar] [CrossRef]
- Shawly, T.; Alsheikhy, A.A. Fire Identification Based on Novel Dense Generative Adversarial Networks. Artif. Intell. Rev. 2024, 57, 207. [Google Scholar] [CrossRef]
- Radke, D.; Hessler, A.; Ellsworth, D. Firecast: Leveraging deep learning to predict wildfire spread. In Proceedings of the 28th International Joint Conference on Artificial Intelligence (IJCAI’19), Macao China, Menlo Park, CA, USA, 10–16 August 2019; pp. 4575–4581. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).