Abstract
Formic acid is a promising candidate fuel that can be produced by reacting renewable hydrogen with carbon dioxide. However, the burning safety characteristics of formic acid–air mixtures have not been fully studied. This paper presents an extensive theoretical study of the adiabatic explosion pressure of formic acid–air premixed laminar flames at various initial conditions (composition of formic acid: 17–38% volume; initial pressure: 0.1–1.5 bar; initial temperature: 333–500 K), using the GASEQ software package. GASEQ software calculates chemical equilibria based on ideal gas behavior and is based on the hypothesis of adiabatic expansion inside a closed containment that allows ideal expansion. The influence of the initial conditions (pressure, temperature, and concentration) of formic acid–air mixtures on the adiabatic explosion pressures, maximum flame temperature, and peak concentrations of the main reaction intermediates is investigated and discussed. It is found that the adiabatic peak explosion pressure (calculated equilibrium pressure) of the studied concentrations decreases with increasing initial temperature and increases linearly with increasing initial pressure.
1. Introduction
Due to limited crude oil reserves and climate change, the development of alternative fuels has attracted much attention. Hydrogen, for example, has the potential to be a highly efficient and emission-free energy source and is produced from a variety of energy sources, including biomass, solar, wind, geothermal, ocean, and hydro technologies []. However, traditional storage systems suffer from the inevitable trade-off between storage density and efficiency. Therefore, storage of hydrogen in the liquid phase utilizing chemical hydrides, such as formic acid, has attracted significant interest. With the increasing progress in new energy sources, formic acid as a hydrogen carrier has become a topic of interest [].
At room temperature, formic acid is a kinetically stable colorless liquid with a pungent, penetrating odor. Its dehydrogenation to H2 and CO2 is thermodynamically favorable (ΔG° = −32.9 kJ/mol at room temperature) but kinetically blocked; the side reaction to form water and carbon monoxide is also thermodynamically feasible [,,]:
| HCOOH(l) ↔ H2(g) + CO2(g) | ΔG° = −32.9 kJ/mol |
| HCOOH(l) ↔ H2O(l) + CO(g) | ΔG° = −12.4 kJ/mol |
Available processes for formic acid production are hydrocarbon oxidation, acidolysis of formate salts, formamide hydrolysis, mineral acid catalysis, and hydrolysis of lower alkyl formats [,]. Recently, advances have been made in the formic acid production and dehydrogenation processes, and an analysis of the recent process configurations could consider formic acid as a feasible option for a liquid organic hydrogen carrier []. Its efficiency and high environmental compatibility make it ideal for a wide range of applications. It is an organic acid that is widely used as a food additive, as a preservative in silage and animal feed, as a bactericide, and in industrial feed and textiles, leather tanning, deicing, and fuel cells (it can be used directly in formic acid fuel cells and indirectly in hydrogen fuel cells) and fuel gas desulfurization [].
Formic acid is a well-established hydrogen storage component, due to its decomposition into CO2 and H2, with the possibility of the reverse reaction to restore formic acid, thereby acting as a medium for chemical energy storage [,,,,]. On the other hand, the catalytic decarboxylation of formic acid ideally leads to the formation of CO2 and H2, which can be used in fuel cells. A large number of transition metal-based homogeneous catalysts with high activity and selectivity have been reported for the selective dehydrogenation of formic acid []. In addition, formic acid is a major product of biomass-derived carbohydrates and is attracting increasing attention as a sustainable hydrogen source [], due to its high volumetric hydrogen density of 53 g of H2 per liter []; therefore, many studies have been reported recently. For example, the evaporation of formic acid was investigated experimentally and numerically by [] who pointed out the low reactivity of formic acid and mixed it with octanol at different concentrations to increase its reactivity []. The performance of formic acid fuel oxidation in a solid polymer electrolyte membrane (PEM) fuel cell at 60 °C was reported by Rice et al. [] who observed that formic acid is an excellent fuel for a fuel cell. In their study, Muller et al. [] compared and evaluated several process options using formic acid for energy storage. Another study carried out by Onishi et al. [] showed that formic acid can be one of the most promising and safest materials for hydrogen storage due to its high hydrogen content (4.4 wt%) in the liquid state at room temperature []. A comprehensive experimental and kinetic study of the low-temperature oxidation and pyrolysis of formic acid was carried out by Yin et al. []. They performed the measurements of species profiles in a jet-stirred reactor (JSR) in the temperature range of 600–1100 K under atmospheric pressure, with a fixed residence time of 2.0 s and for equivalence ratios ranging from 0.5 to ∞ (pyrolysis). In another study, formic acid was employed as a liquid organic hydrogen carrier to power a 25 kW integrated and compact formic acid-to-power system to power a full-size city bus or serve as a stand-alone carbon-neutral electricity generator []. Along with these, formic acid is an important intermediate produced during the combustion of vast oxygenated and unsaturated hydrocarbon fuels [,,,,].
The relevant data and safety characteristics of the formic acid are provided in Table 1 [].

Table 1.
Relevant data and safety characteristics of the formic acid [].
In order to explore the possibility of formic acid as a potential fuel in engines, apart from its use as a hydrogen carrier, it is necessary to know its combustion process in detail. However, as the literature studies show, the combustion of formic acid has not yet been fully explored [].
Few studies have been conducted to determine its laminar burning velocity even though formic acid vapors are flammable and its combustion characteristics are very important. An early study about the burning velocities of mixtures of methyl alcohol, formaldehyde, or formic acid with oxygen was presented by de Wilde and Van Tiggelen []. They compared the results obtained with those of previous work on methane–oxygen flames, which showed a similarity, and proposed a kinetic interpretation []. An experimental and modeling study of laminar burning velocities of methane–formic acid–air flames is presented by Lavadera et al. [] by the heat flux method at an initial gas temperature of 353 K and 1 bar; for fuel mixtures containing a 75 or 50% mole fraction of formic acid (equivalence ratios: 0.7–1.3), and in the stoichiometric mixtures, the fuel composition varied from pure methane to 85% formic acid. They compared their data with data predicted from the literature and suggested a modification of the rate constant of the reaction HOCO (+M) = H + CO2 (+M) to improve the performance of the kinetic model []. Osipova et al. [] present an experimental and kinetic modeling study of laminar premixed formic acid/H2/O2/Ar flames, as well as laminar flame speed, at different equivalence ratios, stabilized on a flat burner at atmospheric pressure. Both of them (flame structure and laminar flame speed) were simulated using three different chemical kinetic mechanisms proposed for formic acid oxidation. It was observed that the components in the fuel mixture present different consumption profiles, and formic acid is consumed faster than hydrogen []. Sarathy et al. [] presented a study about the laminar burning velocities and kinetic modeling of formic acid and its mixtures with H2 and CO2. They observed that in formic acid combustion, the principal intermediate is the HOCO radical, and H2 addition stimulated the decomposition of the HOCO radical, thus growing the burning velocities []. Yin et al. [] presented an experimental and kinetic study of laminar flame speeds of formic acid at equivalence ratios of 0.4–1.6, an initial temperature of 423–453 K, and atmospheric pressure. Furthermore, the pathway analysis from this study shows that the HCOOH is mainly consumed by abstraction reaction with OH to form OCHO radicals, which rapidly dissociate to H + CO2 []. On the other hand, Wako et al. [] developed a simplified kinetic mechanism and a detailed kinetic mechanism derived from a rate-based selection algorithm. Their study aimed to characterize the chemistry of oxygenated species, with specific reference to formic acid at low initial temperatures.
Given the growing concern about the significance of formic acid chemistry in contemporary chemical societies and energy sectors, the study of the influence of initial conditions (concentrations, pressure, and temperature) on other explosion characteristics (e.g., explosion pressures) of formic acid–air mixtures is essential. For example, theoretical knowledge of the adiabatic peak pressure of the formic acid–air explosions propagating in closed vessels at various initial pressures and temperatures is beneficial for a thorough understanding of this flammable mixture, which cannot be found in the literature.
Many processes in the chemical industry are faced with increasing or decreasing pressures or temperatures in order to reduce fuel consumption, operating costs, and pollutant emissions, and to improve quality, flexibility, and capacity. Preventing and mitigating unwanted explosions demands knowledge of explosion safety characteristics. Available explosion data are not always adequate for utilization in certain applications. As an example, estimating the behavior of flammable gas or vapor explosions at lower or higher initial conditions of pressure and temperature should be based on the explosion data obtained at those pressures and temperatures and not at atmospheric conditions.
Therefore, the present theoretical study aims to model the influence of the initial composition, pressure, and temperature on the adiabatic explosion pressure, maximum adiabatic flame temperature, and peak concentrations of the main reaction intermediates of flame propagation in formic acid–air mixtures. In this respect, the GASEQ chemical equilibrium program [] was used to calculate pex, ad (adiabatic explosion pressure), Tf, ad (maximum adiabatic flame temperature), and the main reaction intermediates and species of flame propagation (Xi).
2. Numerical Studies
GASEQ software was used in this theoretical study, in order to evaluate the safety characteristics of formic acid–air mixtures []. GASEQ developed by Chris Morley is the most interesting combustion software package, distributed free of charge on the internet. The fundamentals of the program are based on complex, balanced chemical calculations []. The method is based on the minimization of free energy (NASA method). GASEQ can solve the following: composition at a defined temperature and pressure; adiabatic temperature and composition at constant pressure; composition at a defined temperature and constant volume; adiabatic temperature and composition at constant volume; adiabatic compression and expansion; equilibrium constant calculations. GASEQ software can calculate chemical equilibria involving ideal gases and is based on the hypothesis of adiabatic expansion inside the vessel. More information is given in [].
In their studies, Mitu and Brandes [,] compared experimental data and those obtained theoretically with the GASEQ program for alcohol–air [] and ethanol–air–nitrogen mixtures at different concentrations of inert gas (nitrogen) []. Considering the basis of the calculation of the adiabatic flame temperature under idealized assumptions, it was observed that the theoretical values had higher values than the experimental ones. Even if the calculated values correspond to the principal curve progression of experimental values, up to about 0.9 for equivalence ratios, φ, the calculated values are higher. In the case of ethanol–air diluted with nitrogen mixtures with equivalence ratios (φ) higher than 0.9, the differences are greater. Slight differences (≈0.5 bar) were found in the maximum explosion pressure, pmax. One of the causes for the differences could be that the GASEQ program is based on the calculation of the adiabatic flame temperature using ideal suppositions. The calculation of flame temperatures with the GASEQ program was also reported by Mitu et al. (2021) [].
3. Results and Discussion
Gas explosions are exothermic reactions due to oxidation processes; during oxidation, temperature and pressure increase. An explosion of a fuel–air mixture is possible when the flammable gas concentration is between the lower explosion limit (LEL) and the upper explosion limit (UEL). The LEL of formic acid is 16.4 vol% (temperature of LEL: 100 °C) and the UEL is 45.5 vol% [].
The concentrations and the corresponding equivalence ratios, φ, of formic acid–air mixtures used for the present theoretical study are presented in Table 2. The equivalence ratio, φ, is defined as φ = {[fuel]/[oxygen]}/{[fuel]/[oxygen]st}, where “st” refers to the stoichiometric concentration of the fuel–air mixture.

Table 2.
The equivalence ratios, φ, and the corresponding concentrations of formic acid–air mixtures used for the present theoretical study.
3.1. Influence of the Initial Pressure, Temperature, and Concentration on the Adiabatic Peak Explosion Pressures
The peak explosion pressure is a fundamental pressure-related characteristic parameter for the deflagration of fuel–air mixtures in enclosed vessels. The explosions of gaseous flammable mixtures in closed vessels are characterized by important damaging effects: maximum explosion pressures 7–10 times higher than the initial pressure, which are reached in a very short time (for example, less than one second, for experimental laboratory vessels with small volumes) [,]. The explosion pressure is an essential parameter for explosion risk assessment, for analyzing and predicting different engine or combustor performances, and for designing sufficient mechanical strength for equipment where flammable mixtures could be formed [,]. In addition, the explosion pressures are an important parameter for calculating the laminar burning velocity under various conditions. The explosion pressure is defined as the peak pressure developed in a confined deflagration of an explosive mixture. It depends on the initial conditions (pressure, temperature, and composition) of confined gas explosions, the size and shape of the explosion vessel, and the type, energy, and location of the ignition source [,].
The calculated adiabatic explosion pressure at ambient initial pressure in preheated formic acid–air mixtures is given in Figure 1a for several lean mixtures (φ: 0.5–0.9) and the stoichiometric mixture (φ: 1.0). Similar plots for rich mixtures (φ: 1.1–1.5) are shown as well (Figure 1b).
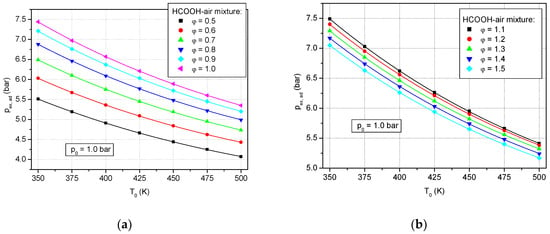
Figure 1.
Calculated adiabatic peak explosion pressure of formic acid–air mixtures versus initial temperatures at p0 = 1.0 bar: (a) lean and stoichiometric mixtures; (b) rich mixtures.
Figure 2a,b show that the dimensionless explosion pressures πex = pex/p0 versus the reciprocal values of initial temperature correlate linearly (as shown in Equation (1)).
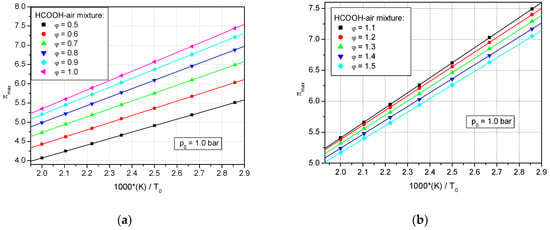
Figure 2.
Variation of dimensionless adiabatic peak explosion pressures at p0 = 1.0 bar, in correlation with the reciprocal temperature of lean and stoichiometric formic acid–air mixtures: (a) lean and stoichiometric mixtures; (b) rich mixtures.
The intercepts and slopes of the correlations found are given in Table 3. In the literature, such behavior was reported both for the calculated values and the experimental ones: methane–air, by Pekalski et al. []; ethane–air, by Mitu et al. []; propane–air, by Desoky et al. [] and by Razus et al. []; and methanol–air and ethanol–air by Mitu and Brandes [,]. The observed decrease of peak pressures in preheated flammable mixtures was explained by the decrease of density for the burning charge, which thus releases a lower heat amount.

Table 3.
Parameters of linear correlations between the dimensionless adiabatic peak explosion pressure and the reciprocal temperature, for formic acid–air mixtures at p0 = 1.0 bar.
For a constant initial pressure, the calculated adiabatic equilibrium pressure decreases with an increase of the initial temperature of the stoichiometric formic acid–air mixture, as shown in Figure 3.
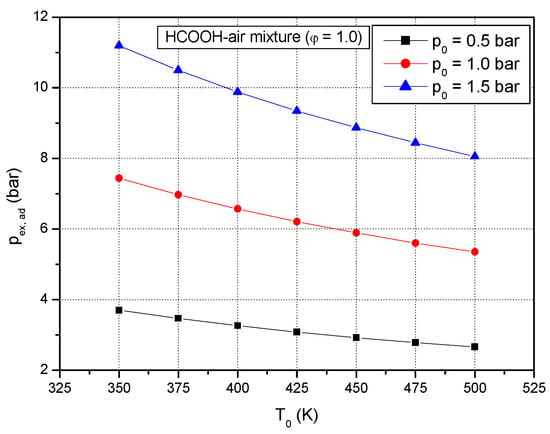
Figure 3.
Calculated adiabatic peak explosion pressure of stoichiometric formic acid–air mixture versus initial temperatures at various initial constant pressures p0: 0.5 bar, 1.0 bar, 1.5 bar.
In Figure 4, the influence of initial pressure on peak adiabatic explosion pressure for a stoichiometric formic acid–air mixture is shown. Figure 5 shows the variation of the calculated adiabatic explosion pressure of various concentrations of formic acid–air mixtures versus initial pressure at initial temperature T0 = 373 K: Figure 5a for lean and stoichiometric mixtures, and Figure 5b for rich mixtures. At constant initial temperature, the calculated adiabatic peak pressure is correlated with the initial pressure by the linear equation:
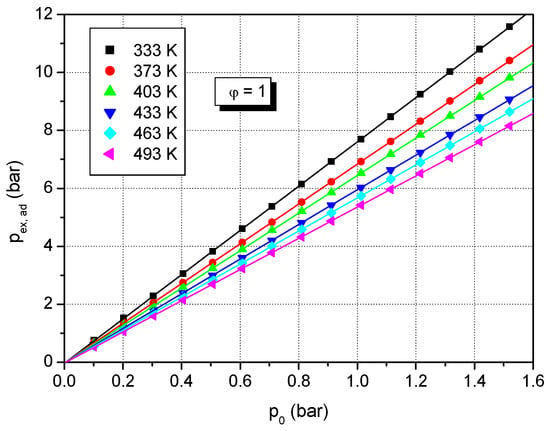
Figure 4.
Calculated adiabatic peak explosion pressure of stoichiometric formic acid–air mixtures versus initial pressure at various initial temperatures.
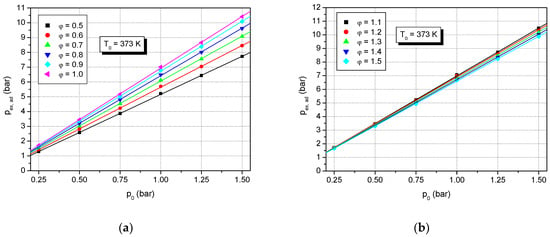
Figure 5.
Calculated adiabatic peak explosion pressure of various concentrations of formic acid–air mixtures versus initial pressure at initial temperature T0 = 373 K: (a) lean and stoichiometric mixtures; (b) rich mixtures.
The slope (α), the intercept (β), and the determination coefficients (rn) of such equations are given in Table 4 and Table 5. In the literature, linear correlations between the adiabatic peak explosion pressure and the initial pressure of gaseous or vapor fuel–air mixtures were reported for different explosions of quiescent mixtures, in deflagration regimes, e.g., methane–air [,], ethane–air [], propane–air [,], propylene–air [], methanol–air [] and ethanol–air []. As expected, both the slope and intercept of the linear correlation are dependent on the fuel concentration of the flammable mixture when initial pressure and temperature are constant.

Table 4.
The fit parameters of linear correlations between the adiabatic peak explosion pressure and the initial pressure (Equation (2)) for a set of data for stoichiometric formic acid–air mixtures, at various initial temperatures.

Table 5.
The fit parameters of linear correlations between the adiabatic peak explosion pressure and the initial pressure (Equation (2)) for data obtained at various initial concentrations of formic acid–air mixtures, at initial temperature T0 = 373 K.
Figure 6 and Figure 7 show the plots of formic acid–air mixture adiabatic peak pressures at different initial temperatures and pressures. Thereby, the variation of calculated equilibrium pressure with equivalence ratio at ambient initial pressure and different initial temperatures (T0: 373 K and 433 K) is presented in Figure 6. Two sets of data obtained of calculated equilibrium pressure at ambient initial pressure and two different initial temperatures, 373 K and 433 K, are plotted in Figure 6 versus equivalence ratio. They were fitted against formic acid concentration (equivalence ratio) by second-degree polynomials:
p0 = 1 bar, T0 = 373 K: pex,ad (bar) = 1.394 + 9.707·φ − 4.168·φ2; rn = 0.992 (11 points)
p0 = 1 bar, T0 = 433 K: pex,ad (bar) = 1.388 + 8.133·φ − 3.474·φ2; rn = 0.993 (11 points)
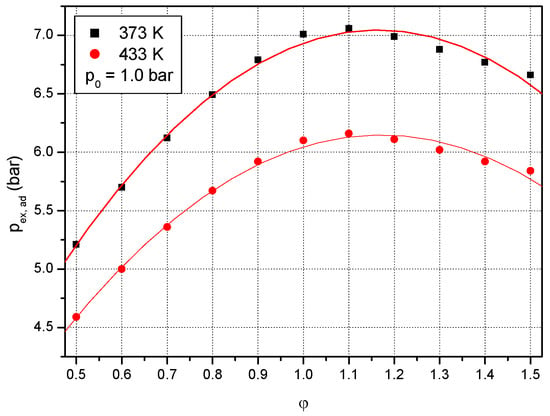
Figure 6.
Effect of equivalence ratio on adiabatic peak explosion pressure of formic acid–air mixtures at ambient initial pressure and two different initial temperatures: 373 K and 433 K.
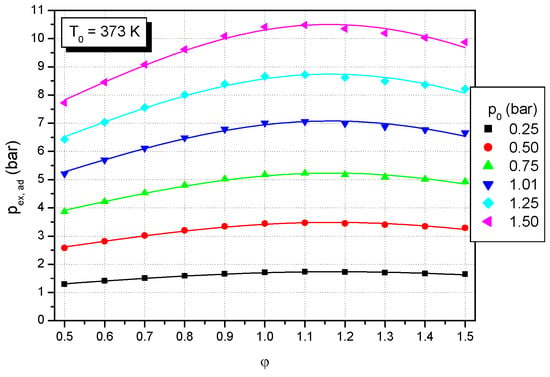
Figure 7.
Effect of equivalence ratio on adiabatic peak explosion pressure of formic acid–air mixtures at a constant initial temperature (T0: 373 K) and various initial pressures.
The influence of initial composition (equivalence ratio) on calculated equilibrium pressure was determined at constant initial temperature and various initial pressures. The sets of calculated equilibrium pressures at a constant initial temperature (T0: 373 K) and different initial pressures are plotted in Figure 7 versus the equivalence ratio. They were fitted against the equivalence ratio of formic acid (11 points) by second-degree polynomials:
T0 = 373 K, p0 = 0.25 bar: pex,ad (bar) = 0.414 + 2.228·φ − 0.944·φ2; rn = 0.995
T0 = 373 K, p0 = 0.50 bar: pex,ad (bar) = 0.747 + 4.653·φ − 1.988·φ2; rn = 0.994
T0 = 373 K, p0 = 0.75 bar: pex,ad (bar) = 1.074 + 7.089·φ − 3.038·φ2; rn = 0.993
T0 = 373 K, p0 = 1.00 bar: pex,ad (bar) = 1.394 + 9.707·φ − 4.168·φ2; rn = 0.992
T0 = 373 K, p0 = 1.25 bar: pex,ad (bar) = 1.714 + 12.008·φ − 5.160·φ2; rn = 0.991
T0 = 373 K, p0 = 1.50 bar: pex,ad (bar) = 2.019 + 14.515·φ − 6.246·φ2; rn = 0.991
As observed by other flammable substances, the highest value of the calculated equilibrium pressure of formic acid–air mixtures is found at the equivalence ratio of 1.1 for all investigated initial conditions (as shown in Figure 6 and Figure 7), as reported for other fuel–air mixtures.
As shown in Figure 7, the adiabatic peak pressure increases with increasing initial pressures; this could be explained due to the increased charge of the mass of formic acid and oxidizer in the combustion vessel and therefore the increased total heat released [,,]. Likewise, another explanation could be that increased initial pressure can increase the kinetic energy or gas–particle collision of the flammable gases and enhance the chemical reaction [,].
Such calculated correlations between equilibrium pressures, initial pressure, initial temperatures, and initial compositions of formic acid–air mixtures are useful for predicting the explosion pressures of flammable mixtures at lower or elevated temperatures and/or pressures when direct measurements are not available.
The peak pressure could be used to evaluate the performance of combustion devices because the peak pressure of a combustible mixture could describe the quantity of energy produced from the combustion of the fuel mixture [].
3.2. Structure of Premixed Formic Acid–Air Flames
The premixed flame structure is described by several important parameters, such as the flame temperature and concentrations of chemical species within the flame front. The examination of the species (radicals or products) distribution within the flame front is necessary to find the main radicals and dominant reactions that are the basis for control of the reaction pathways of hydrocarbon oxidation. The GASEQ software by Morley [] was used to determine the adiabatic flame temperatures and concentrations of chemical species (intermediate radicals, main products) within the flame front, for formic acid–air mixtures at various initial conditions (temperature, pressure, and equivalence ratio).
Figure 8 and Figure 9 show the calculated adiabatic flame temperatures of stoichiometric formic acid–air mixtures at various initial temperatures and various initial pressures. It is observed that at constant initial pressure, the adiabatic flame temperature of stoichiometric formic acid–air mixtures increases linearly with an increase of initial temperature, and at the same initial pressure of the stoichiometric formic acid–air mixture, the adiabatic flame temperature increases non-linearly with increase the initial pressure.
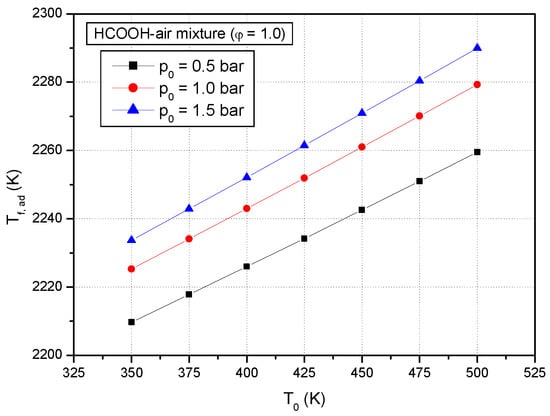
Figure 8.
Predicted adiabatic flame temperatures of premixed stoichiometric formic acid–air flames versus initial temperatures at various initial pressures (p0: 0.5 bar, 1.0 bar, 1.5 bar).
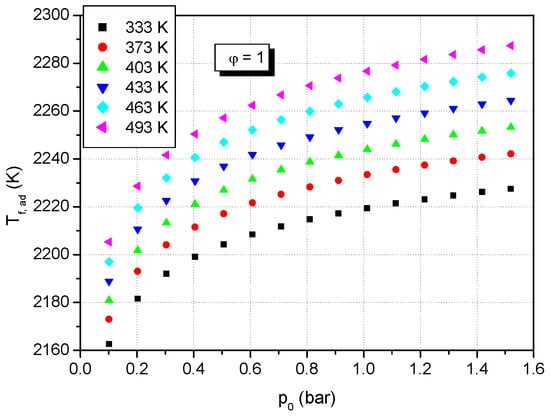
Figure 9.
Predicted adiabatic flame temperature of premixed stoichiometric formic acid–air flames versus initial pressure at various initial temperatures (T0: 333–493 K).
The predicted species mole fraction of O2, H2, and HCO· for premixed stoichiometric formic acid–air flames versus initial temperatures at various initial pressures are presented in Figure 10: (a) p0 = 0.5 bar, (b) p0 = 1.0 bar, (c) p0 = 1.5 bar. It is observed that all these species increase with increasing the initial temperature and decrease with increasing initial pressures.
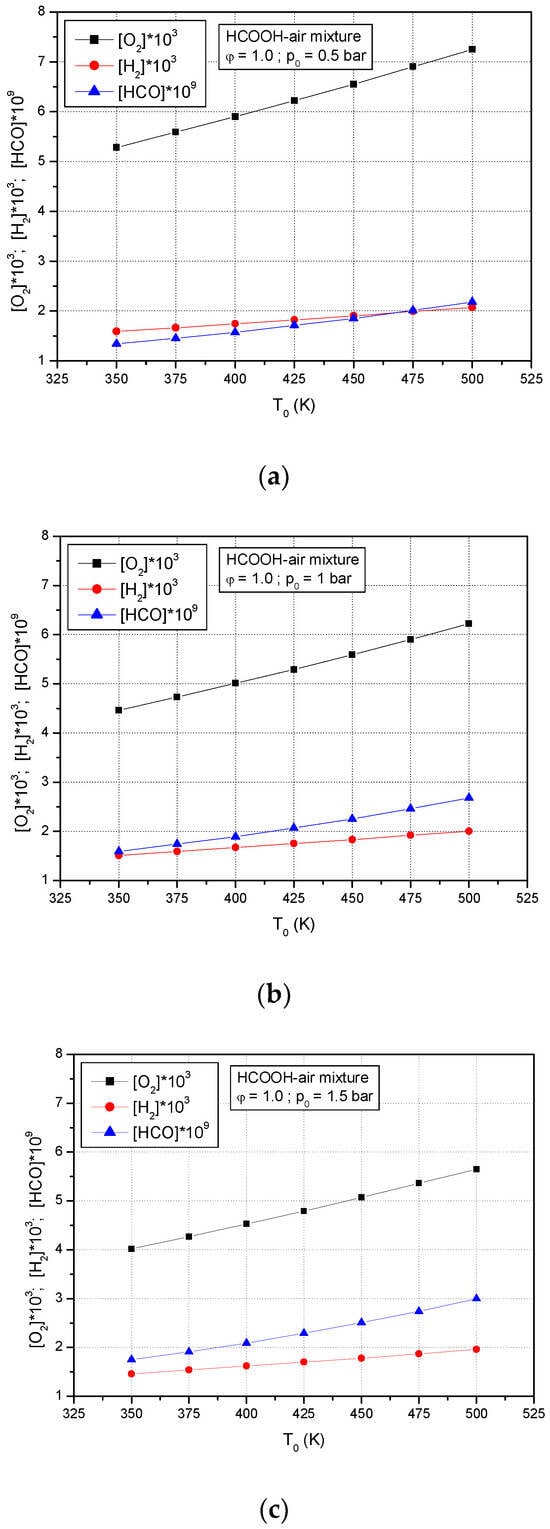
Figure 10.
Predicted species mole fraction of O2, H2, and HCO· of premixed stoichiometric formic acid–air flames versus initial temperatures at various initial pressures: (a) p0 = 0.5 bar, (b) p0 = 1.0 bar, (c) p0 = 1.5 bar.
The active radicals, namely, H, O, and OH, have a significant impact on the explosions of the formic acid–air mixtures. Figure 11 shows the predicted peak mole fractions of H, O, and OH radicals at various initial temperatures and initial pressures for a stoichiometric formic acid–air mixture. It can be seen from Figure 11 that the peak mole fractions of the active radicals increase monotonously with elevated initial temperature, which implies that the chemical effect on the formic acid–air explosion increases. At the same initial temperature, the peak mole fractions of H, O, and OH radicals decrease with elevated initial pressures.
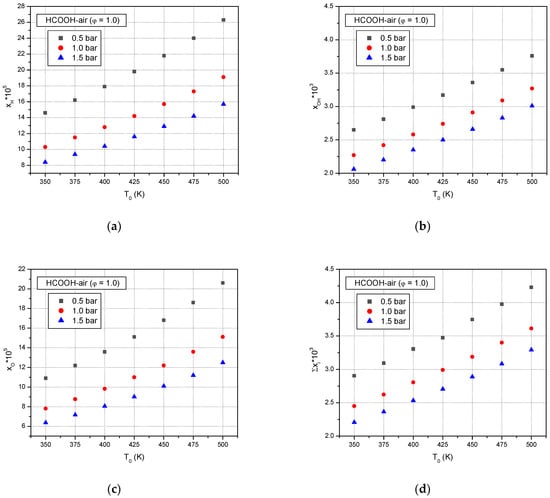
Figure 11.
Predicted peak mole fractions of H, OH, and O (a–c), and the sum of their peak mole fractions (d) in premixed stoichiometric formic acid–air flames versus initial temperatures at various initial pressures.
To further investigate the explosion behavior of formic acid–air mixtures, the peak mole fractions of NO at different initial conditions (pressure, temperature, and equivalence ratio) (Figure 12a–c) together with the peak mole fraction of HCO (Figure 12d) are calculated.
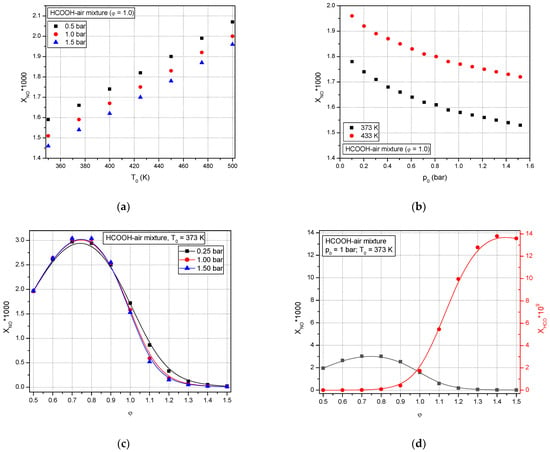
Figure 12.
Predicted mole fraction of NO of premixed stoichiometric formic acid–air flames versus initial conditions: (a) temperatures, (b) pressures, (c) equivalence ratio, and (d) equivalence ratio, together with variation of predicted species of XHCO.
For the stoichiometric formic acid–air mixture, the concentration of the NO species increases linearly with an increase of the initial temperature (Figure 12a), but it is observed that at a constant initial temperature, the increase of initial pressure conducted to decrease of NO concentrations Figure 12b.
Figure 12c shows the variation of the predicted concentration of NO versus the equivalence ratio of formic acid–air mixtures. It is observed that for the lean formic acid–air mixture (0.6 < φ < 1.0), the NO concentration is higher at lower initial pressure, while at the stoichiometric and rich mixtures (φ: 1.0–1.5), the NO concentration decreases with an increase in the initial pressure of the flammable mixture. A comparison of the variation of predicted concentrations of NO and radical species HCO from flames versus the equivalence ratio of formic acid–air mixtures is presented in Figure 12d. It is observed that while the NO concentration decreases, the radical species HCO concentration increases for mixtures richer than φ: 0.8, at p0 = 1 bar and T0 = 373 K.
This study showed that for rich concentrations of formic acid–air mixtures, at a constant initial temperature, a decrease in combustion pressure is efficient for lowering NO concentrations in the burned gas.
Knowledge of these theoretical explosion characteristics of formic acid at high pressures and high temperatures could be a benefit in industrial applications, due to safety concerns in technical applications in which it is involved.
In addition, it is mentioned that the specialized literature presents new intelligence systems that have been applied to generally elucidate the classification and regression problems of fires; some of these relate to the methodology for predicting fire danger rating levels [], a supervised machine learning technique [], and predicting the fire danger rating by using the application of state-of-the-art unsupervised and supervised machine learning techniques [].
4. Conclusions
Formic acid as a hydrogen carrier (as a hydrogen storage component) and as a renewable green fuel, formic acid could be used to reduce carbon dioxide emissions into the atmosphere when adopted as a transportation fuel. Therefore, it is important to have a good understanding of its combustion characteristics for its potential application in combustion devices. In this regard, this work provides a detailed investigation of hazardous formic acid–air mixtures using a validated program, GASEQ []. The GASEQ program delivered the adiabatic peak pressure, adiabatic flame temperature, and chemical species concentrations from the flame of a flammable mixture. The explosion pressure characteristic for explosions of fuel-air mixtures in closed spaces is a fundamental safety parameter for assessing the hazard of processes running in confined vessels and designing enclosures capable of being resistant to explosions or of using their vents as relief devices. Thus, the adiabatic peak pressures of flammable formic acid–air mixtures were systematically investigated at various initial pressures (0.1–1.5 bar), various initial temperatures (333–500 K), and various equivalence ratios (φ: 0.5–1.5) using numerical investigations. For the same initial conditions, the adiabatic flame temperature and the concentrations of the most important chemical species (H2, O2, H, OH, O, NO, HCO) within the flame front of formic acid–air mixtures were also obtained and presented.
The results that were obtained for this large range of initial conditions depict a scientific novelty since until now, no data about explosion pressures of formic acid have been presented.
The major conclusions of this study are summarized as follows:
- -
- The adiabatic peak pressures of the formic acid–air mixture increased with increasing initial pressures and decreased with increasing initial temperatures.
- -
- The adiabatic peak explosion pressures versus the total initial pressure (or initial temperature) of the flammable formic acid–air mixture are correlated by linear dependences for all examined mixtures, with both the slope and intercept of such correlations being influenced by the composition of the flammable mixtures.
- -
- For all investigated flammable formic acid–air mixtures, the maximum adiabatic peak pressures occur around equivalence ratio φ = 1.1.
- -
- This study showed that for rich concentrations of formic acid–air mixtures, at the constant initial temperature, a decrease in combustion pressure is efficient for lowering NO concentrations in the burned gas.
Even if the data presented in this paper are only theoretical, they deliver helpful results, thus completing the literature regarding the formic acid–air deflagrations occurring in enclosures. For that reason, the present results represent significant data for several applications, for example, safety recommendations for industrial activities, design of burners and vessels capable of resisting deflagrations, scaling explosions occurring in enclosures, and detailed modeling of the combustion process.
This theoretical study provides a foundation for future experimental or theoretic modeling studies on the combustion of formic acid. To validate the predicted data from the present paper, further studies should experimentally determine explosion pressure and measure species (for example, NO) concentrations in the flame of formic acid–air mixtures. Future research will focus on the experimental study of the effect of initial pressure and temperature to monitor the severity of explosions produced in formic acid–air mixtures, taking into consideration that industrial applications take place at variable initial pressures and temperatures higher than ambient.
Funding
This research received no external funding.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors on request.
Acknowledgments
The present study was partially financed by the Romanian Academy under the research project “Dynamics of fast oxidation and decomposition reactions in homogeneous systems” of Ilie Murgulescu Institute of Physical Chemistry.
Conflicts of Interest
The author declares no conflicts of interest.
References
- Koumi Ngoh, S.; Njomo, D. An overview of hydrogen gas production from solar energy. Renew. Sustain Energy Rev. 2021, 16, 6782–6792. [Google Scholar] [CrossRef]
- Dutta, I.; Chatterjee, S.; Cheng, H.; Parsapur, R.K.; Liu, Z.; Li, Z.; Ye, E.; Low, J.S.C.; Lai, Z.; Loh, X.J.; et al. Formic Acid to Power towards Low-Carbon Economy. Adv. Energy Mater. 2022, 12, 2103799. [Google Scholar] [CrossRef]
- Mellmann, D.; Sponholz, P.; Junge, H.; Beller, M. Formic acid as a hydrogen storage material–development of homogeneous catalysts for selective hydrogen release. Chem. Soc. Rev. 2016, 45, 3954–3988. [Google Scholar] [CrossRef] [PubMed]
- Loges, B.; Boddien, A.; Gärtner, F.; Junge, H.; Beller, M. Catalytic generation of hydrogen from formic acid and its derivatives: Useful hydrogen storage materials. Top. Catal. 2010, 53, 902–914. [Google Scholar] [CrossRef]
- Wang, X.; Meng, Q.; Gao, L.; Jin, Z.; Ge, J.; Liu, C.; Xing, W. Recent progress in hydrogen production from formic acid decomposition. Int. J. Hydrogen Energy 2018, 43, 7055–7071. [Google Scholar] [CrossRef]
- Eversole, J.F. Manufacture of Formic acid. Patent US2160064 A, 30 May 1939. [Google Scholar]
- Jogunola, O.; Salmi, T.; Warna, J.; Mikkola, J.P.; Tirronen, E. Kinetics of methyl formate hydrolysis in the absence and presence of a complexing agent. Ind. Eng. Chem. Res. 2011, 50, 267–276. [Google Scholar] [CrossRef]
- Kim, C.; Lee, Y.; Kim, K.; Lee, U. Implementation of Formic Acid as a Liquid Organic Hydrogen Carrier (LOHC): Techno-Economic Analysis and Life Cycle Assessment of Formic Acid Produced via CO2 Utilization. Catalysts 2022, 12, 1113. [Google Scholar] [CrossRef]
- BASF. Applications of Formic Acid. 2022. Available online: https://products.basf.com/global/en/ci/formic-acid.html (accessed on 8 November 2022).
- Eppinger, J.; Huang, K.W. Formic acid as a hydrogen energy carrier. ACS Energy Lett. 2017, 2, 188–195. [Google Scholar] [CrossRef]
- Alvarez, A.; Bansode, A.; Urakawa, A.; Bavykina, A.V.; Wezendonk, T.A.; Makkee, M.; Gascon, J.; Kapteijn, F. Challenges in the greener production of formates/formic acid, methanol, and DME by heterogeneously catalyzed CO2 hydrogenation processes. Chem. Rev. 2017, 117, 9804–9838. [Google Scholar] [CrossRef]
- Sordakis, K.; Tang, C.; Vogt, L.K.; Junge, H.; Dyson, P.J.; Beller, M.; Laurenczy, G. Homogeneous catalysis for sustainable hydrogen storage in formic acid and alcohols. Chem. Rev. 2018, 118, 372–433. [Google Scholar] [CrossRef]
- Guan, C.; Pan, Y.; Zhang, T.; Ajitha, M.J.; Huang, K.W. An update on formic acid dehydrogenation by homogeneous catalysis. Chem.–Asian J. 2020, 15, 937–946. [Google Scholar] [CrossRef]
- Valentini, F.; Kozell, V.; Petrucci, C.; Marrocchi, A.; Gu, Y.; Gelman, D.; Vaccaro, L. Formic acid, a biomass-derived source of energy and hydrogen for biomass upgrading. Energy Environ. Sci. 2019, 12, 2646–2664. [Google Scholar] [CrossRef]
- Maharjan, S.; Elbaz, A.M.; Roberts, W.L. Investigation on the formic acid evaporation and ignition of formic acid/octanol blend at elevated temperature and pressure. Fuel 2022, 313, 122636. [Google Scholar] [CrossRef]
- Rice, C.; Ha, S.; Masel, R.I.; Waszczuk, P.; Wieckowski, A.; Barnard, T. Direct formic acid fuel cells. J. Power Sources 2002, 111, 83–89. [Google Scholar] [CrossRef]
- Müller, K.; Brooks, K.; Autrey, T. Hydrogen storage in formic acid: A comparison of process options. Energy Fuels 2017, 31, 12603–12611. [Google Scholar] [CrossRef]
- Onishi, N.; Laurenczy, G.; Beller, M.; Himeda, Y. Recent progress for reversible homogeneous catalytic hydrogen storage in formic acid and in methanol. Coord. Chem. Rev. 2018, 373, 317–332. [Google Scholar] [CrossRef]
- Yin, G.; Xu, J.; Hu, E.; Gao, Q.; Zhan, H.; Huang, Z. Experimental and kinetic study on the low temperature oxidation and pyrolysis of formic acid in a jet-stirred reactor. Combust. Flame 2021, 223, 77–87. [Google Scholar] [CrossRef]
- van Putten, R.; Wissink, T.; Swinkels, T.; Pidko, E.A. Fuelling the hydrogen economy: Scale-up of an integrated formic acid-to-power system. Int. J. Hydrogen Energy 2019, 44, 28533–28541. [Google Scholar] [CrossRef]
- Lavadera, M.L.; Konnov, A.A. Laminar burning velocities of methane + formic acid + air flames: Experimental and modeling study. Combust. Flame 2021, 225, 65–73. [Google Scholar] [CrossRef]
- Osipova, K.N.; Sarathy, S.M.; Korobeinichev, O.P.; Shmakov, A.G. Chemical structure of atmospheric pressure premixed laminar formic acid/hydrogen flames. Proc. Combust. Inst. 2021, 38, 2379–2386. [Google Scholar] [CrossRef]
- Sarathy, S.M.; Brequigny, P.; Katoch, A.; Elbaz, A.M.; Roberts, W.L.; Dibble, R.W.; Foucher, F. Laminar burning velocities and kinetic modeling of a renewable e-fuel: Formic acid and its mixtures with H2 and CO2. Energy Fuels 2020, 34, 7564–7572. [Google Scholar] [CrossRef]
- Yin, G.; Gao, Q.; Hu, E.; Xu, J.; Zhou, M.; Huang, Z. Experimental and kinetic study on laminar flame speeds of formic acid. Combust. Flame 2020, 220, 73–81. [Google Scholar] [CrossRef]
- Wako, F.M.; Pio, G.; Salzano, E. Modeling formic acid combustion. Energy Fuels 2022, 36, 14382–14392. [Google Scholar] [CrossRef]
- CHEMSAFE. 2024. Available online: https://www.chemsafe.ptb.de/ (accessed on 10 June 2024).
- de Wilde, E.V.; van Tiggelen, A. Burning velocities in mixtures of methyl alcohol, formaldehyde or formic acid with oxygen. Bulletin des Sociétés Chimiques Belges 1968, 77, 67–75. [Google Scholar] [CrossRef]
- Morley, C. Gaseq—A Chemical Equilibrium Program for Windows. 2004. Available online: http://www.gaseq.co.uk (accessed on 10 June 2024).
- Mitu, M.; Brandes, E. Sicherheitstechnische Kenngroßen von Alkohol/Luft-Gemischen-Explosionsdruck, zeitlicher Druckanstieg, Verbrennungsgeschwindigkeit. In Proceedings of the Proceedings 13. BAM-PTB-Kolloquium zur Chemischen und Physikalischen Sicherheitstechnik, Braunschweig, Germany, 18–19 June 2013. [Google Scholar]
- Mitu, M.; Brandes, E.; Hirsch, W. Mitigation effects on the explosion safety characteristic data of ethanol/air mixtures in closed vessel. Process Saf. Environ. Prot. 2018, 117, 190–199. [Google Scholar] [CrossRef]
- Mitu, M.; Brandes, E.; Zakel, S.; Hirsch, W. Explosion regions and limiting oxygen concentrations of methyl propionate, methyl acetate, dimethyl carbonate with air and inert gas mixtures. J. Loss Prev. Process Ind. 2021, 69, 104384. [Google Scholar] [CrossRef]
- Steen, H.; Hattwig, M. (Eds.) Handbook of Explosion Prevention and Control; Wiley-VCH: London, UK; New York, NY, USA, 2004; Chapter 3. [Google Scholar]
- Razus, D.; Brinzea, V.; Mitu, M.; Oancea, D. Temperature and pressure influence on explosion pressures of closed vessel propane–air deflagrations. J. Hazard. Mater. 2010, 174, 548–555. [Google Scholar] [CrossRef] [PubMed]
- Pekalski, A.A.; Schildberg, H.P.; Smallegange, P.S.D.; Lemkowitz, S.M.; Zevenbergen, J.F.; Braithwaite, M.; Pasman, H.J. Determination of the explosion behaviour of methane and propene in air or oxygen at standard and elevated conditions. Procces Saf. Environ. Prot. 2005, 83, 421–429. [Google Scholar] [CrossRef]
- Mitu, M.; Giurcan, V.; Razus, D.; Oancea, D. Temperature and pressure influence on ethane–air deflagration parameters in a spherical closed vessel. Energy Fuels 2012, 26, 4840–4848. [Google Scholar] [CrossRef]
- Desoky, A.A.; Abdel-Ghafar, Y.A.; El-Badrawy, R.M. Hydrogen, propane and gasoline laminar flame development in a spherical vessel. Int. J. Hydrogen Energy 1990, 15, 895–905. [Google Scholar] [CrossRef]
- Mitu, M.; Brandes, E. Explosion parameters of methanol–air mixtures. Fuel 2015, 158, 217–223. [Google Scholar] [CrossRef]
- Mitu, M.; Brandes, E. Influence of pressure, temperature and vessel volume on explosion characteristics of ethanol/air mixtures in closed spherical vessels. Fuel 2017, 203, 460–468. [Google Scholar] [CrossRef]
- Gieras, M.; Klemens, R.; Rarata, G.; Wolański, P. Determination of explosion parameters of methane-air mixtures in the chamber of 40 dm3 at normal and elevated temperature. J. Loss Prev. Process. Ind. 2006, 19, 263–270. [Google Scholar] [CrossRef]
- Razus, D.; Oancea, D.; Chirila, F.; Ionescu, N.I. Transmission of an explosion between linked vessels. Fire Safety J. 2003, 38, 147–163. [Google Scholar] [CrossRef]
- Cui, G.; Wang, S.; Liu, J.; Bi, Z.; Li, Z. Explosion characteristics of a methane/air mixture at low initial temperatures. Fuel 2018, 234, 886–893. [Google Scholar] [CrossRef]
- Li, Q.; Cheng, Y.; Huang, Z. Comparative assessment of the explosion characteristics of alcohol-air mixtures. J. Loss Prev. Process. Ind. 2015, 37, 91–100. [Google Scholar] [CrossRef]
- Oppong, F.; Zhongyang, L.; Li, X.; Song, Y.; Xu, C.; Diaby, A.L. Methyl pentanoate laminar burning characteristics: Experimental and numerical analysis. Renewable Energy 2022, 197, 228–236. [Google Scholar] [CrossRef]
- Zhang, B.; Xiu, G.; Bai, C. Explosion characteristics of argon/nitrogen diluted natural gas-air mixtures. Fuel 2014, 124, 125–132. [Google Scholar] [CrossRef]
- Kamran, M.; Shahani, N.M. Decision Support System for the Prediction of Mine Fire Levels in Underground Coal Mining Using Machine Learning Approaches. Min. Metall. Explor. 2022, 39, 591–601. [Google Scholar] [CrossRef]
- Kamran, M.; Wattimena, R.K.; Armaghani, D.J.; Asteris, P.G.; Jiskani, I.M.; Mohamad, E.T. Intelligent based decision-making strategy to predict fire intensity in subsurface engineering environments. Process Saf. Environ. Prot. 2023, 171, 374–384. [Google Scholar] [CrossRef]
- Kamran, M.; Chaudhry, W.; Wattimena, R.K.; Rehman, H.; Martyushev, D.A. A multi-criteria decision intelligence framework to predict fire danger ratings in underground engineering structures. Fire 2023, 6, 412. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).