State-to-State Rate Constants for the O(3P)H2(v) System: Quasiclassical Trajectory Calculations
Abstract
1. Introduction
2. Methodology
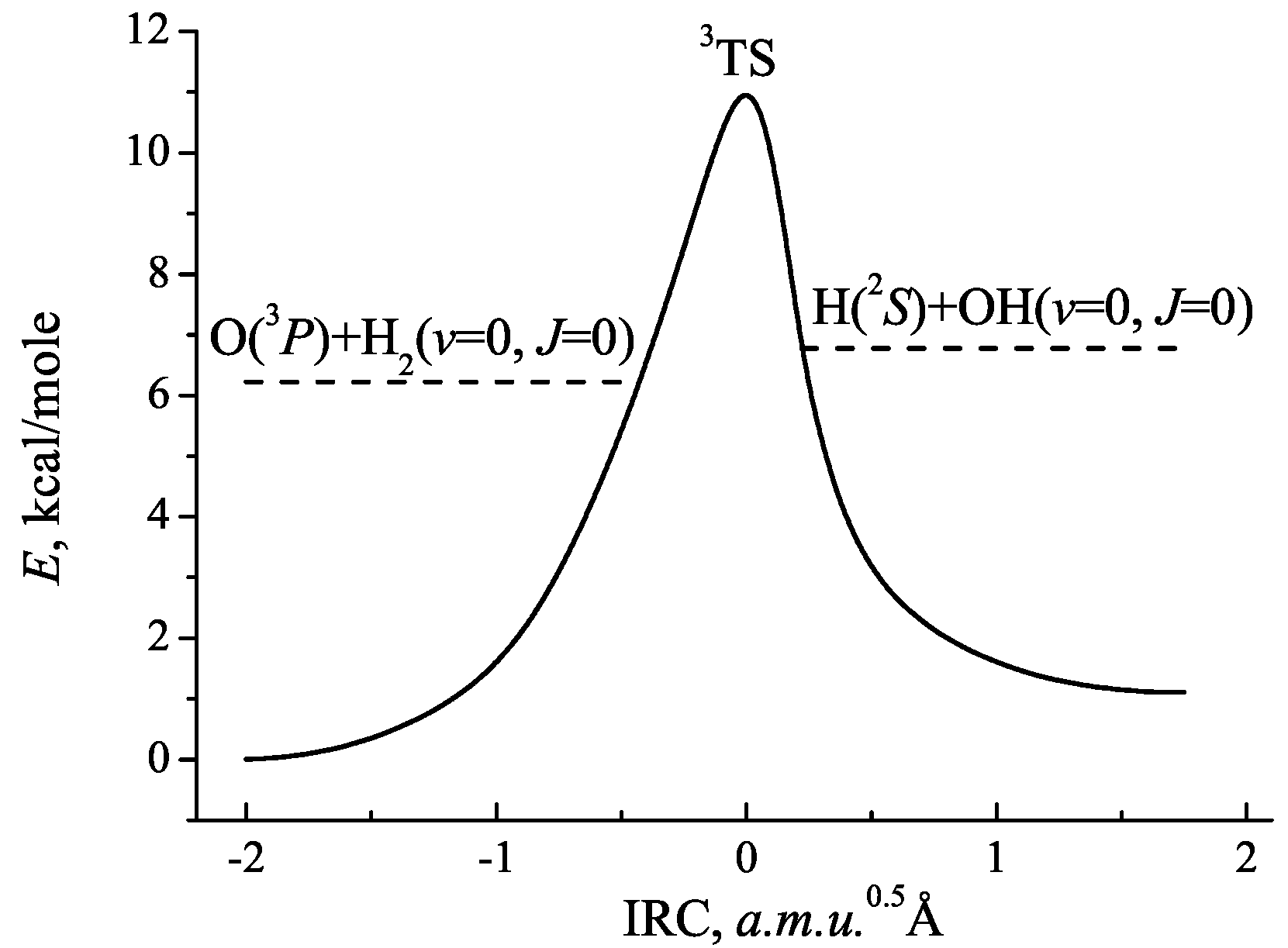
2.1. PES Approximation
2.2. Rate Constant Estimation
3. Results and Discussion

4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| QCT | quasiclassical trajectory |
| PES | Potential energy surface |
| ZPE | zero point energy |
| VT relaxation | vibrational–translational relaxation |
| PIP-NN | permutation invariant polynomials–neural network |
| XMCQDPT2 | extended multi-configuration quasi-degenerate second-order perturbation theory |
| DW-CASSCF | dynamically weighted complete active space self-consistent field method |
References
- Shchepakina, E.A.; Zubrilin, I.A.; Kuznetsov, A.Y.; Tsapenkov, K.D.; Antonov, D.V.; Strizhak, P.A.; Yakushkin, D.V.; Ulitichev, A.G.; Dolinskiy, V.A.; Hernandez Morales, M. Physical and Chemical Features of Hydrogen Combustion and Their Influence on the Characteristics of Gas Turbine Combustion Chambers. Appl. Sci. 2023, 13, 3754. [Google Scholar] [CrossRef]
- Rolo, I.; Costa, V.A.F.; Brito, F.P. Hydrogen-Based Energy Systems: Current Technology Development Status, Opportunities and Challenges. Energies 2024, 17, 180. [Google Scholar] [CrossRef]
- Skrebkov, O.V.; Kostenko, S.S.; Smirnov, A.L. Vibrational nonequilibrium in reaction hydrogen with oxygen (review). Zhurnal Tekhnicheskoj Fiz. 2023, 93, 1073–1093. (In Russian) [Google Scholar] [CrossRef]
- Urzay, J.; Kseib, N.; Davidson, D.F.; Iaccarino, G.; Hanson, R.K. Uncertainty-quantification analysis of the effects of residual impurities on hydrogen-oxygen ignition in shock tubes. Combust. Flame 2014, 161, 1–15. [Google Scholar] [CrossRef]
- Voelkel, S.; Masselot, D.; Varghese, P.L.; Raman, V. Analysis of Hydrogen-Air Detonation Waves with Vibrational Nonequilibrium. AIP Conf. Proc. 2016, 1786, 070015. [Google Scholar]
- Shi, L.; Shen, H.; Zhang, P.; Zhang, D.; Wen, C. Assessment of vibrational non-equilibrium effect on detonation cell size. Combust. Sci. Technol. 2017, 189, 841–853. [Google Scholar] [CrossRef]
- Kadochnikov, I.N.; Arsentiev, I.V. Modelling of vibrational nonequilibrium effects on the H2–air mixture ignition under shock wave conditions in the state-to-state and mode approximations. Shock Waves 2020, 30, 491–504. [Google Scholar] [CrossRef]
- Smirnov, V.N.; Vlasov, P.A. Effects of hydrocarbon impurities, vibrational relaxation, and boundary-layer-induced pressure rise on the ignition of H2–O2–Ar mixtures behind reflected shock waves. Int. J. Hydrogen Energy 2021, 46, 9580–9594. [Google Scholar] [CrossRef]
- Skrebkov, O.V.; Kostenko, S.S.; Smirnov, A.L. Vibrational nonequilibrium and reaction heat effect in diluted hydrogen-oxygen mixtures behind reflected shock waves at 1000<T<1300 K. Int. J. Hydrogen Energy 2020, 45, 3251–3262. [Google Scholar]
- Barbet, M.C.; Burke, M.P. Impact of “missing” third-body efficiencies on kinetic model predictions of combustion properties. Proc. Combust. Inst. 2021, 38, 425–432. [Google Scholar] [CrossRef]
- Bertolino, A.; Frassoldati, A.; Cuoci, A.; Parente, A. Estimation of third body efficiencies from experimental data: Application to hydrogen combustion. Int. J. Hydrogen Energy 2023, 48, 24504–24520. [Google Scholar] [CrossRef]
- Houston, P.L. Chemical Kinetics and Reaction Dynamics; Courier Corporation: Chelmsford, MA, USA, 2012. [Google Scholar]
- Henriksen, N.E.; Hansen, F.Y. Theories of Molecular Reaction Dynamics: The Microscopic Foundation of Chemical Kinetics; Oxford University Press: Oxford, UK, 2018. [Google Scholar]
- Herschbach, D.R. Molecular Dynamics of Elementary Chemical Reactions (Nobel Lecture). Angew. Chem. Int. Ed. Engl. 1987, 26, 1221–1243. [Google Scholar] [CrossRef]
- Leone, S.R. State-Resolved Molecular Reaction Dynamics. Annu. Rev. Phys. Chem. 1984, 35, 109–135. [Google Scholar] [CrossRef]
- Capitelli, M.; Armenise, I.; Gorse, C. State-to-state approach in the kinetics of air components under re-entry conditions. J. Thermophys. Heat Transfer 1997, 11, 570–578. [Google Scholar] [CrossRef]
- Kadochnikov, I.N.; Loukhovitski, B.I.; Starik, A.M. Kinetics of plasmachemical processes in the expanding flow of nitrogen plasma. Phys. Scr. 2013, 88, 058306. [Google Scholar] [CrossRef]
- Colonna, G.; Capitelli, M. Self-consistent model of chemical, vibrational, electron kinetics in nozzle expansion. J. Thermophys. Heat Transf. 2001, 15, 308–316. [Google Scholar] [CrossRef]
- Campoli, L.; Kustova, E.; Maltseva, P. Assessment of Machine Learning Methods for State-to-State Approach in Nonequilibrium Flow Simulations. Mathematics 2022, 10, 928. [Google Scholar] [CrossRef]
- Park, C. Review of chemical-kinetic problems of future NASA missions. I-Earth entries. J. Thermophys. Heat Transf. 1993, 7, 385–398. [Google Scholar] [CrossRef]
- Zhang, W.; Wang, X.; Zhang, Z.; Su, T. Numerical Investigation on the Jet Characteristics and the Heat and Drag Reductions of Opposing Jet in Hypersonic Nonequilibrium Flows. Aerospace 2022, 9, 554. [Google Scholar] [CrossRef]
- Kustova, E.; Mekhonoshina, M.; Bechina, A.; Lagutin, S.; Voroshilova, Y. Continuum Models for Bulk Viscosity and Relaxation in Polyatomic Gases. Fluids 2023, 8, 48. [Google Scholar] [CrossRef]
- Treanor, C.E.; Adamovich, I.V.; Williams, M.J.; Rich, J.W. Kinetics of nitric oxide formation behind shock waves. J. Thermophys. Heat Transf. 1996, 10, 193–199. [Google Scholar] [CrossRef]
- Kustova, E.V.; Nagnibeda, E.A.; Shevelev, Y.D.; Syzranova, N.G. Comparison of different models for non-equilibrium CO2 flows in a shock layer near a blunt body. Shock Waves 2011, 21, 273–287. [Google Scholar] [CrossRef]
- Surzhikov, S.; Reynier, P.; Seller, G.; Taccogna, F. Radiative aerothermodynamics of entering space vehicles: Toward the use of state-to-state approach. Open Plasma Phys. J 2014, 7, 127–154. [Google Scholar] [CrossRef]
- Gimelshein, S.F.; Wysong, I.J.; Fangman, A.J.; Andrienko, D.A.; Kunova, O.V.; Kustova, E.V.; Morgado, F.; Garbacz, C.; Fossati, M.; Hanquist, K.M. Kinetic and continuum modeling of high-temperature air relaxation. J. Thermophys. Heat Transf. 2022, 36, 870–893. [Google Scholar] [CrossRef]
- Aiken, T.T.; Boyd, I.D. Analysis of Critical Rate Processes for Ionization in Shock-Heated Air. In Proceedings of the AIAA AVIATION 2023 Forum, San Diego, CA, USA, 12–16 June 2023; p. 3330. [Google Scholar]
- Zhang, P.; Gao, W.; Niu, Q.; Dong, S. Numerical Analysis of Aerodynamic Thermal Properties of Hypersonic Blunt-Nosed Body with Angles of Fire. Energies 2023, 16, 1740. [Google Scholar] [CrossRef]
- Guy, A.; Bourdon, A.; Perrin, M.Y. Consistent multi-internal-temperatures models for nonequilibrium nozzle flows. Chem. Phys. 2013, 420, 15–24. [Google Scholar] [CrossRef]
- Zidane, A.; Haoui, R.; Sellam, M.; Bouyahiaoui, Z. Numerical study of a nonequilibrium H2-O2 rocket nozzle flow. Int. J. Hydrogen Energy 2019, 44, 4361–4373. [Google Scholar] [CrossRef]
- Starikovskiy, A.; Aleksandrov, N. Plasma-assisted ignition and combustion. Prog. Energy Combust. Sci. 2013, 39, 61–110. [Google Scholar] [CrossRef]
- Popov, N.A. Kinetics of plasma-assisted combustion: Effect of non-equilibrium excitation on the ignition and oxidation of combustible mixtures. Plasma Sources Sci. Technol. 2016, 25, 043002. [Google Scholar] [CrossRef]
- Pietanza, L.D.; Colonna, G.; Capitelli, M. Activation of vibrational-induced CO2 dissociation in cold non-equilibrium plasma. Plasma Phys. Control. Fusion 2023, 65, 044004. [Google Scholar] [CrossRef]
- Kadochnikov, I.N.; Arsentiev, I.V.; Loukhovitski, B.I.; Sharipov, A.S. State-to-state vibrational kinetics of diatomic molecules in laser-induced ignition of a syngas-air mixture: Modeling study. Chem. Phys. 2022, 562, 111669. [Google Scholar] [CrossRef]
- Mankelevich, Y.A.; Rakhimova, T.V.; Voloshin, D.G.; Chukalovskii, A.A. Vibrationally Excited Ozone in Kinetics of O/N/Ar Mixtures after Ozone Photolysis. Russ. J. Phys. Chem. A 2023, 97, 1033–1045. [Google Scholar] [CrossRef]
- Capitelli, M.; Ferreira, C.M.; Gordiets, B.F.; Osipov, A.I. Plasma Kinetics in Atmospheric Gases; Springer Series on Atomic, Optical, and Plasma Physics; Springer: Berlin/Heidelberg, Germany, 2000; Volume 31. [Google Scholar]
- Veselinova, A.; Agúndez, M.; Goicoechea, J.R.; Menéndez, M.; Zanchet, A.; Verdasco, E.; Jambrina, P.; Aoiz, F.J. Quantum study of reaction O(3P)+H2(v,j)→OH+H: OH formation in strongly UV-irradiated gas. Astron. Astrophys. 2021, 648, A76. [Google Scholar] [CrossRef] [PubMed]
- Zannese, M.; Tabone, B.; Habart, E.; Goicoechea, J.R.; Zanchet, A.; van Dishoeck, E.F.; van Hemert, M.C.; Black, J.H.; Tielens, A.G.; Veselinova, A.; et al. OH as a probe of the warm-water cycle in planet-forming disks. Nat. Astron. 2024. [Google Scholar] [CrossRef]
- Truhlar, D.G.; Muckerman, J.T. Reactive scattering cross sections III: Quasiclassical and semiclassical methods. In Atom-Molecule Collision Theory: A Guide for the Experimentalist; Springer: Berlin/Heidelberg, Germany, 1979; pp. 505–566. [Google Scholar]
- Gray, S.K.; Balint-Kurti, G.G. Quantum dynamics with real wave packets, including application to three-dimensional (J = 0) D + H2 = HD + H reactive scattering. J. Chem. Phys. 1998, 108, 950–962. [Google Scholar] [CrossRef]
- Gorse, C.; Capitelli, M.; Bacal, M.; Bretagne, J.; Laganà, A. Progress in the non-equilibrium vibrational kinetics of hydrogen in magnetic multicusp H-ion sources. Chem. Phys. 1987, 117, 177–195. [Google Scholar] [CrossRef]
- Pogosbekian, M.J.; Sergievskaia, A.L.; Losev, S.A. Verification of theoretical models of chemical exchange reactions on the basis of quasiclassical trajectory calculations. Chem. Phys. 2006, 328, 371–378. [Google Scholar] [CrossRef]
- Esposito, F.; Armenise, I.; Capitelli, M. N–N2 state to state vibrational-relaxation and dissociation rates based on quasiclassical calculations. Chem. Phys. 2006, 331, 1–8. [Google Scholar] [CrossRef]
- Bender, J.D.; Valentini, P.; Nompelis, I.; Paukku, Y.; Varga, Z.; Truhlar, D.G.; Schwartzentruber, T.; Candler, G.V. An improved potential energy surface and multi-temperature quasiclassical trajectory calculations of N2 + N2 dissociation reactions. J. Chem. Phys. 2015, 143. [Google Scholar] [CrossRef] [PubMed]
- Andrienko, D.A.; Boyd, I.D. State-specific dissociation in O2–O2 collisions by quasiclassical trajectory method. Chem. Phys. 2017, 491, 74–81. [Google Scholar] [CrossRef]
- Macdonald, R.L.; Jaffe, R.L.; Schwenke, D.W.; Panesi, M. Construction of a coarse-grain quasi-classical trajectory method. I. Theory and application to N2–N2 system. J. Chem. Phys. 2018, 148. [Google Scholar] [CrossRef] [PubMed]
- Vargas, J.; Monge-Palacios, M.; Lacoste, D.A. State-Specific Dissociation and Inelastic Rate Constants for Collisions of H2 with H and He. J. Thermophys. Heat Transf. 2023. [Google Scholar] [CrossRef]
- Garrido, J.d.D.; Ballester, M.Y. A Theoretical Study of the N2+H2 Reactive Collisions for High Vibrational and Translational Energies. Atmosphere 2021, 12, 1349. [Google Scholar] [CrossRef]
- Hong, Q.; Bartolomei, M.; Coletti, C.; Lombardi, A.; Sun, Q.; Pirani, F. Vibrational Energy Transfer in CO + N2 Collisions: A Database for V–V and V–T/R Quantum-Classical Rate Coefficients. Molecules 2021, 26, 7152. [Google Scholar] [CrossRef]
- Tu, Z.; Li, J.; Wang, Y.; Song, H. Quasi-Classical Trajectory Dynamics Study of the Reaction OH + H2S→H2O + SH and Its Isotopic Variants: Comparison with Experiment. Symmetry 2023, 15, 256. [Google Scholar] [CrossRef]
- Espinosa-Garcia, J.; Rangel, C.; Garcia-Chamorro, M.; Corchado, J.C. Quasi-Classical Trajectory Study of the CN+NH3 Reaction Based on a Global Potential Energy Surface. Molecules 2021, 26, 994. [Google Scholar] [CrossRef] [PubMed]
- Celiberto, R.; Capitelli, M.; Colonna, G.; D’Ammando, G.; Esposito, F.; Janev, R.K.; Laporta, V.; Laricchiuta, A.; Pietanza, L.D.; Rutigliano, M.; et al. Elementary Processes and Kinetic Modeling for Hydrogen and Helium Plasmas. Atoms 2017, 5, 18. [Google Scholar] [CrossRef]
- Kuntz, P.J.; Nemeth, E.M.; Polanyi, J.C.; Rosner, S.D.; Young, C.E. Energy distribution among products of exothermic reactions. II. Repulsive, mixed, and attractive energy release. J. Chem. Phys. 1966, 44, 1168–1184. [Google Scholar] [CrossRef]
- Sharipov, A.S.; Loukhovitski, B.I. Energy disposal into the vibrational degrees of freedom of bimolecular reaction products: Key factors and simple model. Chem. Phys. 2021, 544, 111098. [Google Scholar] [CrossRef]
- Dawes, R.; Thompson, D.L.; Guo, Y.; Wagner, A.F.; Minkoff, M. Interpolating moving least-squares methods for fitting potential energy surfaces: Computing high-density potential energy surface data from low-density ab initio data points. J. Chem. Phys. 2007, 126. [Google Scholar] [CrossRef]
- Jiang, B.; Li, J.; Guo, H. Potential energy surfaces from high fidelity fitting of ab initio points: The permutation invariant polynomial-neural network approach. Int. Rev. Phys. Chem. 2016, 35, 479–506. [Google Scholar] [CrossRef]
- Meuwly, M. Machine Learning for Chemical Reactions. Chem. Rev. 2021, 121, 10218–10239. [Google Scholar] [CrossRef] [PubMed]
- Manzhos, S.; Carrington, T.J. Neural Network Potential Energy Surfaces for Small Molecules and Reactions. Chem. Rev. 2021, 121, 10187–10217. [Google Scholar] [CrossRef] [PubMed]
- Braunstein, M.; Adler-Golden, S.; Maiti, B.; Schatz, G. Quantum and classical studies of the O(3P)+H2(v=0–3, j=0)→OH+H reaction using benchmark potential surfaces. J. Chem. Phys. 2004, 120, 4316–4323. [Google Scholar] [CrossRef]
- Wang, W.; Rosa, C.; Brandão, J. Theoretical studies on the O(3P)+H2→OH+H reaction. Chem. Phys. Lett. 2006, 418, 250–254. [Google Scholar] [CrossRef]
- Xu, Z.H.; Zong, F.J.; Han, B.R.; Dong, S.H.; Liu, J.Q.; Ji, F. Effects of a reagent’s rotational and vibrational excitations on reaction O(3P)+H2(ν = 0, 3, j = 0, 3, 5, 7, 9, 12, 15)→OH+H. Chin. Phys. B 2012, 21, 093103. [Google Scholar] [CrossRef]
- Granovsky, A.A. Extended Multi-Configuration Quasi-Degenerate Perturbation Theory: The New Approach to Multi-state Multi-Reference Perturbation Theory. J. Chem. Phys. 2011, 134, 214113. [Google Scholar] [CrossRef]
- Pelevkin, A.V.; Loukhovitski, B.I.; Sharipov, A.S. Reaction of H2 with O2 in excited electronic states: Reaction pathways and rate constants. J. Phys. Chem. A 2017, 121, 9599–9611. [Google Scholar] [CrossRef]
- Pelevkin, A.V.; Sharipov, A.S. Reactions of electronically excited molecular nitrogen with H2 and H2O molecules: Theoretical study. J. Phys. D Appl. Phys. 2018, 51, 184003. [Google Scholar] [CrossRef]
- Pelevkin, A.V.; Loukhovitski, B.I.; Sharipov, A.S. Interaction of Electronically Excited CO (a3Πr) Molecules with H, H2, and H2O: Potential Energy Surfaces and Reaction Kinetics. Phys. Chem. Res. 2023, 11, 837–851. [Google Scholar]
- Sharipov, A.S.; Loukhovitski, B.I.; Pelevkin, A.V.; Korshunova, M.R. A detailed kinetic submechanism for OH* chemiluminescence in hydrogen combustion revisited. Part 1. Combust. Flame 2024, 263, 113407. [Google Scholar] [CrossRef]
- Deskevich, M.P.; Nesbitt, D.J. Dynamically weighted multiconfiguration self-consistent field: Multistate calculations for F+H2O→HF+OH reaction paths. J. Chem. Phys. 2004, 120, 7281. [Google Scholar] [CrossRef] [PubMed]
- Pelevkin, A.V.; Loukhovitski, B.I.; Sharipov, A.S. Reaction of the N Atom with Electronically Excited O2 Revisited: A Theoretical Study. J. Phys. Chem. A 2021, 125, 8294–8312. [Google Scholar] [CrossRef] [PubMed]
- Kendall, R.A.; Dunning, T.H., Jr.; Harrison, R.J. Electron Affinities of the First-Row Atoms Revisited. Systematic Basis Sets and Wave Functions. J. Chem. Phys. 1992, 96, 6796–6806. [Google Scholar] [CrossRef]
- Helgaker, T.; Klopper, W.; Koch, H.; Noga, J. Basis-set convergence of correlated calculations on water. J. Chem. Phys. 1997, 106, 9639–9646. [Google Scholar] [CrossRef]
- Halkier, A.; Helgaker, T.; Jørgensen, P.; Klopper, W.; Olsen, J. Basis-set convergence of the energy in molecular Hartree–Fock calculations. Chem. Phys. Lett. 1999, 302, 437–446. [Google Scholar] [CrossRef]
- Lesiuk, M.; Jeziorski, B. Complete basis set extrapolation of electronic correlation energies using the Riemann zeta function. J. Chem. Theory Comput. 2019, 15, 5398–5403. [Google Scholar] [CrossRef]
- Granovsky, A.A. Firefly V. 8.2.0. 2016. Available online: http://classic.chem.msu.su/gran/firefly/index.html (accessed on 1 June 2024).
- Schmidt, M.W.; Baldridge, K.K.; Boatz, J.A.; Elbert, S.T.; Gordon, M.S.; Jensen, J.H.; Koseki, S.; Matsunaga, N.; Nguyen, K.A.; Su, S.; et al. General Atomic and Molecular Electronic Structure System. J. Comput. Chem. 1993, 14, 1347–1363. [Google Scholar] [CrossRef]
- Abadi, M.; Agarwal, A.; Barham, P.; Brevdo, E.; Chen, Z.; Citro, C.; Corrado, G.S.; Davis, A.; Dean, J.; Devin, M.; et al. TensorFlow: Large-Scale Machine Learning on Heterogeneous Systems, Software. 2015. Available online: https://www.tensorflow.org/ (accessed on 1 June 2024).
- Paszke, A.; Gross, S.; Chintala, S.; Chanan, G.; Yang, E.; DeVito, Z.; Lin, Z.; Desmaison, A.; Antiga, L.; Lerer, A. Automatic differentiation in PyTorch. In Proceedings of the 31st Conference on Neural Information Processing Systems (NIPS 2017), Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Chollet, François and Others. Keras. GitHub. 2015. Available online: https://github.com/fchollet/keras (accessed on 1 June 2024).
- Braams, B.J.; Bowman, J.M. Permutationally invariant potential energy surfaces in high dimensionality. Int. Rev. Phys. Chem. 2009, 28, 577–606. [Google Scholar] [CrossRef]
- Bosma, W.; Cannon, J.; Playoust, C. The Magma algebra system I: The user language. J. Symb. Comput. 1997, 24, 235–265. [Google Scholar] [CrossRef]
- Decker, W.; Greuel, G.M.; Pfister, G.; Schönemann, H. Singular 4-1-2—A Computer Algebra System for Polynomial Computations. 2019. Available online: http://www.singular.uni-kl.de (accessed on 1 June 2024).
- Polak, L.S.; Goldenberg, M.J.; Levickij, A.A. Vychislitel’nye Metody v Himicheskoj Kinetike [Computational Methods in Chemical Kinetics]; Nauka: Moscow, Russia, 1984. [Google Scholar]
- Abdel-Halim, H.M.; Jaafreh, S.M. Reaction rate constants from classical trajectories of atom-diatomic molecule collisions. Z. Naturforschung A 2008, 63, 159–169. [Google Scholar] [CrossRef]
- Le Roy, R.J. LEVEL: A computer program for solving the radial Schrödinger equation for bound and quasibound levels. J. Quant. Spectrosc. Radiat. Transf. 2017, 186, 167–178. [Google Scholar] [CrossRef]
- Rogers, S.; Wang, D.; Kuppermann, A.; Walch, S. Chemically Accurate ab Initio Potential Energy Surfaces for the Lowest 3A′ and 3A′′ Electronically Adiabatic States of O(3P)+H2. J. Phys. Chem. A 2000, 104, 2308–2325. [Google Scholar] [CrossRef]
- Zanchet, A.; Menéndez, M.; Jambrina, P.G.; Aoiz, F.J. New global potential energy surfaces of the ground 3A′ and 3A′′ states of the O(3P)+H2 system. J. Chem. Phys. 2019, 151. [Google Scholar] [CrossRef] [PubMed]
- Varga, T.; Olm, C.; Nagy, T.; Zsély, I.G.; Valkó, É.; Pálvölgyi, R.; Curran, H.J.; Turányi, T. Development of a joint hydrogen and syngas combustion mechanism based on an optimization approach. Int. J. Chem. Kinet. 2016, 48, 407–422. [Google Scholar] [CrossRef] [PubMed]
- Starik, A.M.; Sharipov, A.S.; Titova, N.S. Intensification of syngas ignition through the excitation of CO molecule vibrations: A numerical study. J. Phys. D Appl. Phys. 2010, 43, 245501. [Google Scholar] [CrossRef]
- Atkinson, R.; Baulch, D.L.; Cox, R.A.; Hampson, J.R.F.; Kerr, J.A.; Troe, J. Evaluated Kinetic and Photochemical Data for Atmospheric Chemistry. Supplement IV. J. Phys. Chem. Ref. Data 1992, 21, 1125. [Google Scholar] [CrossRef]
- Tsang, W.; Hampson, R.F. Chemical Kinetic Data Base for Combustion Chemistry. J. Phys. Chem. Ref. Data. 1986, 15, 1087–1280. [Google Scholar] [CrossRef]
- Cohen, N.; Westberg, K.R. Chemical kinetic data sheets for high-temperature chemical reactions. J. Phys. Chem. Ref. Data 1983, 12, 531–590. [Google Scholar] [CrossRef]
- Dove, J.E.; Teitelbaum, H. The vibrational relaxation of H2. I. Experimental measurements of the rate of relaxation by H2, He, Ne, Ar, and Kr. Chem. Phys. 1974, 6, 431–444. [Google Scholar] [CrossRef]
- Cacciatore, M.; Capitelli, M.; Billing, G. Vibration-to-translation energy exchanges in H2 colliding with highly vibrationally excited H2 molecules. Chem. Phys. Lett. 1989, 157, 305–308. [Google Scholar] [CrossRef]
- Millikan, R.C.; White, D.R. Systematics of vibrational relaxation. J. Chem. Phys. 1963, 39, 3209–3213. [Google Scholar] [CrossRef]





| Structure | , Å | , Å |
|---|---|---|
| O−HH | 2.828 (2.996) 1 | 0.741 (0.729) 1 |
| OH−H | 0.970 () 1 | 2.691 (4.079) 1 |
| 3TS | 1.239 (1.193) 1 | 0.882 (0.872) 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pelevkin, A.V.; Arsentiev, I.V.; Kadochnikov, I.N.; Zubrilin, I.A.; Filinov, E.P.; Yakushkin, D.V. State-to-State Rate Constants for the O(3P)H2(v) System: Quasiclassical Trajectory Calculations. Fire 2024, 7, 220. https://doi.org/10.3390/fire7070220
Pelevkin AV, Arsentiev IV, Kadochnikov IN, Zubrilin IA, Filinov EP, Yakushkin DV. State-to-State Rate Constants for the O(3P)H2(v) System: Quasiclassical Trajectory Calculations. Fire. 2024; 7(7):220. https://doi.org/10.3390/fire7070220
Chicago/Turabian StylePelevkin, Alexey V., Ilya V. Arsentiev, Ilya N. Kadochnikov, Ivan A. Zubrilin, Evgeny P. Filinov, and Denis V. Yakushkin. 2024. "State-to-State Rate Constants for the O(3P)H2(v) System: Quasiclassical Trajectory Calculations" Fire 7, no. 7: 220. https://doi.org/10.3390/fire7070220
APA StylePelevkin, A. V., Arsentiev, I. V., Kadochnikov, I. N., Zubrilin, I. A., Filinov, E. P., & Yakushkin, D. V. (2024). State-to-State Rate Constants for the O(3P)H2(v) System: Quasiclassical Trajectory Calculations. Fire, 7(7), 220. https://doi.org/10.3390/fire7070220






