Abstract
The traditional concept of compartmentation guaranteed by fire resistance is mainly concerned with the problem of destructive internal spread potential. External convective spread potential pertains to the loss of compartmentation associated with windows and facade systems. As such, it is assumed that internal fire spread occurs following mechanisms of excessive heat conduction and/or successive failure of the compartment boundaries, which can be, in most cases, conservatively characterised using traditional methods of performance assessment such as fire resistance. Nevertheless, external fire spread represents a potentially more effective route by which fire can spread through the convective advancement of flames and hot gases. This is particularly important in cases such as timber construction, where the presence of exposed timber can result in increased convective spread potential and where loss of compartmentation can result in disproportionate consequences. A simplified compartment fire model is proposed with the objective of quantifying the fuel contribution of exposed timber elements to the compartment fire and determining the impact of variable percentages of exposed timber on the convective spread potential. The overall results show that the convective fire spread potential increases with the increasing percentage of available timber.
1. Introduction
Compartment fires can be divided into five stages, each with specific characteristic timescales [1]: ignition, growth, flashover, fully developed, and decay stages. A common approach used to design a fire safety strategy is to address each stage separately while including only the elements of protection associated with the specific characteristic timescale of each stage of the fire. Thus, evacuation, detection, and suppression are traditionally linked to the ignition and growth stages, while structural integrity and firefighting are linked to the fully developed and decay stages [2].
In the context of high-rise buildings, due to the long evacuation times, the characteristic timescales associated with egress can overlap with those related to the behaviour of the structural systems and the preservation of compartmentation [3]. It is, therefore, critical to maintain structural integrity (compartmentation and stability) to allow for safe evacuation, effectiveness of fire protection systems, and intervention of fire services. Therefore, the separation of these different processes is not always possible. As a consequence, in high-rise buildings, specific compartmentation requirements are necessary to design detection and alarm systems, automatic suppression systems, and smoke management strategies that enable egress.
In fire-safe design, compartmentation has historically been exploited as a means of limiting the probability of fire spreading beyond the compartment of origin for a long time. As a consequence, different forms of compartmentation permeate most prescriptive codes under the implicit assumption that fire resistance-rated structures will serve as barriers that the fire needs to breach before it involves another compartment [4]. So, compartmentation has historically dealt with the destructive internal spread potential. Nevertheless, fires can also spread by the spilling of flames out of the compartment of origin, i.e., external convective spread potential through windows and along facade systems, even when the internal compartmentation is still in place and no structural breach of its boundaries has occurred. As such, it is assumed that internal fire spread occurs through mechanisms of excessive heat conduction and/or successive failure of the compartment boundaries, which can, in most cases, be conservatively characterised using traditional methods of performance assessment such as fire resistance. However, external fire spread represents a potentially more effective route by which fire can spread through the convective advancement of flames and hot gases, as shown in Figure 1.
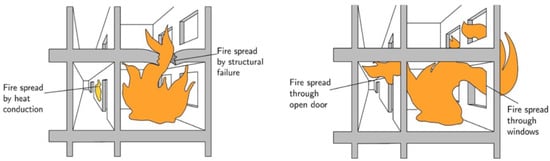
Figure 1.
Classically assumed vs. actual mechanisms of fire spread (based on a figure in [5]).
The historical concept of the compartmentation strategy limiting the probability of fire spread implies that if compartmentation fails (i.e., probability = 1), then the fire spreads at its maximum potential rate beyond the compartment of origin. If compartmentation resists (i.e., probability = 0), then there is no fire spread beyond the compartment of origin. In the case of timber buildings, the structure can become involved in the fire, adding an additional level of complexity. If the structure continues to burn beyond the consumption of the building furnishings, then structural integrity (compartmentation and stability) can be compromised in a manner not anticipated by conventional structural design approaches and structural performance assessment methods (i.e., fire resistance). Fire growth supported by the structure, therefore, has the potential to further challenge conventional fire safety design premises and firefighting protocols. This study takes the more conservative approach that compartmentation will fail at some point. Therefore, the role of compartmentation is not to limit the probability but to reduce the rate of fire spread across the entire building when analysing the total timeline of the fire: from ignition to burnout or self-extinction (when dealing with timber structures) assuming no fire brigade intervention. This approach also intrinsically considers the consecutive failure of compartments’ fire resistance (and ultimately failure) as a more realistic scenario, as opposed to treating the single compartment of origin as a pass-fail criterion.
Finally, fire growth supported by the structure has the potential to result in a multiple-floor fire that could involve the entire high-rise building. A fire that exceeds one floor has the potential to increase the consequences of a fire beyond the building where the fire originated, given that minimum separation distances are generally predicated on one-floor fires (Section 14.2, Approved document B, UK. [6]). This has been reported extensively in fires occurring in timber structures under construction, which, due to their fire strategy not being fully operational, are typically more vulnerable to fire spread.
Thus, when designing high-rise timber structures, it is essential to revisit the principles by which building performance is expected to support the fire safety strategy, particularly the performance expected from components that are intended to limit the size of the fire. This research draws attention to the crucial need for a reliable methodology to characterise and quantify the potential for fire spread beyond the floor of origin in timber buildings. Internal fire spread has been heavily studied, and research has highlighted the performance assessment approaches associated with fire containment. Research has highlighted the need to guarantee that the structural timber does not ignite, either through non-combustible encapsulation or, when structural timber is exposed, by ensuring that the required structural performance is maintained through an analysis that demonstrates self-extinction of the structural timber once the combustible furnishings have burnt out [7].
The fundamental backbone of a classic fire safety strategy for a building with a non-combustible structure is that the fire will burn out once the combustible furnishings are consumed. For such a strategy to be valid in a timber-structured building, it is necessary to assess the conditions leading to the self-extinction of the structural timber. Several authors have reported on the mechanisms and conditions of self-extinction in timber compartments both at the material scale [8,9,10,11] and the compartment scale [12,13]. The phenomenon has typically been reported to occur below a minimum external heat flux. Nevertheless, Cuevas et al. [8] found that self-extinction cannot be defined solely based on the maximum external incident heat flux on the timber surface; oxygen concentration also needs to be considered. This multi-variable dependency of extinction conditions challenges the sole use of the external incident heat flux as a surrogate to define the occurrence of self-extinction in fire safety engineering design [13,14].
Recent research [12] involving medium- and full-scale fire compartments with exposed timber surfaces has shown that external flames are larger and protrude further horizontally as more exposed timber is present. These studies reveal the potential for enhanced convective spread. In combination with a potentially combustible facade, as may be the case in timber buildings, this increased external flaming results in a fire spread potential that has yet to be fully characterised. This study focuses on the relationship between compartment fire dynamics and the external fire plume, attempting to fully characterise the fire process and quantify, through the application of a model, the relative contribution of increasing exposed timber surfaces on the rate of heat released within and outside the fire compartment.
2. Materials and Methods
2.1. The Burning of Wood
The burning of wood involves a series of tightly coupled processes that ultimately depend on the geometric configuration of the fuel package.
When wood is heated to a certain temperature, it undergoes thermochemical degradation (pyrolysis). As a result, combustible volatiles are released, and char is formed. The heat necessary for pyrolysis stems from the balance between incident heat (from the flame that results from the combustion of the volatiles and/or external heating), char oxidation, and losses to the virgin wood. The char separates the gas phase from the pyrolysis zone, generating two zones of interest: the interface between the char and the gas phase (‘char surface’) and the interface between the virgin wood and the char (‘pyrolysis surface’). If the energy balance at the char surface is negative, char oxidation will cease, and if the energy balance at the pyrolysis surface is negative, pyrolysis will cease. Extensive studies have been conducted to characterise these energy balances, showing the critical coupling between both fronts. Therefore, the burning rate of wood depends on the rate of heat supply to the material and the relative rates of conversion of wood into char and char into gas-phase oxidation products.
Nevertheless, there is still controversy surrounding the fundamental theory of compartment fires regarding the underlying mechanism of burning cellulosic fuel packages (e.g., experimental wood cribs as opposed to real furnishings). Traditionally, it is assumed that flame radiation is the main source of heat that sustains pyrolysis. If internal flaming is limited by the supply of oxygen, then this supply would also limit the burning rate. However, Harmathy’s model of burning wood [15] states that the rate of the decomposition reactions (i.e., the pyrolysis rate) is largely controlled by the rate of heat supply to the decomposing fuel. In the case of cellulosic materials, the primary source of heat is the combustion of charcoal, the rate of which is controlled by the rate of flow of air enveloping the charring surfaces, i.e., the rate of oxygen transport to the wood surface. In other words, in an ideal quiescent surrounding atmosphere, the rate of pyrolysis, and consequently the burning rate, is thus only limited by the rate of char oxidation. This, in turn, is limited by the supply of oxygen to the fuel [16].
2.2. Regimes of Behaviour and External Flaming
Studies based on the compartment fire framework [17,18] establish two regimes for fully developed fires: small- and large-opening regimes. The first regime, or Regime I, is known as the “well-mixed” or “one-zone” case, which assumes that the smoke layer reaches the floor, and the entire enclosure is filled with almost stationary gases at a uniformly elevated temperature. During this stage, the pressure, and thus the velocity of the air drawn to the fire zone, is determined by the compartment acting as a suction pump with the opening size being the throttle. When relatively larger openings exist, the second regime, the fuel-controlled regime, or Regime II, occurs and is described as follows: a rapidly moving flow around the flame zone is observed, and there is little or no part of the enclosure where the gases may be regarded as nearly stationary. In this case, the air drawn to the fire zone will not be determined by the compartment but by the turbulent entrainment into a flame with significant vertical pressure accelerations, resembling an exterior buoyant plume.
It has become customary to assume [2] that the reason behind external flaming in Regime I fires is an oxygen-starved internal atmosphere that forces the fuel gases to burn outside once they mix with fresh air. This has led to this regime being termed ventilation-limited. Nevertheless, Thomas [17] and Harmathy [19,20] revealed that in Regime I fires, the ratio of the rate of inflow air to the rate of volatile production could be much higher than the stoichiometric air requirement for the combustion of wood.
Thomas found evidence of this much earlier [21], explaining that in Regime I situations, the maximum velocity of air is proportional to the height of the opening, , while the maximum velocity of the fuel gases is proportional to the square of the ratio of the burning rate to the opening area, . He stated that if the latter was large compared to the former, combustion could not further occur within the compartment and there would be insufficient heat received by the fuel to sustain the combustion process. Therefore, he supported the idea that there is an upper limit on the ratio of these two maximum velocity heads and hence on the burning rate inside the compartment, which, in turn, promotes the typically observed external flaming in Regime I fires:
Thomas’s explanation is the only theoretical link to the empirical equation found by Kawagoe [22] (derived as Equation (4) later in this work), which describes the burning rate, R, in a Regime I fire as follows:
Harmathy estimated that the stoichiometric fuel–air ratio for the combustion of wood is approximately 4.2 [23], while the ratio of the airflow into the compartment and the burning rate, , is never less than 5.3:
The assumption that external flaming is a consequence of oxygen starvation in Regime I fires is thus not supported by evidence. Moreover, in relation to the presumed oxygen starvation, for the reasons explained in Section 2.1 above, Harmathy [19] redefined the terminology of Regime I from “ventilation-limited” to ventilation-controlled fires instead. This redefinition acknowledges that the rate of air inflow literally controls—and not limits—the rate of burning in an indirect way by regulating the rate of heat supply to the fuel.
Another indicator for the claim that external flaming is not linked to the lack of oxygen is the fact that even in Regime II fires, where the overall fuel-air ratio is recognised to be well above the stoichiometric ratio, external flaming can still occur. In this case, there is no doubt that external flaming is due to either insufficient mixing or high momentum of the flow that carries the flames outside (or a combination of both). The characteristics of external flaming, in both regimes, must thus be the result of the system’s flow conditions where the overall stoichiometry is lean, but the compartment is broadly divided into a very rich zone (deeper in the compartment), a close stoichiometric zone (where it is burning), and a very lean zone close to the opening.
Considering the above, it can be conjectured that the compartment will define a flame length, and therefore the characteristics of the compartment could be a predictor of the occurrence of external flaming. The length of the flame inside the compartment is defined by the size of the fuel bed (total amount of fuel surface area, , where is the specific surface area of the fuel in , and G is the fire load in kg) or the buoyant entrainment (dependent on the ventilation through the ventilation factor, , in ). The former has a characteristic length scale consistent with the compartment’s floor area when dealing with fully developed fires (), while the latter has a characteristic length scale consistent with the compartment height, (see Figure 2). Thus, considering the oversimplified scaling, if it occurs to any extent, external flaming () can be related to the ratio, where is the compartment height and l is the flame length. This ratio serves as a simplified surrogate for the chemical and physical processes behind the behaviour of the fire within the compartment, rendering this approach a coarse assessment tool.
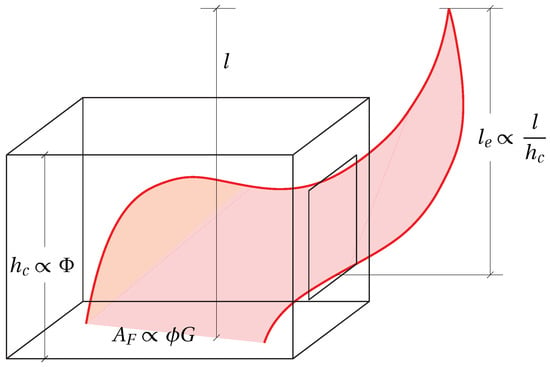
Figure 2.
Simplified compartment and flame scaling.
2.3. The Model
The model and its application are explained in detail in the original publication [24]. It numerically characterises both the potential for destructive fire spread (H) and convective fire spread () in terms of the fire’s ability to retain heat in the compartment or expel heat outwards into a fire plume. To obtain a quantitative assessment of both fire spread potentials, the model relies on input information related to the compartment, the fuel, and the ambient atmosphere, as well as the calculation of empirical factors and variables. It calculates 6 dependent variables, which are as follows:
- 1.
- R: The burning rate of fuel [].
- 2.
- : The flow rate of air [kg/s].
- 3.
- Q: The rate of heat evolution from the fuel within the compartment [kW].
- 4.
- : The penetration heat flux absorbed by the compartment boundaries, averaged over all internal surfaces apart from the floor [kW/m2].
- 5.
- : The duration of a fully developed fire [s].
- 6.
- : The temperature of the compartment gases, averaged over the compartment volume [K].
These six dependent variables not only define the overall characteristics of a given fire scenario but also serve as inputs for calculating the destructive spread potential (H) within the compartment, which, in combination with the convective spread potential () external to the compartment, estimates the inherent fire severity of a given scenario. The explicit forms of equations for most of these factors and variables are presented next, detailing the entire process that allows for the calculation of both H and , following the sequence shown in Figure 3.
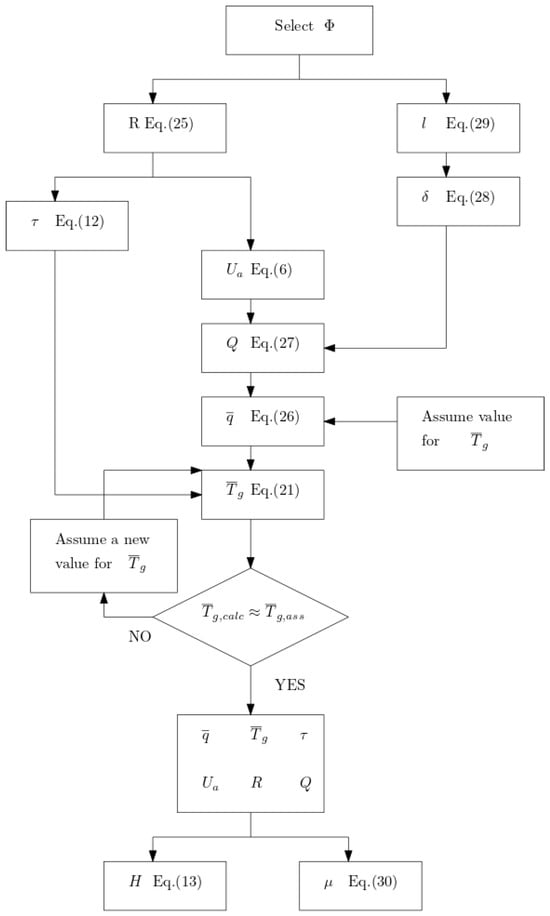
Figure 3.
Flowchart for calculating all 6 process variables and the final convective fire spread. Adapted from [24]. Equation numbers correspond to original paper.
As described in Section 2.2, there are two distinct regimes that need to be characterised: Regime I, which is dominated by momentum induced at the compartment opening and thus by the ventilation factor, and Regime II, which is dominated by momentum induced by the fire and thus is characterised by the fuel area.
The amount of fuel produced is defined by the heat transferred internally from the oxidation of the char into the virgin wood and externally from the flames and smoke towards the fuel surface. Thus, it is controlled by the manner in which air is driven towards the glowing surface of the fuel and towards the flame. The following empirical equations [19] for the burning rate, R, at Regime I and Regime II, respectively, were introduced by Harmathy:
where is the specific surface area of the fuel, which, for conventional furniture, is taken to be 0.13 m2/kg; G is the fire load in kg; is the model’s adjusted ventilation parameter; and is referred to as the ventilation factor, :
where, is the density of the air in kg/m3, Av is the area of the opening in m2, g is the gravity acceleration in m/s2, and hv is the height of the opening in m.
This adjustment—referred to from now on as the safety factor, s, and set to 5 as an arbitrary but conservative design value [24]—is due to the fact that in real compartments, there is often more than one opening, either intentional (such as open windows and doors for ventilation) or unintentional (such as broken windows due to the fire), inducing a cross-draft which increases the ventilation of the in comparison to the classic laboratory draft-free case. This scenario represents the minimum ventilation condition that can occur in real-world fires. Therefore, the model’s ventilation factor, , is used as the input variable for the calculation of . In Equation (5), is the density of the atmospheric air, is the area of the ventilation opening, is the height of the opening, and g is the acceleration due to gravity.
The ratio () in Equation (4) clearly defines the breakpoint between Regime I and Regime II, with the transition occurring at a well-defined critical value. It is recognised that this concept is oversimplified, given that it is more likely that both regimes are separated by a critical regime rather than an exact breakpoint value. Nevertheless, it provides a useful framework to define the transition. Thus, Equation (4) (top) applies to Regime I fires, whereas Equation (4) (bottom), applies to Regime II fires, as explained above. The former describes a scenario where the air supply is limited by a small value of relative to the fuel area (). In this case, the momentum induced by the compartment controls the air intake through the opening, leading to Regime I, and thus the burning rate is dominated by the ventilation factor. In contrast, Equation (4) (bottom) describes a Regime II scenario, where an increase in fire size results in greater momentum, with the flame getting closer to the fuel surface and an increased burning rate. The result is a burning rate dominated by the fire size.
Harmathy introduced the concept of a normalised heat load to account for the comparison of destructive potential comparison in enclosures with different boundary materials, represented by their thermal inertia (). Therefore, the normalised heat load, or destructive spread potential, H, is defined and calculated as follows:
where is the net heat flux to the compartment surfaces in W/m2 and is the thermal inertia of the enclosure boundaries in J/(m2 K).
Simplified approaches have been proposed for this variable; they can be found in [7,24] but will not be further discussed here. Similarly, the characterisation of other variables relevant to the destructive spread potential, H, (e.g., ) can be found in [7,24]. These are not the subject of this study and, therefore, will not be discussed any further.
The final variable of reference is the characteristic duration of the fire or the burn-out time, . The simple equation for the duration of the fully developed fire can be written as follows:
2.3.1. Convective Fire Spread
The model defines the potential for convective spread as the ratio of the evolution of the rate of heat outside the fire compartment to the evolution of the total heat release rate from the fuel:
The ratio depends on a series of parameters related to the combustion process of the solid cellulosic fuel inside the compartment, as both the production of volatiles and their combustion are the result of a highly sensitive combined heat balance coupled with the availability of fresh air to feed the reaction, as explained in Section 2.1 and Section 2.2.
The heat release rate from the fire can be expressed by the following simple formulation:
where is theheat of combustion of volatiles and is the heat of oxidation char.
The constants and add up to one and are empirical approximations of the fraction of the energy used for char formation and volatile production, respectively. Assuming that is the fractional heat evolution within the fire compartment () and that all the heat produced outside the compartment is the result of volatile combustion, then the heat released outside the compartment is given by:
So, the explicit form of Equation (8) can be expressed as:
The denominator in Equation (11) reflects the fact that the evolution of heat in the compartment is attributable partly to the combustion of the volatile products of pyrolysis and partly to the oxidation of the char. The factor in the numerator, in turn, reflects the part of the heat of combustion of the volatile decomposition products that burns outside the compartment. Thus, by including the factor , account is taken of the fact that, in general, only part of the heat of combustion of the volatile decomposition products is released inside the compartment [25], so this variable relates to the potential for convective fire spread quantification.
The factor is quantified through empirical equations suggested by Harmathy after analysing a large amount of experimental data [26] and finding that the compartment height has an important bearing on external flaming. These equations depend on the relationship between the model’s flame length (l) and the compartment height (). The relationship between these two variables is a surrogate for the physical and chemical processes responsible for the relationship between internal and external flaming, as explained in Section 2.2.
where l is the effective flame height, which can be empirically estimated as follows:
Equation (13) (top and bottom) illustrates two different cases. Equation (13) (top) describes a scenario where the fuel area () is large relative to the air supply . In this case, the momentum induced by the compartment controls the air intake through the opening, leading to Regime I. Thus, in Equation (13) (top), the flame length is dominated by the ventilation factor. It is important to note that this cannot be seen as a flame length controlled by fuel and air supply to combust at stoichiometric conditions. In such a scenario, an increase in air supply would result in a reduction in the flame length. In a compartment fire, regardless of the regime, there will be excess air. Thus, under Regime I conditions, air supply controls the overall production of gaseous fuel and the burning rate. Therefore, an increase in will increase the flame length (as per Equation (13) (top). In contrast, Equation (13) (bottom) describes a Regime II scenario where, once again, there is excess air. Consequently, an increase in fire size will result in greater momentum, flame getting closer to the fuel surface, and an increased burning rate. The result is a flame length dominated by the fire size.
At this point, can be calculated in the model.
2.3.2. Destructive Fire Spread
As mentioned above, the model has been designed to calculate 6 process variables that define the overall characteristics of a given fire scenario and serve as inputs for calculating the destructive spread potential, H. Although the design for fire safety in regard to fire spread potential has these two well-defined components—convective and destructive—this part of the study is mainly concerned with the former, not only due to the historical urge to start considering it but also due to the fact that the addition of available fuel in timber buildings, the main focus of this research, enhances the convective spread mode.
2.3.3. Preliminary Diagnosis for μ
After investigating the model’s background equations, assumptions, and suggestions, the following can be concluded prior to and in support of any analysis of the parametric results for , which is the focus of this study:
- (i)
- ranges from 0 to a maximum value of (when substituting appropriate heats of combustion , ).
- (ii)
- In Regime I fires, depends on and increases/decreases with the increase/decrease in the ventilation factor , i.e., the window height and area.
- (iii)
- In Regime II fires, depends on and increases/decreases with the increase/decrease in the effective fuel load density , i.e., the specific area of exposed fuel, that is, on the type, arrangement and total amount of fuel in the compartment.
- (iv)
- For both regimes, ultimately depends on and increases/decreases with the ratio of the flame length and the compartment height
3. Results
In this parametric study, some variables embedded in the process variables mentioned above were chosen to remain constant while others—all compartment-related—were varied to reveal their relative influence on and sensitivity to the overall results.
The parametric constants chosen were the average air temperature (), the average density (), the X-factor (≥1) that accounts for the coupling by the fire plume between the streams of air and hot fire gases, the single opening location, the furnishing-specific fuel load () that depends on the occupancy, the average specific heat capacity of the fire gases (), the heat of gasification for pyrolysis (), the heat of gasification for volatiles (), the heat of oxidation of the char (), the empirical factor () that accounts for the slight spatial non-uniformity of the temperature of the fire gases, the height of the window (), and the temperature of the gases (). Although evidently not a constant, the calculation of is independent of it.
The parameters chosen were varied one at a time while leaving all other parameters constant. These parametric variables were the compartment height (), the window width (), the compartment floor area (), and the safety factor (s). These variables were analysed for different scenarios that exhibit increasing timber influence.
The introduction of exposed timber surfaces is complex because the surfaces can correspond to vertical elements (walls) or the ceiling. These will have a different impact on the manner in which momentum is generated by buoyancy [12]. Nevertheless, in this case, the impact of timber exposure will be introduced through the combined variable , and thus the burning area, independent of its particular configuration.
Therefore, by combining these parametric variables (one at a time), the following variations were obtained:
- (i)
- Overall compartment dimensions [m3] through changes to the floor area [m2] or compartment height [m].
- (ii)
- Timber panelling, which added extra fuel load [kg], and therefore contributed to changes in the total fuel load (G).
- (iii)
- Average specific surface area of fuel φ [m2/kg]. This was calculated by averaging the specific surface area of timber furnishing (0.13 m2/kg) with that of timber panelling, estimated at 0.07 m2/kg. These values were determined considering a density of 600 kg/m3 and a panel thickness of 2.5 cm).
- (iv)
- The effective fuel load exposed surface (φG) was varied as a result of the combination of variations of both variables mentioned above, i.e., (ii) and (iii).
- (v)
- Ventilation regime: The fire was regarded as either ventilation-controlled or fuel-controlled depending on the threshold . The ventilation regime determines the burning rate (R) and flame length (l) equations (and, therefore, the d factor, which accounts for the part of the heat of combustion of the volatile decomposition products that is released inside/outside the compartment and directly affects μ and indirectly affects H through q.
- (vi)
- Overall thermal inertia (): This also depends on the extent of the timber panelling variations mentioned in (ii).
Figure 4, Figure 5, Figure 6 and Figure 7 show graphs where the convective fire spread potential is quantified and represented by the µ-factor on the ordinate axis. These graphs compares changes in each parametric variable—compartment height (Figure 4), window width (Figure 5), compartment floor area (Figure 6), and safety factor (Figure 7)—shown on the respective abscissa. The analysis considers five different scenarios of increasing timber panelling exposure while leaving all other parameters constant. In relation to the safety factor (Figure 7), its purpose is to address drafty conditions, which are not considered in this model or in any classic compartment fire framework correlation.
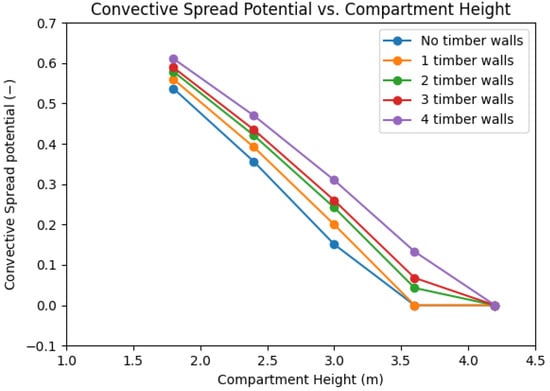
Figure 4.
Convective spread potential over the compartment height.
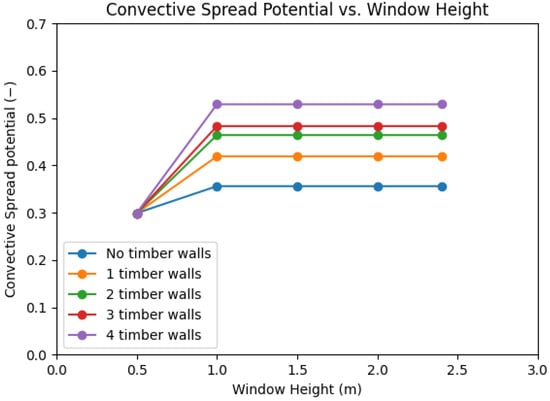
Figure 5.
Convective spread potential over the window height.
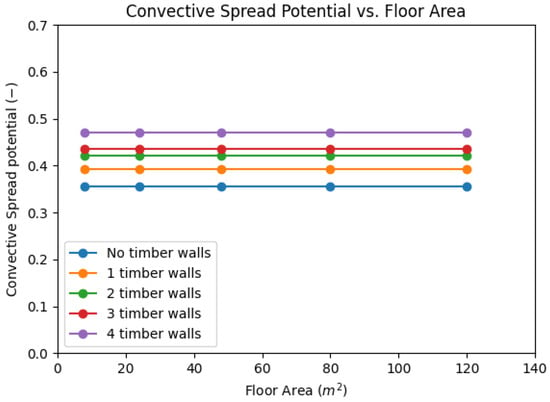
Figure 6.
Convective spread potential over the floor area.
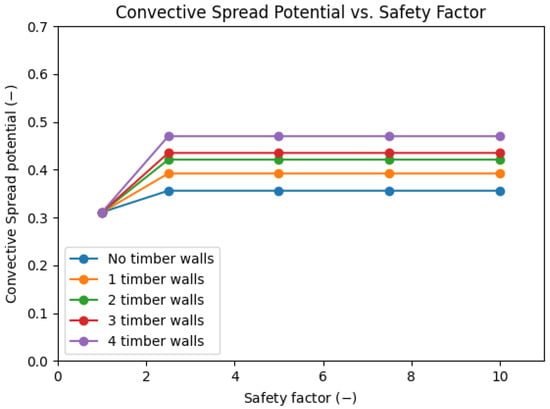
Figure 7.
Convective spread potential over the safety factor.
Figure 4 shows that the convective fire spread potential increases with greater exposure of timber and decreases as the compartment height increases, eventually reaching a point where it vanishes, depending on the amount of exposed timber. These results were expected, as mentioned earlier, as ultimately depends on the ratio of flame length to compartment height (), with ratios causing flames to escape the compartment (either externally and/or internally to an adjacent compartment or corridor). Therefore, the taller the compartment, the higher the probability of containing the flames within it, thereby preventing convective flame escape and reducing the convective fire spread potential originating from the original fire cell. For the 4.2 m height compartment, the flame remains completely contained within the compartment in all five scenarios, resulting in a quantified convective spread potential of nil for each. It is important to note that the model was designed for non-combustible compartments; therefore, the flame height is estimated assuming a fuel package evenly distributed and centred at floor level. This means that the model does not consider flames emerging from the walls at higher levels or their impact on the overall compartment fire dynamics (e.g., flow, pressure, and temperature fields), as reported by several authors after testing the contribution of timber panelling and consequent modifications to the classic compartment fire framework [19].
Figure 5 shows that the convective fire spread potential increases with a higher percentage of timber panelling for constant window widths. The plateau (i.e., constant ) beyond the 3 m window width for all timber scenarios reveals the breakpoint between behaviour regimes [2]. After this point, all scenarios fall under Regime II, where the convective spread potential in this model becomes independent of the ventilation factor and thus the window size. Below a certain window width, the convective spread potential decreases. With this fuel load configuration, this decrease occurs only for very low window widths, specifically when the ventilation-to-fuel ratio is low enough to induce Regime I behaviour in a compartment fire, where the convective spread potential is proportional to the ventilation factor . In this regime, the convective spread potential in this model is independent of the fuel load; hence, the m window width data point is the same for all five scenarios.
Figure 6 again shows the increase in convective spread potential as the timber panelling increases. It also shows that remains constant in all timber scenarios, regardless of variations in the compartment floor area. The model has incorporated the typical specific fire load density for an office building [27], in addition to the extra fuel load brought about by increasing the area of internal timber panelling. Thus, ’s trend responds to the fact that while the total fuel load increases proportionally with the increase in the compartment floor area, ventilation remains constant. Therefore, their relationship pushes the behaviour regime towards Regime I, where the convective fire spread potential does not depend on fuel load, only on ventilation. It is evident in the graph that the breakpoint between behaviour regimes was not reached within this range of floor area range, so all scenarios fall under Regime II.
Finally, Figure 7 shows an increase in the convective fire spread potential in all situations as the amount of timber panelling increases. At the same time, it reveals that the breakpoint between regimes falls somewhere between 1 and for all configurations, demonstrating that they all fall under Regime II beyond , where the model’s convective spread potential quantification is independent of the ventilation. It is important to note that the model’s recommended adjusted ventilation parameter, or ventilation factor, i.e., , as a random input variable, is conservative. Even after doubling it, there is no increase in the convective spread potential in any scenario. This is due to the fact that the safety factor affects F in a proportional/direct way. Therefore, increasing the safety factor while keeping the effective fuel load of the exposed surface () constant, tends the compartment fire towards Regime II behaviour, where the convective spread potential becomes independent of the ventilation factor , as explained above.
4. Discussion
The limitations of the analytical model and analysis are as follows:
- (i)
- The model assumes a post-flashover situation with full involvement of the combustibles within the compartment evenly distributed and centred at floor level. Consequently, the flow field is not influenced by the fuel location or position, especially with respect to the opening, or by the buoyant and inertial forces generated by the burning walls [19].
- (ii)
- It is a single- and vertical-opening model, i.e., no cross-drafts are considered beyond the adjusted ventilation parameter.
- (iii)
- Determination of fire load G [kg]: The extra structural timber or that from the interior compartment linings is accounted for directly as extra fuel load density. The model does not consider the vertical or horizontal configuration influence that the extra timber would have, nor its distance with respect to the ventilation and other combustible surfaces.
- (iv)
- Determination of the -factor: This ultimately depends on the model’s flame length (l) in relation to the compartment height (). In turn, the flame length depends only on (ventilation, i.e., window height and area) when falling within Regime I fires, or on the effective fuel load density () (specific area of exposed fuel, i.e., type and arrangement of fuel, and total fuel load) when falling within Regime II fires.
5. Conclusions
The safety case, particularly for tall timber buildings, must explicitly address the increased hazard of fire spread beyond the compartment of origin. In principle, self-extinction could render a timber building fire strategy equal to that of a non-combustible building, as long as the fire is contained in the compartment of origin. However, without full containment, a feasible self-extinction strategy is not possible. External convection dominates the fire spread in real-world fires, so preventing the fire from spreading by cutting off the main routes of convective spread is crucial to achieving tall timber building fire safety. This is why the convective fire spread potential must be addressed, especially in timber-lined compartments where this spread mode appears to be enhanced. The present study introduces an existing model to characterise and quantify the convective spread potential out of the compartment of origin in timber buildings and introduces a formal method to address the -factor. Beyond the inherent limitations of the model’s simplicity, this study provides guidance for designers regarding variables that enhance the convective fire spread potential. The convective fire spread potential is enhanced by the exposure of timber surfaces and the window width and height (through the window area), while increases in the compartment height decrease it. Safety factors beyond the model’s proposed five and the floor area have a negligible impact on the convective fire spread potential.
Author Contributions
Conceptualisation, J.L.T. and A.H.M.; methodology, A.H.M.; software, I.C.; formal analysis, A.H.M. and I.C.; investigation, A.H.M.; writing—original draft preparation, A.H.M. and I.C.; writing—review and editing, J.L.T. and W.J.; visualisation, I.C.; supervision, W.J. All authors have read and agreed to the published version of the manuscript.
Funding
The APC was funded by ANID BASAL FB210015 (CENAMAD).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
No new data were created.
Acknowledgments
A.H. Majdalani, I. Calderón, and W. Jahn would like to acknowledge the financial support provided by the Timber Innovation Center UC and ANID BASAL FB210015 (CENAMAD).
Conflicts of Interest
The authors declare no conflicts of interest.
References
- The Society of Fire Protection Engineers. SFPE Handbook of Fire Protection Engineering, 3rd ed.; National Fire Protection Association: Quincy, MA, USA, 2009. [Google Scholar]
- Majdalani, A. Compartment Fire Analysis for Contemporary Architecture. Ph.D. Thesis, The University of Edinburgh, Edinburgh, UK, 2014. [Google Scholar]
- Frangi, A.; Fontana, M.; Knobloch, M. Fire Design Concepts for Tall Timber Buildings. Struct. Eng. Int. 2008, 18, 148–155. [Google Scholar] [CrossRef]
- Hou, L.F.; Li, M.; Cui, W.-Y.; Liu, Y.-C. Numerical Simulation and Analysis of On-building High-rise Building Fires. Procedia Eng. 2011, 11, 127–134. [Google Scholar] [CrossRef]
- Harmathy, T.Z. Design of Buildings for Fire Safety—Part I. Fire Technol. 1976, 12, 95–108. [Google Scholar] [CrossRef]
- Government of the United Kingdom. Fire Safety: Approved Document B; Government of the United Kingdom: London, UK, 2019. [Google Scholar]
- Torero, J.; Majdalani, A.; Abecassis-Empis, C.; Cowlard, A. Revisiting the Compartment Fire. Fire Saf. Sci. 2014, 11, 28–45. [Google Scholar] [CrossRef]
- Cuevas, J.; Torero, J.L.; Maluk, C. Flame extinction and burning behaviour of timber under varied oxygen concentrations. Fire Saf. J. 2021, 120, 103087. [Google Scholar] [CrossRef]
- Crielaard, R.; van de Kuilen, J.W.; Terwel, K.; Ravenshorst, G.; Steenbakkers, P. Self-extinguishment of cross-laminated timber. Fire Saf. J. 2019, 105, 244–260. [Google Scholar] [CrossRef]
- Emberley, R.; Inghelbrecht, A.; Yu, Z.; Torero, J.L. Self-extinction of timber. Proc. Combust. Inst. 2017, 36, 3055–3062. [Google Scholar] [CrossRef]
- Emberley, R.; Do, T.; Yim, J.; Torero, J.L. Critical heat flux and mass loss rate for extinction of flaming combustion of timber. Fire Saf. J. 2017, 91, 252–258. [Google Scholar] [CrossRef]
- Gorska, C. Fire Dynamics in Multi-Scale Timber Compartments. Ph.D. Thesis, The University of Queensland, Brisbane, Australia, 2020. [Google Scholar] [CrossRef]
- Xu, H.; Pope, I.; Gupta, V.; Cadena, J.; Carrascal, J.; Lange, D.; McLaggan, M.S.; Mendez, J.; Osorio, A.; Solarte, A.; et al. Large-scale compartment fires to develop a self-extinction design framework for mass timber—Part 1: Literature review and methodology. Fire Saf. J. 2022, 128, 103523. [Google Scholar] [CrossRef]
- Cuevas, J.I.; Guibaud, A.; Maluk, C.; Torero, J.L. Understanding flame extinction in timber under external heating using high-activation energy asymptotics. Combust. Flame 2022, 235, 111645. [Google Scholar] [CrossRef]
- Harmathy, T.Z. Mechanism of burning of fully-developed compartment fires. Combust. Flame 1978, 31, 265–273. [Google Scholar] [CrossRef]
- Harmathy, T.Z. Thermal Inertia or Thermal Absorptivity? Fire Technol. 1985, 21, 146–149. [Google Scholar] [CrossRef]
- Thomas, P.H.; Heselden, M.; Law, M. Fully-Developed Compartment Fires; Fire Research Station: Boreham Wood, UK, 1967. [Google Scholar]
- Thomas, P.H.; Heselden, A.J.M. Fully-Developed Fires in Single Compartments: A Co-Operative Research Programme of the Conseil International Du Batiment; Fire Research Station: Hertfordshire, UK, 1972. [Google Scholar]
- Harmathy, T. A new look at compartment fires, part I. Fire Technol. 1972, 8, 196–217. [Google Scholar] [CrossRef]
- Harmathy, T.Z. Designers Option: Fire Resistance or Ventilation; Technical Paper No. 436; National Research Council of Canada–Division of Building Research: Ottawa, ON, Canada, 1978. [Google Scholar]
- Thomas, P.H. Some General Questions in the Study of Fires in Rooms; Fire Research Note No. 429; Fire Research Station: Boreham Wood, UK, 1960. [Google Scholar]
- Kawagoe, K. Fire Behaviour in Rooms; Technical Report 27; The Building Research Institute, Ministry of Construction: Tokyo, Japan, 1958. [Google Scholar]
- Harmathy, T.Z. The possibility of characterizing the severity of fires by a single parameter. Fire Mater. 1980, 4, 71–76. [Google Scholar] [CrossRef]
- Harmathy, T.Z. Fire Severity: Basis of Fire Safety Design; Fire Research Station: Hertfordshire, UK, 1980. [Google Scholar]
- Harmathy, T.Z.; Oleszkiewicz, I. Fire drainage system. Fire Technol. 1987, 23, 26–48. [Google Scholar] [CrossRef]
- Butcher, E.G.; Ashton, L.A.; Chitty, T.B. The Temperature Attained by Steel in Building Fires; [Fire Research Technical Paper. no. 15.]; HMSO: London, UK, 1966. [Google Scholar]
- Pettersson, O.; Magnusson, S.E.; Thor, J. Fire Engineering Design of Steel Structures; Technical Report 52; Lund Institute of Technology: Lund, Sweden, 1976. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).